Forecasting Electricity Demand in Turkey Using Optimization and Machine Learning Algorithms
Abstract
1. Introduction
- To evaluate the effectiveness of different methods, an analysis of Key Performance Indicators (KPIs) is used to assess prediction accuracy. In this context, commonly used measures such as MAE in the literature result in the omission of crucial quality factors such as the highest forecast error and the distribution of error. By avoiding the mutual counteraction negative and positive errors in the prediction, RMSE, and MAE evaluate, respectively, how closely the anticipated value difference resembles the true value. While MAPE emphasizes the accuracy of the forecasting methodologies, MSE illustrates the difference between the actual data and the anticipated value. When different data sets are utilized, MAPE aids in examining how well the estimating methods function.
- The model hyper-parameters fine-tuning, data pre-processing methods, the validation and training data set selection, and the outcomes graphical display.
- The findings and precision verification of the large dataset collected for the mainland.
- In this study, multi-objective forecasting models were created using various traditional ML methods and a new optimization method, WOA, to improve forecasting accuracy. In the Turkey case study, forecast performances were verified with error metrics by using inter-year data in electrical energy demand forecasting. The predicted results provided reliable and informative references for annual energy demand for the coming decades.
- The effect of independent inputs used for electrical energy demand forecasting on forecast output has been investigated with MLR subsets and different combinations.
- Statistical performance error metrics are included to effectively improve forecast accuracy and demonstrate the effectiveness of the method used.
- It includes the technical analysis of determining the optimal parameters of methods by means of input-output correlation matrices. Thus, it is determined how much the independent variables affect the dependent variable.
- The effective electricity demand estimation made in this study prevents extra reserves and limited operation of the system.
2. Exploration, Pre-Processing, and Data Sources
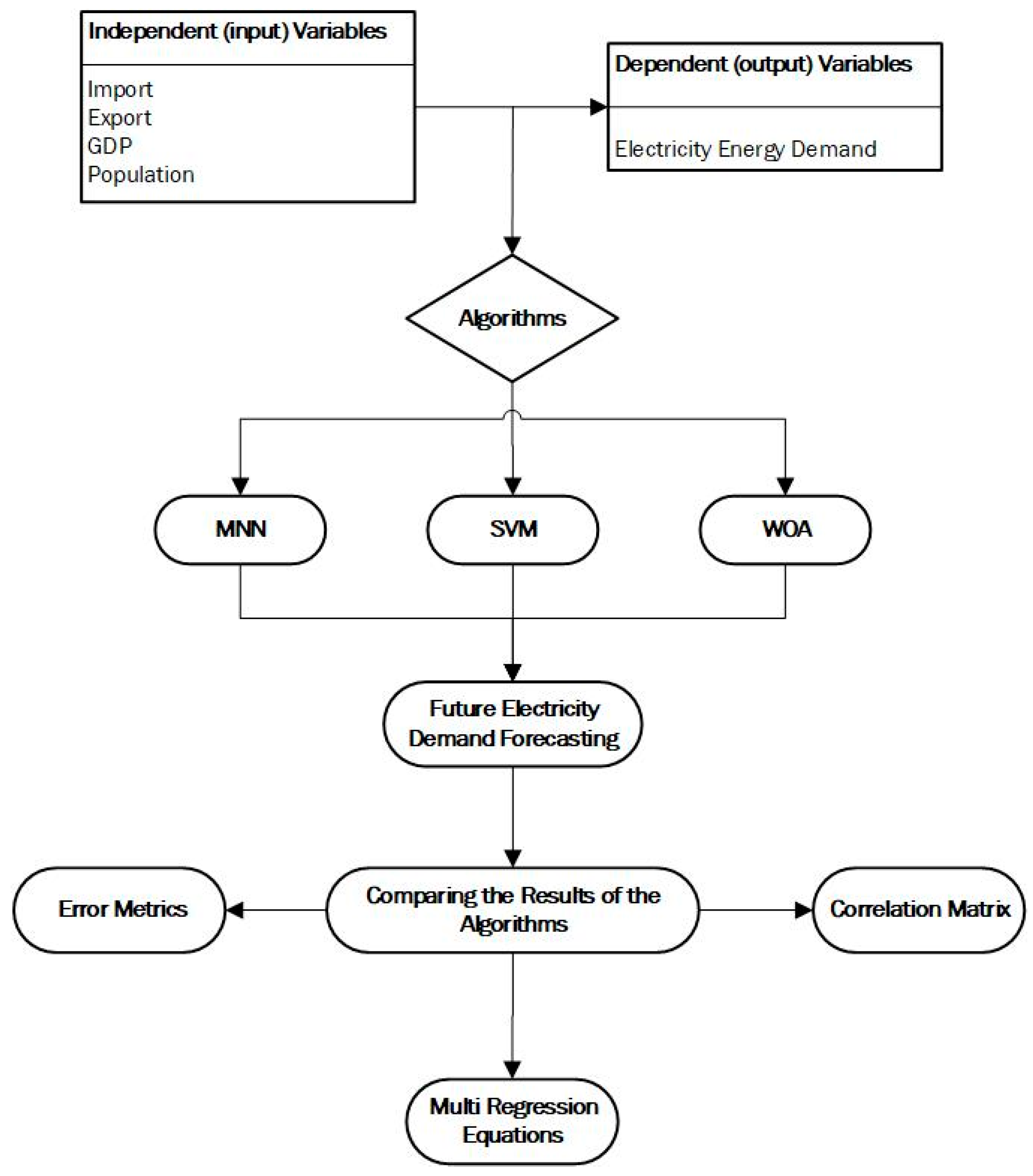
3. Materials and Methods
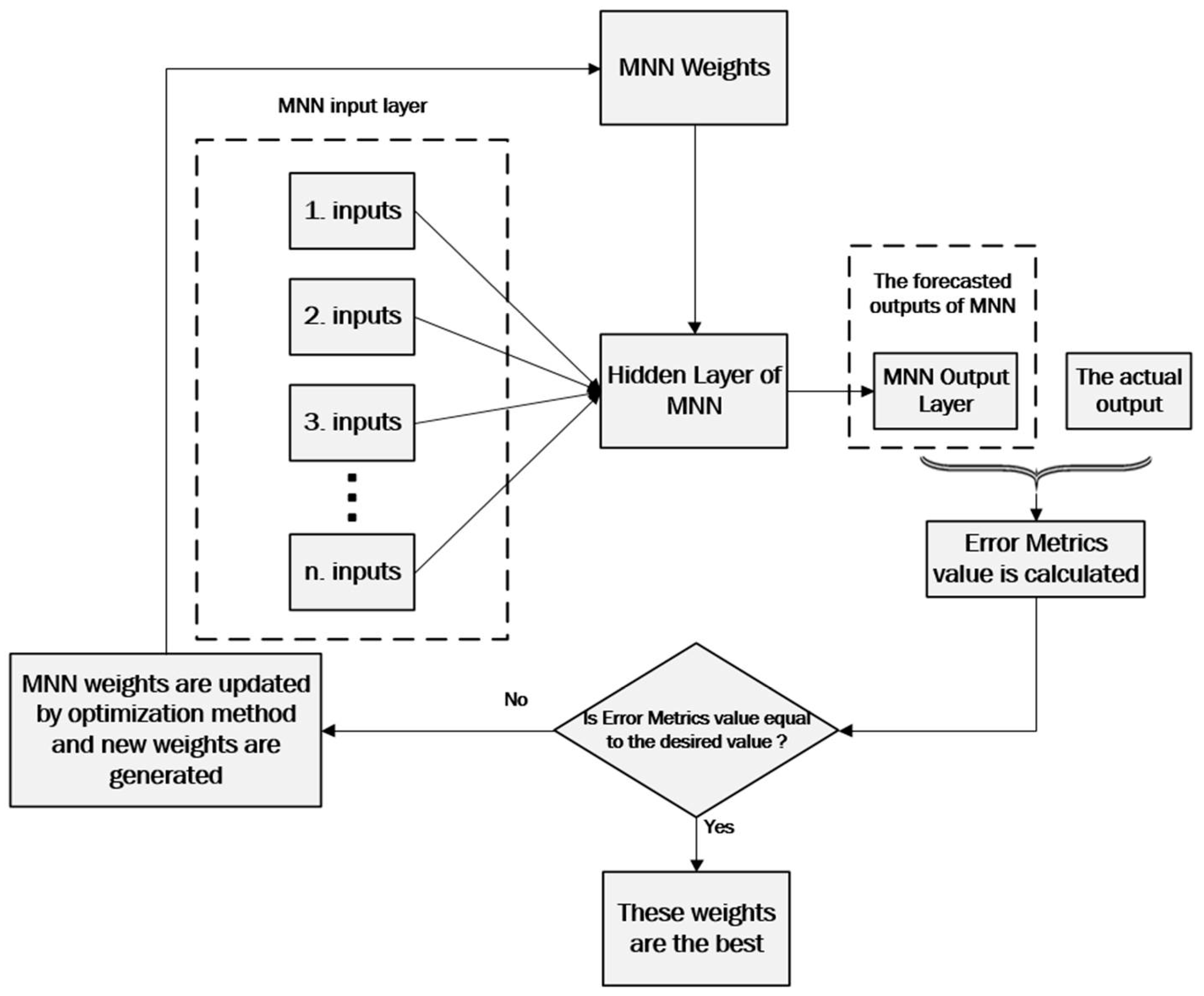
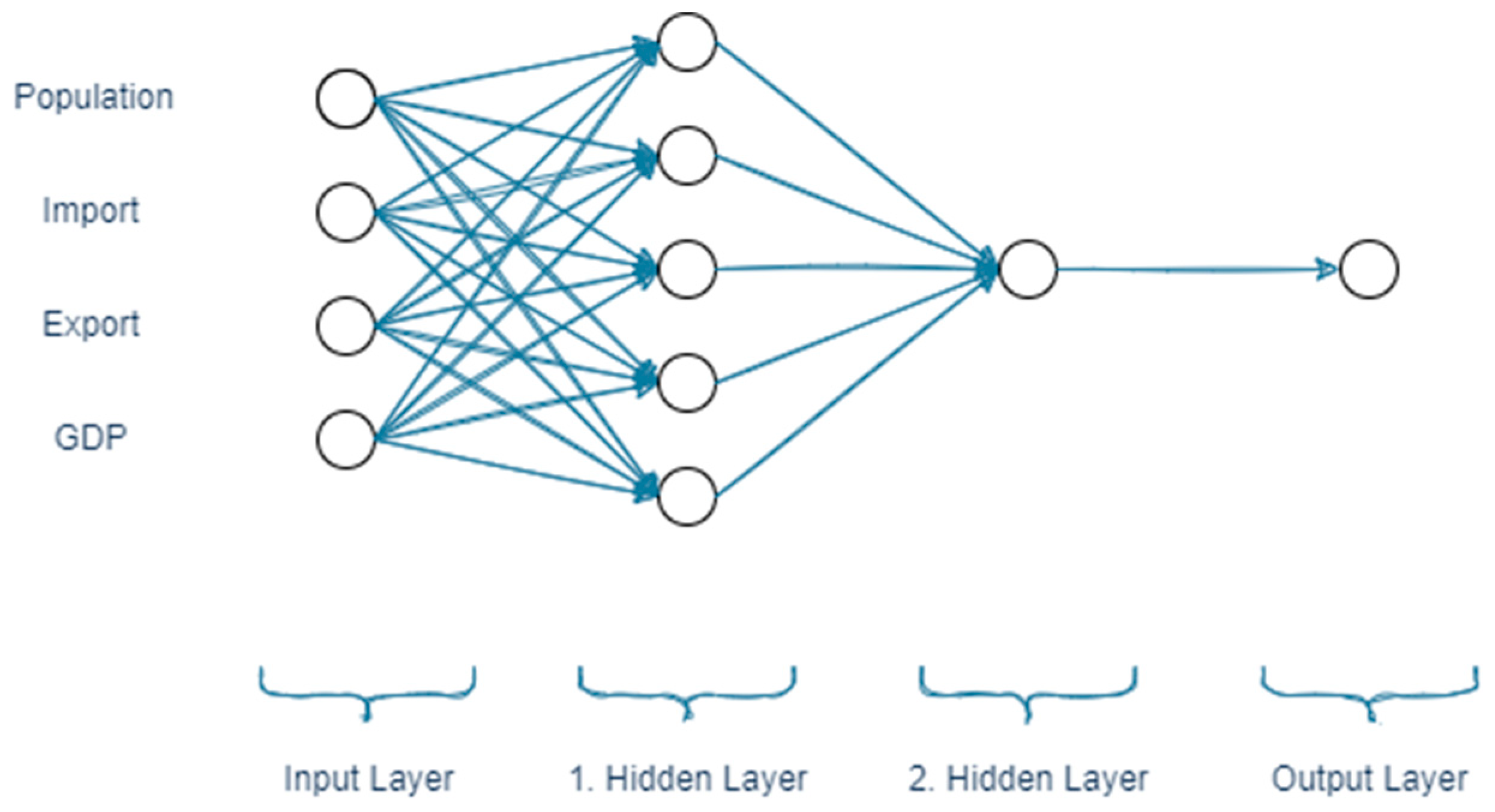
3.1. Medium Neural Networks (MNN)
3.2. Support Vector Machine
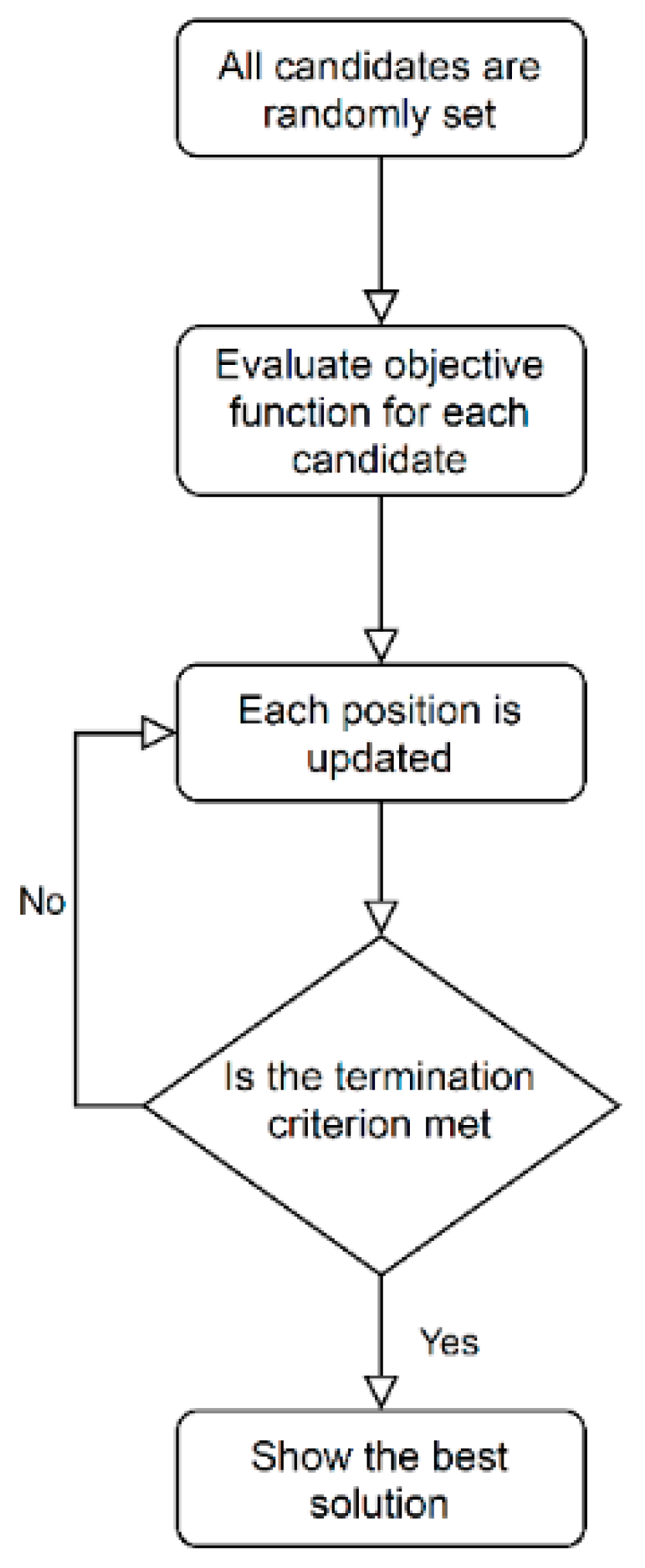
3.3. Whale Optimization Algorithm
3.3.1. Encircling Prey
3.3.2. Bubble-Net Attacking Method
3.3.3. Search for Prey
3.4. Error Metrics
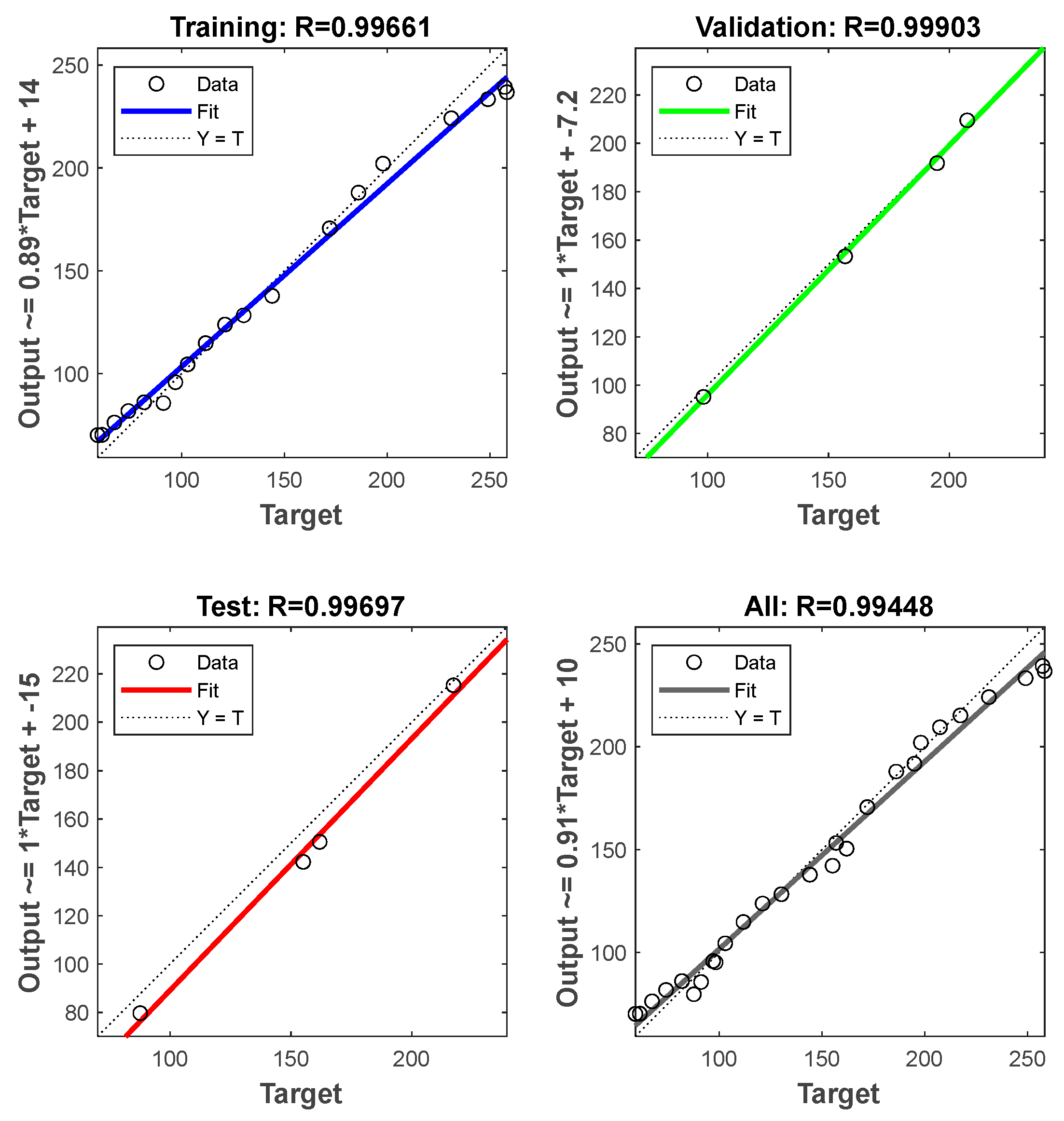
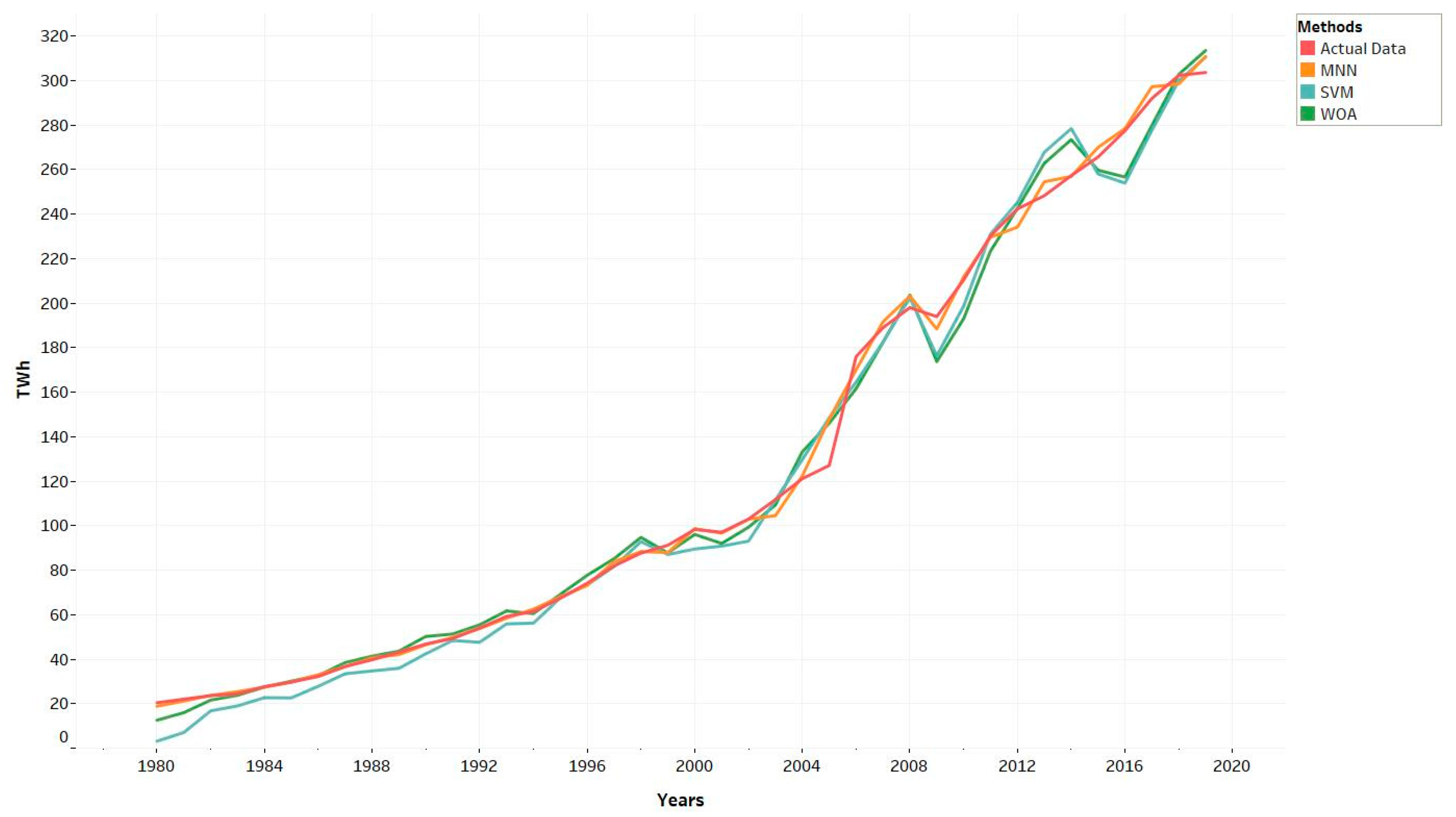
4. Analysis and Results
4.1. Electricity Demand Forecasting
4.2. Error Metrics
4.3. Multi Regression Equations
4.4. Correlation Matrix
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nie, R.X.; Tian, Z.P.; Long, R.Y.; Dong, W. Forecasting household electricity demand with hybrid machine learning-based methods: Effects of residents’ psychological preferences and calendar variables. Expert Syst. Appl. 2022, 206, 117854. [Google Scholar] [CrossRef]
- Gunay, M.E. Forecasting annual gross electricity demand by artificial neural networks using predicted values of socio-economic indicators and climatic conditions: Case of Turkey. Energy Policy 2016, 90, 92–101. [Google Scholar] [CrossRef]
- Sultana, N.; Hossain, S.M.; Almuhaini, S.H.; Düştegör, D. Bayesian Optimization Algorithm-Based Statistical and Machine Learning Approaches for Forecasting Short-Term Electricity Demand. Energies 2022, 15, 3425. [Google Scholar] [CrossRef]
- Beşkirli, A.; Beşkirli, M.; Haklı, H.; Uğuz, H. Comparing Energy Demand Estimation Using Artificial Algae Algorithm: The Case of Turkey. J. Clean Energy Technol. 2018, 6, 349–352. [Google Scholar] [CrossRef]
- Wang, T.; Wen, Y.Y.; Lin, B.Q. Energy consumption and the influencing factors in China: A nonlinear perspective. J. Clean Prod. 2020, 249, 119375. [Google Scholar] [CrossRef]
- Yu, Y.T.; Zhang, N.; Kim, J.D. Impact of urbanization on energy demand: An empirical study of the Yangtze River economic belt in China. Energy Policy 2020, 139, 111354. [Google Scholar] [CrossRef]
- Liu, S.; Zeng, A.; Lau, K.; Ren, C.; Chan, P.W.; Ng, E. Predicting long-term monthly electricity demand under future climatic and socioeconomic changes using data-driven methods: A case study of Hong Kong. Sustain. Cities Soc. 2021, 70, 102936. [Google Scholar] [CrossRef]
- Mutschler, R.; Rüdisüli, M.; Heer, P.; Eggimann, S. Benchmarking cooling and heating energy demands considering climate change, population growth and cooling device uptake. Appl. Energy 2021, 288, 116636. [Google Scholar] [CrossRef]
- Román-Portabales, A.; López-Nores, M.; Pazos-Arias, J.J. Systematic review of electricity demand forecast using ann-based machine learning algorithms. Sensors 2021, 21, 4544. [Google Scholar] [CrossRef]
- Cebekhulu, E.; Onumanyi, A.J.; Isaac, S.J. Performance Analysis of Machine Learning Algorithms for Energy Demand–Supply Prediction in Smart Grids. Sustainability 2022, 14, 2546. [Google Scholar] [CrossRef]
- Saglam, M.; Spataru, C.; Karaman, O.A. Electricity Demand Forecasting with Use of Artificial Intelligence: The Case of Gokceada Island. Energies 2022, 15, 5950. [Google Scholar] [CrossRef]
- Baba, A. Advanced AI-based techniques to predict daily energy consumption: A case study. Expert Syst. Appl. 2021, 184, 115508. [Google Scholar] [CrossRef]
- Shams, M.H.; Niaz, H.; Hashemi, B.; Liu, J.J.; Siano, P.; Anvari-Moghaddam, A. Artificial intelligence-based prediction and analysis of the oversupply of wind and solar energy in power systems. Energy Convers. Manag. 2021, 250, 114892. [Google Scholar] [CrossRef]
- Sekhar, C.; Dahiya, R. Robust framework based on hybrid deep learning approach for short term load forecasting of building electricity demand. Energy 2023, 268, 126660. [Google Scholar] [CrossRef]
- Sen, D.; Tunç, K.M.; Günay, M.E. Forecasting electricity consumption of OECD countries: A global machine learning modeling approach. Util. Policy 2021, 70, 101222. [Google Scholar] [CrossRef]
- Ağbulut, Ü. Forecasting of transportation-related energy demand and CO2 emissions in Turkey with different machine learning algorithms. Sustain. Prod. Consum. 2022, 29, 141–157. [Google Scholar] [CrossRef]
- Şahin, U.; Ballı, S.; Chen, Y. Forecasting seasonal electricity generation in European countries under COVID-19-induced lockdown using fractional grey prediction models and machine learning methods. Appl. Energy 2021, 302, 117540. [Google Scholar] [CrossRef]
- Tun, Y.L.; Thar, K.; Thwal, C.M.; Hong, C.S. Federated Learning based Energy Demand Prediction with Clustered Aggregation. In Proceedings of the Conference: 2021 IEEE International Conference on Big Data and Smart Computing, Jeju Island, Republic of Korea, 17–20 January 2021; pp. 164–167. [Google Scholar]
- Ramsami, P.; King, R.T.A. Neural Network Frameworks for Electricity Forecasting in Mauritius and Rodrigues Islands. In Proceedings of the 2021 IEEE PES/IAS PowerAfrica, Nairobi, Kenya, 23–27 August 2021; pp. 1–5. [Google Scholar]
- Kazemzadeh, M.-R.; Amjadian, A.; Amraee, T. A hybrid data mining driven algorithm for long term electric peak load and energy demand forecasting. Energy 2020, 204, 117948. [Google Scholar] [CrossRef]
- del Real, A.J.; Dorado, F.; Durán, J. Energy Demand Forecasting Using Deep Learning: Applications for the French Grid. Energies 2020, 13, 2242. [Google Scholar] [CrossRef]
- Bedi, J.; Toshniwal, D. Deep learning framework to forecast electricity demand. Appl. Energy 2019, 238, 1312–1326. [Google Scholar] [CrossRef]
- Bannor, E.; Acheampong, A.O. Deploying artificial neural networks for modeling energy demand: International evidence. Int. J. Energy Sect. Manag. 2020, 14, 285–315. [Google Scholar] [CrossRef]
- Abdulsalam, K.A.; Babatunde, O.M. Electrical energy demand forecasting model using artificial neural network: A case study of Lagos State Nigeria. Int. J. Data Netw. Sci. 2019, 3, 305–322. [Google Scholar] [CrossRef]
- Hao, J.; Sun, X.; Feng, Q. A Novel Ensemble Approach for the Forecasting of Energy Demand Based on the Artificial Bee Colony Algorithm. Energies 2020, 13, 550. [Google Scholar] [CrossRef]
- Kaytez, F. A hybrid approach based on autoregressive integrated moving average and least-square support vector machine for long-term forecasting of net electricity consumption. Energy 2020, 197, 117200. [Google Scholar] [CrossRef]
- Di Leo, S.; Caramuta, P.; Curci, P.; Cosmi, C. Regression analysis for energy demand projection: An application to TIMES-Basilicata and TIMES-Italy energy models. Energy 2020, 196, 117058. [Google Scholar] [CrossRef]
- Angelopoulos, D.; Siskos, Y.; Psarras, J. Disaggregating time series on multiple criteria for robust forecasting: The case of long-term electricity demand in Greece. Eur. J. Oper. Res. 2019, 275, 252–265. [Google Scholar] [CrossRef]
- Hou, R.; Li, S.; Wu, M.; Ren, G.; Gao, W.; Khayatnezhad, M. Assessing of impact climate parameters on the gap between hydropower supply and electricity demand by RCPs scenarios and optimized ANN by the improved Pathfinder (IPF) algorithm. Energy 2021, 237, 121621. [Google Scholar] [CrossRef]
- Pegalajar, M.; Ruíz, L.G.B.; Cuéllar, M.P.; Rueda, R. Analysis and enhanced prediction of the Spanish Electricity Network through Big Data and Machine Learning techniques. Int. J. Approx. Reason. 2021, 133, 48–59. [Google Scholar] [CrossRef]
- Bendaoud, N.M.M.; Farah, N.; Ben Ahmed, S. Applying load profiles propagation to machine learning based electrical energy forecasting. Electr. Power Syst. Res. 2022, 203, 107635. [Google Scholar] [CrossRef]
- Porteiro, R.; Hernández-Callejo, L.; Nesmachnow, S. Electricity demand forecasting in industrial and residential facilities using ensemble machine learning. Rev. Fac. De Ing. 2022, 102, 9–25. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, G. A load forecasting model based on support vector regression with whale optimization algorithm. Multimed. Tools Appl. 2023, 82, 9939–9959. [Google Scholar] [CrossRef]
- Emami Javanmard, M.; Tang, Y.; Wang, Z.; Tontiwachwuthikul, P. Forecast Energy Demand, CO2 Emissions and Energy Resource Impacts for the Transportation Sector. Appl. Energy 2023, 338, 120830. [Google Scholar] [CrossRef]
- Rao, C.; Zhang, Y.; Wen, J.; Xiao, X.; Goh, M. Energy Demand Forecasting in China: A Support Vector Regression-Compositional Data Second Exponential Smoothing Model. Energy 2023, 263, 125955. [Google Scholar] [CrossRef]
- Li, S.; Kong, X.; Yue, L.; Liu, C.; Khan, M.A.; Yang, Z.; Zhang, H. Short-Term Electrical Load Forecasting Using Hybrid Model of Manta Ray Foraging Optimization and Support Vector Regression. J. Clean. Prod. 2023, 388, 135856. [Google Scholar] [CrossRef]
- Huang, J.; Kaewunruen, S. Forecasting Energy Consumption of a Public Building Using Transformer and Support Vector Regression. Energies 2023, 16, 966. [Google Scholar] [CrossRef]
- Huang, J.; Algahtani, M.; Kaewunruen, S. Energy Forecasting in a Public Building: A Benchmarking Analysis on Long Short-Term Memory (LSTM), Support Vector Regression (SVR), and Extreme Gradient Boosting (XGBoost) Networks. Appl. Sci. 2022, 12, 9788. [Google Scholar] [CrossRef]
- Velasquez, C.E.; Zocatelli, M.; Estanislau, F.B.; Castro, V.F. Analysis of time series models for Brazilian electricity demand forecasting. Energy 2022, 247, 123483. [Google Scholar] [CrossRef]
- Pallonetto, F.; Jin, C.; Mangina, E. Forecast electricity demand in commercial building with machine learning models to enable demand response programs. Energy AI 2022, 7, 100121. [Google Scholar] [CrossRef]
- May, E.C.; Bassam, A.; Ricalde, L.J.; Soberanis, M.E.; Oubram, O.; Tzuc, O.M.; Alanis, A.Y.; Livas-García, A. Global sensitivity analysis for a real-time electricity market forecast by a machine learning approach: A case study of Mexico. Int. J. Electr. Power Energy Syst. 2022, 135, 107505. [Google Scholar]
- Niu, W.J.; Feng, Z.K.; Li, S.S.; Wu, H.J.; Wang, J.Y. Short-term electricity load time series prediction by machine learning model via feature selection and parameter optimization using hybrid cooperation search algorithm. Environ. Res. Lett. 2021, 16, 055032. [Google Scholar] [CrossRef]
- Luzia, R.; Rubio, L.; Velasquez, C.E. Sensitivity analysis for forecasting Brazilian electricity demand using artificial neural networks and hybrid models based on Autoregressive Integrated Moving Average. Energy 2023, 274, 127365. [Google Scholar] [CrossRef]
- Işık, G.; Öğüt, H.; Mutlu, M. Deep learning based electricity demand forecasting to minimize the cost of energy imbalance: A real case application with some fortune 500 companies in Türkiye. Eng. Appl. Artif. Intell. 2023, 118, 105664. [Google Scholar] [CrossRef]
- Albuquerque, P.C.; Cajueiro, D.O.; Rossi, M.D.C. Machine learning models for forecasting power electricity consumption using a high dimensional dataset. Expert. Syst. Appl. 2022, 187, 115917. [Google Scholar] [CrossRef]
- Rick, R.; Berton, L. Energy forecasting model based on CNN-LSTM-AE for many time series with unequal lengths. Eng. Appl. Artif. Intell. 2022, 113, 104998. [Google Scholar] [CrossRef]
- Maaouane, M.; Chennaif, M.; Zouggar, S.; Krajaci’c, G.; Duic, N.; Zahboune, H.; ElMiad, A.K. Using neural network modelling for estimation and forecasting of transport sector energy demand in developing countries. Energy Convers Manag. 2022, 258, 115556. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Rajasekar, E.; Natarajan, S.; McCullen, N. A comparative assessment of SARIMA, LSTM RNN and Fb Prophet models to forecast total and peak monthly energy demand for India. Energy Pol. 2022, 168, 113097. [Google Scholar] [CrossRef]
- Turkish Electricity Transmission Corporation. Available online: https://www.teias.gov.tr/en-US/interconnections (accessed on 23 May 2022).
- Turkish Statistical Institute. Available online: https://data.tuik.gov.tr/Kategori/GetKategori?p=nufus-ve-demografi-109&dil=1 (accessed on 18 September 2021).
- Binici, M. Turkey’s Energy Consumption Forecast by Using Mathematical Modeling. Master’s Thesis, Sivas Cumhuriyet University, Sivas, Turkey, 2019. [Google Scholar]
- Aghay Kaboli, S.H.; Selvaraj, J.; Rahim, N.A. Long-term electric energy consumption forecasting via artificial cooperative search algorithm. Energy 2016, 115, 857–871. [Google Scholar] [CrossRef]
- International Monetary Fund (IMF). Available online: https://www.imf.org/en/Data (accessed on 19 June 2022).
- World Bank. Available online: https://data.worldbank.org/?intcid=ecr_hp_BeltD_en_ext (accessed on 2 May 2022).
- Aslan, M.; Beşkirli, M. Realization of Turkey’s Energy Demand Forecast with the Improved Arithmetic Optimization Algorithm. Energy Rep. 2022, 8, 18–32. [Google Scholar] [CrossRef]
- Efekemo, E.; Saturday, E.G.; Ofodu, J.C. Electricity Demand Forecasting: A Review. Educ. Res. IJMCER 2022, 4, 279–301. [Google Scholar]
- Alhendi, A.A.; Al-Sumaiti, A.S.; Elmay, F.K.; Wescaot, J.; Kavousi-Fard, A.; Heydarian-Forushani, E.; Alhelou, H.H. Artificial intelligence for water–energy nexus demand forecasting: A review. Int. J. Low-Carbon Technol. 2022, 17, 730–744. [Google Scholar] [CrossRef]
- Moustris, K.; Kavadias, K.A.; Zafirakis, D.; Kaldellis, J.K. Medium, short and very short-term prognosis of load demand for the Greek Island of Tilos using artificial neural networks and human thermal comfort-discomfort bio-meteorological data. Renew Energy 2020, 147, 100–109. [Google Scholar] [CrossRef]
- Birecikli, B.; Karaman, O.A.; Çelebi, S.B.; Turgut, A. Failure load prediction of adhesively bonded GFRP composite joints using artificial neural networks. J. Mech. Sci. Technol. 2020, 34, 4631–4640. [Google Scholar] [CrossRef]
- Karaman, O.A.; Tanyıldızı Ağır, T.; Arsel, İ. Estimation of Solar Radiation Using Modern Methods. Alex. Eng. J. 2021, 60, 2447–2455. [Google Scholar] [CrossRef]
- Akbal, B. Hybrid GSA-ANN Methods to Forecast Sheath Current of High Voltage Underground Cable Lines. J. Comput. 2018, 13, 417–425. [Google Scholar] [CrossRef]
- Onaolapo, A.K.; Carpanen, R.P.; Dorrell, D.G.; Ojo, E.E. A Comparative Assessment of Conventional and Artificial Neural Networks Methods for Electricity Outage Forecasting. Energies 2022, 15, 511. [Google Scholar] [CrossRef]
- Korkut, F.G. Prediction of Interactions between SARS-CoV-2 Protein and Human Protein Using Machine Learning Methods. Master’s Thesis, Yalova University, Yalova, Turkey, 2022. [Google Scholar]
- Dinsever, L.D.; Gümüş, V.; Şimşek, O.; Avşaroğlu, Y.; Kuş, M. Adıyaman ve Gaziantep İstasyonlarındaki Güneşlenme Şiddetinin Destek Vektör Makineleri ile Tahmini. Bilecik Şeyh Edebali Üniversitesi Fen Bilim. Derg. 2021, 8, 753–769. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Gholizadeh, H. A Comprehensive Survey: Whale Optimization Algorithm and Its Applications. Swarm Evol. Comput. 2019, 48, 1–24. [Google Scholar] [CrossRef]
- Aydın, Z.E. Missing Data Imputation Methods Based on Whale Optimization Algorithm and Random Subspaces. Ph.D. Thesis, Eskisehir Technical University, Eskisehir, Turkey, 2021. [Google Scholar]
- Shang, Z.; He, Z.; Song, Y.; Li, L.; Chen, Y. A Novel Combined Model for Short-Term Electric Load Forecasting Based on Whale Optimization Algorithm. Neural Process. Lett. 2020, 52, 1207–1232. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, L.; Wang, J.; Niu, X. Hybrid system based on a multi-objective optimization and kernel approximation for multi-scale wind speed forecasting. Appl. Energy 2020, 277, 115561. [Google Scholar] [CrossRef]
- Houimli, R.; Zmami, M.; Ben-Salha, O. Short-term electric load forecasting in Tunisia using artificial neural networks. Energy Syst. Berl. Period. 2020, 11, 357–375. [Google Scholar] [CrossRef]
- Shah, I.; Jan, F.; Ali, S. Functional Data Approach for Short-Term Electricity Demand Forecasting. Math. Probl. Eng. 2022, 2022, 6709779. [Google Scholar] [CrossRef]
- Soyler, I.; Izgi, E. Electricity Demand Forecasting of Hospital Buildings in Istanbul. Sustainability 2022, 14, 8187. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Moayyed, H.; Zare, K.; Mohammadi-Ivatloo, B. Short-term electricity demand forecasting via variational autoencoders and batch training-based bidirectional long short-term memory. Sustain. Energy Technol. Assess. 2022, 52, 102209. [Google Scholar] [CrossRef]
- Aponte, O.; McConky, K.T. Forecasting an electricity demand threshold to proactively trigger cost saving demand response actions. Energy Build. 2022, 268, 112221. [Google Scholar] [CrossRef]
- Brown, S.H. Multiple linear regression analysis: A matrix approach with MATLAB. Ala. J. Math. 2009, 34, 1–3. [Google Scholar]
- Kaya, N.; Guler, H. Examining the Solution-focused Thinking and Hope Levels of Turkish Midwifery Students During Distance Education: A Cross-sectional Study. Mod. Care J. 2023, 20, e131139. [Google Scholar] [CrossRef]
- Khelouf, N.; Haoud, K.; Meziani, S.; Fizir, M.; Ghomari, F.N.; Khaled, M.B.; Kadi, N. Effect of infant’s gender and lactation period on biochemical and energy breast milk composition of lactating mothers from Algeria. J. Food Compos. Anal. 2023, 115, 104889. [Google Scholar] [CrossRef]
- Steiger, J.H. Tests for comparing elements of a correlation matrix. Psychol. Bull. 1980, 87, 245. [Google Scholar] [CrossRef]

| Method | Forecasting for | Variables | Author |
|---|---|---|---|
| ANN, Gaussian regression, k-nearest neighbors, LR, random forest, and SVM | electricity supply and demand | system hourly demand, renewable generation sources | Cebekhulu et al. [10] |
| MLR, ANN, and PSO | island electricity demand | import, car numbers, passenger (tourist) numbers, export | Saglam et al. [11] |
| ANN- Generic Algorithm for power grid management | daily energy consumption | day data | Baba [12] |
| RT, GBT, RF, ANN, LSTM, and SVR | solar and wind energy oversupply in power system | biomass/geothermal units, output power of thermal power plants, load demands, power imports, nuclear units, wind turbines, solar farms, large hydro units, and WSPC | Shams et al. [13] |
| Bilateral long short-term memory (BILSTM), CNN, GWO, Time Series Prediction | Short-term electricity demand forecast | Buildings’ electricity consumption times series data | Sekhar and Dahiya [14] |
| SVM and ANN | electricity consumption | The population, inflation rate, GDP and unemployment rate | Sen et al. [15] |
| deep learning, SVM, and ANN | transportation energy demand | year, population, GDP, vehicle kilometer | Agbulut [16] |
| grey prediction model and SVM method | seasonal electricity generation | Eurostat database | Sahin et al. [17] |
| RNN | energy demand | past energy usage values | Tun et al. [18] |
| RNN, ANN, and adaptive network-based fuzzy inference system | electricity demand | historical electricity data | Ramsami and King [19] |
| SVR and PSO-ARIMA-ANN | long term electricity demand and peak load | energy and load data | Kazemzadeh et al. [20] |
| ANN, CNN, and compare with traditional ANN-ARIMA | energy demand | hours, week of the year, holidays, day of the week | Real et al. [21] |
| ANN, SVR, and RNN | electricity demand | electricity consumption dataset | Bedi and Toshniwal [22] |
| MLP optimization and ANN | energy demand for India, ustralia, China, the USA and France | Financial development, energy price, industrialization, FDI, economic growth, population, urbanization, | Bannor and Acheampong [23] |
| ANN and RNN | electrical energy demand | population, GDP, temperature, energy consumption | Abdulsalam and Babatundea [24] |
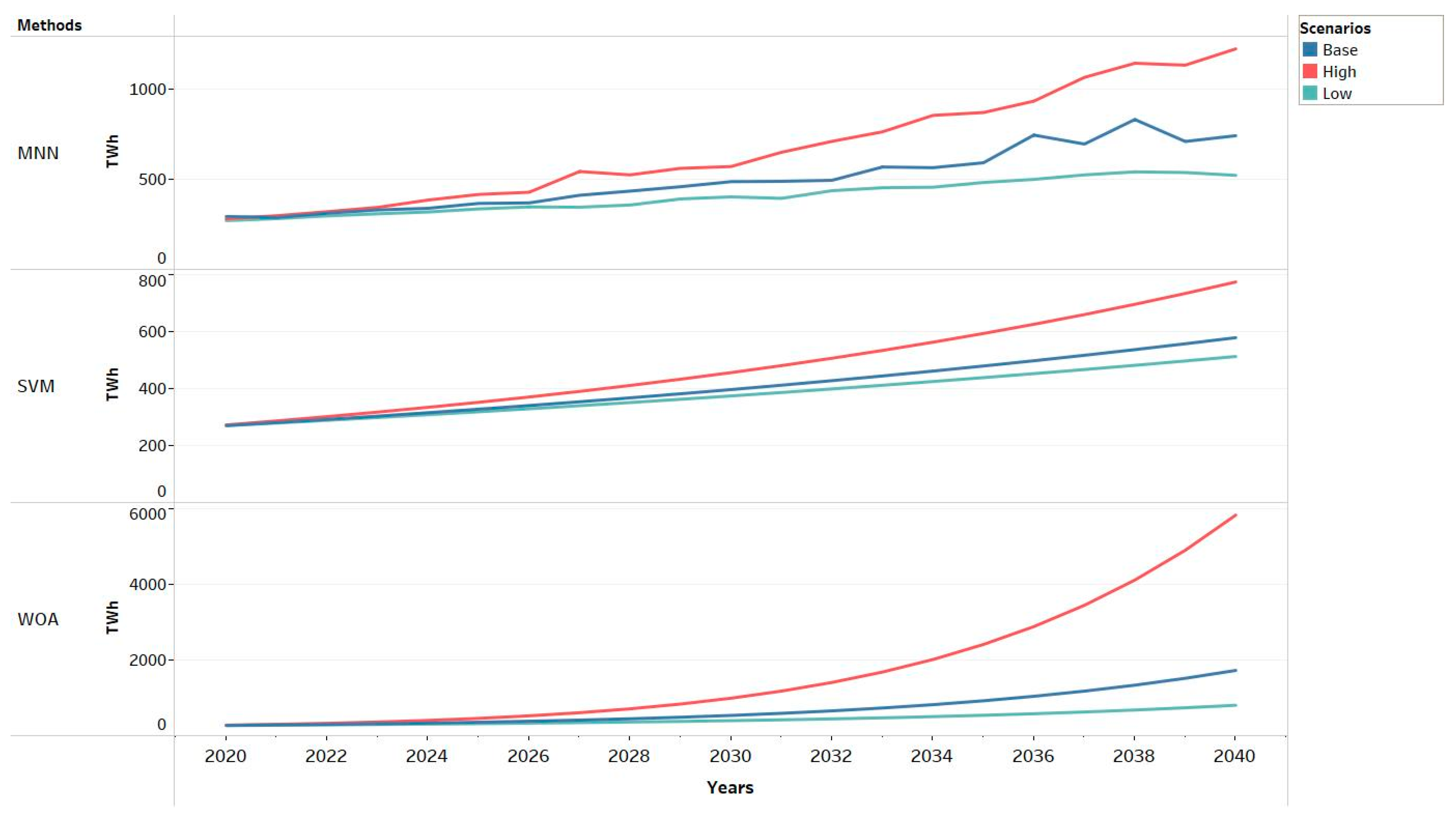
| Input Variables | Mainland | ||
|---|---|---|---|
| Low Scenario | Base Scenario | High Scenario | |
| Import | 1% | 2% | 3% |
| Export | 3% | 5% | 6% |
| GDP | 3% | 4.5% | 6% |
| Population | 1% | 2% | 3% |
| Methods | Mainland | |
|---|---|---|
| R2 | SVM | 0.9978 |
| WOA | 0.9966 | |
| MNN | 0.9984 | |
| RMSE | SVM | 3.4335 |
| WOA | 2.9873 | |
| MNN | 5.325 × 10−14 | |
| MSE | SVM | 11.78 |
| WOA | 8.923 | |
| MNN | 28.35 × 10−28 | |
| MAE | SVM | 2.9982 |
| WOA | 2.3276 | |
| MNN | 2.5 × 10−14 | |
| Eq No | Parameters | Multi Regression Equations | R2 | p-Value |
|---|---|---|---|---|
| 1 | a, b, c, d | F = −49.914 + 0.089284 ∗ a + 0.48065 ∗ b + 0.15825 ∗ c + 0.78607 ∗ d | 0.995 | 3.53 × 10−39 |
| 2 | b, c, d | F = −47.462 + 0.61379 ∗ b + 0.14806 ∗ c + 0.78086 ∗ d | 0.994 | 0.03 × 10−40 |
| 3 | a, c, d | F = −64.02 + 0.3626 ∗ a + 0.21054 ∗ c + 0.08503 ∗ d | 0.993 | 4.07 × 10−39 |
| 4 | c, d | F = −102.91 + 0.32548 ∗ c + 1.1863 ∗ d | 0.98 | 4.41 × 10−32 |
| 5 | a, b, d | F = −82.719 − 0.12819 ∗ a + 1.0247 ∗ b + 2.0838 ∗ d | 0.99 | 5.48 × 10−36 |
| 6 | b, d | F = −90.488 + 0.8576 ∗ b + 2.2348 ∗ d | 0.99 | 1.96 × 10−37 |
| 7 | a, d | F = −166.68 + 0.5579 ∗ a + 3.763 ∗ d | 0.98 | 3.74 × 10−32 |
| 8 | a, b, c | F = −16.317 + 0.086601 ∗ a + 0.49675 ∗ b + 0.1895 ∗ c | 0.994 | 4.1 × 10−40 |
| 9 | b, c | F = −14.155 + 0.62581 ∗ b + 0.17942 ∗ c | 0.994 | 9.28 × 10−42 |
| 10 | a, c | F = −28.091 + 0.36962 ∗ a + 0.24634 ∗ c | 0.993 | 3.85 × 10−40 |
| 11 | a, b | F = 23.942 − 0.30766 ∗ a + 1.5105 ∗ b | 0.984 | 5.42 × 10−34 |
| Variables | Import | Export | GDP | Population | Electricity Consumption |
|---|---|---|---|---|---|
| Import | 1 | 0.9895 | 0.946 | 0.9232 | 0.9742 |
| Export | 0.9895 | 1 | 0.9727 | 0.9478 | 0.991 |
| GDP | 0.946 | 0.9727 | 1 | 0.9684 | 0.9892 |
| Population | 0.9232 | 0.9478 | 0.9684 | 1 | 0.9669 |
| Electricity Consumption | 0.9742 | 0.991 | 0.9892 | 0.9669 | 1 |
| Methods | Actual Data | MNN | SVM | WOA |
|---|---|---|---|---|
| Actual Data | 1 | 0.9988 | 0.9952 | 0.9957 |
| MNN | 0.9988 | 1 | 0.996 | 0.9967 |
| SVM | 0.9952 | 0.996 | 1 | 0.9994 |
| WOA | 0.9957 | 0.9967 | 0.9994 | 1 |
| Methods | Variables | Coefficient | 95% Confidence Internal | t | p > |t| | |
|---|---|---|---|---|---|---|
| Real | import | 0.72 | 0.053 | 1.387 | 2.24 | 0.035 |
| export | −0.771 | −1.438 | −0.103 | −2.4 | 0.025 | |
| GDP | 9.925 | 6.044 | 13.807 | 5.3 | 0 | |
| population | 5.198 | 4.135 | 6.26 | 10.15 | 0 | |
| MNN | import | 0.913 | 0.054 | 1.772 | 2.18 | 0.036 |
| export | −0.693 | −1.254 | −0.133 | −2.1 | 0.026 | |
| GDP | 9.698 | 6.088 | 13.29 | 5.39 | 0 | |
| population | 5.432 | 4.368 | 6.497 | 10.04 | 0 | |
| SVM | import | 0.72 | 0.298 | 1.142 | 3.54 | 0.002 |
| export | −0.77 | −1.193 | −0.348 | −3.78 | 0.001 | |
| GDP | 9.931 | 7.472 | 12.39 | 8.38 | 0 | |
| population | 5.197 | 4.524 | 5.871 | 16.02 | 0 | |
| WOA | import | 0.72 | 0.389 | 1.051 | 4.52 | 0 |
| export | −0.771 | −1.102 | −0.44 | −4.83 | 0 | |
| GDP | 9.912 | 7.986 | 11.838 | 10.67 | 0 | |
| population | 5.202 | 4.674 | 5.729 | 20.46 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saglam, M.; Spataru, C.; Karaman, O.A. Forecasting Electricity Demand in Turkey Using Optimization and Machine Learning Algorithms. Energies 2023, 16, 4499. https://doi.org/10.3390/en16114499
Saglam M, Spataru C, Karaman OA. Forecasting Electricity Demand in Turkey Using Optimization and Machine Learning Algorithms. Energies. 2023; 16(11):4499. https://doi.org/10.3390/en16114499
Chicago/Turabian StyleSaglam, Mustafa, Catalina Spataru, and Omer Ali Karaman. 2023. "Forecasting Electricity Demand in Turkey Using Optimization and Machine Learning Algorithms" Energies 16, no. 11: 4499. https://doi.org/10.3390/en16114499
APA StyleSaglam, M., Spataru, C., & Karaman, O. A. (2023). Forecasting Electricity Demand in Turkey Using Optimization and Machine Learning Algorithms. Energies, 16(11), 4499. https://doi.org/10.3390/en16114499







