1. Introduction
Jackfruit (
Artocarpus heterophyllus Lam.) is a familiar tropical fruit from the
Moraceae family that has high nutritional value and well-documented health benefits [
1]. Jackfruit is considered as a major fruit in Bangladesh, India, Thailand, and southern China since it is preferred by multifarious consumers and is rich in vitamins, cellulose, minerals, sugar, and various other nutrients [
2,
3]. This oval-shaped fruit is mostly distinguished by its mass (usually 5–30 kg) [
4]. Jackfruit pulp is golden-yellow in colour and organised in fleshy bulbs (approximately 30–35% of fruit’s weight), with each bulb comprising a single seed [
5,
6]. The challenges pertaining to the storage and preservation of this nutritious fruit, along with its high perishability once it ripens, make it difficult to commercialise. Drying is an effective approach to ensure longer shelf lives for jackfruit. Food researchers have conducted various drying experiments to analyse the drying kinetics of jackfruit [
7,
8,
9]. The convective drying of jackfruit bulbs was conducted to evaluate the kinetics of drying [
10]. The experiment was carried out at temperatures of 50, 60, and 70 °C to achieve a moisture content of 21.3% dry basis. Drying kinetics experimental data were well fitted to a Page model. The total carotenoids and colour degradation kinetics of jackfruit bulb slices were analysed considering hot air dying to provide a possible solution to the surplus production problem of jackfruit [
11]. An attempt was made to determine the thermophysical properties of jackfruit with varying temperature and moisture content [
12]. The optimization and quality evaluation of jackfruit bulbs with the application of combination drying was conducted to determine the potential of commercialisation for dried products [
3]. Instant controlled pressure drop-assisted freeze drying was developed to investigate the influence of drying methods on the physicochemical characteristics and microstructure of jackfruit bulb chips [
13]. A refractance window drying approach was employed to optimise the drying conditions for jackfruit pulp, and quality analysis was carried out [
14].
The aforesaid description confirms that, although numerous research works have been carried out to investigate the drying kinetics of jackfruit, many have ignored the analysis of basic drying physics. To obtain better-quality dried products and facilitate a reduction in cost, proper analysis of fundamental heat–mass transfer process is crucial since drying involves various physico-chemical changes such as shrinkage and case hardening [
15]. It is indispensable to check the structural changes and physical phenomena that occur during drying to correlate it with the dried product quality [
16]. Shrinkage significantly influences the drying kinetics; hence, it should be considered when predicting basic heat–mass transfer phenomena [
17]. In this respect, mathematical modelling and the simulation of basic drying processes along with shrinkage can provide an in-depth understanding of the underlying physics related to jackfruit drying [
18,
19]. Mathematical modelling provides a wide range of virtual scenarios and enables us to predict the process design outcomes, optimisation parameters, and cost development [
20].
Table 1 represents available Jackfruit drying kinetics models with the best model outcomes.
The existing mathematical models for jackfruit drying are mostly empirical in nature and only describe the drying kinetics for a specific drying condition. These models overlook the fundamental analysis of heat–mass transfer mechanisms and prediction of shrinkage when drying jackfruit samples. As far as the authors know, research works considering the use of a theoretical mathematical model for predicting jackfruit drying kinetics are still scarce, particularly with respect to shrinkage phenomena. Additionally, comparative assessment between the model outcomes with and without consideration of the shrinkage process has not yet been reported for jackfruit drying. However, jackfruit’s potential application in the food industry is well known [
26,
27].
Hence, the present study aims to develop a theoretical single phase drying model to investigate the temperature and moisture variation characteristics along with shrinkage prediction. Due to the absence of reported mechanical properties such as Young’s modulus and Poisson’s ratio for jackfruit in the literature and the lack of current facilities for measuring them, the use of a constitutive material model in the drying experiment would yield erroneous results. In other words, the solution of the theoretical mathematical model requires the characterization of the material, and the unavailability of these essential mechanical properties (which vary with drying conditions) hinders the accurate validation of theoretical shrinkage models, including fractional viscoelastic and classical models.
To address this issue, a semi-theoretical shrinkage model is employed in this study, utilizing the shrinkage velocity approach expressed as a function of effective moisture diffusivity and density. The shrinkage velocity approach has been chosen to predict the shrinkage of jackfruit during drying and fulfil our aim of simplifying the complexity and minimising errors in deformation prediction [
28,
29].
Finally, validation of the developed shrinkage-based drying model was performed through comparison with the experimental outcomes and statistical error analysis. The findings of this model will facilitate further ideas towards developing a multiphase model regarding the advanced analysis of jackfruit drying.
2. Materials and Methods
2.1. Sample Preparation
Fresh jackfruit was collected from the local market (Rajshahi, Bangladesh) and then stored at 4 °C in the refrigerator until it was time to begin the drying experiment. The jackfruit bulbs were separated from the whole fruit and the proper bulbs were selected depending on the characteristics of identical freshness, size, maturity, and integrity. After peeling and the removal of the seed, jackfruit bulbs were cut into unform cylindrical slices approximately 25 mm in diameter and 6 mm in thickness using a cutting tool (Cork borer (JH-1225)) made from stainless steel. The initial moisture content of 5.25 kg/kg dry basis was obtained by heating the sample at 105 °C for 24 h in a hot air oven to obtain the bone-dry mass.
2.2. Experimental Procedure
To carry out the drying experiment, a multi tray convective dryer (with temperature range 35–70 °C, 50 Hz, 245 W, 220–240 V) was used. The samples were horizontally placed on the dryer tray. To achieve a steady state drying condition, the dryer was started 30 min before every drying run.
In this study, the drying experiment was conducted at three different temperatures (50 °C, 60 °C, and 70 °C) to observe the influence of temperature variations on drying kinetics. The outcomes of the experiment for different drying temperatures were utilised to determine the effective moisture diffusivity () and activation energy (). Hot air with an air velocity of 1.1 m/s was supplied throughout the experiment. Total 30.25 gm (10 samples) jackfruit slices were used. In every 30 min interval, jackfruit samples were taken out of the dryer and weighed using a digital electronic balance (Model BB3000; Mettler-Toledo AG, Grefensee, Switzerland, having a measurement range of 0–100 g and accuracy of 0.01 g). The experiment was replicated three times. The temperature data were recorded using a thermal imaging camera. The dimensions of jackfruit slices (diameter and thickness) were measured using a digital vernier calliper (Moore and Wright, Europe, ±0.01 mm) at a fixed time interval of 30 min. The dimension readings were recorded at different positions of the sample since the diameter and thickness changes were not uniform throughout the drying process. Volume calculation of samples was performed using average dimension values. All the experiments were conducted in a laboratory at the Rajshahi University of Engineering & Technology (RUET), Bangladesh. The computational facilities provided by Queensland University of Technology (QUT), Australia were also utilised to simulate the shrinkage model.
3. Mathematical Model Development
A single-phase theoretical 2D drying model considering the axisymmetric coordinate system of the cylindrical jackfruit samples was developed. The moisture-dependent diffusivity approaches were employed to build the model. The assumptions for the developed model are as follows: (i) Homogenization of transport properties are considered within the model domain; (ii) Constant drying air properties; (iii) Uniform distribution of initial temperature and moisture content of the sample; (iv) Thermo-physical properties change with moisture content; (v) Moisture migration from the sample inside towards the surface takes place through diffusion process; (vi) Internal heat generation is neglected.
3.1. Heat and Mass Transfer Governing Equations
3.1.1. Energy Balance Equation
Energy balance is described employing Fourier’s law of heat transfer [
30,
31].
where
T is the instantaneous temperature (K),
ρ is the sample density (kg/m
3),
cp is the material specific heat capacity (J/kg·K), and
k is the thermal conductivity of the sample (W/m·K). The value of
Q is zero due to there being no internal heat generation.
3.1.2. Mass Conservation Equation
Fick’s law of diffusion is utilised to characterise mass transport, as represented by Equation (2).
where
C is instantaneous moisture concentration (mol/m
3),
t is the time (s), and
is the effective moisture diffusivity (m
2/s).
3.2. Deformation Prediction
During drying, the water removal from the sample results in a pressure imbalance between the inner material and external pressure. This induces contracting stress and leads to shape changes, material shrinkage, or collapse. Macroscopic shrinkage is generally defined as the ratio of the sample volume at a given drying time to the initial volume, as given by Equation (3).
where
and
are the sample volumes at any time t and initial time (t = 0), respectively.
In this study, shrinkage velocity method, expressed as a function of effective moisture diffusivity and density, is utilised to predict volumetric deformation because moisture migration is given by the following:
where
is the shrinkage velocity (m/s),
is the effective moisture diffusivity in (m
2/s), density ratio
is the ratio of water density and particle density, respectively, and L is the half thickness of the sample (m). The considered shrinkage velocity of the solid matrix during drying is calculated using the mass-average approach. This approach considers the change in mass of the entire solid matrix during drying and assumes that the velocity is zero when the mass of the solid matrix does not change.
Moreover, the displacement of the centre of inertia due to shrinkage may lead to the existence of a velocity term that was not accounted for in the equation for avoiding the complexity of numerical solution at this stage. Arbitrary Lagrangian Eulerian (ALE) formulation was implemented to describe the shrinkage of jackfruit during drying.
3.3. Initial Conditions and Input Parameters
The required initial conditions and required properties of food materials are presented in the following section:
3.3.1. Initial and Boundary Conditions
The initial conditions for energy balance and mass transport are described by the following:
where C
o represents initial moisture concentration of the sample (mol/m
3).
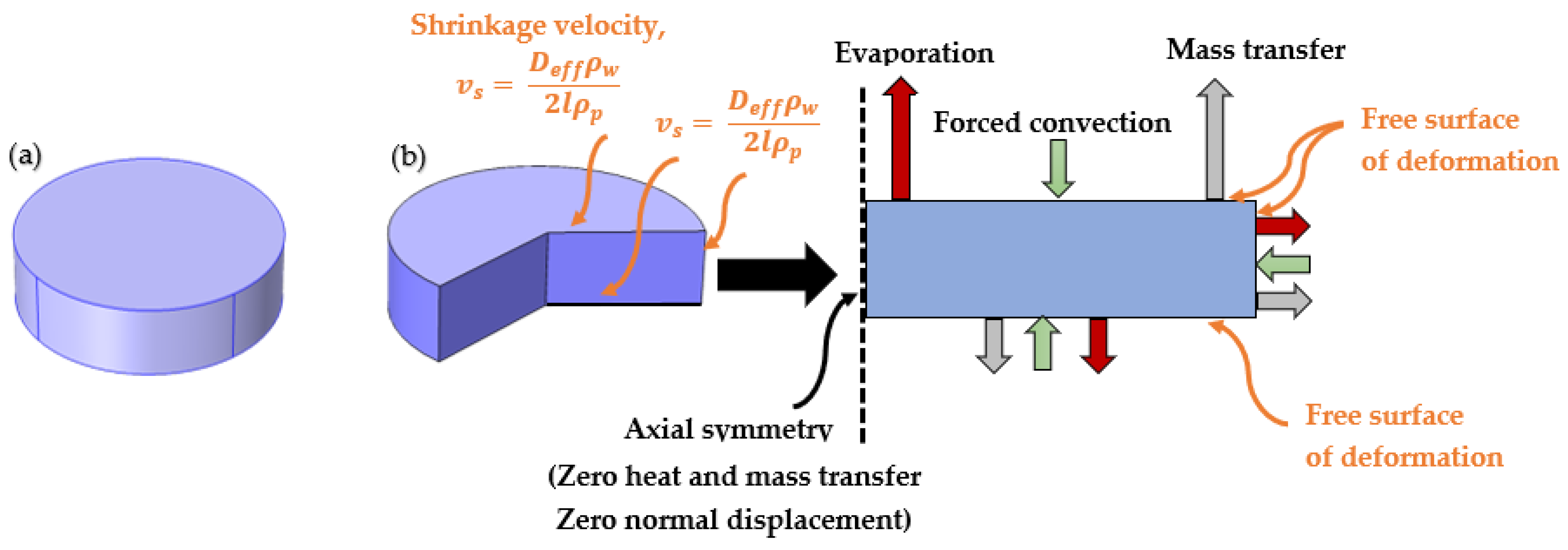
The boundary conditions for heat and mass transfer considered in this study are presented in
Figure 1. Both the convective heat transfer and loss of heat due to evaporation occurring at the surface are considered as the heat transfer boundary conditions for the external boundaries as defined by the following:
With being the temperature of drying air (K), being the heat transfer coefficient (W/m2. K), being the mass transfer coefficient (m/s), as the latent heat of evaporation (J/kg), as the molar mass of water (kg/mol), R as the universal gas constant, and and being the equilibrium vapour pressure (Pa) and vapour pressure of ambient air (Pa), respectively.
There is no known equation of equilibrium vapour pressure of jackfruit available in the literature. The approximate equilibrium vapour pressure of jackfruit can be taken from the widely used literature [
32] and is as follows:
where
is the moisture content (kg/kg dry basis) and
is the saturated vapour pressure of water (Pa). Saturated vapour pressure is defined in [
33],
The mass flux at the outward boundaries is considered as:
The final boundary condition at the symmetry is defined as:
3.3.2. Input Parameters
Most of the input parameters are listed in
Table 2, and the remainder are described in the subsequent section.
Thermophysical Properties of Jackfruit Sample
The thermal conductivity, k (W/m·K) and specific heat,
(J/kg·K) of jackfruit sample are considered as a function of wet bases moisture content (
) [
12,
36].
Moisture Effective Diffusivity
Effective diffusivity used in this research is based on the moisture content. Shrinkage-dependent effective diffusivity is expressed as a function of moisture content considering the drying sample undertaking deformation and can be defined as [
37,
38]:
where
represents reference effective diffusivity (m
2/s),
and
are the sample thickness (m) at initial time and time t, respectively. The thickness ratio is found from the following equation [
39,
40]:
Here, is the initial moisture content (wet basis) and is the density of water (kg/m3).
Determination Effective Moisture Diffusivity
The moisture ratio (MR) is calculated using the following equation:
where
is the moisture content (kg/kg dry basis) of the sample at drying time t,
is the initial moisture content (kg/kg dry basis), and
is the equilibrium moisture content (kg/kg dry basis). In this experiment, the value of
is relatively small (0.1–0.2 kg/kg dry basis). It is worth noting that although the equilibrium moisture content may have a small value compared to the initial value, it is still an important factor to consider in the drying process. Ignoring this factor may lead to a slight mismatch between the simulations and experimental data, especially at the later stages of the process. However, to simplify the modelling, this is the widely used practice. Therefore, Equation (14) can be simplified as [
1,
41]:
The effective moisture diffusivity (
) is calculated using the following:
where
is the effective moisture diffusivity in (m
2/s), L is the half thickness of the sample (m), and t is the drying time (s).
The
values for the present study were found to be varied within the range of 1.64 × 10
−10–3.15 × 10
−10 m
2/s for the temperature ranges of 50–70 °C, which closely agrees the values seen in the literature [
22,
23].
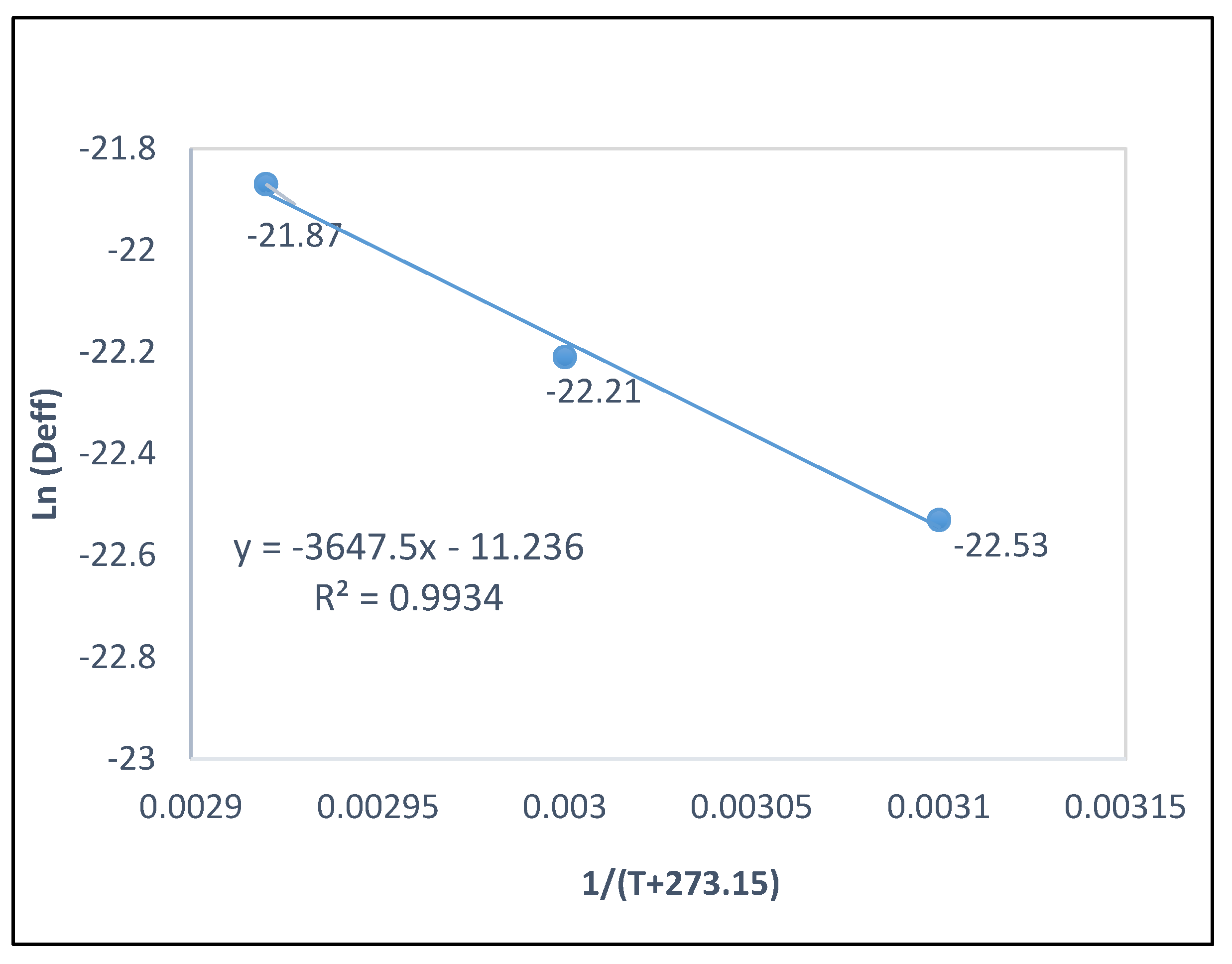
The activation energy and integration constant are calculated from the slope of ln (
) versus 1/T plot (Arrhenius plot), as represented in
Figure 2.
Determination of Heat and Mass Transfer Coefficient
The heat and mass transfer coefficients are calculated using the following correlation of Nusselt number:
where
L is the characteristics length (m), Re is the Reynolds number, and
Pr is the Prandlt number.
Mass transfer coefficient is calculated from the Sherwood number (
Sh) and Schmidt number (
Sc), as given by the following equations:
Here,
is the binary diffusivity of vapour and air (m
2/s). The values of
Re,
Sc, and
Pr numbers are calculated by Equations (19)–(21), respectively.
where
is the density of air (kg/m
3),
is the drying air velocity (m/s),
is the dynamic viscosity of air (Pa·s),
is the thermal conductivity of air (W/mK), and
is the specific heat capacity of air (J/kg·K).
3.4. Simulation Methodology
The simulation strategy for the model is represented in
Figure 3. COMSOL Multiphysics 6.0 (a finite element-based simulation software) was used to conduct the simulation. All the modelling steps consisting of developing geometry, meshing, physics specifying, solving, and the visualization of results were performed by the software. The simulation procedure was simplified considering the 2D axisymmetric mode. The model was built to predict the simultaneous heat–mass transfer process and shrinkage. The conservation of mass and energy were solved using the transport of dilute species and heat transfer in solids module, respectively. Moving mesh and solid momentum balancing were achieved using the Arbitrary–Lagrangian–Eulerian (ALE) framework and the Non-linear Solid Mechanics module to simulate deformation in COMSOL Multiphysics software. For the analysis of food shrinkage, the systems of partial differential equations were assigned to a time-dependent deformed mesh. The variation of the integration domain with time was described using the ALE method, which imparts structural shrinkage along with domain mesh movement [
42]. The ALE method applies a moving mesh to follow a simultaneous boundary change. More accurately, in the ALE approach, the problem domain coordinate system moves in a particular authorised way. This allows for the tracking of the boundary movement during the simulation, while the governing equations are solved on a fixed mesh [
43].
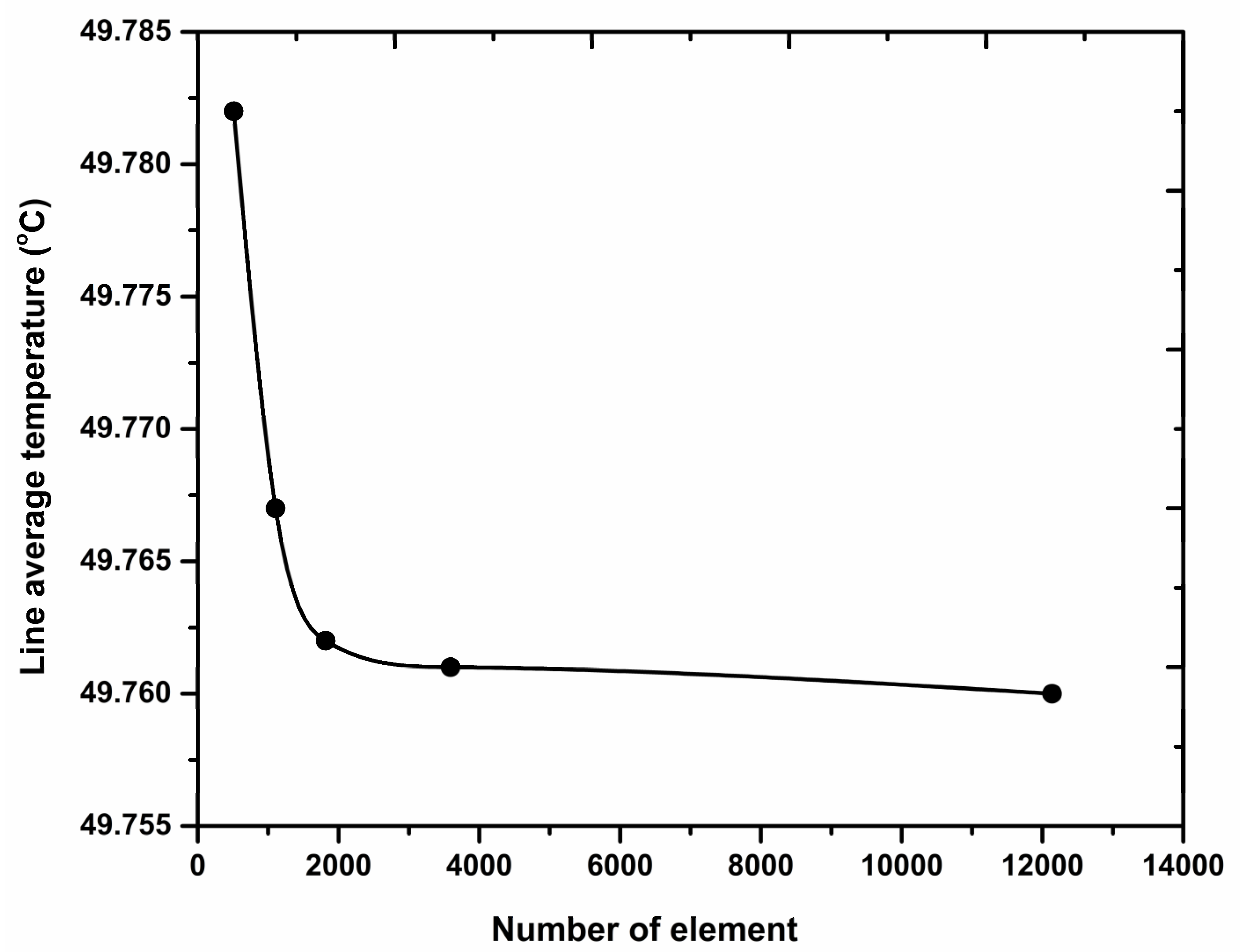
To conduct a mesh independence analysis, a grid sensitivity test was carried out. Five different mesh configurations were examined, with varying numbers of mesh elements: 512, 1104, 1816, 3592, and 12,136. The average temperature variations with respect to the number of mesh elements are depicted in
Figure 4. It can be observed that the average temperature exhibits significant variations up to 2000 elements, but reaches a temperature difference within an acceptable range after 4000 cells. This indicates that the simulation results are independent of the mesh density. A triangular grid was utilised to discretise the computational domain, with an average element quality of 0.9082.
The results from the energy and mass conservation using Equations (1) and (2), respectively, were employed to predict shrinkage, along with the application of Equation (4). The input parameters and variables were updated in the respective sections after each cycle if any changes were required. The time-dependent study was performed using an intel core i7 processor with 12 GB RAM workstation, employing a direct linear solver with a time step of 10 s up to 17,000 s.
4. Results and Discussion
4.1. Moisture Content and Distribution
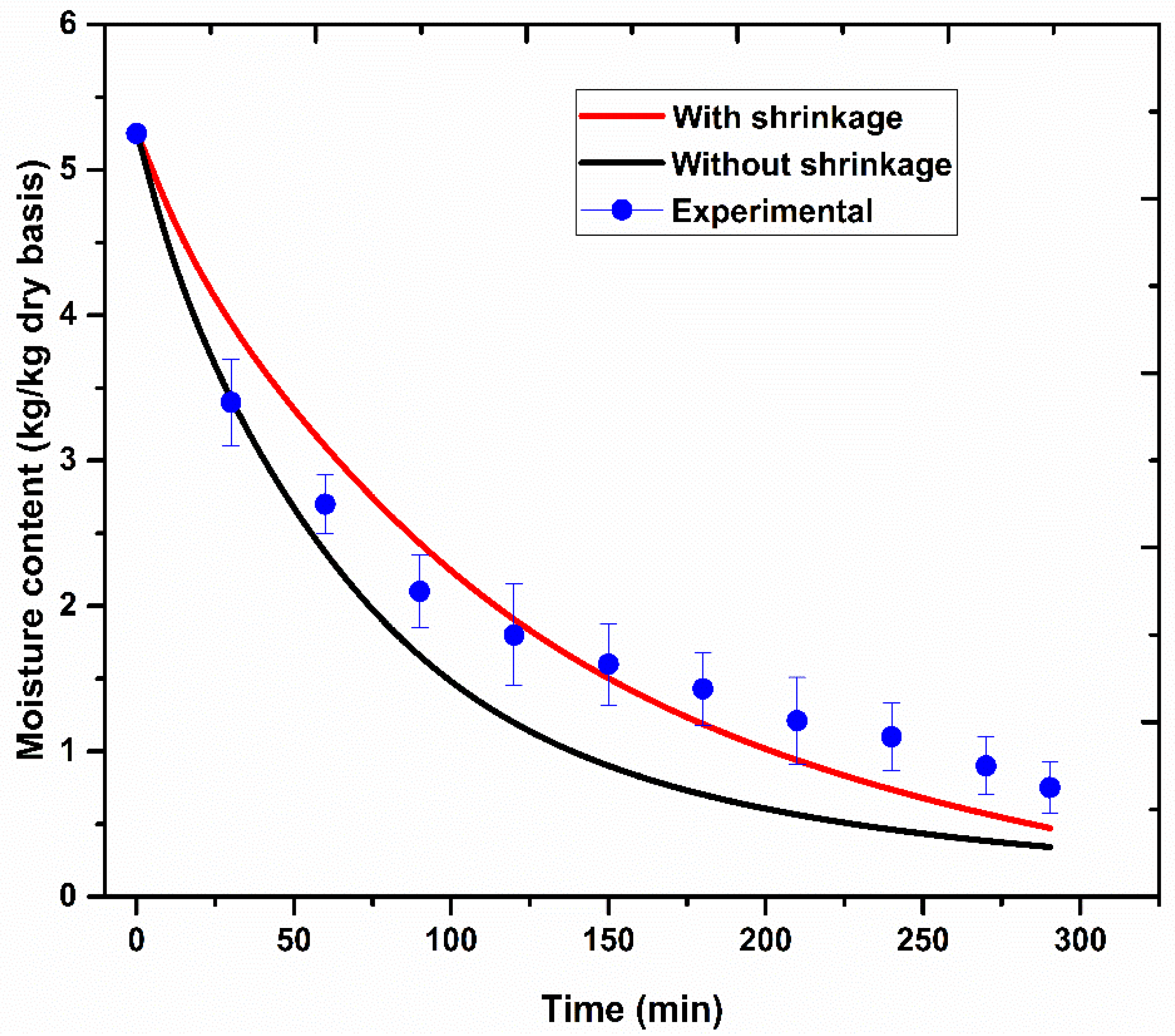
The comparison of simulated average moisture contents of jackfruit at 60 °C with experimental results is presented in
Figure 5. The simulation results for the drying kinetics with and without shrinkage phenomena have been compared.
From
Figure 5, it is clear that the moisture removal rate is higher in samples modelled without shrinkage compared to those modelled with shrinkage. The consideration of shrinkage effects allows the model to consider the surface area change of the sample, which results in a comparative reduction in the moisture removal rate with a smaller diffusion coefficient. Similar outcomes have been found during the convective drying of potato samples [
17]. Additionally, the lower temperature development in the shrinkage model compared to the model without shrink gave results that were lower in terms of moisture migration. The shrinkage induced model yielded 27.66% reduced moisture migration compared to the model without shrinkage.
Initially, the mass transfer rate was found to be higher for all the scenarios, whereas a reduced drying rate was found as soon as the first falling rate period started. This may be due to reduced heat flux and additional internal resistance with respect to the moisture migration [
30]. The rate falls again and shows values that are minimal at the second falling rate period of drying. A diffusion mechanism occurring due to the concentration gradient results in moisture migration from the sample interior sections to the surface. In the falling rate period, due to a lower moisture gradient and shrinkage, diffusion rate also decreases, resulting in longer drying periods. The accuracy of the model was determined based on the mean absolute error (MAE) and mean relative error (MRE) between the experimental and predicted results, as presented in
Table 3. It can be observed that the moisture content variations for the shrinkage-induced model are in good agreement with the experimental outcomes with a lower MAE value of 0.27 kg/kg dry basis compared to the model without shrinkage, which had an MAE value of 0.46 kg/kg dry basis, as shown in
Figure 5.
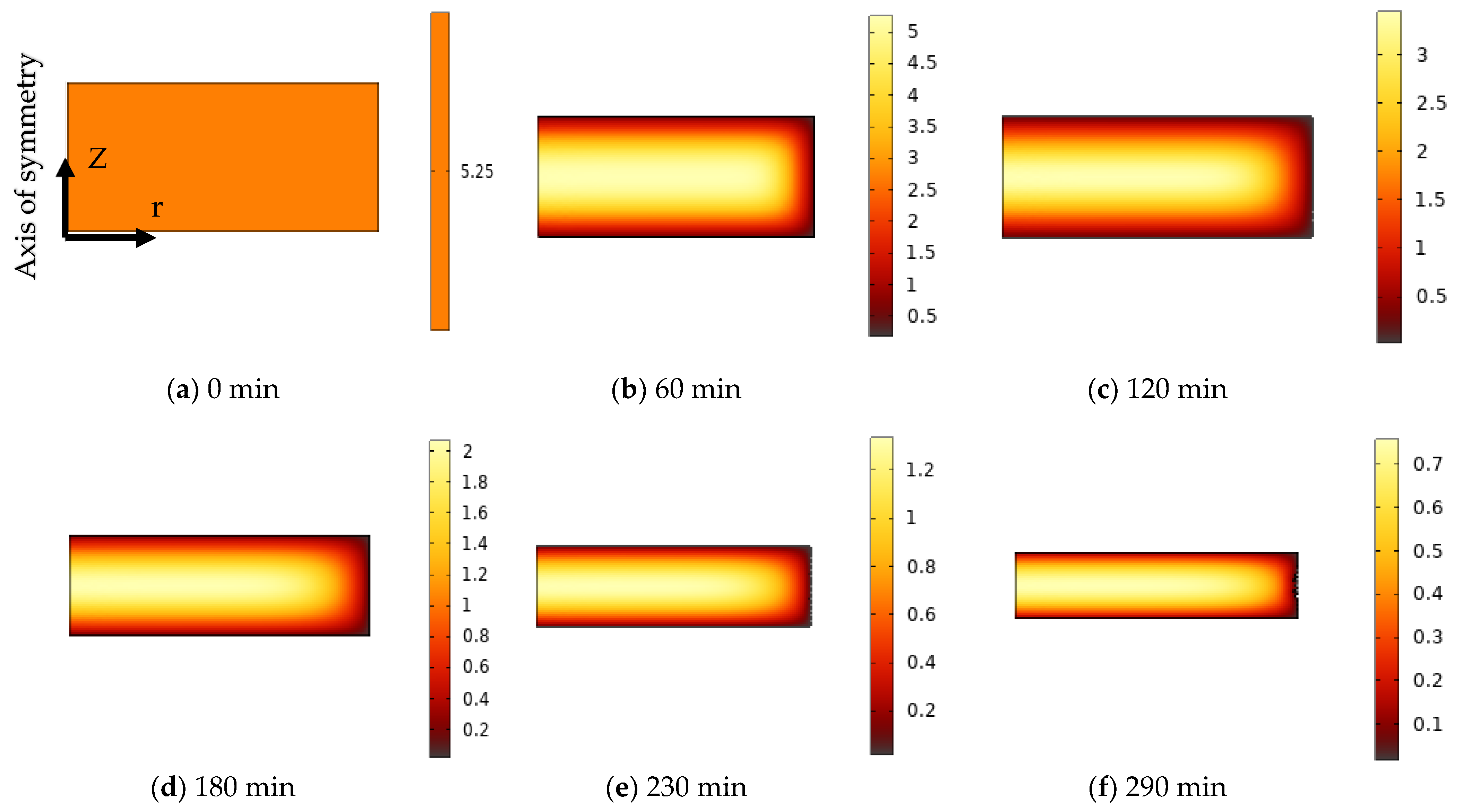
The axisymmetric moisture profiles to demonstrate the moisture variation between the core and surfaces along with shrinkage at different drying times are included in
Figure 6. It is clear that there is simultaneous area reduction with the loss of moisture content. At the same time, it can be found that uniform drying throughout the sample has not occurred since a considerable amount of moisture can be seen inside the sample; however, the exterior sections appear to be completely dried. This is because the moisture at the sample core needs to be dried for longer and consumes a higher amount of energy for migration compared to the moisture near the surfaces [
37].
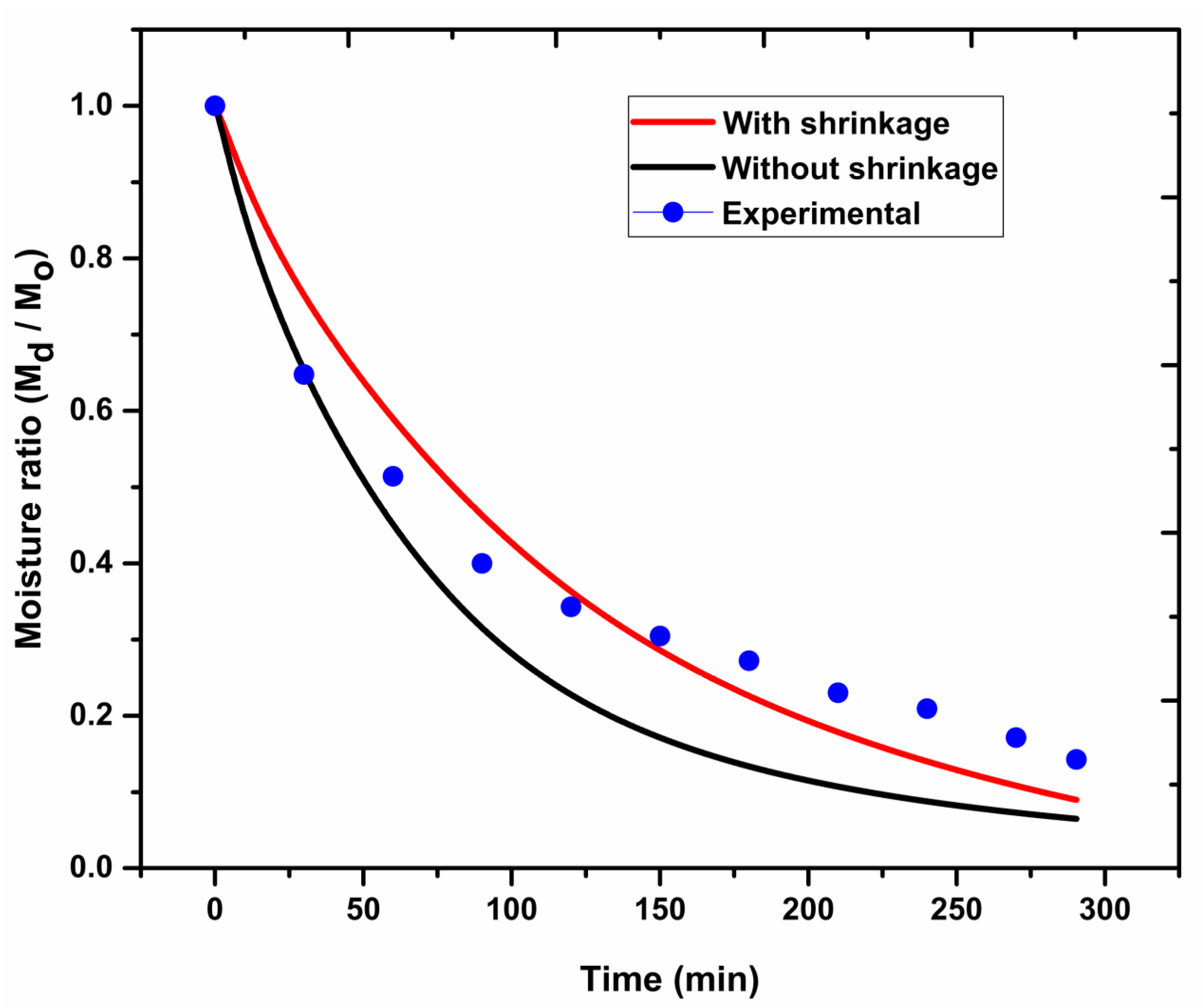
The comparative analysis of the moisture ratio variation with drying time among the model predictions and experimental results is represented in
Figure 7. The moisture ratio variation follows the similar trend of moisture content reduction, as shown in
Figure 5. The continuous moisture ratio reduction confirms that the internal mass transfer is governed by the diffusion process. It can be observed from
Figure 7 that, without the consideration of shrinkage, the model overpredicts moisture content at the later stages of drying. This can be attributed due to the assumption of constant diffusivity during drying.
Moisture ratio values are found to be 0.089 and 0.064 at the end of drying for the with and without shrinkage models, respectively. Similar moisture ratio variations can be found in the literature for different jackfruit drying processes, but all of these studies in which the different drying processes can be found have ignored the consideration of shrinkage [
23,
25].
4.2. Average Sample Temperature
The temperature profiles obtained from the models with and without the consideration of shrinkage phenomena are presented in
Figure 8, and a comparison is made with the experimental data. A rapid increase in temperature can be observed in the early drying stages. In the later periods, the process is almost steady, with a slower increase in temperature being observed. This is due to the diffusive mechanism of moisture migration among other reasons found in the literature [
17,
30].
It can be observed from
Figure 8 that the temperature rise is lower for the model with shrinkage compared to the model without shrinkage. Since there is no consideration of surface area changes in the without shrinkage model, higher heat and mass transfer takes place, resulting in the generation of higher temperatures. Due to lower moisture migration from the sample and the consideration of shrinkage phenomena, the model considering shrinkage predicts lower temperature values in comparison to the model without shrinkage. The model without shrinkage predicts temperature values that are 6.32% higher compared to those of the model with shrinkage. The validation of the temperature predictions was conducted through a comparison between the predicted and experimental values and the determination of statistical errors. The MAE values for the with and without shrinkage models were 2.07 and 2.93 °C, respectively. The shrinkage model also provided a good fit with the experimental outcomes, with 33.33% lower MRE value compared to the without shrinkage model. Hence, the shrinkage model more accurately matches the experimental outcomes compared to the model without shrinkage.
The prediction of temperature profiles from the simulation results at various drying times for the convective drying of jackfruit is depicted in
Figure 9. It can be found that the temperature predictions are always higher for the surface compared to the sample core. Since the surfaces are closely exposed to the drying environment, these sections experience faster drying rates, which results in higher moisture migration and temperature gain compared to the sample core.
It is worth noting that while non-Fickian and non-Fourier approaches may better capture the complexity of the physical phenomena, they are outside of the scope of this current model. The focus of our model is on a simplified representation of the system that can be applied more easily in practical applications. Incorporating non-Fickian and non-Fourier approaches may introduce additional complexities that are not required for the model’s current intended application.
4.3. Shrinkage Profile
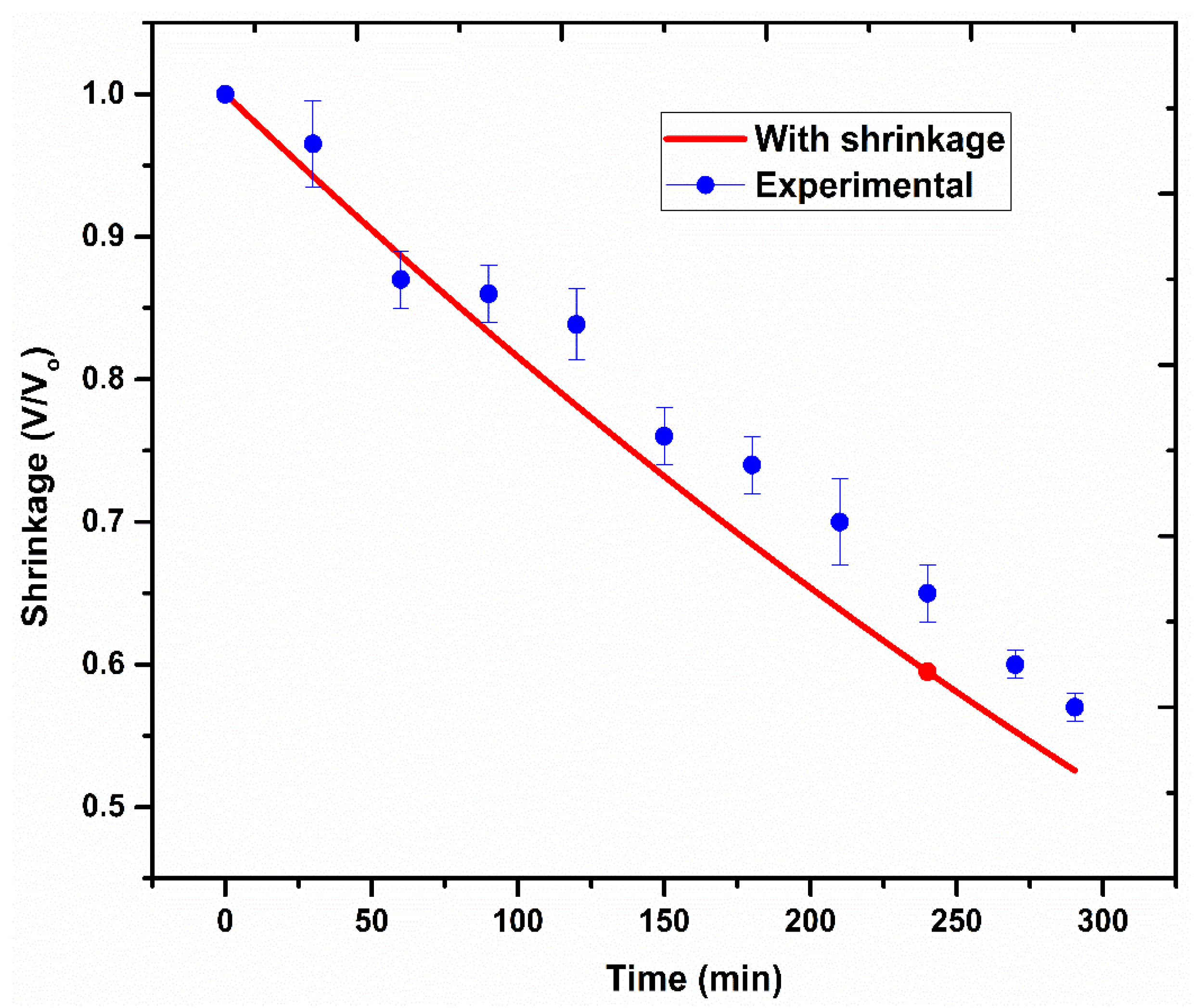
The shrinkage profile of jackfruit with respect to time is represented in
Figure 10. It can be observed that the sample shrinkage almost linearly correlates with drying time. A similar situation was observed during the drying of potato samples [
17]. The tissue structure deforms due to the disturbance of the mechanical equilibrium of the cell walls (initially by the moisture removal from the surface pores of the sample). The exterior tissue cell walls undergo tension due to the formation of void spaces, whereas the interior cell walls stay intact, causing shrinkage due to inward contractions moving toward the sample centre. Uniform shrinkage may occur when the velocity of moisture migration is equal to the shrinkage velocity, as found in
Figure 10. The shrinkage value reduces from 1 to 0.53 after 300 min of drying. The lower values of MAE and MRE of 0.04 and 0.05, respectively, for shrinkage (
Table 3) represent good agreement between the predicted and experimental results.
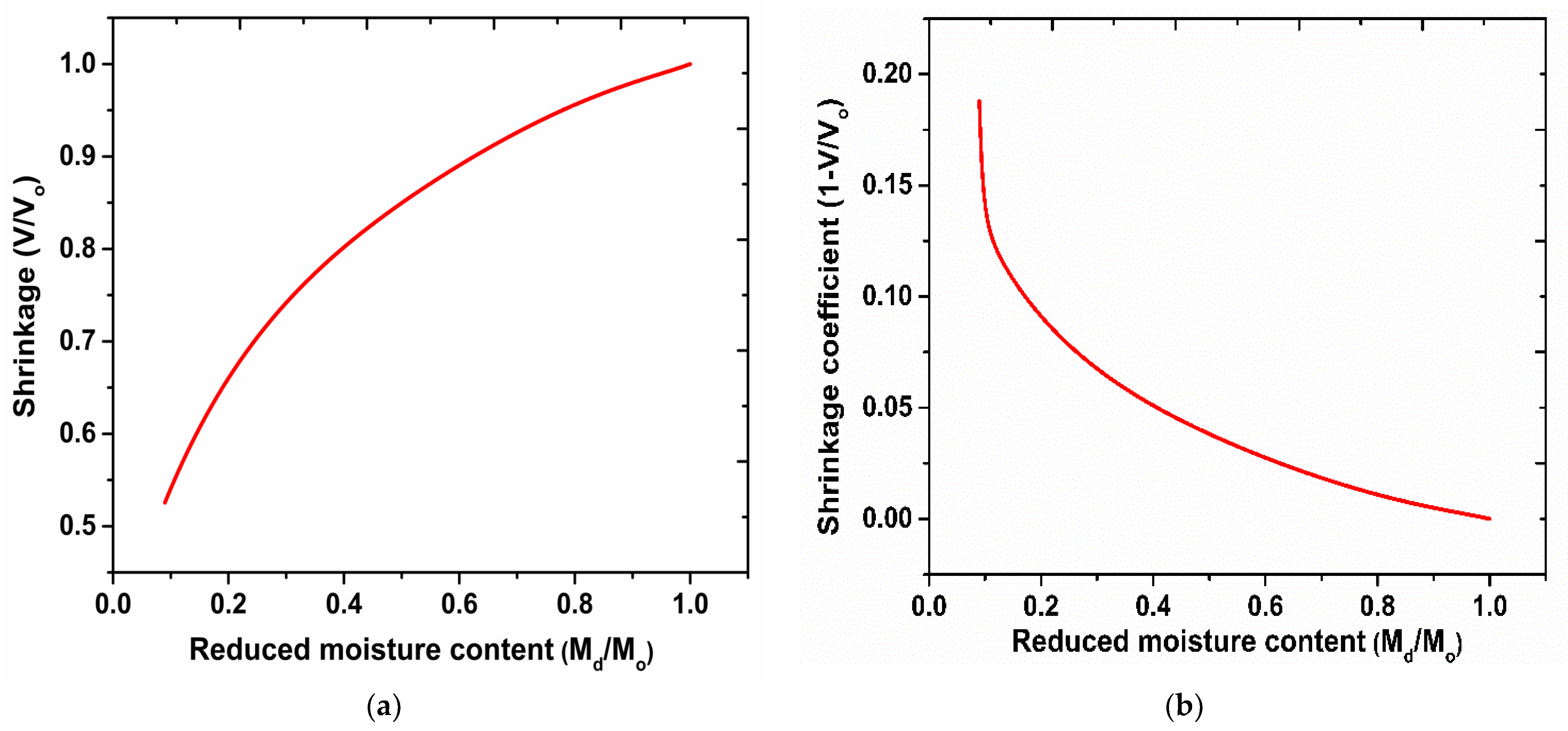
The variation of shrinkage (volume ratio) and shrinkage coefficient with reduced moisture content are shown in
Figure 11a,b, respectively. Moisture loss significantly influences the nature of shrinkage curves. The reduction in volume ratio (V/V
o) with reduced moisture content for jackfruit can be found in
Figure 11a.
On the contrary, shrinkage coefficient increases with the diminution of reduced moisture content. These results may be due to the lowering of the drying rate at low temperatures. Additionally, the deformation rate is comparatively slow because of the case-hardening phenomena occurring at the later drying periods, which results in the complete drying of the outer surfaces; however, the interior portions still contain lots of moisture.
It is worth noting that both models did not fully predict the moisture and temperature behaviour observed in the experiments. This discrepancy can be interpretated as follows: The overprediction of moisture content by the model without shrinkage is due to the assumption of constant diffusivity during drying. On the other hand, the underestimation of moisture content by the shrinkage model at longer drying times could be attributed to the assumption of constant shrinkage rate. The switching behaviour of the shrinkage model around 100 min may be caused due to this constant shrinkage velocity.
The accuracy of the model can be improved by considering the time-dependent diffusivity and shrinkage rate, as well as accounting for other non-Fickian and non-Fourier effects. Moreover, multiphase and multiscale modelling approaches can improve the simulation result. This is something which the authors’ research group is currently working towards.
5. Conclusions
The present study develops a shrinkage model considering the shrinkage velocity approach for the prediction of drying kinetics along with shrinkage phenomena during the convective drying of jackfruit. The model validation was performed through comparison between the predicted and experimental results in terms of temperature, moisture content, and shrinkage, and model accuracy was determined by statistical error analysis. Throughout the total drying time, the moisture content reduced from 5.25 kg/kg dry basis to 0.47 kg/kg dry basis, with a temperature generation of up to 54 °C for the shrinkage-induced model. On the other hand, the model without shrinkage provided a moisture content reduction of up to 0.34 kg/kg dry basis with a maximum temperature gain of 57 °C. The consideration of surface area changes in the shrinkage-induced model provided lower moisture migration and temperature distribution compared to the model without shrinkage. A linear trend of shrinkage variation with dying time was observed from the model outcomes. The correlation with reduced moisture migration is also presented. The shrinkage-induced model provided better agreement with low MAE values of 0.27 kg/kg dry basis for moisture content, 2.07 °C for temperature variation, and 0.04 for shrinkage, respectively, compared to the model without shrinkage. It should be noted that shrinkage greatly influences the drying kinetics; therefore, it cannot be neglected when modelling dying phenomena. Since no previous studies have reported such theoretical shrinkage model outcomes for jackfruit, the results of this research will provide further recommendations and ideas for industrial jackfruit drying and could be used as a robust tool for the proper selection of drying conditions to optimise the drying process.