Cluster Partition-Based Voltage Control Combined Day-Ahead Scheduling and Real-Time Control for Distribution Networks
Abstract
1. Introduction
- (1)
- A coupling quality function is proposed as the cluster index of DNs, which can describe the electrical coupling degree among nodes. Additionally, based on the community-finding algorithm, a fast cluster partition algorithm is proposed to divide the PVs into a number of clusters.
- (2)
- Based on the cluster partition, a DAS strategy is proposed for the OLTC and PV inverters, which is optimized with the objective of minimizing the operation costs of each cluster.
- (3)
- Based on the cluster partition, an SOCP-based model for the RTVC strategy is drawn up in each cluster. Additionally, the RTVC strategy can correct the day-ahead scheduling with the objective of minimizing the output deviation of PVs from the day-ahead scheduling.
2. Coupling Quality Function-Based Cluster Partition Method
2.1. Coupling Quality Function of Cluster Partition
- (1)
- Inner Density Index:where T is the total number of clusters. πα is the α-th cluster. N represents the number of nodes in the DN. Nα is the number of nodes in the α-th cluster. Aij is the power–voltage sensitivity weight between node i and node j. Aij can describe the coupling quality between node i and node j. Aij can be obtained as follows:where , , and represent the ij-th and ji-th elements of matrix ZQU, respectively. ZQU can be obtained from the Jacobian matrix [14,15]:where Δδ is the matrix of variation in phase angle. ΔU is the matrix of variation in voltage magnitude. ZPδ and ZQδ represent the sensitivity matrix of the phase angle to active and reactive power injection, respectively. ZPU and ZQU represent the sensitivity matrix of the voltage magnitude to active and reactive power injection, respectively. ΔP and ΔQ represent the matrix of variation in active and reactive power injection.
- (2)
- Outer Density Index:
2.2. Fast Cluster Partition Strategy
3. The Model of the DAS Strategy
3.1. Objective Function
3.2. Constraints of the DAS Strategy
- (1)
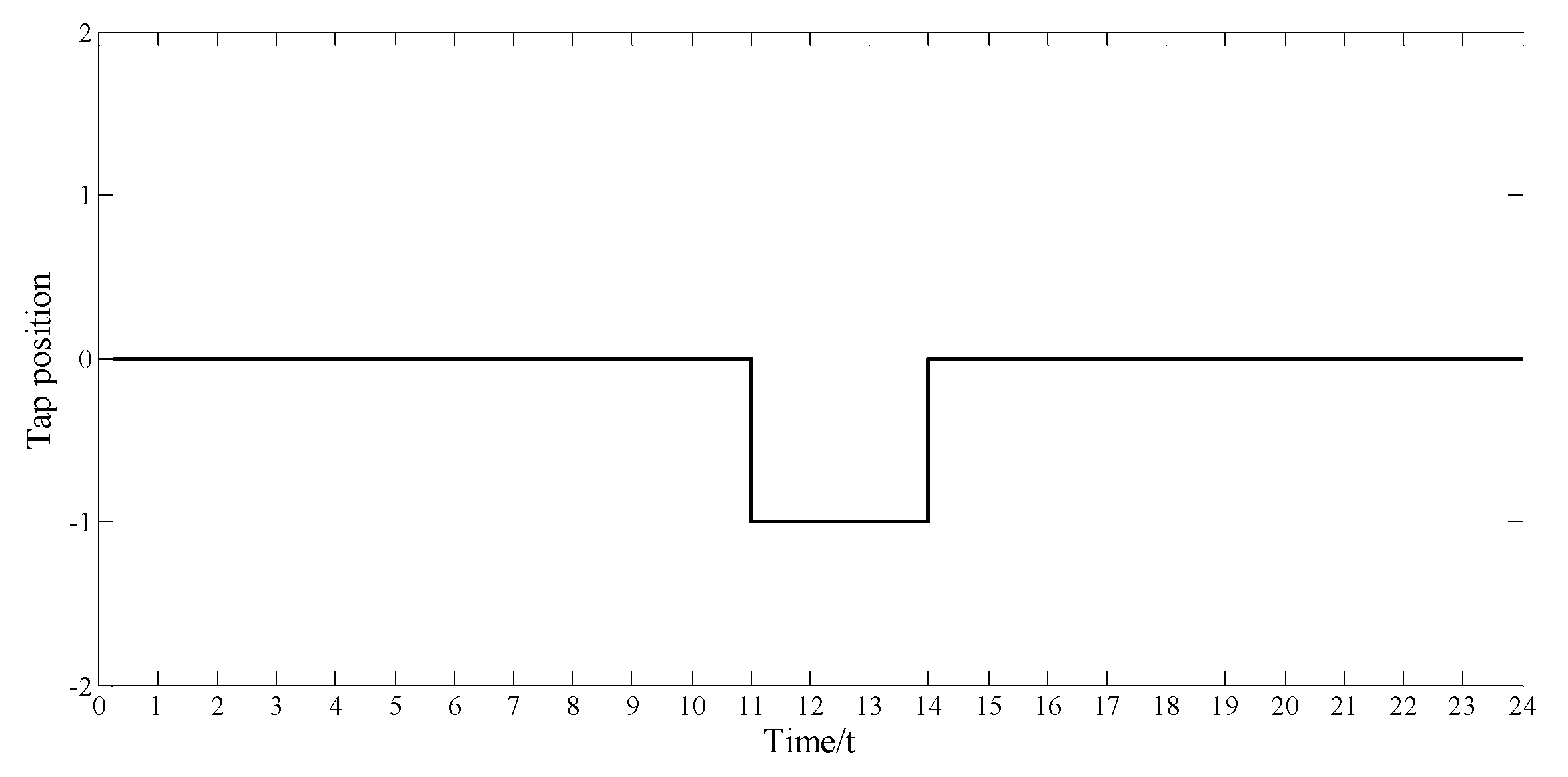
- OLTC constraints:where Equation (10) denotes the limit of the number of tap changes for the OLTC. Equation (11) denotes the tap-position limits of the OLTC. is the number of tap changes allowed in a day. and represent the minimum and maximum tap position of the OLTC, respectively.
- (2)
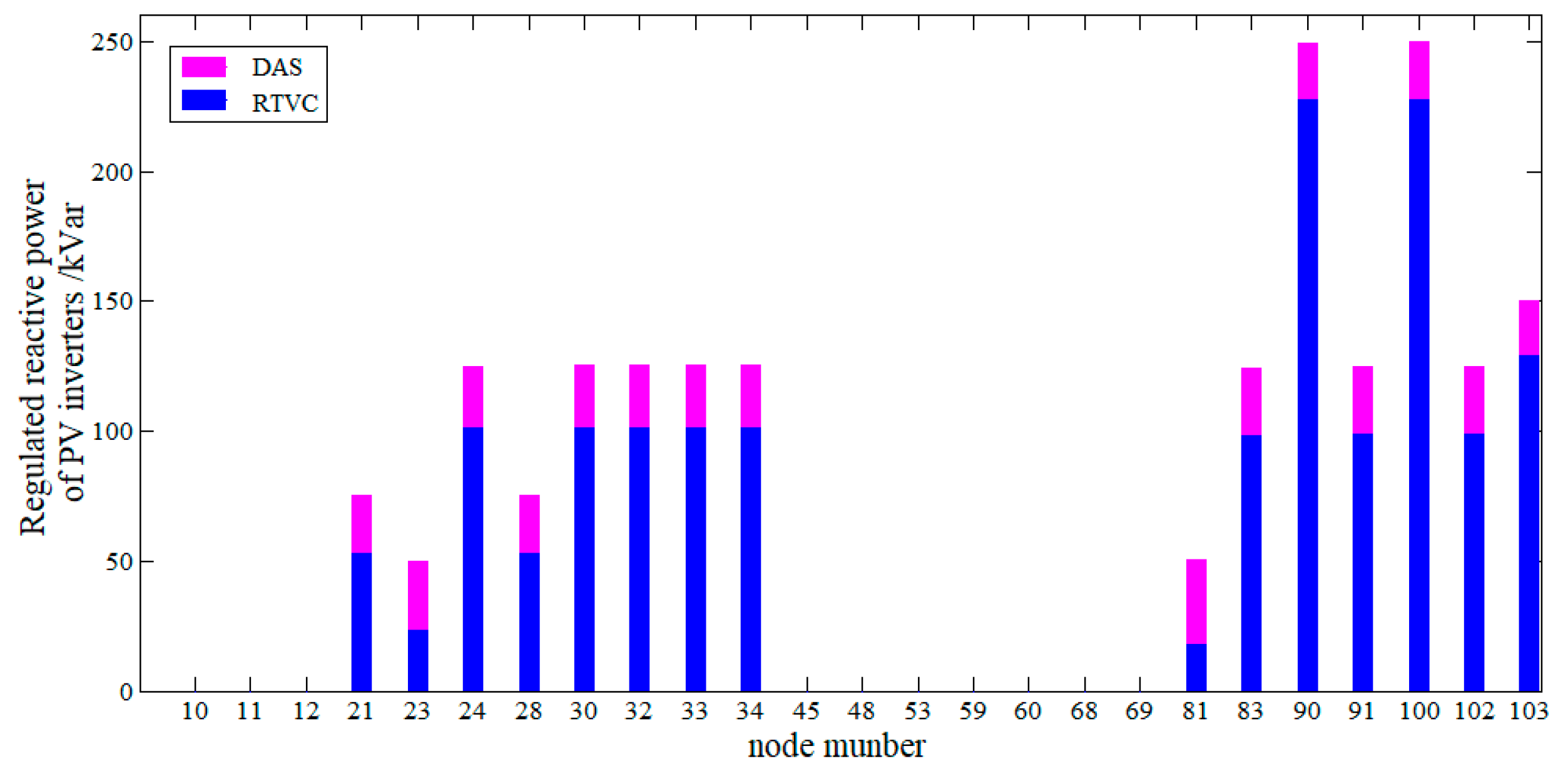
- PV constraints:where Equation (12) denotes the PV output limits. Equation (13) denotes the power factor limits of PV inverters. Equation (14) denotes the regulated reactive power limits of PV inverters. is the predicted PV outputs at node j at time t. represents the maximum allowable regulated reactive power of PV inverter at i-th node.
- (3)
- Network constraints:where Equation (15) represents the active power balance constraints. Equation (16) is the reactive power balance constraints. Equation (17) is the nodal voltage relationship limits. Equation (18) is the nodal voltage magnitude limits. and are the demands of active power and reactive power at node j at time t, respectively. Pij,t and Qij,t are the active power and reactive power through line i–j at time t, respectively. Ui,t is the voltage-magnitude at node j at time t. xij is the reactance in line i–j. Φ(j) is the child bus set of node j. Λ(j) is the parent bus set of node j. To solve the proposed model, the improved particle swarm optimization algorithm (IPSO) is utilized to carry out the optimization; the detailed introduction of IPSO can be found in [19].
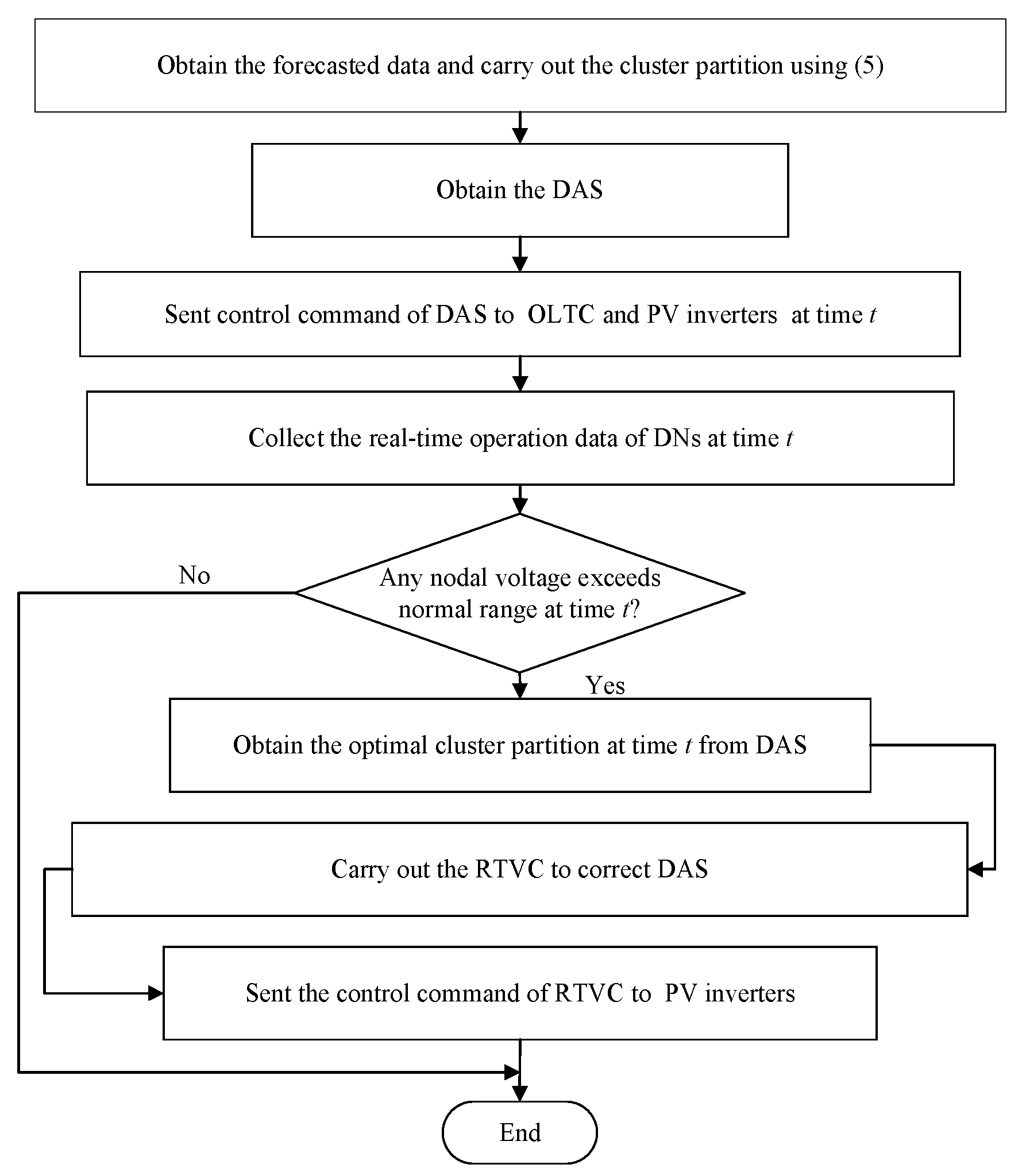
4. DAS Combined RTVC Strategy
4.1. The Model of RTVC Strategy
4.2. Implement of the DAS Combined RTVC Strategy
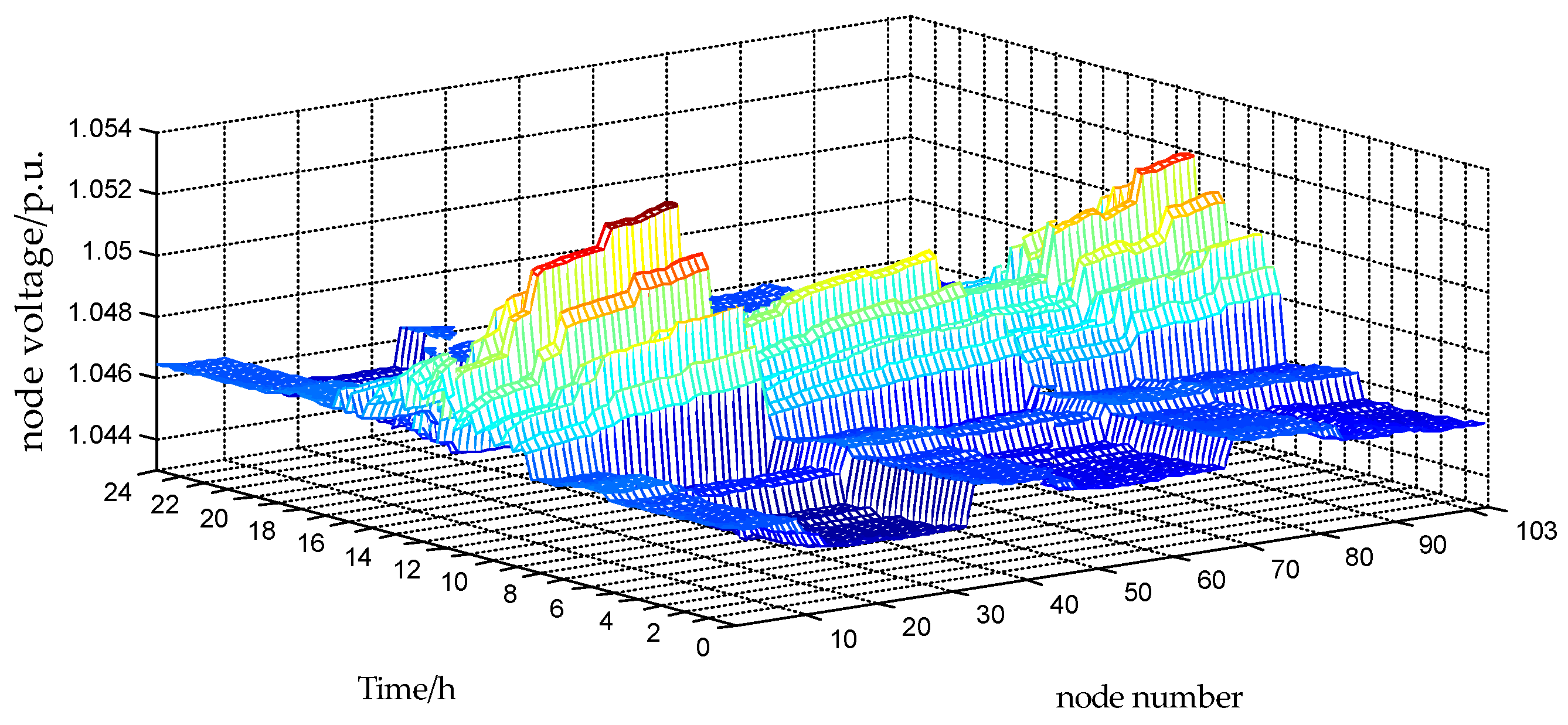
5. Case Study
5.1. Case Study System
5.2. Cluster Partition for the Feeder
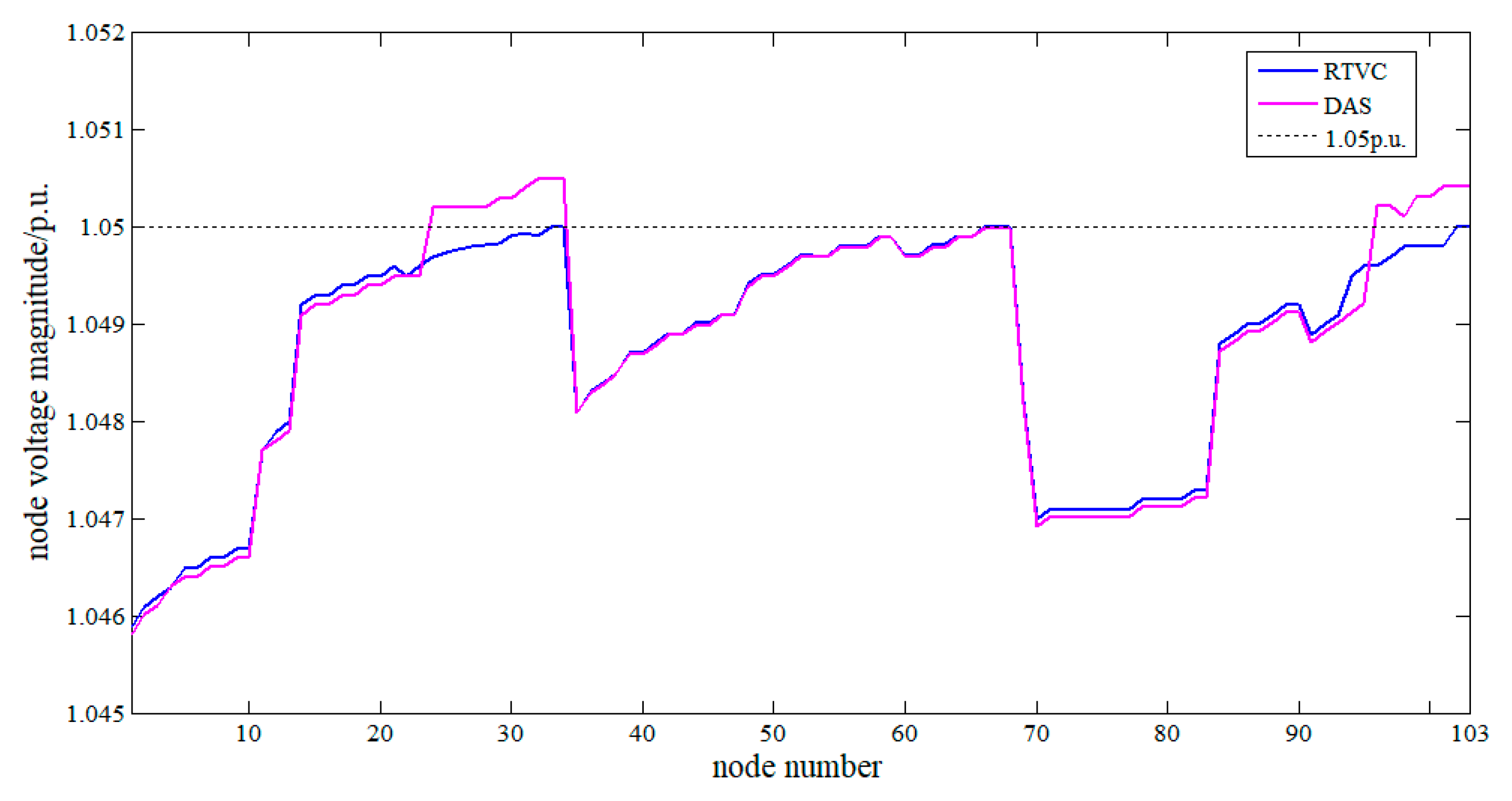
5.3. DAS Combined RTVC Strategy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Confrey, J.; Etemadi, A.; Stuban, S.M.F.; Eveleigh, T.J. Energy Storage Systems Architecture Optimization for Grid Resilience with High Penetration of Distributed Photovoltaic Generation. IEEE Syst. J. 2020, 14, 1135–1146. [Google Scholar] [CrossRef]
- Koutsoukis, N.; Georgilakis, P.; Hatziargyriou, N. Multistage coordinated planning of active distribution networks. IEEE Trans. Power Syst. 2018, 33, 32–44. [Google Scholar] [CrossRef]
- Li, Z.; Wu, L.; Xu, Y. Temporally-coordinated optimal operation of a multi-energy microgrid under diverse uncertainties. Appl. Energy 2019, 240, 719–729. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Y.; Wang, S.; Liang, D.; Zhao, Q.; Zhao, X. Voltage Regulation Strategy for DC Distribution Networks Based on Coordination of Centralized Control and Adaptive Droop Control. IEEE Trans. Power Deliv. 2022, 37, 3730–3739. [Google Scholar] [CrossRef]
- Afandi, I.; Agalgaonkar, A.; Perera, S. Integrated Volt/Var Control Method for Voltage Regulation and Voltage Unbalance Reduction in Active Distribution Networks. Energies 2022, 15, 2225. [Google Scholar] [CrossRef]
- Hu, K.; Yin, R.; Shi, M. Distributed Photovoltaic Cluster Partition and Reactive Power Optimization Strategy Based on Improved Particle Swarm Optimization Algorithm. Power Capacit. React. Power Compens. 2021, 42, 14–21. [Google Scholar]
- Dou, B.; Chang, M.; Ni, H.; Duan, M.; Ge, D.; Wu, J. Multi-level Dispatching and Control of Active Distribution Network for Virtual Cluster of Distributed Photovoitaic. Autom. Electr. Power Syst. 2018, 42, 21–31. [Google Scholar]
- Bi, R.; Liu, F.; Ding, M.; Fang, H.; Zhang, J.; Chen, F. Renewable Energy Generation Cluster Partition Method Aiming at Improving Accommodation Capacity. Proc. CSEE 2019, 39, 6583–6592. [Google Scholar]
- Yan, D.; Cai, H.; Sha, J.; Lv, P.; Xu, Z. Distribution Network Cluster Division and Voltage Control with High Proportion of New Energy Access. Power Demand Side Manag. 2021, 23, 8–13. [Google Scholar]
- Chai, Y.; Liu, X.; Wang, S.; Guo, L.; Zhao, Z.; Gao, S. Coordinated voltage control for dis-tributed pvs clusters with incomplete meas-urements. Proc. CSEE 2019, 39, 2202–2212. [Google Scholar]
- Wei, B.; Qiu, Z.; Deconinck, G. A mean-field voltage control approach for active distribution networks with uncertainties. IEEE Trans. Smart Grid 2022, 12, 1455–1466. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Danon, L.; Díaz-Guilera, A.; Arenas, A. The effect of size heterogeneity on community identification in complex networks. J. Stat. Mech. Theory Exp. 2006, 11, P11010. [Google Scholar] [CrossRef]
- Xiao, C.; Sun, L.; Ding, M. Multiple Spatiotemporal Characteristics-Based Zonal Voltage Control for High Penetrated PVs in Active Distribution Networks. Energies 2020, 13, 249. [Google Scholar] [CrossRef]
- Xiao, C.; Ding, M.; Sun, L.; Chung, C.Y. Network partition-based two-layer optimal scheduling for active distribution networks with multiple stakeholders. IEEE Trans. Ind. Inform. 2021, 17, 5948–5960. [Google Scholar] [CrossRef]
- Cohen, J. Graph Twiddling in a map reduce World. Comput. Sci. Eng. 2009, 11, 29–41. [Google Scholar] [CrossRef]
- Li, Z.; Wu, L.; Xu, Y. Risk-Averse Coordinated Operation of a Multi-Energy Microgrid Considering Voltage/Var Control and Thermal Flow: An Adaptive Stochastic Approach. IEEE Trans. Smart Grid 2021, 12, 3914–3927. [Google Scholar] [CrossRef]
- Li, Z.; Wu, L.; Xu, Y.; Moazeni, S.; Tang, Z. Multi-Stage Real-Time Operation of a Multi-Energy Microgrid with Electrical and Thermal Energy Storage Assets: A Data-Driven MPC-ADP Approach. IEEE Trans. Smart Grid 2022, 13, 213–226. [Google Scholar] [CrossRef]
- Xiao, C.; Zhao, B.; Ding, M.; Li, Z.; Ge, X. Zonal voltage control combined day-ahead scheduling and real-time control for distribution networks with high proportion of PVs. Energies 2017, 10, 1464. [Google Scholar] [CrossRef]
- Li, J.; Yang, H. Research on realization and comparison of community division algorithms in network. Comput. Digit. Eng. 2019, 47, 2861–2865. [Google Scholar]






| Cluster | Coupling Quality Function | Modularity Function |
|---|---|---|
| π1 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 |
| π2 | 16, 17, 18, 19, 20, 21, 22, 23, 24 | 12, 13, 14, 15 |
| π3 | 25, 26, 27, 28, 29, 30, 31, 32, 33, 34 | 17, 18, 19, 20, 21, 22, 23, 24 |
| π4 | 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48 | 16, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34 |
| π5 | 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 | 35, 36, 37, 38, 39, 40 |
| π6 | 61, 62, 63, 64, 65, 66, 67, 68, 69 | 41, 42, 43, 44, 45, 46, 47, 48 |
| π7 | 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83 | 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 |
| π8 | 84, 85, 86, 87, 88, 89, 90, 91 | 61, 62, 63, 64, 65, 66, 67, 68, 69 |
| π9 | 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103 | 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84 |
| π10 | 85, 86, 87, 88, 89, 90, 91, 92, 93 | |
| π11 | 94, 95, 96, 97, 98, 99, 100, 101, 102, 103 | |
| Total regulation cost (USD) | 927.12 | 1241.47 |
| Case | Reactive Power of PV Inverters | Active Power Curtailments of PVs | Tap Position of OLTC | Time |
| CVC method | 2765.34 kVar | 328.56 kW | Change 6 times | 89.63 s |
| Proposed method | 1599.67 kVar | 445.24 kW | Change 2 times | 9.86 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; He, G. Cluster Partition-Based Voltage Control Combined Day-Ahead Scheduling and Real-Time Control for Distribution Networks. Energies 2023, 16, 4375. https://doi.org/10.3390/en16114375
Sun W, He G. Cluster Partition-Based Voltage Control Combined Day-Ahead Scheduling and Real-Time Control for Distribution Networks. Energies. 2023; 16(11):4375. https://doi.org/10.3390/en16114375
Chicago/Turabian StyleSun, Wenwen, and Guoqing He. 2023. "Cluster Partition-Based Voltage Control Combined Day-Ahead Scheduling and Real-Time Control for Distribution Networks" Energies 16, no. 11: 4375. https://doi.org/10.3390/en16114375
APA StyleSun, W., & He, G. (2023). Cluster Partition-Based Voltage Control Combined Day-Ahead Scheduling and Real-Time Control for Distribution Networks. Energies, 16(11), 4375. https://doi.org/10.3390/en16114375







