1. Introduction
As a necessary means towards carbon-neutral energy systems, power systems operation is undergoing a paradigm shift. More devices are becoming electrified, e.g., vehicles and heating devices; the uptake of distributed generation (DG) is increasing; and demand-side flexibility is attracting increasing attention in providing flexibility services for power system operation [
1]. These developments are leading to changes in consumption and production patterns, which might stress the low-voltage (LV) distribution power systems that were originally not designed for these conditions. Meanwhile, operational observability in LV grids is generally nonexistent or very low. As a result, to ensure the reliable operation of grids, distribution system operators (DSOs) require techniques to improve grid observability.
Although smart meters are being installed on a large scale in Europe, they offer limited potential for improving the observability of distribution grids. In [
2], the authors state that it is not the smart meters that carry the largest cost but rather the required communication infrastructure. Moreover, smart meter communication systems could be subject to cyber-attacks; data are often delayed and not available in near-real time (e.g., residential smart meters that collect data only once a day) and have a slower sampling frequency than phase measurement units (PMUs). Hence, to infer the values of the system’s state variables using a limited number of data, distribution system state estimation (DSSE) is required.
While state estimation is common practice in transmission grids, some factors complicate the application of the same state estimation methods in distribution grids, such as low X/R ratios, unbalanced operation, and fast changes in the configuration of distribution grids [
3]. Thus, new methods are proposed in the literature for DSSE that can be categorized from different viewpoints. In general, DSSE problems are voltage-based or branch-current-based. The main focus of this paper is on voltage-based methods. However, several branch-current-based studies can be found in the literature, e.g., [
4,
5,
6].
Among voltage-based DSSE methods, many studies try to apply or modify the weighted least square (WLS) approach as the most commonly used method in transmission system state estimation [
7] for DSSE. For instance, Lin et al. [
8] proposed a fast decoupled DSSE method taking into account the virtual measurements, i.e., perfect information about the grid, as an equality constraint in the problem formulation. A penalty factor was defined and added to the standard WLS problem that enforces satisfaction of this equality constraint. This method needs no assumptions about voltage magnitudes and phase angles. Chen et al. [
9] proposed a methodology for DSSE in cases where only the aggregated data of smart meters are available in order to respect the customers’ privacy. The variance of the smart meters’ measurement errors was used to construct the weight matrix in the WLS optimization problem. A power flow analysis was performed to create time series of active and reactive power data for the study. The problem of DSSE for areas with high numbers of electric vehicles (EVs) was addressed by Nie et al. [
10]. To provide more reliable and accurate results, a new quasi-Newton method was used to solve the WLS problem. The effectiveness of the method was evaluated by applying it to the IEEE 14-bus and 30-bus test systems using real travel survey statistics and base load records. Simulation results showed better performance of the proposed method than standard WLS and extended Kalman filter methods, especially when the number of EVs increased. The DSSE solvers of the WLS problems may face the issue of numerical instability and high sensitivity to the choice of initial values. To address this issue, Yao et al. [
11] proposed a semi-definitive programming (SDP) approach for the DSSE problem obtained by convex relaxation of the original WLS problem. The method was evaluated by applying it to IEEE 13-bus, 34-bus, and 123-bus test systems. Similarly, Zhu et al. [
12] proposed a distributed SDP approach to formulating the DSSE problem, which can be used for areas with several DSOs and minimal data exchange among DSOs due to data confidentiality concerns.
WLS-based approaches are fast and simple, but they could be susceptible to bad data [
3]. This has led to the introduction of robust state estimation approaches. Some research papers upgrade the WLS-based approaches to improve the robustness of state estimation. For instance, Wu et al. [
13] developed a DSSE method for a grid with limited real-time measurements or with delayed information from smart meters. To provide robust results, a machine learning approach was used to create inputs for the weight matrix of the WLS problem in the state estimator. The test data were generated using power flow analysis at each time interval, and then errors were intentionally added to the system to simulate different measurement errors. Simulation results confirm the robustness of the results against the measurement errors; the type, location, and accuracy of measurements; and the temporary failure of the communication system. Liu et al. [
14] proposed a methodology based on the matrix completion approach to perform a robust DSSE. The matrix completion approach uses the known elements in the matrix to estimate the missing elements by solving a rank minimization problem. In the proposed approach, system information is used to form the system state–measurement matrix. The distribution grid model and Ohm’s law are added to the rank minimisation problem as constraints. A decentralized PMU-based robust state estimation method for distribution grids, including a utility grid and several micro-grids, was introduced by Lin et al. [
15]. The state estimation problem was formulated as a quadratic optimization problem for the utility grid and micro-grids. Each micro-grid was assumed to be responsible for evaluating its bad data measurements and an iterative algorithm with minimum data exchange between operators was proposed to perform robust DSSE. Fast convergence and scalability are the two main features of this method. Dahale et al. [
16] proposed robust formulations for four sparsity-based DSSE approaches (1) 1-D compressive sensing, (2) 2-D compressive sensing, (3) matrix completion, and (4) tensor completion. Simulation results highlight the great performance of compressive-sensing-based approaches compared to tensor completion and matrix completion methods. Furthermore, Raghuvamsi et al. [
17] developed a data-driven denoising autoencoder approach for their DSSE model that is robust to false data injection attacks. Their model showed improvements compared to other denoising autoencoder approaches and was able to identify the location of the false data injection and replace the measurements.
Data-driven methods are one of the most recently introduced approaches in DSSE. These methods can be an auxiliary tool in solving the DSSE problem, such as using a neural network (NN) method to generate initial points to solve the main optimization problem [
18] or applying machine learning to exploit pseudo-measurements (i.e., artificial measurements, typically acquired from another model or simulated data) [
19]. Data-driven approaches could also be used to solve the DSSE problem. NN is one of the most common data-driven approaches for DSSE [
20,
21,
22]. Kim et al. [
20] introduced a modified long short-term NN for state estimation in hybrid DC/AC distribution grids. Zamzam et al. [
21] proposed a NN method that utilizes the structure of the power grid for DSSE. The proposed architecture reduces the number of coefficients required for mapping from the measurements to the network state, which prevents overfitting and reduces the complexity of the training stage. Among other data-driven approaches, Weng et al. [
23] introduced a data-driven DSSE approach that uses the power system patterns and physics to clean data. Supervised learning was used to learn the relationship between the measurement and the system’s state using historical data. Moreover, an approach was suggested to speed up the estimation by 1000 times. To benefit from the advantages of both data-driven and classical methods, Anubi et al. [
24] proposed an enhanced resilient DSSE algorithm, which combines a data-driven model with the compressive sensing regression method. Using this algorithm helps the system estimator to recover the true state of the system if faced with false data injection attacks, which mislead regression-based algorithms.
Although the abovementioned studies have covered a wide range of issues and solutions for DSSE, it is worth noting that all these studies are focused on medium-voltage (MV) distribution grids, i.e., voltage levels higher than 0.4 kV. Low-voltage (LV) distribution grids, i.e., 0.4 kV, have characteristics that make them different from MV grids. For instance, LV systems are typically more unbalanced than MV systems. Since customer loads are connected to different phases, uneven load distribution between the phases often arises, marking the need for per-phase voltage estimations. Moreover, MV loads are not as volatile as the aggregate customer loads from the connected LV networks, resulting in lower load variance, supposedly easier to estimate. Additionally, there are DSSE methods for MV distribution grids that rely on more measurements than those that are practically feasible in LV networks. Hence, new methods must be developed for state estimation in LV systems. With this in mind, it is worth mentioning that the authors in [
25] developed an NN approach to estimate voltages in a 0.4 kV distribution grid. However, it seems that the method is developed based on confidential customer data, and it could be questioned whether these data inputs should be used for operational purposes. Meanwhile, the reported root mean squared error (RMSE) is 0.59 V and the method requires retraining after 20 days. In [
26], the authors derive a method for voltage control in LV grids with high levels of photovoltaic (PV) system uptake, including a remote voltage estimation technique. However, the method relies on the load estimations of customers and the number of customers to produce a generic feeder and is rather designed for voltage control in networks with on-load-tap-changers, limiting the applicability in the context of this study. Mokaribolhassan et al. [
27] developed a DSSE method using the augmented complex Kalman filter, also in a power system with PV systems. However, the authors here apply a technique where they separate the PV generation from the customer loads. Testing their model on one month of data for one LV feeder, the authors obtain a mean average error of 0.3% in their simulated studies. Furthermore, in [
28], a remote voltage estimation method for radial LV grids is developed, combining a series of power flow calculations and polynomial regression. While the model shows good accuracy, it relies on pseudo-measurements, which can complicate the required retraining of the model; hence, applicable and relevant pseudo-measurements need to be ensured. The model is also tested based on simulated data, and the computation time to fit the model is 0.79 h.
Our comprehensive literature review of DSSE shows that methods for estimating remote voltages in radial LV grids are scarce, as opposed to the many methods found for MV grid DSSE. Furthermore, it would be advantageous in the DSO grid operation to have methods that place an emphasis on providing an estimation of the error components of the model, whereas most methods in the literature focus on mean value prediction. Methods with higher accuracy and a lower computational burden are also crucial for the DSOs to fully realize remote voltage estimation techniques for grid operation. In addition, methods relying on a few measurements that are based on and validated for real-world data are needed. In light of this, the present paper contributes to the field by
Proposing a data-driven approach for nodal voltage estimation in unbalanced LV grids;
Combining a grey-box modeling approach to gain explainability and a generalized additive modeling approach to reduce the computational burden significantly, which makes the method practical for online monitoring;
Deriving the method for a real-world experimental setup and validating the results with high accuracy.
Through the real-world experimental setup, it is ensured that the method is based on input variables that are practical for the DSO to measure because of hardware installations, unlike pseudo-measurements that rely on simulated data. In addition, the experimental setup also includes a new type of electronic measuring device from Linc.world.
The rest of the paper is structured as follows.
Section 2 defines the problem.
Section 3 provides a generic description of the proposed method.
Section 4 describes the experimental setup with electronic measuring devices in a radial LV grid in Denmark. In
Section 5, the applied method is presented, including an analysis of the data collected in the experimental setup, a workflow for the model selection process, as well as the applied grey-box and generalized additive modeling approaches. In
Section 6, the results from the model selection process are presented and analyzed. The paper is concluded in
Section 7 and improvements that could form the basis for future work are also suggested.
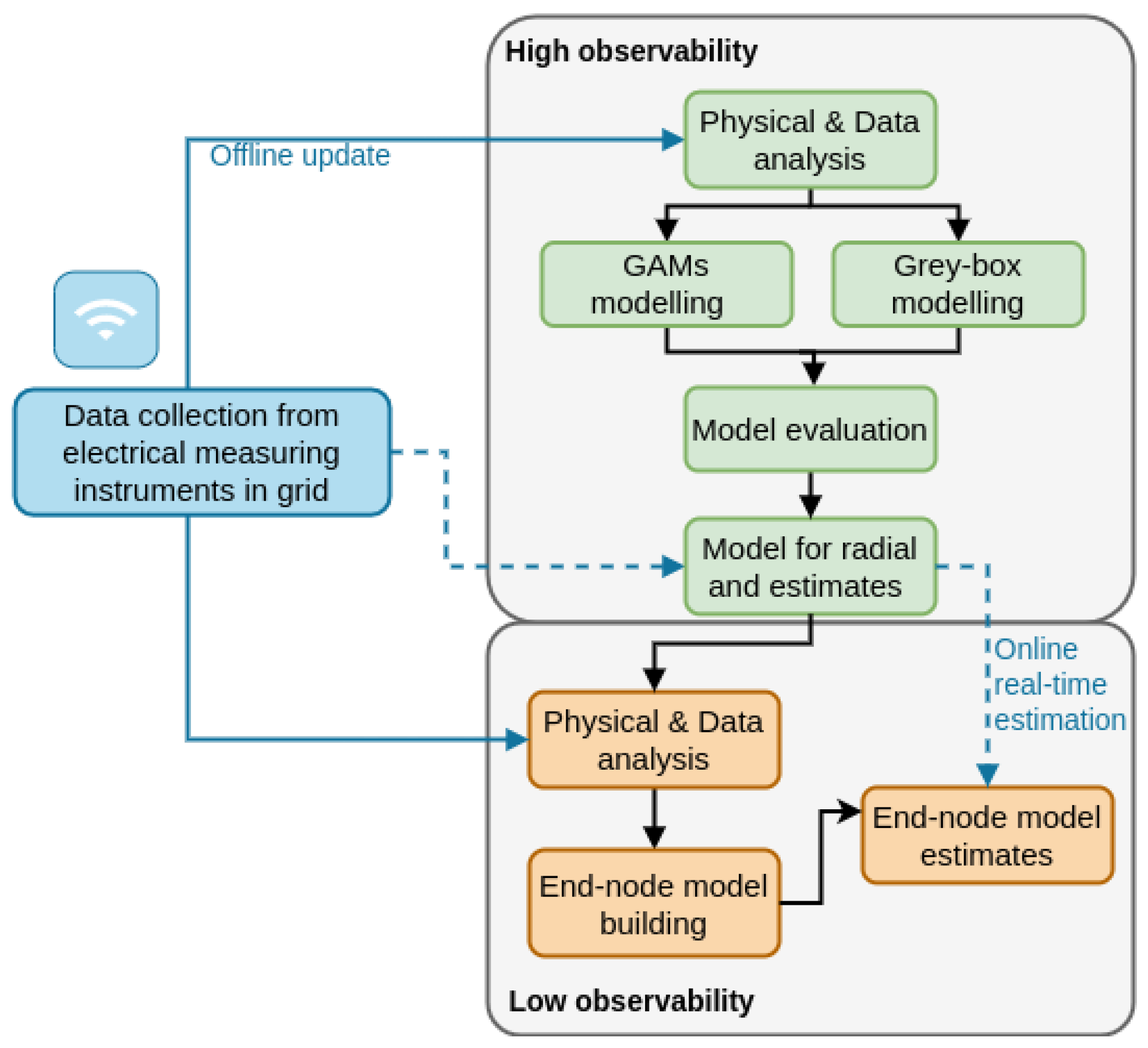
3. Workflow of the Proposed Method for Voltage Estimation
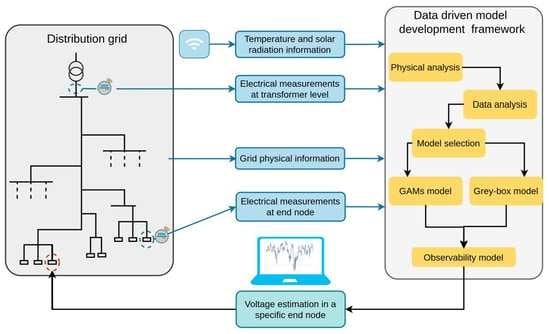
The workflow of the proposed method is illustrated in
Figure 1. To build the data-driven model shown in the workflow, in addition to the transformer measurements, we use an end node for which we have data through measurement devices, i.e., an end node with high observability. Then, we adapt the model to estimate voltages at other end nodes without real-time measurements, i.e., the nodes with low observability. The end node was chosen instead of a middle node because it is prioritized in the DSO operation to obtain the end node voltage and the entire voltage drop along one radial feeder with very high certainty through direct measurement, to add robustness to the model setup in case of disturbances.
End node voltage estimation is performed in two steps. First, the proposed workflow is followed to estimate the voltage in a node at the middle of the radial using the data from upper levels and the available data from the end node with high observability. Then, we use the estimated value for the middle node and follow the workflow again to estimate the voltages in other end nodes with low observability.
To perform the voltage estimation, we start with data analysis. In this step, all the data collected from measurement devices, including the available voltage and current measurement data from phases and neutral conductors and weather information, e.g., solar radiation and ambient temperatures, are considered. The information from the data analysis, such as correlation, is then utilized to choose parameters to construct the model.
In the next step, these parameters should be applied to a data-driven approach to perform the voltage estimation. Our investigations indicated that different methods can show different accuracy levels and advantages in voltage estimation at different nodes. Thus, it is suggested to choose two data-driven approaches, (1) a generalized additive model (GAM) and (2) grey-box modeling, for state estimation. For each approach, we apply the data to both approaches, fit the models, evaluate the results, and choose the best model for state estimation.
It is worth mentioning that other time series modeling approaches, such as Autoregressive Moving Average eXogenous (ARMAX) models, could also be alternative modeling techniques. However, GAMs and grey-box models were found to provide satisfactory results for the problem. Therefore, we focus on these approaches in this paper.
Note that the solid arrows in
Figure 1 represent the model fitting path of the workflow and might include measurements from more devices for model validation. The idea is that the model fitting could occur when an entire data set is collected by the DSO, e.g., daily. The real-time estimation path of the workflow is represented by the dotted arrows and is based on a few measurement devices and could occur in real time. Thereby, a lower burden on the communication system could be achieved.
Since the proposed method is data-driven and deals directly with data, we cannot present the approach in detail without using real data. Hence, in the next sections, first, the experimental setup is introduced as the case study. Then, the abovementioned approach is applied to this setup step by step to explain how the method should be applied to a real grid. Although there might be differences in applying the method to different grids, such as differences in the parameters with a high correlation or the results of model selection, the main approach will be the same as in
Figure 1.
5. Method
The models designed and developed in this research are physics-informed (physics-based) and data-driven. This means that the physics and known theories are used to build the first structure of the model, while the data, together with statistical and analytical tools, guide the process of finding the final model (e.g., a grey-box model). The data reflect the system of interest, including disturbances, which are not always possible to foresee or measure directly. Thus, a probabilistic model that reflects the real-world system, namely the power system in the experimental setup, is achieved. In this section, we first describe the physics of the system utilized to build the end node voltage estimation models, followed by analysis of the data collected in the experimental setup. We then present how generalized additive models (GAMs) and grey-box models are applied in the model selection process.
5.1. Physics of the System—Voltage Drop
Since the model is developed for a radial LV network, the equations that guide the first structure of the model are voltage drop equations. For a meshed network, power flow equations might be more suitable, but due to the low ratio in LV grids, this would directly become a set of non-linear equations.
It should further be noted that the common voltage drop equations are used to calculate line-to-neutral voltage drops [
29]. Since the LV grids are unbalanced, the neutral conductor might carry currents; hence, the neutral conductor voltage might not be zero [
30,
31]. Thus, we will investigate whether a term for the neutral current voltage drop,
, should be included in the voltage drop equations such that
where
is the sending-end voltage (i.e., the voltage at the node upstream of the network) and
is the receiving-end voltage (i.e., the voltage at the node downstream of the network).
Looking at
Figure 2, we can see that using the nodes with installed devices as sending-end and receiving-end voltage inputs (
and
) in Equation (
1), there will be loads not only at the receiving end but also along the feeder. The effective cable length (or impedance) in the voltage drop equations was discussed in [
32], where the authors suggested calculating the load center distance as it varies with the total ampere distribution along the feeder. However, their suggested method becomes impractical for a real-time algorithm as it requires real-time data from all households. Instead, we will fit a parameter in the model, based on available data, that reflects the effective resistance and reactance of the feeder. The resistance also increases with temperature. This might lead to seasonal deviations in the model, which will be investigated as well.
Since distribution networks are quite large and the installation needs to be scalable, another objective of this work is to devise a technique that requires the minimum number of extra measurements from the network. This avoids extra capital investment for the DSOs when rolling out the solution at scale. For example, the distribution network studied in this paper has 22 end nodes. Assuming that the DSO owns 1000 such grids, installing one measurement unit at each end node will result in 22,000 measuring devices, which is an expensive solution. However, if the proposed solution can reduce the number of measurement units to one at each branch, they would only need 5000 units. Turning to classical WLS state estimation is not an option here as it would require more devices to provide enough observability or accurate pseudo-measurements in at least the same time resolution as the model (minimum 10 min). Instead, we use the data at hand to develop a model that estimates the states of concern, i.e., the states at the customer premises.
5.2. Data Analysis
To avoid redundant discussion, the data analysis only presents data for the third phase, L3. The input parameters used in the model selection process are listed in
Table 1. The training data set is from 18 April 2022 to 30 April 2022 and the test data set is from 1 May 2022 to 31 May 2022.
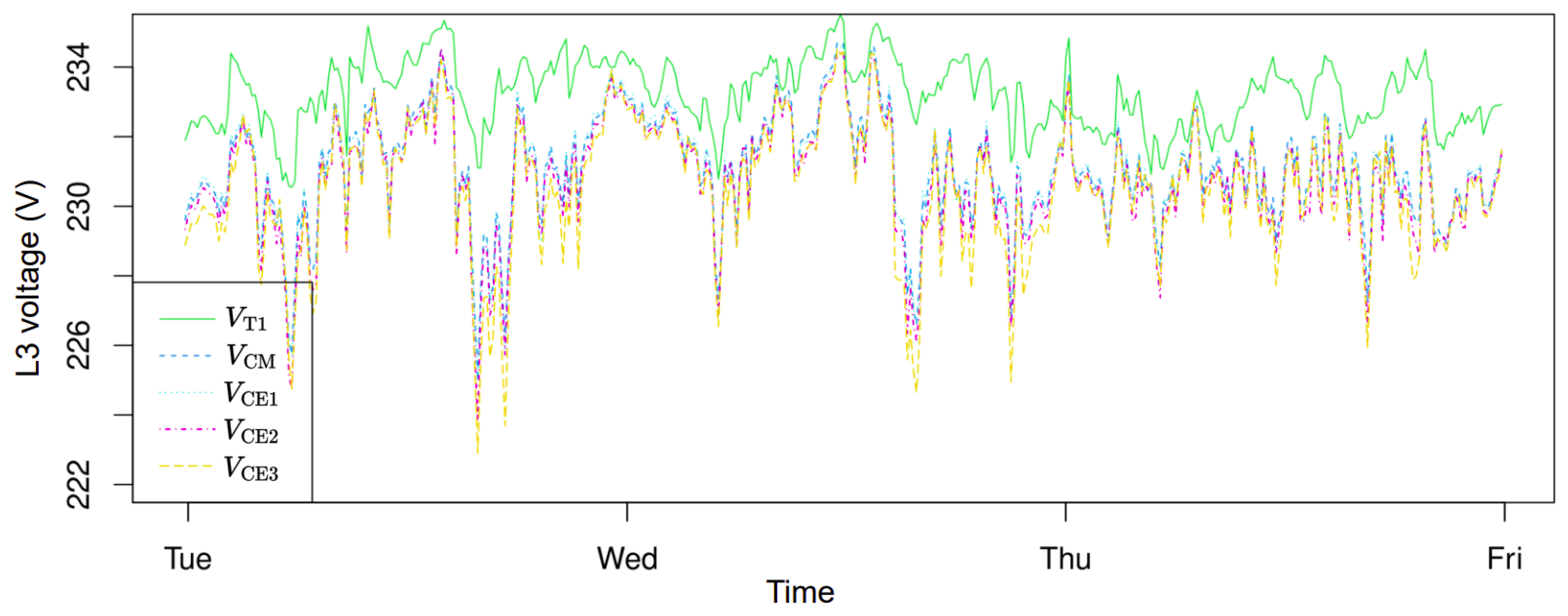
The voltage time series is shown in
Figure 3 for feeder
C in the grid (see
Figure 2). It can be seen that there is a significant voltage drop from the transformer (device
) to the nodes at the edge of the radial (e.g., device
) and that the variations in voltage drop seem quite correlated. In
Figure 4, scatter plots and correlations of the same voltage measurements (as in
Figure 3) and also the neutral currents along radial
C (i.e.,
) can be seen. The behavior seen in
Figure 3 is further supported by
Figure 4, where higher correlations are seen between the node voltages (at
,
,
, and
) than between the nodes and the transformer voltages.
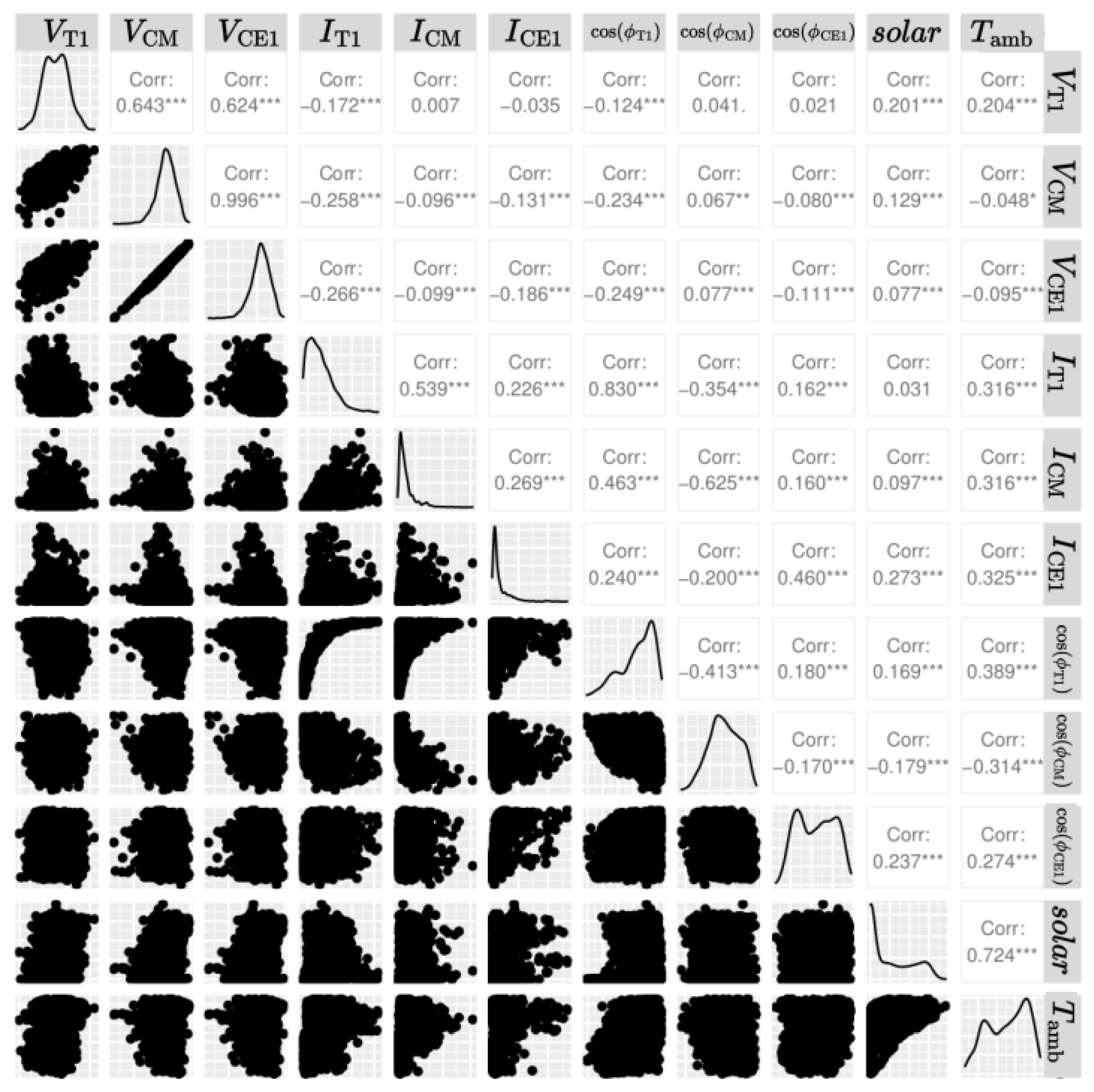
Figure 5 presents scatter plots, data density, and correlations for relevant input parameters. It is noteworthy that although the
voltage has a higher correlation with the other edge voltages, the current for
has a higher correlation with the edge voltages than the current at
. Ambient temperature has a very low correlation and will be excluded as a potential input. Solar radiation, on the other hand, has a higher correlation with the voltages. However, it may not necessarily be an explanatory variable as it probably coincides with a higher load. Therefore, the current should be a better input variable as the voltage drop equation supports it. Nevertheless, this observation will be further investigated in
Section 5.4 and
Section 5.5. Interestingly,
Figure 4 suggests a high correlation between neutral currents and the nodal voltages, which will be further explored in the model selection process.
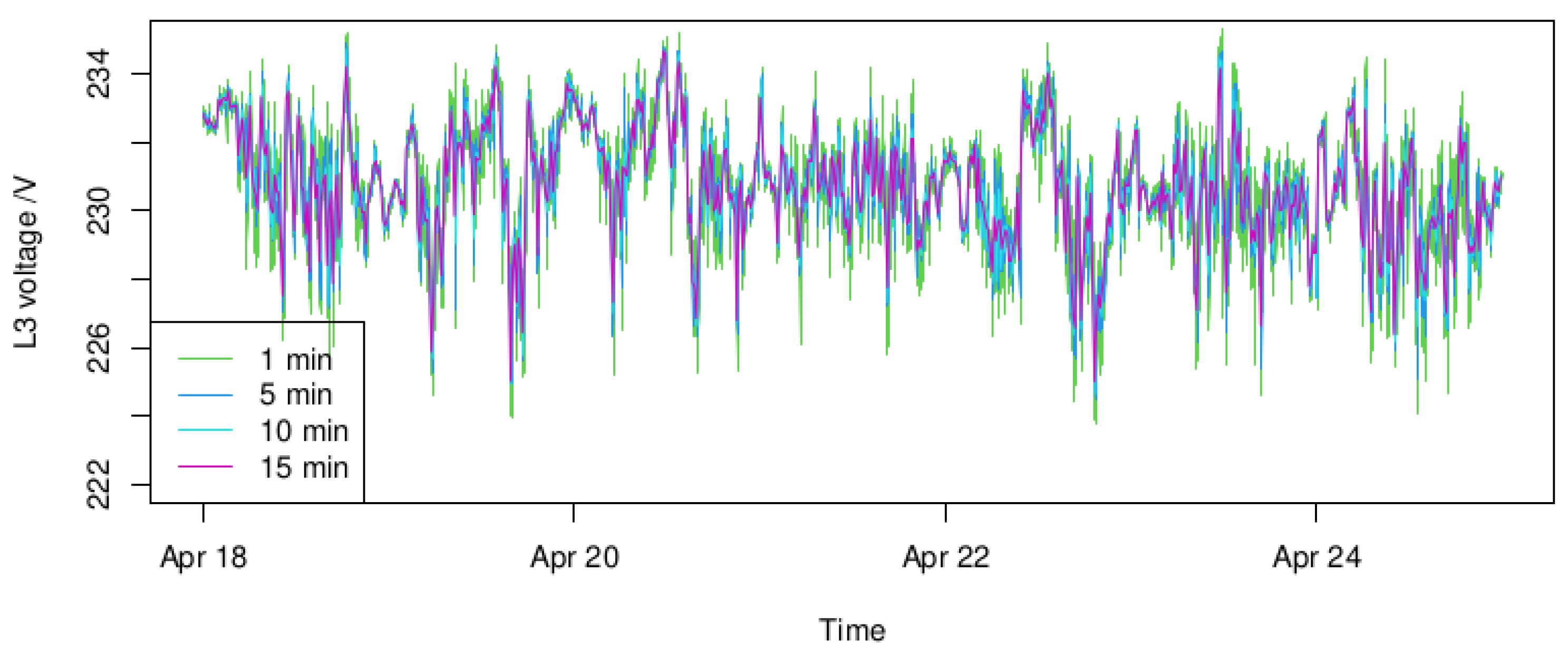
The original data are collected at a 1 second resolution. Therefore, filtering is required to manage the large data set. In
Figure 6, filtering to time resolutions of 1, 5, 10, and 15 min can be seen for the
third phase voltage. Comparing time resolutions of 1 min to 15 min, it can be seen that the voltage peaks and drops appear smoothed, and the time series is less volatile, which is a natural outcome of low-pass filtering. As persistent voltage peaks and drops are of concern for power system operation to avoid outages, we instead aim to find a suitable model for time resolutions of 5 or 10 min, which should be sufficient for DSO operation while having a manageable data throughput (or computational burden). Voltage data in lower resolutions would be less meaningful for the DSO to detect any voltage stability issues due to the volatile behavior. Higher time resolutions might, on the other hand, result in control strategies that are too volatile and miss the overall voltage behavior over time. However, higher time resolutions could be of interest for other voltage dynamic stability issues, but this is beyond the scope of this paper. Ten-minute filtering is initially chosen to offer the possibility of incorporating environmental data, which have a time resolution of 10 min.
5.3. Model Selection
To build the initial end node voltage estimation model, data collected from feeder
C in the grid (see
Figure 2) were utilized. As previously stated, one of the objectives of the proposed method was to minimize the number of required measuring devices. However, it was realized early in the model selection process that using only the measurements at the transformer level was insufficient to model the end node voltages. Instead, a workflow using devices at specific locations in the feeder was derived (see
Figure 1).
GAM and grey-box modeling approaches were used to build the observability model, which will be discussed in detail in
Section 5.4 and
Section 5.5. In both approaches, a forward selection process was followed for model evaluation, as described in
Section 5.6.
To better understand the workflow, let us consider feeder
C in
Figure 2 as an example. The goal is to estimate the voltage in one of the end nodes, such as
or
. To this end, we need one measurement in addition to the measurements in the transformer level. Both
and
measurements can be used. However, in the case of using
, one end node voltage will be known by the DSO with very high accuracy. Furthermore, if the voltage drop along the feeder is known, it will supposedly be easier to derive models for other end nodes in the network. Thus, measurements in transformer
and one of the end nodes, e.g.,
, are used to build the model. Considering the two measurements and node
, two voltage drop equations can be expressed as below:
where
,
, and
are the phase-to-ground voltages at devices
,
, and
, respectively.
is the voltage drop between devices
and
, and
is the voltage drop between devices
and
. Both the GAMs and grey-box model structures are derived assuming that
is partly described by Equation (
2) and partly by Equation (
3) such that
where
k are measurement instants in time;
,
a, and
b are coefficients to scale the contributions from Equations (
2) and (
3), respectively; and
are independent and identically distributed errors assumed to be Gaussian white noise,
. Both modeling approaches start with this formula as an initial model structure.
To estimate the end node voltages at low-observability radial feeders, estimates from a high-observability feeder are then utilized as model inputs.
5.4. GAM Model
GAMs are investigated in this subsection as possible structures to obtain the voltage estimation model. The general expression for GAMs is
where
is the expected value of a response variable
.
represents the parametric part of the model with explanatory variables
and parameters
, and
represents smooth functions of variables
[
33]. For more details of the GAM models, the reader is referred to [
33].
The initially derived GAM model from Equation (
4) has the following structure:
where the inputs are described in
Table 1 and
t is the time variable.
and
represent smooth functions using B-splines. The parameters were estimated using the
gam() and
gamm() functions in R package mgcv version 1.8–40 [
33,
34,
35,
36,
37]. Furthermore, a Gaussian distribution was used.
The initial formula in Equation (
6) is derived using only the terms associated with the resistance of the voltage drop equations. Following the data analysis in
Section 5.2 and the voltage drop description in
Section 5.1, various extensions of the inputs were explored:
Adding a smooth term relating to the reactive-current term in the voltage drop equation by using the line current and as inputs, where is the power factor measured by device d. This was done to investigate the impact of the reactance in the cable.
Adding voltage drop terms using and to investigate the impact of the voltage drop in the neutral conductor. It was impossible to use the neutral current data in due to a lack of data availability.
Adding the temperature as an input by incorporating it into the smooth functions related to cable resistance () to investigate whether the temperature has an impact on the resistance.
Adding a smooth term for solar radiation to investigate the potential impact of PV panels in the network. Here, a smooth term was used due the complicated functional relationship.
Adding a seasonal term to investigate whether there is an additional daily or hourly variation not explained by other data. This was done using cubic splines with periodic incremental time step inputs (i.e., a vector …, where m is the period length of a day or hour).
Additionally, variations of the smooth functions were explored.
5.5. Grey-Box Model
Grey-box models were also explored as another modeling approach because they have proven useful when developing data-driven models for physical systems (e.g., in [
38,
39]). In grey-box models, a known theory of a physical system is used to build the first structure for the model, while statistics and data are used to develop the model further, as well as to estimate the parameters of the model [
40]. Thus, it is a mixture of deterministic modeling, relying purely on the known theory, and black-box models, relying purely on statistics and data. Grey-box models, consisting of a set of stochastic differential equations, can be described in a continuous–discrete time state-space representation as follows:
where
k are points in time,
, of measurements;
is the state vector;
is the vector of measured outputs;
is the vector of input variables;
is a vector of unknown parameters;
,
, and
are linear or nonlinear functions;
are
m-dimensional standard Wiener processes; and
are the measurement errors [
41]. The Wiener processes are associated with the system error and we assume that they are independent, and the measurement errors are assumed to be Gaussian white noise
and uncorrelated to other measurement errors. We further assume that the Wiener processes and the measurement errors are independent.
The initial grey-box model in the model selection process is described as follows:
where
k are points in time,
, of measurements;
a,
b,
c, and
f are parameters to be estimated;
and
are cable resistances;
is the discrete differential of the current at
to the previous time step, i.e.,
(since only discrete measurements are available); consequently,
is the discrete differential of the current at
(
) and other inputs are described in
Table 1. Note that the time indices in the system equations are omitted here for simplicity. The state equations are derived by taking the derivative of the voltage drop equation.
Again, various extensions to the model structure were explored:
The parameters were estimated using the maximum likelihood method as implemented in the R package CTSM-R [
40,
42].
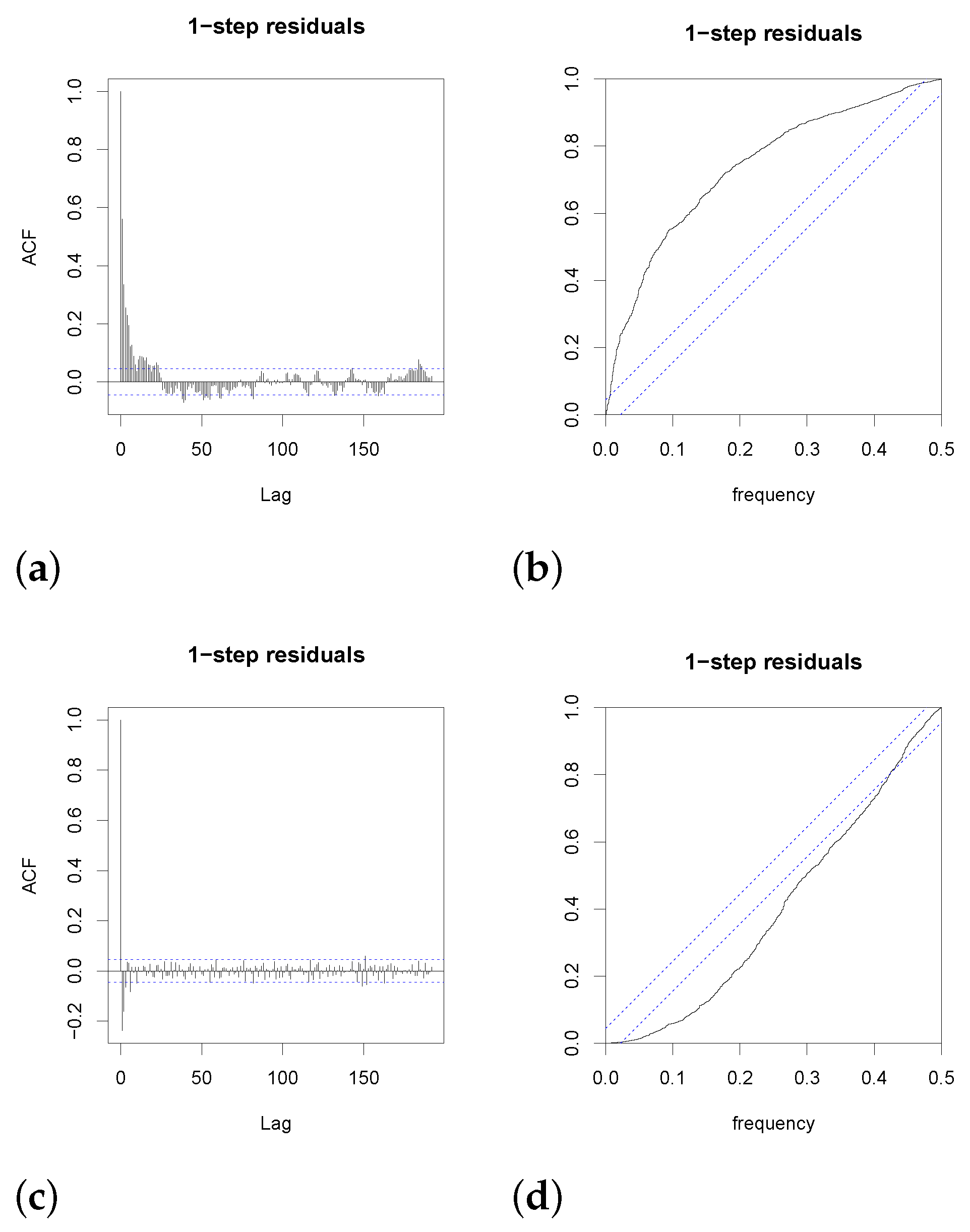
5.6. Model Evaluation
To evaluate the models in the forward model selection process, we used a similar approach to that described in [
38]. For each tested model, the autocorrelation function (ACF) and cumulated periodogram for the residuals were evaluated to investigate whether the model assumption of residual white noise had been achieved and whether there were any patterns left in the data that were not captured by the model. Root mean squared errors (RMSE) for both the training and test data sets, along with visual inspection of model estimations on the training set and predictions on the test set, were used to evaluate each model. We also evaluated the significance levels of the estimated parameters, and the model was reduced if higher
p-values than 5% were observed. Log-likelihood was also used in the grey-box modeling approach and the Akaike Information Criterion (AIC) in the GAM approach to compare candidate models.
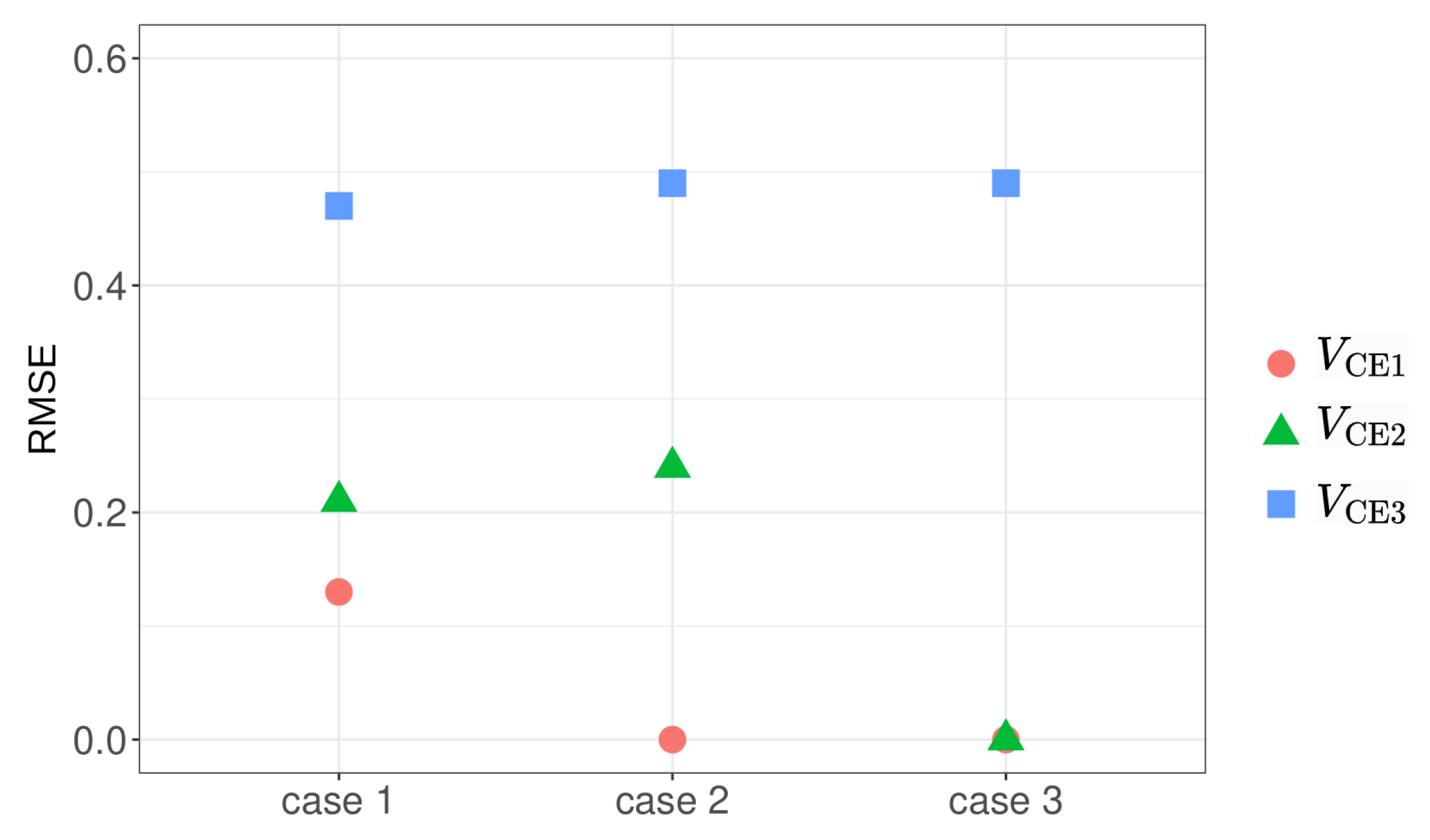
7. Conclusions
In this work, a data-driven nodal voltage estimation method for the real-time monitoring of radial LV grids has been developed. The method uses input from only one device at the end of a feeder and is designed to provide phase voltages. Such estimations are useful for distribution system operation as these grids are typically characterized by low or zero observability in the presence of voltage and current unbalance. With increasing volatility in consumption and production patterns, grid parameters, e.g., voltage and current, will show volatile behavior, especially if implementing flexibility services at this topological level in the grid. Therefore, real-time observability is of increasing importance for DSOs to avoid system failure and replace grid equipment in time.
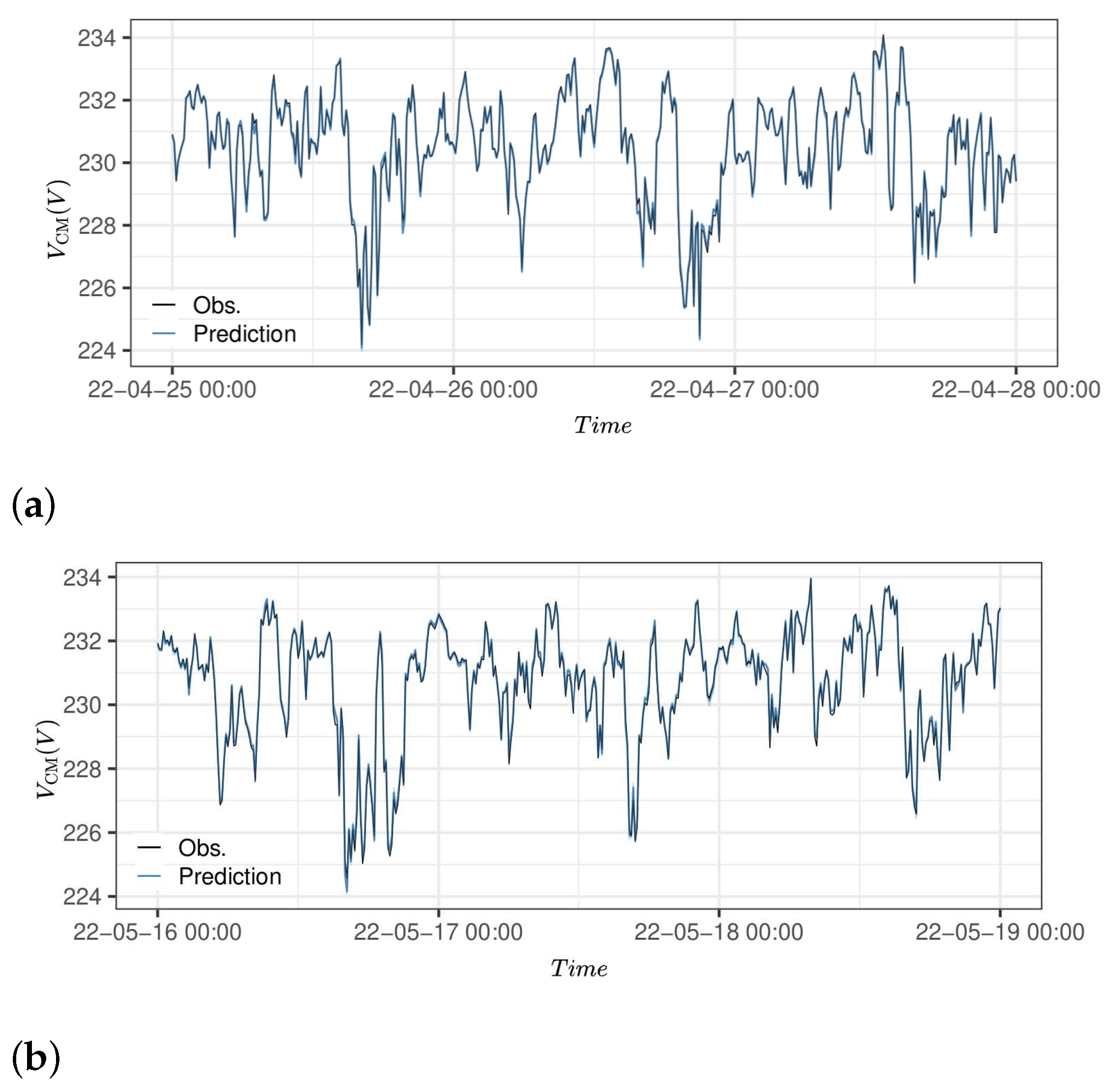
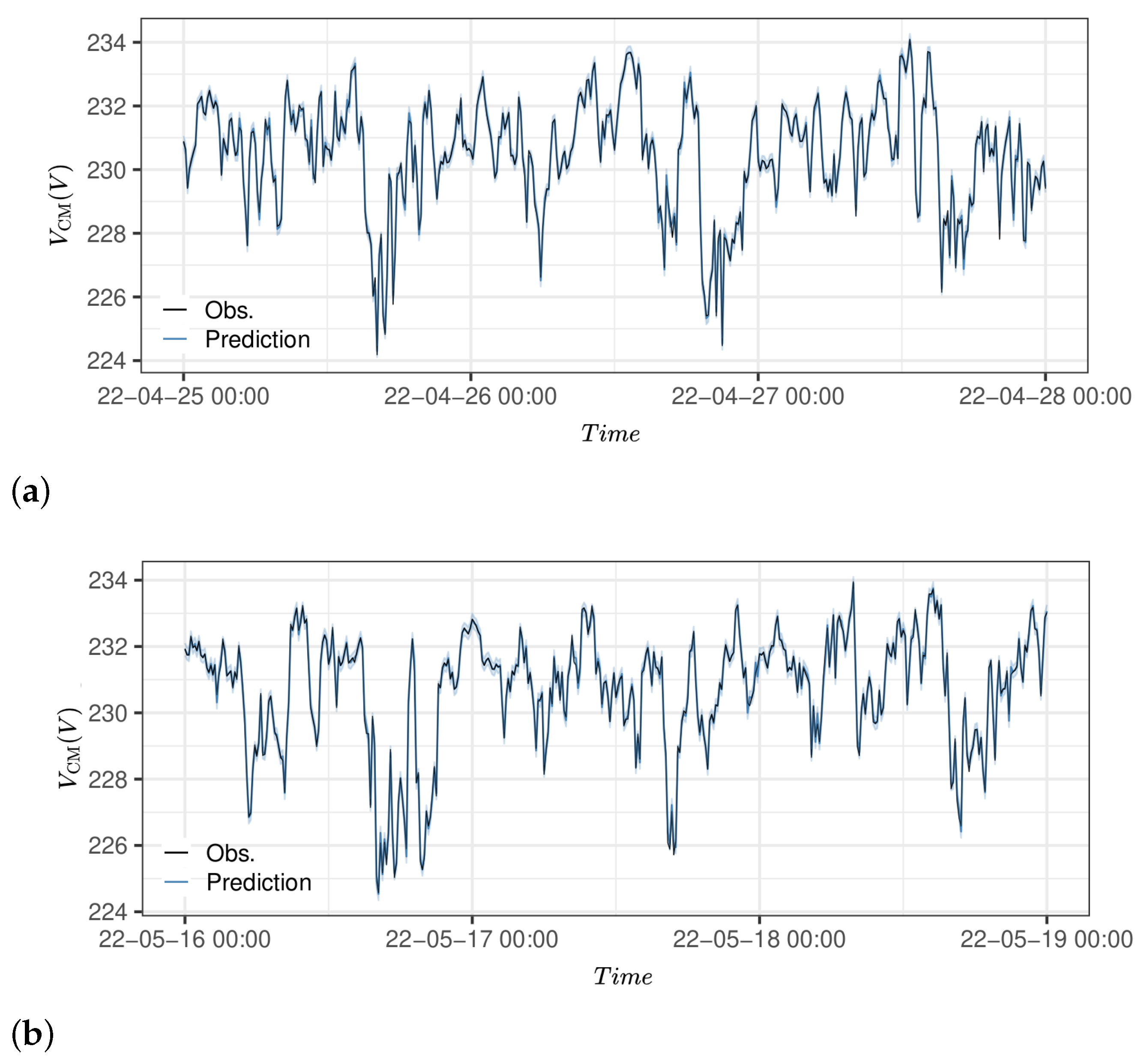
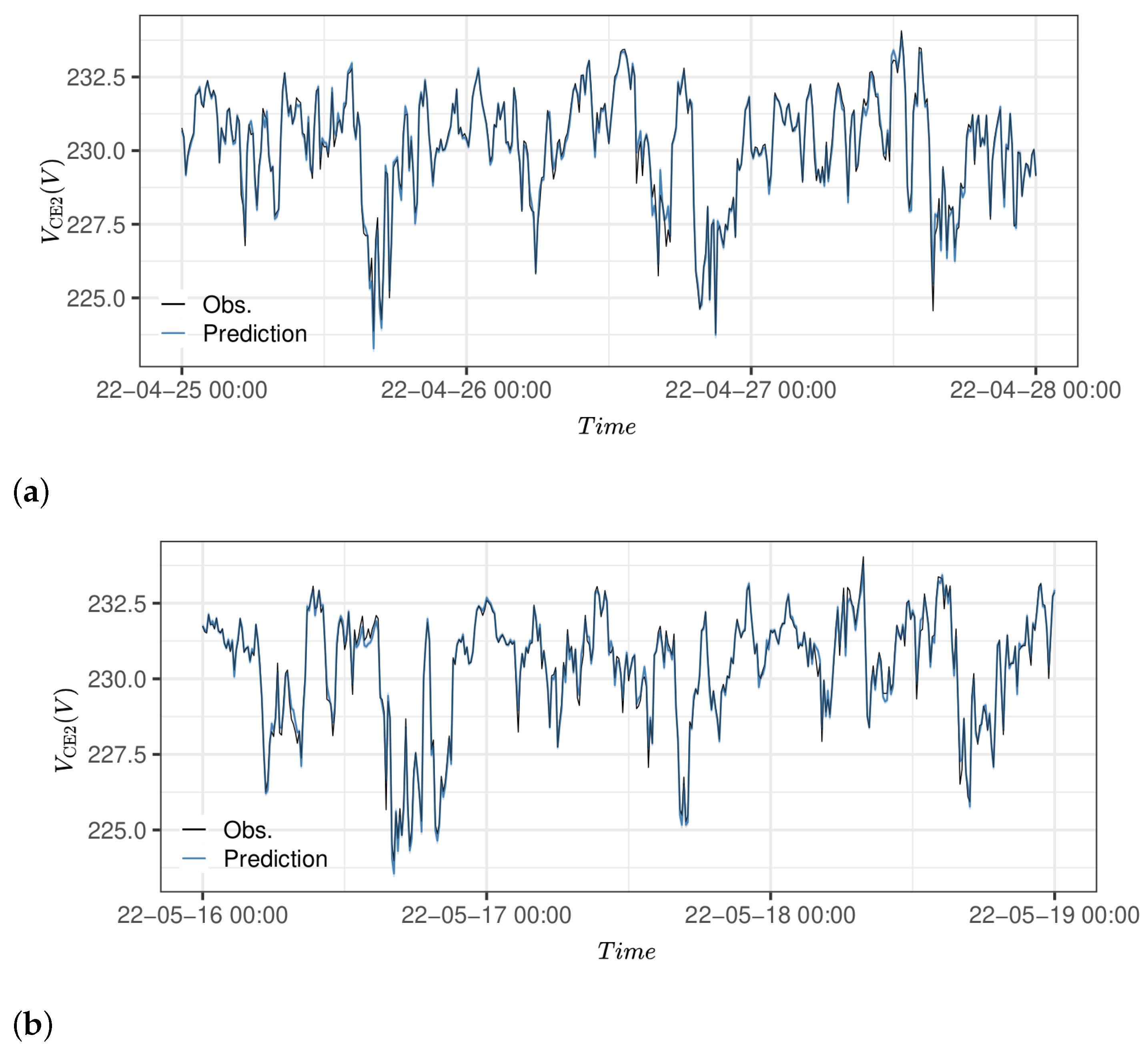
The presented workflow uses both grey-box and GAM modeling techniques. Both methods have been proven to give reasonable estimations on both the training data set (13 days) and the test data set (31 days), with RMSEs of 0.0004–0.002 per unit (p.u.) for the studied nodes (for comparison, the voltage stability limits are p.u.). The grey-box model provides explainability in describing the voltage drop along parts of a feeder, which could be used as input to the computationally lighter GAM model. The method also provides confidence intervals, which give the DSO the opportunity to apply risk-informed strategies.
The proposed method has a low computational burden, which makes it useful for online monitoring algorithms, as opposed to other techniques relying on large data flows and high-bandwidth communication infrastructures. The computational time for optimizing the grey-box model parameters was 13.7 s, while the time required to optimize the GAM models was less than 2 s for each model.
Furthermore, the method was derived using data from a real-world radial LV grid. Working with real-world data and data-driven methods, such as the methods described in this paper, jointly offers a considerable contribution toward the application of observability models in DSO grids, as it reflects the real system with unavoidable disturbances, not captured through simulations in ideal conditions.
Future Work
From analyzing and using the data in the model’s development, useful insights have been gained and a few improvements to the experimental setup can be suggested. The improvements involve more comprehensive measurements at the end node used for model building, as well as at the middle node (). It is suggested that both improvements are implemented and the resulting models evaluated to obtain better model performance, and it is recommended further to install the setup in different LV grids to evaluate the scalability of the method.