Time-Series Well Performance Prediction Based on Convolutional and Long Short-Term Memory Neural Network Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Basic Theory of Convolutional Network
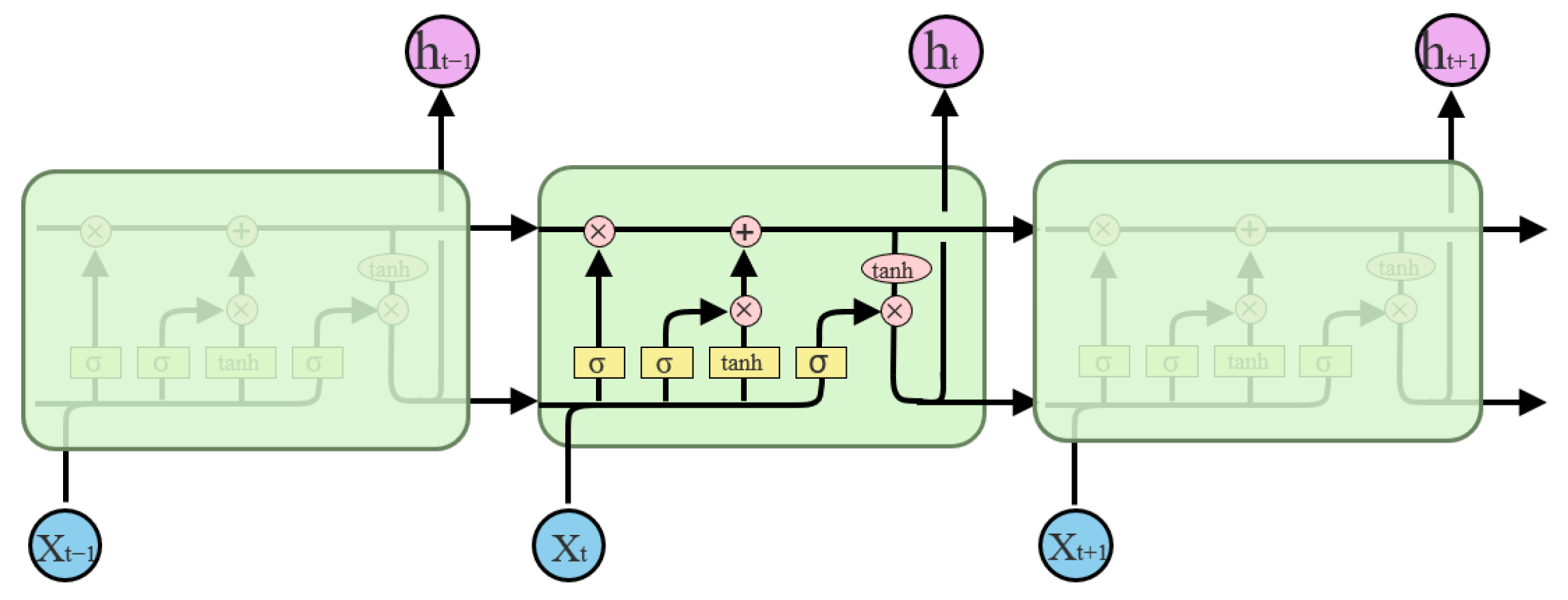
2.2. Basic Theory of LSTM Neural Network
- (a)
- Forget gate: Calculate forget gate by inputting data and outputting data through the input gate, output a value (0~1) and transfer it to the cell state information , and consider whether the previous cell state is retained.
- (b)
- Input Gate: Update input information and candidate cell state .
- (c)
- Update cell state: According to the updated candidate cell state and the cell state of the previous time step , the cell state of t time step is updated.
- (d)
- Output gate: Use output gate and output cell state to obtain output data .where , and are the forget gate’s input weights, recurrent weights and bias, respectively, , and are the input gate’s input weights, recurrent weights and bias, respectively, , and are the output gate’s input weights, recurrent weights and bias, respectively. Activation function is expressed as
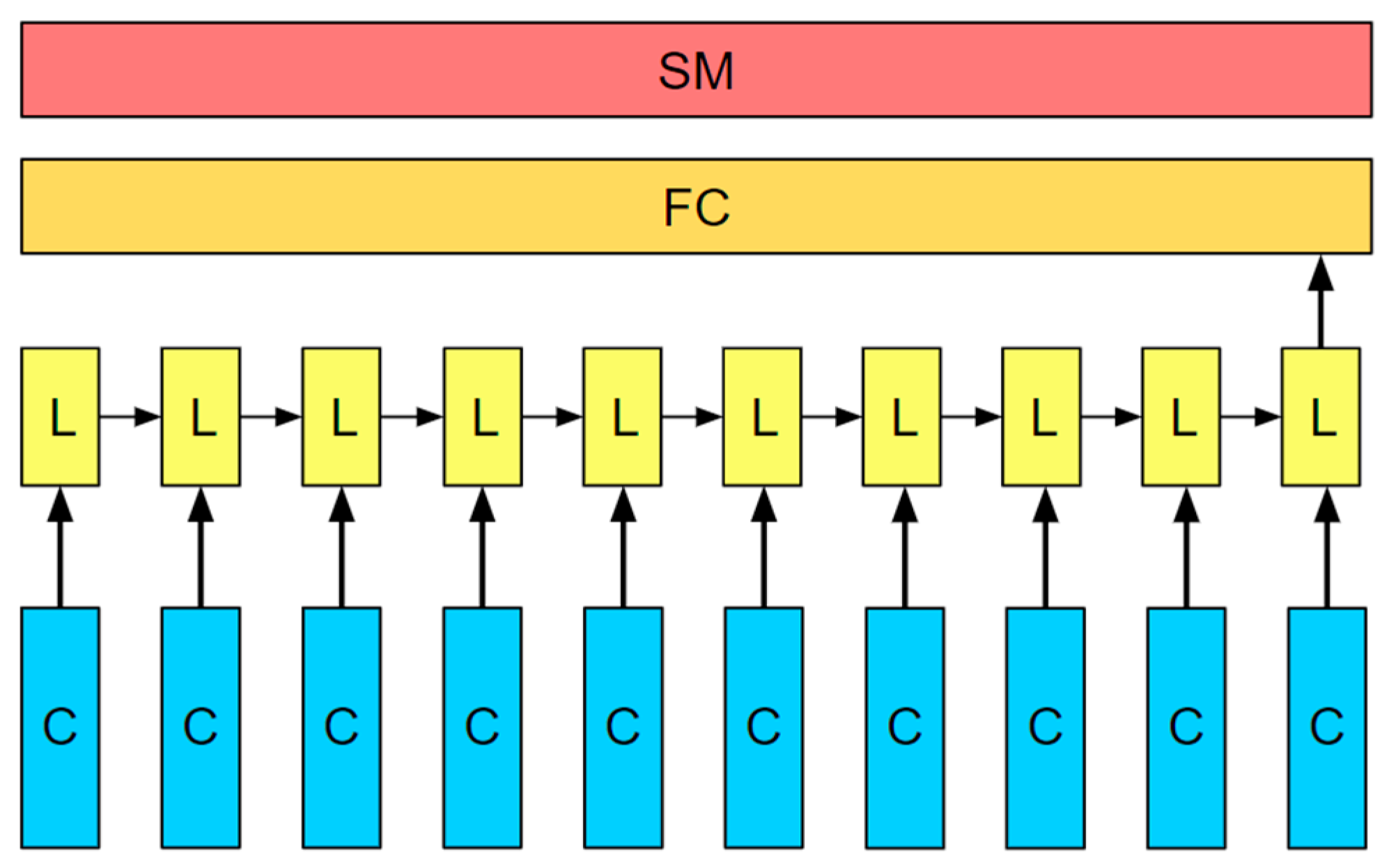
2.3. The CNN-LSTM Framework
2.4. Basic Theory of PSO
2.5. Description of Mathematical Model
2.6. Model Evaluation Criteria
3. Results and Discussion
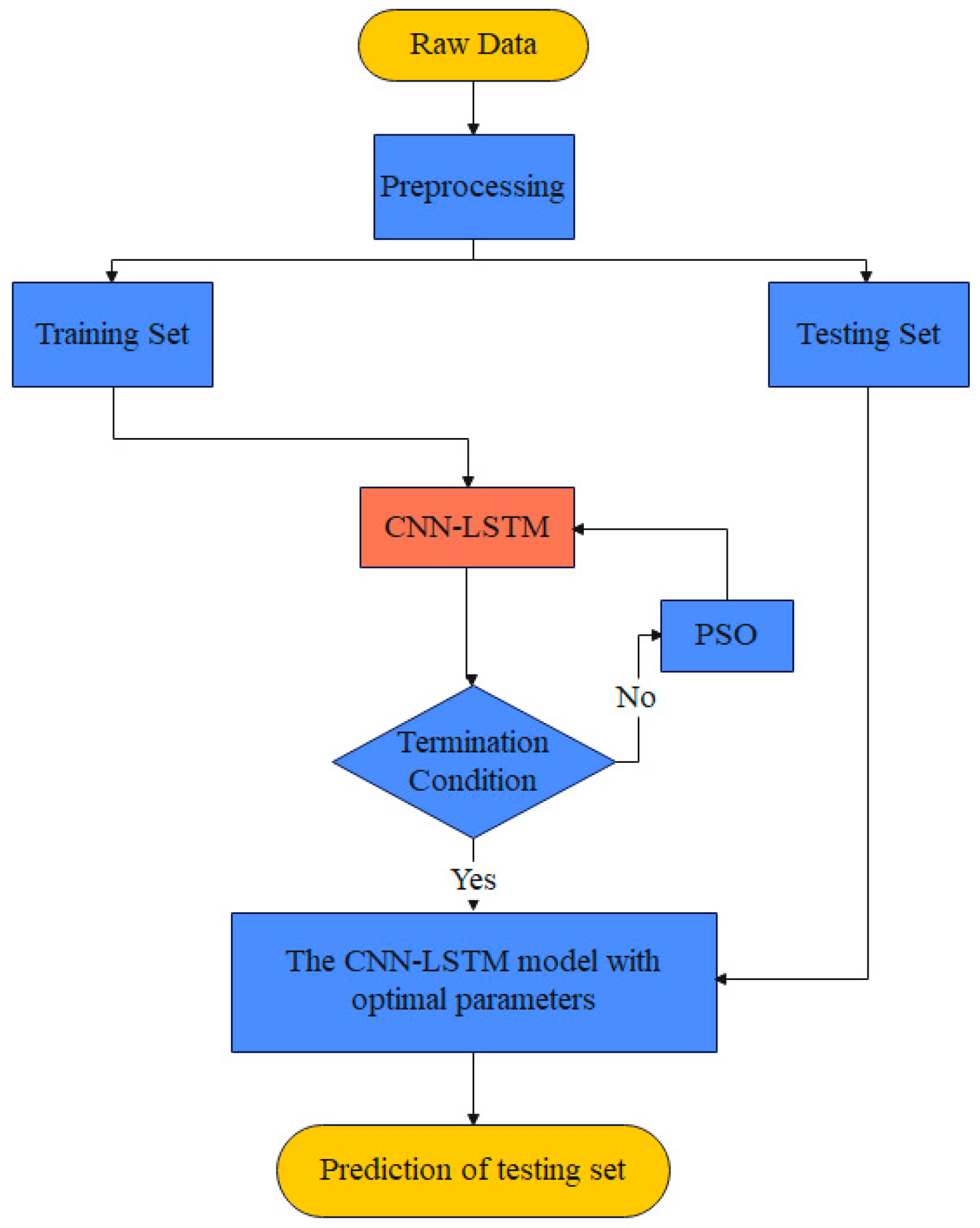
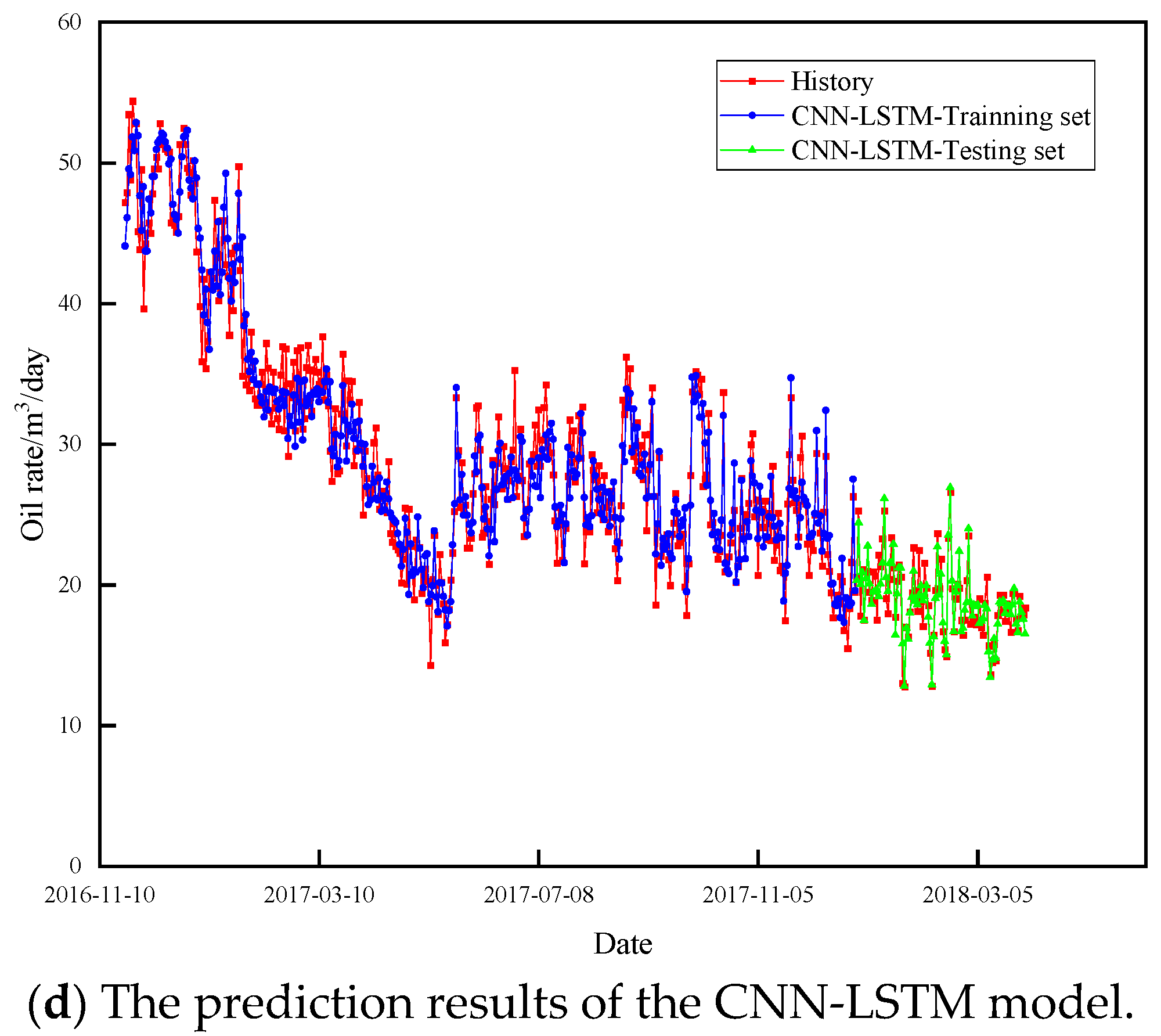
3.1. The Complete Workflow of the Case Study
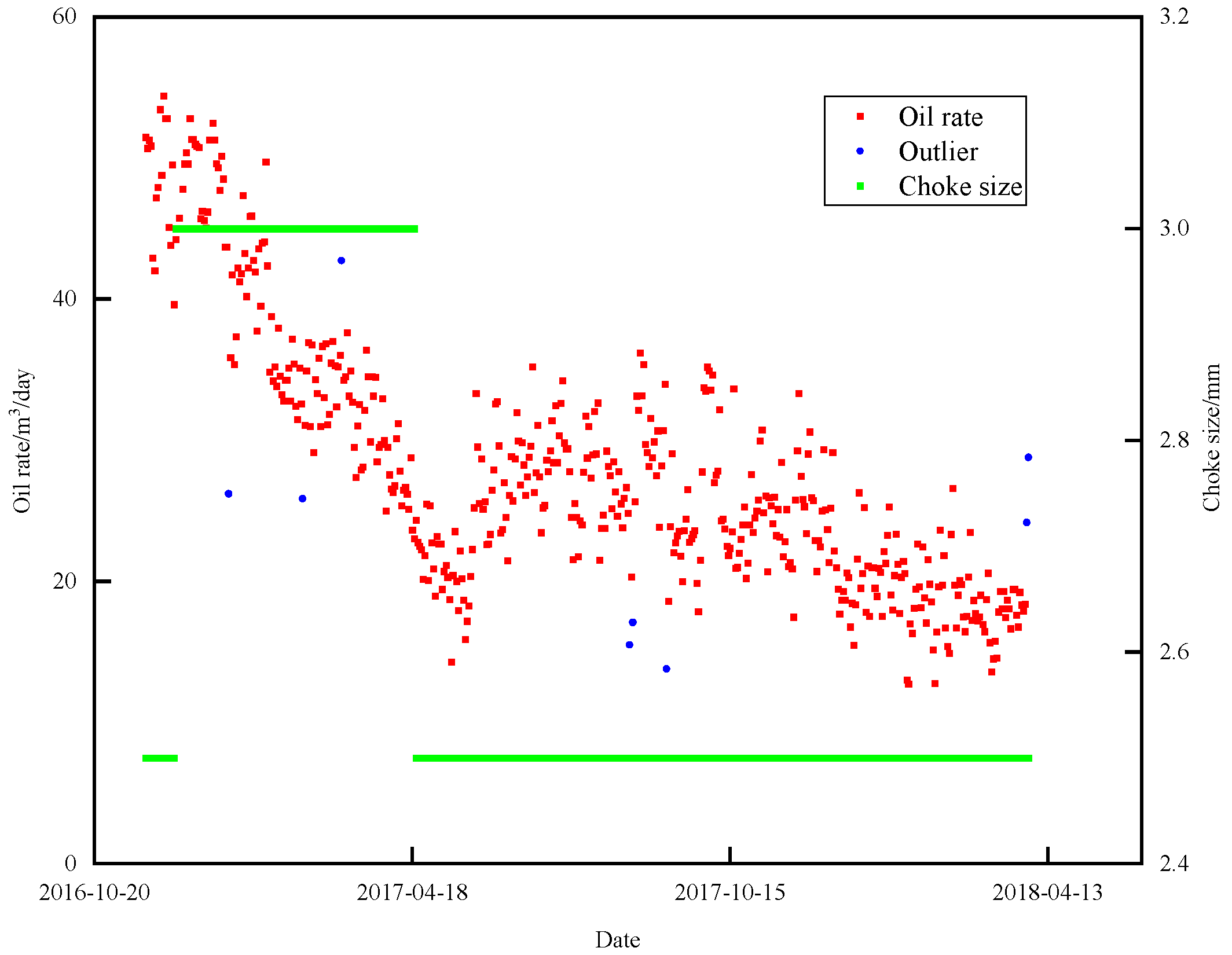
3.2. Complex Production Variation
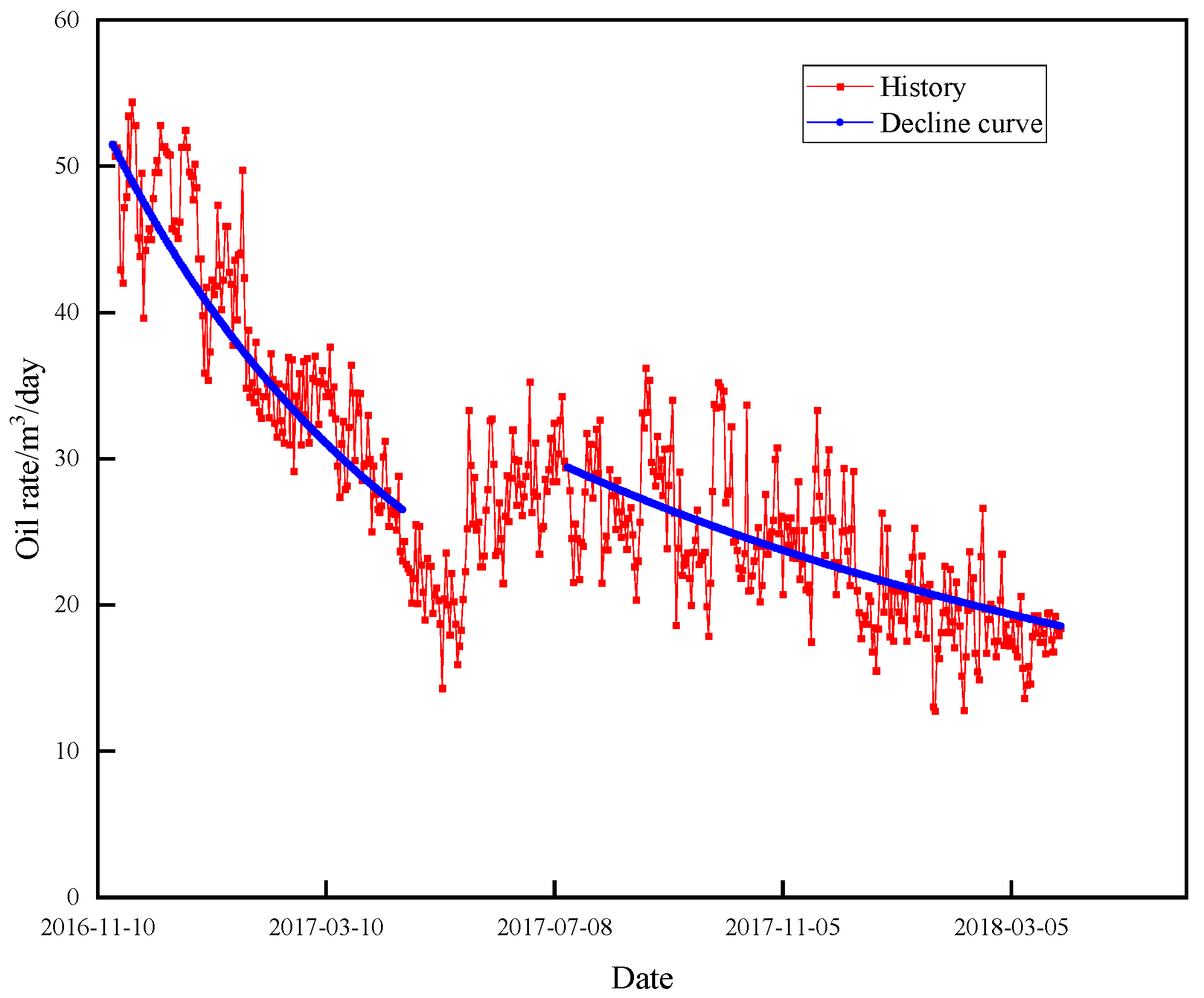
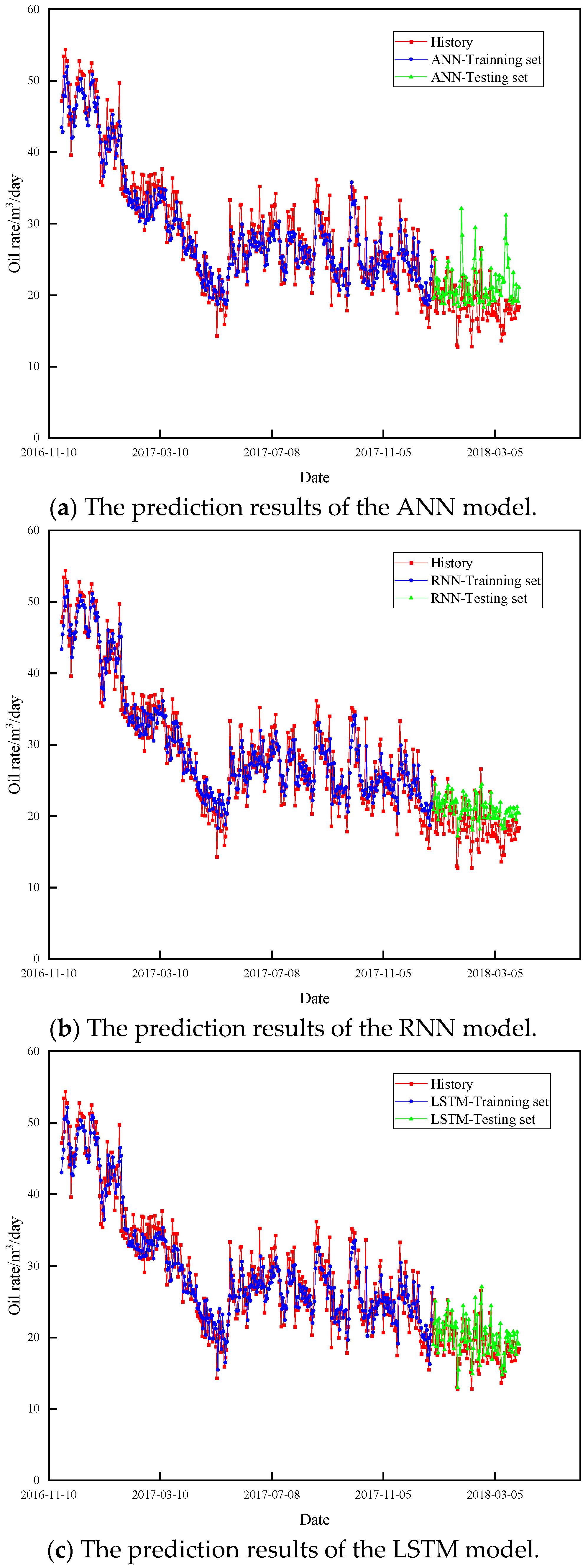
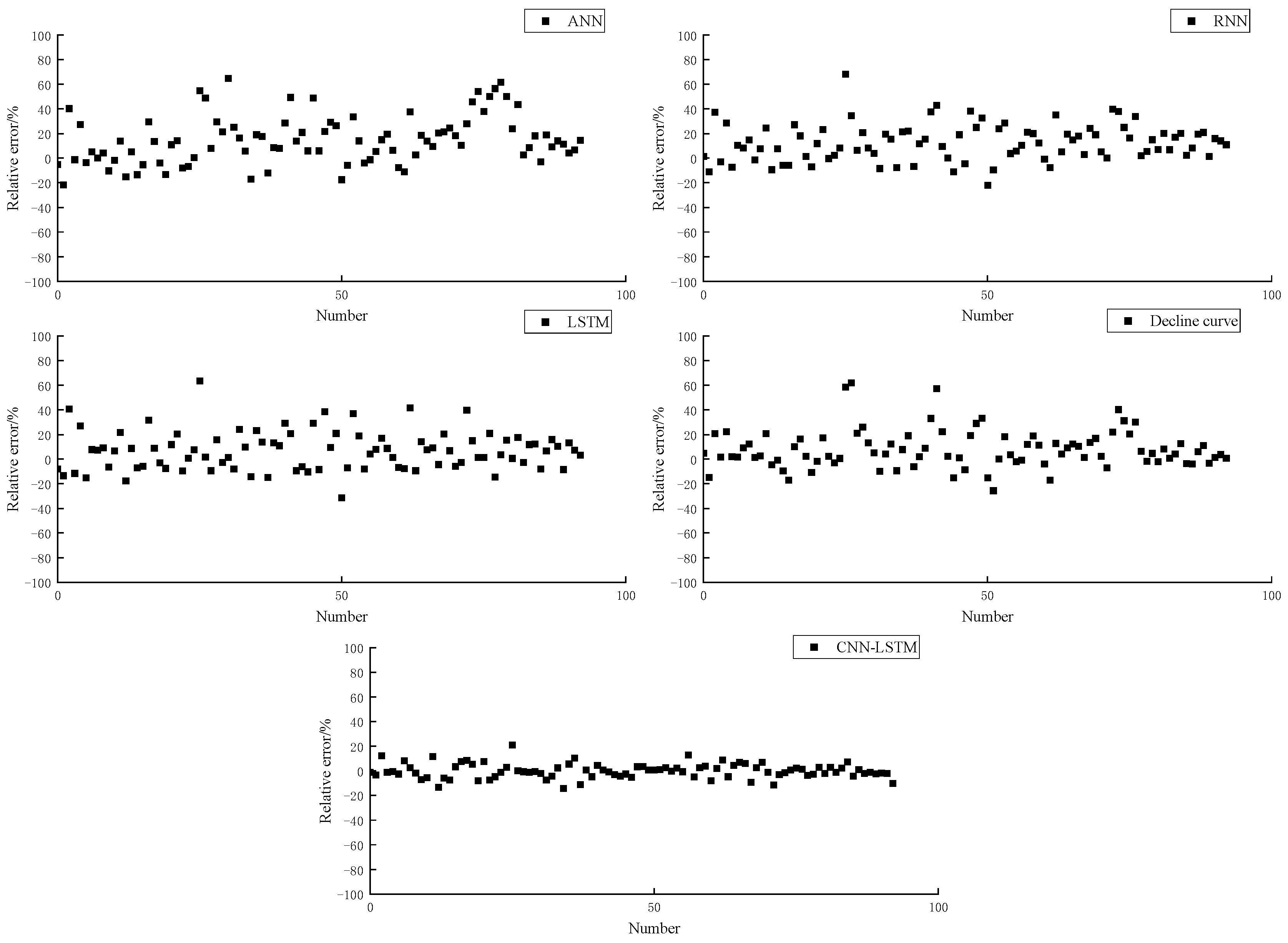
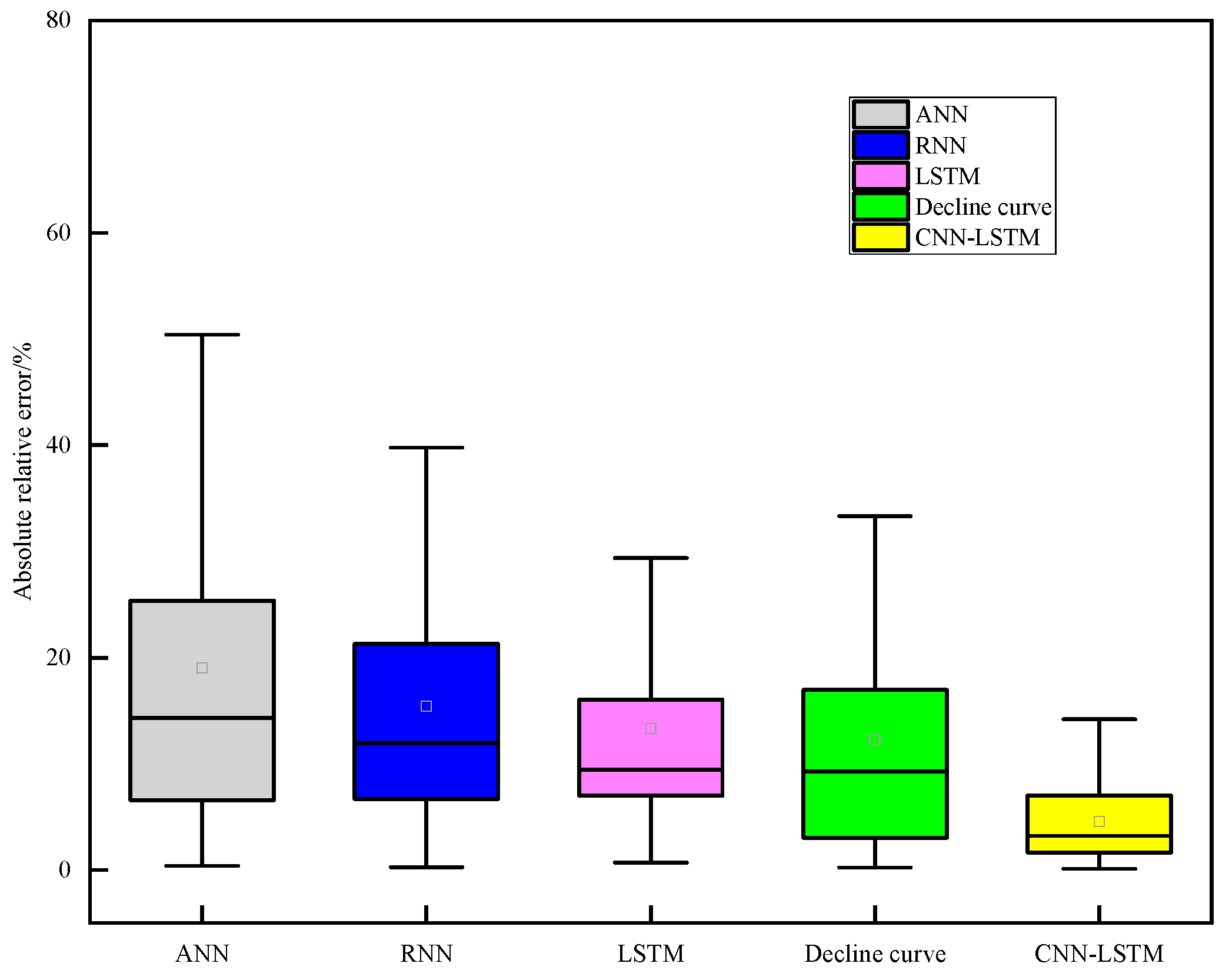
3.3. Comparison and Discussion with Decline Curve Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Amirian, E.; Dejam, M.; Chen, Z. Performance forecasting for polymer flooding in heavy oil reservoirs. Fuel 2018, 216, 83–100. [Google Scholar] [CrossRef]
- Nwaobi, U.; Anandarajah, G. Parameter determination for a numerical approach to undeveloped shale gas production estimation: The UK Bowland shale region application. J. Nat. Gas Sci. Eng. 2018, 58, 80–91. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Williams-Kovacs, J.D. History-matching and forecasting tight/shale gas condensate wells using combined analytical, semi-analytical, and empirical methods. J. Nat. Gas Sci. Eng. 2015, 26, 1620–1647. [Google Scholar] [CrossRef]
- Kalra, S.; Tian, W. A numerical simulation study of CO 2 injection for enhancing hydrocarbon recovery and sequestration in liquid-rich shales. Pet. Sci. 2018, 15, 103–115. [Google Scholar] [CrossRef]
- Zhang, R.H.; Zhang, L.H.; Tang, H.Y. A simulator for production prediction of multistage fractured horizontal well in shale gas reservoir considering complex fracture geometry. J. Nat. Gas Sci. Eng. 2019, 67, 14–29. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Qanbari, F. A semi-analytical method for forecasting wells completed in low permeability, undersaturated CBM reservoirs. J. Nat. Gas Sci. Eng. 2016, 30, 19–27. [Google Scholar] [CrossRef]
- Du, D.F.; Wang, Y.Y.; Zhao, Y.W. A new mathematical model for horizontal wells with variable density perforation completion in bottom water reservoirs. Pet. Sci. 2017, 14, 383–394. [Google Scholar] [CrossRef][Green Version]
- Schuetter, J.; Mishra, S.; Zhong, M.; LaFollette, R. A data-analytics tutorial: Building predictive models for oil production in an unconventional shale reservoir. SPE J. 2018, 23, 1–75. [Google Scholar] [CrossRef]
- Luo, G.; Tian, Y.; Bychina, M.; Ehlig-Economides, C. Production optimization using machine learning in Bakken shale. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018. [Google Scholar]
- Wang, S.; Chen, S. Insights to fracture stimulation design in unconventional reservoirs based on machine learning modeling. J. Pet. Sci. Eng. 2019, 174, 682–695. [Google Scholar] [CrossRef]
- Panja, P.; Velasco, R.; Pathak, M.; Deo, M. Application of artificial intelligence to forecast hydrocarbon production from shales. Petroleum 2018, 4, 75–89. [Google Scholar] [CrossRef]
- Han, B.; Bian, X. A hybrid PSO-SVM-based model for determination of oil recovery factor in the low-permeability reservoir. Petroleum 2018, 4, 43–49. [Google Scholar] [CrossRef]
- Zhong, M.; Schuetter, J.; Mishra, S. Do data mining methods matter? A Wolfcamp Shale case study. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, Woodlands, TX, USA, 23–25 January 2018. [Google Scholar]
- Cao, Q.; Banerjee, R.; Gupta, S.; Li, J.; Zhou, W.; Jeyachandra, B. Data driven production forecasting using machine learning. In Proceedings of the SPE Argentina Exploration and Production of Unconventional Resources Symposium, Buenos Aires, Argentina, 1–3 June 2016. [Google Scholar]
- Ahmadi, M.A.; Ebadi, M.; Shokrollahi, A.; Majidi, S.M.J. Evolving artificial neural network and imperialist competitive algorithm for prediction oil flow rate of the reservoir. Appl. Soft Comput. 2013, 13, 1085–1098. [Google Scholar] [CrossRef]
- Fulford, D.S.; Bowie, B. Machine learning as a reliable technology for evaluating time-rate performance of unconventional wells. SPE Econ. Manag. 2015, 8, 23–39. [Google Scholar] [CrossRef]
- Li, D.; Wang, Z.; Zha, W.; Wang, J.; He, Y.; Huang, X.; Du, Y. Predicting production-rate using wellhead pressure for shale gas well based on Temporal Convolutional Network. J. Petrol. Sci. Eng. 2022, 216, 110644. [Google Scholar] [CrossRef]
- Wang, H.; Mu, L.; Shi, F.; Dou, H. Production prediction at ultra-high water cut stage via recurrent neural network. Petrol. Explor. Dev. 2020, 47, 1084–1090. [Google Scholar] [CrossRef]
- Cheng, Y.; Yang, Y. Prediction of oil well production based on the time series model of optimized recursive neural network. Petrol. Sci. Technol. 2021, 39, 303–312. [Google Scholar] [CrossRef]
- Al-Shabandar, R.; Jaddoa, A.; Liatsis, P.; Hussain, A.J. A deep gated recurrent neural network for petroleum production forecasting. Mach. Learn. Appl. 2020, 3, 100013. [Google Scholar] [CrossRef]
- Mahzari, P.; Emambakhsh, M.; Temizel, C.; PJones, A. Oil production forecasting using deep learning for shale oil wells under variable gas-oil and water-oil ratios. Petrol. Sci. Technol. 2022, 40, 445–468. [Google Scholar] [CrossRef]
- Zha, W.; Liu, Y.; Wan, Y.; Luo, R.; Li, D.; Yang, S.; Xu, Y. Forecasting monthly gas field production based on the CNN-LSTM model. Energy 2022, 260, 124889. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Y.; Meng, J. Synthetic well logs generation via recurrent neural networks. Pet. Explor. Dev. 2018, 45, 598–607. [Google Scholar] [CrossRef]
- Qin, Y.; Li, K.; Liang, Z.; Lee, B.; Zhang, F. Hybrid forecasting model based on long short term memory network and deep learning neural network for wind signal. Appl. Energy 2019, 236, 262–272. [Google Scholar] [CrossRef]
- Han, S.; Qiao, Y.H.; Yan, J. Mid-to-long term wind and photovoltaic power generation prediction based on copula function and long short term memory network. Appl. Energy 2019, 239, 181–191. [Google Scholar] [CrossRef]
- Li, Y.; Cao, H. Prediction for tourism flow based on LSTM Neural Network. Procedia Comput. Sci. 2018, 129, 277–283. [Google Scholar] [CrossRef]
- Tong, W.; Li, L.; Zhou, X.; Hamilton, A.; Zhang, K. Deep learning PM2.5 concentrations with bidirectional LSTM RNN. Air Qual. Atmos. Health 2019, 12, 411–423. [Google Scholar] [CrossRef]
- Xuanyi, S.; Yuetian, L.; Liang, X. Time-series well performance prediction based on Long Short-Term Memory (LSTM) neural network model. J. Pet. Sci. Eng. 2020, 186, 1–14. [Google Scholar]
- Xue, L.; Gu, S.; Wang, J.; Liu, Y. Production dynamic prediction of gas well based on particle swarm optimization and long short-term memory. Oil Drill. Prod. Technol. 2021, 45, 525–531. [Google Scholar]
- Zheng, J.; Du, J.; Liang, Y. Research into real-time monitoring of shutdown pressures in multi-product pipelines. Pet. Sci. Bull. 2021, 4, 648–656. [Google Scholar]
- Luo, G.; Xiao, L.; Shi, Y.; Shao, R. Machine learning for reservoir fluid identification with logs. Pet. Sci. Bull. 2022, 1, 24–33. [Google Scholar]
- Hu, X.; Tu, Z.; Luo, Y.; Zhou, F.; Li, Y.; Liu, J.; Yi, P. Shale gas well productivity prediction model with fitted function-neural network cooperation. Pet. Sci. Bull. 2022, 03, 394–405. [Google Scholar]
- Song, X.; Yao, X.; Li, G.; Xiao, L.; Zhu, Z. A novel method to calculate formation pressure based on the LSTM-BP neural network. Pet. Sci. Bull. 2022, 1, 12–23. [Google Scholar]
- Spandonidis, C.; Theodoropoulos, P.; Giannopoulos, F.; Galiatsatos, N.; Petsa, A. Evaluation of deep learning approaches for oil & gas pipeline leak detection using wireless sensor networks. Eng. Appl. Artif. Intell. 2022, 113, 104890. [Google Scholar]
- Spandonidis, C.; Theodoropoulos, P.; Giannopoulos, F. A Combined Semi-Supervised Deep Learning Method for Oil Leak Detection in Pipelines Using IIoT at the Edge. Sensors 2022, 22, 4105. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Shi, Y.; Lin, R.; Qiao, W.; Ba, W. A novel oil pipeline leakage detection method based on the sparrow search algorithm and CNN. Measurement 2022, 204, 112122. [Google Scholar] [CrossRef]
- Xueqing, Z.; Fang, L. Real time prediction of China’s carbon emissions based on CNN-LSTM model. China Arab. Sci. Technol. Forum 2022, 2022, 5. [Google Scholar]
- Ke, Z.; Renchuan, Z. A CNN-LSTM Ship Motition Extrem Value Prediction Mode. J. Shanghai Jiaotong Univ. 2022, 89, 5. [Google Scholar]
- LeCun, Y. Generalization and network design strategies. In Technical Report CRG-TR-89-4; University of Toronto: Toronto, ON, Canada, 4 June 1989. [Google Scholar]
- Zhao, J.; Bai, G.; Li, Y. Short-term wind power predicttion based on CNN-LSTM. Pro. Auto. Instru. 2020, 41, 37–41. [Google Scholar]
- Niknam, T. A new fuzzy adaptive hybrid particle swarm optimization algorithm for non-linear, non-smooth and non-convex economic dispatch problem. Appl. Energy 2010, 87, 327–339. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27–30 November 1995. [Google Scholar]
- Pytorch Documentation. Available online: https://pytorch.org (accessed on 1 June 2022).
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the SIGMOD/PODS00: ACM International Conference on Management of Data and Symposium on Principles of Database Systems, Dallas, TX, USA, 15–18 May 2000. [Google Scholar]
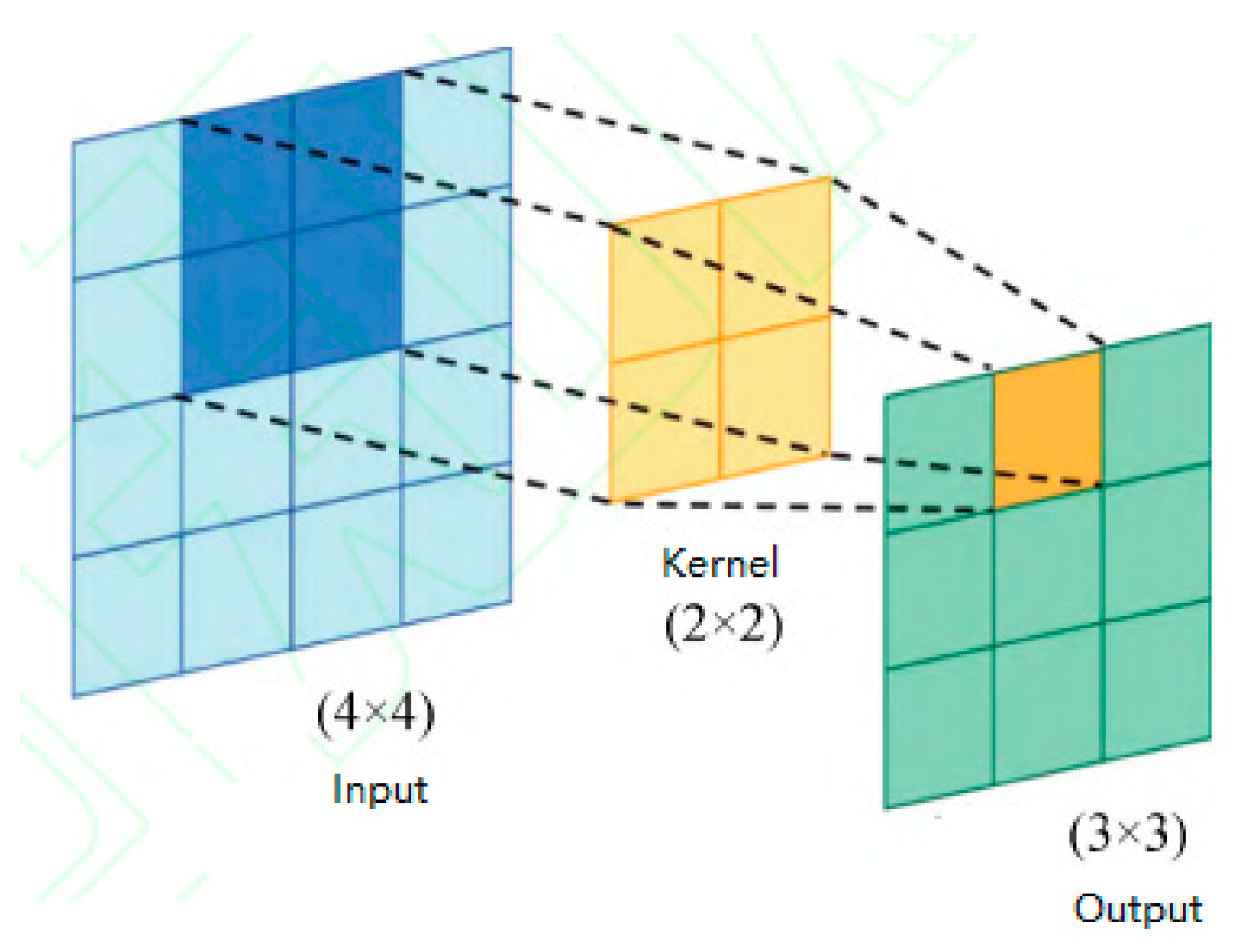
| Symbol | Description |
|---|---|
| the kernel between the ith feature map of the k−1th layer and the jth feature map of the kth layer | |
| the ith feature map’s output value from the k−1th layer | |
| the jth feature map’s bias from the kth layer | |
| the jth feature map’s output value from kth layer | |
| convolution | |
| the collection of input feature maps | |
| activation function, which is usually sigmoid function or rectified linear unit (ReLU) |
| Model | MAPE | MAE | RMSE |
|---|---|---|---|
| ANN | 18.69 | 3.33 | 4.23 |
| RNN | 15.41 | 2.71 | 3.26 |
| Decline curve analysis | 14.15 | 2.31 | 2.73 |
| LSTM | 13.53 | 2.18 | 2.48 |
| CNN-LSTM | 5.49 | 1.15 | 1.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Qiang, X.; Ren, Z.; Wang, H.; Wang, Y.; Wang, S. Time-Series Well Performance Prediction Based on Convolutional and Long Short-Term Memory Neural Network Model. Energies 2023, 16, 499. https://doi.org/10.3390/en16010499
Wang J, Qiang X, Ren Z, Wang H, Wang Y, Wang S. Time-Series Well Performance Prediction Based on Convolutional and Long Short-Term Memory Neural Network Model. Energies. 2023; 16(1):499. https://doi.org/10.3390/en16010499
Chicago/Turabian StyleWang, Junqiang, Xiaolong Qiang, Zhengcheng Ren, Hongbo Wang, Yongbo Wang, and Shuoliang Wang. 2023. "Time-Series Well Performance Prediction Based on Convolutional and Long Short-Term Memory Neural Network Model" Energies 16, no. 1: 499. https://doi.org/10.3390/en16010499
APA StyleWang, J., Qiang, X., Ren, Z., Wang, H., Wang, Y., & Wang, S. (2023). Time-Series Well Performance Prediction Based on Convolutional and Long Short-Term Memory Neural Network Model. Energies, 16(1), 499. https://doi.org/10.3390/en16010499





