Analysis of Low-Density Heat Flux Data by the Wavelet Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology of Evaluating Thermal Resistance
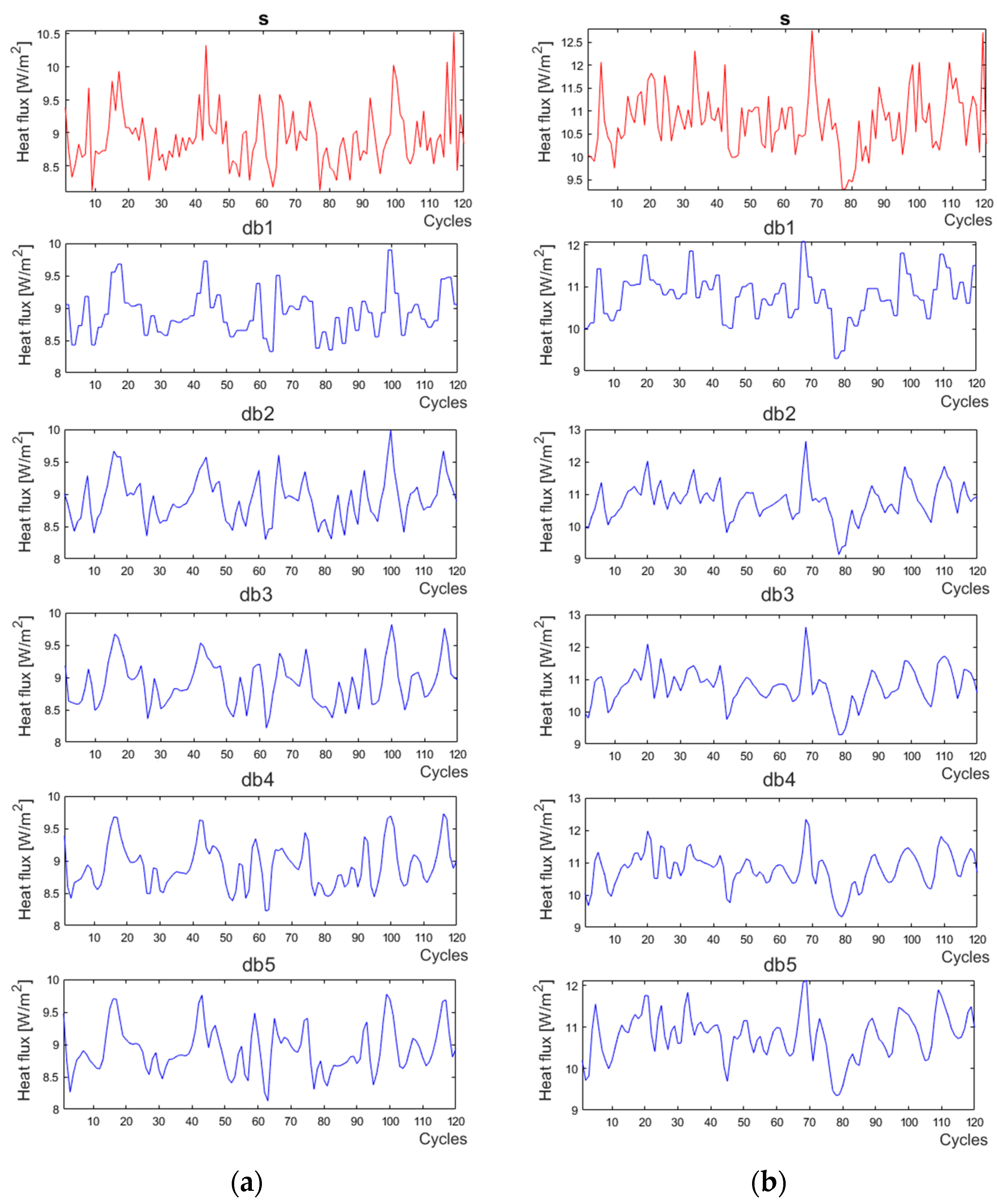
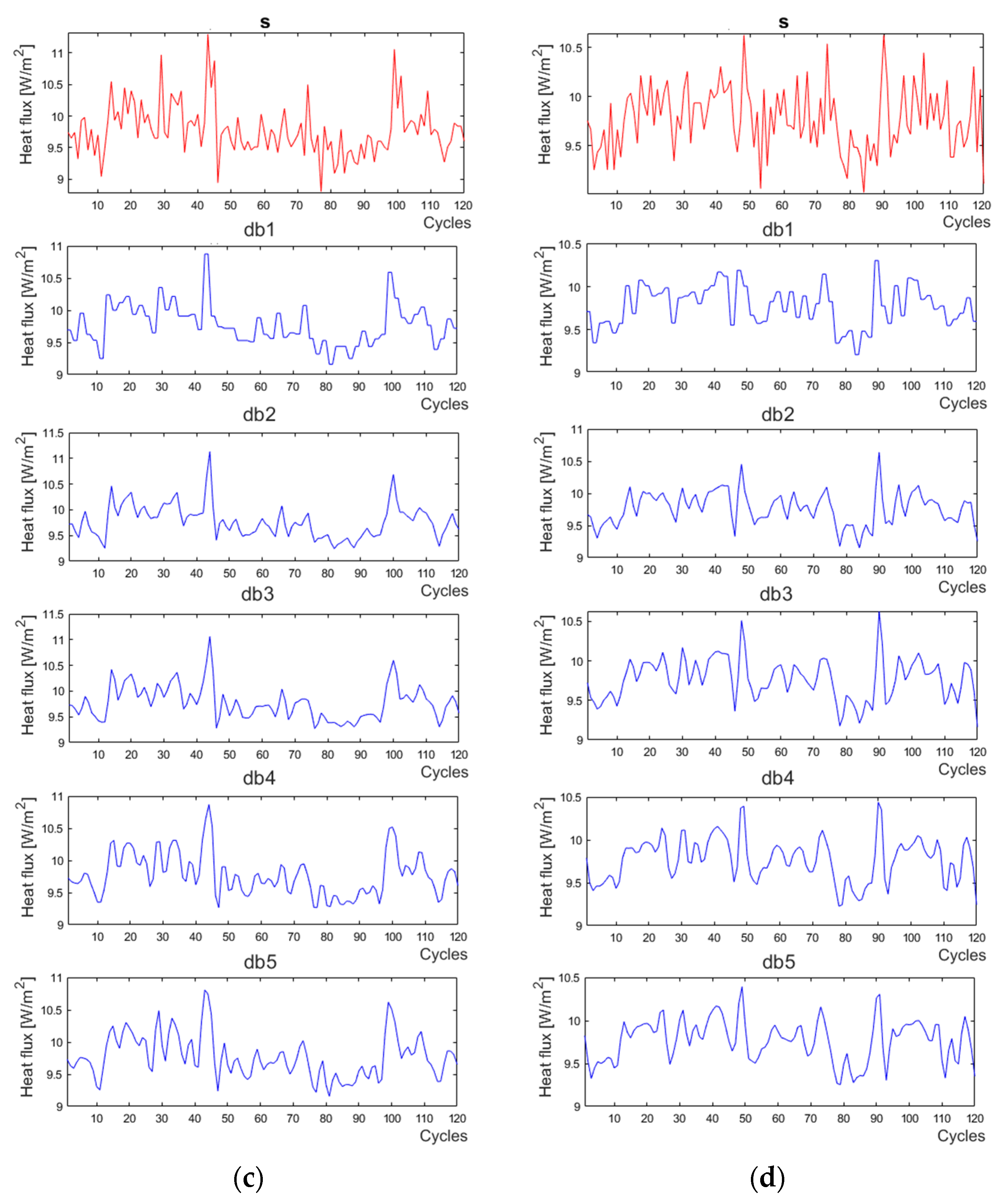
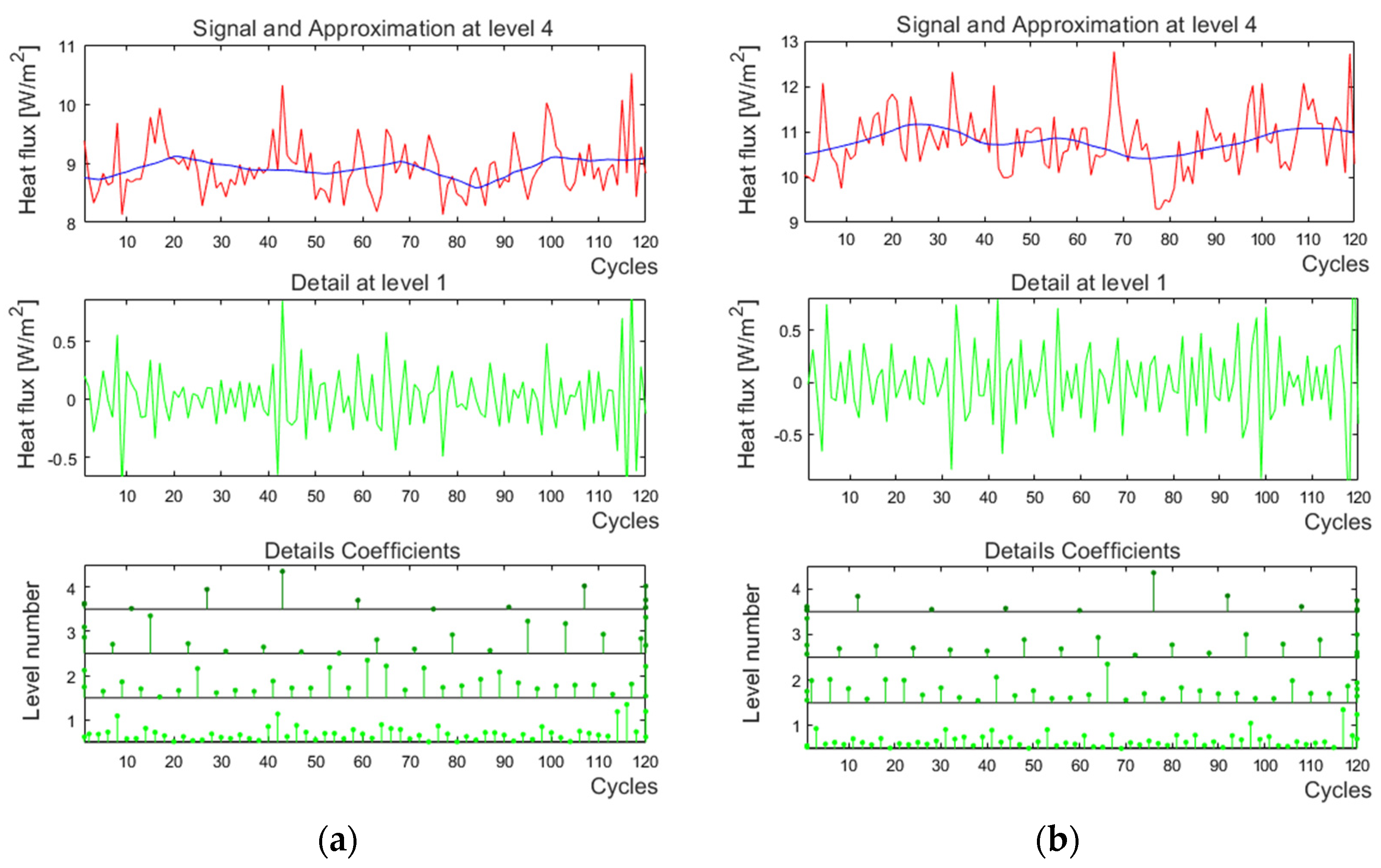
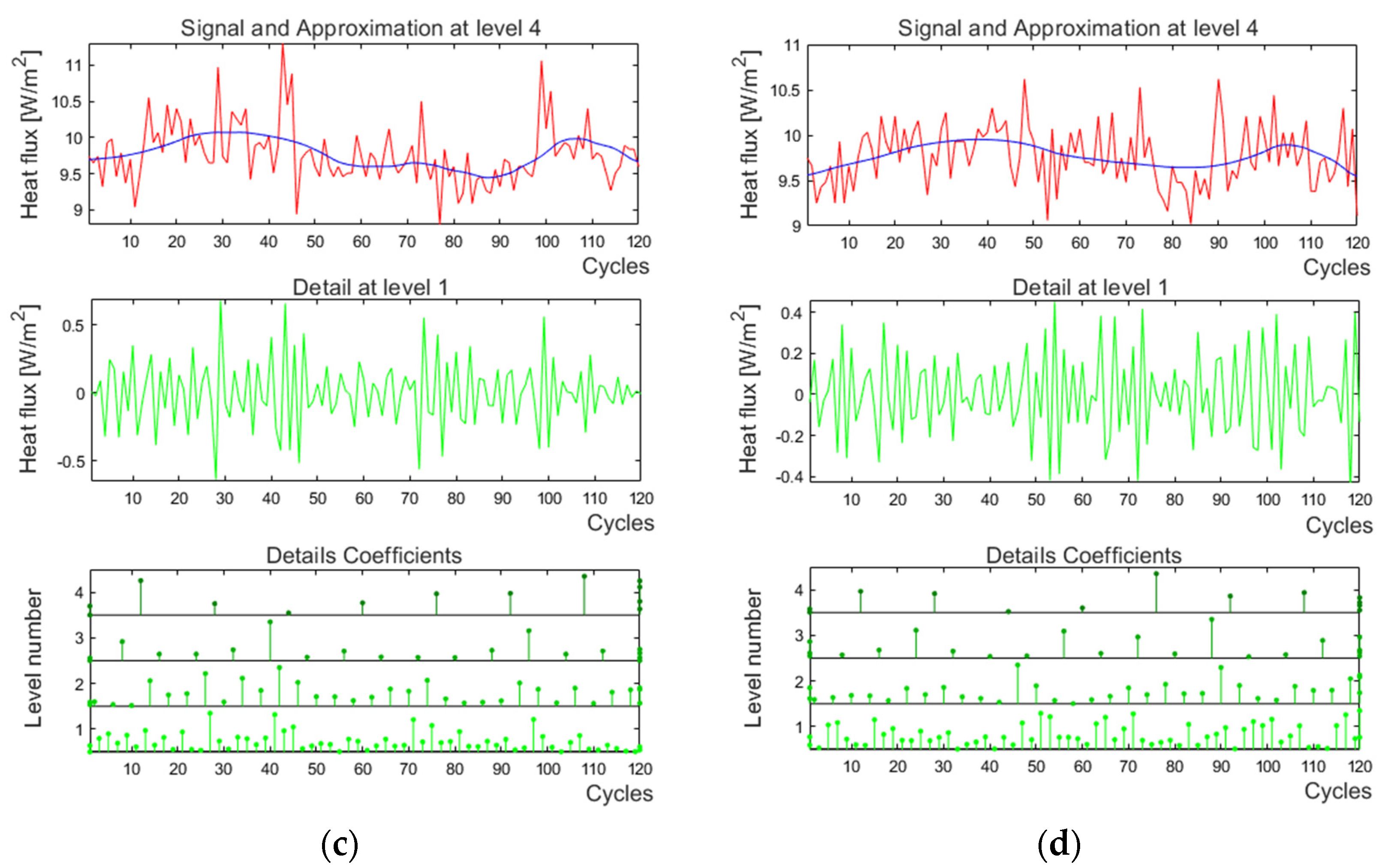
2.2. Methods of Data Processing
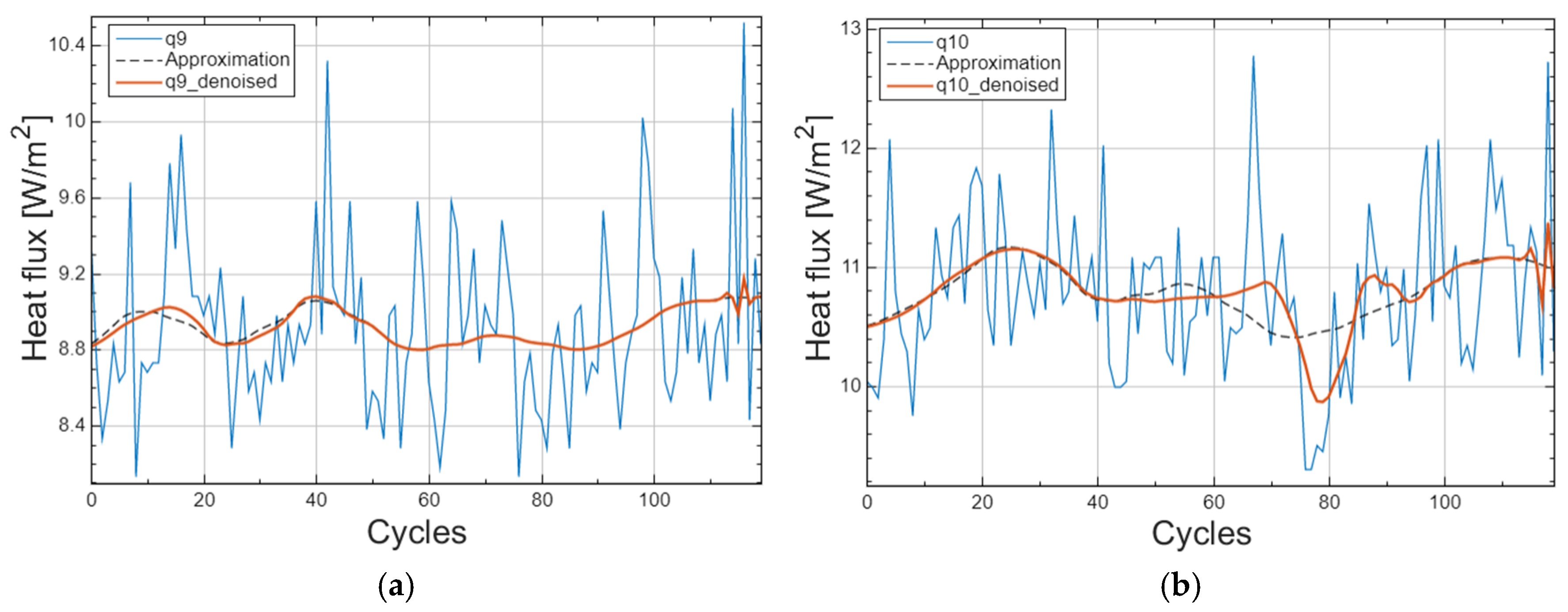
3. Results and Discussion
- An 8-channel ADC; 16 bits; a conversion rate of 10 Hz;
- Dynamic range setting and calibration;
- Support for industrial interface RS-485 and addressing, which makes it possible to create a measuring network.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| E | signal parameter (voltage) generated by heat flux sensor (mV) |
| K | calibration coefficient of heat flux sensor (W/(mV·m2)) |
| qi | heat flux density (W/m2) |
| Tsi | internal surface temperature (°C) |
| Tse | external surface temperature (°C) |
| Rc | theoretical value of thermal resistance calculated according to ISO 9869 (m2 K W−1) |
| thermal resistance obtained by heat flow meter (HFM) method (m2 K W−1) | |
| f(t) | discrete inverse wavelet transform of signal |
| wavelet | |
| signal | |
| m | scale factor |
| n | shift factor |
References
- Final Energy Consumption by Sector. Report of the European Parliamentary Research Service. Available online: https://epthinktank.eu/2022/06/16/monitoring-the-energy-situation-in-the-eu-june-2022/final-energy-consumption-by-sector/ (accessed on 20 November 2022).
- Ch, K.R.; Porpandiselvi, S.; Vishwanathan, N. A three-leg resonant converter for two output LED lighting application with independent control. Int. J. Circ. Theory Appl. 2019, 47, 1173–1187. [Google Scholar] [CrossRef]
- Devara, V.B.; Vishnuram, N.; Maity, T.; Shunmugam, P. Capacitor-sharing two-output series-resonant inverter for induction cooking application. IET Power Electron. 2016, 9, 2240–2248. [Google Scholar] [CrossRef]
- Vishnuram, P.; Ramachandiran, G. A simple multi-frequency multiload independent power control using pulse density modulation scheme for cooking applications. Int. Trans. Electr. Energ. Syst. 2021, 31, e12771. [Google Scholar] [CrossRef]
- Mroczka, J. The cognitive process in metrology. Measurement 2013, 46, 2896–2907. [Google Scholar] [CrossRef]
- ISO 9869-1; Thermal Insulation—Building Elements—In-Situ Measurement of Thermal Resistance and Thermal Transmittance—Part 1: Heat Flow Meter Method. ISO: Geneva, Switzerland, 2014.
- Lucchi, E. Thermal transmittance of historical brick masonries: A comparison among standard data, analytical calculation procedures, and in situ heat flow meter measurements. Energy Build. 2017, 134, 171–184. [Google Scholar] [CrossRef]
- ISO 6946; Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Method. ISO: Geneva, Switzerland, 2007.
- De Wilde, P. The gap between predicted and measured energy performance of buildings: A framework for investigation. Autom. Constr. 2014, 41, 40–49. [Google Scholar] [CrossRef]
- Danielski, I. Large variations in specific final energy use in Swedish apartment buildings: Causes and solutions. Energy Build. 2012, 49, 276–285. [Google Scholar] [CrossRef]
- Raposo, P.C.; Andrade, M.; Correia, J.A.F.O.; Salavessa, M.E.; Reis, C.; Oliveira, C.; de Jesus, A. Non-destructive structural wood diagnosis of a medieval building. Procedia Struct. Integr. 2017, 5, 1147–1152. [Google Scholar] [CrossRef]
- Costamagna, E.; Santana Quintero, M.; Bianchini, N.; Mendes, N.; Lourenço, P.B.; Su, S.; Paik, Y.M.; Min, A. Advanced non-destructive techniques for the diagnosis of historic buildings: The Loka-Hteik-Pan temple in Bagan. J. Cult. Herit. 2020, 43, 108–117. [Google Scholar] [CrossRef]
- Soares, N.; Martins, C.; Goncalves, M.; Santos, P.; da Silva, L.S.; Costa, J.J. Laboratory and in-situ non-destructive methods to evaluate the thermal transmittance and behavior of walls, windows, and construction elements with innovative materials: A review. Energy Build. 2019, 182, 88–110. [Google Scholar] [CrossRef]
- Teni, M.; Krstić, H.; Kosiński, P. Review and comparison of current experimental approaches for in-situ measurements of building walls thermal transmittance. Energy Build. 2019, 203, 109417. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Moyano, J.; Marín, D.; Fresco-Contreras, R. Review of in situ methods for assessing the thermal transmittance of walls. Renew. Sustain. Energy Rev. 2019, 102, 356–371. [Google Scholar] [CrossRef]
- Ahmad, A.; Maslehuddin, M.; Al-Hadhrami, L.M. In situ measurement of thermal transmittance and thermal resistance of hollow reinforced precast concrete walls. Energy Build. 2014, 84, 132–141. [Google Scholar] [CrossRef]
- Meng, X.; Yan, B.; Gao, Y.; Wang, J.; Zhang, W.; Long, E. Factors affecting the in situ measurement 383 accuracy of the wall heat transfer coefficient using the heat flow meter method. Energy Build. 2015, 86, 754–765. [Google Scholar] [CrossRef]
- Cucumo, M.; Ferraro, V.; Kaliakatsos, D.; Mele, M. On the distortion of thermal flux and of surface temperature induced by heat flux sensors positioned on the inner surface of buildings. Energy Build. 2018, 158, 677–683. [Google Scholar] [CrossRef]
- Evangelisti, L.; Guattari, C.; Asdrubali, F. Comparison between heat-flow meter and Air-Surface Temperature Ratio techniques for assembled panels thermal characterization. Energy Build. 2019, 203, 109441. [Google Scholar] [CrossRef]
- Hoffmann, C.; Geissler, A. The prebound-effect in detail: Real indoor temperatures in basements and measured versus calculated U-values. Energy Procedia 2017, 122, 32–37. [Google Scholar] [CrossRef]
- Gaspar, K.; Casals, M.; Gangolells, M. Review of criteria for determining HFM minimum test duration. Energy Build. 2018, 176, 360–370. [Google Scholar] [CrossRef]
- Gori, V.; Elwell, C.A. Estimation of thermophysical properties from in-situ measurements in all seasons: Quantifying and reducing errors using dynamic grey-box methods. Energy Build. 2018, 167, 290–300. [Google Scholar] [CrossRef]
- Evangelisti, L.; Guattari, C.; Asdrubali, F. Influence of heating systems on thermal transmittance evaluations: Simulations, experimental measurements and data postprocessing. Energy Build. 2018, 168, 180–190. [Google Scholar] [CrossRef]
- Tao, T.; Ji, C.; Han, C.; Wang, J.; Sun, W. Study on the noise contents of different measurements in industrial process and their impact on process monitoring. Comput. Aided Chem. Eng. 2022, 51, 1057–1062. [Google Scholar] [CrossRef]
- Mittal, R.C.; Pandit, S. Numerical simulation of unsteady squeezing nanofluid and heat flow between two parallel plates using wavelets. Int. J. Therm. Sci. 2017, 118, 410–422. [Google Scholar] [CrossRef]
- Massa, L. Multiresolution Reconstruction of the Hypersonic Heat Flux. Int. J. Heat Mass Transf. 2022, 190, 122772. [Google Scholar] [CrossRef]
- Kegerise, M.A.; Rufer, S.J. Unsteady heat-flux measurements of second-mode instability waves in a hypersonic flat-plate boundary layer. Exp. Fluids 2016, 57, 130. [Google Scholar] [CrossRef]
- Chuli, F.; Chunyu, Q. Wavelet and error estimation of surface heat flux. J. Comput. Appl. Math. 2003, 150, 143–155. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, T.; Zhu, X.; Yang, K.; Ge, Q.; Wang, M.; Yang, Q. Inverse estimation of hot-wall heat flux using nonlinear artificial neural networks. Measurement 2021, 181, 109648. [Google Scholar] [CrossRef]
- Pagliarini, L.; Cattani, L.; Bozzoli, F.; Mameli, M.; Filippeschi, S.; Rainieri, S.; Marengo, M. Thermal characterization of a multi-turn pulsating heat pipe in microgravity conditions: Statistical approach to the local wall-to-fluid heat flux. Int. J. Heat Mass Transf. 2021, 169, 120930. [Google Scholar] [CrossRef]
- Iwata, N.; Bozzoli, F.; Pagliarini, L.; Cattani, L.; Vocale, P.; Malavasi, M.; Rainieri, S. Characterization of thermal behavior of a micro pulsating heat pipe by local heat transfer investigation. Int. J. Heat Mass Transf. 2022, 196, 123203. [Google Scholar] [CrossRef]
- Gong, M.; Wang, J.; Bai, Y.; Li, B.; Zhang, L. Heat load prediction of residential buildings based on discrete wavelet transform and tree-based ensemble learning. J. Build. Eng. 2020, 32, 101455. [Google Scholar] [CrossRef]
- Kumbinarasaiah, S.; Raghunatha, K.R. The applications of Hermite wavelet method to nonlinear differential equations arising in heat transfer. Int. J. 2021, 9, 100066. [Google Scholar] [CrossRef]
- Aznam, S.M.; Ghani, N.A.C.; Chowdhury, M.S.H. A numerical solution for nonlinear heat transfer of fin problems using the Haar wavelet quasilinearization method. Results Phys. 2019, 14, 102393. [Google Scholar] [CrossRef]
- Jahangiri, A.; Mohammadi, S.; Akbari, M. Modeling the one-dimensional inverse heat transfer problem using a Haar wavelet collocation approach. Phys. A Stat. Mech. Its Appl. 2019, 525, 13–26. [Google Scholar] [CrossRef]
- Awati Vishwanath, B.; Kumar, N.M.; Wakif, A. Haar wavelet scrutinization of heat and mass transfer features during the convective boundary layer flow of a nanofluid moving over a nonlinearly stretching sheet. Partial. Differ. Equ. Appl. Math. 2021, 4, 100192. [Google Scholar] [CrossRef]
- Hotra, O.; Kovtun, S.; Dekusha, O.; Grądz, Ż. Prospects for the Application of Wavelet Analysis to the Results of Thermal Conductivity Express Control of Thermal Insulation Materials. Energies 2021, 14, 5223. [Google Scholar] [CrossRef]
- ISO 8301; Thermal Insulation—Determination of Steady-State Thermal Resistance and Related Properties—Heat Flow Meter Apparatus. ISO: Geneva, Switzerland, 1991.
- Białasiewicz, J.T. Falki i Aproksymacje; WNT: Warszaw, Poland, 2000. [Google Scholar]
- Lina, J.-M.; Turcotte, P.; Goulard, B. Complex Dyadic Multiresolution Analyses. In Advances in Imaging and Electron Physics; Hawkes, P.W., Ed.; Elsevier: Amsterdam, The Netherlands, 1999; Volume 109, pp. 163–197. [Google Scholar] [CrossRef]
- Shen, X.; Walter, G. Meyer wavelet regularization. Numer. Funct. Anal. Optim. 2006, 23, 195–215. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Hotra, O.; Kovtun, S.; Dekusha, O. Analysis of the characteristics of bimetallic and semiconductor heat flux sensors for in-situ measurements of envelope element thermal resistance. Measurement 2021, 182, 109713. [Google Scholar] [CrossRef]
- Babak, V.; Dekusha, O.; Kovtun, S.; Ivanov, S. Information-measuring system for monitoring thermal resistance. CEUR Workshop Proc. 2019, 2387, 102–110. Available online: http://ceur-ws.org/Vol-2387/20190102.pdf (accessed on 25 November 2022).
- ISO 6781; Thermal Insulation—Qualitative Detection of Thermal Irregularities in Building Envelopes—Infrared Method. ISO: Geneva, Switzerland, 2015.
- EN 13187; Thermal Performance of Buildings—Qualitative Detection of Thermal Irregularities in Building Envelopes—Infrared Method. CEN: Brussels, Belgium, 2000.
- Ding, Y.; Zhang, Q.; Yuan, T.; Yang, K. Model input selection for building heating load prediction: A case study for an office building in Tianjin. Energy Build. 2018, 159, 254–270. [Google Scholar] [CrossRef]







| Material | Thickness, m | Thermal Conductivity, W/(m·K) |
|---|---|---|
| PUF | 0.03 | 0.0346 |
| Concrete blocks | 0.40 | 0.5200 |
| Signals of Heat Flux Sensors | Average Heat Flux, W/m2 | Maximum Heat Flux, W/m2 | Minimum Heat Flux, W/m2 | Standard Deviation |
|---|---|---|---|---|
| q9 | 9.02 | 10.52 | 8.13 | 0.44 |
| q10 | 10.89 | 12.77 | 9.30 | 0.67 |
| q11 | 9.87 | 11.30 | 8.80 | 0.41 |
| q12 | 9.85 | 10.62 | 9.02 | 0.33 |
| Signals of Heat Flux Sensors | Standard Deviation | Standard Deviation after Denoising |
|---|---|---|
| q9 | 0.44 | 0.09 |
| q10 | 0.67 | 0.22 |
| q11 | 0.41 | 0.19 |
| q12 | 0.33 | 0.11 |
| q9, W/m2 | Tsi9, °C | Tse9, °C | q10, W/m2 | Tsi10, °C | Tse10, °C | q11, W/m2 | Tsi11, °C | Tse11, °C | q12, W/m2 | Tsi12, °C | Tse12, °C | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Averaged | 9.02 | 17.40 | 2.87 | 10.89 | 17.89 | 2.52 | 9.87 | 17.57 | 2.71 | 9.85 | 17.79 | 2.88 |
| Denoised | 8.92 | 17.42 | 2.61 | 10.79 | 17.89 | 2.53 | 9.78 | 17.61 | 2.42 | 9.77 | 17.83 | 2.62 |
| RHFM9, (m2·K)/W | RHFM10, (m2·K)/W | RHFM11, (m2·K)/W | RHFM12, (m2·K)/W | |
|---|---|---|---|---|
| Averaged | 1.611 | 1.420 | 1.500 | 1.510 |
| Denoised | 1.661 | 1.420 | 1.550 | 1.558 |
| Averaged RHFM, (m2·K)/W | Denoised RHFM, (m2·K)/W | Theoretical Rc, (m2·K)/W | |
|---|---|---|---|
| Value | 1.543 | 1.591 | 1.637 |
| DEV (%) | 5.74 | 2.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hotra, O.; Kovtun, S.; Dekusha, O.; Grądz, Ż.; Babak, V.; Styczeń, J. Analysis of Low-Density Heat Flux Data by the Wavelet Method. Energies 2023, 16, 430. https://doi.org/10.3390/en16010430
Hotra O, Kovtun S, Dekusha O, Grądz Ż, Babak V, Styczeń J. Analysis of Low-Density Heat Flux Data by the Wavelet Method. Energies. 2023; 16(1):430. https://doi.org/10.3390/en16010430
Chicago/Turabian StyleHotra, Oleksandra, Svitlana Kovtun, Oleg Dekusha, Żaklin Grądz, Vitalii Babak, and Joanna Styczeń. 2023. "Analysis of Low-Density Heat Flux Data by the Wavelet Method" Energies 16, no. 1: 430. https://doi.org/10.3390/en16010430
APA StyleHotra, O., Kovtun, S., Dekusha, O., Grądz, Ż., Babak, V., & Styczeń, J. (2023). Analysis of Low-Density Heat Flux Data by the Wavelet Method. Energies, 16(1), 430. https://doi.org/10.3390/en16010430







