Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Improved Variational Mode Decomposition and Machine Learning Algorithm
Abstract
1. Introduction
- (1)
- A new method for predicting the RUL of lithium-ion batteries is proposed. First, the measured battery capacity sequence is decomposed by the VMD algorithm, and the capacity data are decomposed into residual components and capacity regeneration components. Second, the residual component is predicted by the LSTM algorithm, and the capacity regeneration component is predicted by the GPR algorithm. Last, the predicted components are added to predict the RUL of the battery. This method solved the problem of low accuracy of individual models and the inability to fully predict the battery degradation trend.
- (2)
- An improved variational modal decomposition algorithm is proposed. The value of modal layers K and the penalty parameter α in the VMD algorithm are generated by the WOA with the minimum envelope entropy as the fitness function. The decomposed components are more easily captured by the subsequent prediction algorithms, which improve the prediction accuracy and are verified in subsequent RUL prediction experiments.
2. Prediction Model
2.1. Vmd Algorithm
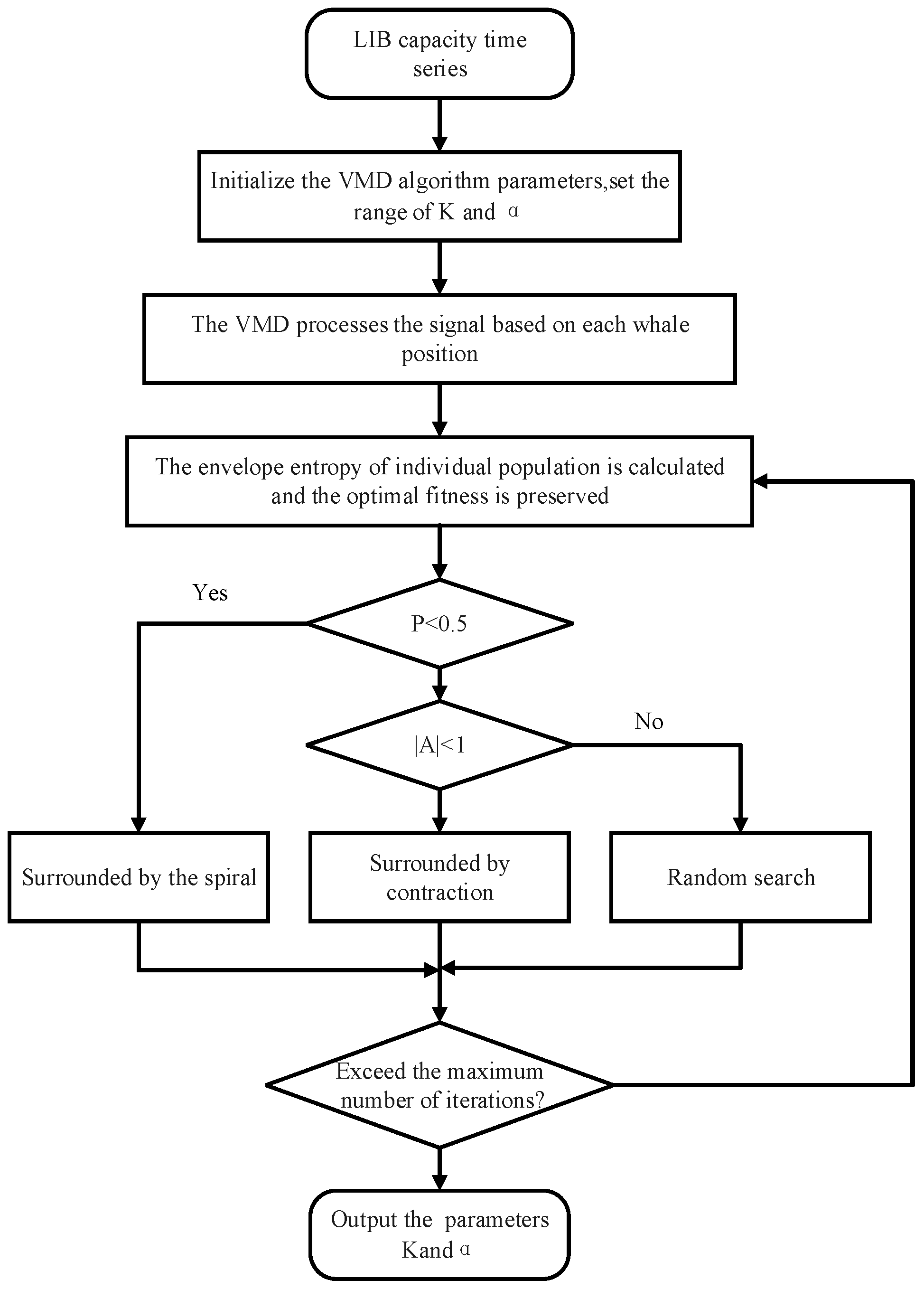
2.2. Improvement of the VMD Algorithm
- (1)
- The lithium-ion battery capacity sequence is input, the parameter ranges of K and α are set in VMD, and the main parameters in the WOA, including the size of the population, maximum number of iterations, and number of variables, are initialized.
- (2)
- VMD decomposition is performed on the input capacity sequence, where the number of modal component K and penalty factor α are optimized by the WOA, the envelope entropy corresponding to each whale individual is calculated, and the optimal individual position is recorded.
- (3)
- The location of individual whales is updated.
- (4)
- Repeat steps (2) to (4) and output the best parameter combination (K, α) when the minimum envelope entropy value or the maximum number of iterations is reached;
- (5)
- VMD decomposition is performed on the signal according to the output parameter combination (K, α).
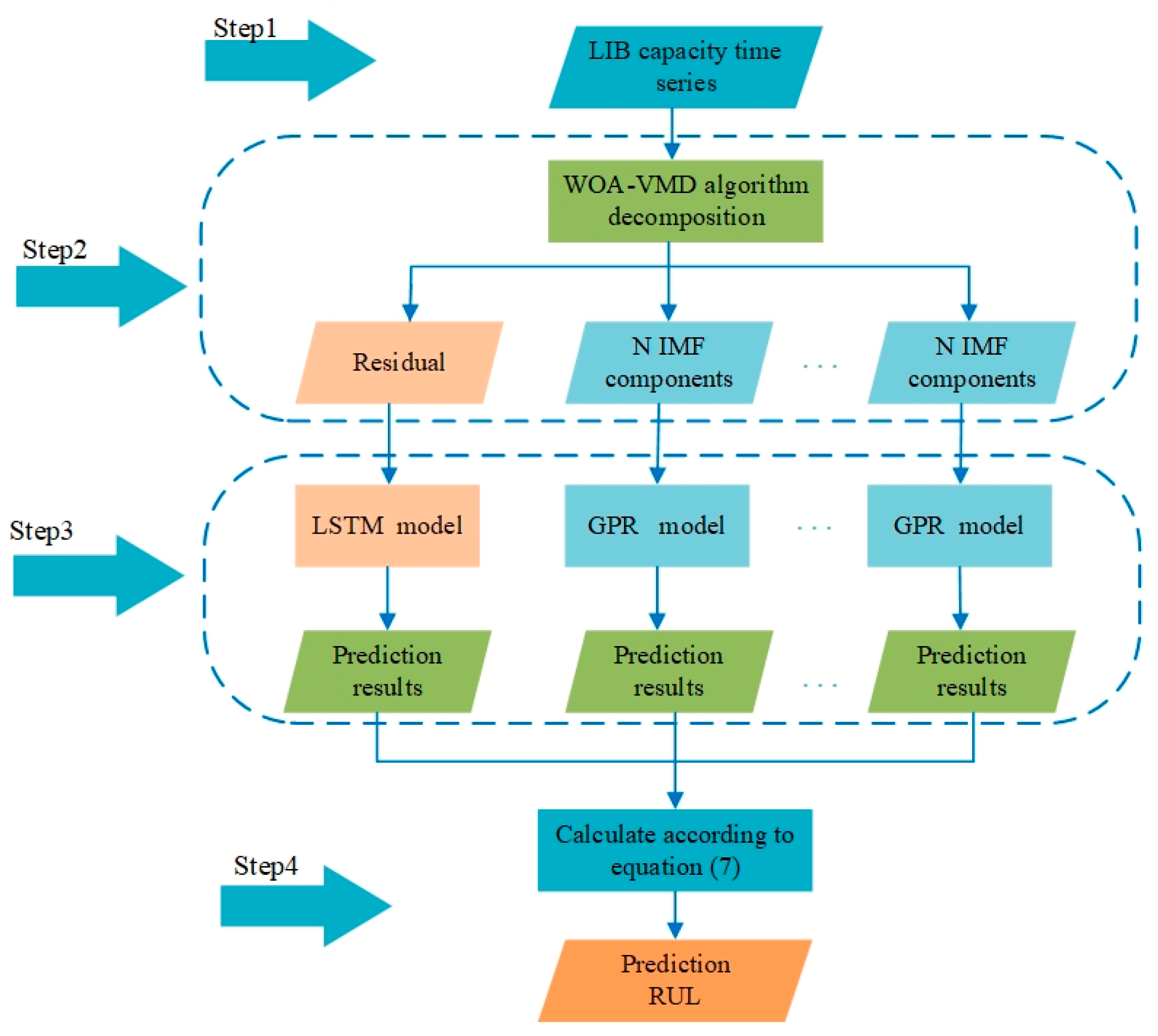
2.3. Experimental Procedures
- (1)
- Obtain the measured lithium-ion battery capacity degradation data.
- (2)
- Based on the improved VMD algorithm, the optimal parameter combination [K, α] is selected. The lithium-ion battery capacity degradation sequence is decomposed into residual and capacity recovery components through WOA-VMD.
- (3)
- The residual component obtained after decomposition is trained and predicted by the LSTM network. The residual component reflects the overall degradation trend of the battery and has stability. The LSTM algorithm has a good effect on time series prediction. The decomposed capacity recovery component reflects the capacity regeneration phenomenon of the battery, so the GPR algorithm is selected for fitting prediction.
- (4)
- The predicted residual component and capacity recovery components are added according to Formula (7) to obtain the predicted capacity data and to simultaneously calculate the RUL of the battery.
3. Experimental Verification and Analysis
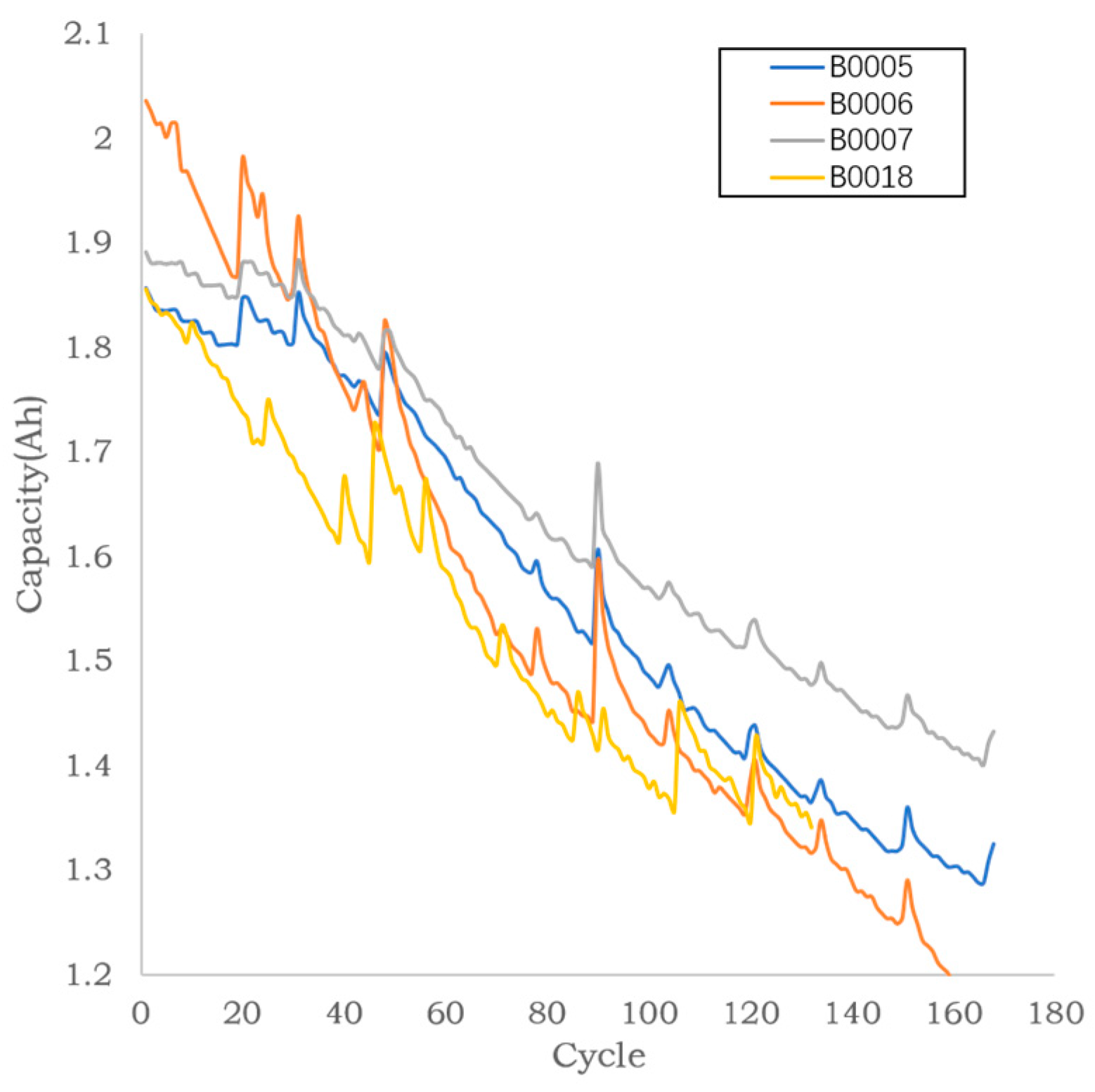
3.1. Datasets
3.2. Evaluation Criterion
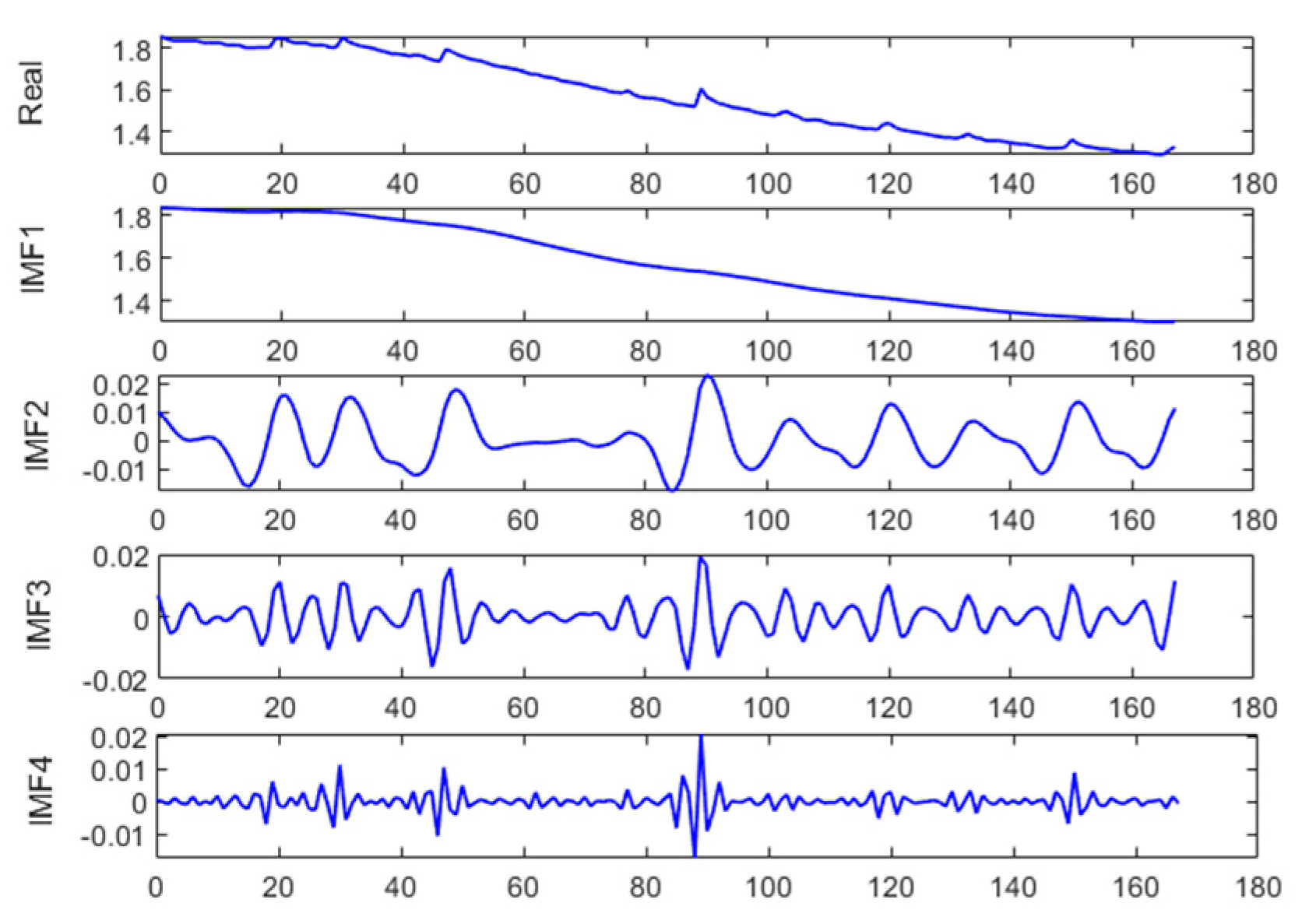
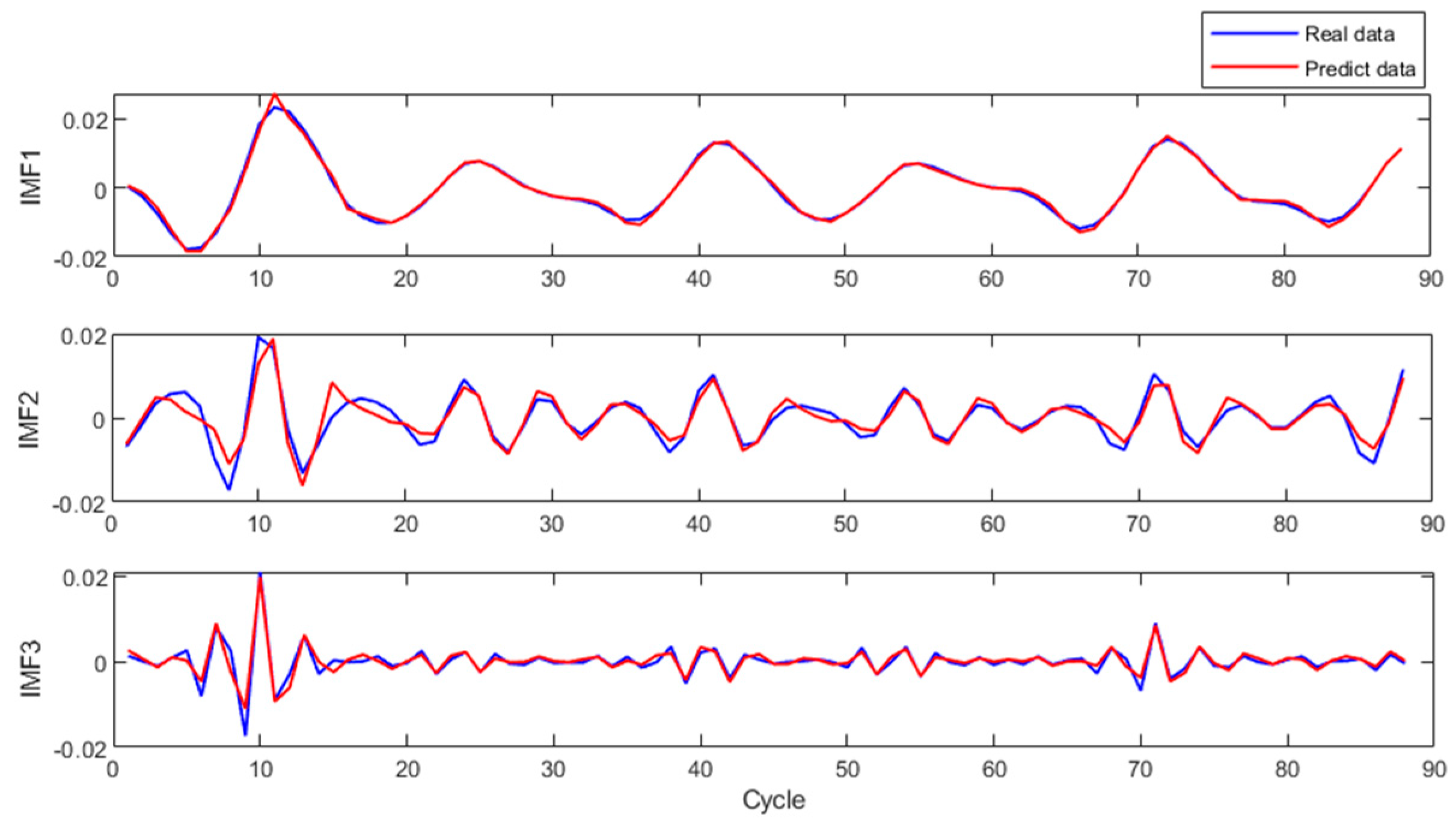
3.3. Decomposition of Lithium-Ion Battery Capacity Squence by WOA-VMD
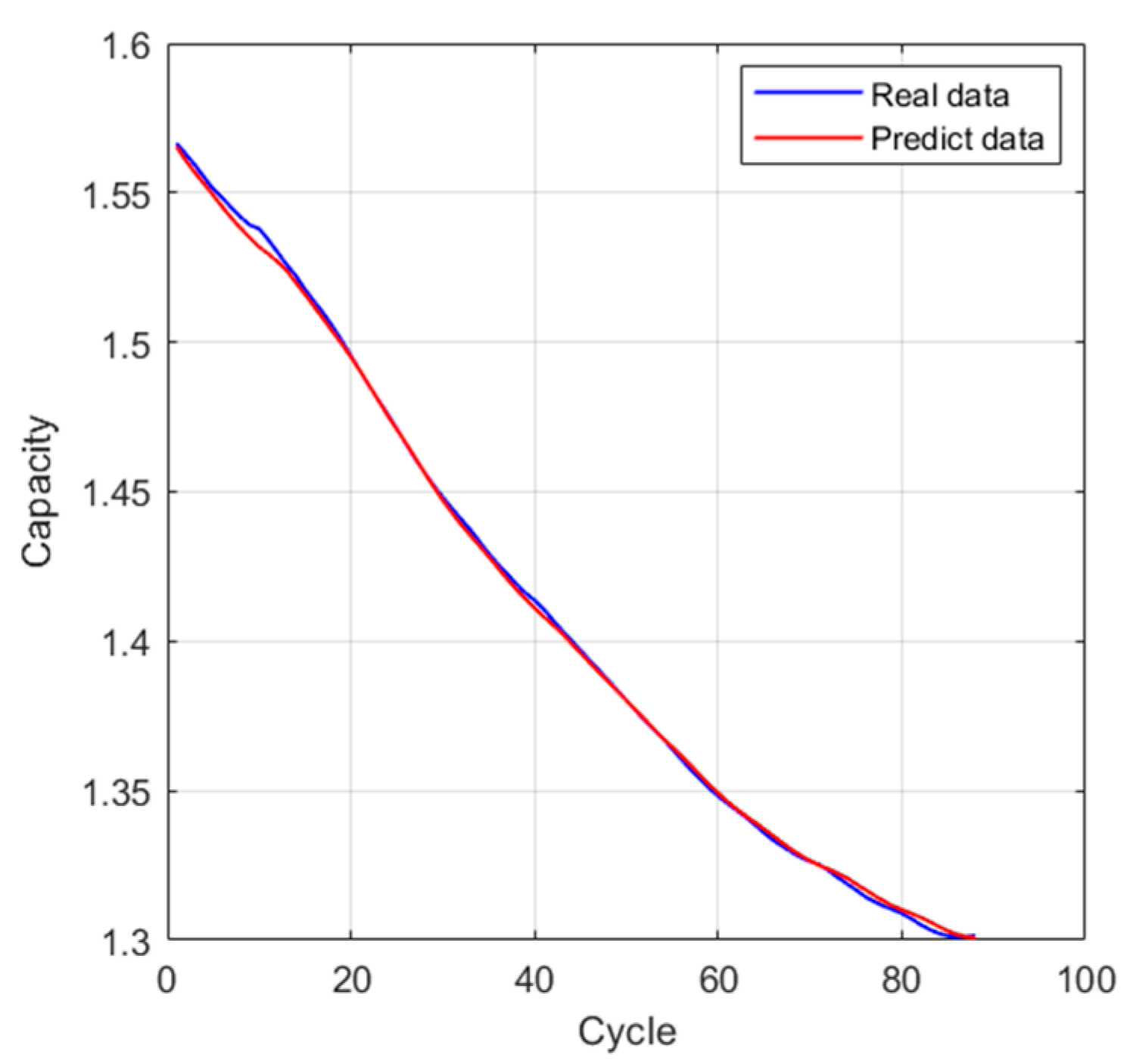
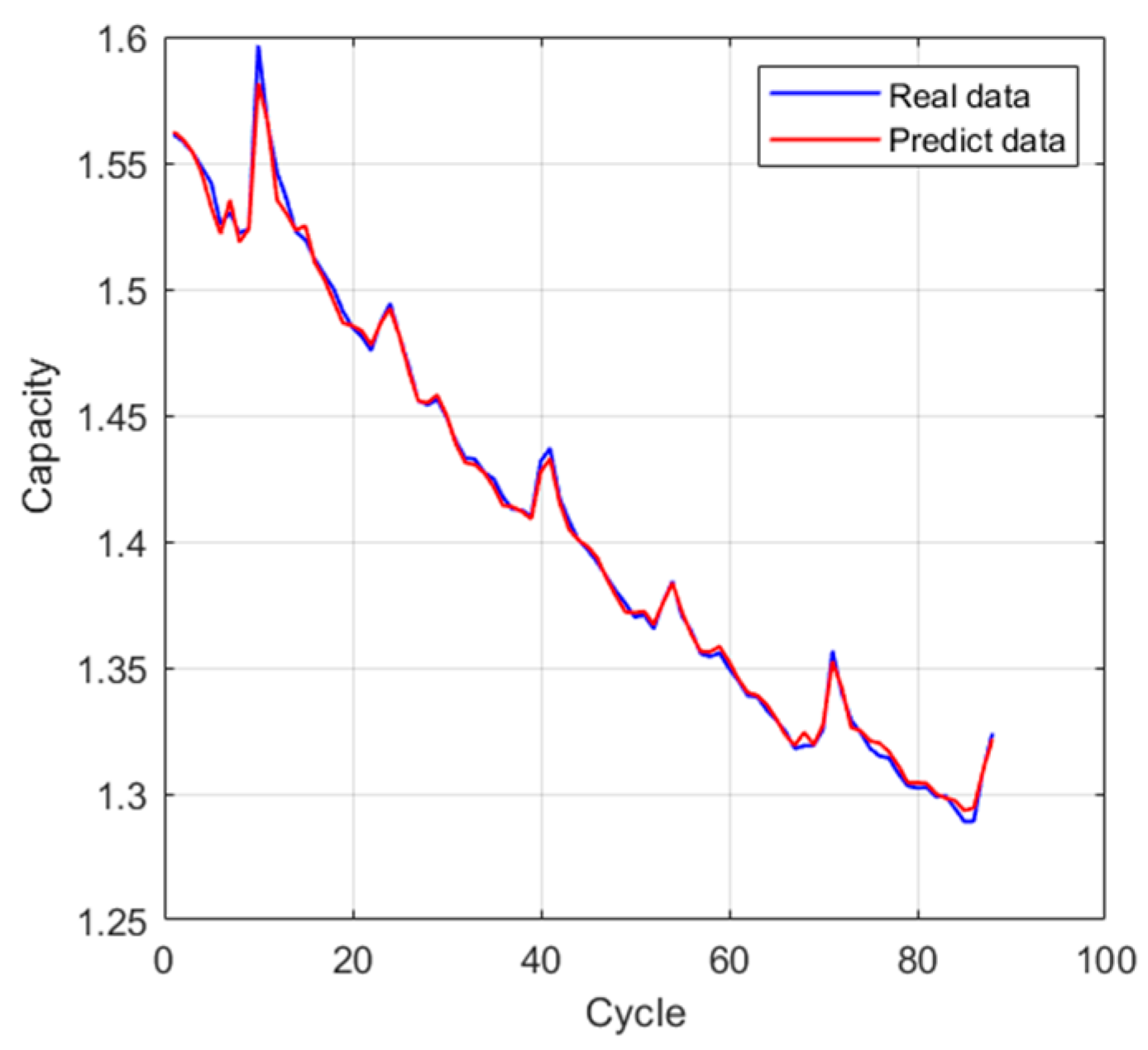
3.4. RUL Prediction of LIBs
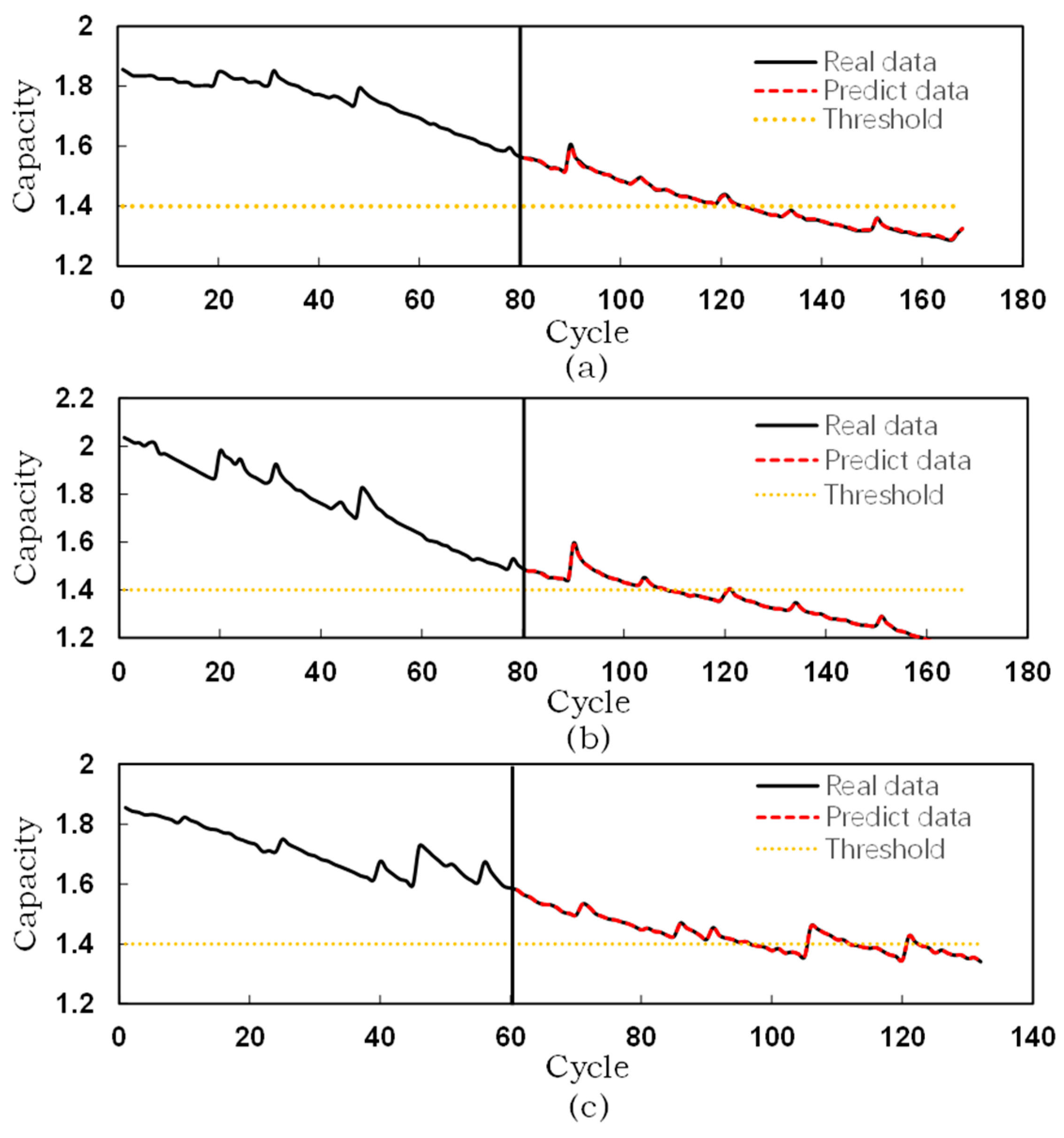
3.5. Battery RUL Prediction and Comparison with Different Prediction Starting Points
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Swornowski, P.J. Destruction mechanism of the internal structure in Lithium-ion batteries used in aviation industry. Energy 2017, 122, 779–786. [Google Scholar] [CrossRef]
- Pang, X.; Huang, R.; Wen, J.; Shi, Y.; Jia, J.; Zeng, J. A Lithium-ion Battery RUL Prediction Method Considering the Capacity Regeneration Phenomenon. Energies 2019, 12, 2247. [Google Scholar] [CrossRef]
- Wang, F.-K.; Mamo, T. A hybrid model based on support vector regression and differential evolution for remaining useful lifetime prediction of lithium-ion batteries. J. Power Sources 2018, 401, 49–54. [Google Scholar] [CrossRef]
- Yun, Z.; Qin, W.; Shi, W.; Ping, P. State-of-Health Prediction for Lithium-Ion Batteries Based on a Novel Hybrid Approach. Energies 2020, 13, 4858. [Google Scholar] [CrossRef]
- Khan, H.; Nizami, I.F.; Qaisar, S.M.; Waqar, A.; Krichen, M.; Almaktoom, A.T. Analyzing Optimal Battery Sizing in Microgrids Based on the Feature Selection and Machine Learning Approaches. Energies 2022, 15, 7865. [Google Scholar] [CrossRef]
- Tian, H.; Qin, P.; Li, K.; Zhao, Z. A review of the state of health for lithium-ion batteries: Research status and suggestions. J. Clean. Prod. 2020, 261, 120813. [Google Scholar] [CrossRef]
- Shimamoto, A.T.; Tanaka, B.R.; Tanaka, C.K. A study on evaluation method for the Lithium-ion battery life performance for stationary use. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; pp. 115–119. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on Dempster–Shafer theory and the Bayesian Monte Carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, Z.; Sun, C. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Exponential Model and Particle Filter. IEEE Access 2018, 6, 17729–17740. [Google Scholar] [CrossRef]
- He, Z.; Gao, M.; Xu, J. EKF-Ah Based State of Charge Online Estimation for Lithium-ion Power Battery. In Proceedings of the 2009 International Conference on Computational Intelligence and Security, Beijing, China, 11–14 December 2009; pp. 142–145. [Google Scholar]
- Xiong, R.; Zhang, Y.; He, H.; Zhou, X.; Pecht, M.G. A Double-Scale, Particle-Filtering, Energy State Prediction Algorithm for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2017, 65, 1526–1538. [Google Scholar] [CrossRef]
- Kim, S.; Park, H.J.; Choi, J.-H.; Kwon, D. A Novel Prognostics Approach Using Shifting Kernel Particle Filter of Li-Ion Batteries Under State Changes. IEEE Trans. Ind. Electron. 2020, 68, 3485–3493. [Google Scholar] [CrossRef]
- Xu, J.; Zhen, A.; Cai, Z.; Wang, P.; Gao, K.; Jiang, D. State of Health Diagnosis and Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Multi-Feature Data and Mechanism Fusion. IEEE Access 2021, 9, 85431–85441. [Google Scholar] [CrossRef]
- Qiu, X.; Wu, W.; Wang, S. Remaining useful life prediction of lithium-ion battery based on improved cuckoo search particle filter and a novel state of charge estimation method. J. Power Sources 2020, 450, 227700. [Google Scholar] [CrossRef]
- Xiong, W.; Mo, Y.; Yan, C. Online State-of-Health Estimation for Second-Use Lithium-Ion Batteries Based on Weighted Least Squares Support Vector Machine. IEEE Access 2020, 9, 1870–1881. [Google Scholar] [CrossRef]
- Zhang, S.; Zhai, B.; Guo, X.; Wang, K.; Peng, N.; Zhang, X. Synchronous estimation of state of health and remaining useful lifetime for lithiu m-ion battery using the incremental capacity and artificial neural networks. J. Energy Storage 2019, 26, 100951. [Google Scholar] [CrossRef]
- Feng, H.; Song, D. A health indicator extraction based on surface temperature for lithium-ion batteries remaining useful life prediction. J. Energy Storage 2020, 34, 102118. [Google Scholar] [CrossRef]
- Chang, Y.; Fang, H. A hybrid prognostic method for system degradation based on particle filter and relevance vector machine. Reliab. Eng. Syst. Saf. 2019, 186, 51–63. [Google Scholar] [CrossRef]
- Catelani, M.; Ciani, L.; Fantacci, R.; Patrizi, G.; Picano, B. Remaininguseful life estimation for prognostics of lithium-ion batteries basedon recurrent neural network. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Yang, Y. A machine-learning prediction method of lithium-ion battery life based on charge process for different applications. Appl. Energy 2021, 292, 116897. [Google Scholar] [CrossRef]
- Wei, M.; Gu, H.; Ye, M.; Wang, Q.; Xu, X.; Wu, C. Remaining useful life prediction of lithium-ion batteries based on Monte Carlo Dropout and gated recurrent unit. Energy Rep. 2021, 7, 2862–2871. [Google Scholar] [CrossRef]
- Zhu, T.; Li, Y.; Li, Z.; Guo, Y.; Ni, C. Inter-Hour Forecast of Solar Radiation Based on Long Short-Term Memory with Attention Mechanism and Genetic Algorithm. Energies 2022, 15, 1062. [Google Scholar] [CrossRef]
- Zhang, M.; Kang, G.; Wu, L.; Guan, Y. A method for capacity prediction of lithium-ion batteries under small sample conditions. Energy 2022, 238, 122094. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Yan, J. Prognostic health condition for lithium battery using the partial incremental capacity and Gaussian process regression. J. Power Sources 2019, 421, 56–67. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Gaussian process regression for forecasting battery state of health. J. Power Sources 2017, 357, 209–219. [Google Scholar] [CrossRef]
- Yu, J. State of health prediction of lithium-ion batteries: Multiscale logic regression and Gaussian process regression ensemble. Reliab. Eng. Syst. Saf. 2018, 174, 82–95. [Google Scholar] [CrossRef]
- Tong, Z.; Miao, J.; Tong, S.; Lu, Y. Early prediction of remaining useful life for Lithium-ion batteries based on a hybrid machine learning method. J. Clean. Prod. 2021, 317, 128265. [Google Scholar] [CrossRef]
- Ren, L.; Dong, J.; Wang, X.; Meng, Z.; Zhao, L.; Deen, M.J. A Data-Driven Auto-CNN-LSTM Prediction Model for Lithium-Ion Battery Remaining Useful Life. IEEE Trans. Ind. Inform. 2020, 17, 3478–3487. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Wang, Z.; Dong, P. Remaining useful life prediction for lithium-ion batteries based on a hybrid model combining the long short-term memory and Elman neural networks. J. Energy Storage 2019, 21, 510–518. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, X.; He, Y. Remaining useful life and state of health prediction for lithium batteries based on empirical mode decomposition and a long and short memory neural network. Energy 2021, 232, 121022. [Google Scholar] [CrossRef]
- Gai, J.; Shen, J.; Hu, Y.; Wang, H. An integrated method based on hybrid grey wolf optimizer improved variational mode decomposition and deep neural network for fault diagnosis of rolling bearing. Measurement 2020, 162, 107901. [Google Scholar] [CrossRef]
- Li, C.; Peng, T.; Zhu, Y. A Novel Approach for Acoustic Signal Processing of a Drum Shearer Based on Improved Variational Mode Decomposition and Cluster Analysis. Sensors 2020, 20, 2949. [Google Scholar] [CrossRef]
- Lv, H.; Xu, S.; Liu, Y.; Luo, W. Evaluation and Comparison of Air Pollution Governance Performance: An Empirical Study Based on Jiangxi Province. Sustainability 2022, 14, 15397. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, K.; Cheng, R.; Zhang, Y. A Novel Temperature Error Compensation method for MEMS Gyros Based on WOA-SVR. In Proceedings of the 2021 IEEE International Conference on Computer Science, Artificial Intelligence and Electronic Engineering (CSAIEE), Greenville, SC, USA, 20–22 August 2021; pp. 292–295. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K.; Poll, S.; Christophersen, J. Prognostics Methods for Battery H36ealth Monitoring Using a Bayesian Framework. IEEE Trans. Instrum. Meas. 2009, 58, 291–296. [Google Scholar] [CrossRef]
- Qu, J.; Liu, F.; Ma, Y.; Fan, J. A Neural-Network-Based Method for RUL Prediction and SOH Monitoring of Lithium-Ion Battery. IEEE Access 2019, 7, 87178–87191. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.; Kong, C. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on a Mixture of Ensemble Empirical Mode Decomposition and GWO-SVR Model. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Hu, X.; Yang, X.; Feng, F.; Liu, K.; Lin, X. A Particle Filter and Long Short-Term Memory Fusion Technique for Lithium-Ion Battery Remaining Useful Life Prediction. J. Dyn. Syst. Meas. Control 2021, 143, 061001. [Google Scholar] [CrossRef]

| Battery Number | CV/V | DV/V | CC/A | DC/A | TS/AH |
|---|---|---|---|---|---|
| B0005 | 4.2 | 2.7 | 1.5 | 2.0 | 1.4 |
| B0006 | 4.2 | 2.5 | 1.5 | 2.0 | 1.4 |
| B0007 | 4.2 | 2.2 | 1.5 | 2.0 | 1.4 |
| B0018 | 4.2 | 2.5 | 1.5 | 2.0 | 1.4 |
| Battery Number | K | α | Envelope Entropy |
|---|---|---|---|
| B0005 | 4 | 92 | 6.7876 |
| B0006 | 4 | 20 | 6.837 |
| B0007 | 4 | 151 | 6.7489 |
| B0018 | 5 | 709 | 6.5357 |
| Battery Number | Correlation Coefficient | ||||
|---|---|---|---|---|---|
| IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | |
| B0005 | 0.9979 | 0.1025 | 0.0516 | 0.0325 | - |
| B0006 | 0.9954 | 0.1417 | 0.0669 | 0.0419 | - |
| B0007 | 0.9976 | 0.1142 | 0.0535 | 0.0353 | - |
| B0018 | 0.9931 | 0.0922 | 0.0854 | 0.0507 | 0.0467 |
| Model | Parameters | Values |
|---|---|---|
| LSTM | input nodes | 3 |
| output nodes | 1 | |
| optimizer | Adam | |
| learing-rate | 0.01 | |
| batchsize | 40 | |
| iterations | 260 |
| Battery Number | Evaluation Criteria | Propose | LSTM | GPR | EMD-LSTM-GPR | VMD-LSTM | VMD-LSTM-GPR |
|---|---|---|---|---|---|---|---|
| B0005 | MAE | 0.0020 | 0.063 | 0.083 | 0.0093 | 0.0089 | 0.0023 |
| RMSE | 0.0027 | 0.085 | 0.146 | 0.0136 | 0.0122 | 0.0031 | |
| B0006 | MAE | 0.0054 | 0.092 | 0.091 | 0.0097 | 0.013 | 0.0071 |
| RMSE | 0.0081 | 0.113 | 0.105 | 0.0146 | 0.025 | 0.0086 | |
| B0007 | MAE | 0.0021 | 0.055 | 0.073 | 0.0074 | 0.0051 | 0.0024 |
| RMSE | 0.0031 | 0.063 | 0.095 | 0.0112 | 0.0062 | 0.0037 | |
| B0018 | MAE | 0.0028 | 0.039 | 0.062 | 0.0085 | 0.0073 | 0.0043 |
| RMSE | 0.0040 | 0.046 | 0.085 | 0.0108 | 0.0092 | 0.0057 |
| Battery Number | Method | Start | Real | Predict | AE | RE |
|---|---|---|---|---|---|---|
| B0005 | EEMD-GWO-SVR | 80 | 44 | 46 | 2 | 4.5 |
| 100 | 24 | 26 | 2 | 8.3 | ||
| PF-LSTM | 80 | 44 | 41 | 3 | 6.8 | |
| 100 | 24 | 22 | 2 | 8.3 | ||
| RNN | 80 | 44 | 50 | 6 | 13.6 | |
| 100 | 24 | 28 | 4 | 16.7 | ||
| Propose | 80 | 44 | 44 | 0 | 0 | |
| 100 | 24 | 24 | 0 | 0 | ||
| B0006 | EEMD-GWO-SVR | 80 | 28 | 30 | 2 | 7.1 |
| 100 | 8 | 10 | 2 | 25 | ||
| PF-LSTM | 80 | 28 | 30 | 2 | 7.1 | |
| 100 | 8 | 10 | 2 | 25 | ||
| RNN | 80 | 28 | 33 | 5 | 17.9 | |
| 100 | 8 | 7 | 1 | 13 | ||
| Propose | 80 | 28 | 29 | 1 | 3.6 | |
| 100 | 8 | 8 | 0 | 0 | ||
| B0018 | EEMD-GWO-SVR | 60 | 37 | - | - | - |
| 80 | 17 | 17 | 17 | 0 | ||
| PF-LSTM | 60 | 37 | 41 | 4 | 10.8 | |
| 80 | 17 | 18 | 1 | 5.9 | ||
| RNN | 60 | 37 | - | - | - | |
| 80 | 17 | 16 | 1 | 5.9 | ||
| Propose | 60 | 37 | 36 | 1 | 2.8 | |
| 80 | 17 | 18 | 1 | 5.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Qu, A.; Zhang, J.; Shi, Q.; Jia, Z. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Improved Variational Mode Decomposition and Machine Learning Algorithm. Energies 2023, 16, 313. https://doi.org/10.3390/en16010313
Sun C, Qu A, Zhang J, Shi Q, Jia Z. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Improved Variational Mode Decomposition and Machine Learning Algorithm. Energies. 2023; 16(1):313. https://doi.org/10.3390/en16010313
Chicago/Turabian StyleSun, Chuang, An Qu, Jun Zhang, Qiyang Shi, and Zhenhong Jia. 2023. "Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Improved Variational Mode Decomposition and Machine Learning Algorithm" Energies 16, no. 1: 313. https://doi.org/10.3390/en16010313
APA StyleSun, C., Qu, A., Zhang, J., Shi, Q., & Jia, Z. (2023). Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Improved Variational Mode Decomposition and Machine Learning Algorithm. Energies, 16(1), 313. https://doi.org/10.3390/en16010313








