Gas Turbine Model Identification Based on Online Sequential Regularization Extreme Learning Machine with a Forgetting Factor
Abstract
:1. Introduction
- We improve the ELM algorithm using the Tikhonov regularization principle to reduce the complexity of the model and thus improve the algorithm’s performance in handling noisy data.
- An ELM is a batch learning algorithm while data acquisition for gas turbines is a continuous process, and it is impossible to obtain the complete data set at one time. When some new data arrive, batch learning has to repeat the training with old and new data, so it takes a lot of time. This paper improves the ELM algorithm by using an online learning method to process the data sequentially, which saves training time.
- A forgetting factor adaptive update strategy is designed to forget the old sample data selectively. This forgetting mechanism can eliminate the adverse effects of old data which do not match with current characteristics of model training and solve the problem of low training accuracy caused by the time-varying nature of gas turbines.
2. The Traditional Algorithms
3. The Proposed Algorithm
- 4.
- Prior knowledge learning phase:
- 5.
- Online updating phase:
| Algorithm 1: FOS_RELM |
| Input:, N0 Output:
while∈do
|
4. Results and Discussion
4.1. Performance Evaluation of Simulation
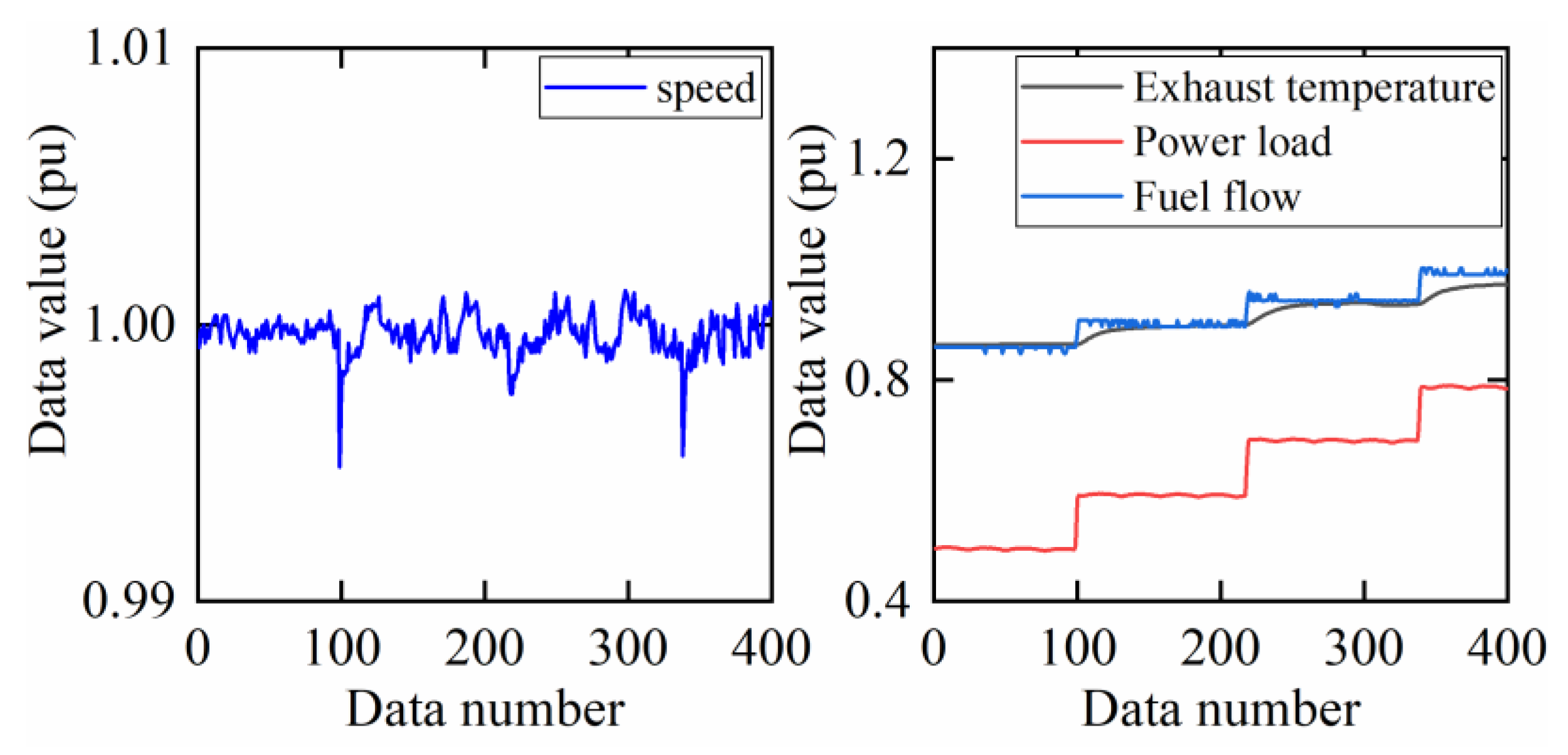
4.1.1. Input Signal Selection
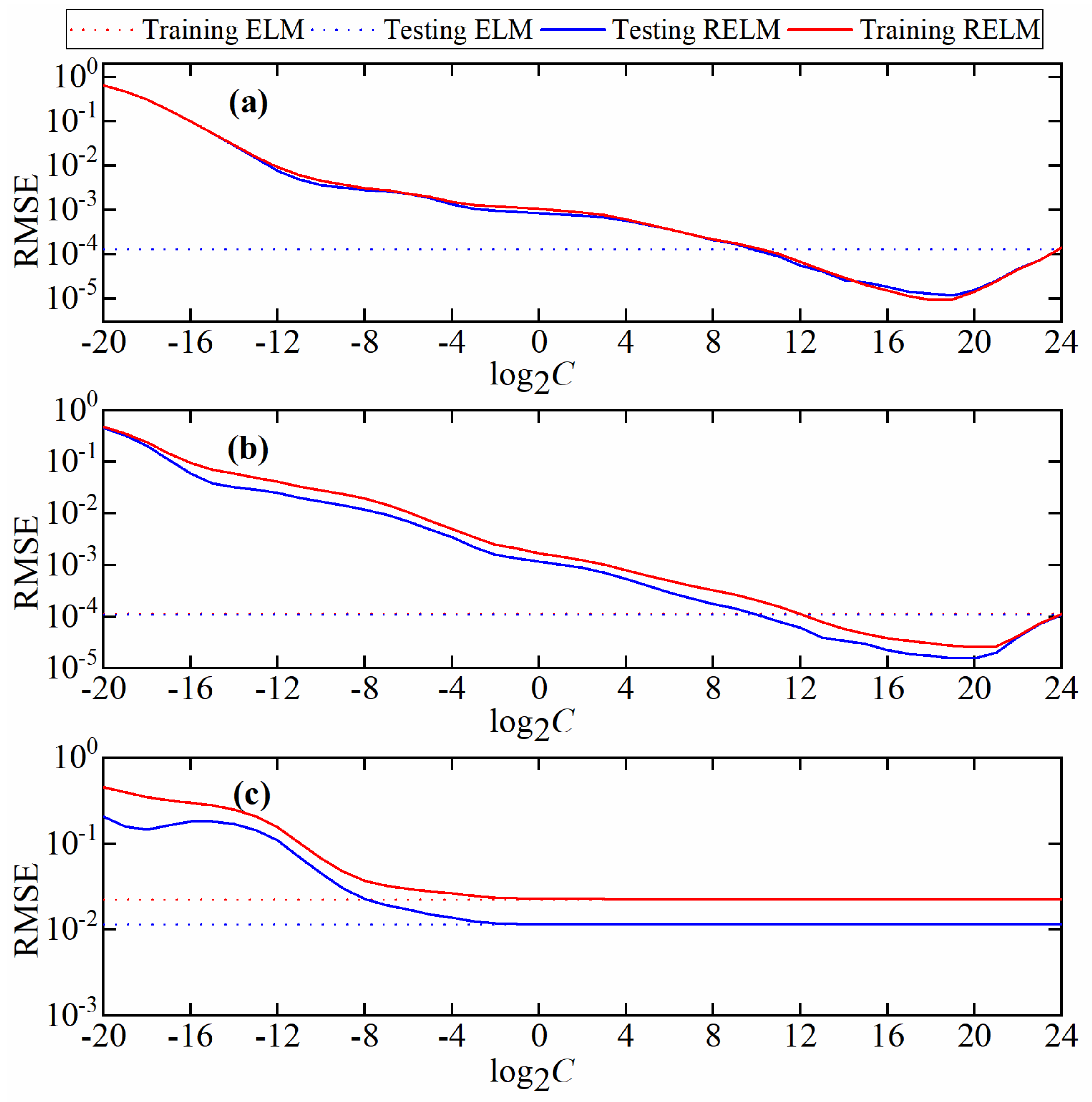
4.1.2. Network Architecture Design
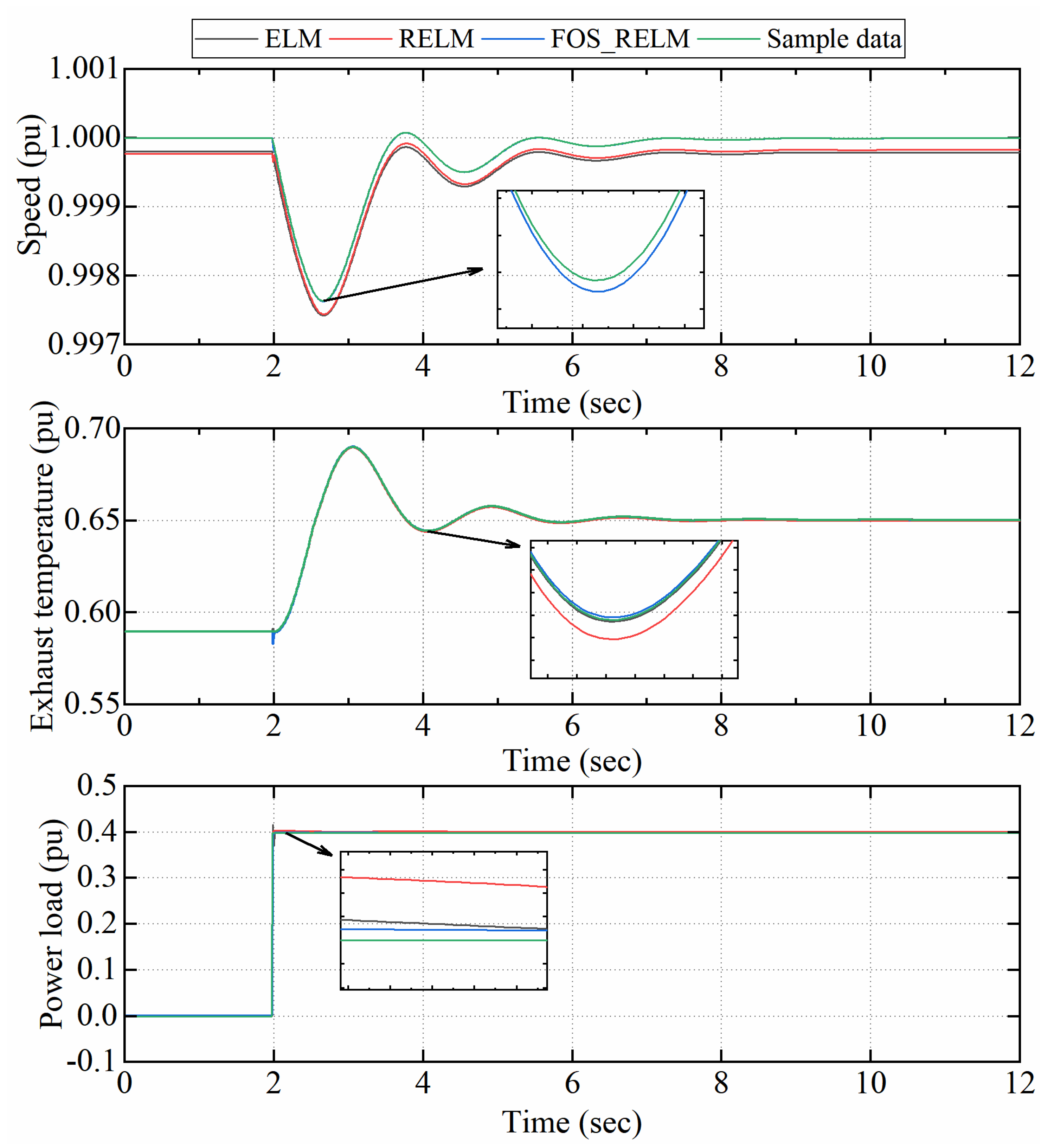
4.1.3. Robustness Testing
4.2. Performance Evaluation of the Experiment
4.2.1. Performance Test of Noise Resistance
4.2.2. Robustness Testing
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| L | Number of nodes in the hidden layer |
| The randomly generated node parameters of the hidden layer | |
| The output weight coefficient | |
| The nonlinear activation function | |
| H | The hidden nodes output matrix |
| E | The modeling error matrix |
| The modeling error of the ith sample | |
| m | The input nodes |
| C | The regularization factor |
| λ | The forgetting factor |
| The standard training error | |
| The set minimum forgetting factor | |
| Gas turbine fuel flow | |
| Turbine output speed | |
| Exhaust temperature | |
| Turbine output power | |
| S | Training data set |
| T | Target value |
| S0 | The initialized training set |
| N0 | Number of initial training samples |
| N | Number of the training samples |
| RMSE | The root mean square error |
| FOS_RELM | Online sequential regularization extreme learning machine algorithm based on forgetting factor |
| GT | Gas turbine |
| SLFNs | Single hidden layer feedforward networks |
| ELM | Extreme learning machine |
| OS_ELM | Online sequential extreme learning machine |
| ERM | Empirical risk minimization |
| SRM | Structural risk minimization |
| RELM | Regularized extreme learning machine |
| SVMs | Support vector machines |
| BP | Backpropagation |
References
- Mohamed, O.; Khalil, A. Progress in modeling and control of gas turbine power generation systems: A survey. Energies 2020, 13, 2358. [Google Scholar] [CrossRef]
- Liu, Y.; Meenakshi, V.; Karthikeyan, L.; Maroušek, J.; Krishnamoorthy, N.; Sekar, M.; Nasif, O.; Alharbi, S.A.; Wu, Y.; Xia, C. Machine learning based predictive modelling of micro gas turbine engine fuelled with microalgae blends on using LSTM networks: An experimental approach. Fuel 2022, 322, 124183. [Google Scholar] [CrossRef]
- Hanachi, H.; Mechefske, C.; Liu, J.; Banerjee, A.; Chen, Y. Performance-based gas turbine health monitoring, diagnostics, and prognostics: A survey. IEEE Trans. Reliab. 2018, 67, 1340–1363. [Google Scholar] [CrossRef]
- Mohamed, O.; Wang, J.; Khalil, A.; Limhabrash, M. Predictive control strategy of a gas turbine for improvement of combined cycle power plant dynamic performance and efficiency. SpringerPlus 2016, 5, 980. [Google Scholar] [CrossRef] [Green Version]
- Asgari, H. Modelling, Simulation and Control of Gas Turbines Using Artificial Neural Networks. Ph.D. Theis, University of Canterbury, Christchurch, New Zealand, 2014. [Google Scholar] [CrossRef]
- Talaat, M.; Gobran, M.H.; Wasfi, M. A hybrid model of an artificial neural network with thermodynamic model for system diagnosis of electrical power plant gas turbine. Eng. Appl. Artif. Intell. 2018, 68, 222–235. [Google Scholar] [CrossRef]
- Jurado, F. Modelling micro-turbines using Hammerstein models. Int. J. Energy Res. 2005, 29, 841–855. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Wilamowski, B.M.; Cotton, N.J.; Kaynak, O.; Dundar, G. Computing gradient vector and Jacobian matrix in arbitrarily connected neural networks. IEEE Trans. Ind. Electron. 2008, 55, 3784–3790. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.; Siew, C. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; Volume 2. [Google Scholar] [CrossRef]
- Wang, J.; Lu, S.; Wang, S.-H.; Zhang, Y.-D. A review on extreme learning machine. Multimed. Tools Appl. 2021, 81, 41611–41660. [Google Scholar] [CrossRef]
- Cao, F.; Liu, B.; Park, D.S. Image classification based on effective extreme learning machine. Neurocomputing 2013, 102, 90–97. [Google Scholar] [CrossRef]
- Wong, K.I.; Wong, P.K. Adaptive air-fuel ratio control of dual-injection engines under biofuel blends using extreme learning machine. Energy Convers. Manag. 2018, 165, 66–75. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Hu, Q.-K.; Xu, J.-G.; Li, B.; Huang, G.; Pan, Y.-T. A robust extreme learning machine for modeling a small-scale turbojet engine. Appl. Energy 2018, 218, 22–35. [Google Scholar] [CrossRef]
- Berghout, T.; Mouss, L.-H.; Kadri, O.; Saïdi, L.; Benbouzid, M. Aircraft engines remaining useful life prediction with an improved online sequential extreme learning machine. Appl. Sci. 2020, 10, 1062. [Google Scholar] [CrossRef] [Green Version]
- Creech, G.; Jiang, F. The application of extreme learning machines to the network intrusion detection problem. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2012; Volume 1479, No. 1. [Google Scholar] [CrossRef]
- Martínez-Martínez, J.M.; Escandell-Montero, P.; Soria-Olivas, E.; Martín-Guerrero, J.D.; Magdalena-Benedito, R.; Gómez-Sanchis, J. Regularized extreme learning machine for regression problems. Neurocomputing 2011, 74, 3716–3721. [Google Scholar] [CrossRef]
- Deng, W.; Zheng, Q.; Chen, L. Regularized extreme learning machine. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence and Data Mining, Nashville, TN, USA, 30 March–2 April 2009. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B 2011, 42, 513–529. [Google Scholar] [CrossRef] [Green Version]
- Liang, N.-Y.; Huang, G.-B.; Saratchandran, P.; Sundararajan, N. A fast and accurate online sequential learning algorithm for feedforward networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Z.; Park, D.S. Online sequential extreme learning machine with forgetting mechanism. Neurocomputing 2012, 87, 79–89. [Google Scholar] [CrossRef]
- Wang, X.; Han, M. Online sequential extreme learning machine with kernels for nonstationary time series prediction. Neurocomputing 2014, 145, 90–97. [Google Scholar] [CrossRef]
- De Sa, A.; Al Zubaidy, S. Gas turbine performance at varying ambient temperature. Appl. Therm. Eng. 2011, 31, 2735–2739. [Google Scholar] [CrossRef]
- Han, M.; Liu, C. Endpoint prediction model for basic oxygen furnace steel-making based on membrane algorithm evolving extreme learning machine. Appl. Soft Comput. 2014, 19, 430–437. [Google Scholar] [CrossRef]
- Bartlett, P.L. The sample complexity of pattern classification with neural networks: The size of the weights is more important than the size of the network. IEEE Trans. Inf. Theory 1998, 44, 525–536. [Google Scholar] [CrossRef] [Green Version]
- Salehi, A.; Montazeri-Gh, M. Black box modeling of a turboshaft gas turbine engine fuel control unit based on neural NARX. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2019, 233, 949–956. [Google Scholar] [CrossRef]
- Deflorian, M.; Zaglauer, S. Design of experiments for nonlinear dynamic system identification. IFAC Proc. Vol. 2011, 44, 13179–13184. [Google Scholar] [CrossRef]
- Nelles, O.; Isermann, R. Identification of nonlinear dynamic systems classical methods versus radial basis function networks. In Proceedings of the 1995 American Control Conference-ACC’95, Seattle, WA, USA, 21–23 June 1995; Volume 5. [Google Scholar]
- Nelles, O.; Isermann, R. Basis function networks for interpolation of local linear models. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; Volume 1. [Google Scholar]
- Boomadevi, P.; Paulson, V.; Samlal, S.; Varatharajan, M.; Sekar, M.; Alsehli, M.; Elfasakhany, A.; Tola, S. Impact of microalgae biofuel on microgas turbine aviation engine: A combustion and emission study. Fuel 2021, 302, 121155. [Google Scholar] [CrossRef]
- Tan, D.; Wu, Y.; Lv, J.; Li, J.; Ou, X.; Meng, Y.; Lan, G.; Chen, Y.; Zhang, Z. Performance optimization of a diesel engine fueled with hydrogen/biodiesel with water addition based on the response surface methodology. Energy 2023, 263, 125869. [Google Scholar] [CrossRef]








| FOS_RELM | |
|---|---|
| L | 100 |
| sigmoid | |
| C | 219 |
| 0.01 | |
| 0.98 | |
| ELM | RELM | FOS_RELM | ||
|---|---|---|---|---|
| Training RMSE | 1.30 × 10−4 | 9.46 × 10−6 | 6.60 × 10−6 | |
| 1.12 × 10−4 | 2.78 × 10−5 | 2.67 × 10−5 | ||
| 0.0226 | 0.0226 | 0.0226 | ||
| Testing RMSE | 1.29 × 10−4 | 1.16 × 10−5 | 1.01 × 10−5 | |
| 1.12 × 10−4 | 1.55 × 10−5 | 1.46 × 10−5 | ||
| 0.0115 | 0.0115 | 0.0115 | ||
| Training time (s) | 0.0809 | 0.0879 | 0.6609 | |
| Algorithm | OS_ELM | FOS_ELM | FOS_RELM | |
|---|---|---|---|---|
| Testing RMSE | 1.06 × 10−5 | 9.71 × 10−6 | 8.93 × 10−6 | |
| 2.18 × 10−4 | 1.17 × 10−4 | 1.19 × 10−4 | ||
| 0.011 | 0.011 | 0.011 | ||
| Training time (s) | 25.82 | 25.52 | 26.08 | |
| Rated Speed | Rated Output Power | Rated Power Generation Efficiency | Dimensions (Length × Width × Height) | Compressor Type | Turbine Type | Combustion Chamber Type | Weight |
|---|---|---|---|---|---|---|---|
| 51,000 rpm | 125 kW | 15% | 2950 × 2200 × 2450 mm3 | Single-stage centrifugal type | Two-stage axial flow type | Single cylinder type | 4.3 t |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Liu, Y.; He, X.; Liu, Z. Gas Turbine Model Identification Based on Online Sequential Regularization Extreme Learning Machine with a Forgetting Factor. Energies 2023, 16, 304. https://doi.org/10.3390/en16010304
Yang R, Liu Y, He X, Liu Z. Gas Turbine Model Identification Based on Online Sequential Regularization Extreme Learning Machine with a Forgetting Factor. Energies. 2023; 16(1):304. https://doi.org/10.3390/en16010304
Chicago/Turabian StyleYang, Rui, Yongbao Liu, Xing He, and Zhimeng Liu. 2023. "Gas Turbine Model Identification Based on Online Sequential Regularization Extreme Learning Machine with a Forgetting Factor" Energies 16, no. 1: 304. https://doi.org/10.3390/en16010304
APA StyleYang, R., Liu, Y., He, X., & Liu, Z. (2023). Gas Turbine Model Identification Based on Online Sequential Regularization Extreme Learning Machine with a Forgetting Factor. Energies, 16(1), 304. https://doi.org/10.3390/en16010304





