Independent Power Producer Approach to Optimal Design and Operation of IES with Wind Power Plants

Abstract

In South Korea, Renewable Energy Sources (RES) have been increasing with the application of energy policies, such as Feed in Tariff (FIT) and the Renewable Portfolio Standard (RPS). However, a rapid increase in RES supply leads to an uncertain power supply due to the intermittent output of RES. A representative example is the curtailment of Wind Turbines (WT), which frequently occurs in Jeju Island, South Korea. The proportion of RES power on Jeju Island is 67%, and there are cases where WT is curtailed among the operable sections to maintain the balance of power supply and demand. This paper applies Power-to-Gas (P2G) technology to hydrogenate, store, and utilize unused power to solve this problem. In this paper, Aewol-eup in Jeju Island is selected as a target site for case study. An Integrated Energy System (IES) for various energy operations is designed to control RES output. This paper proposes the optimal facility configuration and finally drives the optimal design and operation solution of IES by analyzing the objective functions and focusing on the Independent Power Producer (IPP) perspective.

1. Introduction

The distribution of Renewable Energy Sources (RES) in South Korea has been steadily increasing as part of South Korea’s energy policy, such as Feed in Tariff (FIT) in which the government pays fixed prices to operators of RES according to power generation of RES. Renewable Portfolio Standard (RPS) mandates power generation through RES for power generation operators with a power generation capacity of 500 MW or higher. South Korea has raised nationally dedicated contributions through the 2021 United Nations Climate Change Conference. Therefore, a goal was selected to reduce greenhouse gas by more than 40% compared to 2018 by 2030, and accordingly, a plan is being made to gradually reduce the capacity of coal-fired power generation facilities, which are the leading cause of carbon emissions, and replace the capacity of reduced coal-fired power generation facilities with RES capacity. As a result, the spread of RES in South Korea is expected to accelerate further. As a way to implement the decarbonization policy, many countries have adopted green hydrogen energy. South Korea also announced a roadmap for revitalizing the hydrogen economy in 2019 and implementing hydrogen production and utilization policies. The Clean Hydrogen Portfolio Standard (CHPS) is scheduled to be implemented as a policy. CHPS is a policy that independently implements the RPS system on hydrogen power generation obligations and is scheduled to be implemented for the first time in 2022. Laws are currently pending in the Korean National Assembly. With the introduction of CHPS, the supply of RES-linked hydrogen production facilities and produced hydrogen operation facilities is also expected to accelerate.

Representative facilities of RES include Wind Turbine (WT) and Photovoltaic (PV), and WT and PV are classified as Uncontrolled Generators (UCG), the operator cannot control the output. Although UCG is on the rise due to national policy, power supply and demand imbalances occur due to RES output exceeding load due to unpredictable power generation that occurs at a specific time zone or intermittently as the proportion of UCG increases. One of the problems caused by the uncertain output of UCG is the Duck-Curve phenomenon caused by PV. The Duck-Curve phenomenon is a phenomenon in which the amount of power supplied from the grid decreases sharply in the afternoon when the output of PV is concentrated. The Duck-Curve phenomenon may cause problems in power quality, such as voltage and frequency fluctuations in the system. In addition, due to the rapid expansion of PV, PV that produces over-output is curtailed, and the power supply from PV is stopped during the corresponding time [1]. In addition, when overpowering occurs due to unpredictable changes in wind speed, in order to match the power balance of the power system, the WT is curtailed [2]. Since the curtailment of UCG reduces IPP benefits by causing a decrease in power transaction volume, IPP needs to reduce UCG’s curtailment by utilizing IES.

Deep learning, which has been implemented relatively recently, is part of a method to reduce the curtailment of UCG. Through Deep learning, a stable facility plan, including UCG and a power supply operation plan, are established based on the predicted insolation and wind speed. However, the technology has a clear limit to prediction accuracy, and the prediction-dependent development plan has uncertainty and cannot be a definite solution [3]. Therefore, this paper proposes a method to eliminate the uncertain output of UCG and reduce the curtailment of WT economically using Independent Energy System (IES).

One of the ways to eliminate the output of the uncertain UCG proposed in this paper is to link and utilize Battery Energy Storage System (BESS) with UCG. BESS can reduce UCG’s curtailment by storing the excess power generation of UCG. In [4], the degree to which the curtailment of WT is reduced was analyzed using BESS based on the two-stage optimization technique. Another way to eliminate the uncertain output of UCG is using an IES based on Sector Coupling (SC) technology. SC technology designs an integrated energy operation system, by converting energy, such as power, heat, and gas into each other. Recently, the supply of hydrogen production and utilization facilities has increased rapidly following South Korea’s hydrogen utilization policy, and hydrogen has been adopted as a critical energy source for SC technology based on these policy moves.

Power to Gas (P2G) technology, a hydrogen utilization technology among SC technologies, is a representative green hydrogen production technology that produces hydrogen and oxygen by electrolyzing water using an Electrolyzer (Elz). Oxygen generated by P2G technology is emitted into the atmosphere, and hydrogen is stored in the Hydrogen Energy Storage System (HESS). Furthermore, it may supply fluid power and thermal energy using a Fuel Cell (FC), which generates water and electricity by combining hydrogen and oxygen at the judgment of the system operator [5]. P2G technology has a significant advantage in terms of UCG operational efficiency because it can operate Elz with the output of UCG, and the generated hydrogen can be injected into the gas system to commercialize hydrogen itself or produce synthetic natural gas [6]. In addition, FC supplies power and thermal energy simultaneously, and load following operation is possible due to its excellent responsiveness [7]. Since Elz and FC do not emit carbon, the operation of SC technology based on P2G technology is adopted as an energy operation technology that perfectly meets the purpose of the carbon-neutral policy.

Unlike the existing single-energy operating system, IES is unsure of its operating entity. In most research cases, an objective function of an IES is selected to minimize system design and operation costs. In this paper, the objective functions are classified to minimize the curtailment of RES and IES’s investment and operation cost. Then, both objective functions are applied to optimization, respectively. In addition, previous studies on IES constitute a single topology of IES, assuming the facility configuration of IES. However, additional injection of equipment must be considered in IES as various energy facilities are applied. Therefore, this paper considers whether various energy conversion and storage facilities are input from the facility configuration perspective of IES. Finally, in this paper, the optimal design and operation solution of IES is derived for each facility configuration of IES, and the optimal facility configuration of IES is proposed based on the results. In this paper, the objective functions are derived from an Independent Power Producer (IPP) perspective that assists power supply to the IES and an optimal design and operation solution of IES through Mixed-Integer Linear Programming -based optimization.

2. Structure of Integrated Energy System

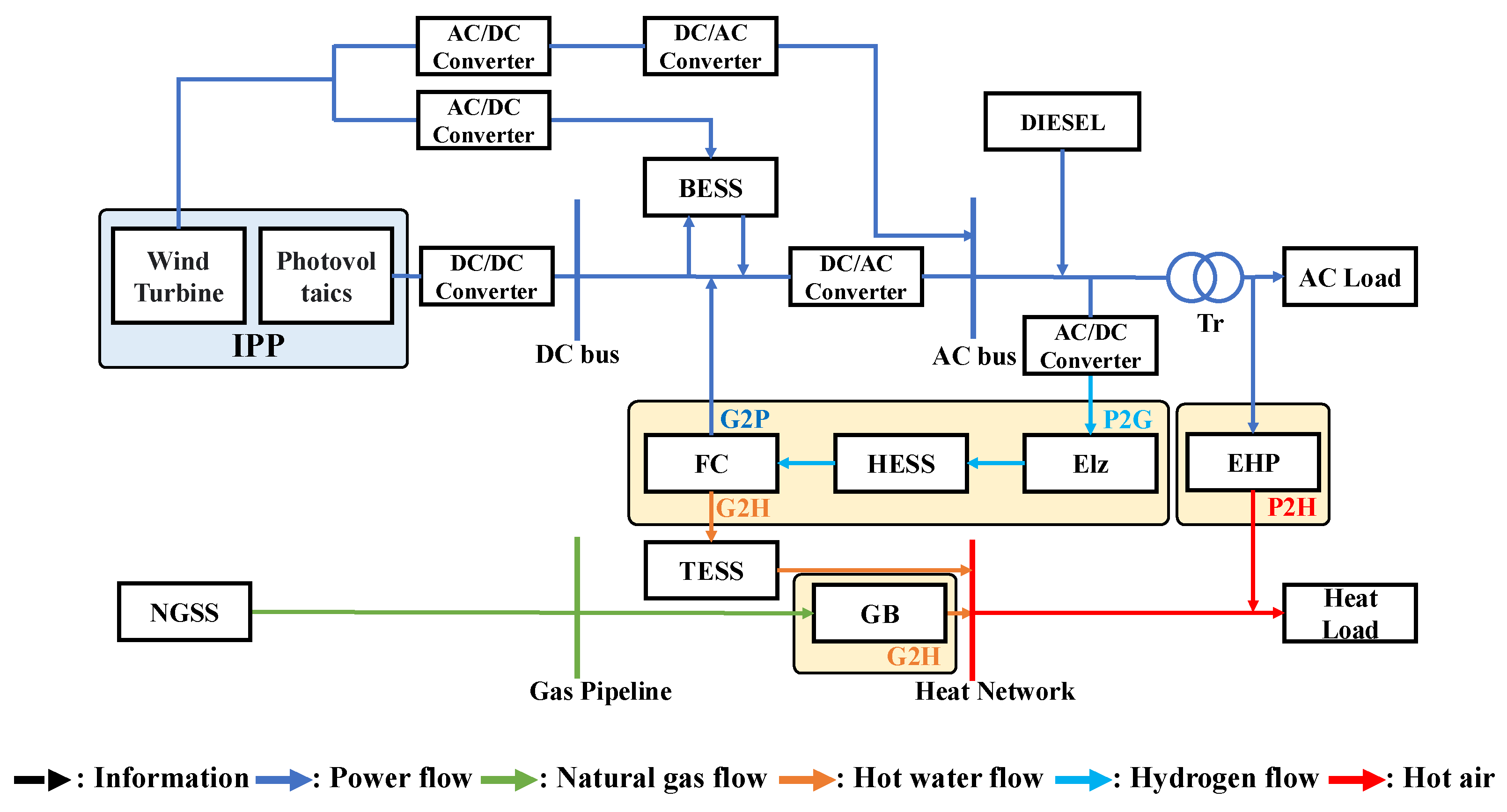
In this paper, IES utilizes power and gas as energy sources and supplies energy to power and thermal loads, respectively, through P2G, Power to Heat (P2H), Gas to Power (G2P), and Gas to Power (G2H) technologies. Figure 1 is the structure of IES proposed in this paper.

In Figure 1, the energy storage facilities include BESS, HESS, and Thermal Energy Storage System (TESS), and the natural gas storage system is operated as a supply facility for natural gas. Energy conversion facilities include Elz, FC, Gas Boiler (GB), and Electric Heat Pump (EHP). Elz produces and supplies hydrogen in the process of electrolyzing water. FC supplies power in the process of combining hydrogen as opposed to Elz. Technologies that supply energy through Elz and FC are called P2G and G2P technologies, respectively. GB supplies heat as a medium for hot water through the combustion of natural gas. A process commonly referred to as G2H technology. EHP supplies heat to the air as a medium from heat conversion of power, and this process is commonly referred to as P2H technology. It is assumed that the power supply is supplied through the Diesel Generator (DG) to simulate 100% self-reliance of the target site.

2.1. Power Supply Facilities

2.1.1. Modeling of Wind Turbine

The output characteristics of the WT vary depending on the wind speed. The power generation output section of the WT is largely determined by cut-in speed, rated speed, and cut-off speed [8].

$$P_{WT,t}=\frac{1}{2}\cdot {\rho }_v\cdot A\cdot V^3,V\in \left\{Cu{t}_{in},Rate,Cu{t}_{off}\right\}$$

(1)

$$P_{WT,t}=P_{WT,w,t}^{CT}+P_{WT,w,t}^N$$

(2)

In Equation (1), $P_{WT,t}$, ${\rho }_v\cdot A, \mathrm{and} v$ refer to the output of WT [kWh], density of the wind [kg/m³], the area of the blade [m²], and the velocity of the wind [m/s], respectively. Cut_in, Rate, and Cut_off wind speeds, with values of 3, 15, and 25 [m/s], respectively. The total output of the W^Th in this paper is classified into $P_{WT,w,t}^N$ operated output of WT and $P_{WT,w,t}^{CT}$ curtailed output of WT, as shown in Equation (2).

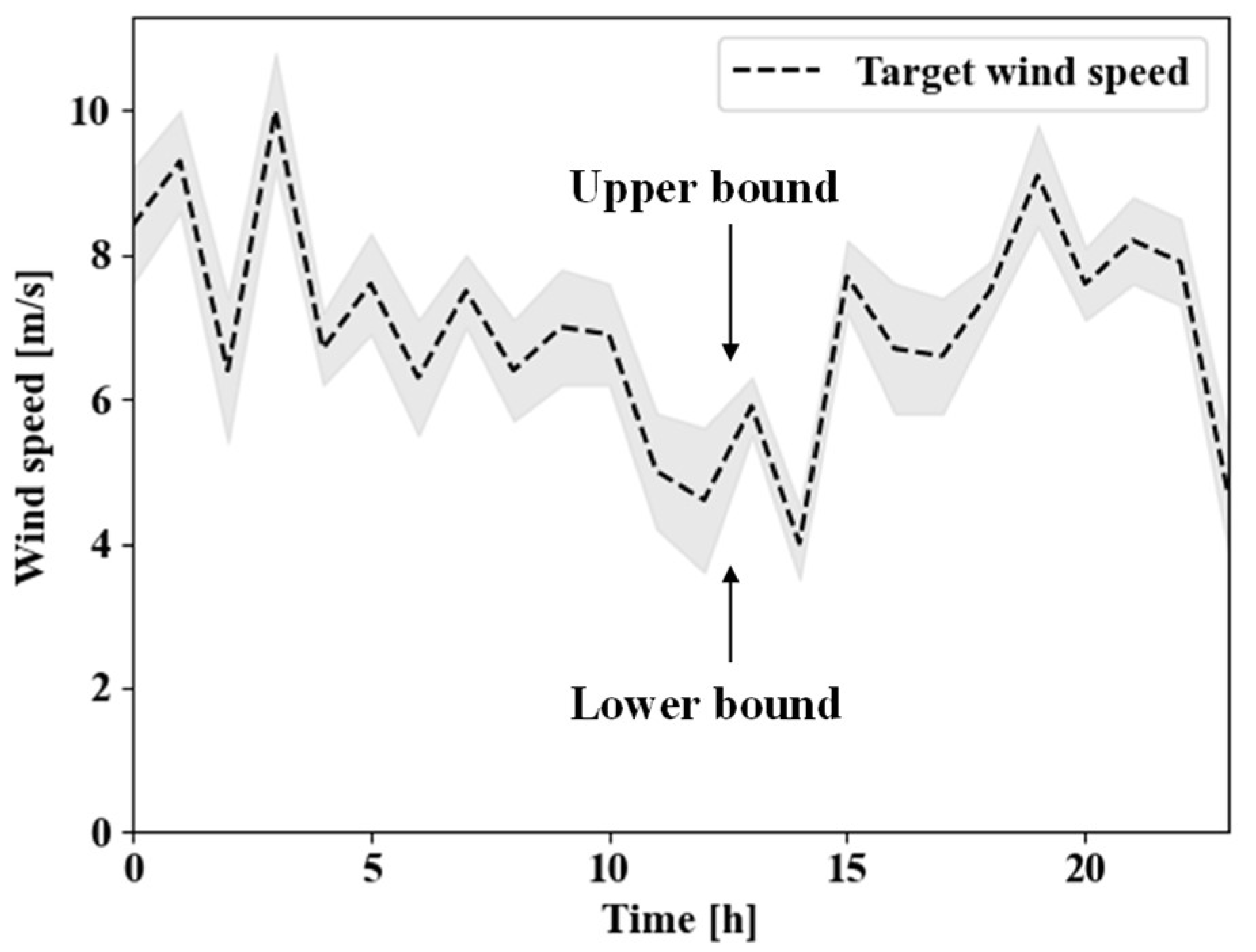
This paper utilizes the observed wind speed data of Jeju Island in 2021. It calculates the error range of the measured data based on a 5% error in the seasonal and hourly Weibull distribution of the observed data to consider the output uncertainty of the WT. Weibull distribution’s shape and scale factors are applied with 2 and 5, respectively. Figure 2 shows the lower and upper bound of wind speed data derived based on an error of 5% in the Weibull distribution by seasonal and hourly wind speed data and a wind speed sample of 24 h. In this paper, random data of wind speeds within range is applied to consider the output uncertainty of WT.

2.1.2. Modeling of Photovoltaic

In Equation (3), $P_{pv,t}, C_{pv}, f, G_t, \sigma , T_{cell}, \mathrm{and} T_{cell,STC}$ refer to the output of PV [kWh], the capacity of PV, [kW] the yield of the solar radiation [m²], solar radiation [kWh/m²], constant for loss, temperature [$℃$], and standard temperature [$℃$], respectively. The amount of insolation generally utilizes the amount distributed according to the beta distribution or normal distribution [9]. However, similar to wind speed data, actual insolation data from Aewol-eup during 2020 is used. Furthermore, as the output of PV is proportional to the insolation, the predicted output volatility is equal to that of WT. Thus, only WT with relatively high output uncertainty among UCG is considered the target for curtailment. Therefore, PV output is used to store and convert energy for the optimal operation of IES, and PV facilities are not considered curtailment targets.

$$P_{pv,t}=C_{pv}\cdot f\cdot \left(\frac{G_t}{1000}\right)\cdot \left[1+\sigma \left(T_{cell}-T_{cell,STC}\right)\right]$$

(3)

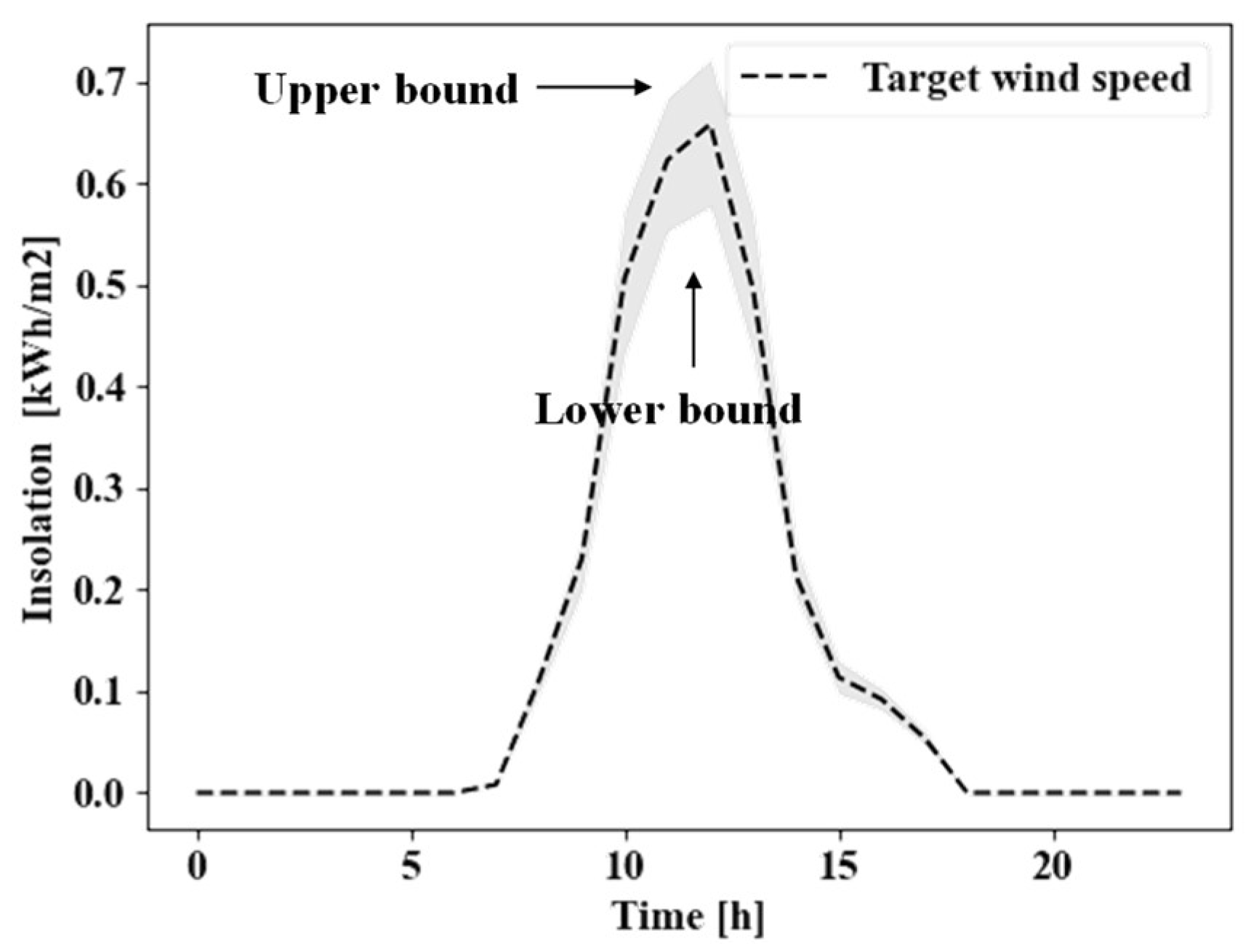
This paper utilized the observed solar radiation of Jeju Island in 2021. It calculates the error range of the measurement data based on an error of 5% in the standard distribution by the seasonal and hourly observation data to consider PV output uncertainty. Figure 3 shows the lower and upper bound of solar radiation data derived based on an error of 5% in the standard distribution by solar radiation and shows a solar radiation sample of 24 h. In this paper, random data of solar radiation within the range is applied to consider the output uncertainty of WT.

2.1.3. Modeling of Diesel Generator

A Diesel Generator (DG)is capable of load-following operation. It is in charge of the load-following operation for power balance if there are no other power generation facilities capable of load-following operations. Therefore, it is assumed that the fuel of DG consumed is infinite. DG is modeled through Equation (4).

$$P_{dg,t}=\frac{Q_t · E · {\eta }_{dg}}{860 · cos\theta }$$

(4)

In Equation (4), $P_{dg,t}$ is the output of DG [kWh] $Q_t$ is the amount of fuel consumed [kg-oil], ${\eta }_{dg}$ is the efficiency of DG, and E is the amount of heat generated by fuel [Kcal/kg-oil].

2.2. Heat Supply Facilities

2.2.1. Modeling of Gas Boiler

Gas Boiler (GB) utilizes G2H technology to convert natural gas into thermal energy. For the gas network, the gas flow can be interpreted using the Weymouth equation considering the hydraulic pressure and flow rate of gas in the pipeline [10]. This paper does not interpret gas flow because it focuses on energy operations based on the UCG output within IES. Therefore, it is assumed that the gas fuel supply through the natural gas storage system is infinite. GB is modeled through Equation (5).

$$T_{gb,t}=G_{gb,t}\cdot {\eta }_{gb}\cdot HH{V}_{ng}$$

(5)

In Equation (5), $T_{gb,t}$, $G_{gb,t}$, and ${\eta }_{gb}$ refer to the output [kWh], input [kg-ng], and efficiency of GB, respectively. $HH{V}_{ng}$ is a higher heating value of natural gas [kWh/kg-ng]. Natural gas supplied from the natural gas storage system is expressed in kg. Therefore, to convert the amount of energy,$HH{V}_{ng}$ of natural gas is applied and converted [11].

2.2.2. Modeling of Electric Heat Pump

An Electrical Heat Pump (EHP) utilizes P2H technology to convert electrical energy into thermal energy. The EHP supplies the heat generated through electrical resistance to thermal energy in the form of air and is modeled through Equation (6).

$$T_{ehp,t}=P_{ehp,t}\cdot {\eta }_{ehp,t}, \forall t$$

(6)

In Equation (6), $T_{ehp,t}$, $P_{ehp,t}$, and ${\eta }_{ehp}$ refer to the output [kWh], input [kWh], and efficiency of EHP, respectively.

2.3. Hydrogen Operation Facilities

2.3.1. Modeling Electrolyzer

An Electrolyzer (Elz) produces hydrogen and oxygen through electrolysis, wherein the hydrogen is stored in HESS. Generally, Elz’s electrolysis is expressed in Equations (7) and (8).

$${\mathrm{H}}_2\mathrm{O}\to \frac{1}{2}{\mathrm{O}}_2+2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}:\mathrm{Anode}$$

(7)

$$2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}\to {\mathrm{H}}_2:\mathrm{Cathode}$$

(8)

Elz is classified into a proton exchange membrane electrolyzer (PEMEL), alkaline electrolyzer (AEL), and solid oxide electrolyzer (SOEL) based on the catalyst. In this paper, Elz assumes a PEM type [12]; it experiences a loss of movement during its initial operation, and research [13] has been conducted to minimize the loss of mobility and produce stable hydrogen through Elz’s switch control. Therefore, in this paper, Elz’s switch control was applied as a constraint for its modeling. Elz is modeled as shown in Equation (9).

$$H_{elz,t}^{total}=P_{elz,t}\cdot {\eta }_{elz}/HH{V}_{H2}$$

(9)

In Equation (9), $H_{elz,t}^{total}$, $P_{elz,t}$, and ${\eta }_{elz}$, refer to produced hydrogen [kg], input of Elz [kWh] and efficiency of Elz, respectively. $HH{V}_{H2}$ is higher heating value of hydrogen [kWh/kg-H₂].

2.3.2. Modeling of Fuel Cell

As shown in Equations (10) and (11), a FC produces electricity and heat simultaneously in the anode and the cathode through the combination of hydrogen and oxygen, respectively. That is, an FC is a facility that simultaneously utilizes the G2P and G2H technologies [14].

$${\mathrm{H}}_2\to 2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}:\mathrm{Anode}$$

(10)

$$2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}+\frac{1}{2}{\mathrm{O}}_2\to {\mathrm{H}}_2\mathrm{O}:\mathrm{Cathode}$$

(11)

FC is classified into alkaline fuel cell (AFC), proton exchange member fuel cell (PEMFC), molten carbonate fuel cell (MCFC), and solid oxide fuel cell (SOFC), depending on the catalyst [15]. This paper assumes that the FC is of the PEMFC type. The modeling of FC is expressed as Equations (12) and (13).

$$P_{fc,t}=H_{fc,t}\cdot {\eta }_{fc}^P\cdot HH{V}_{H2}$$

(12)

$$T_{fc,t}=H_{fc,t}\cdot {\eta }_{fc}^T\cdot HH{V}_{H2}$$

(13)

In Equation (12), $P_{fc,t}$, $H_{fc,t}$, and ${\eta }_{fc}^P$ refer to electric output of FC [kWh], input of FC [kg-H₂], and efficiency of FC’s electric output, respectively. In Equation (13), $T_{fc,t}$ refers to thermal output of FC [kWh], and ${\eta }_{fc}^P$ refers to efficiency of FC’s thermal output.

2.4. Energy Storage Facilities

In this paper, the operation characteristics of each energy storage device, except for the natural gas storage system are commonly applied using Equations (14)–(22) [16].

$$SO{C}_{s,t}=SO{C}_{s,t-1}+E_{s,t}^{ch}\cdot {\eta }_s-E_{s,t}^{dch}/{\eta }_s,s\in \left\{BESS,HESS,TESS\right\}$$

(14)

$$\underset{¯}{SO{C}_s}\le SO{C}_{s,t}\le \overline{SO{C}_s},s\in \left\{BESS,HESS,TESS\right\}$$

(15)

$$E_{s,t}^{ch}\le C-rat{e}_s\cdot \overline{C_s},s\in \left\{BESS,HESS,TESS\right\}$$

(16)

$$E_{s,t}^{dch}\le C-rat{e}_s\cdot \overline{C_s},s\in \left\{BESS,HESS,TESS\right\}$$

(17)

$$E_{s,t}^{ch}\le {\alpha }_{s,t}^{ch}\le M\cdot b_{s,t}^{ch},s\in \left\{BESS,HESS,TESS\right\}$$

(18)

$$E_{s,t}^{dch}\le {\alpha }_{s,t}^{dch}\le M\cdot b_{s,t}^{dch},s\in \left\{BESS,HESS,TESS\right\}$$

(19)

$$b_{s,t}^{ch}\le {\beta }_{s,t}^{ch}\le E_{s,t}^{ch},s\in \left\{BESS,HESS,TESS\right\}$$

(20)

$$b_{s,t}^{dch}\le {\beta }_{s,t}^{dch}\le E_{s,t}^{dch},s\in \left\{BESS,HESS,TESS\right\}$$

(21)

$$b_{s,t}^{ch}+b_{s,t}^{dch}\le 1,s\in \left\{BESS,HESS,TESS\right\}$$

(22)

Equation (14) represents the state of charge (SOC) of the ESS at each time t. Equation (15) implies the minimum and maximum operating ranges of the SOC. In Equations (14)–(22), $E_{s,t}^{ch}$ and $E_{s,t}^{dch}$ refers to amount of charge and discharge for each ESS [kWh]. $C_s$ is capacity of each ESS [kW]. ${\alpha }_{s,t}^{ch}$, ${\alpha }_{s,t}^{dch}$, ${\beta }_{s,t}^{ch}$ and ${\beta }_{s,t}^{dch}$ refer to linear variables for charge and discharge of each ESS, auxiliary variables for charge and discharge of each ESS, respectively. $b_{s,t}^{ch}$ and $b_{s,t}^{dch}$ refer to binary operation variables for each ESS.

3. Energy Operation Analysis of IES

Equation (23) means the power balance of the IES.

$$\begin{gathered} P_{dg,t}\cdot {\eta }_{dg}+{\displaystyle \sum }_{\forall w}{P}_{wt,w,t}\cdot {\eta }_{wt}+P_{pv,t}\cdot {\eta }_{pv}+E_{bess,t}^{dch}\cdot {\eta }_{bess} \\ -E_{bess,t}^{cha}/{\eta }_{bess}-P_{ehp,t}/{\eta }_{ehp}-P_{elz,t}/{\eta }_{elz}=P_{load,t} \end{gathered}$$

(23)

This paper considers the power supply and demand imbalance caused by the excess output of UCG. As UCG utilizes confirmed facilities, it is necessary to maintain a balance between power supply and demand by reducing the excess power when UCG is overpowered.

The first excess power elimination mode reduces excess power by curtailing a part of the WT operating when excess power occurs. As the curtailed power is determined based on the output of the WT to be curtailed, the operator cannot control it. Therefore, a case in which the total power supply amount is instantaneously lower than the load amount may occur owing to the curtailment of WT. In this case, insufficient power must be supplied through facilities capable of load-following operation. Furthermore, the curtailment of the WT implies that the output of the WT is 0, and additional DG operation is required from the power balance perspective. Therefore, the curtailment of WT generally causes additional power generation costs for the DG.

The second excess power elimination mode stores excess power using the charging mode of BESS when excess power occurs. As the operator can control the BESS operation, BESS can reduce excess power without the further involvement of DG. Due to BESS’s charging and discharging characteristics according to the constraints of Equations (14)–(22), BESS cannot flexibly eliminate excess power. However, the discharging power of BESS has an economic profit of reducing the facility cost and power generation cost of DG by replacing a part of the DG power generation.

The third excess power elimination mode hydrogenates excess power through the P2G technology when excess power occurs. As the operator can control the operation of Elz, P2G technology can reduce the excess power without the further involvement of the DG. HESS can charge and discharge hydrogen independently through Elz and FC. Therefore, it is possible to eliminate excess power more flexibly than BESS.

The fourth excess power elimination mode converts excess power into thermal energy and supplies it through P2H technology through EHP. As the operator can control EHP, it can reduce excess power without the further involvement of DG. This paper does not consider waste heat; therefore, using EHP at a level exceeding the heat load cannot occur.

In the event of an excess power, one or more of the four proposed excess power elimination modes must be applied to maintain the power balance of the IES.

4. Objective Functions of IES

The objective functions for the optimal design and operation of the IES are set differently depending on the operating entity of the IES. In this paper, the objective functions are derived from the perspective of IPP, which assists in power supply through UCG. From the IPP perspective, the objective functions refer to the high utilization rate of UCG operated within the IES. Furthermore, minimize the total system cost. Therefore, after securing the maximum utilization rate of UCG, the optimal economic objective function of IES is applied.

The economic objective function is to minimize all costs incurred in constructing and operating a system. Therefore, the objective function minimizes Investment cost and Maintenance costs. Here, Investment cost implies the facility’s capital cost, and Maintenance cost implies the operation cost and fuel cost. Investment cost and Maintenance cost equations for deriving economic objective functions are expressed as Equations (24) and (25), respectively.

$$C_I=C_{dg}\cdot {\varphi }_{dg}+C_{gb}\cdot {\varphi }_{gb}+C_{ehp}\cdot {\varphi }_{ehp}+C_{elz}\cdot {\varphi }_{elz}+C_{fc}\cdot {\varphi }_{fc}+{\displaystyle \sum }_{\forall s}{C}_s\cdot {\varphi }_s$$

(24)

$$\begin{gathered} C_M=C_{dg}\cdot {\theta }_{dg}+C_{gb}\cdot {\theta }_{gb}+C_{ehp}\cdot {\theta }_{ehp}+C_{elz}\cdot {\theta }_{elz} \\ +C_{fc}\cdot {\theta }_{fc}+{\displaystyle \sum }_{\forall s}{C}_{ess,s}\cdot {\theta }_{ess,s}+{\displaystyle \sum }_{\forall t}{T}_{ng,t}\cdot {\theta }_{ng}+{\displaystyle \sum }_{\forall t}{P}_{dg,t}\cdot {\theta }_{oil} \end{gathered}$$

(25)

$\varphi$ refers to the installation cost for each facility and $\theta$ refers to the operation cost for each facility, and fuel cost. PV is not included in this paper in the curtailment target, so it operates fixedly. Finally, the objective function from an IPP perspective is a function that simultaneously optimizes the investment cost of IES and the curtailment of WT, and It is represented by Equation (26).

$$\min \left(f\right)=\min \left({\displaystyle \sum }_{\forall t}{\displaystyle \sum }_{\forall w}{P}_{WT,w,t}^{CT}+C_I+C_M\right)$$

(26)

In this paper, as random values according to probability distribution and probability distribution are applied to consider the power uncertainty of WT and PV, optimization is implemented 100 times, the observation value is derived, and the result is applied. Equation (27) represents this paper’s observation value of the optimization value.

$$E\left[X\right]={\displaystyle \sum }_{\forall m}{x}_m{f}_m\left(x_m\right)$$

(27)

5. Simulation Result

The simulation result of this paper derives the optimal design and operation solution of IES from an IPP perspective and constructs a composition set based on BESS, Elz, and EHP facilities that can reduce curtailed power and analyzes the simulation result. The case is shown in

Table 1. Composition of IES.

Cases	Facilities
1	(UCG + DG) + (GB + EHP)
2	Case 1 + BESS
3	Case 1 + (Elz + HESS + FC + TESS)
4	Case 3 + BESS

.

Aewol-eup, four WT with a capacity of 2000 kW from No. 1 to 4 and 3000 kW from No. 5 to No. 8 are installed. Load data considers seasonal load characteristics. The cost information of the facilities in the IES is applied. as shown in

Table 2. Facilities economical parameters.

Facilities	CAPEX	OPEX	Eff
BESS	700 [$/kW]	14 [$/kW]	${\eta }_{bess}$:0.98
HESS	574 [$/H2 kg]	11.48 [$/H2 kg]	${\eta }_{hess}$:0.98
TESS	3.2 [$/kWh]	0.064 [$/kWh]	${\eta }_{tess}$:0.98
FC	1000 [$/kW]	20 [$/kW]	${\eta }_{fc}^p:0.3$
			${\eta }_{fc}^t:0.6$
ELZ	760 [$/kW]	21 [$/kW]	${\eta }_{elz}:0.8$
DG	400 [$/kW]	0.5 [$/h]	${\eta }_{cg}:0.35$
GB	220 [$/kWh]	10.76 [$/kWh]	${\eta }_{gb}:0.8$
EHP	690 [$/kW]	4.9 [$/kW]	${\eta }_{ehp}:1$
Oil	-	0.87 [$/kg]
Natural gas	-	0.0047 [$/kWh]

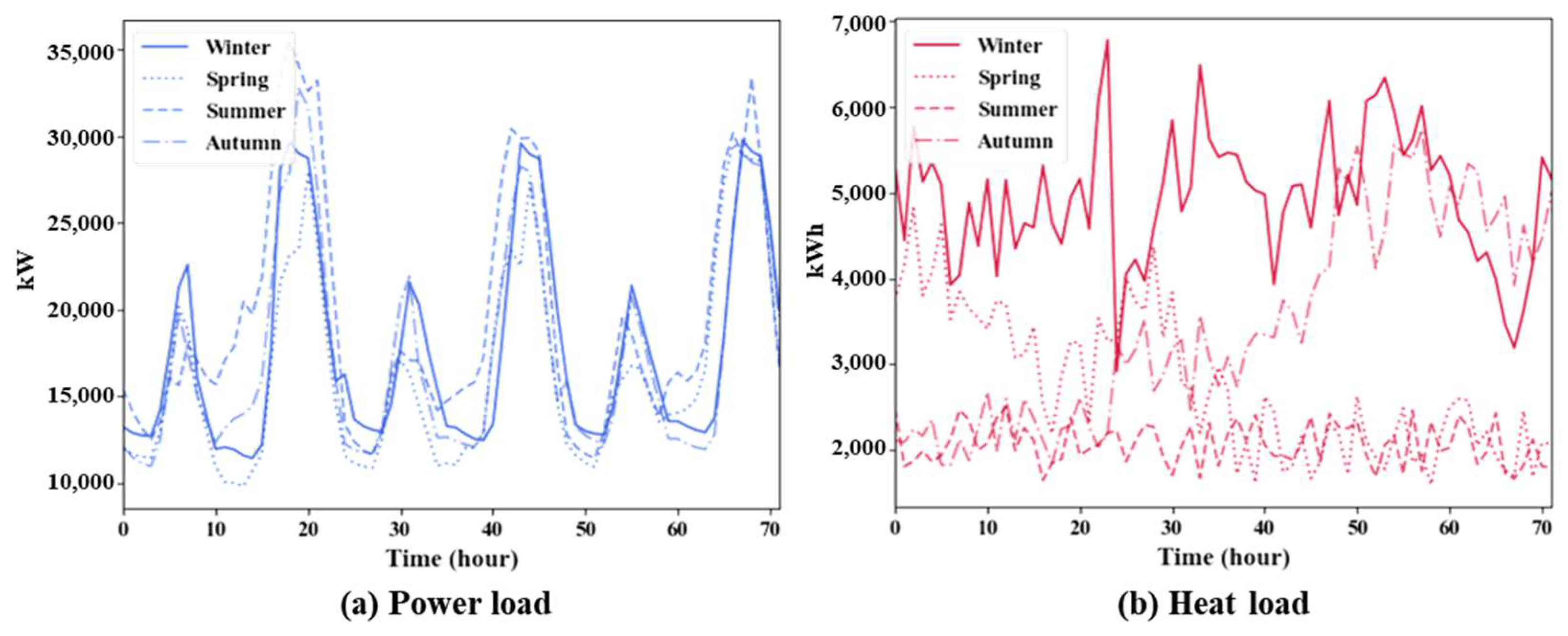
, based on the reference. In Table 2, capital expansion (CAPEX) and operational expansion (OPEX) refer to the investment and operation costs of the facility, respectively. Oil and gas prices are calculated based on the prices distributed in Korea. In this case study of this paper, all scheduling figures are shown based on 70–120 [h], highlighting the plan to reduce curtailed power. The figure below schematically illustrates the time series load data used in this paper, and power and heat show the maximum demand in summer and winter, respectively. The parameters applied to the modeling for each facility are shown in

Table 3. Facilities modeling parameters.

Applied Facility	Parameters	Value	Applied Facility	Parameters	Value
WT	${\rho }_v$	1.225 [kg/m3]	DG	$E$	1000 [kcal/kg-oil]
	$A$	314 [m2]	GB	$HH{V}_{ng}$	15.4 [kWh/kg-ng]
PV	$f$	3000 [m2]	ELZ	$HH{V}_{H2}$	39.4 [kWh/kg-H2]
	$\sigma$	0.75	ESS	$C-rat{e}_s$	0.5
	$T_{Cell,STC}$	$25$

. The seasonal load profile of power and heat are shown in Figure 4.

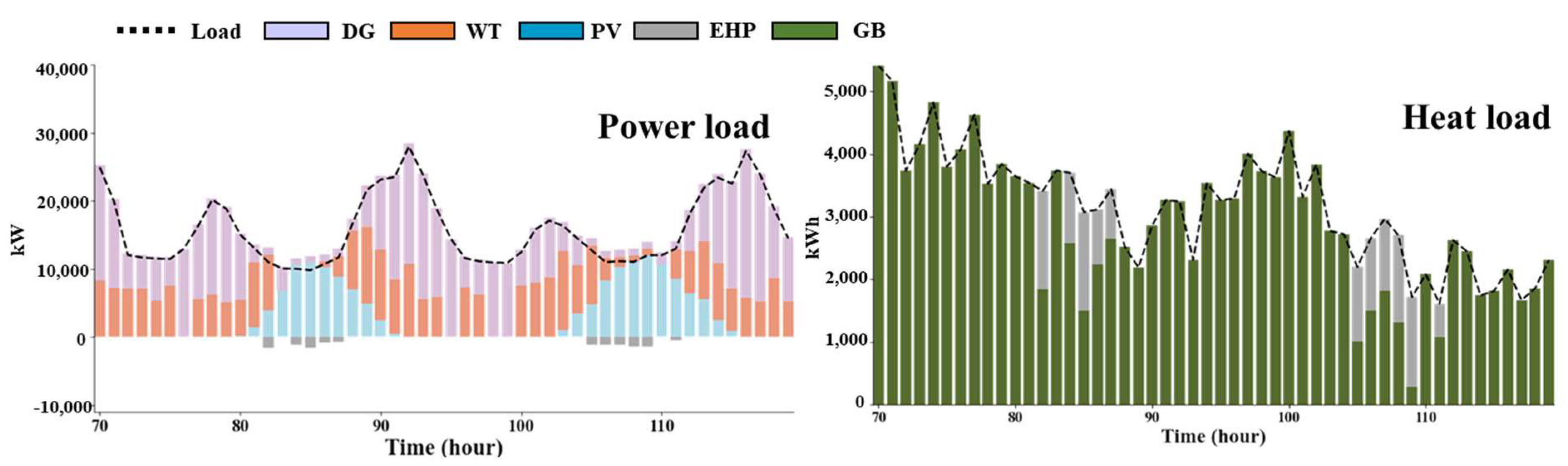
5.1. Case 1: (UCG + DG) + (GB + EHP)

The IES design and operation from an IPP perspective is for the economical operation while always satisfying the constraints that do not occur in the curtailment of WT. In Case 1, the facility used in excess power elimination mode is EHP. Therefore, in Case 1, the curtailed power cannot be removed completely. However, as EHP is the only facility deployed to eliminate excess power, it derives economical design and operation results compared to other cases. Figure 5 shows the scheduling result of Case 1. Figure 5 show the scheduling result of the power load and the heat load, respectively, and it can be confirmed that the operation of the EHP occurs up to the limit in Case 1.

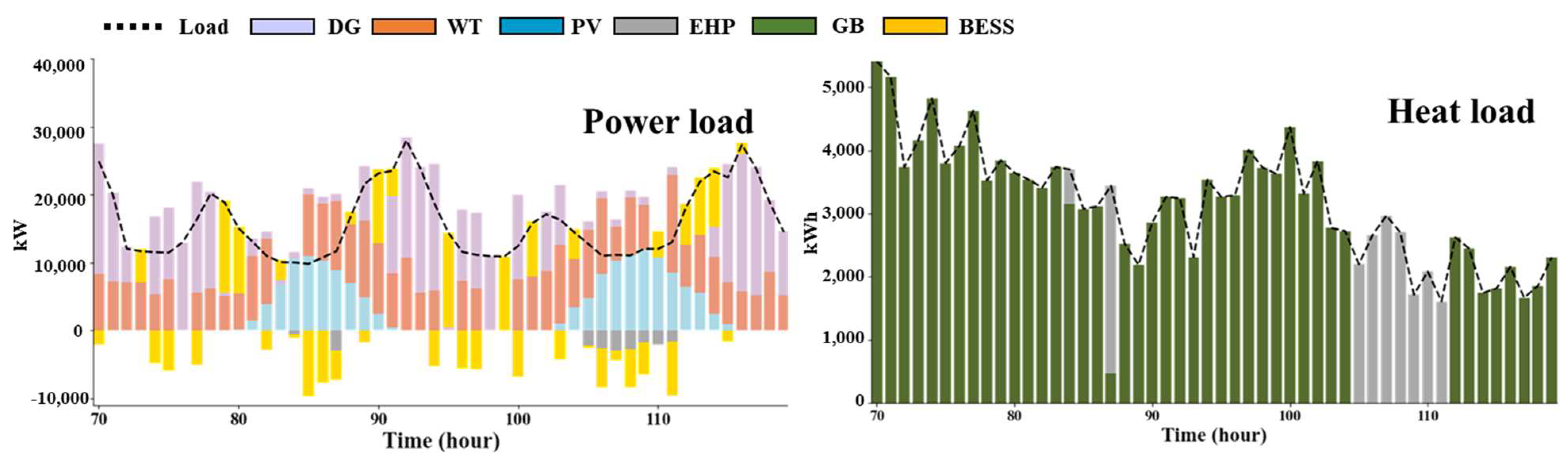
5.2. Case 2: Case 1 + BESS

Case 2 additionally applies BESS in Case 1 as a facility used in excess power elimination. Therefore, excess power is eliminated when excess power occurs by supplying heat energy through EHP and storing power through BESS. In BESS, more than the necessary capacity is selected to reduce continuous excess power by charging and discharging characteristics. Therefore, the design and operation results of the uneconomical IES are derived compared to Case 4 using P2G facilities, and Case 1 and Case 3 are not applied with BESS. Figure 6 demonstrates the scheduling result of Case 2. Figure 6 represent the scheduling result of the power load and the heat load, respectively. Contrary to Case 1, BESS is mainly used to reduce the curtailment of WT, and through this, it can be seen that the operation of EHP is reduced, and the supply of thermal energy is also increased through GB.

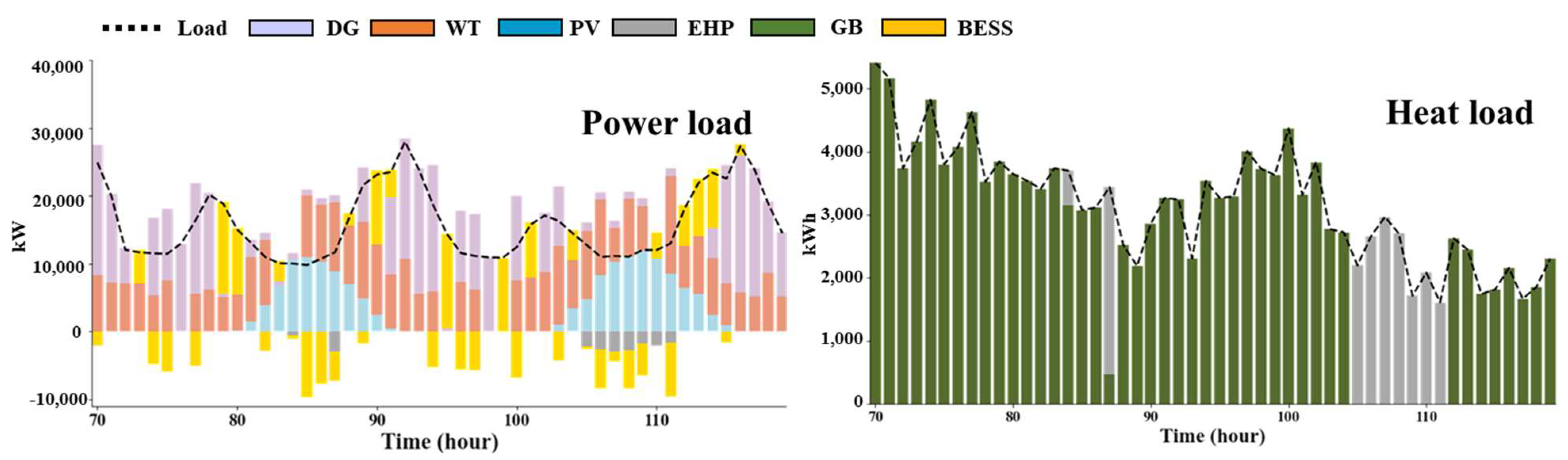
5.3. Case 3: Case 1 + Elz + HESS + FC +TESS

Case 3 is additionally applied by P2G facilities in Case 1 as a facility in excess power elimination. Therefore, when excess power is generated, the excess power is eliminated by supplying heat energy through EHP and hydrogenating power through Elz. Unlike BESS, HESS does not select excess facility capacity for excess power elimination because charging and discharging may occur independently by the FC and Elz. Therefore, although the Elz and FC are additionally applied using P2G, they show more economical operating results than Case 1 and Case 2. Figure 7 is the scheduling result of Case 3. Figure 7 represent the scheduling result of the power load and the heat load, respectively. Elz is mainly used as an operation to reduce the curtailment of WT, and through this, it can be confirmed that the operation of EHP is reduced compared to Case 1, as in Case 2. Additionally, the use of FC occurs from the production of hydrogen energy and the heat supply by FC is added accordingly.

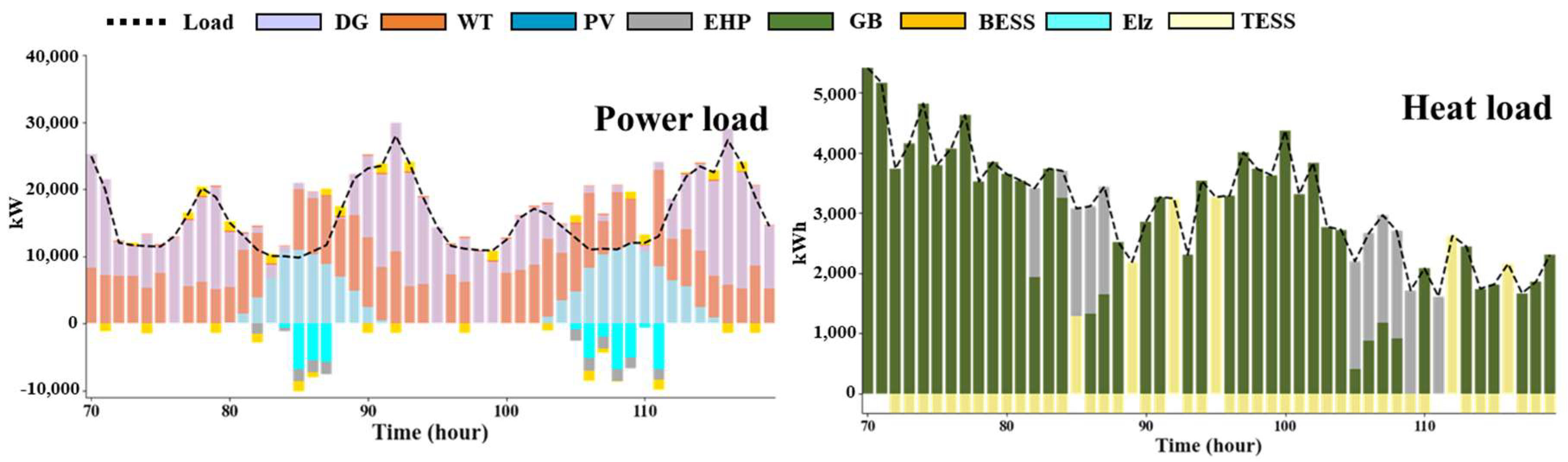
5.4. Case 4: Case 3 + BESS

Case 4 simultaneously applies BESS and P2G facilities in Case 1 as the facilities in excess power elimination. Therefore, when excess power is generated, excess power is eliminated by supplying thermal energy through EHP, storing power through BESS, and hydrogenating power through Elz. As Case 4 includes both BESS and P2G facilities, the operation result is expected to be uneconomical compared to other cases. However, when excess power occurs in the simulation, the capacity of each facility is moderately selected through a complementary operation. Through this, the most economical IES design and operation results are derived while reducing the same level of curtailed power in all cases. Figure 8 is the scheduling result of Case 3. Figure 8 represent the scheduling result of the power load and the heat load, respectively. In Case 5, Elz and BESS are simultaneously used as an operation to reduce the curtailment of WT. Through this, it can be confirmed that the capacity of Elz and BESS is relatively shared compared to Cases 2 and 3, and thus the system cost is reduced. Furthermore, it can be observed that the amount of heat supplied by FC decreases compared to Case 3. The numerical results of each case are shown in

Table 4. Optimization results of each case.

	Case 1	Case 2	Case 3	Case 4
System cost [$ $\times {10}^3$/year]	32,950	50,002	42,170	40,435
Curtailed power [MWh/year]	3197	0	0	0

.

As shown in Table 4, the system cost of Case 1 is the cheapest because the facility combination of Case 1 cannot completely remove the curtailed power, so the investment in the facility is technically limited. However, in Case 2, Case 3, and Case 4, the curtailed power is completely removed, and as mentioned above, the operation of Elz and BESS is dispersed in Case 4, and thus the system cost is the cheapest. Therefore, it is reasonable to use Elz and BESS simultaneously to reduce the economic curtailment of WT.

6. Conclusions

This paper analyzes the measures undertaken to resolve the effects of rapidly increasing UCG output on a power system’s power supply and demand balance. The case study was conducted in Aewol-eup, Jeju Island, South Korea, the target site. Here, WT curtailment occurred due to excess power generation. The designed IES prevented WT’s curtailment based on P2G, P2H, G2P, and G2P technology. The results of this paper first considered the operational efficiency objective function of UCG from the IPP perspective before applying the economic objective function, which is a general objective function. Therefore, IES has the most economical washing and operation solution when the WT curtailment is minimized.

As a result, if only P2H is applied to IES, the curtailment of WT can be partially removed. Where BESS is additionally injected with IES, a high investment cost of BESS is induced by the constraint that the charge and discharge of BESS cannot be operated simultaneously, and as a result, the system cost rises rapidly. If P2G technology is additionally injected with IES instead of BESS, a high capacity of the facility is not caused by an independent charging and discharging operation of the HESS. However, it is verified that the limitations of P2G facilities are clear in the process of reducing the curtailment of discontinuous WT. IF BESS and P2G technology are injected with IES simultaneously, discontinuous curtailment of WT is reduced through charging mode of BESS and the continuous curtailment of WT is reduced through P2G technology. Therefore, this paper proposes a structure in which the optimal facility configuration for reducing the curtailment of WT using IES includes both BESS and P2G facilities.

Many countries worldwide have adopted semi-permanent and highly utilizable hydrogen as next-generation energy and encourage its active use. Accordingly, hydrogen infrastructure construction is being accelerated for the production and utilization of hydrogen. As the hydrogen economy is achieved by building hydrogen infrastructure, the importance of Elz and FC is greatly emphasized. Elz and FC have witnessed a decline in facility costs due to the utilization of hydrogen. The results of this paper include costs resulting from applying the excess power elimination mode. As the facility costs of Elz and FC, which are cheaper than the present, are applied in the future, this paper will achieve excellent economic feasibility and stable WT.

The use of hydrogen employing the P2G technology is essential for energy policies, such as RE100. Accordingly, various profit-generating measures using hydrogen are expected to be proposed following national policy, and Korea’s CHPS will be implemented. This paper derives IES’s optimal design and operation solutions with various structures from an IPP perspective. The results show that it is optimal to operate BESS and P2G technologies simultaneously in the optimization process, and it is determined that WT’s curtailment can be reduced economically. Based on the results, it can be used as a criterion for reasonably calculating CHPS subsidies scheduled to be introduced in South Korea.