Analysis of the Influence of Structure–Soil–Structure Interaction on the Seismic Response for Nuclear Power Plant ASTS
Abstract
1. Introduction
2. Numerical Analysis Methods and Models
2.1. Finite Element Model
2.2. Site Conditions
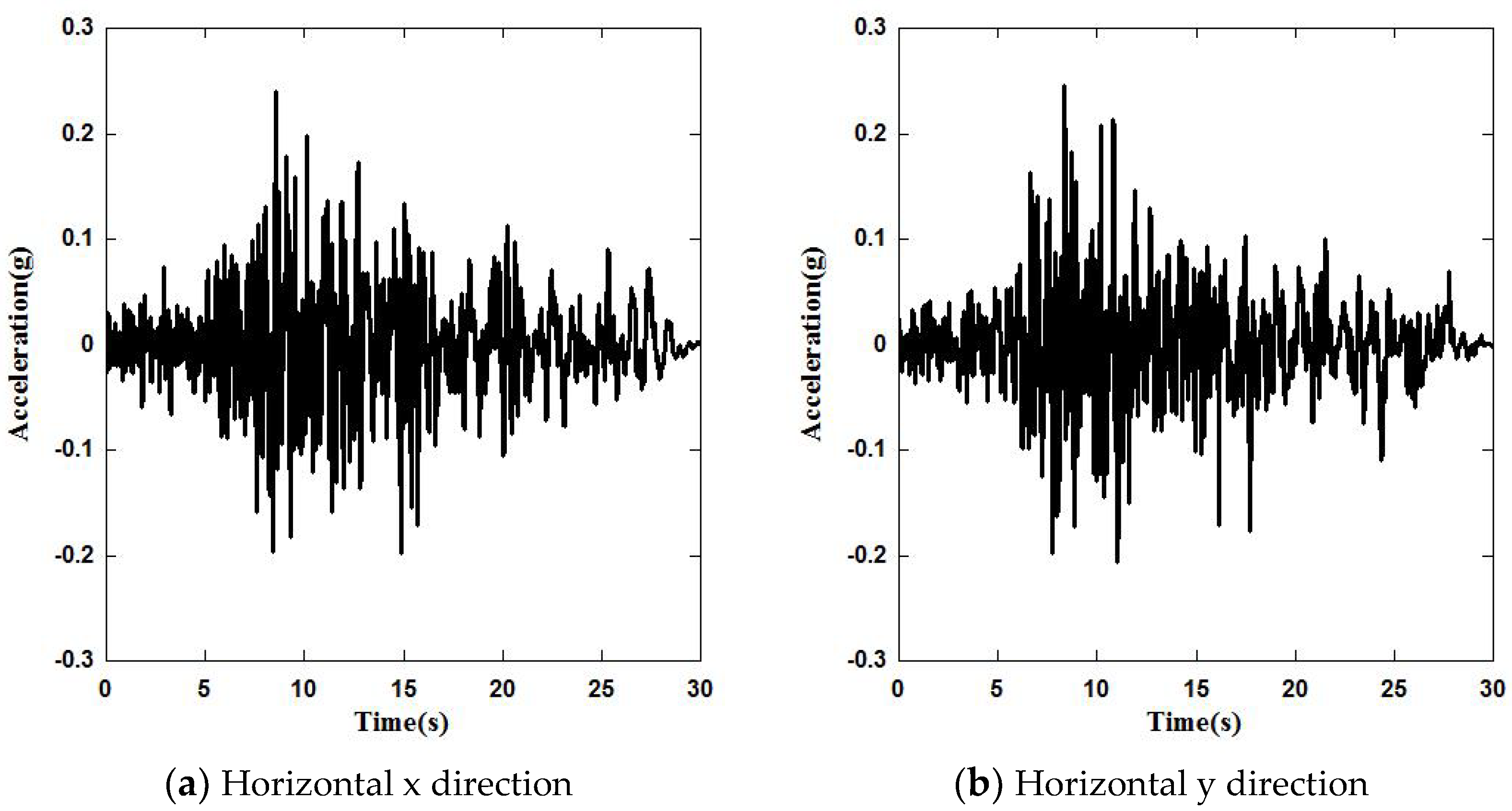
2.3. Ground Motion Input
3. Analysis of Seismic Parameters of Raft Foundation
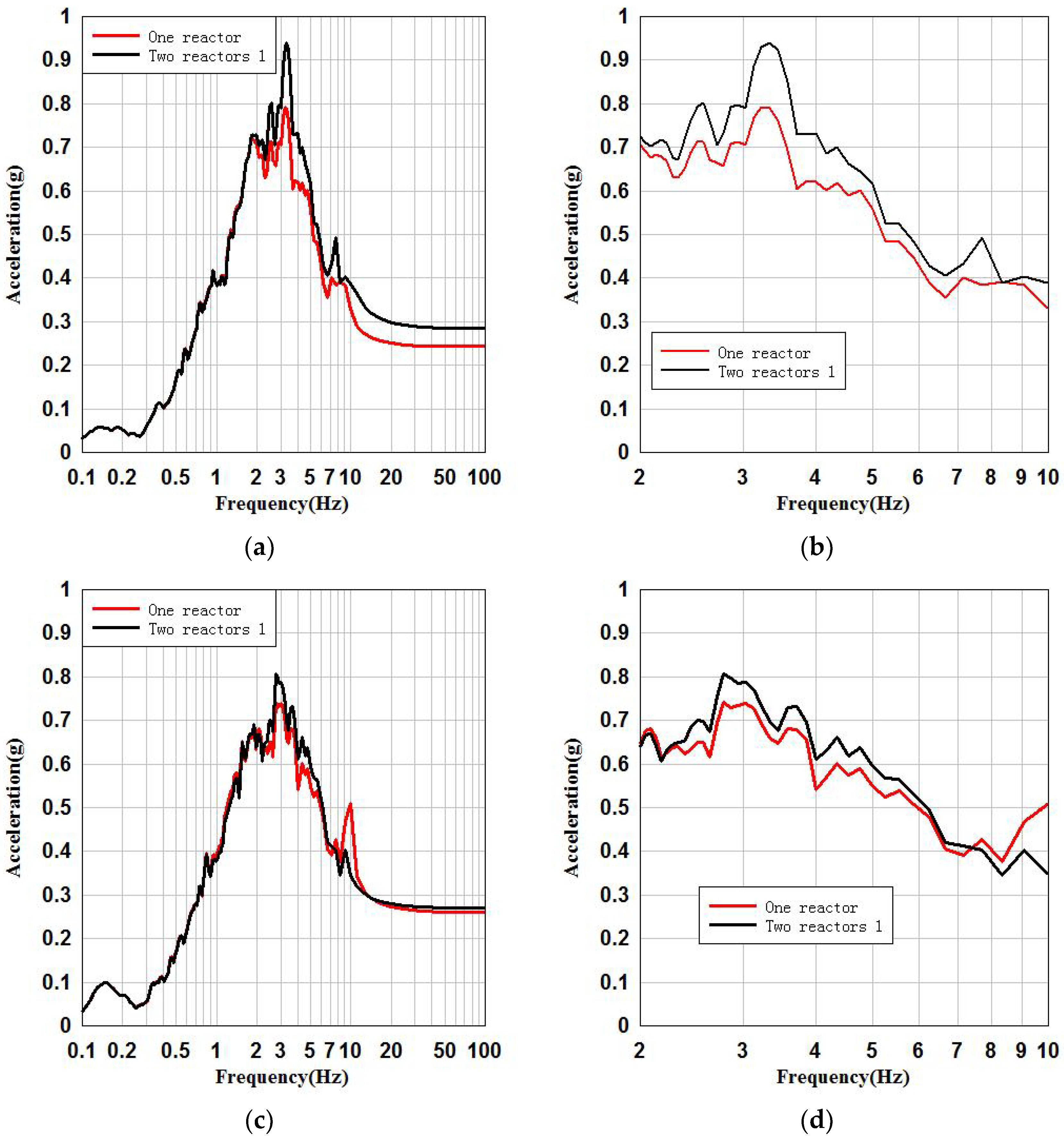
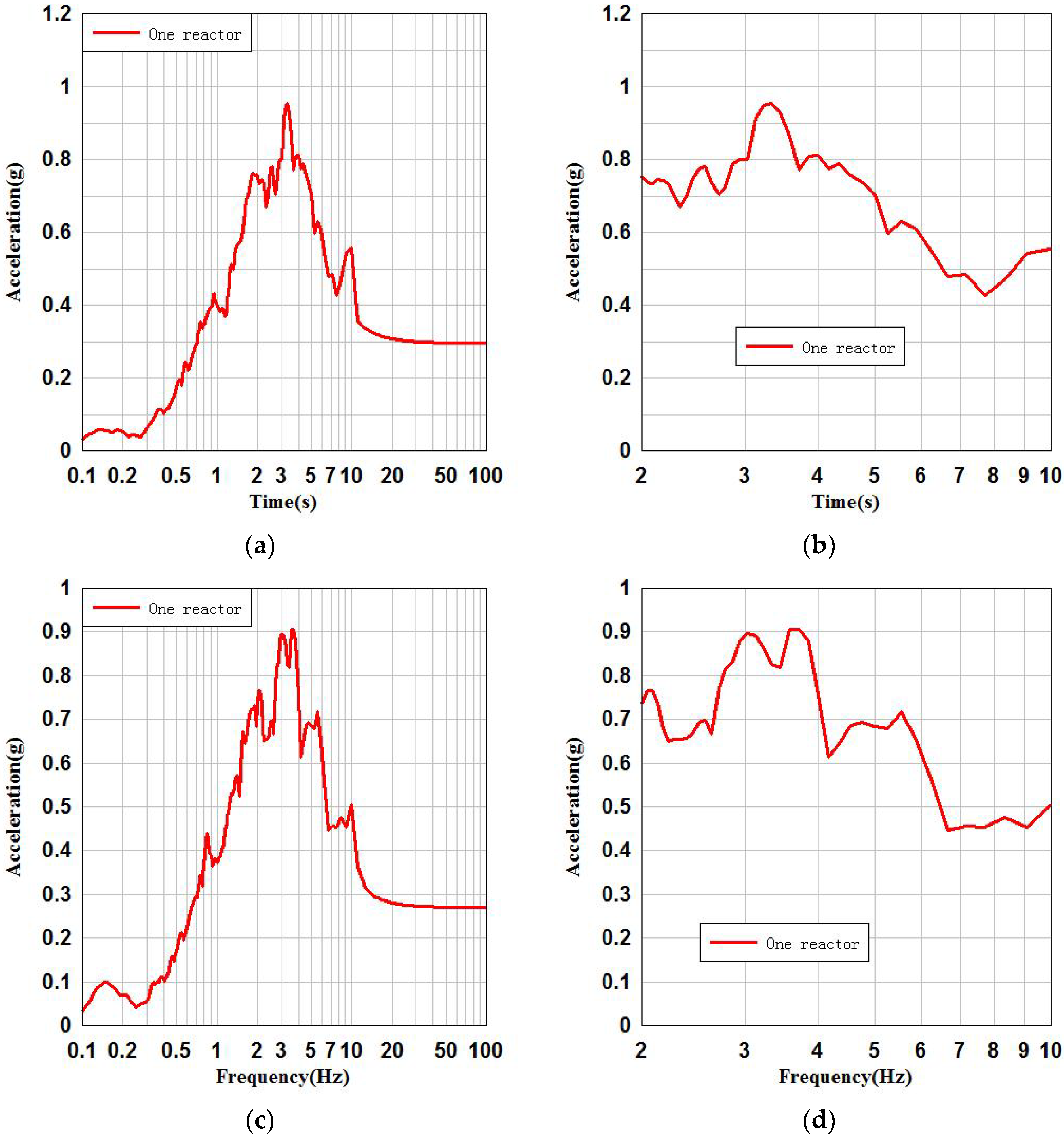
3.1. Seismic Parameter Analysis of Raft Foundation of SSI System
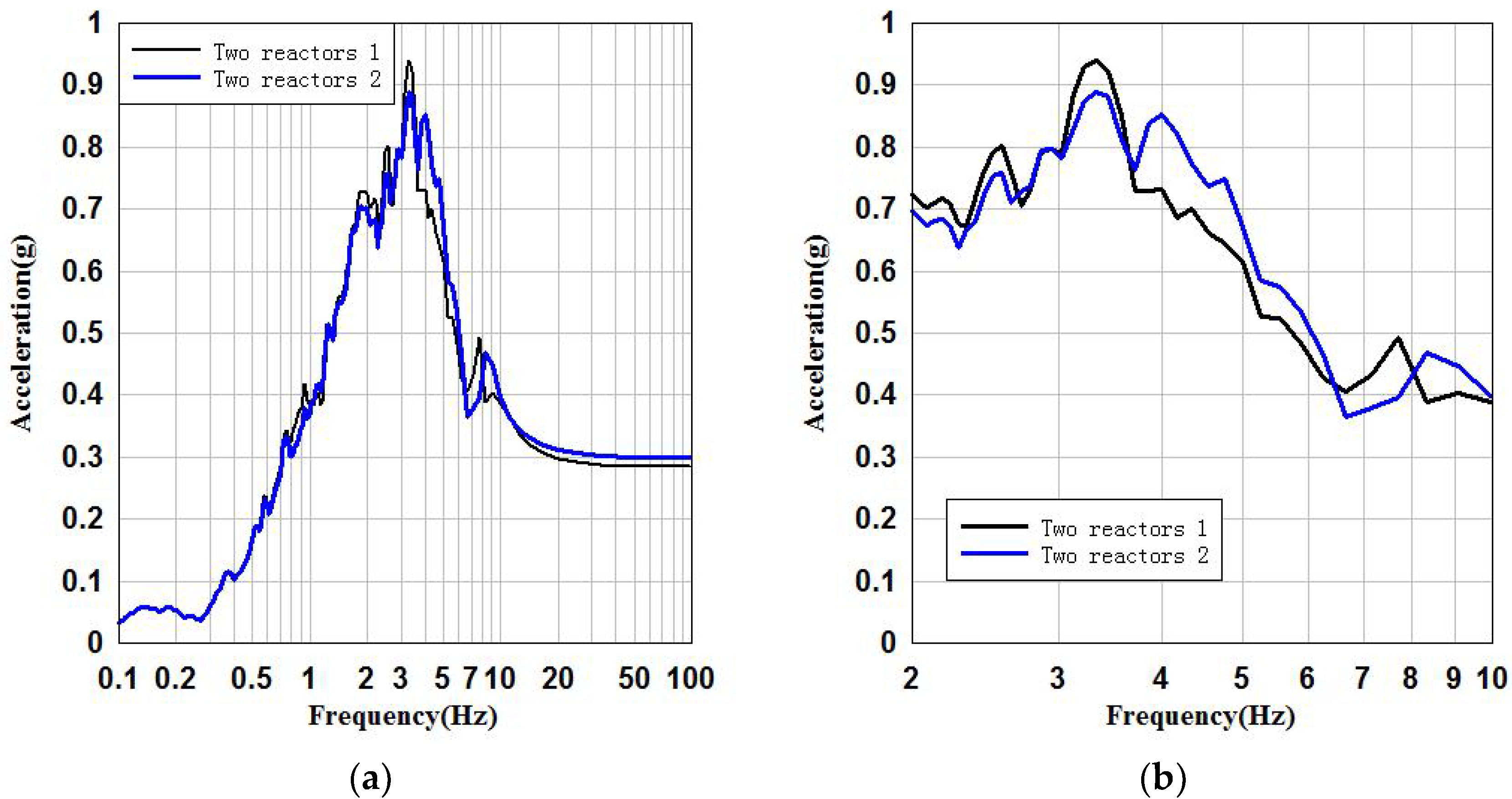
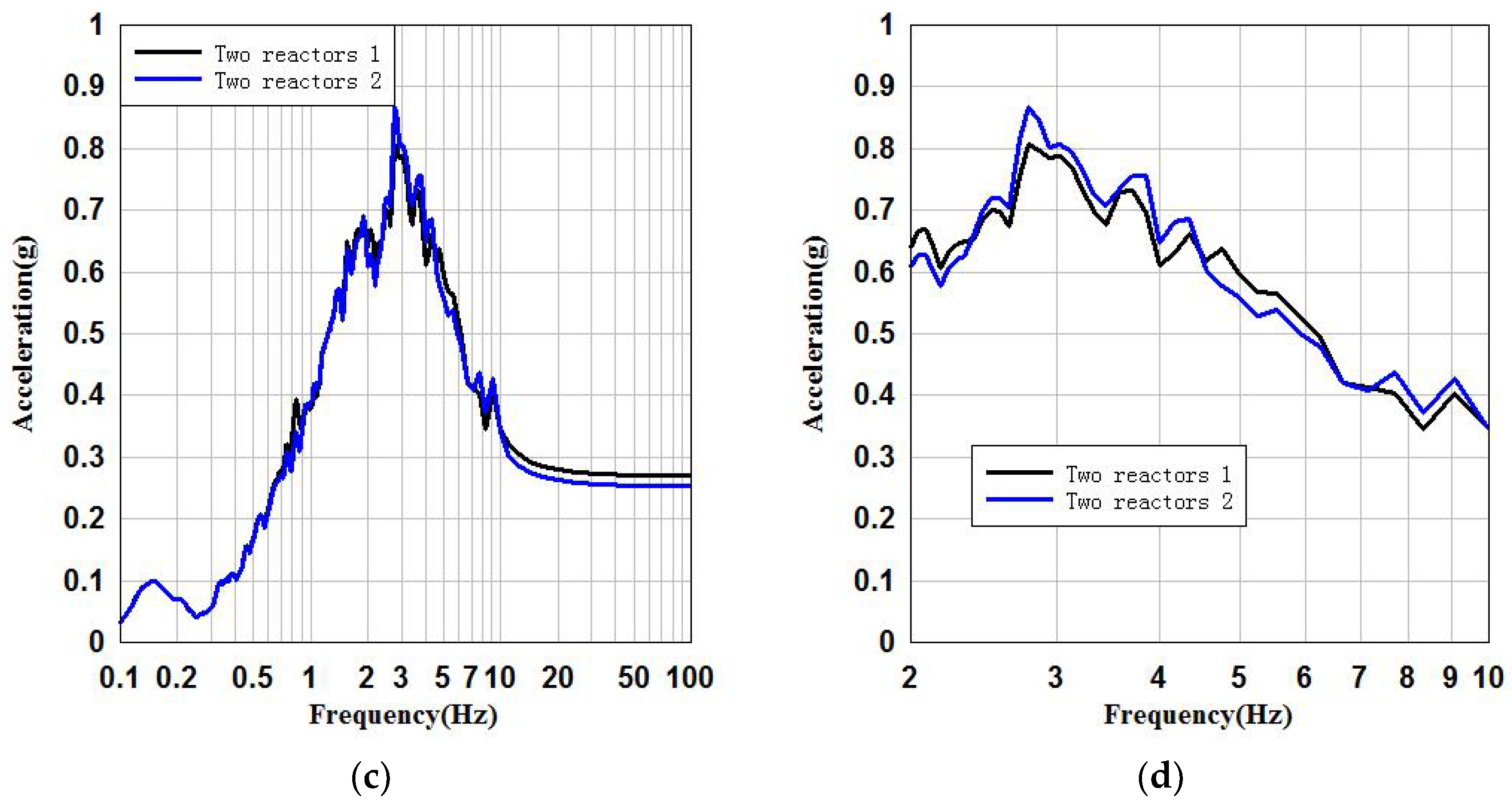
3.2. Seismic Parameter Analysis of SSSI System Raft Foundation
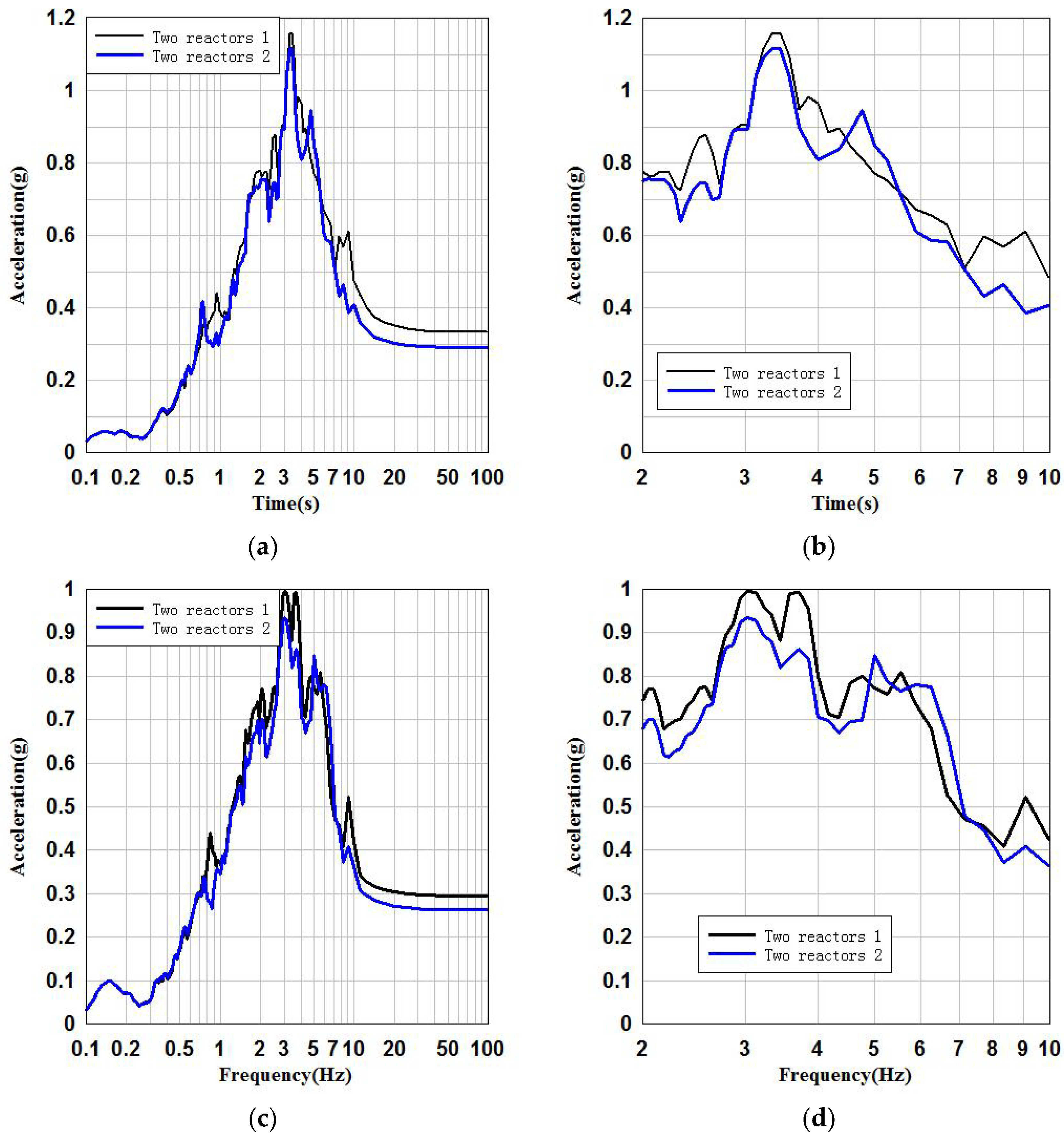
3.3. Comparison and Analysis of Two Reactors at the Same Site
3.4. Comparison of Raft Foundation Ground Motion Parameters between SSI System and SSSI System
4. Analysis of Seismic Parameters of the Key Floor
4.1. Seismic Parameter Analysis of the Key Floor of SSI System
4.2. Seismic Parameter Analysis of the Key Floor of SSI System
4.3. Seismic Parameter Analysis of the Key Floor of SSI System
4.4. Comparison of Ground Motion Parameters of Key Floors between SSI System and SSSI System
5. Conclusions
- (1)
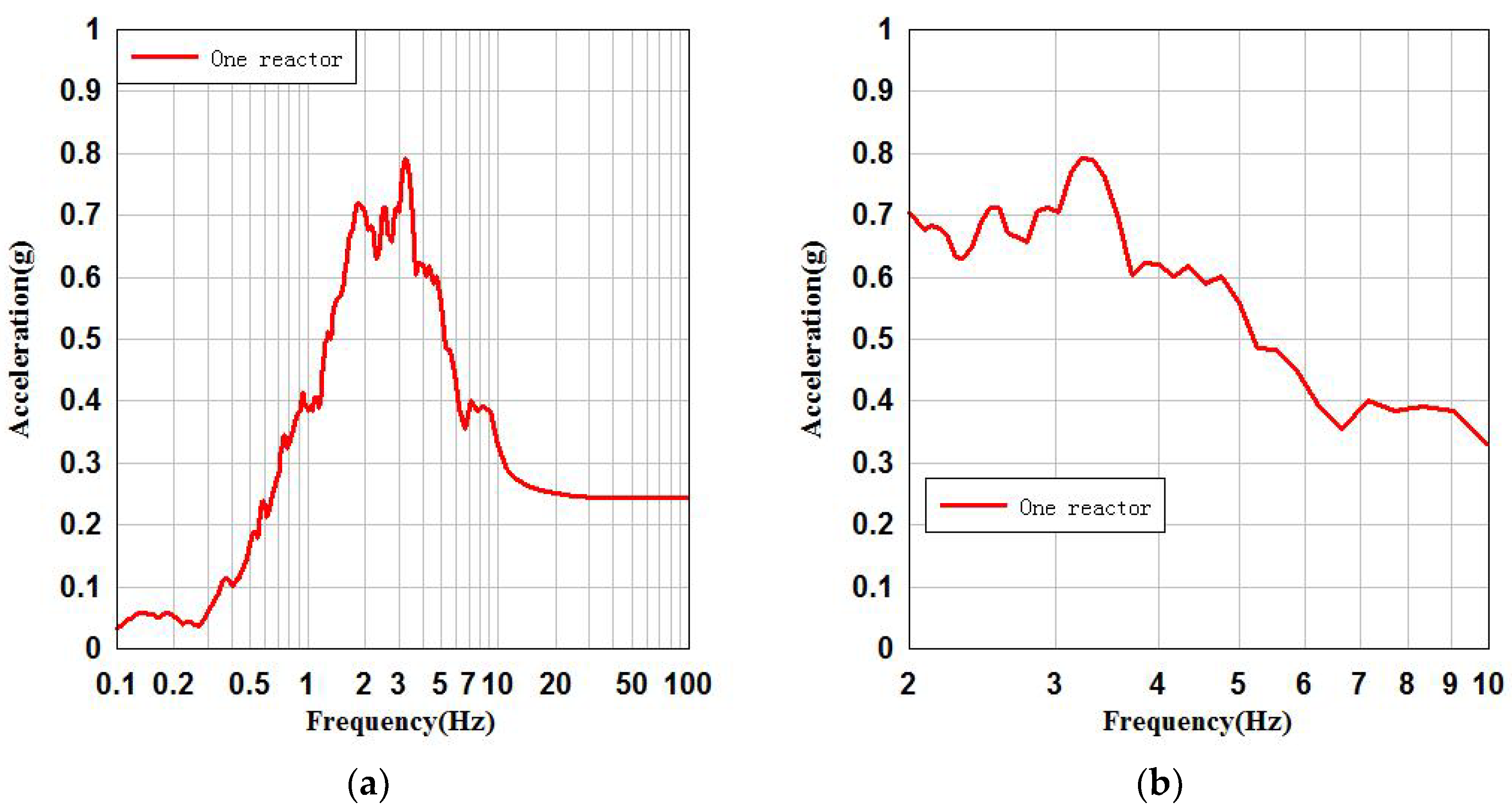
- By comparing the SSI system with the SSSI system for the raft foundation, the peak accelerations of the SSI system and the SSSI system in x and y directions differ by 0.04 g and 0.01 g, respectively. The peak accelerations of the FRS in x and y directions differ by 19% and 18%, respectively. It can be said that the difference between the peak accelerations of the raft foundation reference point of the SSI system and the SSSI system is very small, but the peak values of the FRS are somewhat different. The FRS of raft foundation of SSI system and SSSI system are basically consistent in the low frequency band (below 2 Hz), and have certain differences in the main frequency band (2–10 Hz).
- (2)
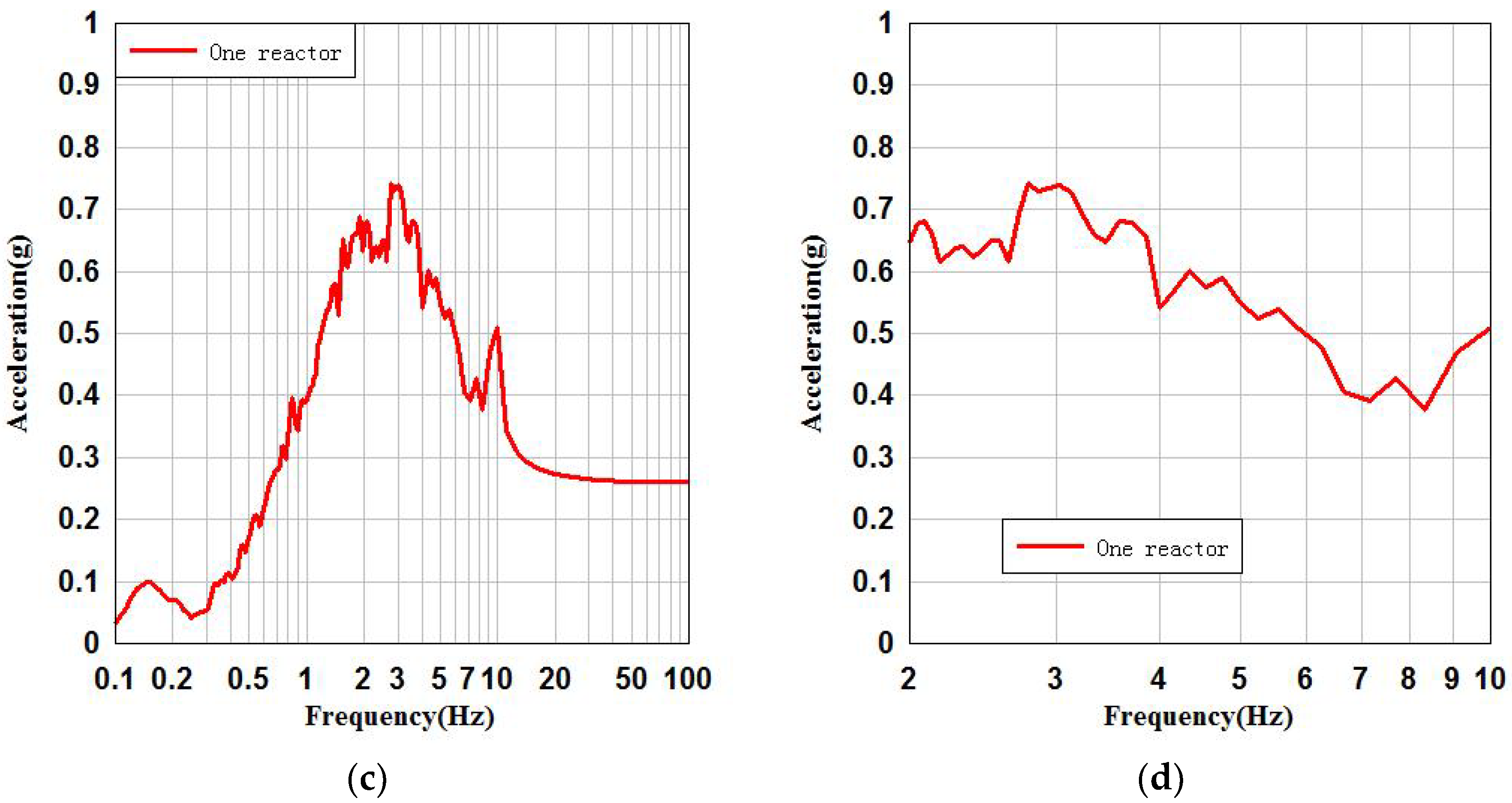
- By comparing the SSI system with the SSSI system for the key floor of the NPP structure, the difference between the peak acceleration of the SSI system and the SSSI system in x and y directions is 0.04 g and 0.02 g, respectively. The peak accelerations of the FRS in x and y directions differ by 22% and 10%, respectively. It can be said that the FRS of the key floor reference points of the NPP structure of the SSI system and the SSSI system are different. The FRS of the key floors of the SSI system and SSSI system are basically consistent in the low frequency band (below 2 Hz), and have certain differences in the main frequency band (2–10 Hz).
- (3)
- Generally, SSSI effect can be ignored for bedrock sites, but for non-bedrock sites, especially those with soft soil site, the influence of SSSI effect shall be considered in the layout position of seismic instruments used for ASTS and the setting of shutdown threshold. SSSI effect shall be reasonably considered according to site conditions during structural analysis for the NPPs ASTS.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Elkhoraibi, T.; Hashemi, A.; Ostadan, F. Probabilistic and deterministic soil structure interaction analysis including ground motion incoherency effects. Nucl. Eng. Des. 2014, 269, 250–255. [Google Scholar] [CrossRef]
- Farahani, R.V.; Dessalegn, T.M.; Vaidya, N.R.; Bazan-Zurita, E. Seismic soil–structure interaction analysis of a nuclear power plant building founded on soil and in degraded concrete stiffness condition. Nucl. Eng. Des. 2016, 297, 320–326. [Google Scholar] [CrossRef]
- Politopoulos, I.; Sergis, I.; Wang, F. Floor response spectra of a partially embedded seismically isolated nuclear plant. Soil Dyn. Earthq. Eng. 2015, 78, 213–217. [Google Scholar] [CrossRef]
- Luco, J.E.; Contesse, L. Dynamic structure-soil-structure interaction. Bull. Seismol. Soc. Am. 1973, 63, 1289–1303. [Google Scholar] [CrossRef]
- Wong, H.L.; Luco, J.E. Dynamic interaction between rigid foundations in a layered half-space. Soil Dyn. Earthq. Eng. 1986, 5, 149–158. [Google Scholar] [CrossRef]
- Wong, H.L.; Luco, J.E. Dynamic structure-to-structure interaction for closely spaced buildings. In Proceedings of the 3rd US National Conference on Earthquake Engineering, Charleston, SC, USA, 24–28 August 1986. [Google Scholar]
- Ostadan, F.; Tseng, W.S.; Liu, A.S. Effect of site soil properties on seismic SSI response of embedded structures. In Proceedings of the ASCE Foundation Engineering Congress, Reston, VA, USA, June 1989. [Google Scholar]
- Kitada, Y.; Hirotani, T.; Iguchi, M. Model test on dynamic structure-structure interaction of nuclear power plant buildings. Nucl. Eng. Des. 1999, 192, 205–216. [Google Scholar] [CrossRef]
- Clouteau, D.; Broc, D.; Devésa, G.; Guyonvarh, V.; Massin, P. Calculation methods of structure-soil-structure interaction (3SI) for embedded buildings. application to NUPEC tests. Soil Dyn. Earthq. Eng. 2012, 32, 129–142. [Google Scholar] [CrossRef]
- Naserkhaki, S.; Pourmohammad, H. SSI and SSSI effects in seismic analysis of twin buildings:Discrete model concept. J. Civ. Eng. Manag. 2012, 18, 890–898. [Google Scholar] [CrossRef]
- Anderson, L.M.; Carey, S.; Amin, J. Effect of structure, soil, and ground motion parameters on structure-soil-structure interaction of large scale nuclear structures. In Structures Congress 2011; ASCE: Las Vegas, NV, USA, 2011; pp. 2862–2873. [Google Scholar]
- Roy, C.; Bolourchi, S.; Eggers, D. Significance of structure-soil-structure interaction for closely spaced structures. Nucl. Eng. Des. 2015, 295, 680–687. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Thusa, B.; Park, H.; Azad, M.S.; Lee, T.H. Efficiency of various structural modeling schemes on evaluating seismic performance and fragility of APR1400 containment building. Nucl. Eng. Technol. 2021, 53, 2696–2707. [Google Scholar] [CrossRef]
- GB50267-2019; Code for Seismic Design of Nuclear Power Plants. China Architecture and Building: Beijing, China, 2019.
- Zhao, M.; Wang, X.; Zhong, Z. Study on seismic responses of nuclear island structure in non-bedrock site under obliquely incidence of p waves. Eng. Mech. 2020, 37, 43–51. [Google Scholar]
- Frano, R.L.; Forasassi, G. Isolation systems influence in the seismic loading propagation analysis applied to an innovative near term reactor. Nucl. Eng. Des. 2010, 240, 3539–3549. [Google Scholar] [CrossRef]
- Du, X.L.; Zhao, M. A local time-domain transmitting boundary for simulating cylindrical elastic wave propagation in infinite media. Soil Dyn. Earthq. Eng. 2010, 30, 937–946. [Google Scholar] [CrossRef]
- Zhao, M.; Gao, Z.D.; Wang, L.T.; Du, X. Obliquely incident earthquake input for soil-structure interaction in layered half space. Earthq. Struct. 2017, 13, 573–588. [Google Scholar]
- Seismic Instrumentation System and Its Use in Post-earthquake Decision Making at Nuclear Power Plants; IAEA TECDOC-1956; International Atomic Energy Agency: Viena, Austria, 2021.


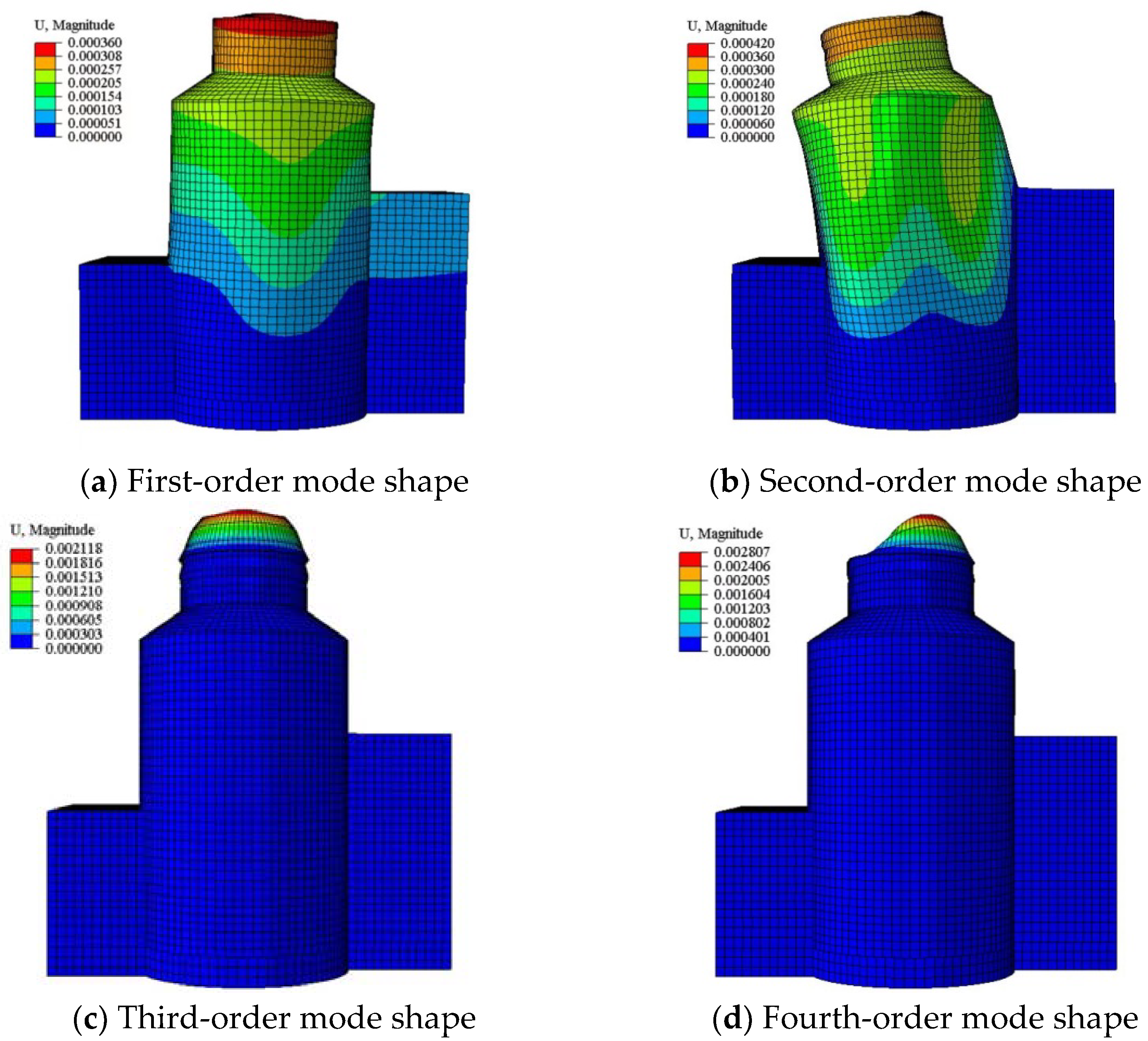

| Mode | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Frequency (Hz) | 4.11 | 4.46 | 5.00 | 5.81 |
| Depth (m) | Shear Velocity (m/s) | Density (kg/m3) | Elastic Modulus (MPa) | Poisson Ratio |
|---|---|---|---|---|
| 5 | 967.071596 | 1910 | 4923 | 0.378 |
| 15 | 458.45863 | 2020 | 1092 | 0.286 |
| 20 | 1146.22413 | 2460 | 8539 | 0.321 |
| 40 | 756.684691 | 2470 | 3612 | 0.277 |
| Direction | Condition | Amax (g) | |
|---|---|---|---|
| x | Two reactors1 | 0.28 | 0.02 |
| Two reactors2 | 0.30 | ||
| y | Two reactors1 | 0.27 | 0.02 |
| Two reactors2 | 0.25 |
| Direction | Condition | Smax (g) | Frequency (Hz) | |
|---|---|---|---|---|
| x | Two reactors1 | 0.94 | 3.33 | 0.05 |
| Two reactors2 | 0.89 | 3.33 | ||
| y | Two reactors1 | 0.81 | 2.77 | 0.06 |
| Two reactors2 | 0.87 | 2.77 |
| Direction | Condition | Smax (g) | Frequency (Hz) | |
|---|---|---|---|---|
| x | Two reactors1 | 0.94 | 3.33 | 0.05 |
| Two reactors2 | 0.89 | 3.33 | ||
| y | Two reactors1 | 0.81 | 2.77 | 0.06 |
| Two reactors2 | 0.87 | 2.77 |
| Variables | Definition | Variables | Definition |
|---|---|---|---|
| the peak acceleration | peak acceleration of the floor response spectrum | ||
| reduction rate of the peak acceleration | reduction rate of peak acceleration of the floor response spectrum | ||
| Amax | maximum of the peak acceleration | Smax | maximum of peak acceleration of the floor response spectrum |
| Direction | Condition | Amax (g) | |
|---|---|---|---|
| x | SSSI | 0.28 | 0.04 |
| SSI | 0.24 | ||
| y | SSSI | 0.27 | 0.01 |
| SSI | 0.26 |
| Direction | Condition | Smax (g) | Frequency (Hz) | |
|---|---|---|---|---|
| x | SSSI | 0.94 | 3.33 | 19 |
| SSI | 0.79 | 3.22 | ||
| y | SSSI | 0.87 | 2.77 | 18 |
| SSI | 0.74 | 2.77 |
| Direction | Condition | Smax (g) | Frequency (Hz) | |
|---|---|---|---|---|
| x | SSSI | 0.94 | 3.33 | 19 |
| SSI | 0.79 | 3.22 | ||
| y | SSSI | 0.87 | 2.77 | 18 |
| SSI | 0.74 | 2.77 |
| Direction | Condition | Amax (g) | |
|---|---|---|---|
| x | Two reactors1 | 0.33 | 0.04 |
| Two reactors2 | 0.29 | ||
| y | Two reactors1 | 0.29 | 0.03 |
| Two reactors2 | 0.26 |
| Direction | Condition | Smax (g) | Frequency (Hz) | |
|---|---|---|---|---|
| x | Two reactors1 | 1.16 | 3.44 | 0.04 |
| Two reactors2 | 1.12 | 3.33 | ||
| y | Two reactors1 | 1.00 | 3.03 | 0.06 |
| Two reactors2 | 0.94 | 3.03 |
| Direction | Condition | Smax (g) | Frequency (Hz) | |
|---|---|---|---|---|
| x | Two reactors1 | 1.16 | 3.44 | 0.04 |
| Two reactors2 | 1.12 | 3.33 | ||
| y | Two reactors1 | 1.00 | 3.03 | 0.06 |
| Two reactors2 | 0.94 | 3.03 |
| Direction | Condition | Amax (g) | |
|---|---|---|---|
| x | SSSI | 0.33 | 0.04 |
| SSI | 0.29 | ||
| y | SSSI | 0.29 | 0.02 |
| SSI | 0.27 |
| Direction | Condition | Smax (g) | Frequency (Hz) | |
|---|---|---|---|---|
| x | SSSI | 1.16 | 3.44 | 22 |
| SSI | 0.95 | 3.33 | ||
| y | SSSI | 1.00 | 3.03 | 10 |
| SSI | 0.91 | 3.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Chen, Q.; Pan, R. Analysis of the Influence of Structure–Soil–Structure Interaction on the Seismic Response for Nuclear Power Plant ASTS. Energies 2023, 16, 194. https://doi.org/10.3390/en16010194
Li L, Chen Q, Pan R. Analysis of the Influence of Structure–Soil–Structure Interaction on the Seismic Response for Nuclear Power Plant ASTS. Energies. 2023; 16(1):194. https://doi.org/10.3390/en16010194
Chicago/Turabian StyleLi, Liang, Qun Chen, and Rong Pan. 2023. "Analysis of the Influence of Structure–Soil–Structure Interaction on the Seismic Response for Nuclear Power Plant ASTS" Energies 16, no. 1: 194. https://doi.org/10.3390/en16010194
APA StyleLi, L., Chen, Q., & Pan, R. (2023). Analysis of the Influence of Structure–Soil–Structure Interaction on the Seismic Response for Nuclear Power Plant ASTS. Energies, 16(1), 194. https://doi.org/10.3390/en16010194





