Numerical Simulation of Multiarea Seepage in Deep Condensate Gas Reservoirs with Natural Fractures
Abstract
1. Introduction
2. Model and Methods
2.1. Physical Model
2.2. Mathematical Description
2.2.1. Continuity Equation
2.2.2. Motion Equation
2.2.3. Constraint Equation
2.2.4. Phase Equilibrium Equation
2.2.5. State Equation
2.2.6. Boundary Conditions and Initial Conditions
3. Model Validation
3.1. Static Parameters
3.2. Fluid Properties
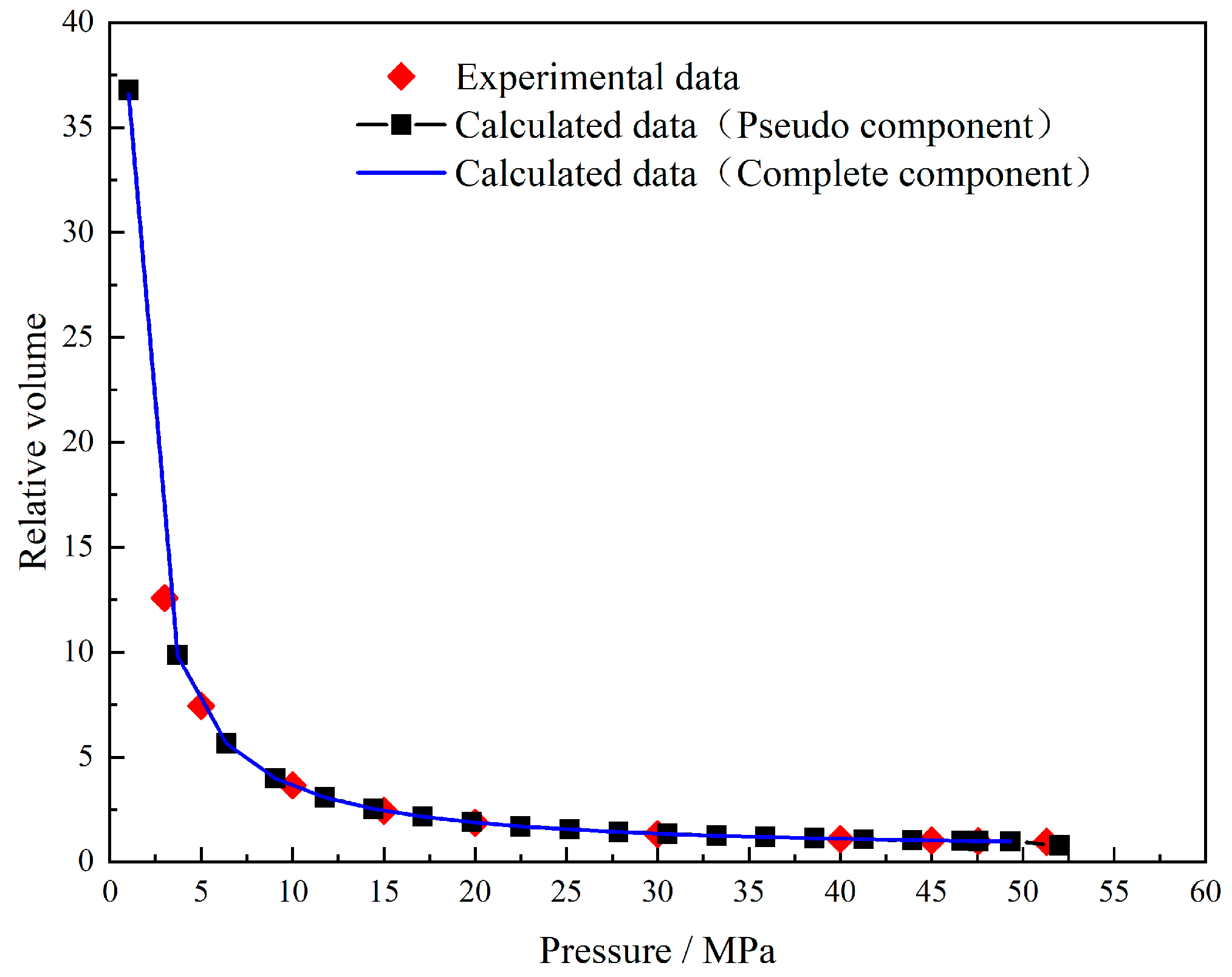
3.3. Validation
4. Simulation Results and Discussion
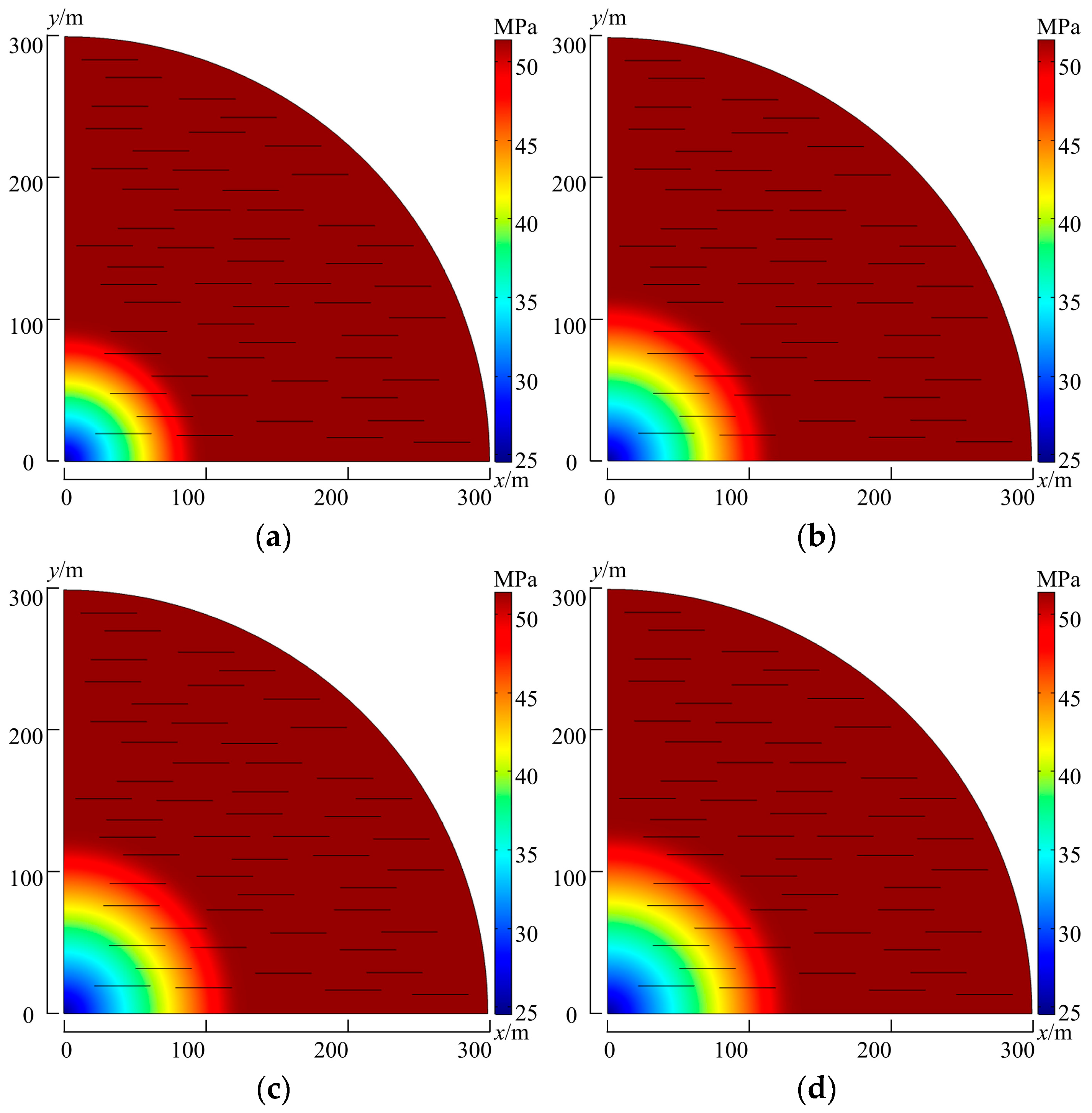
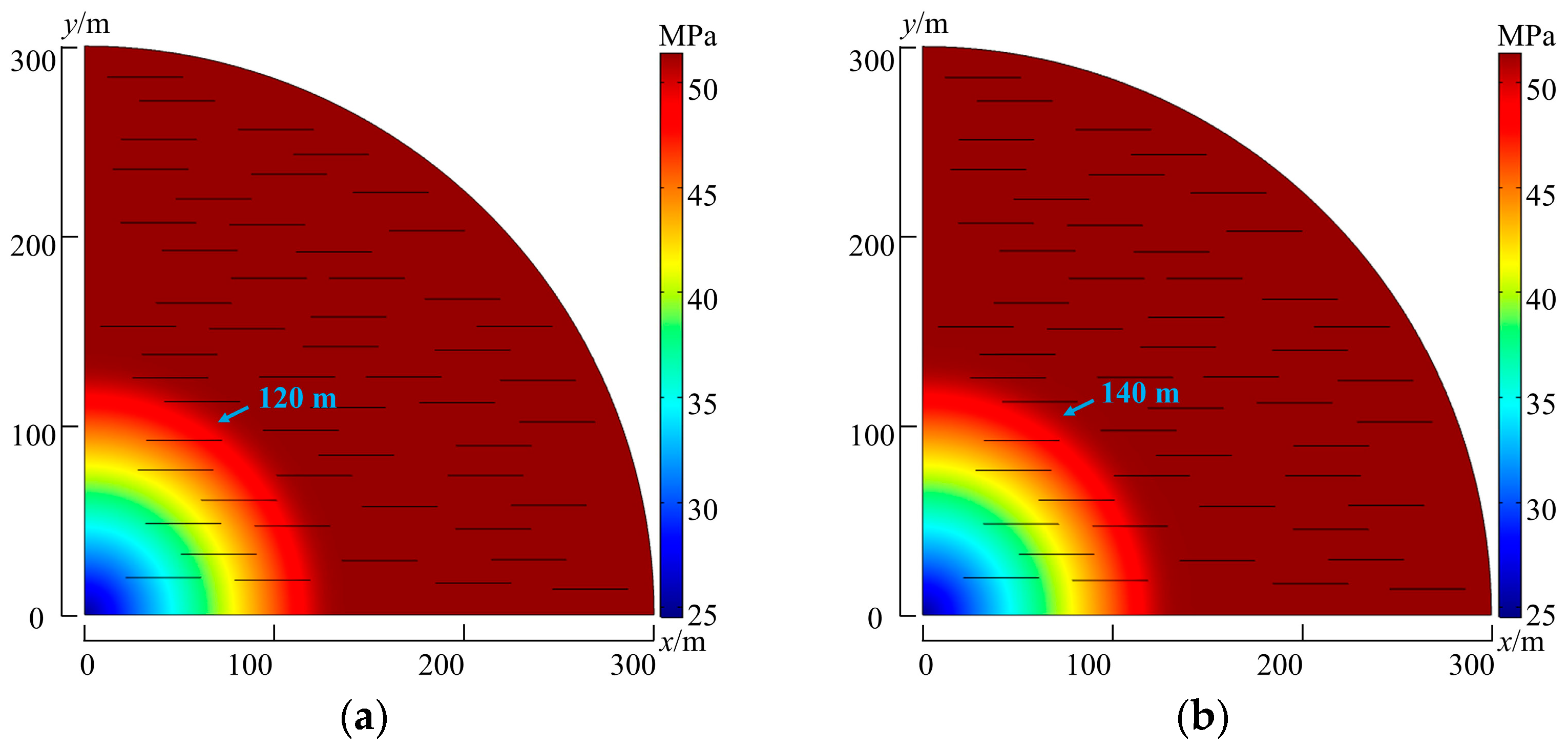
4.1. Formation Pressure Distribution
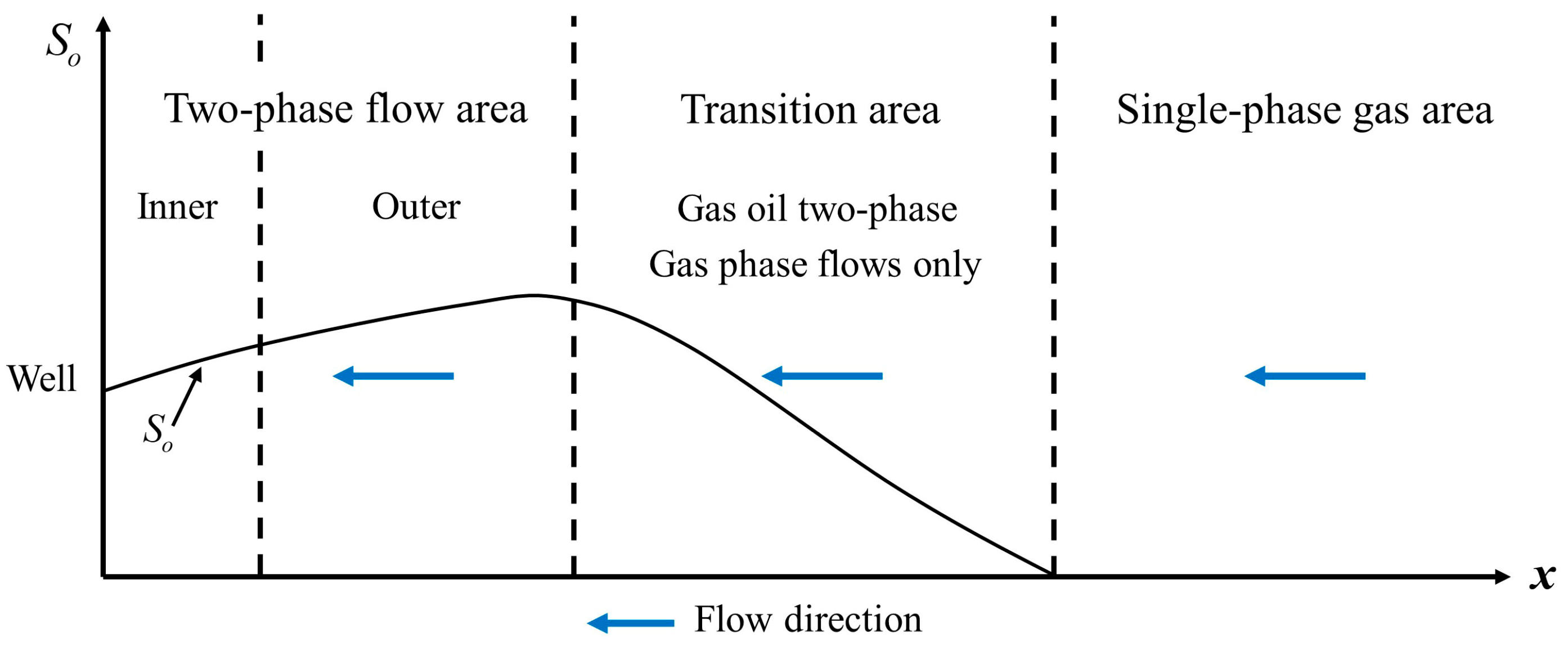
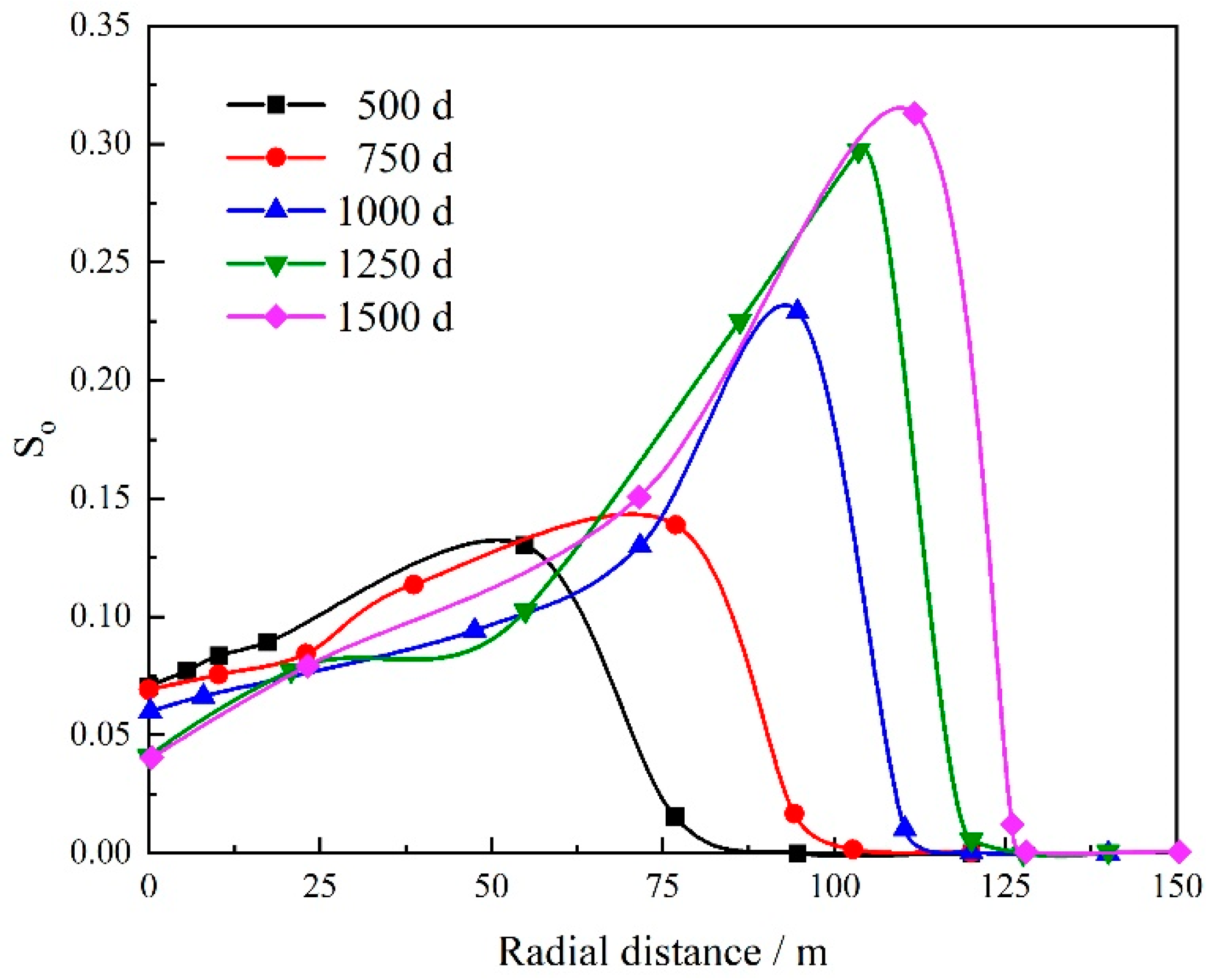
4.2. Condensate Oil Distribution
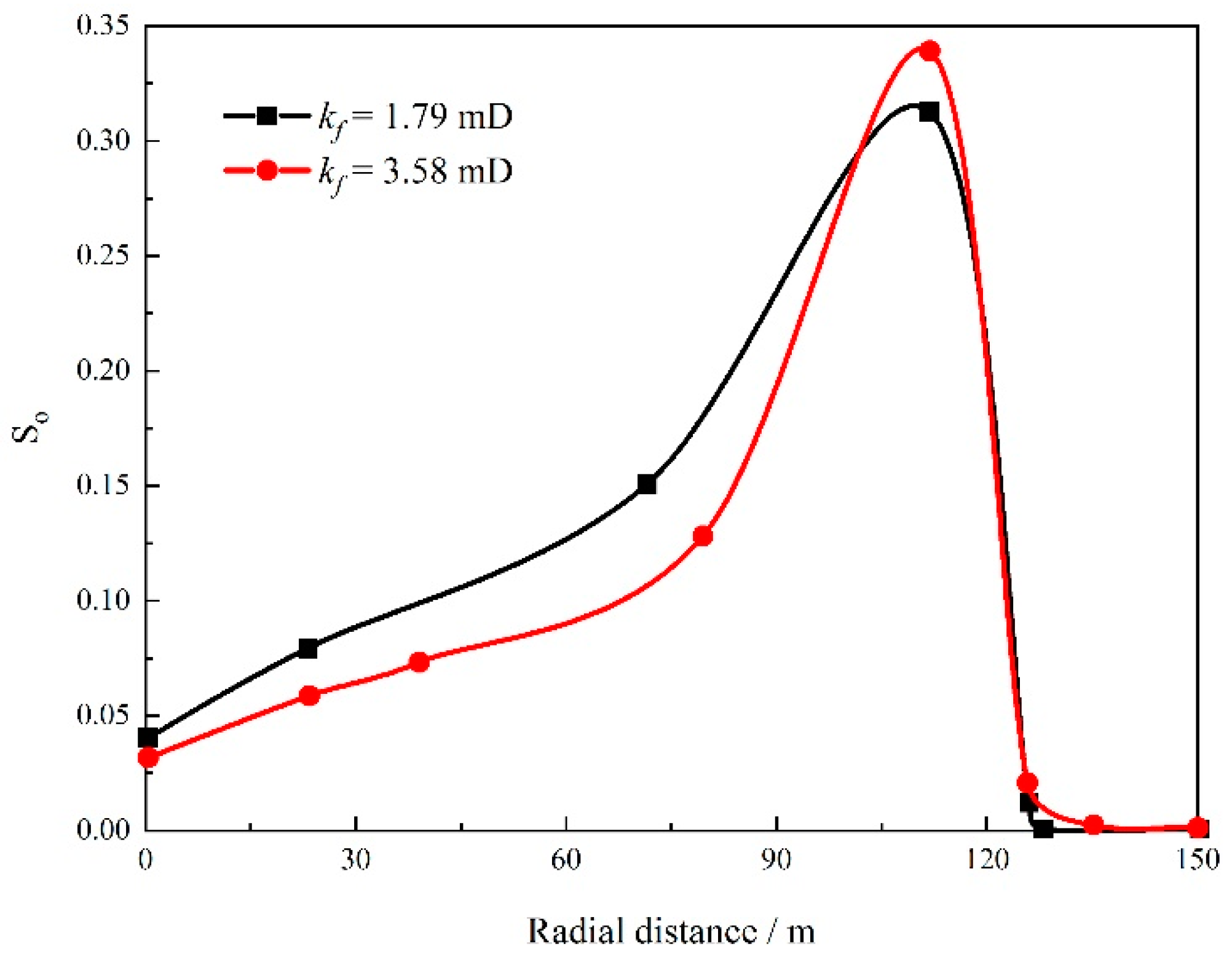
4.3. Influence of Discrete Natural Fractures
5. Conclusions
- The existence of the threshold pressure gradient slows down the propagation speed of pressure to the far side of formation. For the same production interval, the advancing speed of the moving pressure boundary decreases by 55%.
- The condensate oil saturation is not higher when it is closer to the wellbore. The continuous flow of condensate oil itself and the high-speed gas flow can reduce the condensate oil saturation near the wellbore by up to 42.8%.
- The existence of natural fractures is conducive to the expansion of the moving pressure boundary and the utilization of formation and condensate oil. The gas–oil two-phase area becomes larger, and the condensate oil saturation in the middle of the formation increases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Wen, Z.; He, Z.; Song, C.; Liu, X.; Chen, R.; Liu, Z.; Bian, H.; Shi, H. Global condensate oil resource potential and exploration fields. Acta Pet. Sin. 2021, 42, 1556–1565. [Google Scholar]
- Shi, H.; Wang, Q.; Wang, J.; Liu, X.; Feng, C.; Hao, Y.; Pan, W. Discovery and exploration significance of large condensate gas fields in BZ19-6 structure in deep Bozhong sag. China Pet. Explor. 2019, 24, 36–45. [Google Scholar]
- Syed, F.I.; Dahaghi, A.K.; Muther, T. Laboratory to field scale assessment for EOR applicability in tight oil reservoirs. Pet. Sci. 2022, 19, 2131–2149. [Google Scholar] [CrossRef]
- Martyushev, D.A.; Ponomareva, I.N.; Osovetsky, B.M.; Kazymov, K.P.; Tomilina, E.M.; Lebedeva, A.S.; Chukhlov, A.S. Study of the structure and development of oil deposits in carbonate reservoirs using field data and X-ray microtomography. Georesursy 2022, 24, 114–124. [Google Scholar]
- Martyushev, D.A.; Ponomareva, I.N.; Filippov, E.V.; Li, Y. Formation of hydraulic fracturing cracks in complicated carbonate reservoirs with natural fracturing. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2022, 333, 85–94. [Google Scholar]
- Galkin, S.V.; Martyushev, D.A.; Osovetsky, B.M.; Kazymov, K.P.; Song, H. Evaluation of void space of complicated potentially oil-bearing carbonate formation using X-ray tomography and electron microscopy methods. Energy Rep. 2022, 8, 6245–6257. [Google Scholar] [CrossRef]
- Luo, X.; Wang, X.; Wu, Z.; He, T.; Qiu, X.; Yuan, F.; Tan, C. Study on Stress Sensitivity of Ultra-Low Permeability Sandstone Reservoir Considering Starting Pressure Gradient. Front. Earth Sci. 2022, 10, 890084. [Google Scholar] [CrossRef]
- Li, D.; Zha, W.; Liu, S.; Wang, L.; Lu, D. Pressure transient analysis of low permeability reservoir with pseudo threshold pressure gradient. J. Pet. Sci. Eng. 2016, 147, 308–316. [Google Scholar] [CrossRef]
- Wang, R.; Yang, J.; Wang, M.; Zhao, Y.; Chen, W. Effect of Threshold Pressure Gradients on Control Areas Determination of Production Well in CBM Reservoirs. Adv. Polym. Technol. 2019, 2019, 3517642. [Google Scholar] [CrossRef]
- Ren, S.; Shen, F.; Yang, S.; Zhang, X.; Luo, H.; Feng, C. Analysis and Calculation of Threshold Pressure Gradient Based on Capillary Bundle. Math. Probl. Eng. 2021, 2021, 5559131. [Google Scholar] [CrossRef]
- Shi, X.; Wei, J.; Bo, H.; Zheng, Q.; Yi, F.; Yin, Y.; Chen, Y.; Dong, M.; Zhang, D.; Li, J.; et al. A novel model for oil recovery estimate in heterogeneous low-permeability and tight reservoirs with pseudo threshold pressure gradient. Energy Rep. 2021, 7, 1416–1423. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, T. Theoretical and Experimental Study on Nonlinear Flow Starting Pressure Gradient in Low Permeability Reservoir. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 571, p. 012044. [Google Scholar]
- Lu, C.; Qin, X.; Ma, C.; Yu, L.; Geng, L.; Bian, H.; Zhang, K.; Zhou, Y. Investigation of the impact of threshold pressure gradient on gas production from hydrate deposits. Fuel 2022, 319, 123569. [Google Scholar] [CrossRef]
- Bo, N.; Zuping, X.; Xianshan, L.; Zhijun, L.; Zhonghua, C.; Bocai, J.; Xin, Z.; Huan, T.; Xiaolong, C. Production prediction method of horizontal wells in tight gas reservoirs considering threshold pressure gradient and stress sensitivity. J. Pet. Sci. Eng. 2020, 187, 106750. [Google Scholar] [CrossRef]
- Lu, J. Pressure Behavior of a Hydraulic Fractured Well in Tight Gas Formation with Threshold Pressure Gradient. In Proceedings of the SPE Middle East Unconventional Gas Conference and Exhibition, Abu Dhabi, United Arab Emirates, 23–25 March 2012. [Google Scholar]
- Tian, W.; Zhu, W.; Zhu, H.; Zhang, X.; An, Z.; Du, S. Condensate gas reservoir threshold pressure gradient for tight sandstone. J. Cent. South Univ. 2015, 46, 3415–3421. [Google Scholar]
- Martyushev, D.A.; Galkin, S.V.; Shelepov, V.V. The influence of the rock stress state on matrix and fracture permeability under conditions of various lithofacial zones of the tournaisian-fammenian oil fields in the Upper Kama Region. Moscow Univ. Geol. Bull. 2019, 74, 573–581. [Google Scholar] [CrossRef]
- Martyushev, D.A.; Yurikov, A. Evaluation of opening of fractures in the Logovskoye carbonate reservoir, Perm Krai, Russia. Pet. Res. 2021, 6, 137–143. [Google Scholar] [CrossRef]
- Xia, Y.; Jin, Y.; Chen, M.; Chen, K.P. An Enriched Approach for Modeling Multiscale Discrete-Fracture/Matrix Interaction for Unconventional-Reservoir Simulations. SPE J. 2018, 24, 349–374. [Google Scholar] [CrossRef]
- Zidane, A.; Firoozabadi, A. An efficient numerical model for multicomponent compressible flow in fractured porous media. Adv. Water Resour. 2014, 74, 127–147. [Google Scholar] [CrossRef]
- Xia, Y.; Jin, Y.; Oswald, J.; Chen, M.; Chen, K. Extended finite element modeling of production from a reservoir embedded with an arbitrary fracture network. Int. J. Numer. Methods Fluids 2018, 86, 329–345. [Google Scholar] [CrossRef]
- Wang, Y.; Shahvali, M. Discrete fracture modeling using Centroidal Voronoi grid for simulation of shale gas plays with coupled nonlinear physics. Fuel 2016, 163, 65–73. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, G.; Zhang, L.; Wei, Y.; Guo, J.; Chang, C. Numerical simulation of shale gas reservoirs considering discrete fracture network using a coupled multiple transport mechanisms and geomechanics model. J. Pet. Sci. Eng. 2020, 195, 107588. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Al-Lamki, A.; Daungkaew, S.; Mott, R.; Whittle, T.M. Well Test Analysis in Gas-Condensate Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Huang, Z.; Yan, X.; Yao, J. A Two-Phase Flow Simulation of Discrete-Fractured Media using Mimetic Finite Difference Method. Commun. Comput. Phys. 2014, 16, 799–816. [Google Scholar] [CrossRef]
- Forchheimer, P. Wasserbewegung durch boden. Z. Ver. Dtsch. Ing. 1901, 45, 1782–1788. [Google Scholar]
- Blom, S.M.P.; Hagoort, J. The Combined Effect of Near-Critical Relative Permeability and Non-Darcy Flow on Well Impairment by Condensate Drop Out. SPE Reserv. Eval. Eng. 1998, 1, 421–429. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
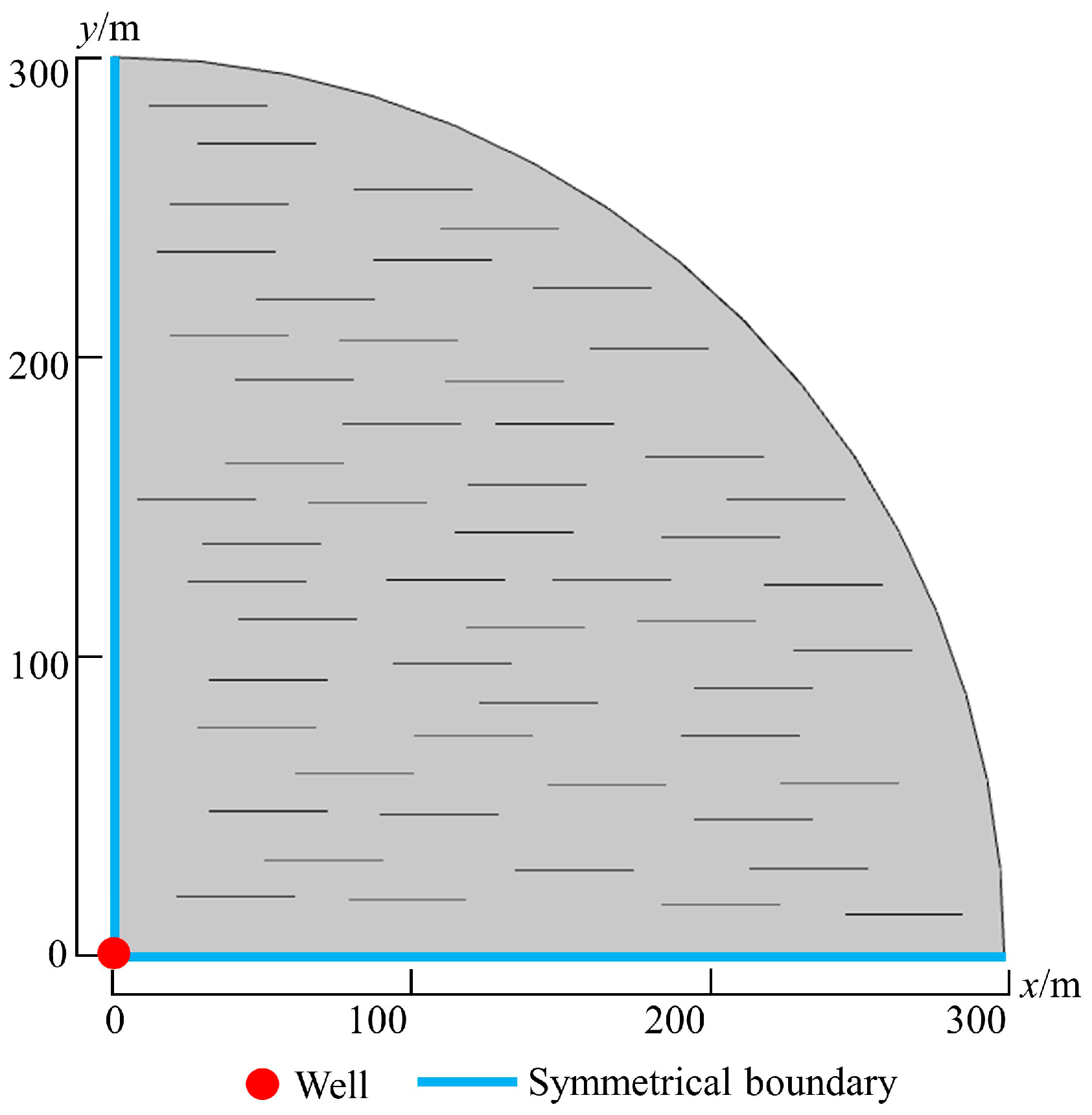




| Parameters | Value |
|---|---|
| Initial formation pressure/MPa | 51.3 |
| Formation temperature/°C | 178.4 |
| Matrix porosity | 0.0335 |
| Fracture porosity | 0.0052 |
| Matrix permeability/mD | 0.26 |
| Fracture permeability/mD | 1.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Bu, W.; Li, N.; Tan, X.; Liu, Y. Numerical Simulation of Multiarea Seepage in Deep Condensate Gas Reservoirs with Natural Fractures. Energies 2023, 16, 10. https://doi.org/10.3390/en16010010
Zhang L, Bu W, Li N, Tan X, Liu Y. Numerical Simulation of Multiarea Seepage in Deep Condensate Gas Reservoirs with Natural Fractures. Energies. 2023; 16(1):10. https://doi.org/10.3390/en16010010
Chicago/Turabian StyleZhang, Lijun, Wengang Bu, Nan Li, Xianhong Tan, and Yuwei Liu. 2023. "Numerical Simulation of Multiarea Seepage in Deep Condensate Gas Reservoirs with Natural Fractures" Energies 16, no. 1: 10. https://doi.org/10.3390/en16010010
APA StyleZhang, L., Bu, W., Li, N., Tan, X., & Liu, Y. (2023). Numerical Simulation of Multiarea Seepage in Deep Condensate Gas Reservoirs with Natural Fractures. Energies, 16(1), 10. https://doi.org/10.3390/en16010010





