Abstract
Hydraulic vibration is a critical factor affecting the stability and health of the hydro-turbine generator unit (HGU). This paper investigates the nonlinear dynamic characteristics of the HGU occurring from the hydraulic vibration. First, using the turbulence flow model, the lift and drag coefficients of the asymmetric airfoil blades are calculated at different Reynolds numbers and angles of attack. Based on the lift and drag coefficients of the asymmetric airfoil blade, a novel nonlinear mathematical model of asymmetric hydraulic forces is proposed for the asymmetric airfoil blade. Then, combining mechanic and electric asymmetric excitations, a coupled nonlinear mathematical model of the HGU is built using Lagrange equations. Moreover, the correctness of this model is verified. Finally, dynamic behaviors of the HGU changing with attack angle, deviation of the outlet blade angle, outlet guide vane angle, and Reynolds number are analyzed by bifurcation diagrams. It is found that increasing the Reynolds number can enhance the hydraulic vibration, which can lead to more complex nonlinear bifurcation and chaotic motions. In addition, some interesting physical phenomena of HGU under critical ranges and values are obtained. More importantly, these results could give theoretical guidance in the designing and stability research of hydropower units.
1. Introduction
Vibration is an inevitable phenomenon of the hydro-turbine generator unit (HGU) and is one of the important factors affecting the safe production of hydropower stations [1,2,3]. An in-depth analysis of the vibration mechanism of the HGU can better ensure the reliability of the unit’s operation, and effectively avoid or reduce the possible harm of vibration failure to the unit, which is of great significance to its safe and stable operation. In recent years, with the rapid development and wide application of hydropower [4,5,6,7,8,9,10,11], vibration problems of the HGU have received scholars’ great attention.
Due to the complex structure of HGUs, there are many reasons to induce vibration [12,13,14,15,16,17,18,19,20,21,22], and it is caused by the comprehensive action of many factors. Here, the vibration stability of the HGU is analyzed from hydraulic, mechanical, and electrical aspects. Mechanical vibration is caused by the interference of friction and other forces of the unit machinery. The main factors include misalignment of the rotor, unbalance of the rotor mass, collision, and so on. Electrical vibration is the vibration caused by the unbalanced magnetic pull force during the operation of the generator. The main factors are the short circuit of the rotor winding and the uneven air gap. Hydraulic vibration in the HGU is mainly caused by hydraulic pressure fluctuations, vortex forces, hydraulic unbalance, and other factors. Moreover, the main factor generating these is the turbulent flow regime, which was detailedly described by Moreno [23]. In order to study the influence of these vibration problems on the stability of the HGU, nonlinear dynamic theory and methods are introduced. Up to now, a great deal of work has been done on mechanical and electrical vibration, mainly focusing on the misalignment of the rotor, unbalance of the rotor mass, collision, and the uneven air gap. For example, Lees [24] analyzed the characteristics of the misalignment subsystem by establishing the misalignment constraint relationship between two rotors and taking dimensionless factors as parameters. Molka et al. [25] analyzed the response of the faulty rotor system under the condition of misalignment angle and put forward the characteristic frequency representing the misalignment fault in the vibration spectrum. Khanlo et al. [26] studied the performance of correlated chaotic motion caused by the collision of the correlated spindle-disk system. Khanlo. et al. [27] studied the nonlinear dynamic behaviors of the flexible disk system due to a lateral-torsional collision. Dirani et al. [28] established a nonlinear two-dimensional finite element model of the HGU with an uneven air gap. On the basis of the model analysis, the specific effects of an air gap on the magnetic force density of a hydro-turbine generator are obtained. Yan et al. [29] developed a nonlinear fractional-order model of the shafting system for a bending-torsional coupled hydro-generator set considering the coupling reaction of the asymmetric magnetic pull, unbalance of the rotor mass, and contact friction faults and the dynamic behaviors of the system were analyzed. Shi et al. [30] established a mathematical model of the bending-torsional coupling vibration for an unbalanced rotor, and investigated nonlinear vibration sensitivities of the HGU with some parameters by bifurcation diagrams. Xu et al. [31] proposed a new method to calculate the turbine torque. Then, considering the misalignment force, rubbing force, and unbalanced magnetic pull force, a nonlinear mathematical model of the hydro-generator set was built. Moreover, based on the model, the sensitivities of some electro-mechanical parameters to the operation of the unit were obtained. Su and Guo [32] presented a method to investigate the overall nonlinear dynamics of a coupled hydro-generator shaft-foundation system under unbalanced magnetic pull force and nonlinear seal forces, and The variable laws and inner mechanism of the coupled system were revealed further. The results of all these analyses have enriched the dynamical behaviors of a coupled hydro-generator shaft-foundation system. Xu et al. [33] introduced the nonlinear modal method to analyze the dynamic modal interactions between subsystems, and the results given by the different methods were compared to verify the method’s feasibility. The effect of the second-order modes was quantified to investigate its effect on the dynamic characteristics of francis hydro-turbine generator unit (FHTGU), and the vibration characteristics affected by the wind generation system were also investigated. As for hydraulic vibration, many scholars have performed studies on hydraulic variability because of the complex water movement [34,35,36,37,38,39]. For example, Dimitriadis et al. [34] identified the stochastic nature of the water movement and intense hydraulic variability in turbulent regimes. Finite systems of deterministic ordinary nonlinear differential equations were designed to represent forced dissipative hydrodynamic flow, and solutions of these equations can be identified with trajectories in phase space [35]. Frisch reviewed, discussed, and defined turbulence and water movement [36]. Shen et al. [37] analyzed pressure fluctuations in the turbine and identified possible exciting sources that may induce hydraulic vibration in hydropower systems by experimental tests and numerical calculations. Zhuang et al. [38] and Xu et al. [39] proposed nonlinear mathematical modeling of unbalanced hydraulic forces based on the fitting formula of the experimental data of lift and drag coefficients under two-dimensional plate flow and analyzed the effects of hydraulic variability on the stability of the HGU.
Based on the above analysis, mechanical and electrical vibration was the main research target in the early studies on vibration problems of the HGU. There are few nonlinear dynamic studies on hydraulic vibration, and the existing studies on hydraulic vibration also have some shortages. Firstly, due to the difficulty in calculating the lift and drag coefficients of the airfoil blade, the nonlinear mathematical model of hydraulic variability forces was derived by using the fitting formula of the experimental data of lift and drag coefficients under two-dimensional plate flow. Since the two-dimensional plates are symmetric, this method can only be applied to symmetric airfoil blades, but not asymmetric airfoil blades. Secondly, the experiment is troublesome and the working conditions are limited, so the experimental data can not be obtained under any working conditions, which means the obtained mathematical model of the hydraulic variability forces is not systematic and regular. In addition, in engineering practice, airfoil blades are asymmetrical. Therefore, to seek a numerical simulation method to calculate the lift and drag coefficients of the asymmetric airfoil blades is not only of engineering practice value but also of profound academic significance to establish the nonlinear mathematical model of hydraulic variability forces.
In light of the above analysis, we conclude the following innovations. Firstly, a method for calculating the lift and drag coefficients of the hydro-turbine blades at different Reynolds numbers by using the S-A turbulence flow model is proposed. The specific series expressions of the lift coefficient and lift-drag ratio with attack angle at different Reynolds numbers are obtained. Second, considering the forces acting on the airfoil blade, based on the mathematical expressions of the lift coefficient and lift-drag ratio, the nonlinear mathematical model of the asymmetric hydraulic forces for the asymmetric airfoil blade is established for the first time containing attack angle (α), deviation of the outlet blade angle (χ), outlet guide vane angle (α1), and Reynolds number (Re). Then the nonlinear dynamic model of the HGU including the hydraulic vibration factors is further obtained by bringing it into the Lagrange equation. Third, based on the established dynamic model of the HGU including hydraulic vibration factors, the influences of attack angle (α), deviation of the outlet blade angle (χ), outlet guide vane angle (α1), and Reynolds number (Re) on the nonlinear dynamic evolution characteristics of the HGU under different Reynolds numbers are analyzed in detail. Besides, the effects of hydraulic instability on the system stability of the HGU are evaluated, which has a certain theoretical guiding significance in the reduction and elimination of hydraulic vibration in practical engineering.
The rest of the paper is organized as follows: In Section 2, the mathematical modeling of asymmetric hydraulic forces for the asymmetric airfoil blade and the establishment of the nonlinear coupled mathematical model of the HGU is presented. Section 3 explains the numerical simulation and analysis. Section 4 presents the conclusions.
2. Mathematical Modeling of HGU
2.1. Modeling of Asymmetric Hydraulic Forces
The manufacturing errors of the outlet flow angle of the hydraulic turbine runner blade have been detected in some engineering observations [15,40], which can cause the inconsistency of the blade channel and lead to strong hydraulic vibration of the HGU. Moreover, when the attack angle of the airfoil blade is large, flow separation and vortex structure will occur that can further enhance the hydraulic vibration. Therefore, it is important and significant to find a mathematical model of asymmetric hydraulic forces for the runner’s airfoil blades to carry out a hydraulic vibration analysis of the HGU.
2.1.1. Radial Hydraulic Force of a Single Airfoil Blade
Force analysis of a single airfoil blade is presented in Figure 1. From Figure 1, when fluid flows over the blade, the pressure difference between the upper and lower surfaces causes lift L. Meanwhile, there is a backward drag D acting on the blade as the water flows. Then, the resultant force R can be estimated. Further, by breaking up the resultant force into radial and peripheral components, the radial force Rm can be obtained.
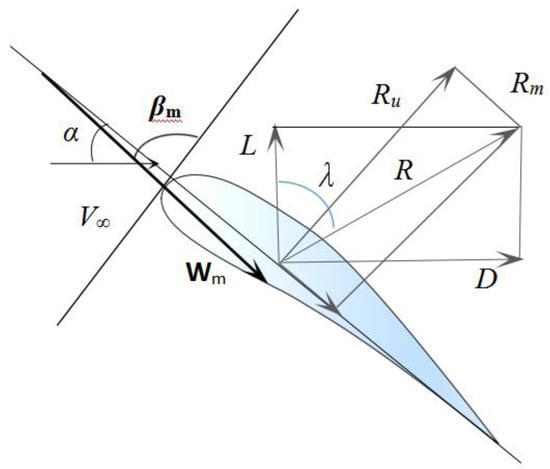
Figure 1.
Force analysis of a single airfoil blade.
Based on Figure 1, the angle between the lift (L) and the resultant force (R) is λ, which can be written as
where CL and Cd are the lift and drag coefficients, separately.
Here, for the convenience of modeling, we define k as the drag-lift ratio, namely that
According to the Kutta-Joukowski theorem [40] and combining Equations (1) and (2), the radial hydraulic force Rm of a single blade can be estimated as
where F is the maximum projected area of turbine blades; Wm is the average relative velocity of the blade, and βm represents its direction angle; γ is the unit volume of liquid weight; g is the gravity coefficient.
From Equation (3), the lift coefficient (CL), drag coefficient (Cd), and average relative velocity of the blade (Wm) are important parameters influencing the radial hydraulic force, whose expressions and values will be discussed in the following.
2.1.2. Lift and Drag Coefficients of the Asymmetric Airfoil Blade
Lift and drag coefficients (CL and Cd) are dimensionless of lift L and drag D, and they can be defined as
and
With the attack angle and Reynolds number changing, lift coefficient CL and drag-lift ratio k will change as a power series function, which can be expressed as follows:
and
where Re is the Reynolds number; α is the attack angle; pi and qj are coefficients of the power series of the lift coefficient CL and drag-lift ratio k, respectively.
2.1.3. Average Relative Velocity of the Blade
Flow velocity in the blade entrance and exit indicated by subscripts 1 and 2, can be broken into relative velocity (W), convected velocity (U), and absolute velocity (V), which are presented in Figure 2 and Figure 3.
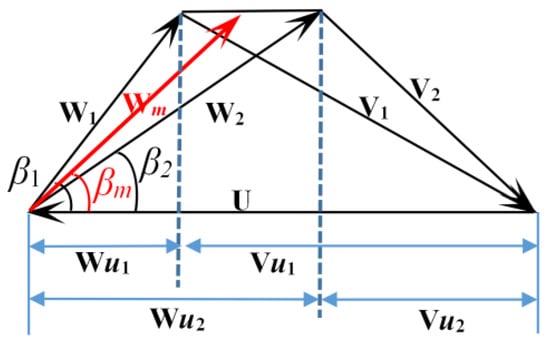
Figure 2.
Decomposition of the velocity triangle.
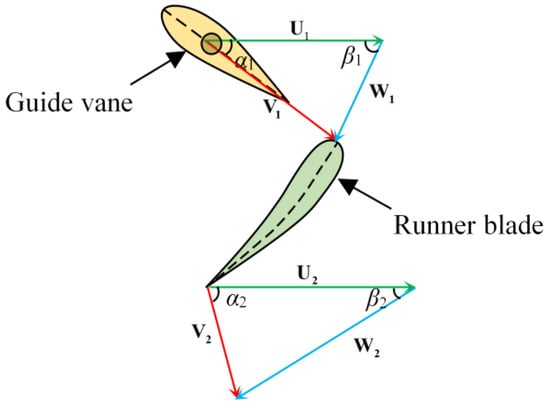
Figure 3.
Velocity triangle at the blade entrance and exit.
From Figure 2, the average relative velocity of the blade Wm can be expressed as
where |Wm|, |W1| and |W2| represent their values, which can be written as
and
where β1 represents inlet blade angle; β2 represents outlet blade angle; Q represents the flow of the hydraulic turbine; F1, F2 are the area of the blade entrance and exit section, respectively, which can be expressed as
and
where Z represents the number of runner blades; Su is the blade thickness; D1 and D2 are the diameters of the blade inlet and outlet, respectively; b0 is the guide vane height.
Based on Equations (6)–(8), |Wm| and βm can be written as
and
2.1.4. Asymmetric Hydraulic Forces of the Turbine Runner
In practical engineering, because of geometrical manufacturing deviations, the outlet blade angles of the runner blades are always inconsistent, which can result in synchronous vibration occurring from an asymmetric hydraulic force rotating with the runner. Here, for the convenience of modeling, we assume that the deviation of the outlet flow angle (χ) only exists in only a pair of blades, χ = βm2 − βm1. The asymmetric hydraulic forces acting on the runner are described in Figure 4.
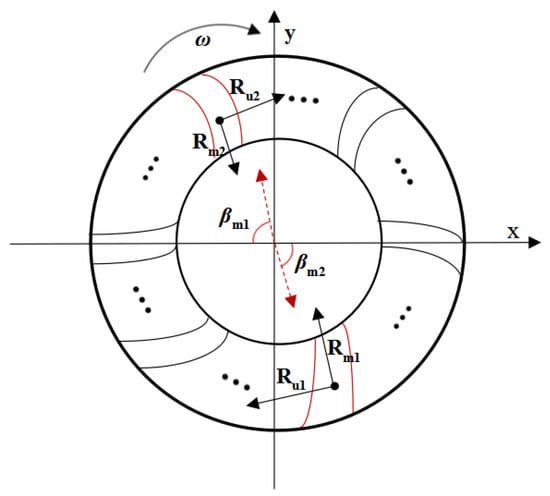
Figure 4.
Asymmetric hydraulic forces acting on the runner.
Assumption 1: Since this study provides a method for calculating the lift and drag coefficients of the airfoil blade, as a preliminary generalized study, not specifically for a particular runner, numerical simulations of the flow characteristics based on a two-dimensional airfoil blade are carried out.
Assumption 2: The turbine blade grille density is small, and the interaction between the runner airfoil blades is little. Thus, the liquid flow around the airfoil blade in the blade grille is close to the flow of a single airfoil blade.
From Figure 4, Rm1 and Rm2 are the radial hydraulic forces of the pair of blades with inconsistent outlet flow angles, respectively, and based on Equations (3)–(5), (11) and (12), they can be written as
Based on this, radial asymmetric hydraulic forces of the runner considering the asymmetry of the airfoil blade Hm can be expressed as
where |Wm1| and |Wm2| are values of the average relative velocity for the pair of blades with inconsistent outlet flow angle, βm1 and βm2 are their direction angles, which are written as
Assuming that the position angle of the pair of blades with inconsistent outlet flow angle is δ, Hm can be decomposed into x and y components as
Combining Equations (14) and (16), the asymmetric hydraulic forces considering the asymmetry of the runner airfoil blade in x and y components can be written as
where δ = δ0 + ωt.
2.2. Modeling of the Mechanic and Electric Asymmetric Forces
Except for the asymmetric hydraulic forces of the runner, the dynamic response of the HGU is also significantly affected by some other asymmetric forces. They are summarized in Table 1, and the specific expressions are shown in the listed references.

Table 1.
Forces acting on different components of the hydro-turbine generator unit (HGU).
2.3. Modeling of the HGU
The shaft system of the HGU is installed in the vertical position. Here, only transverse vibrations are considered and both the rotor and coupling are assumed rigid. The structure of the HGU is presented in Figure 5.
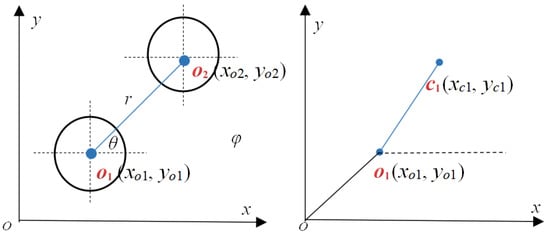
Figure 5.
Structure of the HGU.
From Figure 5, the coordinate relationships [42] of the HGU can be written as
where (xo1, yo1) and (xo2, yo2) are axis coordinates for the rotor and runner, separately; θ0 is the initial phase of the HGU, and θ = ωt + θ0; (xc1, yc1) and e1 are mass coordinates and eccentricity for the rotor, respectively; (xc2, yc2) and e2 represent mass coordinates and eccentricity for the runner, respectively; φ= ωt + φ0.
The Lagrange function [42] of the HGU is
where J1, m1, k1 are the rotation inertia, the mass, and the bearing stiffness of the generator rotor, respectively; J2, m2, k2 are the rotation inertia, the mass, and the bearing stiffness for the turbine runner, respectively.
The Lagrange equations [43] of the HGU are
From the above, Equations (19) and (20) can be combined into
Furthermore, Equation (21) can be rewritten as
3. Numerical Simulation and Analysis
3.1. Calculation and Verification of the Lift and Drag Coefficients
Functions of the lift coefficient CL and drag-lift ratio k of the NACA2415 asymmetric airfoil blade are established in Section 2.1.2. Here, to get the coefficients of the power series of the lift coefficient CL and drag-lift ratio k, the calculation and verification are carried out, and the grid for the single airfoil blade is generated by ICEM CFD, which is presented in Figure 6. The grid extends from −9 chords upstream to 14 chords downstream. The upper and lower boundary extends 10 chords from the profile. The grid presented is a “C”-like structured grid. The independent grid can be obtained by increasing grid nodes until it reaches the stage where the solution will not change with the number of nodes. Here, the number of nodes is set as 28,400.
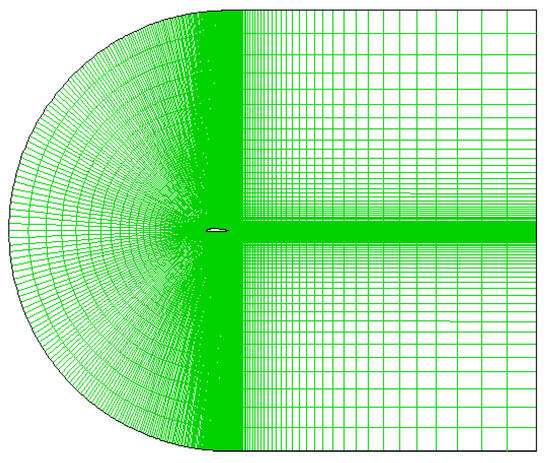
Figure 6.
Calculation grid region of the NACA2415 asymmetric airfoil blade.
FLUENT is used for the numerical calculation of the lift and drag coefficients (CL and Cd), and the Spalart-Allmaras model is used to model the turbulence. The finite volume-based method has been used to convert the governing equations of flow into algebraic equations that can be solved numerically. The pressure-velocity coupling has been achieved by the SIMPLE algorithm. The boundary conditions are pressure far-field boundary conditions. The time step of unsteady flow calculation is 0.001 s, and the number of iterations is 2000. To verify the numerical simulation set-up and ensure the accuracy of the results, a comparison of the calculated lift and drag coefficients with the experimental data [44,45] and results from the thin airfoil theory [46] at Reynolds numbers of 2.0 × 105 are presented in Figure 7.
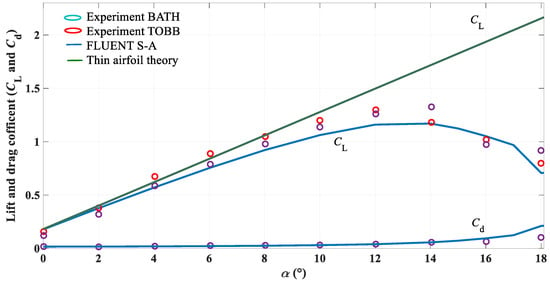
Figure 7.
Comparison of the numerical calculation with the thin airfoil theory and experiment data at Re = 2.0 × 105.
From Figure 7, it can be seen that the lift and drag coefficients obtained by the thin airfoil theory are close to the experimental data [44,45] when the attack angle is smaller than 10 degrees. For the numerical results obtained by the FLUENT S-A turbulence model, the changing curves of lift and drag coefficients are basically consistent with that of the experiment [44,45], and the error is large only around the critical stall attack angle, which is because at high attack angles, there is a separation vortex in the flow field of the airfoil blade, and the accuracy of the turbulent flow model decreases leading to a decrease in the accuracy of the numerical simulation of the lift and drag coefficients of the airfoil blade, which in turn leads to the numerical calculation deviating from the experimental values at high attack angles. Therefore, in general, the study of the unsteady flow around the asymmetric airfoil blade using the FLUNENT Spalart-Allmaras turbulence model in this paper is basically accurate and reliable. Based on this, by numerical simulation, the lift and drag coefficients (CL and Cd) at different Reynolds numbers are obtained, which are presented in Figure 8. Then, using MATLAB, the fitting of lift coefficient CL and drag-lift ratio k by power series are carried out and the fitting results are presented in Figure 9, from which orders 5 and 7 have been chosen for the polynomials of lift coefficient CL and drag-lift ratio k, respectively. The fitting coefficients of the power series of the lift coefficient CL and drag-lift ratio k are shown in Table 2.
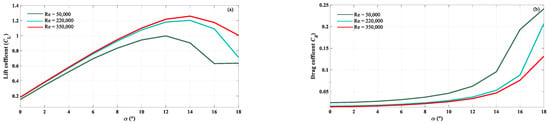
Figure 8.
Lift (a) and drag (b) coefficients (CL and Cd).
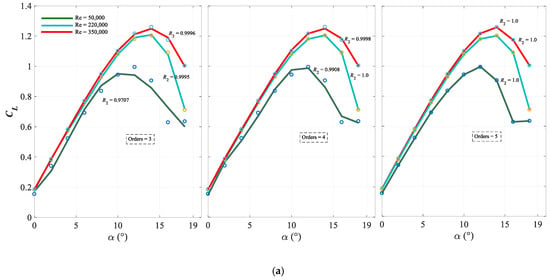
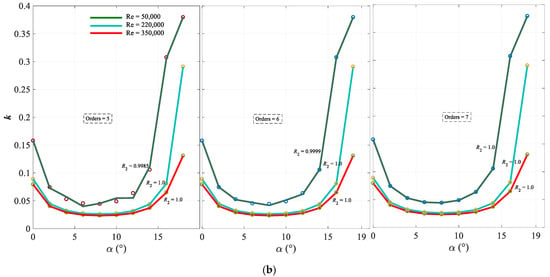
Figure 9.
Fitting results of the lift coefficient CL and drag-lift ratio k. (a) Lift coefficient CL. (b) Drag-lift ratio k.

Table 2.
Fitting coefficients of the power series of the lift coefficient CL and drag-lift ratio k.
3.2. Nonlinear Dynamic Analysis of the HGU
The nonlinear dynamics of the HGU are solved by the numerical calculation method, and by analyzing the nonlinear dynamic behaviors of the HGU system with parameters, the essential characteristics of the unit system can be analyzed. Based on the fitting coefficients of the power series of the lift coefficient CL and drag-lift ratio k obtained in Section 3.1, using MATLAB the effects of the attack angle (α), deviation of outlet blade angle (χ), outlet guide vane angle (α1), and Reynolds number (Re) on the dynamic behaviors of the HGU are investigated. Here, the initial values [42] of the simulation are (xo1, vx, yo1, vy)T = (0.0001, 0.0001, 0.0001, 0.0001). On the basis of references [42,47], detailed parameter values conducted in the simulation are: mo1 = 1.6 × 104 kg, mo2 = 1.0 × 104 kg, ko1 = 8.4 × 107 N/m, ko2 = 6.4 × 107 N/m, e1 = 0.4 mm, e2 = 0.4 mm, ω = 14.28 rad/s, Q = 160.3 m3/s, D1 = 4.34 m, Z = 14, δ0 = 0.6 rad.
3.2.1. Comparison and Verification
According to the solution grid and calculation conditions in Section 3.1, the velocity streamlines and pressure distribution of the asymmetric airfoil blade under different attack angles (α) at Re = 3.5 × 105 are obtained in Figure 10. Meanwhile, the time-domain diagrams of axis coordinates (xo1 and yo1) are presented in Figure 11.
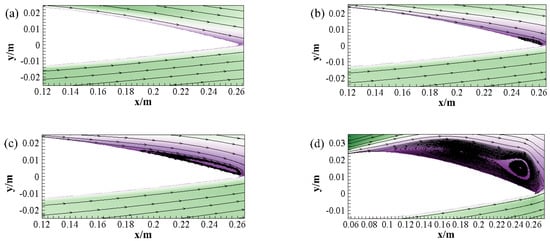
Figure 10.
Velocity streamlines of the asymmetric airfoil blade. (a) α = 6°; (b) α = 11°; (c) α = 13°; (d) α = 19°.
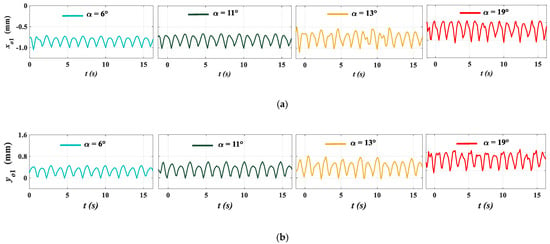
Figure 11.
Time-domain charts of axis coordinates (xo1 and yo1). (a) axis coordinates xo1; (b) axis coordinates yo1.
Comparing Figure 10 and Figure 11, when the attack angle (α) is smaller than 10°, there is no separation in the flow field of the airfoil blade. Meanwhile, the vibration amplitude of the HGU is small. When the attack angle (α) reaches 11°, a small clockwise separation vortex appears at the trailing edge of the airfoil, and accordingly, the vibration amplitude shows a slight increase. Then, when the attack angle (α) increases to 13°, the separation vortex and separation region gradually expand and move along the upper airfoil toward the leading edge. At this point, the axis coordinates (xo1 and yo1) increase towards a larger vibration amplitude. Especially at α = 19°, the separation vortex increases further and the separation region reaches the maximum thickness of the airfoil. Meanwhile, the axis coordinates (xo1 and yo1) enter an oscillation state with a very large vibration amplitude. Based on the above analyses, changes in the separation zone and separation vortex in the flow field of the airfoil blade are basically consistent with the vibration characteristics of the axis coordinates (xo1 and yo1). This is because flow separation can lead to a decrease in the lift-drag ratio and flow performance of the airfoil blade, which can further intensify the hydraulic vibration. In fact, the effects of the separation of the flow field and the separation vortex on the performance of the airfoil blade and the HGU vibration have been detected in engineering observations.
Above all, the proposed nonlinear mathematical model of the HGU can reflect the effects of the flow separation and separation vortex on the vibration of the HGU by attack angle (α) well, which also verifies the accuracy of the nonlinear mathematical model of the HGU.
3.2.2. Effects of Attack Angle (α)
Attack angle (α) and the Reynolds number are two critical parameters that can determine the operating conditions of the airfoil bade. Here, to study the specific effects of these two parameters, dynamic evolutions of asymmetric hydraulic forces (Hx and Hy) and axis coordinates (xo1 and yo1) of the HGU with increasing attack angle (α) at different Reynolds numbers are shown in Figure 12 and Figure 13, respectively.
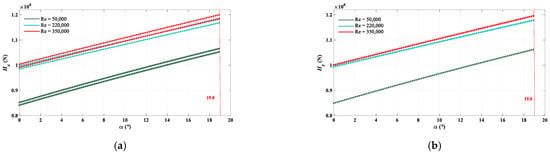
Figure 12.
Dynamic evolutions of asymmetric hydraulic forces (Hx and Hy) with increasing attack angle (α) at different Reynolds numbers. (a) Hydraulic variability force Hx; (b) Hydraulic variability force Hy.
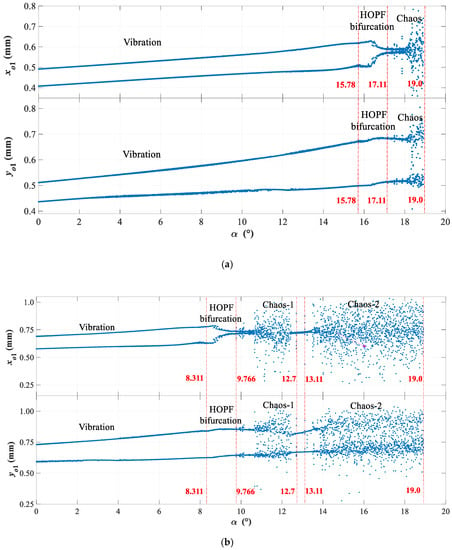
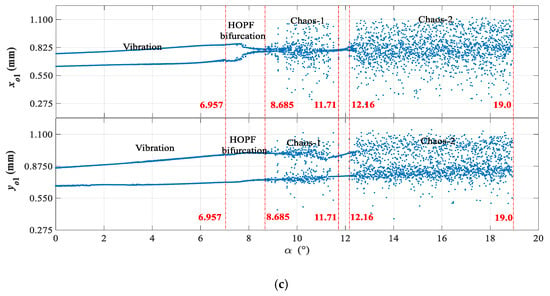
Figure 13.
Dynamic evolutions of axis coordinates (xo1 and yo1) with increasing attack angle (α). (a) Re = 0.5 × 105; (b) Re = 2.2 × 105; (c) Re = 3.5 × 105.
As shown in Figure 12 and Figure 13, from the perspective of vibration amplitude, with the attack angle (α) increasing from 0° to 19°, the asymmetric hydraulic forces (Hx and Hy) increase by approximately 2.0 × 105 N, 2.03 × 105 N and 2.08 × 105 N respectively, at Reynolds numbers of 0.5 × 105, 2.2 × 105 and 3.5 × 105. Meanwhile, under the action of asymmetric hydraulic forces (Hx and Hy), the axis coordinates (xo1 and yo1) of the HGU have an approximate increase of 0.26 mm, 0.43 mm, and 0.46 mm respectively, at Re = 0.5 × 105, 2.2 × 105 and 3.5 × 105. This is because as the attack angle (α) increases, the flow separation zone and separation vortex of the airfoil blade also increase, which can decrease the flow performance of the airfoil blade and further enhance the hydraulic vibration. On the other hand, from the changing process of dynamic evolutions of the HGU, with the attack angle (α) changing from 0° to 19°, the axis coordinates (xo1 and yo1) of the HGU always maintain a two-period oscillation when α < 15.78° at Reynolds numbers of 0.5 × 105. Then, the axis coordinates (xo1 and yo1) remain in an unstable state with high variability. With the Reynolds number increasing to 2.2 × 105, the dynamic behaviors of the HGU become more complex. In detail, the axis coordinates (xo1 and yo1) show a HOPF bifurcation at α = 8.311° and then enter into an irregular and high vibration state at α = 9.766°. Interestingly, when 12.7° < α < 13.11°, the axis coordinates (xo1 and yo1) enter into a short stable state with a two-period oscillation, which changes into an unstable state with high vibration when α > 13.11°. The dynamic evolutions of the axis coordinates (xo1 and yo1) at the Reynolds number of 3.5 × 105 are similar to that with a Reynolds number of 2.2 × 105. Detailedly, when the attack angle is 6.957°, a HOPF bifurcation appears that changes into an unstable state with high variability when α = 8.685°. Then the system breaks out of the high variability state and transforms into a periodic oscillation when 11.71° < α < 12.16°. Especially at α = 12.16°, the shaft coordinates transform into an unstable state with high variability again.
From the above, several conclusions can be drawn. First, with the attack angle (α) increasing, changing trends of axis coordinates (xo1 and yo1) are consistent with those of asymmetric hydraulic forces (Hx and Hy), which means that the hydraulic instability has decisive effects on the vibration amplitude of the HGU. Second, at Re = 0.5 × 105, the shaft system enters into high variability at α = 17.11°. However, at Re = 2.2 × 105 and Re = 3.5 × 105, a phenomenon of high variability appears at α = 9.766° and α = 8.685°, respectively, which indicates that the dynamic evolutions of the HGU with attack angle (α) are very sensitive to the Reynolds number. In other words, with the increase of the Reynolds number, the bifurcation and high variability points of the axis coordinates (xo1 and yo1) move forward. Third, at Re = 2.2 × 105, when α > 8.311°, the hydraulic instability has a large effect on the stability of the HGU. Out of this range, effects are small. Besides, when 12.7° < α < 13.11° at Re = 2.2 × 105 and 11.71° < α < 12.16° at Re = 3.5 × 105, the axis coordinates (xo1 and yo1) are in periodic oscillation rather than a high variability state, indicating that within this range, the hydraulic instability has a weak sensitivity to the operation state of the HGU, while it has a strong sensitivity in other ranges. Finally, in actual engineering, the best safety ranges of the attack angle (α) are from 0° to 15° at Re = 0.5 × 105, from 0° to 8° at Re = 2.2 × 105, and from 0° to 7° at Re = 3.5 × 105.
3.2.3. Effects of the Deviation of Outlet Blade Angle (χ)
The opening value of the blade outlet is an important parameter of the blade design, which is a characterization of the overflow. Additionally, when the opening value of the blade outlet for the turbine runner is inconsistent, the outflow of the turbine runner will be not symmetrical, and then it can lead to the generation of asymmetric hydraulic forces (Hx and Hy), which in turn causes hydraulic vibration of the HGU. Particularly, deviation of the outlet blade angle (χ) is an important parameter characterizing the uneven opening value of the blade outlet. For studying the effects of the deviation of the outlet blade angle (χ), dynamic evolutions of asymmetric hydraulic forces (Hx and Hy) and axis coordinates (xo1 and yo1) at different Reynolds numbers are described in Figure 14 and Figure 15, respectively.
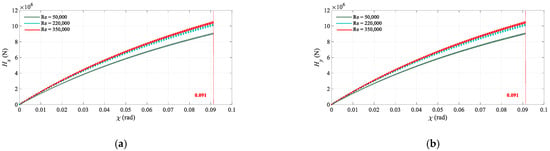
Figure 14.
Dynamic evolutions of the asymmetric hydraulic forces (Hx and Hy) with an increasing deviation of the outlet blade angle (χ) at different Reynolds numbers. (a) Hydraulic variability force Hx; (b) Hydraulic variability force Hy.
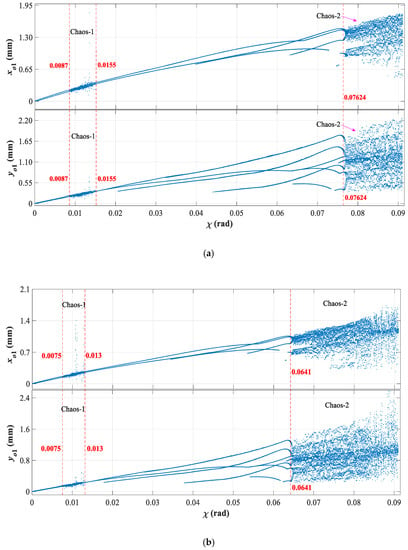
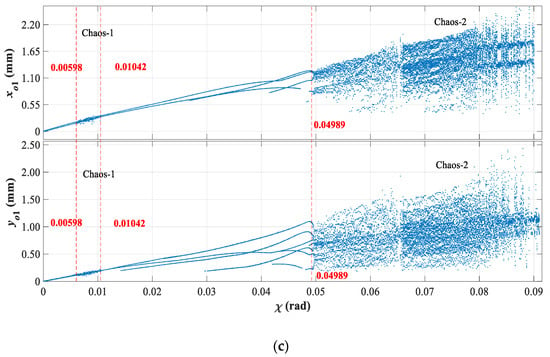
Figure 15.
Dynamic evolutions of axis coordinates (xo1 and yo1) with increasing deviation of outlet blade angle (χ). (a) Re = 0.5 × 105; (b) Re = 2.2 × 105; (c) Re = 3.5 × 105.
As shown in Figure 14 and Figure 15, with the increase of Reynolds number and the deviation of the outlet blade angle (χ), vibration amplitudes of asymmetric hydraulic forces (Hx and Hy) and axis coordinates (xo1 and yo1) both increase, and their changing trends are similar. In detail, with the deviation of outlet blade angle (χ) increasing from 0 rad to 0.091 rad, the asymmetric hydraulic forces (Hx and Hy) increase by approximately 8.97 × 106 N, 1.01 × 107 N, and 1.037 × 107 N respectively, at Reynolds numbers of 0.5 × 105, 2.2 × 105 and 3.5 × 105. Under the action of asymmetric hydraulic forces (Hx and Hy), the axis coordinates (xo1) of the HGU have an approximate increase of 1.75 mm, 2.04 mm, and 2.18 mm respectively, at Re = 0.5 × 105, 2.2 × 105, and 3.5 × 105. Meanwhile, the axis coordinate (yo1) of the HGU increases by 2.2 mm, 2.4 mm, and 2.46 mm respectively, at Re = 0.5 × 105, 2.2 × 105, and 3.5 × 105. These phenomena show that the asymmetric hydraulic forces (Hx and Hy) have determined effects on the stability of the HGU during this changing process. In detail, at Re = 0.5 × 105, 2.2 × 105, and 3.5 × 105, with the deviation of outlet blade angle (χ) increasing from 0 rad to 0.091 rad, the vibration amplitudes of the asymmetric hydraulic forces (Hx and Hy) also increase.
In addition, taking a further study of Figure 15a–f, at Re = 0.5 × 105, 2.2 × 105, and 3.5 × 105, when 0 rad < χ < 0.091 rad, the axis coordinates (xo1 and yo1) of the HGU go through two-period oscillation—high variability state—two-period oscillation—multi-period oscillation—HOPF bifurcation—high variability state. However, it is worth noting that the occurrence points of the high variability state are different when the Reynolds numbers are different. To be specific, at Re= 0.5 × 105, the HGU enter a high variability state when 0.0087 rad < χ < 0.0155 rad and χ > 0.07624 rad. Then, at Re = 2.2 × 105, they come into the high variability state when 0.0075 rad < χ < 0.013 rad and χ > 0.0641 rad. Finally, with the Reynolds numbers increasing to 3.5 × 105, the axis coordinates enter into the high variability state when 0.00598 rad < χ <0.01042 rad, and χ > 0.04929 rad.
The above analyses can lead to several meaningful results. First, the derivation of the outlet blade angle (χ) has decisive effects on the dynamic evolutions of the HGU, meaning that the operating state of the HGU is sensitive to the hydraulic instability. Second, when 0.0087 rad < χ< 0.0155 rad at Re = 0.5 × 105, 0.0075 rad < χ < 0.013 rad at Re = 2.2 × 105 and 0.00598 rad < χ < 0.01042 rad at Re = 3.5 × 105, the value of the asymmetric hydraulic forces (Hx and Hy) is small, but the axis coordinate s (xo1 and yo1) are in the state of high variability, showing that hydraulic instability could intensify mechanic and electric instabilities among these ranges. In addition, with the increase of Reynolds number, occurrence points of the high variability state move forward, and the ranges of instability increase. Namely, the stability of HGU with the derivation of outlet blade angle (χ) is very sensitive to the Reynolds number. Finally, the derivation of outlet blade angle (χ) should avoid these unstable ranges: 0.0087 rad < χ < 0.0155 rad and χ > 0.07624 rad at Re = 0.5 × 105, 0.0075 rad < χ < 0.013 rad and χ > 0.0641 rad at Re = 2.2 × 105, 0.00598 rad < χ < 0.01042 rad and χ > 0.04929 rad Re = 3.5 × 105.
3.2.4. Effects of Outlet Guide Vane Angle (α1)
Outlet guide vane angle (α1) is an important parameter determining the flow condition before the hydraulic turbine runner, which can further affect the asymmetric hydraulic forces (Hx and Hy) and the stability of the HGU.To investigate the influences of the outlet guide vane angle (α1), dynamic evolutions of asymmetric hydraulic forces (Hx and Hy), and axis coordinates (xo1 and yo1) with increasing outlet guide vane angle (α1) at different Reynolds numbers are presented in Figure 16 and Figure 17.
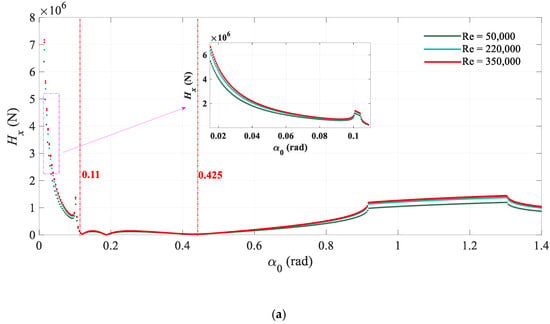
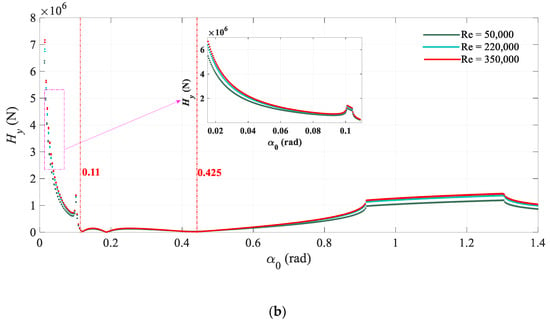
Figure 16.
Dynamic evolutions of the asymmetric hydraulic forces (Hx and Hy) with increasing outlet guide vane angle (α1) at different Reynolds numbers. (a) Hydraulic variability force Hx; (b) Hydraulic variability force Hy.
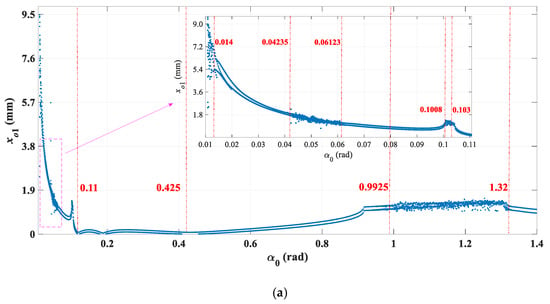
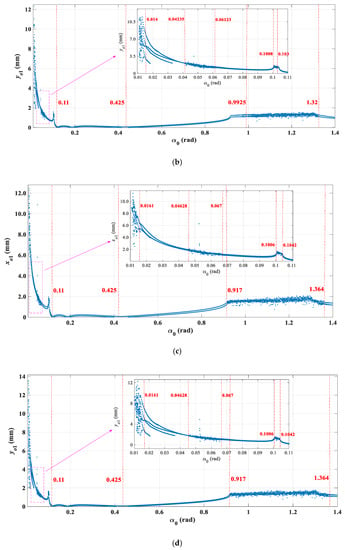
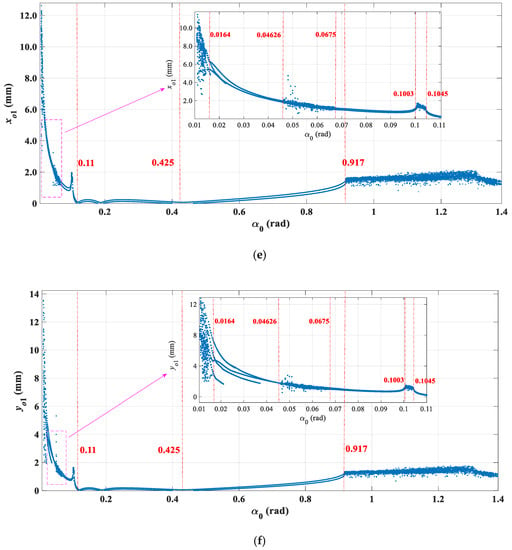
Figure 17.
Dynamic evolutions of axis coordinates (xo1 and yo1) with increasing outlet guide vane angle (α1). (a) and (b) Re = 0.5 × 105 and 2.2 × 105; (c) and (d) Re = 3.5×105, (e) Re = 3.5 × 105, (f) Re = 3.5 × 105.
From Figure 16, at Re = 0.5 × 105, 2.2 × 105, and 3.5 × 105, qualitatively speaking, the dynamic changing process of the asymmetric hydraulic forces (Hx and Hy) are similar. When the outlet guide vane angle (α1) ranges from 0 rad to 0.11 rad, the value of the asymmetric hydraulic forces (Hx and Hy) decreases rapidly. Especially at α1 = 0.11 rad, the value of the asymmetric hydraulic forces (Hx and Hy) decreases to about 0. Moreover, as the outlet guide vane angle (α1) continues to range from 0.11 rad to 0.425 rad, the value of the asymmetric hydraulic forces (Hx and Hy) fluctuates around 0 all the time. Then, with the outlet guide vane angle (α1) increasing further, asymmetric hydraulic forces (Hx and Hy) begin to increase and show a slight jump when it increases to a certain extent. Finally, the asymmetric hydraulic forces (Hx and Hy) get rid of the jump and go into a periodic oscillation. At the same time, it is worth noting that at Reynolds numbers of 2.2 × 105 and 3.5 × 105, the value of the asymmetric hydraulic forces (Hx and Hy) is basically the same, which is larger than that at Reynolds numbers of 0.5 × 105. Moreover, when 0 rad < α1 < 0.11 rad and 0.425 rad < α1 < 1.4 rad, larger differences of the asymmetric hydraulic forces (Hx and Hy) appear at different Reynolds numbers. In addition, quantitatively speaking, with the outlet guide vane angle (α1) increasing from 0 rad to 1.4 rad, the asymmetric hydraulic forces (Hx and Hy) decrease by approximately 5.5 × 106 N at Reynolds numbers of 0.5 × 105. Under the action of asymmetric hydraulic forces (Hx and Hy), the axis coordinates (xo1) and (yo1) of the HGU has an approximate decrease of 8.5 mm and 11 mm at Re = 0.5 × 105. With the Reynolds number increasing to 2.2 × 105 and 3.5 × 105, the asymmetric hydraulic forces (Hx and Hy) decrease by 6.2 × 106 N and 6.4 × 106 N respectively, which have small differences. Therefore, the changes in the vibration amplitudes of the axis coordinates (xo1) and (yo1) are almost the same, decreasing by 10.5 mm and 13 mm.
Based on the above, comparing Figure 16 with Figure 17, some important results can be concluded. First, the variation of the dynamic evolutions of the HGU is determined by the asymmetric hydraulic forces (Hx and Hy). Second, the Reynolds number is less sensitive to the outlet guide vane angle (α1) than to the attack angle (α) and deviation of the outlet blade angle (χ). Dynamic characteristics of the HGU can be affected by large changes in Reynolds number. Third, at Reynolds numbers of 0.5 × 105, 2.2 × 105, and 3.5 × 105, when 0.11 rad< α1 < 0.425 rad, the vibration amplitude of the system maintains at about 0, meaning that this range is close to the optimal working condition. Out of this range, whether the outlet guide vane angle (α1) increases or decreases, the vibration amplitude of the HGU will increase significantly. Because a small outlet guide vane angle (α1) can lead to the water rushing to the front of the guide blade profile, the attack angle is positive, while the outlet guide vane angle (α1) is large, the water flow will rush to the back of the guide blade profile with a negative attack angle. These two conditions will both aggravate the hydraulic instability and affect the efficiency of the HGU. In fact, in engineering practice, when the HGU is in operation, a larger or smaller guide vane opening will both affect the stability and performance of the unit. Third, when the outlet guide vane angle (α1) ranges from 0.1008 rad to 0.103 rad and from 0.9925 rad to 1.32 rad, the coordinates of the shaft system enter into high variability at Reynolds numbers of 0.5 × 105, while at Reynolds numbers of 2.2 × 105, they go into high vibration in the ranges from 0.1006 rad to 0.1042 rad and from 0.917 rad to 1.364 rad, which illustrates that larger Reynolds numbers can enhance the hydraulic instability in these ranges. In other words, the axis coordinates (xo1 and yo1) have a strong sensitivity to the Reynolds number in these ranges. Finally, in order to guarantee the efficient operation of the HGU, the outlet guide vane angle (α1) should be controlled within the range of 0.11 rad to 0.425 rad as far as possible.
4. Conclusions
To investigate the nonlinear dynamics of the HGU under hydraulic vibration, the lift and drag coefficients of the asymmetric airfoil blades are calculated at different Reynolds numbers and angles of attack using the turbulence flow model. Based on the lift and drag coefficients of the asymmetric airfoil blade, a nonlinear mathematical model of the asymmetric hydraulic forces (Hx and Hy) is firstly proposed for the asymmetric airfoil blade. Then, taking the mechanic and electric asymmetric excitations into consideration, a nonlinear coupled mathematical model of the HGU is built, and the correctness of this model is verified. Using the latter, the nonlinear vibration characteristics of the HGU are investigated with the changing of attack angle (α), deviation of the outlet blade angle (χ), outlet guide vane angle (α1), and Reynolds number (Re), and some important physical phenomena are obtained as follows:
- (1)
- In the changing process of attack angle (α), deviation of the outlet blade angle (χ), and outlet guide vane angle (α1), asymmetric hydraulic forces have decisive effects on the vibration amplitude of the HGU.
- (2)
- The Reynolds number is less sensitive to the outlet guide vane angle (α1) than to the attack angle (α) and deviation of the outlet blade angle (χ), and the dynamic characteristics of the HGU with increasing outlet guide vane angle (α1) can only be effected by large changes in the Reynolds number.
- (3)
- Increasing the Reynolds number can enhance the effects of the attack angle (α) and the deviation of outlet blade angle (χ) on dynamic evolutions of the HGU, which leads to the points of the high variability state moving forward. Meanwhile, the stable ranges are respectively analyzed.
- (4)
- A larger or smaller outlet guide vane angle (α1) can both enhance the nonlinear hydraulic vibration, and the best range is from 0.11 rad to 0.425 rad. In addition, in the ranges of outlet guide vane angle (α1) from 0.917 rad to 1.4 rad, the Reynolds number can intensify the nonlinear hydraulic vibration.
The conclusions obtained are a guiding significance to studying the nonlinear dynamics of hydraulic vibration and give theoretical guidance in the designing and stability research of the HGU. Besides, due to the limitations of this study, in future studies, the complex three-dimensional flow characteristics of the hydraulic machinery will be studied in-depth, taking into account the interaction between the turbine blades.
Author Contributions
Conceptualization, K.Z. and L.C.; Formal analysis, S.H.; Software, K.Z. and S.H.; Validation, K.Z. and X.F.; Writing—original draft, K.Z., S.H., X.F. and L.C.; Writing—review & editing, K.Z., S.H. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 51179153) and the National Natural Science Foundation of China (grant number 51439007).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Varney, P.; Green, I. Rough surface contact of curved conformal surfaces: An application to rotor-stator rub. J. Tribol. Trans. ASME 2016, 138, 041401. [Google Scholar] [CrossRef]
- Bovsunovsky, A.P. Efficiency analysis of vibration based crack diagnostics in rotating shafts. Eng. Fract. Mech. 2017, 173, 118–129. [Google Scholar] [CrossRef]
- Ramamurthy, S.T.; Wang, Y.X.; Hughes, T. Electromagnetic response of three-dimensional topological crystalline insulators. Phys. Rev. Lett. 2017, 118, 146602. [Google Scholar] [CrossRef] [PubMed]
- Si, G.Q.; Diao, L.; Zhu, J.W.; Lei, Y.H.; Zhang, Y.B. Attempt to generalize fractional-order electric elements to complex-order ones. Chin. Phys. B 2017, 26, 060503. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Gandhi, B.K. Investigation of a High Head Francis Turbine at Runaway Operating Conditions. Energies 2016, 9, 149. [Google Scholar] [CrossRef]
- Chu, S.; Majumdar, A. Opportunities, and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef]
- Giosio, D.R.; Henderson, A.D.; Walker, J.M.; Henderson, A.D. Rapid Reserve Generation from a Francis Turbine for System Frequency Control. Energies 2017, 10, 496. [Google Scholar] [CrossRef]
- Zhang, L.K.; Ma, Z.Y.; Wu, Q.Q.; Wang, X.N.; Wu, Q.Q.; Fan, Z. Vibration analysis of coupled bending-torsional rotor-bearing system for hydraulic generating set with rub-impact under electromagnetic excitation. Arch. Appl. Mech. 2016, 86, 1665–1679. [Google Scholar] [CrossRef]
- Martinez-Lucas, G.; Sarasua, J.I.; Sanchez-Fernandez, J.A.; Wilhelmi, J.R. Frequency control support of a wind-solar isolated system by a hydropower plant with long tail-race tunnel. Renew. Energy 2016, 90, 362–376. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Tolo, S.; Patelli, E.; Jiang, Y.L. Model validation and stochastic stability of a hydro-turbine governing system under hydraulic excitations. Int. J. Electr. Power Energy Syst. 2018, 95, 156–165. [Google Scholar] [CrossRef]
- Williamson, S.J.; Stark, B.H.; Booker, J.D. Performance of a low-head pico-hydro Turgo turbine. Appl. Energy 2013, 102, 1114–1126. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Gandhi, B.K.; Dahlhaug, O.G. Transient pressure measurements on a high head model Francis turbine during emergency shutdown, total Load rejection, and runaway. J. Fluids Eng. 2014, 136, 121107. [Google Scholar] [CrossRef]
- Williamson, S.J.; Stark, B.H.; Booker, J.D. Low head pico hydro turbine selection using a multi-criteria analysis. Renew. Energy 2014, 61, 43–50. [Google Scholar] [CrossRef]
- Yan, D.L.; Chen, Q.J.; Zheng, Y.; Wang, W.Y.; An, Y.C. Dynamic evolution of a bulb hydroelectric generating unit considering effects of the blades. Energy Convers. Manag. 2019, 185, 183–201. [Google Scholar] [CrossRef]
- Zhang, J.S.; Xu, B.B.; Chen, D.Y. Global sensitivity analysis of hydro power generator unit system. J. Hydroelectr. Eng. 2019, 38, 146–159. (In Chinese) [Google Scholar]
- Qin, W.Y.; Chen, G.R.; Meng, G. Nonlinear responses of a rub-impact overhung rotor. Chaos Solitons Fractals 2004, 19, 1161–1172. [Google Scholar] [CrossRef]
- Yan, D.L.; Wang, W.Y.; Chen, Q.J. Nonlinear Modeling and Dynamic Analyses of the Hydro-Turbine Governing System in the Load Shedding Transient Regime. Energies 2018, 11, 1244. [Google Scholar] [CrossRef]
- Yan, D.L.; Chen, Q.J.; Zheng, Y.; Liu, W.Y. Parameter sensitivity and dynamic characteristic analysis of bulb hydro generating unit with shaft crack fault. Mech. Syst. Signal Process. 2021, 158, 107732. [Google Scholar] [CrossRef]
- Qu, J.X.; Zhang, Z.S. A novel intelligent method for mechanical fault diagnosis based on dual-tree complex wavelet packet transform and multiple classifier fusion. Chaos Solitons Fractals 2016, 171, 837–853. [Google Scholar] [CrossRef]
- Fu, X.Q.; Jia, W.T.; Xu, H.; Song, S.L. Imbalance-misalignment-rubbing coupling faults in hydraulic turbine vibration. Opt. Int. J. Light Electron Opt. 2016, 127, 3708–3712. [Google Scholar] [CrossRef]
- Gasch, R. A survey of the dynamic behaviour of a simple rotating shaft with a transverse crack. J. Sound Vib. 1993, 160, 313–332. [Google Scholar] [CrossRef]
- Darpe, A.K.; Chawla, A.; Gupta, K. Analysis of the response of a cracked Jeffcott rotor to axial excitation. J. Sound Vib. 2002, 249, 429–445. [Google Scholar] [CrossRef][Green Version]
- Moreno, C. Turbulence, Vibrations, Noise and Fluid Instabilities. Practical Approach. In Computational Fluid Dynamics; Intech: Rijeka, Croatia, 2010; p. 420. [Google Scholar]
- Lees, A.W. Misalignment rinrigidly coupled rotors. J. Sound Vib. 2007, 305, 261–271. [Google Scholar] [CrossRef]
- Slim, B.; Molka, A.H.; Mohamed, M.; Fakhfakh, T.; Haddar, M. Dynamic behavior of hydrodynamic journal bearings in presence of rotor spatial angular misalignment. Mech. Mach. Theory 2009, 44, 1548–1559. [Google Scholar]
- Khanlo, H.M.; Ghayour, M.; Ziaei-Rad, S. Chaotic vibration analysis of rotating, flexible, continuous shaft-disk system with a rub-impact between the disk and the stator. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 566–582. [Google Scholar] [CrossRef]
- Khanlo, H.M.; Ghayour, M.; Ziaei-Rad, S. Theeffectsof lateral-torsional couplingonthenonlineardynamicbehaviorofarotatingcontinuousflexible shaft-disk system with rub-impact. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1524–1538. [Google Scholar] [CrossRef]
- Dirani, H.C.; Merkhouf, A.; Giroux, A.M.; Kedjar, B.; Al-Haddad, K. Impact of Real Air Gap Nonuniformity on the Electromagnetic Forces of a Large Hydro-Generator. IEEE Trans. Ind. Electron. 2018, 65, 8464–8475. [Google Scholar] [CrossRef]
- Yan, D.L.; Wang, W.Y.; Chen, Q.J. Fractional-order modeling and dynamic analyses of a bending-torsional coupling generator rotor shaft system with multiple faults. Chaos Solitons Fractals 2018, 110, 1–15. [Google Scholar] [CrossRef]
- Shi, Y.S.; Zhou, J.Z.; Lai, X.J.; Xu, Y.H.; Guo, W.C.; Liu, B.N. Stability and sensitivity analysis of the bending-torsional coupled vibration with the arcuate whirl of hydro-turbine generator unit. Mech. Syst. Signal Process. 2021, 149, 107306. [Google Scholar] [CrossRef]
- Xu, B.B.; Yan, D.L.; Chen, D.Y.; Gao, X.; Wu, C.Z. Sensitivity analysis of a Pelton hydropower station based on a novel approach of turbine torque. Energy Convers. Manag. 2017, 148, 785–801. [Google Scholar] [CrossRef]
- Su, W.Q.; Guo, Z.Q. Mathematical modeling and nonlinear vibration analysis of a coupled hydro-generator shaft-foundation system. Commun. Nonlinear Sci. Numer. Simul. 2021, 98, 105776. [Google Scholar]
- Xu, B.B.; Luo, X.Q.; Egusquiza, M.; Ye, W.; Liu, J.; Egusquiza, E.; Chen, D.Y.; Guo, P.C. Nonlinear modal interaction analysis and vibration characteristics of a francis hydro-turbine generator unit. Renew. Energy 2021, 168, 854–864. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D.; Papanicolaou, P. Stochastic similarities between the microscale of turbulence and hydrometeorological processes. Hydrol. Sci. J. 2016, 61, 1623–1640. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Frisch, U. The Legacy of A.N. Kolmogorov; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Shen, A.Y.; Chen, J.; Zhou, F.; Yang, H.; Cai, F.S. Hydraulic Vibration and Possible Exciting Sources Analysis in a Hydropower System. Appl. Sci. 2021, 11, 5529. [Google Scholar] [CrossRef]
- Zhuang, K.Y.; Gao, C.D.; Li, Z.; Yan, D.L.; Fu, X.Q. Dynamic Analyses of the Hydro-Turbine Generator Shafting System Considering the Hydraulic Instability. Energies 2018, 11, 2862. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Behrens, P.; Ye, W.; Guo, P.C.; Luo, X.Q. Modeling oscillation modal interaction in a hydroelectric generating system. Energy Convers. Manag. 2018, 174, 208–217. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, X.D. Hydraulic Turbine; China Water Resources and Electric Power Press: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Perers, R.; Lundin, U.; Leijon, M. Saturation effects on unbalanced magnetic pullin a hydroelectric generator with an eccentric rotor. IEEE Trans. Magn. 2007, 43, 3884–3890. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Zhang, H.; Zhou, R. Dynamic analysis and modeling of a novel fractional-order hydro-turbine-generator unit. Nonlinear Dyn. 2015, 81, 1263–1274. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, L.X.; Guo, Y.K.; Qian, J.; Zhang, C.L. The generalized Hamiltonian model for the shafting transient analysis of the hydro turbine generating sets. Nonlinear Dyn. 2014, 76, 1921–1933. [Google Scholar] [CrossRef]
- Genç, M.S.; Lock, G.; Kaynak, U. An Experimental and Computational Study of Low Re Number Transitional Flows over an Aerofoil with Leading Edge Slat, AIAA-2008-8877. In Proceedings of the The 26th Congress of ICAS and 8th AIAA ATIO, Anchorage, AK, USA, 14–19 September 2008. [Google Scholar]
- Genç, M.S. Kanat Profilleri Etrafındaki Düşük Reynolds Sayılı Akışın Kontrolü ve Aerodinamik Performansın İncelenmesi. Ph.D. Thesis, Fen Bilimleri Enstitüsü, Erciyes Üniversitesi, Kayseri, Türkiye, 2009. (In Turkish). [Google Scholar]
- He, J.X.; Tang, F.; Xiong, C.; Wang, Z.C. Experiment of Lift Coefficient measurement Based on Thin Airfoil Model of Simple Wind Tunnel. Phys. Eng. 2018, 28, 113–117. [Google Scholar]
- Feng, Y.R.; Gu, M.C.; Fang, R.Z. Modernization transformation of No. 4 generating unit of Fengman Hydropower Plant. Water Power 2000, 1, 38–40. (In Chinese) [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).