Friction Factor and Heat Transfer of Giesekus-Fluid-Based Nanofluids in a Pipe Flow

Abstract

The friction factor and heat transfer of Giesekus-fluid-based nanofluids in a pipe flow were studied in the ranges of 0.5 ≤ Reynolds number (Re) ≤ 500, 1 ≤ Weissenberg number (Wi) ≤ 8, 0.5% ≤ particle volume concentration (Φ) ≤ 3.0%, 0 ≤ viscosity ratio (β₀) ≤ 1, and 0 ≤ mobility parameter (α) ≤ 0.5. Our numerical method was validated by comparing the results with available ones in the literature. The effects of Wi, Φ, β₀, Re, and α on the relative friction factor (C_f/C_fNew), Nusselt number (Nu), and ratio (PEC_nf/PEC_f) of energy performance evaluation criterion for Giesekus-fluid-based nanofluids to those for Giesekus fluid were discussed. The results showed that the values for the C_f/C_fNew and Nu of Giesekus-fluid-based nanofluids were larger than those for Newtonian fluid-based nanofluids and those for pure Giesekus fluid. The values for C_f/C_fNew increased with increasing Φ and Re, but they increased with decreasing β₀ and α. As Wi increased, the values of C_f/C_fNew first increased and then decreased. The values of Nu and PEC_nf/PEC_f were enhanced with increasing Wi, Φ, Re, and α, but with decreasing β₀. It is more effective to use Giesekus-fluid-based nanofluids to improve heat transfer with the conditions of a larger Wi, Φ, Re, and α and a smaller β₀. Finally, the correlation formula for PEC_nf/PEC_f as a function of Wi, Φ, β₀, Re, and α was derived.

1. Introduction

The friction factor and heat transfer of non-Newtonian fluids have aroused extensive concern due to their wide range of applications, e.g., drilling processes, synthesis of composites, paper making, and plastic molding [1,2]. In order to reduce friction and increase the heat transfer of fluid flowing in a pipe and achieve the goal of saving energy, nanofluids, i.e., fluids containing nanoparticles, are used. So far, nanofluids have been extensively used, and their properties have also been widely investigated. For example, adding graphite and carbon nanofibers increases the efficiency of a gear pump-driven hydraulic circuit using ethanol [3]. The thermal efficiency was increased by 13.8%, 1.5%, and 1.3% for nanofluids of water–CuO compared with pure water, water–TiO₂, and water–Al₂O₃, respectively [4]. Low friction factor and high heat transfer were reached when the nanofluids of water-Al₂O₃ and water-SiO₂ were used in a heat exchanger in the range of 10,551 ≤ Re ≤ 17,220 and 17,220 ≤ Re ≤ 31,910, respectively [5].

Newtonian fluid was employed as the base fluid in most of the previous studies. However, there are many occasions where the base fluid is non-Newtonian fluid in applications; only a few studies have focused on non-Newtonian fluid as the base fluid. For instance, the Deborah number had an important impact on convective heat transfer, and the effect of heat conduction of Jeffrey nanofluids was better than that of Oldroyd-B nanofluids [6]. The impacts of fluid relaxation and retardation time parameters on the velocity of Oldroyd-B nanofluids were converse [7]. The heat transfer performance of Jeffrey nanofluids was better than that of the Oldroyd-B nanofluids when taking the thermal radiation, suction, and nonuniform heat source/sink into account [8]. The heat transfer performance was greatly enhanced in the Oldroyd-B nanofluids at higher Biot and Prandtl numbers [9]. The heat transfer rate of EG-Si₃N₄ was higher than that of EG for various nanoparticle concentrations and flow rates [10]. The heat transfer rate of Oldroyd-B nanofluids was much higher than those of Jeffery and Maxwell nanofluids, while the friction factor of Maxwell nanofluids was less than those of Oldroyd-B and Jeffrey nanofluids over a permeable stretching sheet [11]. Polyalphaolefins-based nanofluids with carbon tubes promoted heat conductivity, followed by exfoliated graphite and heat-treated nanofibers [12]. The precipitation of particles on a wall enhanced the heat transfer rate in polyalphaolefins-based nanofluids with exfoliated graphite fibers [13]. The thermophysical properties of polyalphaolefins-based nanofluids containing Al₂O₃ nanoparticles were dependent on particle volume fraction, particle aggregation, and dispersion [14].

The non-Newtonian fluids mentioned above involved Oldroyd-B, Jeffrey, and Maxwell fluids. The constitutive equations of these three non-Newtonian fluids can account for elasticity; hence, they are suited to model viscoelastic fluid but cannot account for the shear-thinning property of fluid. The constitutive equations of Jeffrey and Maxwell fluids are linear, and they can only be used to describe some simple flows. In practical applications, non-Newtonian fluid with both viscoelastic and shear-thinning characteristics is also common. To describe both characteristics, the constitutive equation of Giesekus fluid can be used. Hence, Giesekus fluid has attracted wide attention. However, a literature survey revealed that there is little research available on the friction factor and heat transfer of Giesekus-fluid-based nanofluids. Yang et al. [15] investigated the turbulent flow and heat transfer of Giesekus-fluid-based nanofluids in a channel and drew the conclusion that the viscoelasticity of Giesekus fluid resulted in drag reduction and the enhancement of convective heat transfer. Wang et al. [16] studied drag reduction in the gas–liquid two-phase turbulent flow of Giesekus fluids and indicated that it is better to use polymer drag-reducing agents with high concentrations in high shear flow. With the method of using Giesekus-fluid-based nanofluids, the effects of reducing friction and enhancing heat transfer performance are dependent on the Reynolds number, Weissenberg number, particle volume concentration, viscosity ratio, and mobility parameter, and there is still a lack of research on this issue. In addition, in previous studies, the distribution of particle volume concentration is usually assumed to be uniform without taking particle convection, diffusion, coagulation, or breakage into account. In this work, therefore, a numerical simulation was conducted to investigate the effects of the Reynolds number, the Weissenberg number, rheological properties, and particle concentration on the friction factor and heat transfer performance of Giesekus-fluid-based Al₂O₃ nanofluids in a pipe flow while considering the effects of particle convection, diffusion, coagulation, and breakage.

The rest of this paper is organized as follows. The flow and equations of nanofluids and particle equations are introduced in Section 2 and Section 3, respectively. The numerical method is given in Section 4. In Section 5, the numerical results are presented and discussed. Finally, conclusions are drawn in Section 6.

2. Flow and Equations of Nanofluids

The flow of Giesekus-fluid-based nanofluids in a pipe is shown in Figure 1. For the incompressible flow, the continuity and momentum equations of Giesekus-fluid-based nanofluids are [17]:

$$\nabla \cdot \mathit{u}=0$$

(1)

$${\rho }_{\mathrm{nf}}(\frac{\partial \mathit{u}}{\partial t}+\mathit{u}\cdot \nabla \mathit{u})=\nabla \cdot \mathbf{\sigma }$$

(2)

$$\mathbf{\sigma }=-p\mathit{I}+2{\mu }_{\mathrm{nf}}\mathit{D}+\mathbf{\tau }$$

(3)

where $\nabla$ is the differential operator; u, p, and ρ_nf are the velocity, pressure, and density of nanofluids, respectively; σ is the total stress tensor; I is the unit tensor; μ_nf is the solvent viscosity; τ is the stress tensor; and D is the rate-of-deformation tensor:

$$\mathit{D}=\frac{[\nabla \mathit{u}+{(\nabla \mathit{u})}^{\mathsf{T}}]}{2}$$

(4)

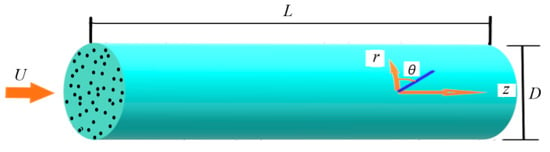
Figure 1. Flow in a pipe and cylindrical coordinate system.

The constitutive equation of Giesekus fluid is:

$$\lambda \stackrel{\nabla }{\mathbf{\tau }}+\frac{\alpha \lambda }{{\mu }_{\mathrm{p}}}\mathbf{\tau }\cdot \mathbf{\tau }+\mathbf{\tau }=2{\mu }_{\mathrm{p}}\mathit{D}$$

(5)

where λ is the fluid relaxation time; μ_p is the contribution of the polymer to viscosity; α is the mobility parameter; and the symbol ∇ is the upper-convected time derivative:

$$\stackrel{\nabla }{\mathbf{\tau }}\equiv \frac{\partial \mathbf{\tau }}{\partial t}+\mathit{u}\cdot \nabla \mathbf{\tau }-{(\nabla \mathit{u})}^{\mathsf{T}}\cdot \mathbf{\tau }-\mathbf{\tau }\nabla \mathit{u}$$

(6)

The density and viscosity of nanofluids in Equations (2) and (3) are [18]:

$${\rho }_{\mathrm{nf}}=(1-\Phi ){\rho }_{\mathrm{f}}+\Phi {\rho }_{\mathrm{p}}, {\mu }_{\mathrm{nf}}={\mu }_{\mathrm{f}}(1+2.5\Phi +6.2{\Phi }^2)$$

(7)

where Φ is the particle concentration and subscripts f and p denote fluid and particles, respectively.

The energy equation is:

$$\frac{\partial T}{\partial t}+\mathit{u}\cdot \nabla T=D_{\mathrm{nf}}{\nabla }^{2}T$$

(8)

where T is the nanofluid temperature and D_nf is the thermal diffusivity coefficient of nanofluids:

$$D_{\mathrm{nf}}=\frac{k_{\mathrm{nf}}}{{(\rho C_{\mathrm{p}})}_{\mathrm{nf}}}$$

(9)

where heat capacitance (ρC_p)_nf and k_nf are [19]:

$$k_{\mathrm{nf}}=k_{\mathrm{f}}\left[\frac{(k_{\mathrm{p}}+2k_{\mathrm{f}})-2\Phi (k_{\mathrm{f}}-k_{\mathrm{p}})}{(k_{\mathrm{p}}+2k_{\mathrm{f}})+\Phi (k_{\mathrm{f}}-k_{\mathrm{p}})}\right], {(\rho C_{\mathrm{p}})}_{\mathrm{nf}}=(1-\Phi ){(\rho C_{\mathrm{p}})}_{\mathrm{f}}+\Phi {(\rho C_{\mathrm{p}})}_{\mathrm{p}}$$

(10)

where k is thermal conductivity.

3. Equations of Particles

Particle concentration Φ in Equations (7) and (10) should be determined before solving Equations (1)–(6). The diffusion, convection, coagulation, and breakage of nanoparticles leads to a nonuniform distribution of Φ in the flow process; hence, it is necessary to solve the equation of particle concentration.

3.1. Dynamics Equation for Nanoparticles

Considering the convection, diffusion, coagulation, and breakage of nanoparticles, the equation of particle volume can be given as follows under a steady condition:

$$\begin{array}{l}\frac{\partial u_{j}n(v)}{\partial x_j}-\frac{\partial }{\partial x_j}[D_{\mathrm{p}}\frac{\partial n(v)}{\partial x_j}]=\frac{1}{2}{\displaystyle \underset{0}{\overset{v}{{\displaystyle \int }}}\beta (v_1,v-v_1)n(v_1)n(v-v_1)\mathrm{d}{v}_1}\\ -{\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}\beta (v_1,v)n(v)}n(v_1)\mathrm{d}{v}_1+\frac{1}{2}{\displaystyle \underset{0}{\overset{v}{{\displaystyle \int }}}\beta (v_1,v-v_1)\overline{n^{\prime }(v_1)n^{\prime }(v-v_1)}\mathrm{d}{v}_1}\\ -{\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}\beta (v_1,v)\overline{n^{\prime }(v)n^{\prime }(v_1)}}\mathrm{d}{v}_1+{\displaystyle \underset{v}{\overset{\infty }{{\displaystyle \int }}}a(v_1)b(v|v_1)}n(v_1)\mathrm{d}{v}_1-a(v)n(v)\end{array}$$

(11)

where u_j is the nanofluids’ velocity; the subscript j indicates summation; n(v) is the distribution function of particle volume; D_p = k_BT/3πμ_nfd_p is the diffusion coefficient of particles with k_B being the Boltzmann constant, μ_nf the viscosity, and d_p the particle diameter; β(v, v₁) is the coagulation kernel for two particles of volume v and v₁; α(v) is the breakage kernel expressing the breakage frequency of particle v; and b(v|v₁) is the breakage distribution function.

3.2. Moment Equation of Nanoparticles

Multiplying Equation (11) with v^k and then integrating over v yields:

$$\begin{array}{c}\frac{\partial u_j{M}_k}{\partial x_j}-\frac{\partial }{\partial x_j}(D_{\mathrm{p}}\frac{\partial M_k}{\partial x_j})=\frac{1}{2}{\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}{\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}[{(v+v_1)}^k-v^k-v_1{}^k]\beta (v,v_1)n(v)n(v_1)\mathrm{d}v\mathrm{d}{v}_1}}\\ +{\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}{v}^k{\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}a(v_1)b(v|v_1)}n(v_1)\mathrm{d}{v}_1\mathrm{d}v}-{\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}{v}^{k}a(v)n(v)}\mathrm{d}v\end{array}$$

(12)

where moment M_k is:

$$M_k={\displaystyle {{\displaystyle \int }}_0^{\infty }{v}^{k}n(v)dv}$$

(13)

Taking k = 0 and 1 yields:

$$M_0={\displaystyle {{\displaystyle \int }}_0^{\infty }n(v)dv}=N, M_1={\displaystyle {{\displaystyle \int }}_0^{\infty }vn(v)dv}=V$$

(14)

where M₀ and M₁ are the total particle number and particle volume, respectively. Based on Equation (14), Φ can be calculated.

3.3. Particle Coagulation and Breakage

The coagulation kernel in Equation (12) is [20]:

$$\beta =B(\frac{1}{v^{1/3}}+\frac{1}{v_1^{1/3}})(v^{1/3}+v_1^{1/3})$$

(15)

where B = 2k_BT/μ_nf with k_B being the Boltzmann constant, T the fluid temperature, and μ_nf the nanofluids’ viscosity.

The particle breakage function is composed of breakage kernel α(v) and breakage distribution function b(v|v₁). The breakage kernel α(v) is [21]:

$$a(v)=k_{\mathrm{B}}{(\frac{{\nu }_{\mathrm{nf}}G}{{\mathbf{\tau }}^{\ast }})}^{\mathrm{q}}{v}_{\mathrm{p}}{}^{1/3}{(\frac{d_{\mathrm{c}}(v)}{d_{\mathrm{p}}})}^{3/D_{\mathrm{f}}}$$

(16)

where ν_nf is the nanofluids’ viscosity; G is the shear rate of flow; τ* is characteristic shear stress and is a strength measure of the coagulated particles; q, v_p, and d_p are constants dependent on Φ; d_c is particle collision diameter and dependent on the number of primary particles; and D_f is the fractal dimension of particles (D_f = 3 for spherical particles).

The breakage distribution function, b(v|v₁), is [22]:

$$b(v\left|v_1\right.)=\left\{\begin{array}{l}2 \mathrm{if} v_1=2v\\ 0 \mathrm{otherwise}\end{array}\right.$$

(17)

Replacing the second term on the right-hand side of Equation (12) with Equation (17) yields:

$${\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}{v}^k{\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}a(v_1)b(v|v_1)}n(v_1)\mathrm{d}{v}_1\mathrm{d}v}={\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}[{\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}{v}^{k}b(\left.v\right|v_1)\mathrm{d}v}}]a(v_1)n(v_1)\mathrm{d}{v}_1={\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}{2}^{1-k}{v}_i{}^{k}a(v_1)n(v_1)\mathrm{d}{v}_1}$$

(18)

3.4. Taylor Series Expansion Moment Method

The Taylor series expansion technique [23,24] is used to solve moment equations. The equations of zero-, first-, and second-order moment can be given by substituting Equations (15)–(18) into Equation (12):

$$\frac{\partial u_j{M}_0}{\partial x_j}-\frac{\partial }{\partial x_j}(D_{\mathrm{p}}\frac{\partial M_0}{\partial x_j})=\frac{B_2(-151M_1^4+2M_2^2{M}_0^2-13M_2{M}_1^2{M}_0)M_0^2}{81M_1^4}$$

(19)

$$\frac{\partial u_j{M}_1}{\partial x_j}-\frac{\partial }{\partial x_j}(D_{\mathrm{p}}\frac{\partial M_1}{\partial x_j})=0$$

(20)

$$\frac{\partial u_j{M}_2}{\partial x_j}-\frac{\partial }{\partial x_j}(D_{\mathrm{p}}\frac{\partial M_2}{\partial x_j})=\frac{2B_2(2M_2^2{M}_0^2-13M_2{M}_1^2{M}_0-151M_1^4)}{81M_1^2}$$

(21)

4. Numerical Method

4.1. Steps of Numerical Simulation

The numerical simulation included the following steps: (1) solving Equations (1)–(7) with Φ = 0 to get u, p, and τ; (2) solving Equations (11)–(21) to get n and Φ; (3) substituting Φ into Equations (7), (9), and (10) to get ρ_nf, μ_nf, D_nf, k_t, and (ρC_p)_nf; (4) substituting Φ, ρ_nf, μ_nf, D_nf, k_t, and (ρC_p)_nf into Equations (1)–(8) to get u, p, τ, and T; (5) turning to Step (2) based on the new values of u, p, and τ if necessary; (6) calculating the Fanning friction factor C_f and Nusselt number Nu:

$$C_{\mathrm{f}}=\frac{\Delta p}{4{\rho }_{\mathrm{nf}}(L/D)(u_{z,\mathrm{av}}^2/2)}, \mathrm{Nu}=\frac{hD}{k_{\mathrm{nf}}}$$

(22)

where u_z,av and ∆p are the mean velocity and pressure drop of the fluid, respectively, and h is the heat transfer coefficient; L and D are shown in Figure 1.

4.2. Numerical Method and Boundary Condition

The finite-volume method was used to solve Equations (2), (5), (8), and (19)–(21). The SIMPLE scheme was employed to handle the term of velocity–pressure coupling, and the power-law scheme was used to handle the convection term. The discretized equations were solved using a staggered mesh system and an alternating direction implicit method. The mesh size was uniform along z and θ directions, while it was refined in r direction. On the wall, the velocity, zero-, first-, and second-order moment were zero; the heat flux was constant. The initial distributions of zero-, first-, and second-order moment and temperature were uniform.

4.3. Parameters

Giesekus fluid has both viscoelasticity and shear-thinning characteristics, and Al₂O₃ nanoparticles have the features of high energy density and thermal conductivity, safety, and low cost. Therefore, the Giesekus fluid and Al₂O₃ nanoparticles were selected as the base fluid and disperse phase, respectively, in the present study. The parameters used in the numerical simulation were: ρ_f = 990 kg/m³, ρ_p= 3970 kg/m³, k_f = 0.65 W/m·K, k_p = 40 W/m·K, C_pf = 4.15 kJ/kg·K, C_pp = 0.765 kJ/kg·K, and k_B = 1.38 × 10⁻²³ J/K. The Reynolds number was defined as Re = ρ_nfUD/μ_nf.

4.4. Validation

The flow field was divided into 128(r) × 32(θ) × 256(z) = 1,048,576 grids, and a test of independence for the grid size was performed, as shown in Table 1. The convergence criterion was that all the residual errors were less than 10⁻⁴.

Table 1. Values of M₀ when changing grid points.

r × θ × S	M0	r × θ × S	M0	r × θ × S	M0
112 × 32 × 256	1.08669	128 × 24 × 256	1.08664	128 × 32 × 216	1.08660
120 × 32 × 256	1.08651	128 × 28 × 256	1.08648	128 × 32 × 236	1.08647
128 × 32 × 256	1.08636	128 × 32 × 256	1.08636	128 × 32 × 256	1.08636
136 × 32 × 256	1.08628	128 × 36 × 256	1.08630	128 × 32 × 276	1.08631
144 × 32 × 256	1.08622	128 × 40 × 256	1.08626	128 × 32 × 296	1.08628

To validate the numerical model used in the present simulation, the present numerical result of the axial velocity profile along the radial direction in the pipe flow of Giesekus fluid was compared with the result given by Vachagina et al. [25], as shown in Figure 2, where u_z is the ratio of local velocity to average velocity and the corresponding parameters are: Wi = 4.29 and λ = 84.25 s⁻¹. The present result of the relationship between the Nusselt number and Weissenberg number in the pipe flow of Giesekus fluid was compared with theoretical results [26], as shown in Figure 3, where Br = ηu_a²/Dq_w with η being zero-shear viscosity, u_a the average velocity, D the pipe diameter, and q_w the heat flux. As can be seen from Figure 2 and Figure 3, our results were in agreement with previous results.

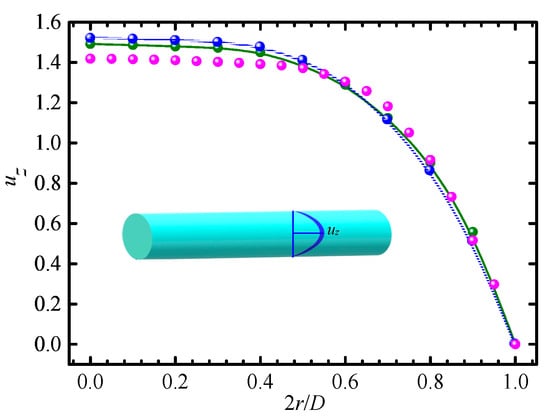
Figure 2. Axial velocity profile along the radial direction. ⸺●⸺: present numerical result; ⸺●⸺: analytical result [25]; ●: experimental result [25].

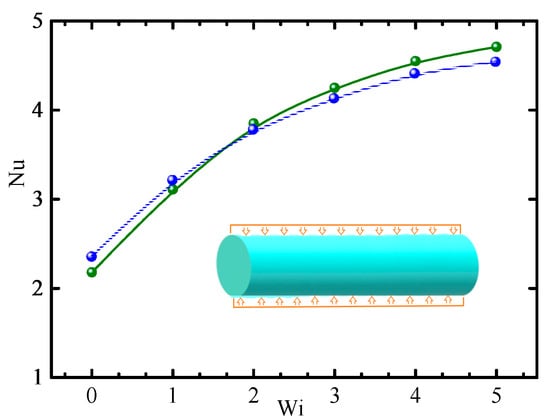
Figure 3. Variation in Nu with Wi (Br = 0.1). ⸺●⸺: present numerical result; ⸺●⸺: theoretical solution [26].

5. Results and Discussion

5.1. Friction Factor

The Fanning friction factor C_f, as shown in Equation (22), was used to express the shear stress exacting on the flow by the wall.

5.1.1. Effect of Weissenberg Number

The relationship between the relative friction factor, C_f/C_fNew, and the modified Weissenberg number, Wi*, for different particle concentrations, Φ, is shown in Figure 4, where the results [27] for pure Giesekus fluid are also given for comparison. The parameters in Figure 4 are: C_fNew is the friction factor for Newtonian fluid; Wi* = 2Wi_τ0/(Re_b0L), where Wi_τ0 = λu_τ²/ν₀ (λ is relaxation time, u_τ is friction velocity, and ν₀ is zero shear-rate kinematic viscosity) is zero shear-rate friction Wi; Re_b0 = Du_b/ν₀ (D is pipe diameter and u_b is bulk average velocity), L is the maximum extensibility parameter of polymer molecules; β₀ = μ_s/μ₀ = μ_s/(μ_s + μ_p), where μ_s is solvent viscosity, μ₀ is zero shear-rate viscosity, and μ_p is viscosity from polymer contributions; and α is a mobility parameter.

Figure 4. Friction factor vs. modified Weissenberg number for different particle concentrations (β₀ = 0.2, Re = 2.5, α = 0.2). ⸺●⸺: Φ = 0% (Giesekus fluid) [27]; ⸺●⸺: Φ = 0% (Giesekus fluid); ⸺●⸺: Φ = 0.5%; ⸺●⸺: Φ = 1.0%; ⸺●⸺: Φ = 2.0%; and ⸺●⸺:Φ = 3.0%.

From Figure 4, we can see that C_f/C_fNew is always larger than 1, i.e., the C_f of Giesekus-fluid-based nanofluids is larger than that of Newtonian fluid. C_f/C_fNew = 1 when Wi* = 0 because Wi* = 2Wi_τ0/(Re_b0L) is the ratio of elastic force to inertial force; Wi* = 0 for Newtonian fluid. As Wi* increases, C_f/C_fNew increases rapidly when 0 < Wi* < 0.5 and slowly when 0.5 < Wi* < 1, and then it decreases slowly when 1 < Wi*< 7. Wi is also the ratio of the first normal stress difference (FNSD) to shear stress. When 0 < Wi* < 1, the increase in Wi* means an increase in FNSD, so as to produce additional extension resistance and result in an increase in C_f. When 1 < Wi* < 7, the effect of the increase in FNSD is weakened; meanwhile, the effect of shear-thinning is increased, resulting in the decrease in C_f. Friction is the result of the combined action of various forces exacting on fluid. Therefore, there exists a maximum C_f for certain rheological and physical properties of nanofluids and certain flow conditions.

5.1.2. Effects of Particle Concentration and Viscosity Ratio

In Figure 4, C_f/C_fNew increases with increasing Φ. The nanoparticles in Giesekus fluid are responsible for energy absorption, leading to a large C_f. In addition, nanofluids’ viscosity, μ_nf, is proportional to Φ, as shown in Equation (7). μ_nf increases with increasing Φ, intensifying the viscous sublayer and resulting in an increase in C_f. As Φ increases, the increase in C_f/C_fNew is large when 0 < Φ < 0.5% but small when 0.5% < Φ < 3.0% because the variation in Φ has little impact on the viscous sublayer in this range of Φ, showing that the effect of particle concentration on C_f is nonlinear. In previous studies, there were different conclusions on the impact of nanoparticles in Newtonian-fluid-based nanofluids on C_f; most conclusions are that nanoparticles lead to an increase in C_f (e.g., [28,29,30,31]). The results in Figure 4 show that nanoparticles in Giesekus-fluid-based nanofluids also lead to an increase in C_f.

Figure 5 shows the relationship between C_f/C_fNew and Wi* for different viscosity ratios, β₀. β₀ = 0 and 1 corresponds to pure polymer and Newtonian fluid because β₀ = μ_s/(μ_s + μ_p). We can see that C_f/C_fNew = 1 for Newtonian fluid (β₀ = 1). As Wi* increases, C_f/C_fNew increases rapidly when 0 < Wi* < 2 and slowly when 2 < Wi* < 7 for the pure polymer (β₀ = 0), showing that C_f is directly proportional to Wi* in the absence of solvent viscosity μ_s. However, C_f/C_fNew first increases and then gradually decreases with the increase in Wi* when 0 < β₀ < 1. Therefore, the changing trend of C_f with Wi* depends on β₀. In addition, C_f/C_fNew increases with decreasing β₀, i.e., a large β₀ should be selected in order to reduce C_f.

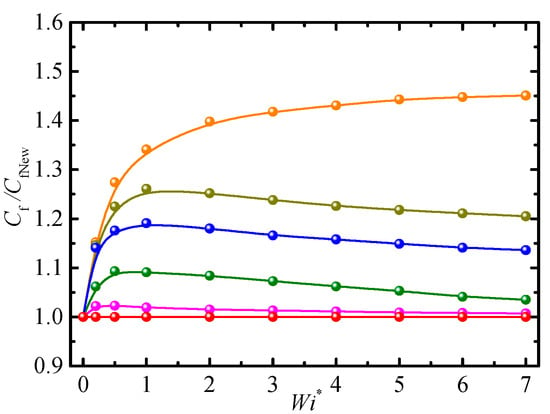
Figure 5. Friction factor vs. modified Weissenberg for different viscosity ratios (Φ =1.0%, Re = 2.5, α = 0.2). ⸺●⸺: β₀ =1.0; ⸺●⸺: β₀ = 0.9; ⸺●⸺: β₀ = 0.3; ⸺●⸺: β₀ = 0.2; ⸺●⸺: β₀ = 0.1; and ⸺●⸺: β₀ = 0.

5.1.3. Effects of Reynolds Number and Mobility Parameter

The Reynolds number represents the ratio of fluid inertia to viscosity, and its value represents the relative importance of the two. The range in Reynolds numbers in this paper was 0.5–500 because this can more fully reflect the situations of inertia or viscosity dominance. The relationship between C_f/C_fNew and Wi* for different Re is shown in Figure 6, where C_f/C_fNew is reduced with increasing Re, but the relationship between the reducing rate of C_f/C_fNew and the increasing rate of Re is nonlinear, i.e., the change rate for C_f/C_fNew is almost the same as the small change rate for Re when 0.5 < Re < 1, and there is a large change rate when 100 < Re < 500. C_f is proportional to viscosity and shear rate, and Re is the ratio of inertia to viscosity. At a small Re, the function of viscosity is large, and the shear rate is large in most regions of flow, so there is a large C_f. At a small Re, the flow is sensitive to changes in Re, so C_f is also sensitive to changes in Re. At a large Re, the inertial force is dominant against the viscous forces with increasing Re, so C_f is less sensitive to changes in Re.

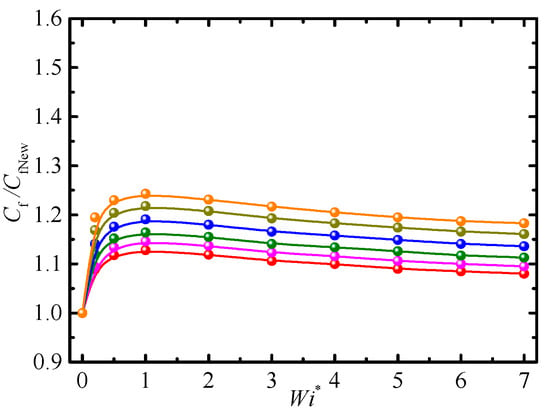
Figure 6. Friction factor vs. modified Weissenberg number for different Reynolds numbers (β₀ = 0.2, Φ = 1.0%, α = 0.2). ⸺●⸺: Re = 500; ⸺●⸺: Re = 100; ⸺●⸺: Re = 10; ⸺●⸺: Re = 2.5; ⸺●⸺: Re = 1; and ⸺●⸺: Re = 0.5.

Figure 7 shows the relationship between C_f/C_fNew and Wi* for different mobility parameters, α; the degree of shear-thinning is proportional to α. Increasing α leads to a decrease in C_f/C_fNew due to an increase in the shear-thinning effect. C_f/C_fNew is smaller for Giesekus-fluid-based nanofluids than for Oldroyd-B-based nanofluids (α = 0) under the same conditions. For a definite α and larger Wi*, the change in C_f/C_fNew becomes unobvious and C_f/C_fNew approaches asymptotic values. Despite the shear-thinning effect, C_f/C_fNew is still larger than 1 because there exists a polymer contribution, μ_p, to viscosity.

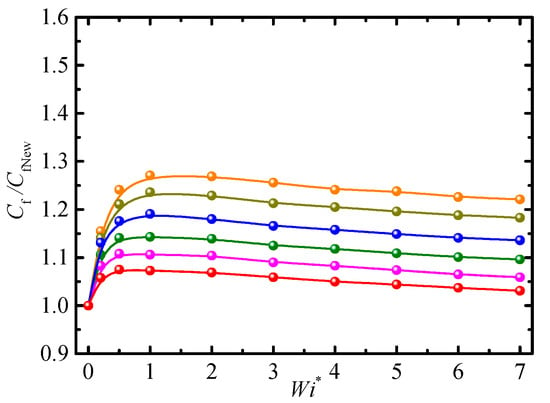
Figure 7. Friction factor vs. modified Weissenberg number for different mobility parameters (Re = 2.5, Φ = 1.0%, β₀ = 0.2). ⸺●⸺: α = 0.5; ⸺●⸺: α = 0.4; ⸺●⸺: α = 0.3; ⸺●⸺: α = 0.2; ⸺●⸺: α = 0.1; and ⸺●⸺: α = 0.

5.2. Heat Transfer

In order to understand the heat transfer performance of Giesekus-fluid-based nanofluids, we explored the impacts of Wi*, Φ, β₀, Re, and α on Nu, which is shown in Equation (22).

5.2.1. Effect of Weissenberg Number

The relationship between Nu and Wi for different Φ is shown in Figure 8, where the results [32] for pure Giesekus fluid are also given. Nu is at its minimum when Wi = 0 for Φ = 0, i.e., the heat transfer effect of Giesekus fluid is better than that of Newtonian fluid. As Wi increases, Nu increases rapidly when 0 < Wi < 2 and slowly when 2 < Wi < 8. For a definite Φ and larger Wi, Nu approaches asymptotic values, indicating that the fluid elasticity has little impact on heat transfer when Wi exceeds a certain value.

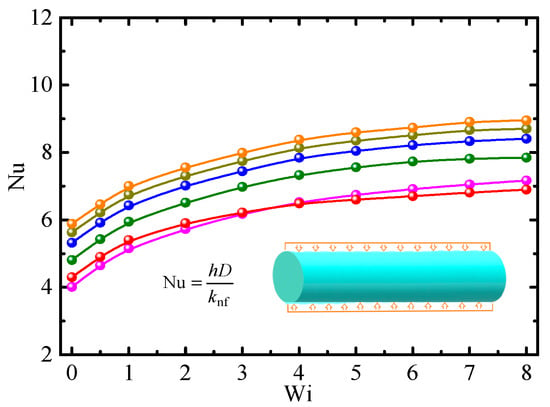
Figure 8. Nusselt number vs. Weissenberg number for different particle concentrations (β₀ = 0.2, Re = 2.5, α = 0.2). ⸺●⸺: Φ = 0% (Giesekus fluid) [32]; ⸺●⸺: Φ = 0% (Giesekus fluid); ⸺●⸺: Φ = 0.5%; ⸺●⸺: Φ = 1.0%; ⸺●⸺: Φ = 2.0%; and ⸺●⸺: Φ = 3.0%.

5.2.2. Effects of Particle Concentration and Viscosity Ratio

In Figure 8, the Nu for Φ≠0 is larger than that for Φ = 0, indicating that adding nanoparticles into fluid can improve heat transfer. An increase in Φ usually leads to an increase in viscosity, as shown in Equation (7), and intensifies the viscous sublayer, which causes a decrease in heat transfer. However, the thermal conductivity of nanofluids is higher than that of pure fluid when adding nanoparticles with high thermal conductivity into fluid, which enhances the heat transfer effect. Therefore, the results in Figure 8 imply that the impact of thermal conductivity enhancement overcomes the impact of viscosity increase, which is consistent with previous results, e.g., [33]. Nu increases with increasing Φ because the interaction between particles is weak at a small Φ, meaning a weak heat transfer. At a large Φ, both frequent particle interaction and movement disturb the flow and enhance heat transfer. The increasing rate of Nu decreases with increasing Φ because the increase in viscosity is far greater than the increase in thermal conductivity at a large Φ. In addition, the nanoparticles with high Φ are easier to coagulate, resulting in a reduction in particle numbers, thereby affecting heat transfer performance.

Figure 9 shows the relationship between Nu and Wi for different viscosity ratios, β₀. The Nu for β₀ < 1 is larger than that for β₀ = 1, i.e., the heat transfer performance of Giesekus-fluid-based nanofluids was better than that of Newtonian-fluid-based nanofluids, which is in agreement with previous conclusions that viscoelastic fluid can enhance heat transfer rates compared to Newtonian fluids, e.g., [34]. Nu decreases with increasing β₀, and the reducing rate was almost the same when 0 < β₀ < 1, showing the enhancement of heat transfer depends linearly on the viscosity ratio.

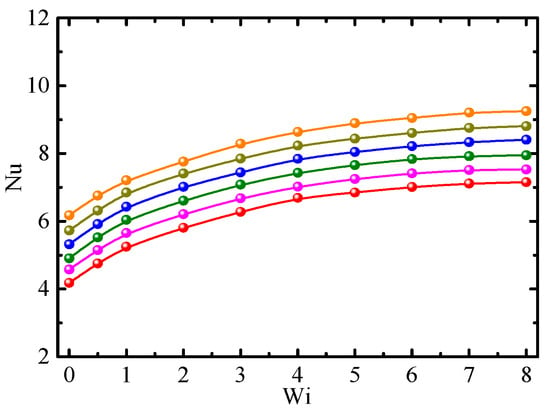
Figure 9. Nusselt number vs. Weissenberg number for different viscosity ratios (Φ = 1.0%, Re = 2.5, α = 0.2). ⸺●⸺: β₀ = 1.0; ⸺●⸺: β₀ = 0.9; ⸺●⸺: β₀ = 0.3; ⸺●⸺: β₀ = 0.2; ⸺●⸺: β₀ = 0.1; and ⸺●⸺: β₀ = 0.

5.2.3. Effects of Reynolds Number and Mobility Parameters

The relationship between Nu and Wi for different Re is shown in Figure 10, where Nu increases with increasing Re. The relationship between the growth rate of Nu and increasing rate of Re was nonlinear. As the flow was laminar in the range of Re in this paper, there are two reasons for why Nu was proportional to Re: (1) the laminar sublayer becomes thinner and shear stress subsequently increases with increasing Re; (2) more heat is carried by a faster moving fluid than a slower one.

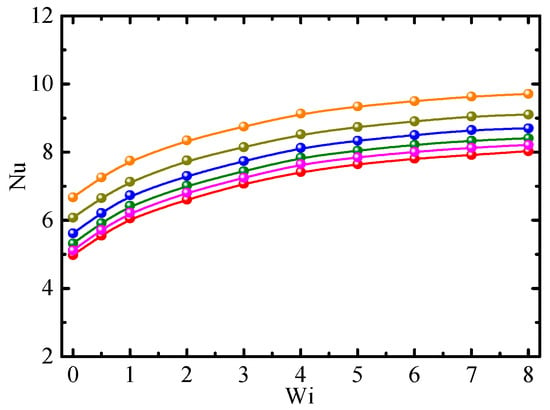
Figure 10. Nusselt number vs. Weissenberg number for different Reynolds numbers (β₀ = 0.2, Φ = 1.0%, α = 0.2). ⸺●⸺: Re = 0.5; ⸺●⸺: Re = 1; ⸺●⸺: Re = 2.5; ⸺●⸺: Re = 10; ⸺●⸺: Re = 100; and ⸺●⸺: Re = 500.

Figure 11 shows the relationship between Nu and Wi for different α. Nu increases with the increase in α, and the growth rate of Nu is almost the same when 0 < α < 0.5, showing the increase in heat transfer depends linearly on α. The larger α is, the more obvious the shear-thinning effect is and the thinner the viscous sublayer is, leading to increases in heat transfer. In Equation (5), α = 0 corresponds to Oldroyd-B fluid; therefore, the heat transfer performance of Giesekus-fluid-based nanofluids is better than that of Oldroyd-B-based nanofluids.

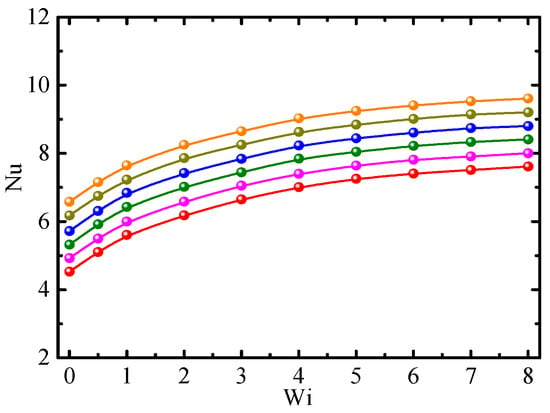
Figure 11. Nusselt number vs. Weissenberg number for different mobility parameters (Re = 2.5, Φ = 1.0%, β₀ = 0.2). ⸺●⸺: α = 0; ⸺●⸺: α = 0.1; ⸺●⸺: α = 0.2; ⸺●⸺: α = 0.3; ⸺●⸺: α = 0.4; and ⸺●⸺: α = 0.5.

5.3. Performance Evaluation Criterion

As shown above, the heat transfer performance of Giesekus-fluid-based nanofluids is better than that of Giesekus fluid, while the friction factor in the former is larger than that in the latter. Therefore, we need to balance the increase in heat transfer and enhancement of consumed power. An energy performance evaluation criterion (PEC) was employed to express the ratio of heat flow rate to required consumed power [35]:

$$\mathrm{PEC}=\frac{(T_{out}-T_{\mathrm{in}}){\displaystyle {{\displaystyle \int }}_{-D/2}^{D/2}2\pi r{u}_z{(\rho C_{\mathrm{p}})}_{\mathrm{nf}}\mathrm{d}r}}{\Delta P{\displaystyle {{\displaystyle \int }}_{-D/2}^{D/2}2\pi r{u}_z\mathrm{d}r}}$$

(23)

where T_in and T_out are the temperatures at the inlet and outlet of the pipe, respectively.

5.3.1. Effects of Various Factors on the PEC

The ratio of PEC for Giesekus-fluid-based nanofluids (PEC_nf) to that for Giesekus fluid (PEC_f) is expressed as PEC_nf/PEC_f. Figure 12, Figure 13, Figure 14 and Figure 15 show PEC_nf/PEC_f as a function of Wi for different Φ, β₀, Re, and α, respectively. At a small Wi (Wi < 3~6), the difference in C_f/C_fNew is larger than that in Nu between Giesekus-fluid-based nanofluids and Giesekus fluid; hence PEC_nf/PEC_f is less than 1. On the contrary, PEC_nf/PEC_f is larger than 1 at a large Wi because the difference in Nu is larger than that in C_f/C_fNew. PEC_nf/PEC_f increases with increasing Wi, Φ, Re, and α, and with decreasing β₀. Therefore, it is more effective to use nanofluids at a large Wi, Φ, Re, and α, but small β₀.

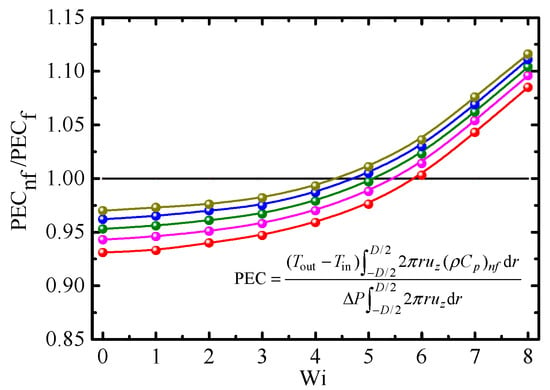
Figure 12. PEC_nf/PEC_f vs. Weissenberg number for different particle concentrations (β₀ = 0.2, Re = 2.5, α = 0.2). ⸺●⸺: Φ = 0% (Giesekus fluid); ⸺●⸺: Φ = 0.5% (Giesekus fluid); ⸺●⸺: Φ = 1.0%; ⸺●⸺: Φ = 2.0%; and ⸺●⸺: Φ = 3.0%.

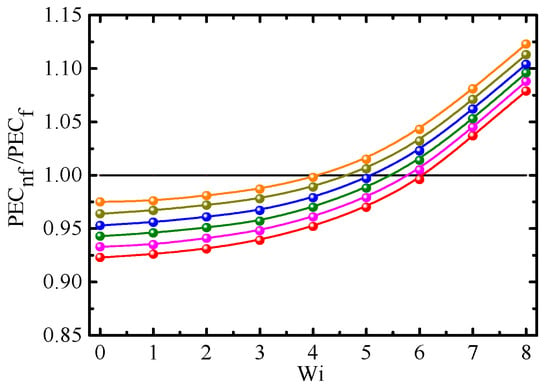
Figure 13. PEC_nf/PEC_f vs. Weissenberg number for different viscosity ratios (Φ = 1.0%, Re = 2.5, α = 0.2). ⸺●⸺: β₀ = 1.0; ⸺●⸺: β₀ = 0.9; ⸺●⸺: β₀ = 0.3; ⸺●⸺: β₀ = 0.2; ⸺●⸺: β₀ = 0.1; and ⸺●⸺: β₀ = 0.

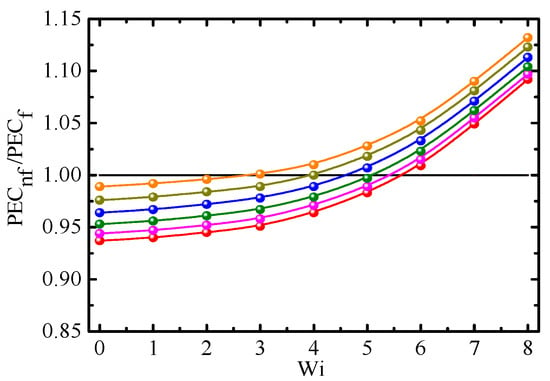
Figure 14. PEC_nf/PEC_f vs. Weissenberg number for different Reynolds numbers (β₀ = 0.2, Φ = 1.0%, α = 0.2). ⸺●⸺: Re = 0.5; ⸺●⸺: Re = 1; ⸺●⸺: Re = 2.5; ⸺●⸺: Re = 10; ⸺●⸺: Re = 100; and ⸺●⸺: Re = 500.

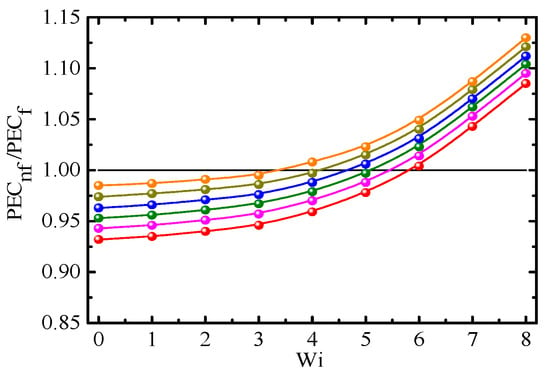
Figure 15. PEC_nf/PEC_f vs. Weissenberg number for different mobility parameters (Re = 2.5, Φ =1.0%, β₀ = 0.2). ⸺●⸺: α = 0; ⸺●⸺: α = 0.1; ⸺●⸺: α = 0.2; ⸺●⸺: α = 0.3; ⸺●⸺: α = 0.4; and ⸺●⸺: α = 0.5.

5.3.2. Correlation Model

In Figure 12, Figure 13, Figure 14 and Figure 15, PEC_nf/PEC_f is proportional to Wi, Φ, Re, and α, but inversely proportional to β₀. In order to describe the impact of related parameters on PEC_nf/PEC_f, we built a correlation model relating PEC_nf/PEC_f to related parameters. Firstly, related parameters were combined into a dimensionless parameter:

$$\xi =\frac{\mathrm{Wi}\Phi \mathrm{Re}\alpha }{{\beta }_0}$$

(24)

We established a relationship between PEC_nf/PEC_f and ξ based on formula (24) and numerical data in Figure 12, Figure 13, Figure 14 and Figure 15 as:

$${\mathrm{PEC}}_{\mathrm{nf}}/{\mathrm{PEC}}_{\mathrm{f}}=-0.17632{\mathrm{e}}^{(\xi /-171.88918)}+1.12805$$

(25)

Figure 16 shows the numerical data in Figure 12, Figure 13, Figure 14 and Figure 15 and formula (25) on a fitted curve.

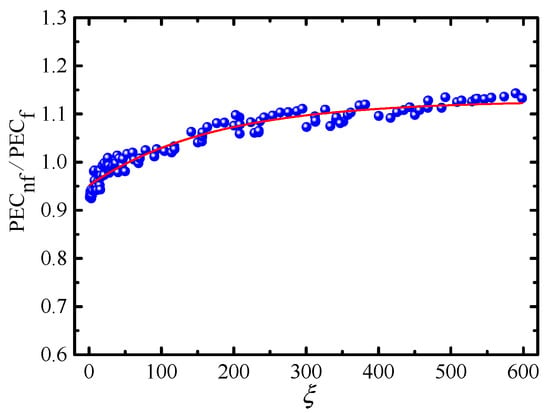
Figure 16. Relationship between PEC_nf/PEC_f and ξ. ●: numerical data; ⸺⸺: Formula (25).

6. Conclusions

The friction factor and heat transfer of Giesekus-fluid-based nanofluids in a pipe flow were investigated in order to understand the function of non-Newtonian-fluid-based nanofluids as a heat transfer medium. The impacts of Wi, Φ, β₀, Re, and α on C_f/C_fNew, Nu, and PEC_nf/PEC_f were discussed. The main conclusions are summarized as follows:

(1) C_f/C_fNew is larger for Giesekus-fluid-based nanofluids than for Newtonian fluid, and there exists a maximum C_f/C_fNew under certain rheological and physical properties of nanofluids and flow conditions. As Wi increases, C_f/C_fNew first increases and then decreases. Nanoparticles in Giesekus-fluid-based nanofluids lead to an increase in C_f/C_fNew. An increase in Φ results in an increase in C_f/C_fNew, and the effect of Φ on C_f/C_fNew is nonlinear. C_f/C_fNew is proportional to Wi in the absence of solvent viscosity, and the changing trend of C_f/C_fNew with Wi depends on β₀. A large β₀ should be selected in order to reduce friction factor. C_f/C_fNew is reduced with increasing Re, but the relationship between the reducing rate of C_f/C_fNew and increasing rate of Re is nonlinear. Increasing α leads to a decrease in C_f/C_fNew, and Giesekus-fluid-based nanofluids have a smaller C_f/C_fNew than Oldroyd-B-based nanofluids.

(2) As Wi increases, Nu increases rapidly when 0 < Wi < 2 and slowly when 2 < Wi < 8, and fluid elasticity has little effect on Nu when Wi exceeds a certain value. Adding nanoparticles into fluid can enhance heat transfer. Nu increases with increasing Φ, and the increasing rate of Nu decreases with the increase in Φ. Giesekus-fluid-based nanofluids have a better heat transfer effect than Newtonian-fluid-based nanofluids. Nu decreases with increasing β₀, and the enhancement of Nu depends linearly on β₀. Nu increases with increasing Re, and the relationship between the growth rate of Nu and increase rate of Re is nonlinear. Nu increases with an increase in α, and the enhancement of Nu depends linearly on α.

(3) PEC_nf/PEC_f increases with increasing Wi, Φ, Re, and α, and with decreasing β₀. It is more effective to use nanofluids at a large Wi, Φ, Re, and α, but small β₀. Finally, the formula of PEC_nf/PEC_f as a function of Wi, Φ, β₀, Re, and α was derived based on numerical data.