Economic Evaluation of Oil and Gas Projects: Justification of Engineering Solutions in the Implementation of Field Development Projects
Abstract
:1. Introduction
- Uniqueness. What makes each project unique [6] is the combination of the geological conditions in the reservoir (including such parameters as permeability, porosity, pressure, and fracture density), the physical and chemical properties of produced fluids, and the equipment used in specific conditions.
- Capital intensity [3,4,5]. For example, it is stated in [2] that the capital costs of the Constellation-X project in Malaysia (an oil and gas field with 250 billion cubic feet of reserves) amount to almost 400 million dollars. Many sources, including [5], state that drilling a single well costs several million dollars.
- Being influenced by oil and gas price volatility [6]. According to the authors’ calculations, daily price volatility for Brent oil has increased by 1.43%, and annual price volatility has grown by 27.3% over the past 10 years (Independent Statistics and Analysis. US Energy Information Administration. Petroleum and other liquids. Available online: https://www.eia.gov/dnav/pet/hist/LeafHandler.ashx?n=PET&s=RBRTE&f=D (accessed on 29 March 2022)).The authors of [9,10,11] state that is both difficult and necessary to factor in oil price fluctuations in the future to create effective plans for the development of oil and gas fields. They also attempt to provide a rationale for price-forecasting methods.
- Knowledge accumulation on the features of the oil and gas field in the development process. At the exploration and testing stage, information on the oil and gas field is rather limited due to the uniqueness of both the geological properties of reservoirs and the physicochemical properties of fluids. As more data are obtained on the field, it may lead to making changes to the initial engineering decisions. For example, Ref. [11] presents an example of a transition from vertical and deviated to horizontal wells.
- Interest on part of the government in producing as much as possible [4], which goes against the company’s interest. The company is interested in maximizing the economic effect of the project, while the government wants more tax money.
- Complexities of project implementation. This is associated with the complexity of the physical processes occurring in the reservoir during the extraction of fluids [7,8] and requires both highly qualified personnel and the company’s exper that oil companies face, an approach is widely ience in applying engineering solutions in specific conditions [13,14].
- Numerous risks, including geological, technical, engineering, operational, financial, political risks, etc. [3]. Risk assessment is an independent and rather complex problem.
- The opportunity to improve or change decisions already made at the design stage in the process of project implementation [15].
- The high technological intensity and complexity of engineering solutions [19].
- The objects are fluids, the reservoir, and the production facility.
- The ability to respond to market conditions [20].
- Reducing costs;
- Choosing optimal production technologies while acquiring new information during operation;
- Adjusting production volumes depending on the situation on global markets, etc.
- To analyze the bias of the DCF model, which limits the economic evaluation of engineering solutions in the implementation of oil and gas field development projects.
- To analyze the tools of economic evaluation of investment projects to eliminate the bias of the DCF model and identify the advantages and limitations of these tools.
- To develop a methodological approach to the economic evaluation of oil and gas projects, taking into account engineering solutions, and to test the resulting approach on a conditional example of an oil and gas field development project with the justification of an engineering solution.
2. Materials and Methods
- Justification for each year of the forecast period of nominal values (excluding discounting) of cash inflows and outflows: revenue, operating costs, capital costs, taxes, etc.
- The use of binary discounting, i.e., separate discounting of inflows and outflows of the project at different rates. For inflows, the discount rate consists of two components: the risk-free rate (reflects the time factor) and the risk rate (reflects the change in the price of oil), which is calculated using a reverting price model. Outflows are discounted at a risk-free rate.
- Application of the real options valuation to calculate the absolute values of premiums for technical risks in the implementation of the project. For the inflows of each year of the project, the calculation of premiums is based on the projected change in production volumes. For outflows, capital expenditure premiums are calculated based on their volatility.
- The use of the real options valuation method to justify engineering decisions that can be made in the future of the project, from the available range of alternatives.
2.1. Economic Evaluation of Oil and Gas Projects as Real Assets: Limitations of the DCF Method
- The capital asset pricing model (CAPM);
- Classifying projects by their basic parameters and assigning a different discount rate for each category (for example, one value for exploration projects, another for R&D projects, a third for development projects, etc.).
- It implies that the project is not changed, and the management follows the original plan regardless of changing circumstances without striving to eliminate uncertainties and increase the value of results;
- It assumes that future cash flows are predictable, which, as a rule, leads to the overestimation or underestimation of some types of projects;
- Insufficient consideration of the specific risks of the project, the need for adjustments increases the initial errors in the choice of the parameter and increases with the increase in the duration of the project.
2.2. Binary Model and Reverting Discounting for the Economic Evaluation of Oil and Gas Projects
- It eliminated the systematic error that occurs when the single discount rate used by the company is applied to evaluate projects of different nature.
- Through discounting the individual determinants of the project, it removes the limitations that total cash flow discounting has.
- It combines risk and cost analyzes of a project by calculating the net present value of a project as the endpoint of all possible scenarios grouped together, as opposed to calculating the cost for each of the scenarios, and then by using this combination of costs in the economic evaluation process.
/((Pt − UOpExt)·Qt − CapExt),
=TimeDFt·(((Ft − UOpExt)·Qt − CapExt)/((Pt − UOpExt)·Qt − CapExt)),
2.3. Application of the Theory of Real Options Valuation to Find the Cost of Risks of an Oil and Gas Development Project
- The influence of geological and technical conditions, which cause changes in the levels of production and costs;
- The situation in hydrocarbon production and transportation sectors;
- Market conditions in energy markets;
- The quality of the hydrocarbons produced at the given field;
- Local tax system, etc.
3. Results
4. Discussion
- Optimization of the reservoir model at the design phase with the emergence of new opportunities to respond to technological and geological challenges through engineering solutions;
- Rationalization of the field development system during production by improving reservoir parameters through engineering solutions, covering a larger area, or improving fluid movement in the reservoir, thereby reducing technical uncertainties and creating prerequisites for increasing the recovery factor;
- Taking into account changes in macroeconomic indicators, in particular, the situation of global energy markets.
5. Conclusions
- The methodological approach to substantiating various discount rates for inflows and outflows during the development of oil and gas fields makes it possible to more realistically take into account the specifics of oil and gas fields development projects, including both long terms and the requirement to intensify production through the use engineering solutions and oil price volatility.
- The implementation of a combination of binary discounting and reverting discounting. By itself, binary discounting allows us to correctly take into account, first of all, the risks of outflows, and reverting discounting—the risks of inflows. Thus, the discount model, which is elaborated due to their combination, enables us to correctly take into account the risks of both types.
- Reasonable choice of the discount rate for inflows, taking into account the reduction in oil price volatility, enables us to obtain more correct values of discounted inflows and improve the economic efficiency of the oil and gas fields’ development project.
- Reasonable choice of the discount rate for outflows, taking into account the absolute magnitudes of risks, including investment flows of engineering solutions produced over a number of years, allows us to obtain more correct values of discounted outflows and make more valid conclusions about the economic efficiency of the oil and gas fields’ development project, including the reduction in economic efficiency.
- The reduction in oil price volatility in the long term is estimated using a logarithmic model. This is an assumption that may not correspond to real conditions in the global market. In modern conditions, in addition to economic factors, the situation on the oil market is influenced by the ESG agenda. That is, the model can be refined and expanded because of the new factors.
- The sensitivity analysis of the results obtained has not been performed, taking into account the structure of cash flows in the financial model for various oil and gas fields: the ratio between inflows and outflows by year, the distribution of cash flows by year, the non-negativity of cash flows by year, the composition of inflows and outflows, the marginality of products, and the composition of taxes.
- The calculation was made for one case. Therefore, it is necessary to continue the economic evaluation of deposits with various types and sizes, with different investment structures and under different tax conditions.
- There is incomplete accounting of the spectrum of risks accompanying the implementation of oil and gas projects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Ministry of Natural Resources and Environment of the Russian Federation. Rules on the Preparation of Technical Projects for the Development of Hydrocarbon Deposits; Ministry of Natural Resources and Environment: Moscow, Russia, 2019. [Google Scholar]
- Ministry of Natural Resources and Environment of the Russian Federation. Rules on the Development of Hydrocarbon Deposits; Ministry of Natural Resources and Environment: Moscow, Russia, 2016. [Google Scholar]
- Clews, R.J. Project Finance for the International Petroleum Industry, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Fermi, D.W.; Yusri, B.A.; Haeryip, S. Monte Carlo net present value for techno-economic analysis of oil and gas production sharing contract. Int. J. Technol. 2019, 10, 829–840. [Google Scholar]
- Jafarizadeh, B.; Bratvold, R.B. Project Economics in the Big-Bets Industry: The Integrated Valuation in Practice. J. Pet. Sci. Eng. 2021, 197, 108095. [Google Scholar] [CrossRef]
- Berntsen, M.; Bøe, K.S.; Jordal, T.; Molnár, P. Determinants of oil and gas investments on the Norwegian Continental Shelf. Energy 2018, 148, 904–914. [Google Scholar] [CrossRef]
- Kh, M.R. Nefteotdacha: Proshloe, Nastoyashchee, Budushchee (Optimizatsiya Dobychi, Maksimizatsiya KIN) (Oil Recovery: Past, Present, Future (Production Optimization, Maximization of Recovery Factor)); Kazan’: FEN Publishing House: Kazan, Russia, 2014; p. 750. [Google Scholar]
- Muslimov, R.K. History and prospects of hydrodynamic methods for oil fields development in Russia. Neftyanoe Khozyaystvo—Oil Ind. 2020, 12, 95–100. [Google Scholar] [CrossRef]
- Tang, B.-J.; Zhou, H.-L.; Chen, H.; Wang, K.; Cao, H. Investment opportunity in China’s overseas oil project: An empirical analysis based on real option approach. Energy Policy 2017, 105, 17–26. [Google Scholar] [CrossRef]
- Jafarizadeh, B.; Bratvold, R.B. Sequential Exploration: Valuation with Geological Dependencies and Uncertain Oil Prices. SPE J. 2020, 25, 2401–2417. [Google Scholar] [CrossRef]
- Salahor, G. Implications of output price risk and operating leverage for the evaluation of petroleum development projects. Energy J. 1998, 19, 13–46. [Google Scholar] [CrossRef]
- Yakupov, R.F.; Mukhametshin, V.S.; Khakimzyanov, I.N.; Trofimov, V.E. Optimization of reserve production from water oil zones of D3ps horizon of Shkapovsky oil field by means of horizontal wells. Georesursy 2019, 21, 55–61. [Google Scholar] [CrossRef]
- Muslimov, R.K. Fundamental problems of oil industry. Neftyanoe Khozyaystvo—Oil Ind. 2017, 1, 6–11. [Google Scholar]
- Adkins, R.; Paxson, D. Rescaling-contraction with a lower cost technology when revenue declines. Eur. J. Oper. Res. 2019, 277, 574–586. [Google Scholar] [CrossRef]
- Bailey, W.; Couët, B.; Bhandari, A.; Faiz, S.; Srinivasan, S.; Weeds, H. Unlocking the value of real options. Oilfield Rev. 2003, 15, 4–19. [Google Scholar]
- Bera, A.; Kumar, T.; Ojha, K.; Mandal, A. Adsorption of surfactants on sand surface in enhanced oil recovery: Isotherms, kinetics and thermodynamic studies. Appl. Surf. Sci. 2013, 284, 87–99. [Google Scholar] [CrossRef]
- Sedaghata, M.H.; Mohammadib, H.; Razmia, R. Application of SiO2 and TiO2 nanoparticles to enhance the efficiency of polymer-surfactant floods. Energy Sources Part A Recovery Util. Environ. Eff. 2016, 38, 22–28. [Google Scholar] [CrossRef]
- Rogachev, M.K.; Aleksandrov, A.N. Justification of a comprehensive technology for preventing the formation of asphalt-resin-paraffin deposits during the production of highly paraffinic oil by electric submersible pumps from multiformation deposits. J. Min. Inst. 2021, 250, 596–605. [Google Scholar] [CrossRef]
- Dvoynikov, M.V. Designing of well trajectory for efficient drilling by rotary controlled systems. J. Min. Inst. 2018, 231, 254–262. [Google Scholar]
- Wang, K.; Vredenburg, H.; Wang, T.; Feng, L. Financial return and energy return on investment analysis of oil sands, shale oil and shale gas operations. J. Clean. Prod. 2019, 223, 826–836. [Google Scholar] [CrossRef]
- Sharpe, W.F. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Financ. 1964, 19, 425–442. [Google Scholar]
- Myers, S.C.; Turnbull, S.M. Capital budgeting and the capital asset pricing model: Good news and bad news. J. Financ. 1977, 32, 321–333. [Google Scholar] [CrossRef]
- Rogachev, M.K.; Mukhametshin, V.V.; Kuleshova, L.S. Improving the efficiency of using resource base of liquid hydrocarbons in jurassic deposits of western Siberia. J. Min. Inst. 2019, 240, 711–715. [Google Scholar] [CrossRef] [Green Version]
- Rogachev, M.K.; Mukhametshin, V.V. Control and regulation of the hydrochloric acid treatment of the bottomhole zone based on field-geological data. J. Min. Inst. 2018, 231, 275–280. [Google Scholar]
- Dvoinikov, M.V.; Kuchin, V.N.; Mintsaev, M.S. Development of viscoelastic systems and technologies for isolating water-bearing horizons with abnormal formation pressures during oil and gas wells drilling. J. Min. Inst. 2021, 247, 57–65. [Google Scholar] [CrossRef]
- Hawas, F.; Cifuentes, A. Valuation of projects with minimum revenue guarantees: A Gaussian copula-based simulation approach. Eng. Econ. 2017, 62, 90–102. [Google Scholar] [CrossRef]
- Shkatov, M.Y.; Sergeev, I.B. The evaluation of cost efficiency of mineral exploration and mining investment projects: Development of the income approach. Mineral Resources of Russia. Econ. Manag. 2007, 1, 38–44. [Google Scholar]
- Fama, E. Risk-adjusted discount rates and capital budgeting under uncertainty. J. Financ. Econ. 1977, 5, 3–24. [Google Scholar] [CrossRef]
- Philbrick, S.W. Accounting for risk margins. Casualty Actuar. Soc. Spring Forum 1994, 1, 1–87. [Google Scholar]
- Robichek, A.A.; Myers, S.C. Conceptual problems in the use of risk-adjusted discount rates. J. Financ. 1966, 21, 727–730. [Google Scholar]
- Viscusi, W.K. Rational discounting for regulatory analysis. Univ. Chic. Law Rev. 2007, 74, 209–246. [Google Scholar]
- Gert, A.A.; Suprunchik, N.A.; Nemova, O.G.; Kuzmina, K.N. Valuation of Oil and Gas Fields and Subsoil Plots, 2nd ed.; OOO Geoinformmark: Moscow, Russia, 2010; ISBN 978-5-98877-038-1. [Google Scholar]
- Gert, A.A.; Volkova, K.N.; Nemova, O.G.; Suprunchik, N.A. Methods and Practical Experience of Valuation of Oil and Gas Reserves and Resources; Science: Novosibirsk, Russia, 2007; ISBN 5-02-032557-0. [Google Scholar]
- Tugan, M.F.; Sinayuc, C. A new fully probabilistic methodology and a software for assessing uncertainties and managing risks in shale gas projects at any maturity stage. J. Pet. Sci. Eng. 2018, 168, 107–118. [Google Scholar] [CrossRef]
- Cherepovitsyn, A.; Metkin, D.; Gladilin, A. An algorithm of management decision-making regarding the feasibility of investing in geological studies of forecasted hydrocarbon resources. Resources 2018, 7, 47. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Zhang, Z.X.; Fan, Y. Overseas oil investment projects under uncertainty: How to make informed decisions? J. Policy Model. 2015, 37, 742–762. [Google Scholar] [CrossRef]
- Marinina, O.A. Classification and methods of the accounting of investment risks of oil and gas projects. J. Min. Inst. 2013, 205, 202–207. [Google Scholar]
- Laughton, D.G. The potential for use of modern asset pricing methods for upstream petroleum project evaluation: Introductory remarks. Energy J. 1998, 19, 1–11. [Google Scholar] [CrossRef]
- Bradley, P.G. On the use of modern asset pricing for comparing alternative royalty systems for petroleum development projects. Energy J. 1998, 19, 47–81. [Google Scholar] [CrossRef]
- Laughton, D. The management of flexibility in the upstream petroleum industry. Energy J. 1998, 19, 83–114. [Google Scholar] [CrossRef]
- Baker, M.P.; Scott Mayfield, E.; Parsons, J.E. Alternative models of uncertain commodity prices for use with modern asset pricing methods. Energy J. 1998, 19, 115–148. [Google Scholar] [CrossRef] [Green Version]
- Laughton, D.G.; Sagi, J.S.; Samis, M.R. Modern asset pricing and project evaluation in the energy industry. West. Cent. Econ. Res. 2000, 56, 3–46. [Google Scholar]
- Samis, M.; Davis, G.A.; Laughton, D.; Poulin, R. Valuing uncertain asset cash flows when there are no options: A real options approach. Resour. Policy 2006, 30, 285–298. [Google Scholar] [CrossRef]
- Guj, P.; Garzon, R. Modern Asset Pricing—A Valuable Real Option Complement to Discounted Cash Flow Modeling of Mining Projects. In Proceedings of the Project Valuation Conference, Melbourne, Australia, 19–20 April 2007. [Google Scholar]
- Espinoza, R.D.; Morris, J.W.F. Decoupled NPV: A simple, improved method to value infrastructure investments. Constr. Manag. Econ. 2013, 31, 471–496. [Google Scholar] [CrossRef]
- Espinoza, R.D. Decoupling time value of money and risk: A step toward the integration of risk management and quantification. Int. J. Proj. Manag. 2014, 32, 1056–1072. [Google Scholar] [CrossRef]
- Espinoza, R.D.; Rojo, J. Towards sustainable mining (Part I): Valuing investment opportunities in the mining sector. Resour. Policy 2017, 52, 7–18. [Google Scholar] [CrossRef]
- Pindyck, R. Investments of uncertain cost. J. Financ. Econ. 1993, 34, 53–76. [Google Scholar] [CrossRef] [Green Version]
- Espinoza, R.D. Contingency estimating using option theory: Closing the gap between theory and practice. Constr. Manag. Econ. J. 2011, 29, 913–927. [Google Scholar] [CrossRef]
- Armstrong, M.; Galli, A.; Bailey, W.; Couët, B. Incorporating technical uncertainty in real option valuation of oil projects. J. Pet. Sci. Eng. 2004, 44, 67–82. [Google Scholar] [CrossRef]
- Ponomarenko, T.V.; Sergeev, I.B. Valuation of mineral assets of a mining company on the basis of the option approach. J. Min. Inst. 2011, 191, 164–175. [Google Scholar]
- Galevsky, S.G. A binary model of discounting cash flows to correct risk assessment for real assets evaluation. Tomsk. State Univ. J. Econ. 2020, 49, 122–140. [Google Scholar] [CrossRef] [PubMed]
- Myers, S.C. Determinants of corporate borrowing. J. Financ. Econ. 1977, 5, 147–176. [Google Scholar] [CrossRef] [Green Version]
- Myers, S.C. Finance theory and financial strategy. Interfaces 1984, 14, 126–137. [Google Scholar] [CrossRef]
- Davis, G.A.; Samis, M. Using Real Options to Value and Manage Exploration. In Wealth Creation in the Minerals Industry: Integrating Science, Business, and Education; Doggett, M.D., Parry, J.R., Eds.; Society of Economic Geologists: Easton, MD, USA, 2006; pp. 273–294. [Google Scholar]
- Shafiee, S.; Topal, E.; Nehring, M. Adjusted real option valuation to maximise mining project value—A case study using century mine. Australas. Inst. Min. Metall. Publ. Ser. 2009, 3, 125–134. [Google Scholar]
- Kruk, M.N.; Nikulina, A.Y. Economic estimation of project risks when exploring sea gas and oil deposits in the Russian arctic. Int. J. Econ. Financ. Issues 2016, 6, 138–150. [Google Scholar]
- Damodaran, A. Investment Valuation: Tools and Techniques for Determining the Value of Any Asset, 2nd ed.; Wiley: Oxford, UK, 2002. [Google Scholar]
- Miller, M.H.; Modigliani, F. Dividend Policy, Growth and the Valuation of Shares. J. Bus. 1961, 34, 411–433. [Google Scholar] [CrossRef]
- Arnold, G.; Hatzopoulos, P.D. The theory practice gap in capital budgeting: Evidence from the United Kingdom. J. Bus. Financ. Account. 2000, 27, 603–626. [Google Scholar] [CrossRef]
- Davies, R.; Goedhart, M.; Koller, T. Avoiding a risk premium that unnecessarily kills your project. McKinsey Q. 2012, 2, 1–4. [Google Scholar]
- Gollier, C. Time horizon and the discount rate. J. Econ. Theory 2002, 107, 463–473. [Google Scholar] [CrossRef] [Green Version]
- Laughton, D.G.; Jacoby, H.D. Reversion, Timing Options, and Long-Term Decision-Making. Financ. Manag. 1993, 22, 225–240. [Google Scholar] [CrossRef]
- Schwartz, E.S. The stochastic behavior of commodity prices: Implications for valuation and hedging. J. Financ. 1997, 52, 923–973. [Google Scholar] [CrossRef]
- Jafarizadeh, B.; Bratvold, R.B. Project valuation: Price forecasts bound to discount rates. Decis. Anal. 2021, 18, 139–152. [Google Scholar] [CrossRef]
- Duffie, D.; Malamud, S.; Manso, G. Information percolation in segmented markets. J. Econ. Theory 2015, 158, 838–869. [Google Scholar] [CrossRef]
- Shang, Y.-L. Multi-type directed scale-free percolation. Commun. Theor. Phys. 2012, 57, 701–716. [Google Scholar] [CrossRef]
- Dixit, A.K.; Pindyck, R.S. Investment under Uncertainty; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Golovina, E.; Pasternak, S.; Tsiglianu, P.; Tselischev, N. Sustainable Management of Transboundary Groundwater Resources: Past and Future. Sustainability 2021, 13, 12102. [Google Scholar] [CrossRef]



| Parameter | Value | Note |
|---|---|---|
| 1. Development and production expenses, million RUB | 962.87 | In Year 0 |
| 2. Planning horizon, years | 10 | Starting from Year 1 |
| 3. Annual decrease in production, % | 10 | - |
| 4. Initial production rate, million m3/year | 254.52 | - |
| 5. Fixed operating expenditures, million RUB/year | 119.16 | 0 in Year 0 |
| 6. Variable operating expenditures, RUB/m3 | 0.13 | 0 in Year 0 |
| Parameter | 0 | 1 | 2 | 3 | 4 | … | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Revenue | 1 037.2 | 928.36 | 830.38 | 742.21 | … | 527.15 | 469.30 | 417.23 | 370.37 | |
| Operating expenditures | 152.30 | 148.99 | 146.00 | 143.32 | … | 136.77 | 135.01 | 133.42 | 132.00 | |
| Capital expenditures | 962.87 | … | ||||||||
| Depreciation | 183.39 | 183.39 | 183.39 | 183.39 | … | 22.95 | - | - | - | |
| Taxes | 371.19 | 331.75 | 295.85 | 263.14 | … | 188.15 | 169.33 | 152.40 | 137.16 | |
| Profit | 330.34 | 264.23 | 205.14 | 152.36 | … | 179.28 | 164.96 | 131.41 | 101.21 | |
| Corporate tax | 66.07 | 52.85 | 41.03 | 30.47 | … | 35.86 | 32.99 | 26.28 | 20.24 | |
| Net profit | 264.27 | 211.39 | 164.11 | 121.89 | … | 143.42 | 131.96 | 105.13 | 80.97 | |
| Cash flow | −962.87 | 447.66 | 394.78 | 347.50 | 305.28 | … | 166.38 | 131.96 | 105.13 | 80.97 |
| Discount factor | 1.00 | 0.87 | 0.76 | 0.66 | 0.57 | … | 0.38 | 0.33 | 0.28 | 0.25 |
| Discounted cash flow | −962.87 | 389.27 | 298.51 | 228.49 | 174.55 | … | 62.55 | 43.14 | 29.88 | 20.01 |
| Accumulated discounted cash flow | −962.87 | −573.60 | −275.09 | −46.60 | 127.94 | … | 409.62 | 452.76 | 482.64 | 502.65 |
| T | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DF | 1.00 | 0.89 | 0.81 | 0.75 | 0.71 | 0.66 | 0.62 | 0.59 | 0.55 | 0.52 | 0.49 |
| r, % | - | 12.59 | 10.94 | 9.86 | 9.12 | 8.60 | 8.22 | 7.93 | 7.71 | 7.54 | 7.40 |
| Parameter | 0 | 1 | 2 | 3 | 4 | … | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Revenue | 921.20 | 754.23 | 626.29 | 523.53 | … | 308.96 | 259.03 | 216.92 | 181.39 | |
| Operating expenditures | 143.49 | 132.25 | 122.10 | 112.92 | … | 90.12 | 83.82 | 78.04 | 72.74 | |
| Capital expenditures | 962.87 | … | ||||||||
| Depreciation | 172.78 | 162.79 | 153.37 | 144.50 | … | 15.13 | 0.00 | 0.00 | 0.00 | |
| Taxes | 349.71 | 294.48 | 247.42 | 207.33 | … | 123.98 | 105.13 | 89.14 | 75.59 | |
| Profit | 255.21 | 164.71 | 103.40 | 58.77 | … | 79.74 | 70.08 | 49.74 | 33.07 | |
| Corporate tax | 51.04 | 32.94 | 20.68 | 11.75 | … | 15.95 | 14.02 | 9.95 | 6.61 | |
| Net profit | 204.17 | 131.77 | 82.72 | 47.02 | … | 63.79 | 56.07 | 39.79 | 26.46 | |
| Cash flow | −962.87 | 376.95 | 294.56 | 236.09 | 191.52 | … | 78.91 | 56.07 | 39.79 | 26.46 |
| Discount factor | 1 | 1 | 1 | 1 | 1 | … | 1 | 1 | 1 | 1 |
| Discounted cash flow | −962.87 | 376.95 | 294.56 | 236.09 | 191.52 | … | 78.91 | 56.07 | 39.79 | 26.46 |
| Accumulated discounted cash flow | −962.87 | −585.92 | −291.36 | −55.27 | 136.25 | … | 474.22 | 530.29 | 570.08 | 596.53 |
| Standard DCF | |
|---|---|
| Discount rate, % | 15 |
| NPV, million RUB | 502.65 |
| Reverting and binary discounting | |
| Discount rate,% | 12.87 |
| NPV, million RUB | 596.53 |
| T, Period | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| σ (Equation (14)) | 20.0% | 19.5% | 19.0% | 18.4% | 17.9% | 17.3% | 16.7% | 16.1% | 15.5% | 14.8% | 14.1% |
| Risk component (Equation (A2)), million RUB | - | 51.65 | 44.46 | 38.14 | 32.60 | 27.74 | 23.49 | 19.78 | 16.55 | 13.73 | 11.28 |
| d1 (Equation (A3)) | - | 0.41 | 0.41 | 0.42 | 0.42 | 0.43 | 0.44 | 0.45 | 0.46 | 0.48 | 0.49 |
| d2 (Equation (A4)) | - | 0.21 | 0.22 | 0.23 | 0.25 | 0.26 | 0.27 | 0.29 | 0.31 | 0.33 | 0.35 |
| Parameter | 0 | 1 | 2 | 3 | 4 | … | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Revenue | 1037.2 | 928.36 | 830.38 | 742.21 | … | 527.15 | 469.30 | 417.23 | 370.37 | |
| Revenue minus risk component (Table 6) | 985.57 | 883.90 | 792.24 | 709.61 | … | 507.37 | 452.75 | 403.50 | 359.09 | |
| Discounted risk-free revenue (based on Table 3) | 875.83 | 718.52 | 597.86 | 500.81 | … | 297.53 | 250.02 | 209.88 | 175.96 | |
| Operating expenditures | 143.49 | 132.25 | 122.10 | 112.92 | … | 90.12 | 83.82 | 78.04 | 72.74 | |
| Capital expenditures (factoring in the risk component) | 1070.27 | … | ||||||||
| Depreciation | 172.78 | 162.79 | 153.37 | 144.50 | … | 15.13 | 0.00 | 0.00 | 0.00 | |
| Taxes | 349.71 | 294.48 | 247.42 | 207.33 | … | 123.98 | 105.13 | 89.14 | 75.59 | |
| Profit | 209.84 | 129.00 | 74,97 | 36.06 | … | 68.30 | 61.08 | 42.70 | 27.63 | |
| Net profit | 167.87 | 103.20 | 59,98 | 28.85 | … | 54.64 | 48.86 | 34.16 | 22.10 | |
| Cash flow | −1070.2 | 340.66 | 265.99 | 213,35 | 173.35 | … | 69.76 | 48.86 | 34.16 | 22.10 |
| Discount factor | 1 | 1 | 1 | 1 | 1 | … | 1 | 1 | 1 | 1 |
| Discounted cash flow | −1070.2 | 340.66 | 265.99 | 213,35 | 173.35 | … | 69.76 | 48.86 | 34.16 | 22.10 |
| Accumulated discounted cash flow | −1070.2 | −729.58 | −463.59 | −250,25 | −76.90 | … | 225.85 | 274.72 | 308.88 | 330.99 |
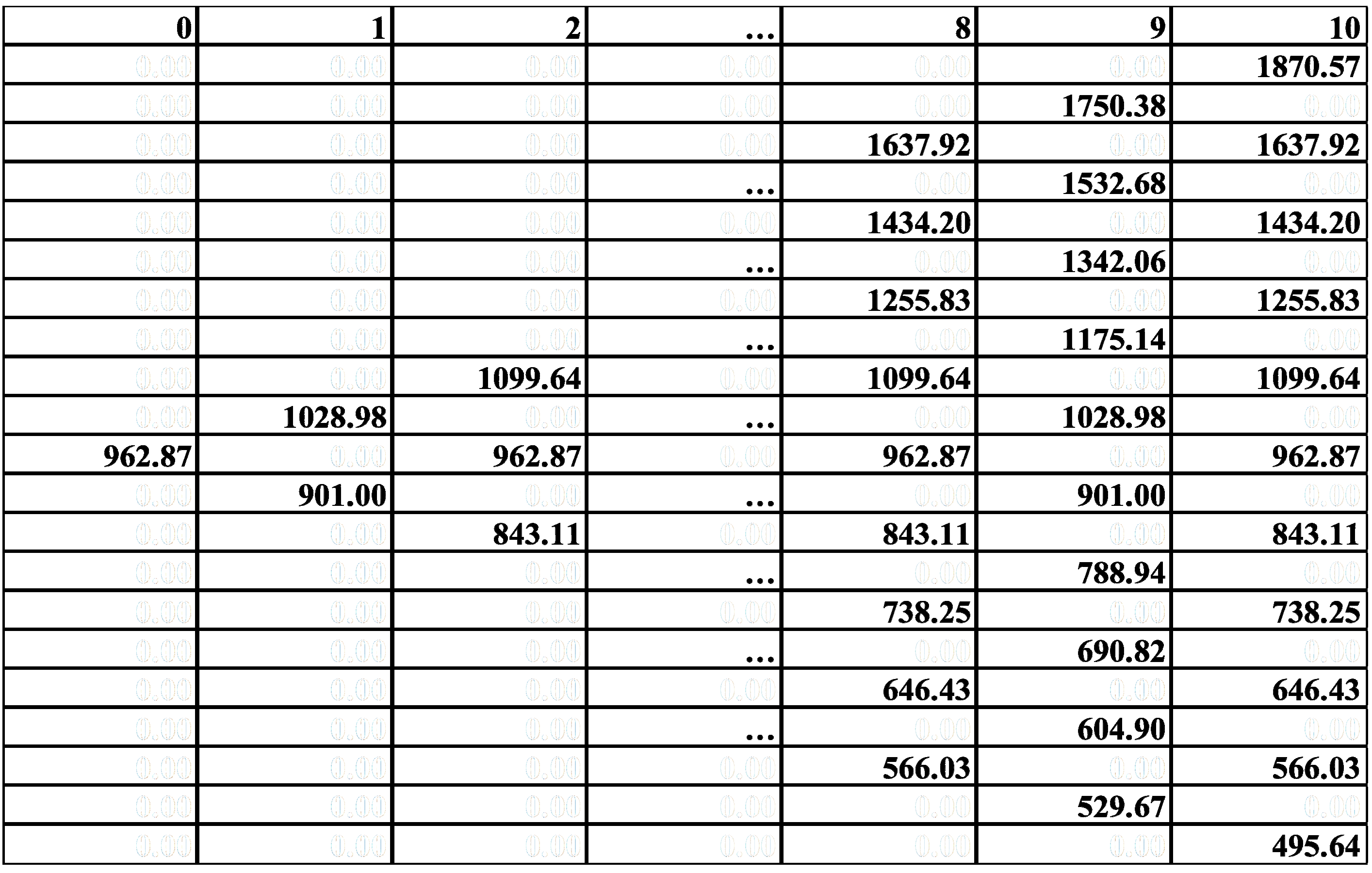
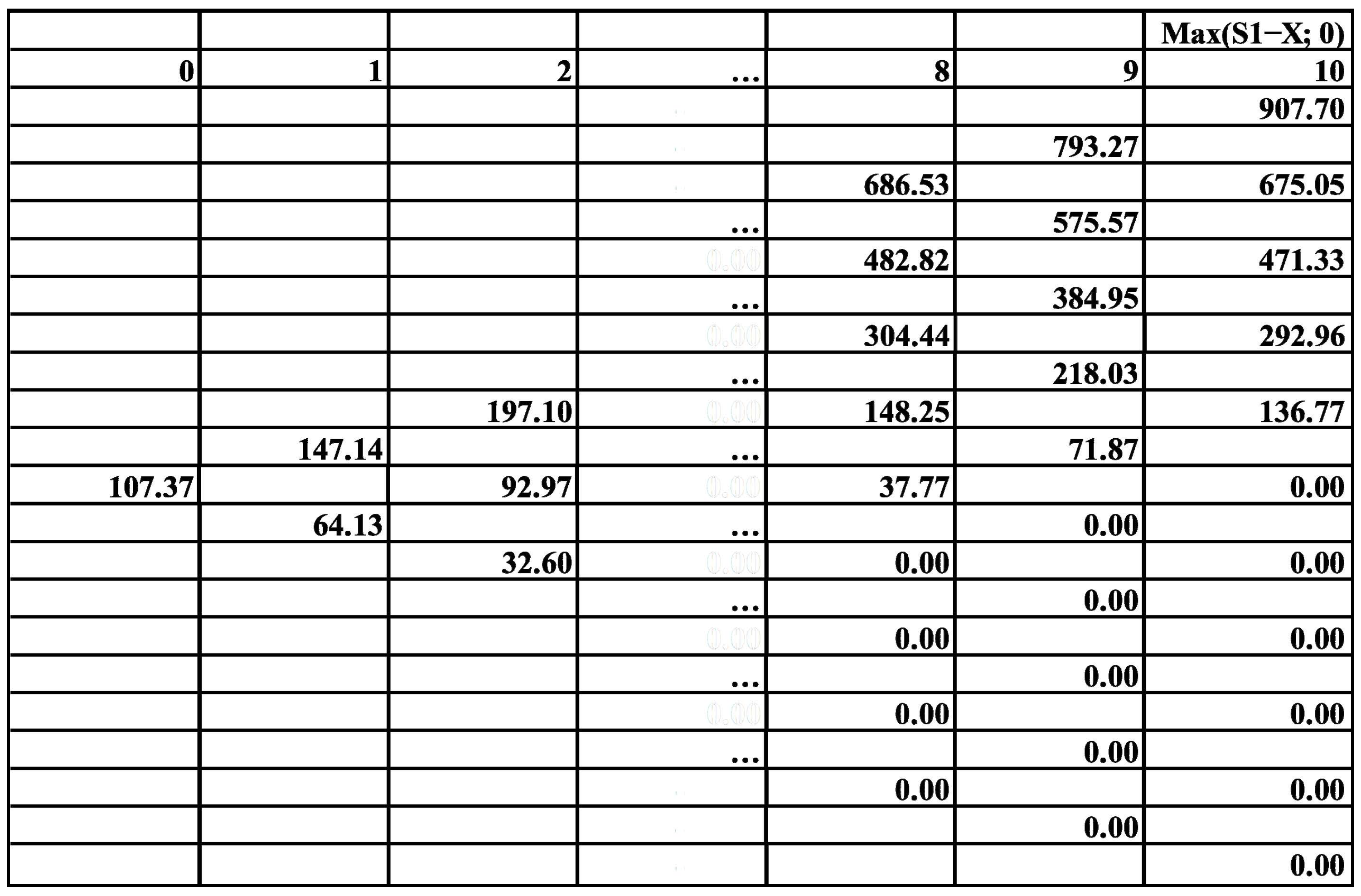
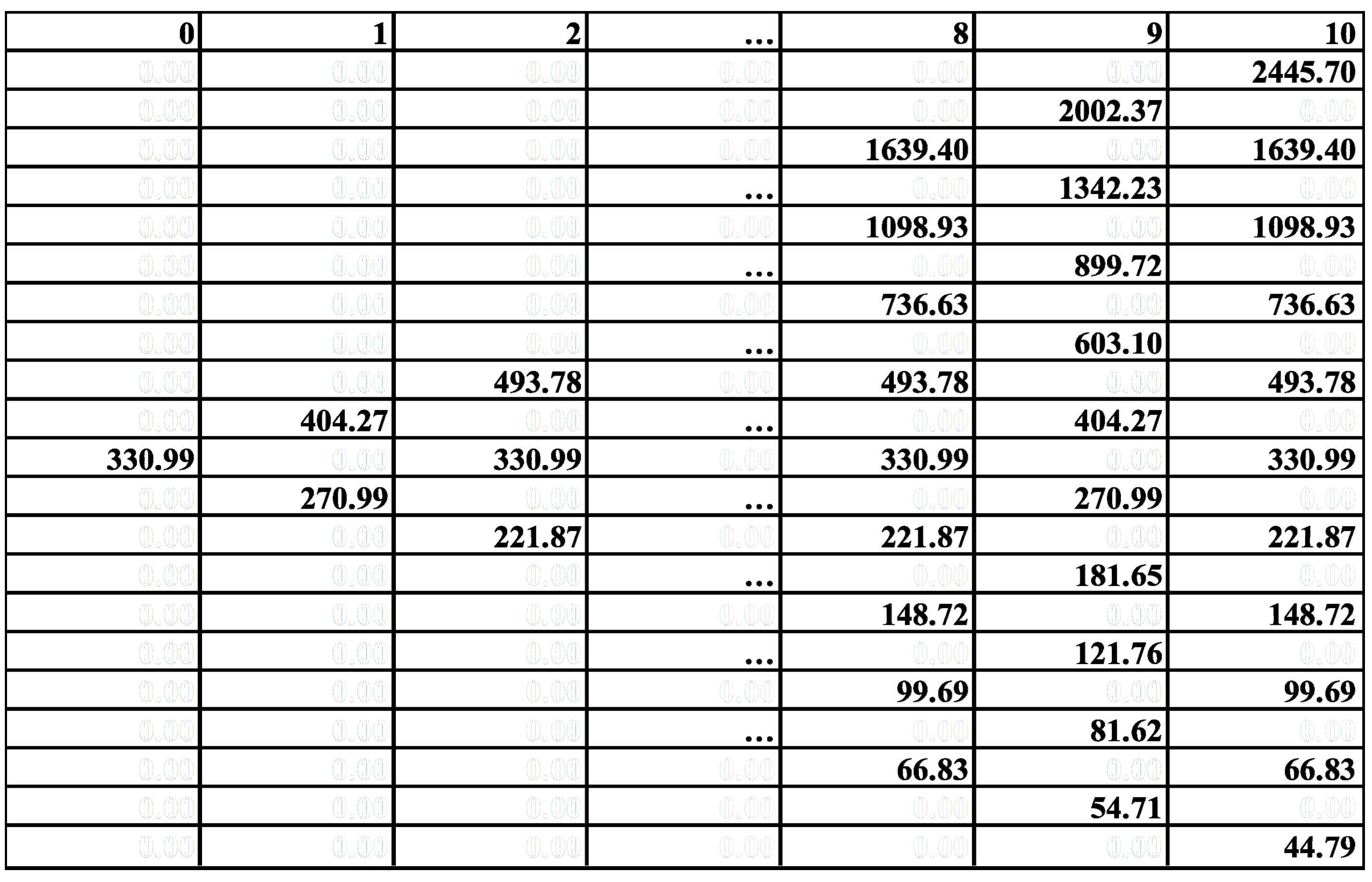
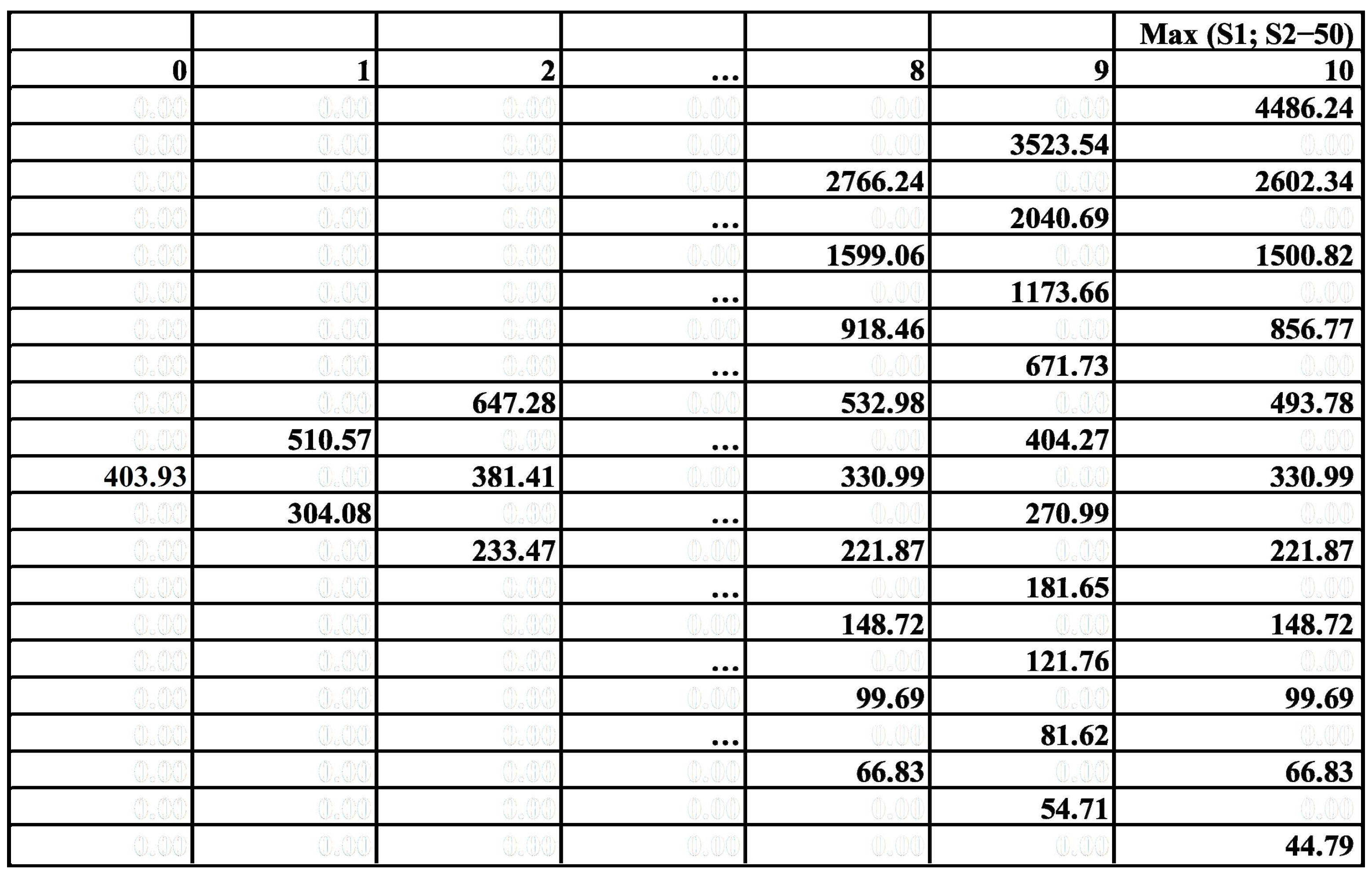
| Parameter | Option 1 | Option 2 |
|---|---|---|
| Volatility, σ | 0.2 | 0.27 |
| ΔT, years | 1 | 1 |
| u | 1.22 | 1.31 |
| d | 0.818 | 0.765 |
| rf | 6.14% | 6.14% |
| X, million RUB | - | 50 (costs associated with the engineering solution) |
| NPV, million RUB | 330.99 | 310 (without factoring in 50 m for drilling) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ponomarenko, T.; Marin, E.; Galevskiy, S. Economic Evaluation of Oil and Gas Projects: Justification of Engineering Solutions in the Implementation of Field Development Projects. Energies 2022, 15, 3103. https://doi.org/10.3390/en15093103
Ponomarenko T, Marin E, Galevskiy S. Economic Evaluation of Oil and Gas Projects: Justification of Engineering Solutions in the Implementation of Field Development Projects. Energies. 2022; 15(9):3103. https://doi.org/10.3390/en15093103
Chicago/Turabian StylePonomarenko, Tatiana, Eugene Marin, and Sergey Galevskiy. 2022. "Economic Evaluation of Oil and Gas Projects: Justification of Engineering Solutions in the Implementation of Field Development Projects" Energies 15, no. 9: 3103. https://doi.org/10.3390/en15093103
APA StylePonomarenko, T., Marin, E., & Galevskiy, S. (2022). Economic Evaluation of Oil and Gas Projects: Justification of Engineering Solutions in the Implementation of Field Development Projects. Energies, 15(9), 3103. https://doi.org/10.3390/en15093103






