Modelling of the Electrically Excited Synchronous Machine with the Rotary Transformer Design Influence †
Abstract
:1. Introduction
2. Methods
2.1. The EESM Model with Vector Control System
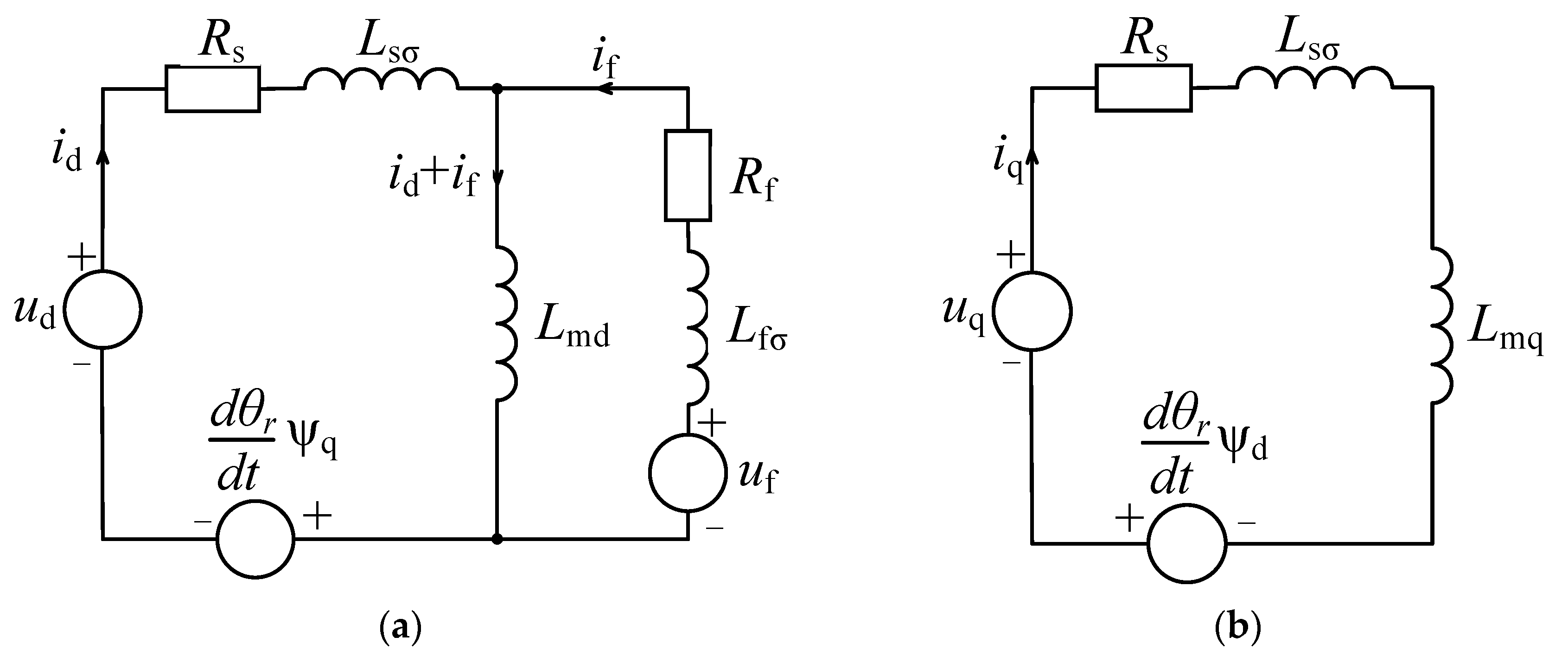
2.1.1. Modeling of the EESM
2.1.2. Calculation of the Field Excitation Current
2.1.3. Transformation Block
2.1.4. Motor Voltage/Current Models
2.2. Selection of the EESM for Modeling and Analysis
Parameters of the Real EESM Used for Modeling
2.3. The Wireless Power Transfer System Applied for the EESM Excitation
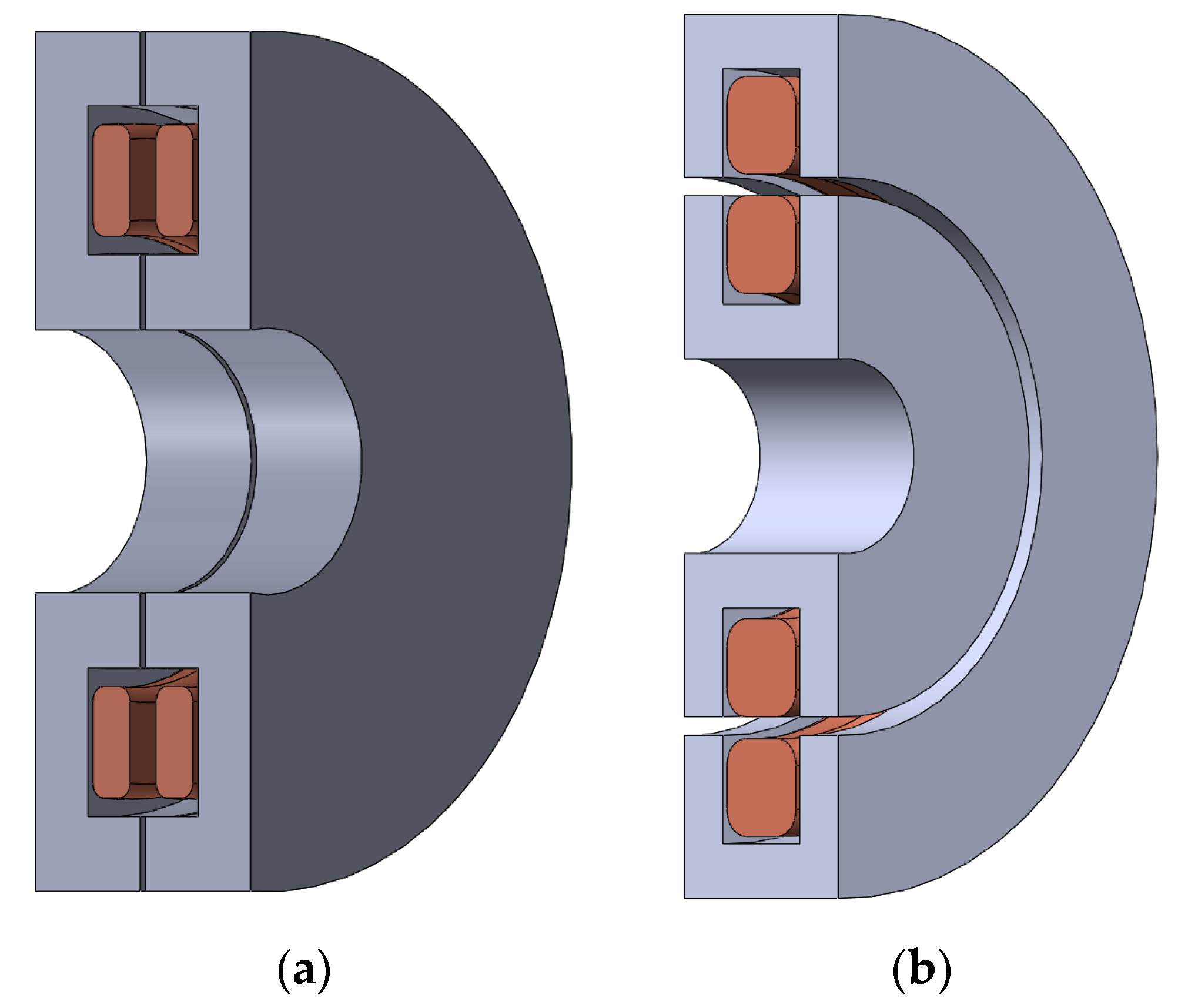
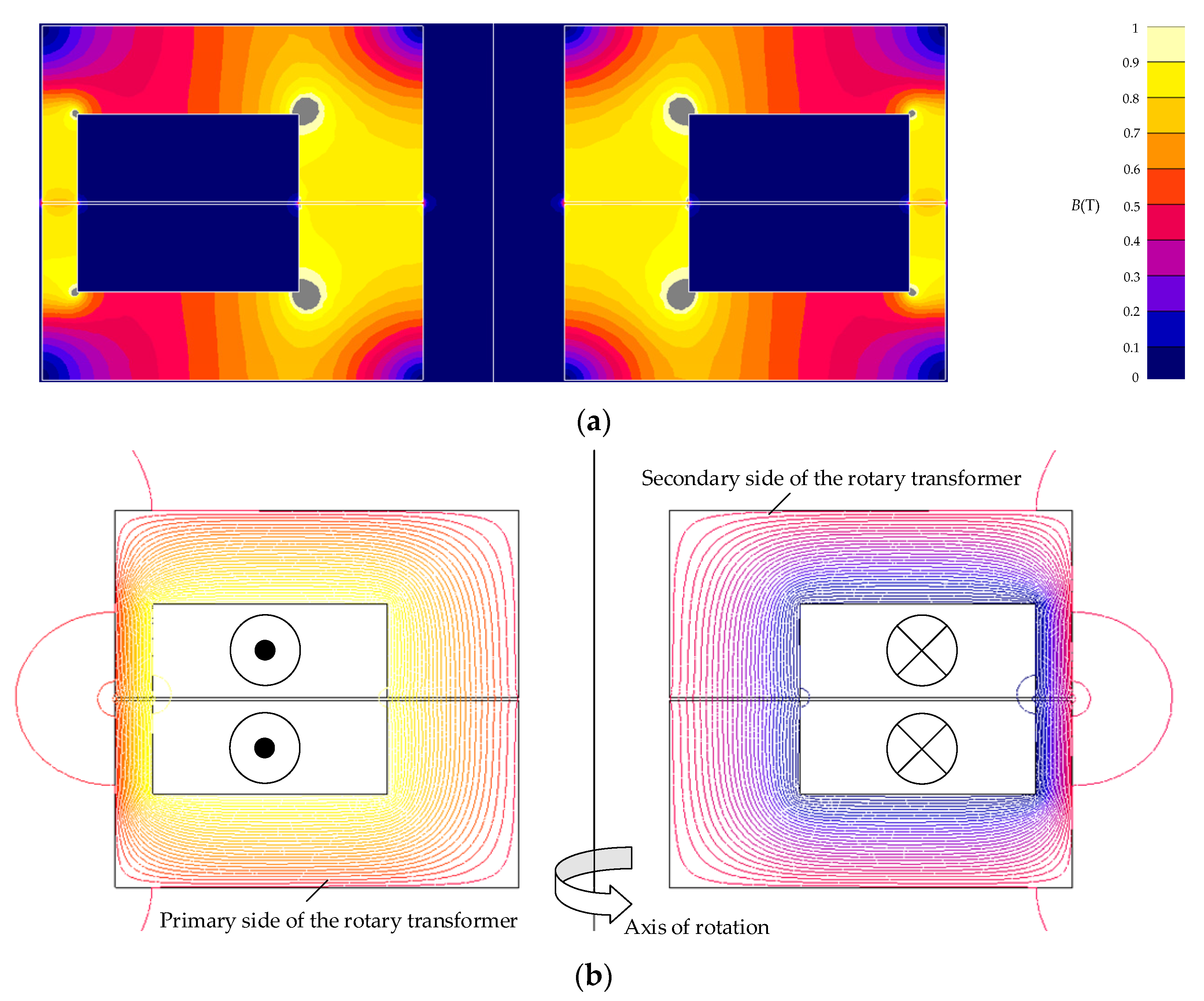
2.3.1. The Geometries of Wireless Power Transfer Systems Applied for EESM Excitation
2.3.2. Analytical Approach for Modeling of Rotary Transformers
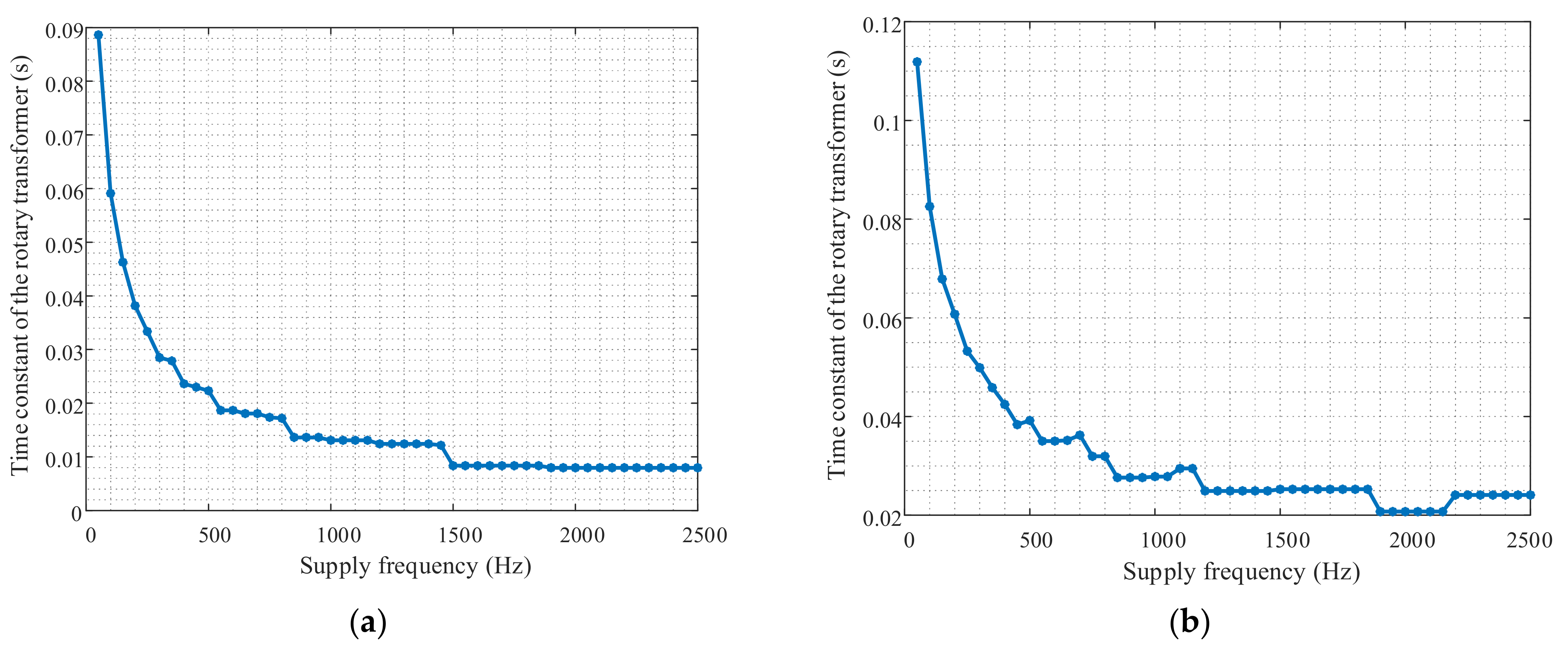
2.3.3. The Time Constant Determination of the Axial and Radial Rotary Transformers
2.4. Estimation of the Change in Dynamic Performance of the EESM Control System Due to the Wireless Power Transfer Excitation
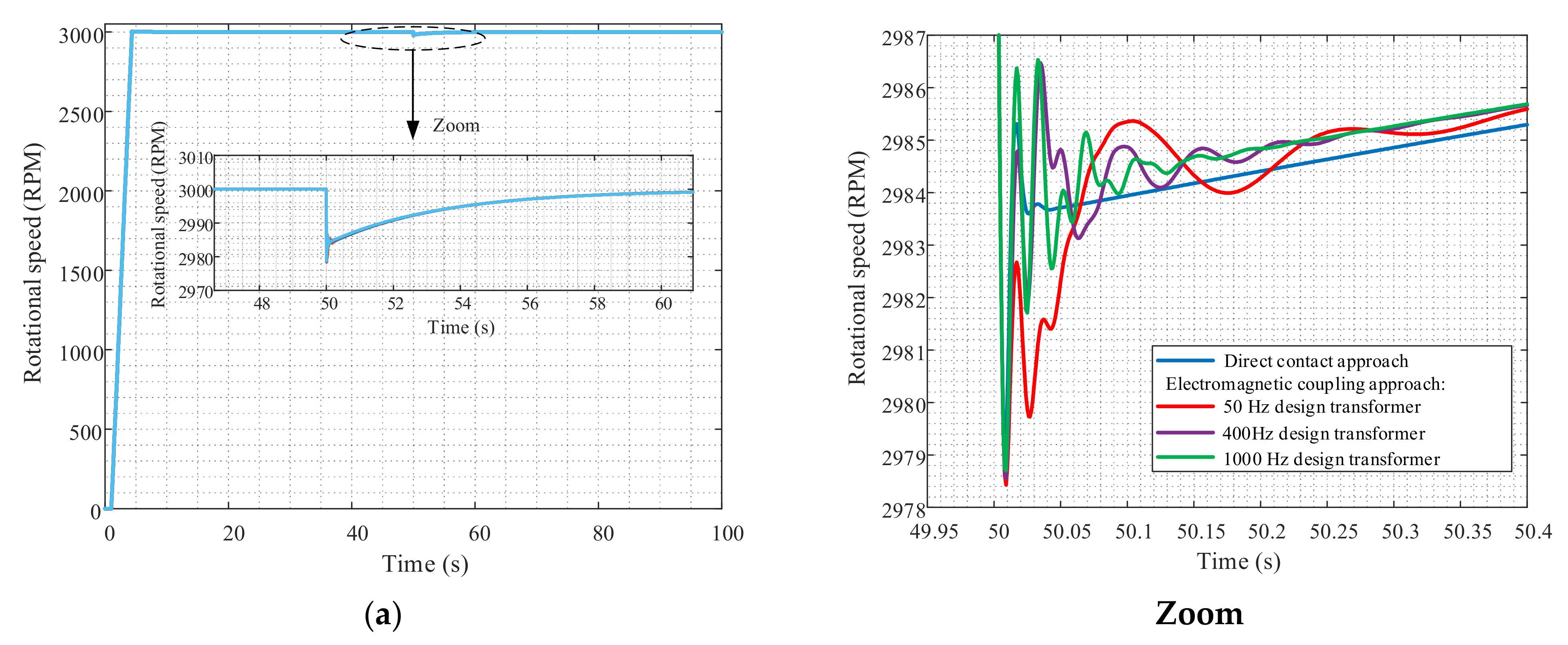
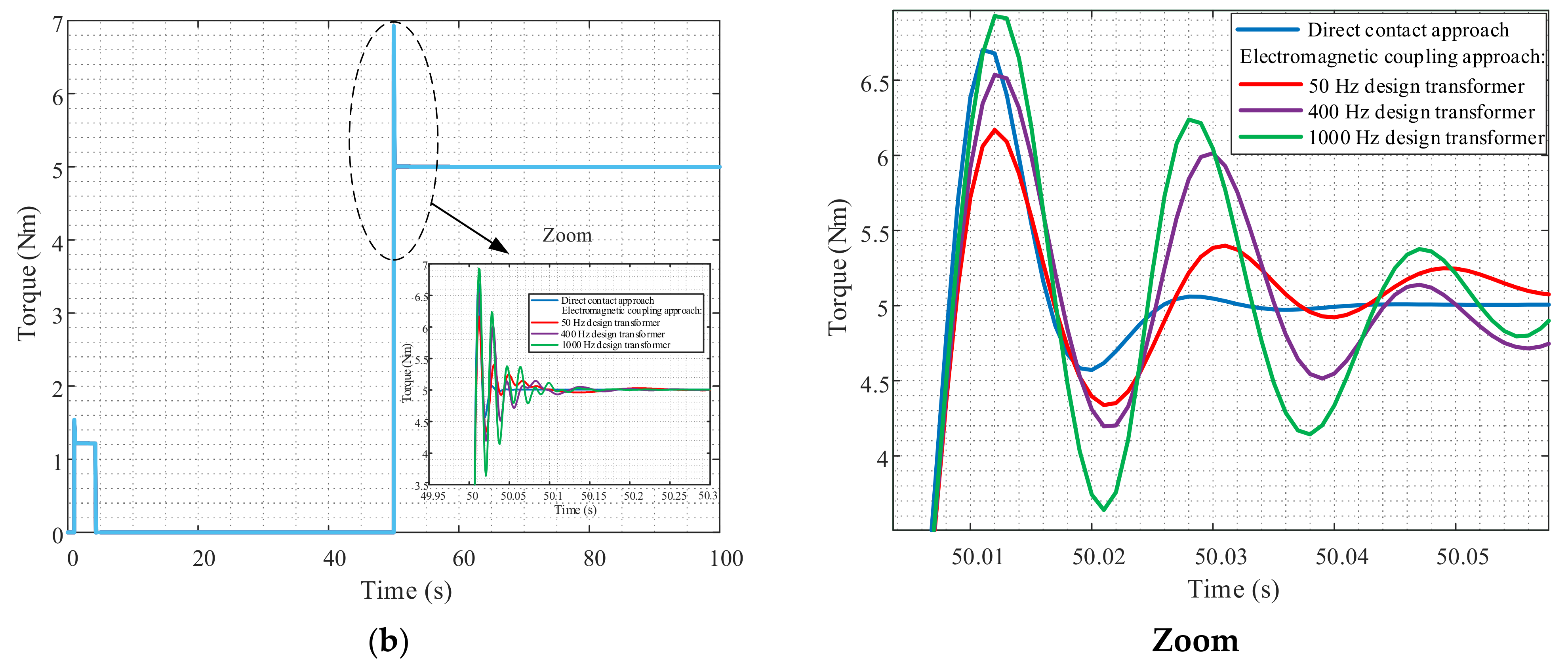
The Method Used for Comparison of the Dynamic Performances between Direct and Electromagnetic Coupling Approaches
3. Results and Discussion
3.1. Results of the Axial and Radial Rotary Transformer Modeling
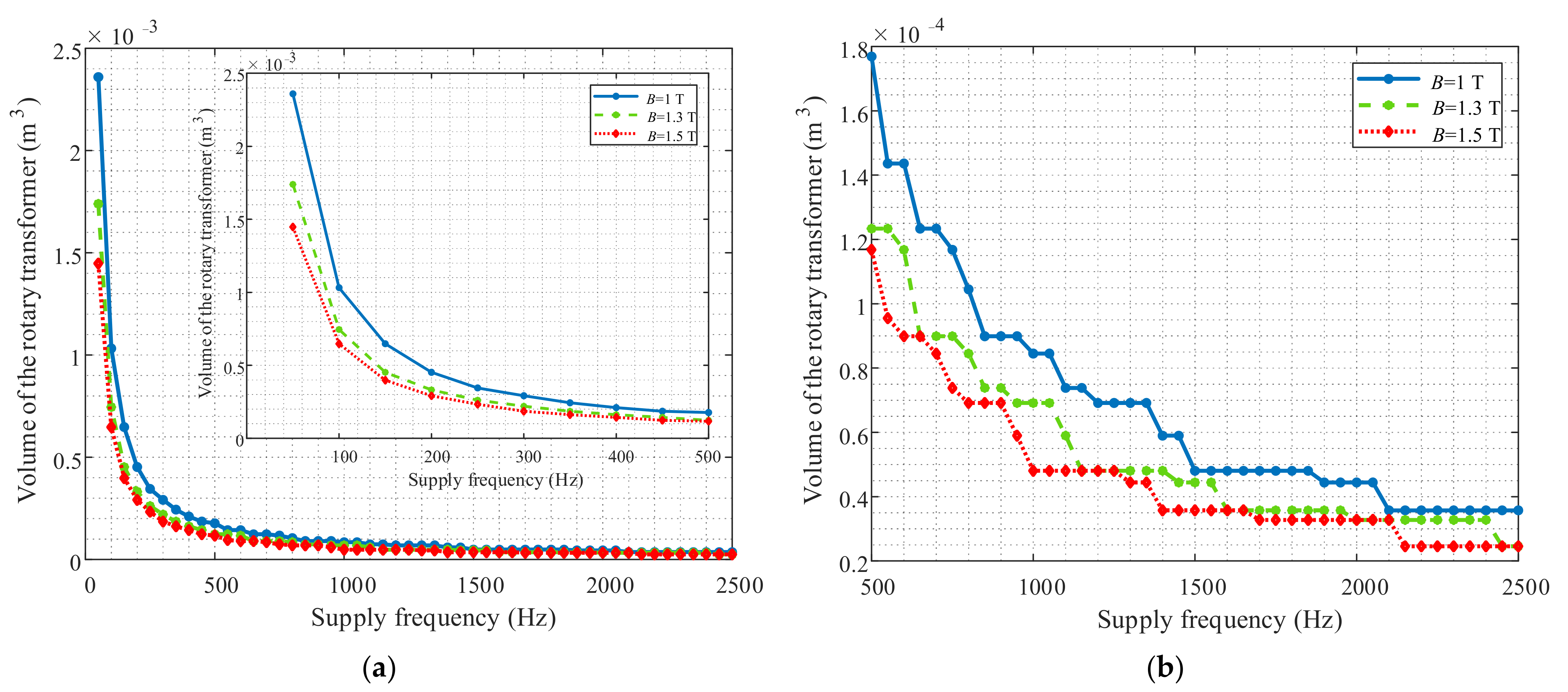
3.1.1. Design Methodology of the Axial and Radial Rotary Transformers with Different Supply Frequencies
3.1.2. The Comparison of the Analytical Models with Numerical Modeling of the Axial and Radial Rotary Transformers Topologies
3.2. Modeling Results of the EESM Control System with Rotary Transformer (i.e., WPT) and Comparison to the Conventional Excitation (i.e., Sliding Contacts)
4. Conclusions
- -
- The axial topology of the rotary transformer outperforms the radial type, since the minimum size with the best magnetic properties can be obtained with the axial topology of the rotary transformer for the same supply frequency. Namely, our results show that the best design in terms of size, time constant and inductance values can be obtained with the axial rotary transformer topology at the supply frequency of 400 Hz. In addition, the rotary transformer supplied with 400 Hz enables the usage of the classic H-bridge inverter which is an important advantage in terms of cost-effectiveness of the WPT system, while at higher frequencies (e.g., 1000 Hz), a special and more expensive high frequency inverter is required.
- -
- The comparison of the analytical and numerical results in 12% difference for both topologies (axial and radial). Thus, the developed analytical tool can be used as an efficient alternative for time-consuming numerical simulations.
- -
- The usage of the rotary transformer instead of direct contact degrades the dynamic performance of the EESM by less than 5.38% in the case of 400 Hz design of the rotary transformer. Further improvement of the dynamic response of the EESM with rotary transformer can be achieved with the proper adjustment of the PI controllers’ gains of the control system. The future work towards improvement of the EESM dynamic response can also include the advanced optimization procedure for tuning the PI gains of the model controllers including the automatic recalculation of the geometry of the rotary transformer based on the rotary transformers’ time constant as an optimization goal. These results may have an important contribution in the field of the development of the power electronics required for the excitation circuits of the EESM.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Value (SI) | Value (pu) | |
|---|---|---|---|
| Apparent power | S | 5500 VA | 1.0011 |
| Nominal active power | Pn | 4400 W | - |
| Nominal voltage | Un | 400 V | 1.2247 |
| Nominal current | In | 7.93 A | 0.7071 |
| Nominal field current | If_no_load Ifn | 1.11 A 4.11 A | 0.0711 0.2639 |
| Nominal field voltage | Ufn | 44 V | 0.124 |
| Stator winding resistance | Rs | 1.5 Ω | 0.0515 |
| Field winding resistance without resistance of brushes | Rf | 7.25 Ω | 0.3378 |
| Field winding time constant | τf | 206.8 ms | - |
| Nominal frequency | f | 50 Hz | - |
| Number of pole pairs | p | 1 | - |
| Moment of inertia | J | 0.0129 kgm2 | - |
| Power factor | cosφ | 0.8 | - |
| Nominal speed | n | 3000 RPM | - |
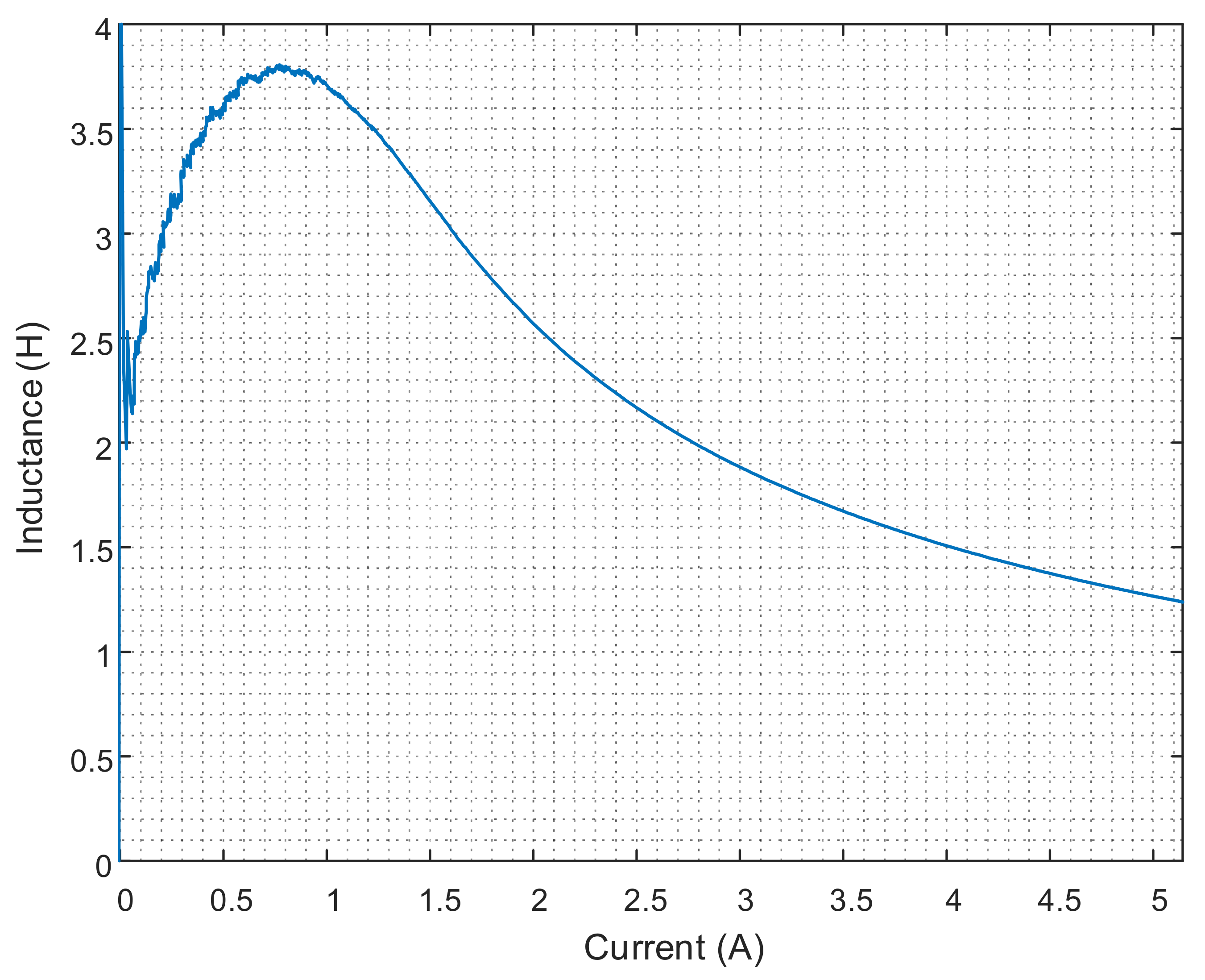
Appendix B
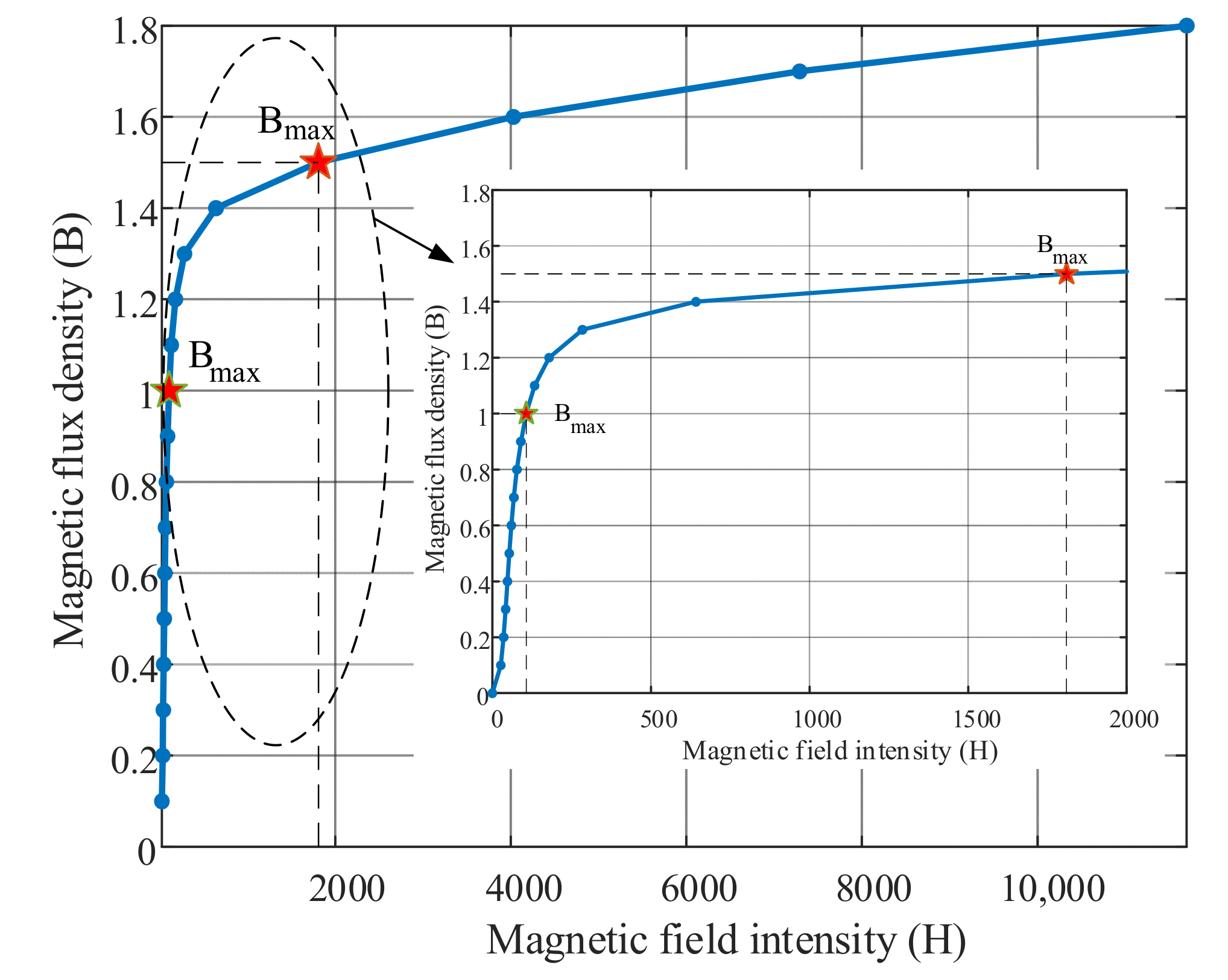
Appendix C
- Direct excitation of the rotor winding via slip rings/brushes. In this case, the supplied AC voltage from the grid via variable transformer have been rectified with the diode rectifier and fed into the rotor windings.
- Indirect excitation of the rotor winding via transformer (with the following parameters obtained from the short circuit test: short circuit resistance Rk = 0.8 Ω and short circuit reactance Xk = 0.5 Ω). In this case, the supplied AC voltage from the grid via variable transformer have been supplied to the primary winding of the conventional transformer. The voltage from the secondary transformer was rectified with the diode rectifier and fed into the rotor windings via slip rings/brushes.


References
- EU European Commission. EU Climate Action and the European Green Deal. Available online: https://ec.europa.eu/clima/policies/eu-climate-action_en (accessed on 11 October 2021).
- EEA Database on Climate Change Mitigation Policies and Measures in Europe. Available online: http://pam.apps.eea.europa.eu (accessed on 11 October 2021).
- Amann, M.; Borken-Kleefeld, J.; Cofala, J.; Hettelingh, J.-P.; Heyes, C.; Hoglund, L.; Holland, M.; Kiesewetter, G.; Klimont, Z.; Rafaj, P.; et al. The final policy scenarios of the EU Clean Air Policy Package; TSAP Report #11; International Institute for Applied Systems Analysis (IIASA): Laxenburg, Austria, 2014. [Google Scholar]
- Standard IEC 60349-2; Electric Traction—Rotating Electrical Machines for Rail and Road Vehicles—Part 2: Electronic Converter-fed Alternating Current Motors. IEC: London, UK, 2010.
- Wang, Z.; Ching, T.W.; Huang, S.; Wang, H.; Xu, T. Challenges Faced by Electric Vehicle Motors and Their Solutions. IEEE Access 2021, 9, 5228–5249. [Google Scholar] [CrossRef]
- Karki, A.; Phuyal, S.; Tuladhar, D.; Basnet, S.; Shrestha, B.P. Status of pure electric vehicle power train technology and future prospects. Appl. Syst. Innov. 2020, 3, 35. [Google Scholar] [CrossRef]
- Staton, D.A.; Goss, J. Open source electric motor models for commercial EV & Hybrid traction motors. Presented at Coil Winding, Insulation & Electrical Manufacturing Exhibition (CWIEME), Berlin, Germany, 20–22 June 2017. [Google Scholar]
- Popescu, M.; Goss, J.; Staton, D.A.; Hawkins, D.; Chong, Y.C.; Boglietti, A. Electrical Vehicles—Practical Solutions for Power Traction Motor Systems. IEEE Trans. Ind. Appl. 2018, 54, 2751–2762. [Google Scholar] [CrossRef] [Green Version]
- Krings, A.; Monissen, C. Review and Trends in Electric Traction Motors for Battery Electric and Hybrid Vehicles. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; pp. 1807–1813. [Google Scholar]
- Čorović, S.; Miljavec, D. Modal Analysis and Rotor-Dynamics of an Interior Permanent Magnet Synchronous Motor: An Experimental and Theoretical Study. J. Appl. Sci. 2020, 10, 5881. [Google Scholar] [CrossRef]
- Maga, D.; Zagirnyak, M.; Miljavec, D. Additional losses in permanent magnet brushless machines. In Proceedings of the EPE-PEMC 2010—14th International Power Electronics and Motion Control Conference, Ohrid, Macedonia, 6–8 September 2010; pp. S412–S413. [Google Scholar] [CrossRef]
- Illiano, E.M. Design of a Highly Efficient Brushless Current Excited Synchronous Motor for Automotive Purposes. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2014. [Google Scholar]
- Di Gioia, A.; Brown, I.P.; Nie, Y.; Knippel, R.; Ludois, D.C.; Dai, J.; Hagen, S.; Alteheld, C. Design and Demonstration of a Wound Field Synchronous Machine for Electric Vehicle Traction with Brushless Capacitive Field Excitation. IEEE Trans. Ind. Appl. 2018, 54, 1390–1403. [Google Scholar] [CrossRef]
- Tang, J.; Liu, Y.; Sharma, N. Modeling and Experimental Verification of High-Frequency Inductive Brushless Exciter for Electrically Excited Synchronous Machines. IEEE Trans. Ind. Appl. 2019, 55, 4613–4623. [Google Scholar] [CrossRef]
- Paszek, S.; Boboń, A.; Berhausen, S.; Majka, Ł.; Nocoń, A.; Pruski, P. Synchronous Generators and Excitation Systems Operating in a Power System; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Ruuskanen, V.; Niemelä, M.; Pyrhönen, J.; Kanerva, S.; Kaukonen, J. Modelling the brushless excitation system for a synchronous machine. IET Electr. Power Appl. 2009, 3, 231–239. [Google Scholar] [CrossRef]
- Manko, R.; Čorović, S.; Miljavec, D. Analysis and Design of Rotary Transformer for Wireless Power Transmission. In Proceedings of the 2020 IEEE Problems of Automated Electrodrive. Theory and Practice (PAEP), Kremenchuk, Ukraine, 21–25 September 2020; pp. 1–6. [Google Scholar]
- Pyrhonen, J.; Hrabovcova, V.; Scott Semken, R. Electrical Machine Drives Control: An Introduction; John Wiley & Sons: Chichester, UK, 2016; p. 504. [Google Scholar]
- Zhang, Y.; Yang, J.; Jiang, D.; Li, D.; Qu, R. Design, manufacture, and Test of a Rotary Transformer for Contactless Power Transfer System. IEEE Trans. Magn. 2022, 58, 8400206. [Google Scholar] [CrossRef]
- Toscani, N.; Brunetti, M.; Carmeli, M.S.; Castelli Dezza, F.; Mauri, M. Design of a Rotary Transformer for Installations on Large Shafts. J. Appl. Sci. 2022, 12, 2932. [Google Scholar] [CrossRef]
- Bastiaens, K.; Krop, D.C.; Jumayev, S.; Lomonova, E. A Optimal design and comparison of high-frequency resonant and non-resonant rotary transformers. Energies 2020, 13, 929. [Google Scholar] [CrossRef] [Green Version]
- Littau, A.; Wagner, B.; Köhler, S.; Dietz, A.; Weber, S. Design of Inductive Power Transmission into the Rotor of an Externally Excited Synchronous Machine. In Proceedings of the Conference on Future Automotive Technology (CoFAT), Munich, Germany, 17–18 March 2014. [Google Scholar]
- Perrottet, M. Transmission Électromagnétique Rotative D’énergie et D’information Sans Contact. Ph.D. Thesis, EPLF, Lausanne, Switzerland, January 2000. [Google Scholar]
- Datasheet of Cogent M250-35A Material. Available online: https://www.tatasteeleurope.com/sites/default/files/m250-35a.pdf (accessed on 10 December 2021).
- Voldek, A.I. Electricheskie Mashiny, 2nd ed.; Energiya: Sankt-Peterburg, Russia, 1974; p. 350. [Google Scholar]
- Datasheet on Three-Phase Synchronous Generator Mecc Alte ET16F-130/A. Available online: https://www.meccalte.com/downloads/ET16F.pdf (accessed on 10 December 2021).


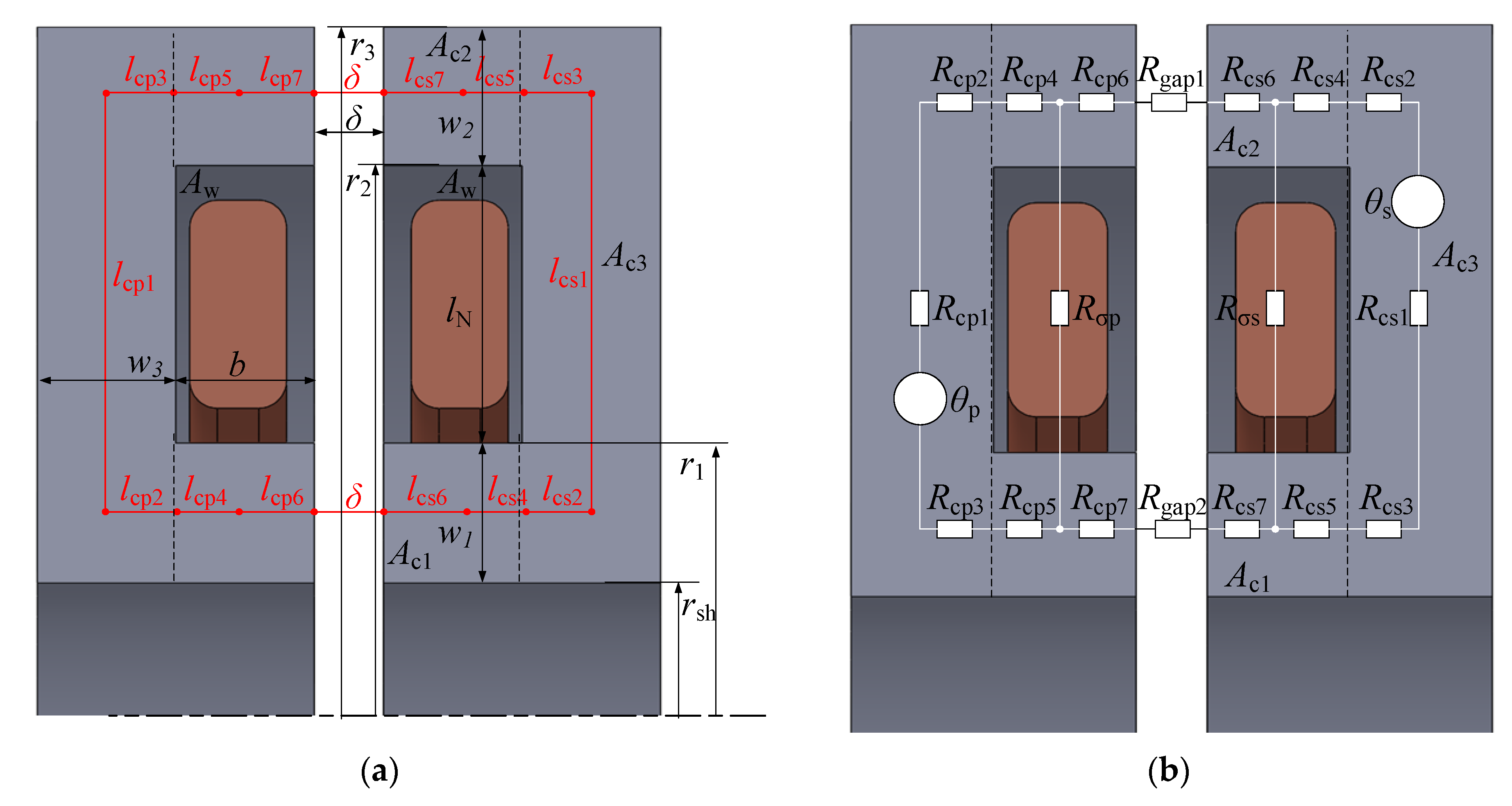
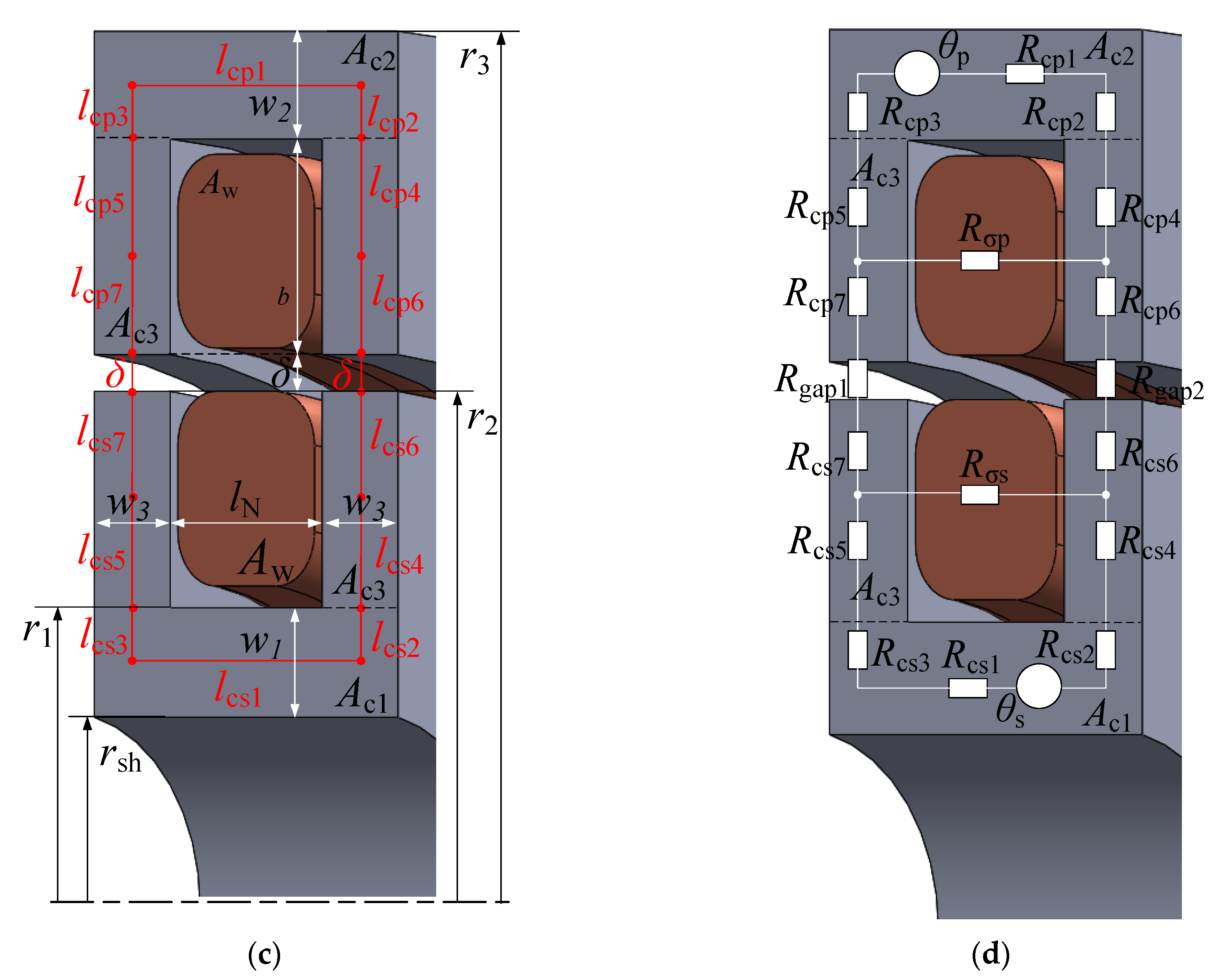
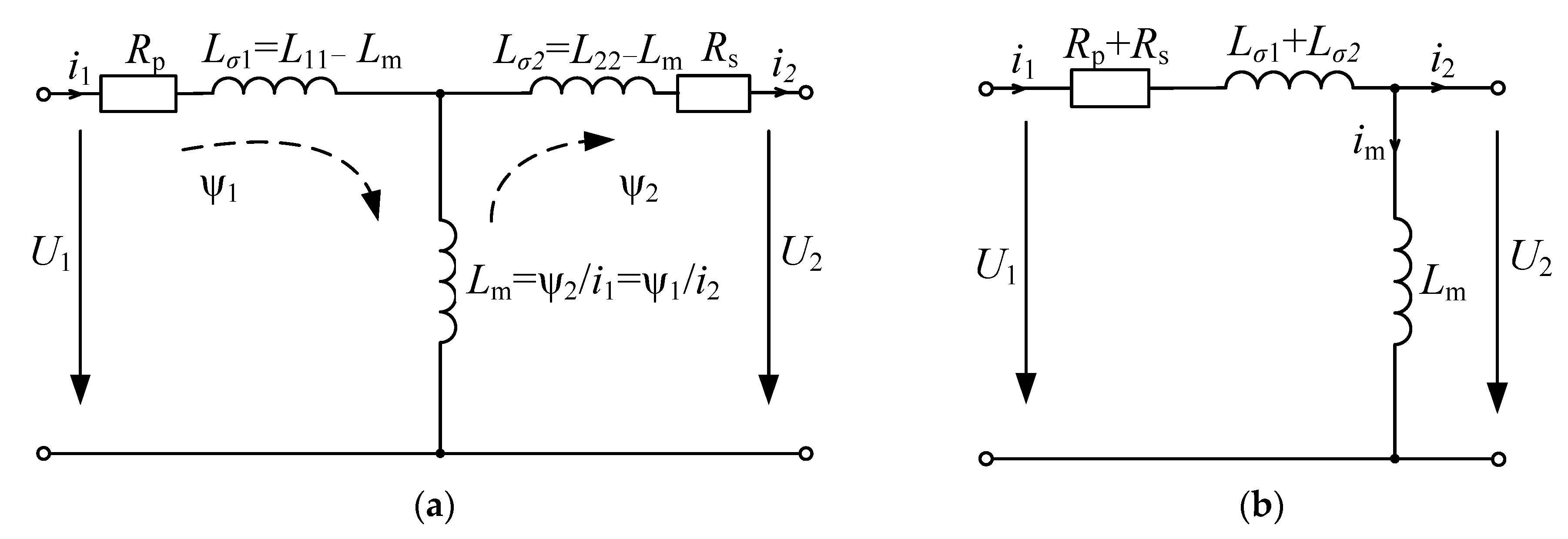

| Parameters | Axial Rotary Transformer Topology | Radial Rotary Transformer Topology |
|---|---|---|
| Outer radius of the core (primary/secondary side) | ||
| Outer radius of the winding window | ||
| Inner radius of the winding window | ||
| Shaft radius | ||
| Height of the winding window | b | |
| Width of the winding window | b | |
| Width of the first main cross-section | ||
| Width of the second main cross-section | ||
| Width of the auxiliary cross-section | ||
| Air gap width | ||
| Winding window cross-section area | ||
| First main cross-section area of the ferromagnetic core | ||
| Second main cross-section area of the ferromagnetic core | ||
| Auxiliary cross-section area of the ferromagnetic core | ||
| Core material | Cogent M250-35A | Cogent M250-35A |
| Parameters | Axial Rotary Transformer Topology | Radial Rotary Transformer Topology | ||||
|---|---|---|---|---|---|---|
| Supply frequency | 50 Hz | 400 Hz | 1000 Hz | 50 Hz | 400 Hz | 1000 Hz |
| 103 mm | 51 mm | 42 mm | 99 mm | 47 mm | 38 mm | |
| 84 mm | 47 mm | 40 mm | 69 mm | 32 mm | 25 mm | |
| 59 mm | 22 mm | 15 mm | 59 mm | 22 mm | 15 mm | |
| 8 mm | 8 mm | 8 mm | 8 mm | 8 mm | 8 mm | |
| 25 mm | 25 mm | 25 mm | 25 mm | 25 mm | 25 mm | |
| 10 mm | 10 mm | 10 mm | 10 mm | 10 mm | 10 mm | |
| 51 mm | 14 mm | 7 mm | 51 mm | 14 mm | 7 mm | |
| 19 mm | 4 mm | 2 mm | 19.7 mm | 4.7 mm | 2.7 mm | |
| 29 mm | 10 mm | 6 mm | 29 mm | 10 mm | 6 mm | |
| δ | 0.3 mm | 0.3 mm | 0.3 mm | 0.3 mm | 0.3 mm | 0.3 mm |
| Total volume | 2.4 × 10−3 m3 | 2.1 × 10−4 m3 | 0.845 × 10−4 m3 | 2.4 × 10−3 m3 | 2.59 × 10−4 m3 | 1.28 × 10−4 m3 |
| Turns (primary/secondary) | 33/33 | 33/33 | 33/33 | 33/33 | 33/33 | 33/33 |
| Winding DC resistance (primary/secondary) | 0.1361 Ω/0.1361 Ω | 0.0657 Ω/0.0657 Ω | 0.0524 Ω/0.0524 Ω | 0.1414 Ω/0.1218 Ω | 0.071 Ω/0.0514 Ω | 0.0577 Ω/0.0381 Ω |
| Parameters | Analytical Calculation | Numerical Calculation | Analytical Calculation | Numerical Calculation | Analytical Calculation | Numerical Calculation |
|---|---|---|---|---|---|---|
| Axial rotary transformer topology | ||||||
| 50 Hz | 400 Hz | 1000 Hz | ||||
| 24.3 mH | 25.5 mH | 3.1 mH | 3.31 mH | 1.3 mH | 1.46 mH | |
| 85.66 μH | 85.28 μH | 41.33 μH | 40.56 μH | 32.94 μH | 31.94 μH | |
| 85.66 μH | 85.28 μH | 41.33 μH | 40.56 μH | 32.94 μH | 31.94 μH | |
| 171.32 μH | 170.56 μH | 82.66 μH | 81.12 μH | 65.88 μH | 63.88 μH | |
| τ | 89.9 ms | 94.3 ms | 23.9 ms | 25.8 ms | 13.3 ms | 14.54 ms |
| Radial rotary transformer topology | ||||||
| 29.3 mH | 29.15 mH | 5.1 mH | 4.8 mH | 2.6 mH | 1.89 mH | |
| 89.01 μH | 86.08 μH | 44.69 μH | 41.71 μH | 36.3 μH | 40.57 μH | |
| 76.67 μH | 79.4 μH | 32.35 μH | 34.87 μH | 23.96 μH | 15.19 μH | |
| 165.68 μH | 165.48 μH | 77.04 μH | 76.58 μH | 60.26 μH | 55.76 μH | |
| τ | 111.9 ms | 111.4 ms | 42.4 ms | 39.84 ms | 27.8 ms | 20.31 ms |
| Supply Frequency of the Rotary Transformer | Rotary Transformer’s Parameters | |
|---|---|---|
| Axial rotary transformer | Time constant value (τ) | RMSE (Δ) |
| 50 Hz | 89.9 ms | 7.86% |
| 400 Hz | 23.9 ms | 5.38% |
| 1000 Hz | 13.3 ms | 6.06% |
| Radial rotary transformer | Time constant value (τ) | RMSE (Δ) |
| 50 Hz | 111.9 ms | 8.76% |
| 400 Hz | 42.4 ms | 6.16% |
| 1000 Hz | 27.8 ms | 6.43% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manko, R.; Vukotić, M.; Makuc, D.; Vončina, D.; Miljavec, D.; Čorović, S. Modelling of the Electrically Excited Synchronous Machine with the Rotary Transformer Design Influence. Energies 2022, 15, 2832. https://doi.org/10.3390/en15082832
Manko R, Vukotić M, Makuc D, Vončina D, Miljavec D, Čorović S. Modelling of the Electrically Excited Synchronous Machine with the Rotary Transformer Design Influence. Energies. 2022; 15(8):2832. https://doi.org/10.3390/en15082832
Chicago/Turabian StyleManko, Roman, Mario Vukotić, Danilo Makuc, Danijel Vončina, Damijan Miljavec, and Selma Čorović. 2022. "Modelling of the Electrically Excited Synchronous Machine with the Rotary Transformer Design Influence" Energies 15, no. 8: 2832. https://doi.org/10.3390/en15082832
APA StyleManko, R., Vukotić, M., Makuc, D., Vončina, D., Miljavec, D., & Čorović, S. (2022). Modelling of the Electrically Excited Synchronous Machine with the Rotary Transformer Design Influence. Energies, 15(8), 2832. https://doi.org/10.3390/en15082832






