1. Introduction
Global warming due to the use of fossil fuels, the main energy source of mankind, has become a major issue in the environment around the world, threatening human life and the earth. Efforts to reduce this adverse environmental impact are required to increase the demand for renewables and promote more efficient energy use [
1,
2,
3]. Lithium-ion batteries (LIBs) are taking an important position in regards to storing and using them as needed in various industrial fields and living areas, from traditional portable devices to the energy storage system (ESS) and electrical vehicles [
4]. In particular, as the electric vehicle market is rapidly expanding, charging speed and mileage are becoming important keys in determining consumer purchasing power, so the main performance factors such as high energy density, high power (quick charge), and high safety of batteries are considered most important [
3,
5,
6,
7].
The cathode and anode electrodes in the LIBs are composed of the current collector that collects electrons, the active material that stores or releases lithium ions, the conductive material to facilitate the flow of electrons between the active materials, and the binder to maintain the bond between the current collector, active material, and conductive material. These components are manufactured through the process of casting on the current collector in the form of a slurry uniformly dispersed in a solvent such as NMP (N-Methyl-2-pyrrolidone) or distilled water using a mixer. To improve the energy density, it is important to increase the amount of active material among the electrode constituent materials and to minimize the conductive material and binder. In addition, increasing the loading amount of the slurry casting on the current collector is an additional energy density improvement method. For quick charging/discharging with a high current, it is important to improve the conductivity of lithium ions and electrons. To this end, numerous researchers have been studying the nanoscale approach of active materials with short lithium-ion diffusion pathways and the formation of composite materials, including various carbon materials such as carbon nanotubes, carbon nanofibers, and graphene [
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. However, these have the drawbacks of lowering the energy density in terms of gravimetric or volumetric energy of the active materials in the electrode. Therefore, there is no doubt that the use of high-conductivity conductive materials and their uniform electrode distribution are important factors to ensure high conductivity and high content of active materials in the electrode.
Among carbon materials, carbon nanotubes (CNTs), which have been widely considered as a conductive carbon material with a one-dimensional (1D) structure, have attracted particular attention in the industry due to their high electrical conductivity [
19]. In the case of LIBs, if CNTs are applied to the electrode instead of carbon black (e.g., Super-P, Ketjen black), the electrical conductivity of the electrode can be improved, so various studies related to this have been reported [
20,
21,
22]. Currently, carbon black is the most widely used conductive material in LIBs. When CNTs replace it, charging/discharging with high current density is possible, resulting in improved charging/discharging speed, and high energy can be achieved by reducing the conductive material content or increasing the active material loading on both the cathode and anode. However, for CNTs to be used as the conductive material, it is easily agglomerated by the high aspect ratio, van der Waals force, and high surface area, which are inherent characteristics of CNTs in slurry preparation [
23,
24], so it must be uniformly dispersed with the active materials in a solvent such as NMP or distilled water. The non-uniformity of material dispersion due to the high inter-particle aggregation of CNTs lowers the electron conductivity of the electrode, weakens the adhesion between the current collector and the electrode constituent materials, thereby increasing the electrode resistance or causing problems such as detachment of the materials from the electrode. This results in the increase of the defect rate due to the generation of impurities in the manufacturing process and high variation in electrochemical performance, make it impossible to achieve high energy density, high power (quick charging), and a long cycle life.
From the perspective of the production process, the traditional way to evaluate the degree of dispersion in the manufacturing process is to measure the viscosity and particle size analysis, and visually check it using a grinder gauge and so on. Furthermore, after electrode manufacturing, a certain portion of the electrode is collected, followed by conductivity measurement physically through the probe-type conductivity meter and direct observation through a scanning electron microscope (SEM); finally, a causal relationship is determined after cell performance evaluations. However, these methods sometimes have the disadvantages of measurement and observer error, lower reproducibility, and taking a long time due to many processes. From these points of view, rapid analysis of materials dispersion and distribution, along with high reliability, will be an important factor that can further save cost and time in the manufacturing process.
In this report, the dispersion characteristics of CNTs in NMP solvent were studied regarding the use of CNTs instead of carbon black, which is mainly used as a conductive material for the cathode in LIBs. Three samples with different dispersion conditions were evaluated for dispersion stability by using a dispersion analyzer, a light transmission method. Each CNTs dispersion sample was prepared with the cathode electrode containing active material NCM622, and then assembled into coin-type half-cells to evaluate cell performance. The correlation between CNTs dispersion stability and electrochemical properties was investigated through prepared electrodes and cell evaluations. In particular, using THz-TDS, a new analysis method for understanding the characteristics of LIBs’s slurry composed of dispersed materials, we confirmed the possibility of accurately and quickly analyzing cathode electrode slurries in a non-destructive way.
3. Results and Discussion
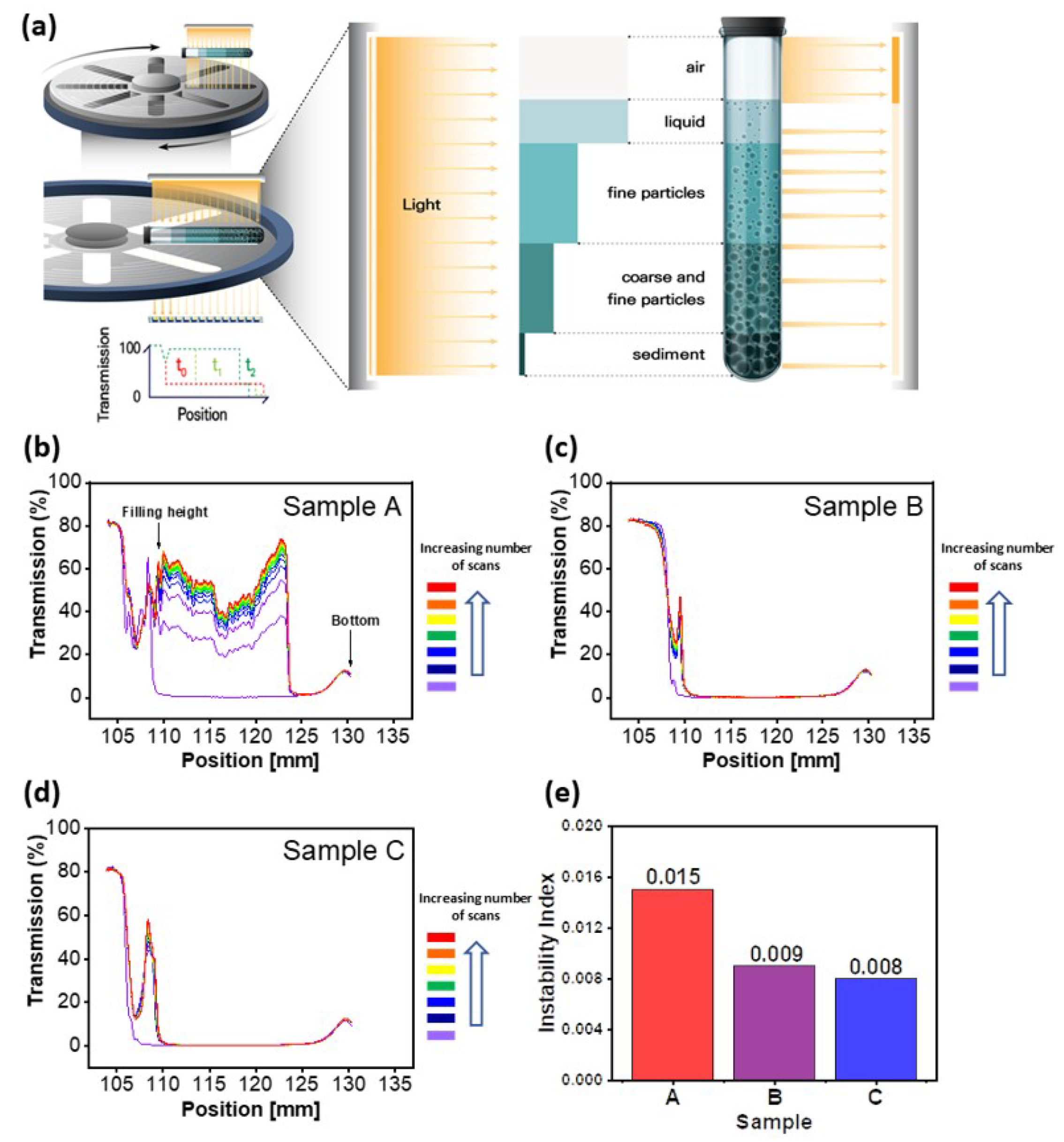
To measure the dispersion stability of the prepared CNTs dispersed samples, it was analyzed by using a dispersion analyzer.
Figure 1a is a schematic view regarding the measurement of the dispersion analyzer. Samples are put in a sampling tube and de-mixing is accelerated by high-speed centrifugation for a set time. During this process, samples are irradiated with near-infrared rays at set time intervals and the degree of transmittance is detected, thereby analyzing the dispersion stability of the samples. Three samples with CNTs dispersed in NMP solvent were each loaded into polyamide tubes in equal amounts and measured every 2 h at a centrifugation speed of 4000 rpm (approx. 1878 G) for 40 h. The peak at a position of approx. 110 mm in
Figure 1b–d indicates the filling height of the sample tube and is due to the boundary between the sample and air in the tube. On the other hand, the broad peak at a position of approx. 130 mm is a phenomenon caused by the scattering of part of the scanned light by the tube bottom structure, which occurs during measurement. In the case of sample A (
Figure 1b), between the positions of approx. 110 mm and approx. 123 mm, the transmission peaks are gradually increasing overall as the number of measurements increases, except for the first graph measured before the start of centrifugation. It is believed that as the measurement time increased, the fine CNTs particles agglomerated while de-mixing was accelerated by centrifugation, which resulted in an increased amount of transmitted light signals. On the other hand, above the 123 mm position, it was shown that the peak change hardly occurred, as the number of measurements increased due to the failure of the light source to penetrate the sediments accumulating from the bottom of the sample tube to a height of approx. 123 mm. Particularly, although the number of measurements increased, the peak at a position of approx. 123 mm, the boundary of the sediments, hardly shifted to a lower position. This phenomenon is believed to be because the sedimentation of the fine particles is formed very slowly or densely, or because the agglomerated fine particles are suspended in the solvent. Unlike sample A, samples B and C showed little increase in transmission, despite the increase in the number of measurements, indicating that samples B and C had better dispersion in the NMP and higher dispersion stability compared to sample A.
Figure 1e showed the instability index based on the measurements for each sample, which can be calculated by dividing the sum of the differences in transmission for each measurement frequency by the maximum possible transmission of the sample, with a higher value indicating lower dispersion stability [
29]. For three calculated samples, sample A showed the highest instability index of 0.015, and samples B and C were 0.009 and 0.008, respectively, indicating a higher dispersion stability than sample A.
To evaluate the effect of the dispersion stability of CNTs on the formation of internal networks between constituent materials during electrode manufacturing, dispersed CNTs samples were used to fabricate electrodes to which NCM622 cathode material was employed. For the fabricated electrodes using samples A and C, a scanning electron microscope (SEM) was employed to observe the dispersion characteristics of the cathode active material and CNTs, and this is shown in
Figure 2. The bright spherical morphologies in the observed SEM images represent the NCM622 cathode materials, and the dark slender morphologies represent CNTs. As shown in
Figure 2b, compared to
Figure 2d from sample C, the CNTs particles from sample A were not evenly distributed and aggregated in some areas. On the other hand, in the case of the cathode electrode containing sample C, it was shown that the CNTs particles were relatively uniformly distributed in the cathode electrode particles.
Figure S1 shows the results of observing the secondary electrons (SE) signal and the backscattered electrons (BSE) signal of the SEM to confirm the difference in this distribution more statistically. The distribution of the color difference between light and dark in SE mode due to the difference in electronic conductivity between materials was subdivided from light gray to dark black, and the composition ratio was extracted from the images. In the BSE mode, as the atomic number difference between the transition metal of the cathode material and the carbon of the CNTs was large; it was observed with the composition ratio by dividing it into white and black images, respectively. It was possible to calculate the area of CNTs distributed on the electrode surface by subtracting the value of the pore (and/or blank) area calculated in SE mode from the black area calculated in BSE mode. In the case of a sample with low dispersion stability of CNTs in the configuration of cathode material and CNTs, the detection area of the cathode material is large and CNTs are reduced by self-agglomeration, while the sample with excellent dispersion stability is evenly distributed with cathode material. The basis of this calculation is that, in the case of a sample with low dispersion stability of CNTs, the surface of the cathode material is greatly exposed due to the aggregation of CNTs, so the detection area of the cathode material is large and the detection area of the CNTs is small. On the other side, in the case of a sample with good dispersion stability, CNTs are uniformly distributed with the cathode material, so the detection area of the cathode material is small and the detection area of the CNTs is larger compared to that of the low dispersion stability. The proportion of CNTs detection area calculated in
Figure S1a,b showed that sample C had a higher area compared to sample A. Through these results, it was confirmed that sample C, which had higher dispersion stability, was more evenly distributed in the electrode manufactured together with the cathode material.
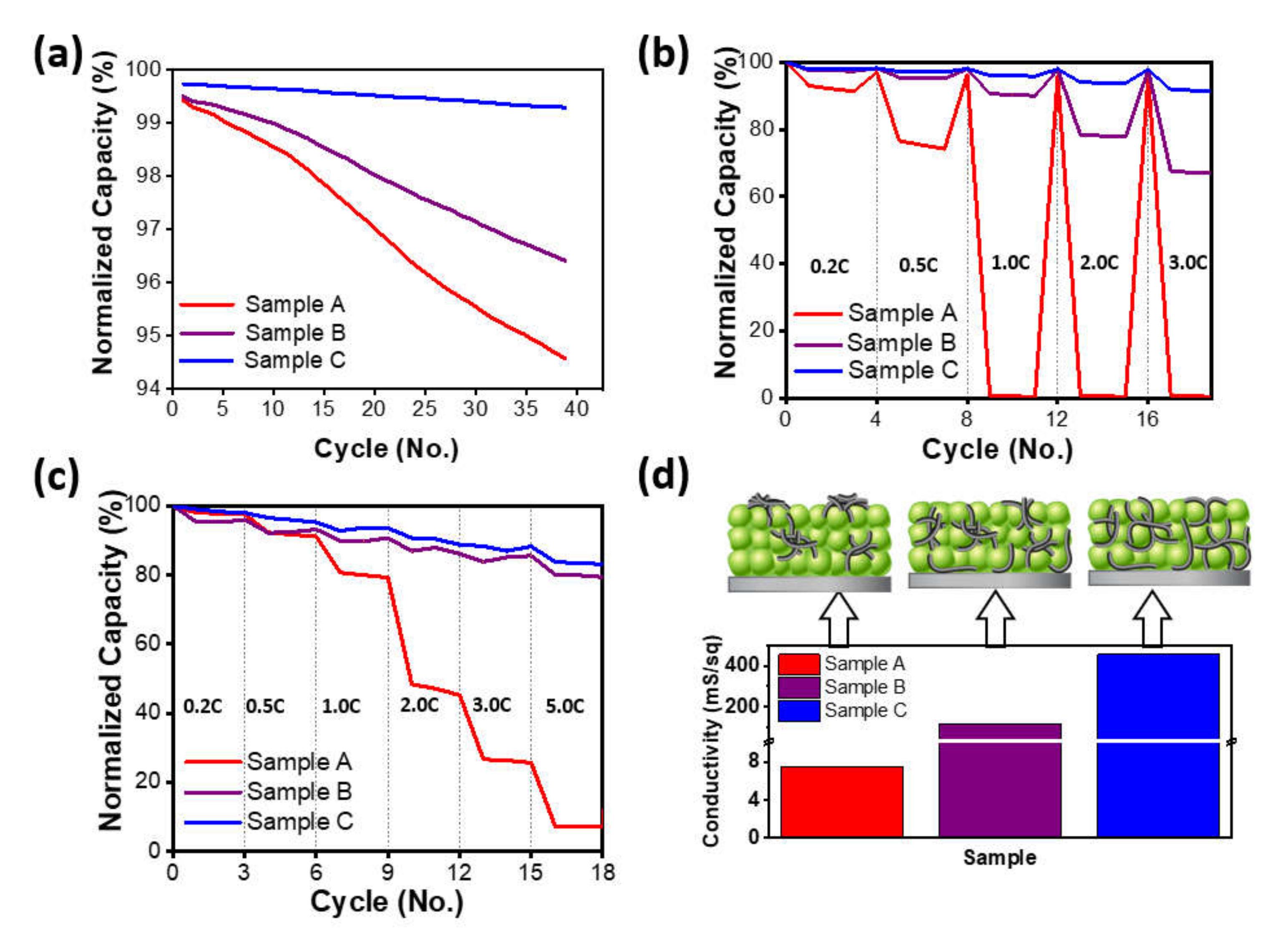
Figure 3 shows the electrochemical properties of the cycle life at 5 C, the charging and discharging rate characteristics under increasing charging or discharging rates up to 3 C and 5 C, respectively, through coin-type half-cells, and the measurement results of electric conductivity via a four-probe contact method for each electrode.
Figure 3a shows the normalized discharging capacity for charging and discharging at 5 C at 25 °C. In the case of sample C, it was 99.7% in the first cycle at 5 C, showing the highest capacity retention compared to samples A and B, which were 99.4% and 99.5%, respectively. After 39 cycles, samples A and B were 94.6% and 96.4%, respectively, representing 4.8% points and 3.1% points, respectively, a capacity decrease compared to those of the first cycle, and sample A showed the largest capacity decrease among all samples. However, for sample C, despite the high C-rate cycling, it decreased only 0.4% points to 99.3% after 39 cycles, indicating the highest capacity retention among all samples. In
Figure 3b, which evaluated the charging characteristics as the charging rate increased, the capacity of sample A was significantly inferior among the three samples, and even at a rate of 1 C or higher, the capacity became zero. Remarkably, in the case of sample C, the third capacities of 2 C and 3 C were 93.7% and 91.5%, respectively, showing the best capacity retention. In
Figure 3c, which evaluated the discharging characteristics as the discharging rate increased, with a similar tendency to the results of the charging characteristics in
Figure 3b, sample A showed a sharp decrease of capacity after 0.5 C, and the third capacity at 3 C and 5 C showed 25.6% and 7.3%, respectively. Sample B and C showed a tendency of high capacity retention even with an increasing discharging rate compared to sample A, and they showed high capacity retention of 79.4% and 83.2%, respectively, even at a 5 C rate. To determine the correlation between these cell evaluation properties and the conductivity characteristics of the electrodes, each electrode was measured with a four-tip probe-type electrical conductivity meter, and the results are shown in
Figure 3d. The electrical conductivities of the prepared electrodes were 7.6 mS/sq, 114.8 mS/sq, and 454.5 mS/sq for samples A, B, and C, respectively. Sample A showed very low electrical conductivity, while sample C showed the highest conductivity among those samples, which corresponds to the results of the cell performance evaluation. These results show that the formation of the network organically between electrode materials composed of CNTs, cathode material, and the current collector not only ensures stable conductivity of the electrode, but also enables the expression of high conductivity properties by CNTs, thereby suppressing the increase in resistance of the cell during fast charging (or fast discharging). Therefore, it was confirmed that securing dispersion stability of materials with low dispersibility such as CNTs is an important factor for application to electrodes.
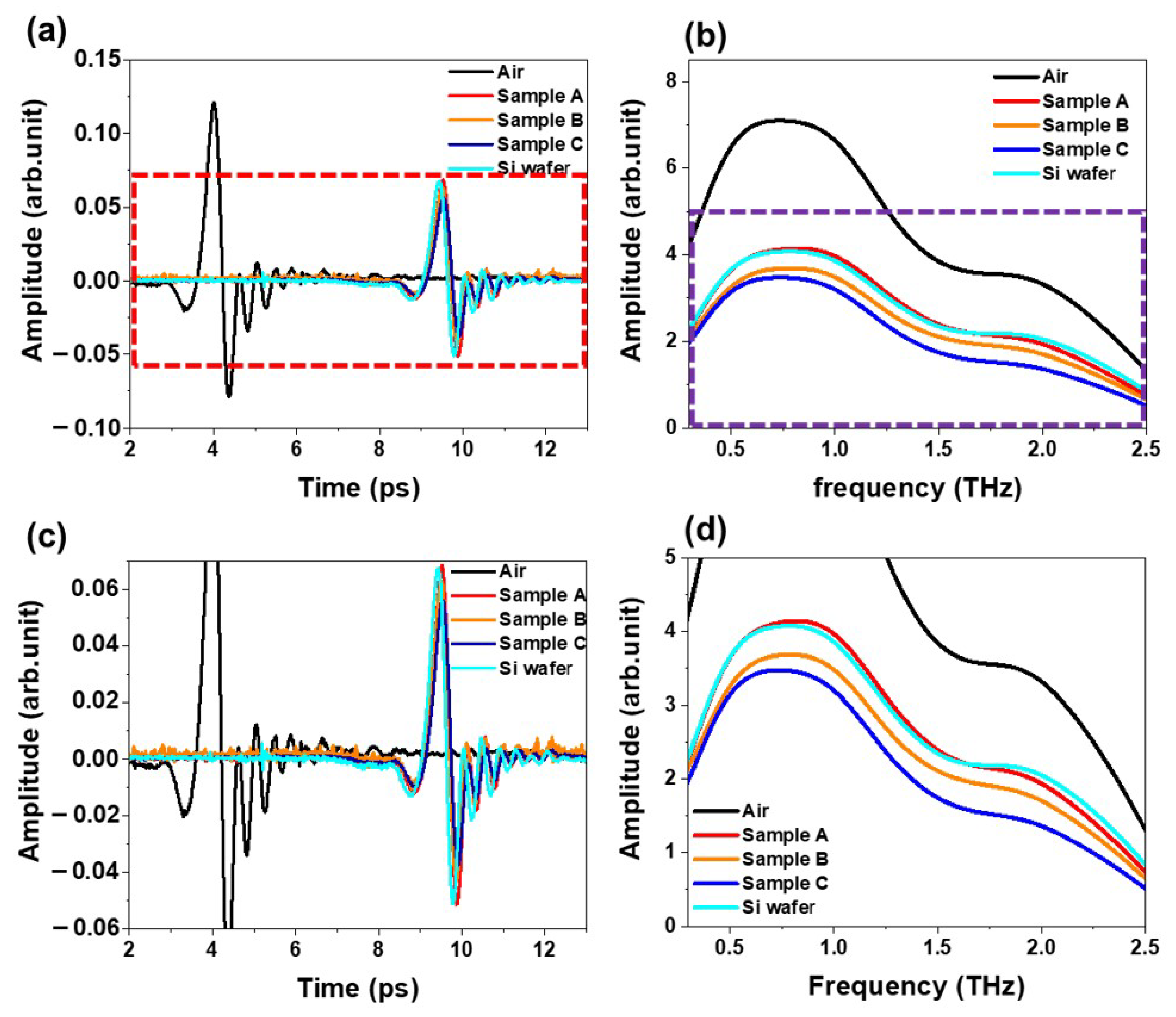
Figure 4 shows the time-domain waveform and their corresponding Fourier-transform frequency spectra of the transmitted THz pulse through the air, bare silicon, and three different cathode films containing CNTs dispersion samples (A, B, and C), respectively. The frequency-domain output THz signals were obtained from the time-domain THz signals using the Fourier-transform analysis of the input and output time-domain THz signals. As expected, the cathode films exhibit a smaller amplitude and a longer arrival time to the detector than that of the air. The relative amplitude of the samples is as follows; sample A > sample B > sample C.
The frequency-domain output THz signal value includes the absorption and refractive index. We obtained the optical constant and conductivity using the transmission amplitude ratio and the following equations. The transmission amplitude ratio
A(
ω) and phase difference
(
ω) of sample and reference fields can be calculated as [
30,
31]:
where
c is the speed of light,
d represents the sample thickness, and
ω is the angular frequency. From Equation (1), we can derive the absorption coefficient
α(
ω) and the real index of refraction
:
The real refractive index
value was obtained from the phase difference between the input and output THz pulse. The complex dielectric constant is related to the index of refraction as follows:
According to the Drude model, the complex dielectric constant and the conductivity are given by [
32]:
where
is the dielectric constant at infinity frequency,
N is a carrier, m is the effective mass of the sample,
e is the electronic charge,
is free-space permittivity, and
is damping rate. We obtained the constant (
N,
,
) by the Drude model fitting on dielectric constant data, and then calculated the frequency-dependent real conductivity.
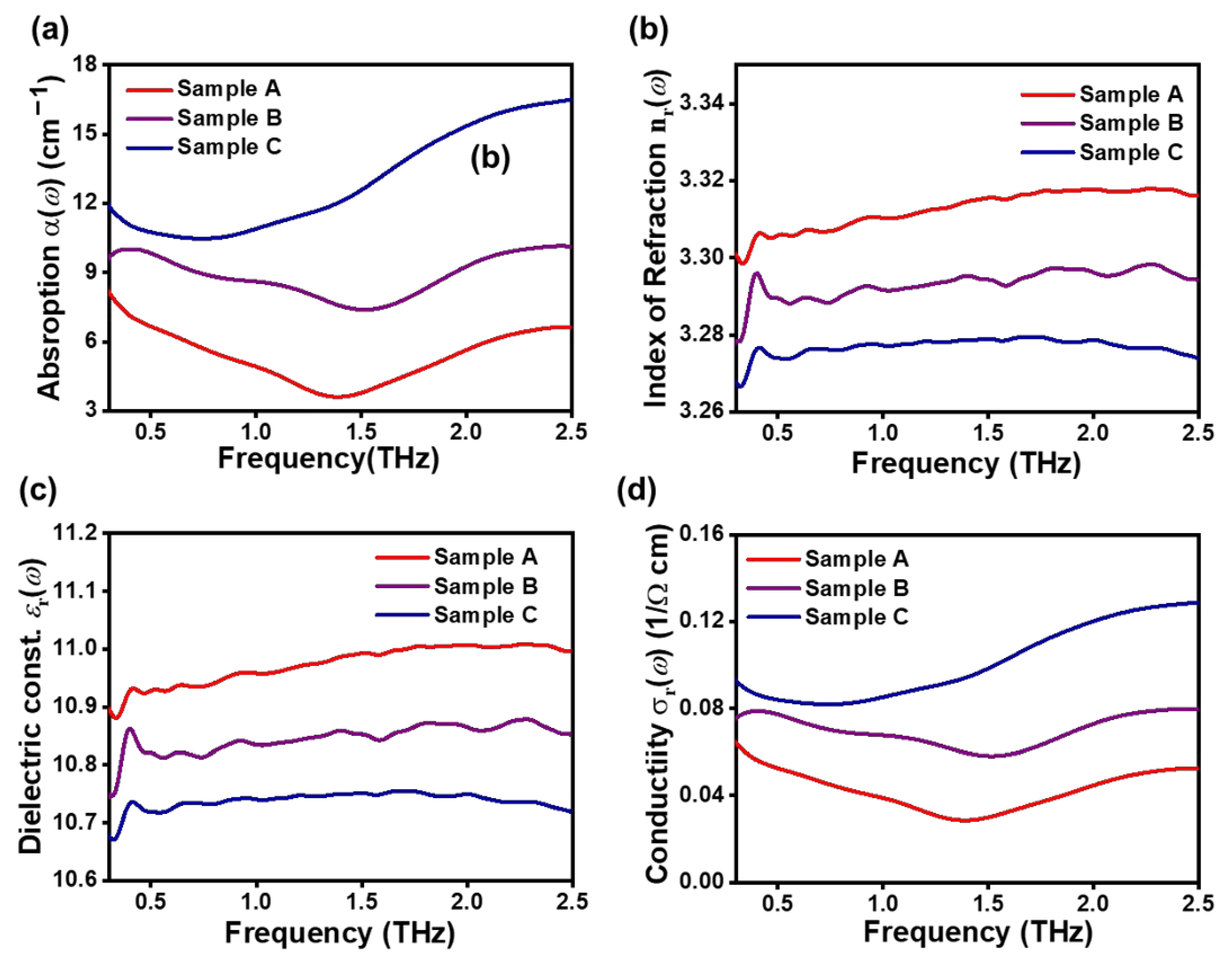
The optical constants and conductivity of the samples are shown in
Figure 5. The absorption coefficient
α(
ω) and the real part index of refraction
obtained from THz-TDS data, using Equations (2) and (3), are presented in
Figure 5a,b respectively. The
α(
ω) value of sample A is smaller than that of samples B and C. The
spectra are almost flat in the range of 0.5–2.5 THz, and the values at 1 THz for samples A, B, and C are 3.27, 3.29, and 3.31, respectively. The different
α(
ω) and
values for the samples A, B, and C are caused by the different states of CNTs dispersion. As previously described, the degree of CNTs dispersion in each sample was different, and sample A was at the lowest degree of CNTs dispersion. Furthermore, its electric conductivity was also the lowest. As explained above, it is calculating the spectra for the relative dielectric constant
knowing the
.
Figure 5c shows the real part of the complex dielectric function spectra for samples A, B, and C. The resulting
spectra are almost flat in the range of 0.5–2.5 THz, as we observed previously for the
dependences presented in
Figure 5b. The conductivity calculation is based on Equations (5) and (6).
Figure 5d displays real conductivity
σ(
) data for the samples. The
σ(
) values decrease in the order C > B > A. This result is in good agreement with the conductivity values obtained from the four-point contact electrical conductivity measurement in
Figure 3d. We found that the conductivity of the electrode prepared from the slurry containing the cathode material increased with an increase in the degree of CNTs dispersion. Therefore, the THz-TDS method may be used as a useful tool to analyze the dispersion degree of slurries containing materials that are difficult to disperse such as CNTs, and to have insight into the fast estimation of electrochemical performances, whereas it takes a long time to get a conventional electrochemical estimation.