Abstract
With the increasing focus on renewable energy, there is a need to improve the efficiency of vertical-axis wind turbines (VAWTs). The Ugrinsky wind turbine is a type of VAWT, but there are few studies on this turbine. Previous studies have shown that the maximum power coefficient of the Ugrinsky wind turbine reaches 0.170, which is 54.5% higher than that of the Savonius type (0.110), and this turbine maintains a high power coefficient over a wide range of tip speed ratios (TSR). In this study, the dimensions of the two semicircles of the Ugrinsky wind turbine were further optimized to obtain a higher power coefficient. An analysis of the effect of the blade dimensions on the performance was conducted. The flow around the turbine was simulated using the regularized lattice Boltzmann method. The geometry of the turbine was simulated using the virtual flux method for the Cartesian grid. The optimization was conducted in terms of the output power coefficient and the average value of the power coefficient for neighboring TSR to consider the fluctuation of the TSR. This study demonstrates that a closer vortex distance favored the growth of the vortex and improved the power coefficient.
1. Introduction
Wind turbines can be classified into horizontal-axis wind turbines (HAWTs) and vertical-axis wind turbines (VAWTs) depending on their rotational axis. They can also be divided into drag-type and lift-type depending on the aerodynamic force that drives their rotation [1]. Vertical-axis drag-type wind turbines, especially the Savonius wind turbines, are often used for small-scale power generation [2]. In particular, these wind turbines can be described as having high torque and high self-starting power, a low potential for noise pollution, a simple and low-cost design, operatable in a wide range of wind conditions, and omnidirectional (independent of the wind direction) [3,4,5]. In recent years, there has been a growing focus on small-scale power generation in urban areas such as buildings and roads [6,7,8]. Due to the characteristics described above, the vertical-axis drag type wind turbine is the most suitable wind turbine for this application. In addition, refugee settlements are in need of efficient, clean, affordable, and reliable renewable energy [9]. With their simple and low-cost design, the vertical-axis drag-type turbine can be an off-grid renewable energy option.
Vertical-axis lift-type wind turbines, including Darrius and H-VAWT, have higher performance than drag-type wind turbines and are also omnidirectional [4]. However, because of the nature of the lift force, their torque is lower than that of drag-type turbines, and their starting characteristics are also inferior to those of drag types [4,5]. Therefore, drag types are more suitable for power generation in urban areas where the wind is not always uniform. To improve their starting characteristics, previous studies have combined a drag-type wind turbine with a lift-type one [10]. However, the tip speed ratio (TSR) to obtain the maximum output from the two types of wind turbines is different, and the lift-type turbines peak at a higher TSR than the drag types. Therefore, to maximize the performance of this combined wind turbine, the diameter of the lift-type wind turbine must be around 6 to 7 times as large as that of the drag-type one and will not be suitable for small-scale power generation [11]. Furthermore, the lift types consists of blades with precise dimensions, such as NACA blades, and are more complex than the drag types, which can be manufactured by combining arc-shaped plates, resulting in higher manufacturing costs.
However, a study suggested that the power coefficient of the Savonius turbine is generally less than half of that of the HAWT [12]. This is explained by the characteristics of the Savonius wind turbine, which consists of two blades. During a cycle, while one blade generates a positive torque, the other blade generates a negative torque. Thus, the net torque is always suppressed by the countering negative torque, resulting in a low power coefficient. To avoid this, various studies have been conducted to find a better design for VAWTs. One example is the installation of shield plates in front of the turbine [13,14]. However, the installation of obstructions to improve efficiency results in the loss of wind direction independence and requires additional land area. Therefore, modifying the blade shape is an effective way to improve efficiency while maintaining wind direction independence. Zhang et al. [5] used a quadratic polynomial curve for the blade shape of a conventional Savonius turbine to improve the power coefficient by 6% while reducing the blade weight by 17.9%. Roy et al. [15] developed a new two-bladed Savonius-type wind turbine, which showed improved the power coefficient by 32.1% compared to the conventional Savonius-type turbine. Matsui et al. [16] introduced sub-blades to the two-blade VAWT, which is similar to the Bach-type wind turbine, and succeeded in increasing the power coefficient by 50.7% over that of the conventional Savonius-type wind turbine by optimizing their positions.
The Ugrinsky wind turbine is a type of VAWT that has a pair of centrosymmetric blades with two identical segments of arcs with different diameters [17]. The source documentation claims that the Ugrinsky turbine performs better than the traditional Savonius wind turbine and produces positive torque at all angles. Our study demonstrated and confirmed that the turbine performs better than the traditional Savonius wind turbine by 54.5%; moreover, it produces positive torque at all angles throughout a cycle at λ = 0.5 [18]. With its high efficiency, this turbine can be a viable option for the future installation of VAWTs. In previous research, the optimal dimensions were (S, L) = (0.35D, 1.3R) for maximum power coefficient and (S, L) = (0.35D, 1.0R) for average power coefficient [19]. These parameters improved the maximum power coefficient by 1.5% and the average value of the power coefficient for neighboring tip speed ratios by 5.9%. However, not all parameters were considered in this study, and it remains possibile to obtain better-performing parameters. Moreover, further analysis of the effect of blade dimensions on performance and fluid structure should be conducted for future improvements. In this paper, as an expansion of the previous study, a wide combination of parameters was examined to further increase the efficiency of the turbine, with a focus on the relationships between blade dimensions and fluid structure in anticipation of further optimization and future employment of the optimized turbine.
2. Numerical Methods
The regularized lattice Boltzmann method (RLBM) was used as a governing equation in this paper for ease of implementation of parallel computing [20]. The virtual flux method was used to describe the blades of the turbines on a Cartesian grid [21,22]. The multi-block method was used for the locally fine grids around the turbines [23]. The simulation was conducted in 2-D, which is known to give acceptable results and shares performance characteristics with 3-D simulation [2,4].
2.1. Regularized Lattice Boltzmann Method
The RLBM is used as a governing equation of the 2D 9-velocity (D2Q9) model for fluid analysis. This method is designed to reduce memory usage and simulate flow at high Reynolds numbers without compromising accuracy compared to the lattice Boltzmann method [24].
The distribution function fα is expressed as
where is the weight coefficient defined by the lattice speed model (w0 = 4/9, w1–4 = 1/9, w5–9 = 1/36 for the D2Q9 model); a0, bi, and cij are determined to satisfy the following relationships:
where ρ is the fluid density, is the fluid velocity component, c is the lattice speed defined as c = δx/δt, δij is the Kronecker delta, and is the non-equilibrium part of the stress tensor. Then, the equilibrium distribution function and the non-equilibrium part of the distribution function are expressed as follows:
where the equilibrium distribution function is expressed by approximating the Maxwell equilibrium distribution function to the quadratic term. Lastly, the time evolution equation in the regularized lattice Boltzmann equation is expressed as
where is the relaxation time.
2.2. Virtual Flux Method
The virtual flux method [20,21] is used to describe the wind turbine shape in a Cartesian grid. This method was chosen due to its simplicity in the algorism with no iterative calculations and easy incorporation into RLBM. Moreover, for the same grid resolution, this method can describe the pressure field around an object more accurately compared to other immersed boundary methods [20,21]. Figure 1 shows a schematic view of the virtual boundary points on the turbine. With the RLBM using the D2Q9 model, virtual boundary points were set at the intersections of discrete velocities in eight directions and the object surface.
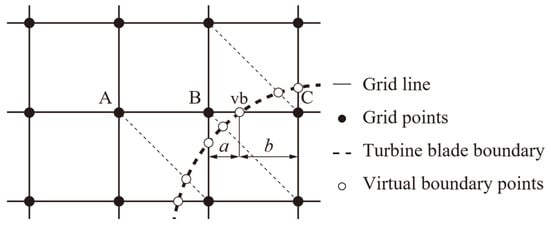
Figure 1.
Schematic view of the turbine blade boundary on a Cartesian grid.
First, the physical quantity on the virtual boundary qvb was considered. The no-slip boundary condition (uvb = uwall) was applied for the velocity of the virtual boundary uvb, where uwall is the velocity on the wall surface of the turbine blade. The Neumann boundary condition (∂pvb/∂n = 0) was applied for the pressure of the virtual boundary pvb, where n is the normal vector on the virtual boundary wall, providing the approximate pressure condition on the surface.
As shown in Figure 1, the case where the distribution function at point “C” moved to point “B” was considered; however, this movement was obstructed by the virtual boundary. Therefore, the virtual distribution function fα,vb was calculated at point “vb” from the distribution function fα,B and the equilibrium distribution function as follows:
Then, the virtual distribution function and the virtual equilibrium distribution function at point “C” were calculated by extrapolation using internal division ratios a and b.
Finally, the distribution function at point “B” for the next time step fα,B was obtained from and as follows:
2.3. Computational Models
The torque and power coefficients for various wind turbine dimensions through numerical fluid dynamics analysis were used for discussion and to determine the optimal dimensions. The original dimensions of the Ugrinsky wind turbine are shown in Figure 2a. The diameter of the semicircular part (Segment 1) was 0.4 with respect to the wind turbine diameter (D), and the radius of the arc part (Segment 2) was equal to the wind turbine radius R (=D/2). The wind turbine diameter is shown as a dashed line in Figure 2. Figure 2b shows the Savonius wind turbine used for the verification, where e and l are the blade diameter and overlap and were set as e = 0.2l, a value considered to provide the highest performance in the previous study [12]. Figure 2c shows a schematic diagram of the multi-block method. The overall computational domain was set to be 30D × 30D with respect to the wind turbine diameter D, and the coordinates of the turbine center were set to (x,y) = (10D,15D). The inflow from the left side had a constant flow velocity, and the velocity and pressure gradients were set to zero at the upper and lower boundaries. The convective outflow condition was set for the outflow on the right side [25]. Finally, the Reyolds number was set to 1000 with respect to the turbine diameter D, and the turbine rotated 0.00557 [°] per timestep for λ = 0.6.
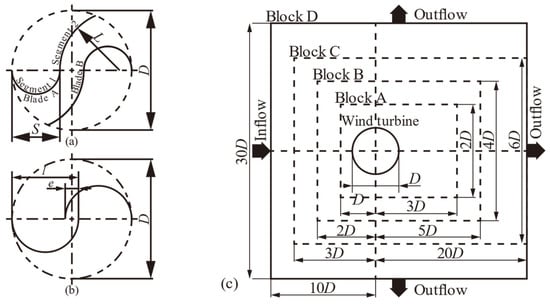
Figure 2.
Top view of (a) the Ugrinsky wind turbine at 0 [°] and (b) the Savonius wind turbine at 0 [°] and (c) schematic view of the multi-block model used in the simulation.
Normally, when evaluating wind turbines in fixed rotation, multiple TSRs are evaluated individually. In such cases, the turbine was rotated several times for the flow field development in the calculation domain, and then evaluation was performed for each TSR. In this study, information regarding the calculation domain from the previous TSR was imported into the calculation of the next TSR in order to reduce the number of revolutions required for flow field development and to shorten the calculation time. For example, when calculating from λ = 0.7 to 0.5 with an interval of 0.1, λ = 0.7 was set as the initial TSR, and a total of 9 cycles were calculated, with the last 3 cycles set as an evaluation period. The blade rotation speed was then gradually decreased using one cycle to satisfy λ = 0.6 at the beginning of the 10th cycle. Then, six cycles were calculated, including three cycles of evaluation. After that, the TSR was reduced to λ = 0.5, and the calculations and evaluations were performed in the same manner as for λ = 0.6. The output and torque coefficients obtained from the evaluation cycles were averaged over the last three cycles.
The torque coefficient CQ, the power coefficient CP, and the TSR λ are defined as
where T is the torque, U is the characteristic velocity, ω is the angular velocity, and is the swept area. The optimal shape is selected by the maximum power coefficient value and the average value of the power coefficient for neighboring TSRs. For example, the average value of the power coefficient for neighboring TSRs at λ = 0.6 is the average value of the power coefficient at λ = 0.5, 0.6, and 0.7. In this way, the TSR fluctuation of the turbine due to non-uniform flow and angle-dependent torque values that occurred during the experiment could be taken into account in the fixed speed simulation.
2.4. Validation
A flow analysis around a 2-D fixed cylinder was performed as a validation of the simulation code. The computational model used in this analysis is shown in Figure 3. The diameter of the cylinder was set to a characteristic length D, the computational domain was set to 30D × 30D in the x and y directions, and the cylinder was placed at (x,y) = (10D,15D). A uniform flow with characteristic velocity U flowed in from the left and out from the upper, lower, and right boundaries. The convective outflow condition was given at the right end, and the other outflow conditions were given a gradient of 0 for both pressure and velocity. Block A, Block B, Block C, and Block D, from the highest to the lowest resolution, were the 4-step multi-blocks, and the lattice widths of each block were δxA = 1.0, δxB = 2.0δxA, δxC = 4.0δxA, and δxD = 8.0δxA, respectively. The Reynolds number was Re = 1000, and the resolutions for the characteristic length D were 128, 184, 256 cells.
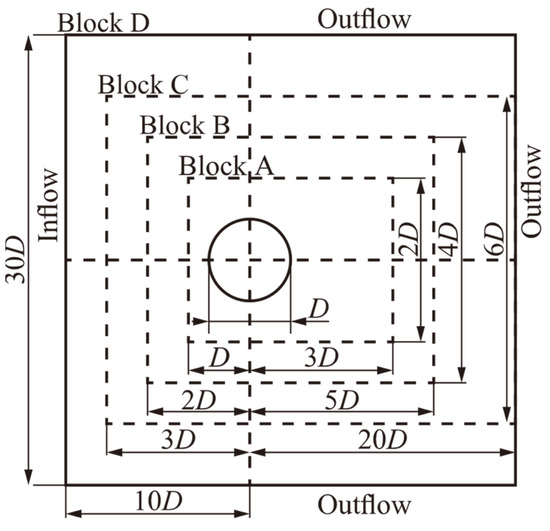
Figure 3.
Schematic view of the flow around a cylinder.
Figure 4 shows the pressure coefficient diagram on the surface of the cylinder, the distribution diagram of the normal direction component of shear stress, and the distribution diagram of the tangential direction component of shear stress when the absolute value of the lift coefficient CL was at minimum. It can be seen that the pressure coefficient values, Cτn values, and Cτt values around the cylinder converged by increasing the grid resolution.
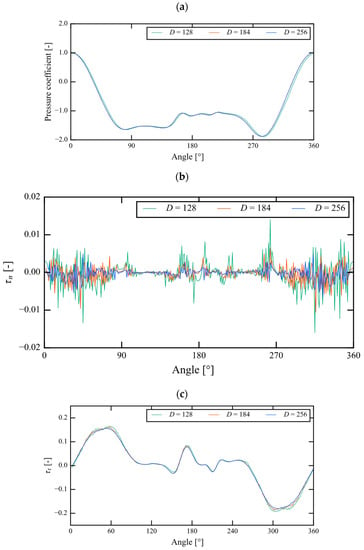
Figure 4.
(a) Pressure coefficient diagram, (b) distribution diagram of the normal direction component of shear stress, and (c) distribution diagram of the tangential direction component of shear stress of a cylinder for Re = 1000.
The time variation of the drag coefficient CD and the lift coefficient CL in the non-dimensional time 450–500 are shown in Figure 5, and the Strouhal number St is shown in Table 1. In Figure 5, it can be seen that the drag coefficient CD and the lift coefficient CL oscillated periodically, and in Table 1, it was confirmed that St was quantitatively valid in comparison with others.
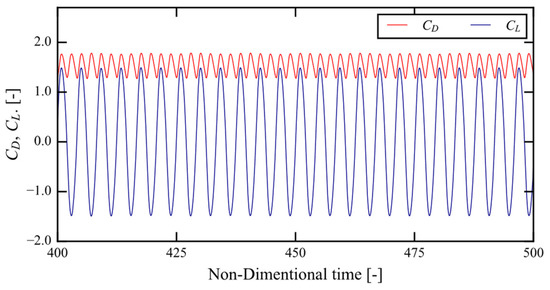
Figure 5.
Time history of drag and lift coefficients for Re = 1000.

Table 1.
Maximum power coefficient values and average value of the power coefficient for neighboring TSRs of different diameters L for Segment 2.
2.5. Verification
A verification study was conducted on the Savonius turbine shown in Figure 2b for Reynolds number Re = 500 at λ = 0.8. The test was conducted with four different grids for the characteristic length (D = 256, 360, 512, 724 cells). The torque coefficient value for the 6th rotation showed the same trend as in other studies [4,5,19]. The number of grids required for the characteristic length is proportional to Re1/2 times according to the boundary layer thickness theory [30]. The average torque coefficient for D = 256 cells showed less than a 3% error compared to that for D = 724 cells at Re = 500 [19]; therefore, D = 360 cells was selected for Re = 1000 condition.
3. Results and Discussion for the Optimization of S = 0.30D and 0.40D Models
In this section, the effects of optimization on Segment 1 and Segment 2 are discussed. The performance of the turbines is described in torque and power coefficients, and the pressure coefficient is used in the pressure contour diagram for visualization.
In the optimization conducted in the previous study, the radius (L) of Segment 2 was fixed for Segment 1 optimization, and there remains possibile to identify a combination with even better performance among the combinations that had not been examined. Therefore, we calculated S = 0.30D and S = 0.40D with various radii L, which were the two combinations with the best performance in the previous study [19].
Figure 6 shows the average power coefficients for different tip speed ratios while Segment 1 was fixed at S = 0.30D. The average value of the power coefficient for neighboring tip speed ratios is shown in Table 2. In Figure 6, except for L = 0.9R, it can be seen that peaks of average power coefficients could be observed at λ = 0.5 and 0.7, similar to L = 1.1R and 1.2R models for S = 0.35D [19]. While the L = 0.9R model reached a low average power coefficient at all calculated tip speed ratios, the L = 1.2R model reached the highest tip speed ratio out among all calculated models at both λ = 0.5 and λ = 0.7. From the stability point of view, while the Ave. CP of L = 1.2R was the highest of the calculated models, the L = 1.3R model showed less fluctuation and a stable average power coefficient, from λ = 0.5 to λ = 0.7, as shown in Figure 6.
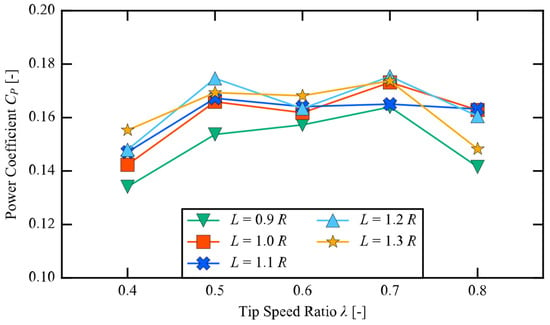
Figure 6.
Power coefficient values of the Ugrinsky wind turbine model with various radii for Segment 2 in dynamic simulation for S = 0.30D.

Table 2.
Maximum power coefficient values and average value of the power coefficient for neighboring TSRs of different diameters L for Segment 2.
Figure 7 shows the average power coefficients for different tip speed ratios while Segment 1 was fixed at S = 0.40D. The average power coefficients and the average value of the power coefficient for neighboring tip speed ratios are shown in Table 3. In particular, the characteristics of the average power coefficient against tip speed ratio of S = 0.40D was different from S = 0.30D and 0.35D [19]. While the peak was at λ = 0.7 for L = 1.3R, the peaks for the other L were at low tip speed ratios (λ = 0.4 or 0.5). In addition, L = 1.2R and 1.3R had low maximum average power coefficient values, unlike the other S values. The peculiar point at λ = 0.4 for L = 1.1R indicates that the evaluation method employed in this study was inadequate. Normally, lower TSRs require a greater number of rotations than higher TSRs to exhibit periodicity, and six cycles are not sufficient; therefore, satisfactory convergence was not seen, resulting in an abnormal value in this case.
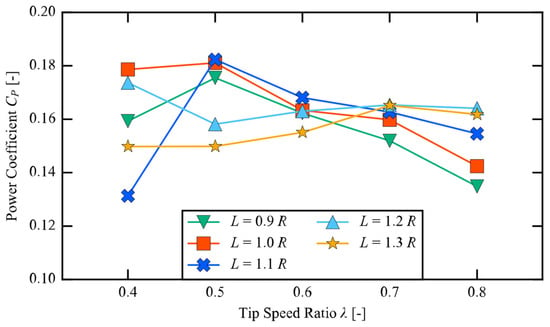
Figure 7.
Power coefficient values of the Ugrinsky wind turbine model with various radii for Segment 2 in dynamic simulation for S = 0.40D.

Table 3.
Maximum power coefficient values and average value of the power coefficient for neighboring TSRs of different diameters L for Segment 2.
Figure 8 shows the torque coefficient throughout a cycle for different diameters S at λ = 0.5, and Figure 9 shows the pressure distribution at 40, 90, 130, and 190 [°] and the velocity contour at 130 [°]. For 0–70 [°]. As Segment 1 diameter S increased, an increase of the torque coefficient could be observed. It can be seen in Figure 9 that the increase in torque was due to the increase in the wind-receiving area (swept area), thus suggesting the dominance of the geometrical shape in this advancing blade region for λ = 0.5. Similarly, at the same angle, the negative torque increased in Segment 2 due to the increase in the length of the torque arm at the tip of Segment 2 with the increase in S. Furthermore, at 130 [°], the edge vortex in Segment 1 also grew with the increase in S, and the detached vortex became the negative pressure in the wake area and pulled the blade in the direction of rotation. The detachment of the vortex of Segment 1 for S = 0.40D was delayed compared to that for S = 0.30D due to the increase in vortex growth as noted above, and this further increased the pull. Likewise, at 190 [°], the edge vortex also grew at the tip of Segment 2, and the growth of the vortex increased as S increased. From the velocity contour diagram at 130 [°], focusing on the velocity between Blade A and Blade B, it can be seen that the model with a larger S had a higher velocity. This is because the model with a large S created a nozzle-like structure with a small distance between blades A and B, increasing the velocity of the inflow from the left side. Furthermore, some of the fluid that passed between the blades flew into the edge vortex of Blade B Segment 2 and BladeA Segment1, and this contributed to the growth of the vortex for models with large S.
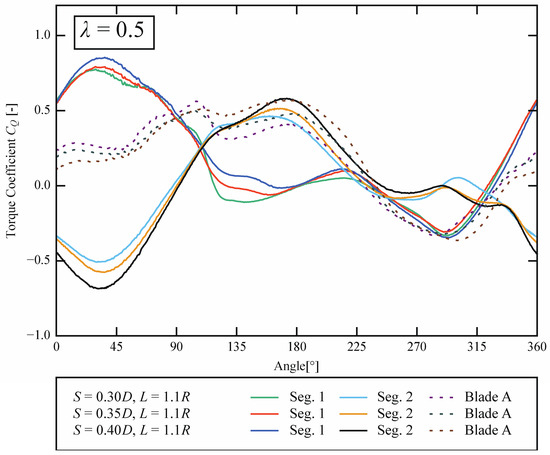
Figure 8.
Power coefficient values of the Ugrinsky wind turbine model with various radii for Segment 2 in dynamic simulation for λ = 0.5.
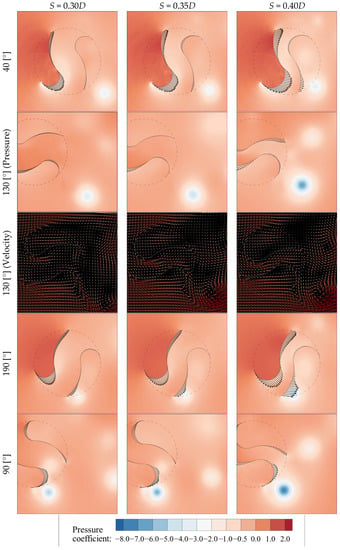
Figure 9.
Pressure coefficient distributions and velocity contour around the Ugrinsky models for different Segment 1 diameters at λ = 0.5. The black vectors represent the torque generated on the blades.
To understand the relationship between the edge vortex and the torque generation, the distance between Blade A Segment 1 vortex and Blade B Segment 2 vortex at 90 [°] is shown in Table 4. When S increased, Blade A Segment 1 and Blade B Segment 2 became geometrically closer. At the same time, the vortex–vortex distances generated at each end became shorter, as shown in Table 4. Focusing on the pressure distribution between the two vortices during the vortex growth phase, the pressure of the edge vortex of S = 0.30D was higher than that of 0.40D. Therefore, it can be said that for S = 0.30D, the vortex–vortex distance was great, and a high-pressure region developed between the vortices, which inhibited the formation and growth of the vortex.

Table 4.
Distance between Blade A Segment 1 vortex and Blade B Segment 2 vortex at 90 [°].
As in the case of λ = 0.5, Figure 10 shows the torque coefficient throughout a cycle for different diameter S at λ = 0.6, and Figure 11 shows the pressure distribution at 40, 90, and 160 [°]. At 40 [°], Segment 1 did not have the maximum power at S = 0.40D, unlike the case of λ = 0.5. This phenomenon was also observed in the case of λ = 0.6 comparisons of Segment 1 optimization [19]. For Segment 2 at 40 [°], similarly to λ= 0.5, the larger S was, the longer the torque arm length became, and the more the negative torque increased. At 90 [°] for Segment 1 and 160 [°] for Segment 2, similarly to λ = 0.5, the larger S was, the larger the size of the edge vortex and the larger the positive torque. For te S = 0.40D model chosen in this comparison, the diameter of Segment 1 was increased, but the radius of Segment 2 was decreased; therefore, the return torque produced was smaller than that in the other models.
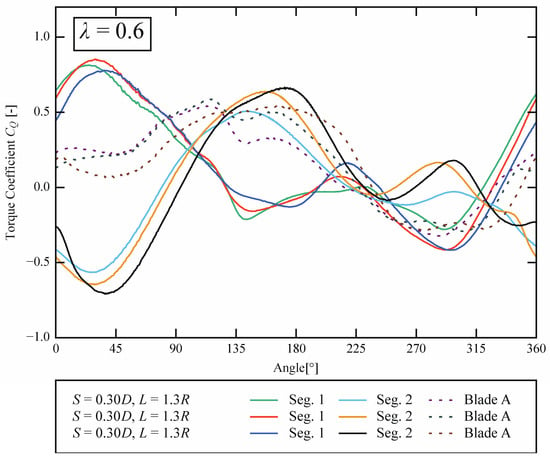
Figure 10.
Power coefficient values of the Ugrinsky wind turbine model with various radii for Segment 2 in dynamic simulation for λ = 0.6.
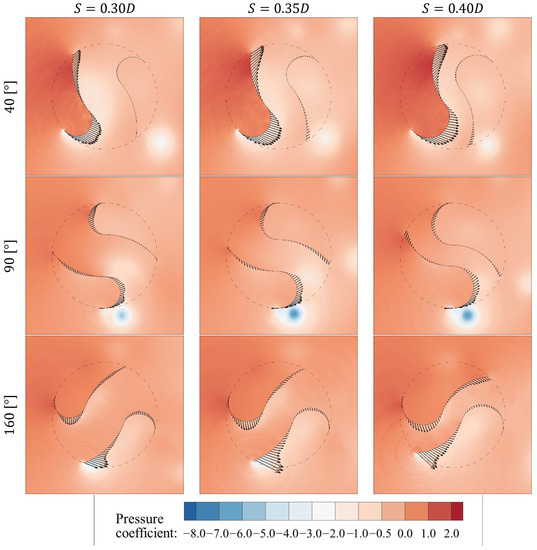
Figure 11.
Pressure coefficient distributions around the Ugrinsky models for different Segment 2 diameters at λ = 0.6. The black arrows are representing the torque vectors generated on the blades.
4. Conclusions
In this paper, the flow around the Ugrinsky wind turbine with various blade dimensions was simulated using the regularized lattice Boltzmann method coupled with the virtual flux method. The remaining parameters from the previous research were calculated to ensure the optimization [19]. In the optimization, the maximum power coefficient values and the average value of the power coefficient for neighboring TSRs were employed for evaluating the optimal dimensions. The latter evaluation method was used to include the fluctuation of the blade speed that occurs in real-life conditions.
The dimension of Segment 1 was fixed to S = 0.30D and 0.40D, while various Segment 2 dimensions were considered, from L = 0.9R to 1.3R, to investigate the effects of each dimension S and L and of TSR on the torque coefficient CQ and the power coefficient CP. The results suggested that, in general, CQ and CP peaked at λ = 0.5–0.6, and their values were correlated with S, torque arm length, and vortex distance. However, in some cases, such as (S, L, λ) = (0.40D, 1.1R, 0.4), the influence of the L value was not determined. To determine the general principle of the turbine and further improve its performance, optimization focusing on blade shapes, overlap ratio, blade length, blockage ratio, etc. was suggested.
This study suggests some principles regarding the Ugrinsky wind turbine:
- The geometrical properties are dominant in the returning blade period of Segment 2 regardless of the TSR, and an increase in torque arm length may increase the negative torque.
- The geometrical properties are dominant in the advancing blade period of Segment 1 at λ = 0.5; however, the increase in the wind-receiving area (swept area) may not benefit at λ = 0.6.
- The distance between edge vortices created on each segment may affect the growth of those vortices. This study demonstrates that a shorter distance benefits the growth of the vortex and lowers the central pressure of the vortex.
Author Contributions
Conceptualization, L.S. and T.F.; methodology, L.S. and T.F.; software, T.F. and K.M.; validation, L.S.; investigation, L.S.; resources, T.F. and K.M.; writing—original draft preparation, L.S.; writing—review and editing, L.S., T.F. and K.M.; visualization, L.S.; supervision, T.F. and K.M.; project administration, T.F. and K.M.; funding acquisition, T.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jang, H.; Kim, D.; Hwang, Y.; Paek, I.; Kim, S.; Baek, J. Analysis of Archimedes Spiral Wind Turbine Performance by Simulation and Field Test. Energies 2019, 12, 4624. [Google Scholar] [CrossRef] [Green Version]
- Roy, S.; Saha, U.K. Review on the numerical investigations into the design and development of Savonius wind rotors. Renew. Sustain. Energy Rev. 2013, 24, 73–83. [Google Scholar] [CrossRef]
- Mitchell, S.; Ogbonna, I.; Volkov, K. Improvement of Self-Starting Capabilities of Vertical Axis Wind Turbines with New Design of Turbine Blades. Sustainability 2021, 13, 3854. [Google Scholar] [CrossRef]
- Tian, W.; Song, B.; Van Zwieten, J.H.; Pyakurel, P. Computational Fluid Dynamics Prediction of a Modified Savonius Wind Turbine with Novel Blade Shapes. Energies 2015, 8, 7915–7929. [Google Scholar] [CrossRef]
- Zhang, B.; Song, B.; Mao, Z.; Tian, W.; Li, B.; Li, B. A Novel Parametric Modeling Method and Optimal Design for Savonius Wind Turbines. Energies 2017, 10, 301. [Google Scholar] [CrossRef] [Green Version]
- Alaimo, A.; Esposito, A.; Milazzo, A.; Orlando, C.; Trentacosti, F. Slotted Blades Savonius Wind Turbine Analysis by CFD. Energies 2013, 6, 6335–6351. [Google Scholar] [CrossRef]
- Chakroun, Y.; Bangga, G. Aerodynamic Characteristics of Airfoil and Vertical Axis Wind Turbine Employed with Gurney Flaps. Sustainability 2021, 13, 4284. [Google Scholar] [CrossRef]
- Müller, G.; Chavushoglu, M.; Kerri, M.; Tsuzaki, T. A resistance type vertical axis wind turbine for building integration. Renew. Energy 2017, 111, 803–814. [Google Scholar] [CrossRef] [Green Version]
- IRENA. Renewables for Refugee Settlements: Sustainable Energy Access in Humanitarian Situations; International Renewable Energy Agency: Abu Dhabi, United Arab Emirate, 2019; p. 4. [Google Scholar]
- Feng, F.; Tong, G.; Ma, Y.; Li, Y. Numerical Simulation and Wind Tunnel Investigation on Static Characteristics of VAWT Rotor Starter with Lift-Drag Combined Structure. Energies 2021, 14, 6167. [Google Scholar] [CrossRef]
- Ushiyama, I. Introduction to Wind Turbine Engineering, 2nd ed.; Morikita Publishing: Tokyo, Japan, 2013; pp. 53–60. (In Japanese) [Google Scholar]
- Ushiyama, I.; Nagai, H.; Shinoda, J. Experimentally determining the optimum design configuration for Savonius rotors. Trans. Jpn. Soc. Mech. Eng. Ser. B 1986, 52, 2973–2981. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, M.; Gábor, J.; Elemér, P.; Dominique, T. Optimization of Savonius turbines using an obstacle shielding the returning blade. Renew. Energy 2010, 35, 2618–2626. [Google Scholar] [CrossRef]
- El-Askary, W.A.; Nasef, M.H.; AbdEL-hamid, A.A.; Gad, H.E. Harvesting wind energy for improving performance of Savonius rotor. J. Wind Eng. Ind. Aerodyn. 2015, 139, 8–15. [Google Scholar] [CrossRef]
- Roy, S.; Ducoin, A. Unsteady analysis on the instantaneous forces and moment arms acting on a novel Savonius-style wind turbine. Energy Convers. Manag. 2016, 121, 281–296. [Google Scholar] [CrossRef]
- Matsui, T.; Fukui, T.; Morinishi, K. Computational fluid dynamics on a newly developed Savonius rotor by adding sub-buckets for increase of the tip speed ratio to generate higher output power coefficient. J. Fluid Sci. Technol. 2020, 15, JFST0009. [Google Scholar] [CrossRef] [Green Version]
- Kazhinsky, B.B. Low-Capacity Free-Flow Hydroelectric Power Plants; Gosenergoizdat: Moscow, Russia, 1950; pp. 30–32. (In Russian) [Google Scholar]
- Sakamoto, L.; Fukui, T.; Morinishi, K. Performance Evaluation of Ugrinsky Wind Turbine using Numerical Simulation. In Proceedings of the Fluids Engineering Conference, Osaka, Japan, 6 November 2020. (In Japanese). [Google Scholar]
- Sakamoto, L.; Fukui, T.; Morinishi, K. Numerical Study on the Performance of 2-D Ugrinsky Wind Turbine Model. WIT Trans. Ecol. Environ. 2021, 254, 113–124. [Google Scholar]
- Izham, M.; Fukui, T.; Morinishi, K. Application of Regularized Lattice Boltzmann Method for Incompressible Flow Simulation at High Reynolds Number and Flow with Curved Boundary. J. Fluid Sci. Technol. 2011, 6, 812–822. [Google Scholar] [CrossRef] [Green Version]
- Tanno, I.; Morinishi, K.; Matsuno, K.; Nishida, H. Validation of Virtual Flux Method for Forced Convection Flow. JSME Int. J. Ser. B 2006, 46, 1141–1148. [Google Scholar] [CrossRef] [Green Version]
- Morinishi, K.; Fukui, T. An Eulerian approach for fluid-structure interaction problems. Comput. Fluids 2012, 65, 92–98. [Google Scholar] [CrossRef]
- Yu, D.; Mei, R.; Shyy, W. A multi-block lattice Boltzmann method for viscous fluid flows. Int. J. Numer. Methods Fluids 2002, 39, 99–120. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Tsutahara, M.; Hiraishi, M. Study of Outflow Boundary Condition for Finite Difference Lattice Boltzmann Method. Trans. Jpn. Soc. Comput. Eng. Sci. 2006, 6, 7–12. [Google Scholar]
- Lei, C.; Cheng, L.; Kavanagh, K. A finite difference solution of the shear flow over a circular cylinder. Ocean Eng. 2000, 27, 271–290. [Google Scholar] [CrossRef]
- Matsumiya, H.; Kieda, K.; Taniguchi, N.; Kobayashi, T. Numerical Simulation of 2D Flow around a Circular Cylinder by the Third- Order Upwind Finite-Difference Method. Trans. Jpn. Soc. Mech. Eng. Ser. B 1993, 59, 2937–2943. [Google Scholar] [CrossRef] [Green Version]
- Mittal, S.; Kumar, V. Flow-induced vibrations of a light circular cylinder at reynolds numbers 103 to 104. J. Sound Vib. 2001, 245, 923–946. [Google Scholar] [CrossRef] [Green Version]
- Stinger, R.M.; Zang, J.; Hillis, A.J. Unsteady RANS computations of flow around a circular cylinder for a wide range of Reynolds numbers. Ocean Eng. 2014, 87, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Fujii, K. Numerical Method for Computational Fluid Dynamics; University of Tokyo Press: Tokyo, Japan, 1994; pp. 174–180. (In Japanese) [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).