Abstract
A frequency response analysis (FRA) is a well-known technique for evaluating the mechanical stability of a power transformer’s active part components. FRA’s measuring practices have been industrialised and are codified in IEEE and IEC standards. However, because there is no valid coding in the standard, the interpretation of FRA data is still far from being a widely acknowledged and authoritative approach. This study proposes an innovative fault segmentation and localisation technique based on FRA data. The algorithm is based on regression analysis to estimate the repeatability and relationship between the FRA fingerprint and the latest measured data. Initially, the measuring frequency is discretised into three regions to narrow the location of the fault; the regression model of the fingerprint and current FRA data are then evaluated. As a benchmark, two statistical indicators are the employed benchmark against the proposed method. Finally, the proposed scheme identifies and characterises various transformer conditions, such as healthy windings, axial and radial winding deformations, core deformation and electrical faults. The database used in this study consists of FRA measurements from 70 mineral-oil-immersed power transformers of different designs, ratings and manufacturers that were physically inspected for various faults and comparable frequency regions. The results achieved corroborate the efficacy of the proposed regression analysis fault recognition algorithm (RAFRA) model for transformer fault diagnosis using FRA. Further recommendations are made to address the reproducibility concerns induced by multiple FRA testing conditions.
1. Introduction
The massive amount of energy usage and power demand in South Africa has led to power transformers operating under abnormal loading conditions. Therefore, the transformer runs a risk of failure due to high-stress operating levels. Generally, this occurs as a result of degradation in the insulation material, which weakens the clamping structure holding the winding core and subjects the transformer to vibrations and short circuit forces [1]. Studies in [2,3] reveal that approximately 70–80% of transformer failures occur as a result of a short circuit. Therefore, early detection of winding faults would be of great interest for power utilities for preventative maintenance management [4,5]. In a survey conducted by CIGRE [6,7] covering 58 power utilities from 21 countries, different transformers were collected and tested according to their standards for assessing the components with a major contribution to transformer failures. The windings were found to have a major contribution of 37.69%. The outcome of the survey is presented in Figure 1. This raises a serious concern since most winding failures occur due to a short circuit. The rate of failures in the survey was calculated according to Equation (1).
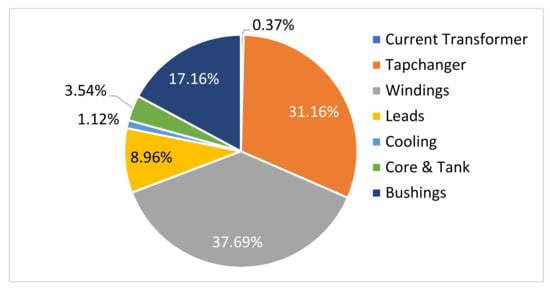
Figure 1.
Failure location of substation above 100 kV.
The rate of failure is calculated as:
where:
number of transformer failures in ith year
number of transformers operating in ith year
Reference period (ranging from 3 years to 11 years)
Apart from economic constraints caused by short circuit forces, the bumping of the transformer during transportation from the factory to the site could also contribute to huge losses. In order to reduce transformer failures, in-depth knowledge of the mechanical integrity of the power transformer, mainly the windings, is advantageous for monitoring the condition of the transformer and its reliability. The evaluation of the mechanical condition of a transformer in good condition after manufacturing requires an extra cost. If the transformer is required to be returned to the factory, there is also an additional cost. Hence, the development of standard diagnostic tools for distinctive testing and interpretation of the mechanical status of the winding and core is imperative [8,9] to make an informed decision whether to return the transformer to the factory or not.
To evaluate the mechanical integrity of the transformer, sweep frequency response analysis (SFRA) is widely accepted as the best approach [9]. This technique was first used by Dick and Erven in 1978 in their paper published by the IEEE [10]. It is a non-destructive test that measures the frequency response of the windings in the frequency range of 20 Hz to 2 MHz. A comparison between two frequency characteristics (the fingerprint and the latest test) is observed to detect discrepancies. If the resultant over-laying of the frequency characteristics reveals any discrepancies, it is an indication that the winding is potentially damaged. To investigate the severity of the fault, there is no definite answer unless the transformer tank is dismantled. The SFRA has great potential to be widely accepted and established as an interpretational scheme such as the dissolved gas analysis (DGA) presented by the authors in [11,12,13,14,15,16,17,18,19,20] for transformer oil analysis. A few hurdles still require investigation, but with the expanding demand for non-intrusive assessment techniques, it has a great future use.
Studying the transformer winding deformation in a real transformer would be very costly if attempted, as the winding would have to be deformed permanently to create various deformations. Considering this rationale, the development of a winding model is more accessible to explore the understanding of SFRA in winding deformations. Unlike an actual transformer, a model can simulate various winding deformations, which is not possible on a real transformer. Simulation software such as MATLAB, ELECNET and MAGNET can be used with reasonable accuracy in studying the frequency responses of the winding. In [12], the IEEE makes recommendations about the use of computer models and simulations in studying various transformer conditions.
In recent studies [15,16], machine learning has been proposed as a methodology to evaluate transformer FRA data. By examining various winding failure modes, the winding frequency response can be understood. Further, the severity of a fault can be established in a model simulation to monitor the condition of a transformer and its reliability. Electrical faults such as inter-turn faults and their severity can also be investigated using SFRA. In general, every winding fault must be investigated to fully understand and interpret the use of SFRA for accurate transformer monitoring.
This work provides a novel regression-analysis-based detection and categorisation scheme using FRA data. The FRA fingerprint taken at the manufacturer’s plant and the latest FRA data underpins the proposed technique. By discretising the measuring frequency band, several numerical indicators are employed as a benchmark. To detect and classify transformer winding abnormalities, regression analysis is used in conjunction with indices.
2. Materials and Methods
Figure 2 shows the stages involved in developing a regression analysis fault recognition algorithm (RAFRA) for a specific FRA data set. The process includes seven major steps, i.e., FRA data preliminaries, measuring frequency discretisation, fingerprint extraction, development of regression analysis model, numerical indicators benchmarking, performance analysis and report findings. If the model’s performance is poor as a result of the unavailability of the initial transformer fingerprint records, the RAFRA proposes using the FRA dataset of a design with similar technical specifications to improve results.
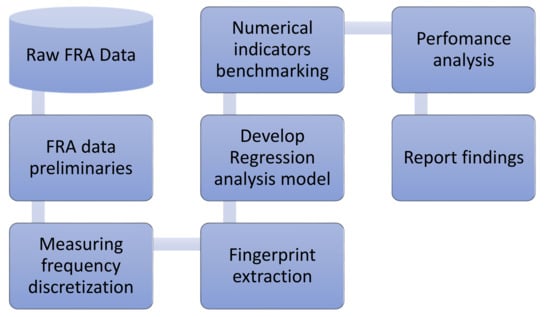
Figure 2.
Flowchart for regression analysis fault detection scheme, FRA—Fault Recognition Algorithm.
2.1. Fault Recognition Algorithm (FRA) Database
The database for this study is comprised 150 FRA results from 70 mineral-oil-immersed power transformers with different designs, ratings and manufacturers that were physically inspected for various faults and comparable frequency regions. Different types of transformers are included in the database, including distribution, transmission and generator step-up units. Thus, every FRA measurement in the database correlates with a certain transformer condition. This study focuses on five transformer mechanical and electrical faults: healthy windings, axial and radial winding deformations, core deformation and electrical faults.
2.2. Fault Recognition Algorithm (FRA) Data Preliminaries
Data labelling and de-noising are the two primary processes involved with FRA data pre-processing. Individual latest FRA test measurements are allotted a label during FRA data labelling. De-noising is performed to ensure that the diversity of noise interferences that might affect SFRA tests, notably in substation surroundings, are eliminated. These interferences may be segmented into narrow-band and broadband noise. The harmonic current interference and its harmonics constitute a quintessential narrow-band noise. The latter is a multiple of the general electric utility total power frequency. The FRA waveforms in the lower-frequency region spanning 30 Hz and 100 Hz are considerably influenced by narrow-band interference. The effects of narrow-band disturbance are relatively uncommon above 300 Hz. Narrow-band noise can also be discovered in power stations with considerable harmonic contamination. In practice, it has also been found that the disturbances may be due to the measurement system. In the frequency region about 3 Hz to 100 Hz, the impacts of disturbances are significant, even though at harmonic frequencies the effects are less apparent but detectable. Interestingly, noise characteristics typically emerge during measurements in an elevated electromagnetic field intensity setting, such as that prevalent in power stations having rated voltages exceeding 380 kV. Typical narrow-band noise interference is illustrated in Figure 3a.
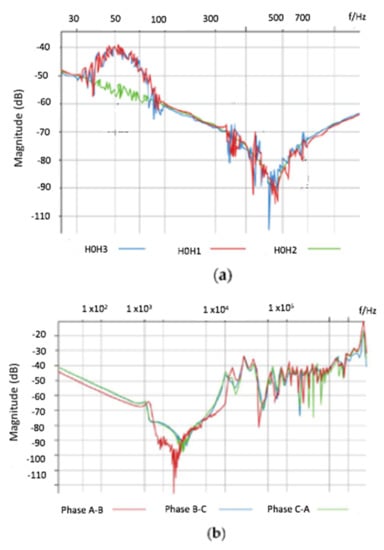
Figure 3.
(a) Typical narrow-band interference. (b) Typical broadband interference.
A noise floor will always emerge during FRA measurements, and this will distort the FRA waveforms. The attached FRA test device is the source of this specific sort of internal noise, which is classed as broadband interference. The dynamic range of the FRA test device defines the extent of disturbance. The noise floor may be defined as the measurement of the signal produced by adding all of the interferences and undesirable signals in a measuring device. It is employed to evaluate the minimal signal intensity that may be detected. The dynamic range of an FRA test device specifies its noise floor. The IEC 60076-18 standard specifies a dynamic range of −90 dB to +10 dB as a threshold. Typical narrow-band noise interference is illustrated in Figure 3b. The measured transfer function (output voltage/input voltage) in the FRA measurement is converted to decibels (dB) by and presented as the magnitude (dB).
Several techniques may be incorporated in the measurement setup to minimise the impact of external disturbances on FRA waveforms. Practically, external interference can be curbed through the use of adequate connection procedures and available noise-suppressing input filters.
2.3. Fault Recognition Algorithm (FRA) Measuring Frequency Discretisation
The frequency response of a transformer is intrinsically linked to the transformer’s active parts components such as core clamps, core, windings, leads, etc. In distinct frequency ranges, the active part components dominate the frequency response. As a result, different faults in transformers may be categorised by distinguishing these ranges. The ranges of these frequency regions are dependent on a variety of parameters, including application, MVA rating, core steel grade and winding conductor configuration, and a generalised range cannot be wholly determined. The segmentation and tracking of distinct FRA profiles is the primary basis for developing a numerical frequency discretisation algorithm. The FRA data from 70 transformers of various applications, MVA rating, and winding configurations are examined in this study. The percentage breakdown of fault conditions of these transformers is demonstrated in Figure 4. Based on these factors, seven transformer conditions identifiers are recognised in various frequency sub-ranges. Table 1 shows the proposed segmentation of FRA waveforms based on distinct features in different frequency sub-bands.
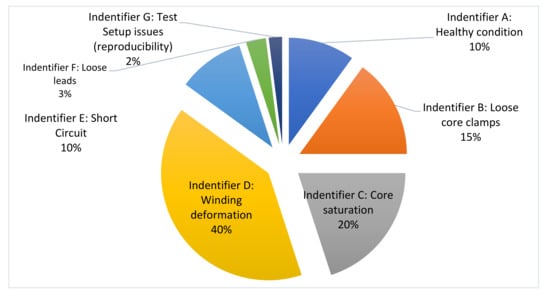
Figure 4.
Segmentation of FRA repository.

Table 1.
Proposed numerical frequency response segmentation.
Categorising the frequency sub-bands according to influencing factors optimises the probability of narrowing down the transformer component that is damaged. Moreover, Table 1 provides a familiar idea of the frequency range. The frequency range for the influenced components will vary in each frequency sub-band. The following assumptions were made in an attempt to formulate the frequency sub-bands in Table 1 and to attempt reproducibility of the latest FRA data:
- The FRA data of investigated transformers with known faults were compared with previous FRA data of the same unit.
- In the case where the fingerprint of the same unit was not available, the latest FRA data was compared with the same MVA unit designed according to the same technical specification.
- The FRA data of one phase were compared with those of another phase of the same unit.
2.4. Development of Regression Analysis Model
After the FRA fingerprint and the latest FRA measurement has been extracted, regression analysis in the application of FRA is proposed and employed. The modelling of the relationship between the latest sweep frequency response data (LSD) and a transformer fingerprint (explanatory variables) is further proposed to contribute to existing statistical indicators.
Prediction requires a unit of association; there should be an entity that relates the two FRA variables. To accommodate inevitable errors in the model, the prediction equation is written as in Equation (2). A simple linear regression model is presented where is the y-intercept (expected response given x), is the slope (or regression coefficient) and is the error term.
The proposed FRA criterion for the proposed method is illustrated in Figure 5. The criterion was segmented into four classes: healthy condition, slightly deformed, deformed and totally deformed.
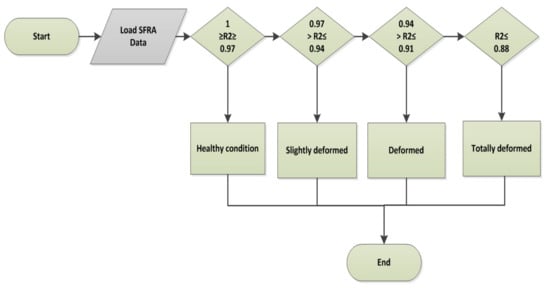
Figure 5.
Proposed FRA regression analysis method.
The criterion for these conditions is formulated based on the statistical evaluation of FRA measurements from 70 mineral-oil-immersed power transformers of different designs, ratings, and manufacturers that were physically inspected for various faults. The correlation of coefficients is a key parameter in specifying the extent to which the latest FRA profile varies from the fingerprint taken at the manufacturer premises during factory acceptance testing.
In [21,22], regression analysis was employed to evaluate the relationship between two or more variables in diagnosing the condition of electrical equipment. In [21], the correlation between various transformer oil properties with water content was studied in a transformer. The results yielded a correlation of more than 90%. In [22], the decomposition of low voltage cables was studied by studying the relationship between the voltage response and the ageing of the insulation material.
2.5. Numerical Indicators Benchmarking
Several statistical indices have been proposed in the standards and literature to analyse deviations in various frequency sub-bands to classify the severity of the deformation. Generally used statistical techniques are cross-correlation (CC) and absolute sum of logarithmic error (ASLE). When there is a perfect correlation between two frequency responses, the CC and ASLE will be 1 and 0, respectively. The analysed response is divided into sub-bands before the numerical techniques are applied to increase the chances of locating the location of the fault, since frequency regions represent specific transformer parts, as presented earlier. After segmenting the FRA measuring frequency into three frequency sub-bands, two numerical indicators (CC and ASLE) are employed as given in Equations (3) and (4). These numerical indicators are evaluated in three sub-bands using the FRA fingerprint and latest FRA measurement. These indicators appraise the divergence patterns for various transformer fault conditions. This process is called benchmarking of the proposed regression model.
Here,
Raw data of the transformer fingerprint
The mean of the transformer fingerprint
The raw data from the latest measurement
The mean for the latest measurement
The total number of data points.
In [23,24,25], various statistical indicators were employed to interpret transformer FRA results. It is impracticable to employ all of them as a benchmark in this work, and hence only CC and ASLE were chosen for comparison with the proposed methodology discussed in the previous section, particularly as they give different results.
2.6. Performance Analysis
The performance analysis is then tabulated where the model’s goodness of fit coefficients are shown. The R2 (coefficient of determination) illustrates the % of the volatility of the LSD variable which is explained by the FRA fingerprint profile. The stronger the relationship, the closer the R2 is to 1. These data are further compared with two statistical indicators as a benchmark to evaluate the performance of RAFRA.
3. Results
In this section, four case studies of field transformers, courtesy of a local transformer manufacturer, power utility and local municipality, are presented. All the case studies hold distinct failure modes and each is interpreted using the benchmarking numerical indicators and the proposed RAFRA. The interpretational tool evaluates the FRA traces in the case studies at the lower-, upper- and higher-frequency regions. The case studies under investigation are presented in Table 2.

Table 2.
Case studies under investigation.
3.1. Measurement Setup
The frequency responses of the units were ascertained from measurements performed personally and contributed by the relevant parties as mentioned above. In some cases, the units were reported to have suspected faults and no internal inspection was performed. Hence, the results of analyses of these units were not verified. Nonetheless, a cautious evaluation of the condition of the transformer is presented using the available information. The performance analysis incorporates the proposed RAFRA and benchmarking statistical indicators. The measurement setup from one of the test cases is shown in Figure 6.

Figure 6.
M5400 FRA Measurement setup.
3.2. Case Studies
3.2.1. Investigating Frequency Response of Transformers in Good Condition
To implement numerical indices on a real test unit, the sub-band frequency responses which are affected by specific transformer parts are presented.
Case Study 1
For the first case, two SFRA traces measured during FAT in 2015 and again in routine maintenance test in 2017 are available for comparison. In Figure 7, a frequency response characteristic based on a fingerprint for the HV winding of Phase A is demonstrated. Bushings with resin impregnated paper (RIP) insulation and lightning impulse withstand voltages of 350 kV and 200 kV on the high-voltage and low-voltage sides were used during the test. The capacitive values of the bushings have great values and have an inconsequential effect on the interpretation of the FRA results.
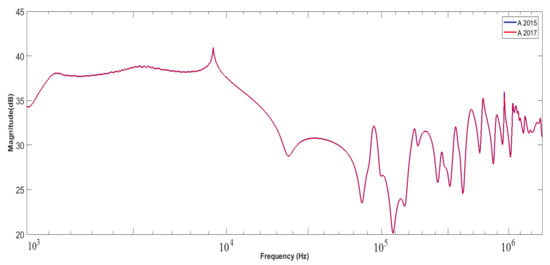
Figure 7.
Frequency response based on a fingerprint comparison.
The transformer had only three years in service and was still relatively new. An analysis of the frequency response for this unit is presented in Table 3 for the chosen numerical techniques after careful consideration in the previous section. Precautions were taken during the measurements to ensure reproducibility of the results taken during FAT in 2015.

Table 3.
Numerical technique for healthy winding condition.
The application of regression analysis on the frequency response is presented in Table 4 and Figure 8. The numerical and regression values appear to be in good agreement across the entire measuring frequency range. There is no deviation identified by the proposed techniques—the winding is indeed in a healthy condition.

Table 4.
Regression analysis for frequency regions in healthy winding conditions.
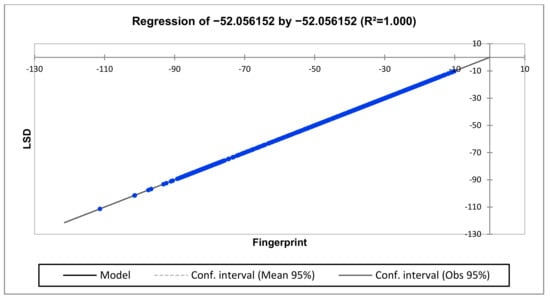
Figure 8.
Regression for healthy winding conditions.
The goodness of fit statistics above shows an R2 of 1, which indicates that the LSD in 2017 perfectly correlates with the transformer fingerprint taken in 2015.
The regression characteristics show that the latest SFRA data has a perfect fit of the fingerprint data across all the frequency regions.
3.2.2. Investigating Frequency Response for Transformers with Winding Damages
Case Study 2
In this case, a 50 MVA 66/11.66 kV, YNd1 transformer winding frequency response is analysed. The transformer fingerprint is compared against the latest SFRA measurement of the unit that is suspected of being faulty and is presented in Figure 9. Bushings with resin impregnated paper (RIP) insulation and lightning impulse withstand voltages of 250 kV and 200 kV on the high-voltage and low-voltage sides were used during the test. The capacitive values of the bushings have large values and result in a negligible effect on the interpretation of the FRA results; accurate analysis of the data can therefore be achieved.
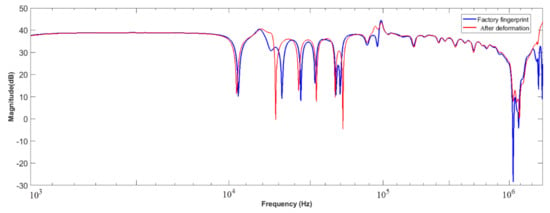
Figure 9.
Frequency responses for a transformer faulty winding based on fingerprint comparison.
There are obvious deviations from the frequency characteristics in the middle-frequency region at about 10 to 100 kHz and again at higher frequencies above 1 MHz. The frequency response analysis of the unit was divided into sub-bands to assess each frequency region separately as shown in Table 5. The results are presented in Figure 10, Figure 11 and Figure 12 and the severity of the observed deviations in the frequencies are presented. The CC and ASLE results agree at lower- and higher-frequency regions except for the middle-frequency region. The CC and ASLE suggest a totally deformed and slightly deformed condition, respectively.

Table 5.
Numerical technique for fingerprint vs. after deformation.
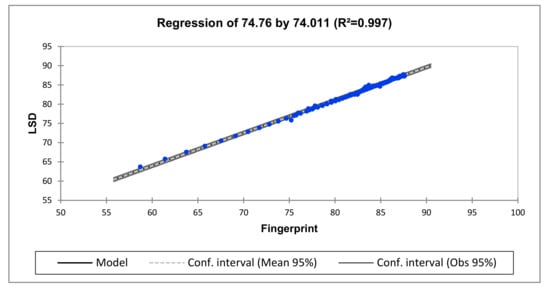
Figure 10.
Regression analysis for fingerprint vs. after deformation (lower-frequency region).
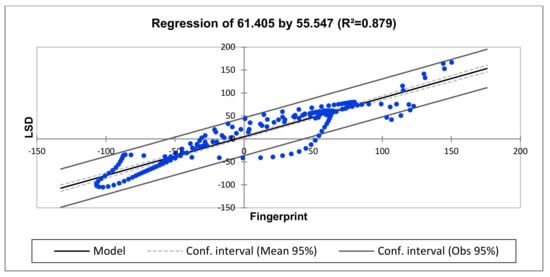
Figure 11.
Regression analysis for fingerprint vs. after deformation (medium-frequency region).
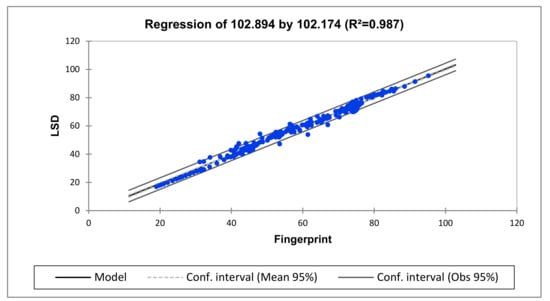
Figure 12.
Regression for fingerprint vs. after deformation (high-frequency region).
To apply regression analysis in this case study, the frequency response data was again divided into sub-bands and the regression for each region is presented in Table 6. The regression analysis shows good agreement with CC and ASLE at the lower-, medium- and higher-frequency regions with R2 = 0.997, R2 = 0.879 and R2 = 0.987, respectively. The middle-frequency region is deformed. Based on the analysis, this unit is likely diagnosed with a winding deformation.

Table 6.
Regression analysis for fingerprint vs. after deformation.
Equation of the model: LSD = 12.745 + 0.854 × Fingerprint
Interpretation (74.76): Given the R2 value, 100% of the variability of the dependent variable LSD is explained by the explanatory variable.
Equation of the model (61.405): LSD = 4.861 + 0.845 × Fingerprint
Interpretation (61.405): Given the R2 value, 88% of the variability of the dependent variable LSD is explained by the explanatory variable.
Equation of the model: LSD = −1.052 + 1.014 × Fingerprint
Interpretation (102.894): Given the R2 value, 99% of the variability of the dependent variable LSD is explained by the explanatory variable.
In the case presented, it can be observed from the equation of the model at each frequency region that in the range of the variable fingerprint that is taken into account here, when the fingerprint increases by one hertz, the LSD increases by 0.854, 0.845 and 1.1013 at the lower-, medium- and high-frequency regions, respectively. With the support of the R2 value obtained for each frequency region and the regression characteristics, the lower- and high-frequency regions seem to indicate a good correlation between the fingerprint and the LSD. However, the R2 value and the regression characteristic of the medium frequency indicate that the LSD does not have a good fit of the fingerprint. In this regard, the regression agrees with the results obtained for C and ASLE across all the frequency regions. The overall deviations observed on the medium-frequency region indicate that there is a deformation within the main or tap windings.
Case Study 3
In this case, a 40 MVA, 132/11 kV 3-Ph 2-Winding transformer is assessed on phase C tap position 1, as shown in Figure 13. The transformer is tested against a fingerprint that was obtained during a factory acceptance test in 2013. The FRA measurements were performed at tap position 1 with bushings fitted. The bushing test tap was used to inject the FRA signal and to alleviate the terminal voltage on account of capacitive dividers.
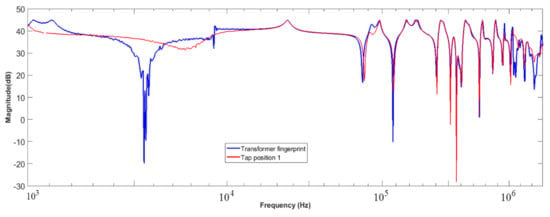
Figure 13.
Comparison between fingerprint and regulator winding (Phase C).
The deviations at about 5.5 kHz and also at about 100 kHz are generally governed by core and tap winding deformation, respectively. The numerical technique results for this frequency response are given in Table 7. The CC shows deformed and slightly deformed conditions at the lower- and middle-frequency regions, respectively. The ALSE shows totally deformed and deformed conditions at the lower- and middle-frequency regions. In this case, the CC and ASLE agree on the higher-frequency region with the ALSE, showing high warning compared to the CC across all the frequency regions.

Table 7.
Numerical technique results for regulator winding.
The frequency response regression parameters and equations for this test case are shown in Table 8 and Table 9. Regression analysis shows R2 = 0.251, R2 = 0.935 and R2 = 0.838 at the lower-, medium- and higher-frequency regions, respectively. The regression analysis shows totally deformed, healthy and slightly deformed conditions at the lower-, middle- and high-frequency regions. Based on this result, the regression analysis is sensitive to the deviations observed on the resonances at higher frequencies. A graphical representation of the regression results is shown in Figure 14, Figure 15 and Figure 16. This unit is likely to be diagnosed with core deformation and shorted turns on the tap winding (Winding C or regulator) due to the slight deviation observed at the lower-frequency region and 100 kHz.

Table 8.
Regression analysis for frequency regions at tap position 1.

Table 9.
Equation of the model for frequency regions at tap position 1.
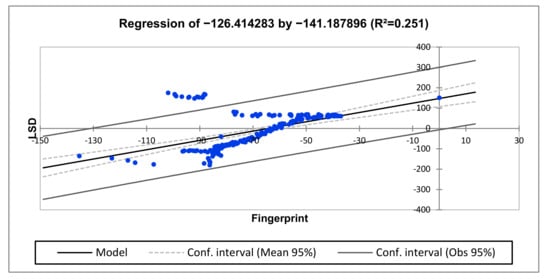
Figure 14.
Regression of Phase C, tap position 1 (lower-frequency region).
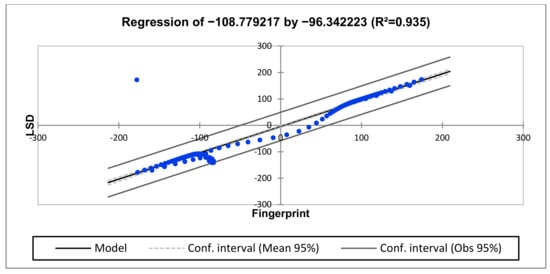
Figure 15.
Regression of Phase C, tap position 1 (medium-frequency region).
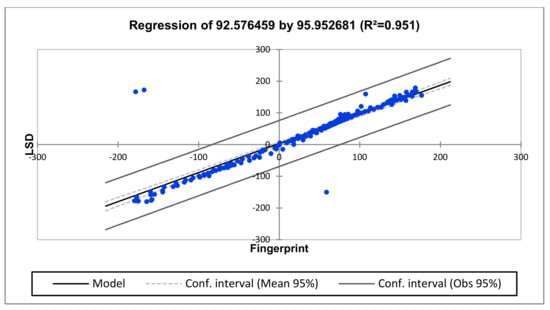
Figure 16.
Regression of Phase C, tap position 1 (higher-frequency region).
In Case III, it can be observed from the equation of the model in Table 9 for each frequency region that in the range of the variable fingerprint that is considered here, when the fingerprint increases by one hertz, the LSD increases by 2.286, 0.9963 and 0.9187 at the lower-, medium- and high-frequency regions, respectively. When the fingerprint is increased by one hertz, it increases by approximately two hertz, indicating an obvious deformation at the lower-frequency regions. This is supported by the measured frequency characteristic in Figure 16.
Case Study 4
In this case, a transformer manufactured in 1983 and taken out of service in 2016 is tested for frequency response analysis on the HV winding. The results of the SFRA measurements are shown in Figure 17. Since there were no established SFRA measurements during the manufacturing of the transformer, no fingerprint is available for comparison. Hence, the SFRA measurements were performed by comparing different phases of the transformer. Obvious deformations can be seen between H2-H1 and H3-H2 at the middle-frequency region (10–100 kHz) and again at about 550 kHz. The magnitude of the responses also decreases gradually at about 500 kHz compared to the deviations at 10–100 kHz. A good correlation is maintained amongst the phases in the lower-frequency region (1–10 kHz) and at about 100–500 kHz. The transformer was tested with the tank filled with oil and the bushing test tap grounded. The bushings’ capacitive values are consistent throughout a broad frequency range, and this alleviates the camouflaging of the actual transformer FRA profile on account of the bushing’s frequency response.
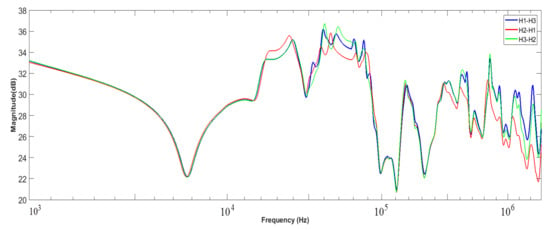
Figure 17.
Frequency response of the HV winding for the transformer of steel mill 2.
The interpretation of the SFRA results using numerical techniques is presented in Table 10, Table 11 and Table 12. To determine the winding to be used as a fingerprint in this case study, the highest value of CC and lowest value of ASLE were chosen from the results since they show great constancy in the previous cases. The comparison between H1-H3 vs. H2-H1, H2-H1 vs. H3-H2 and H3-H2 vs. H1-H3 reveals that H3-H2 has the lowest deviations compared with the other phases. It will thus be taken as the baseline (fingerprint) since it is healthier than the other phases.

Table 10.
Numerical technique for H1-H3 vs. H2-H1.

Table 11.
Numerical technique for H2-H1 vs. H3-H2.

Table 12.
Numerical technique for H3-H2 vs. H1-H3.
To apply the regression analysis, all the responses are presented by comparing different phases, as shown in Table 13, Table 14 and Table 15. The comparison between H1-H3 vs. H2-H1 indicates that there is a slight deformation in the middle- and higher-frequency regions, as shown in Figure 18, Figure 19 and Figure 20.

Table 13.
Regression analysis for H1-H3 vs. H2-H1.

Table 14.
Regression analysis for H2-H1 vs. H3-H2.

Table 15.
Regression analysis for H3-H2 vs. H1-H3.
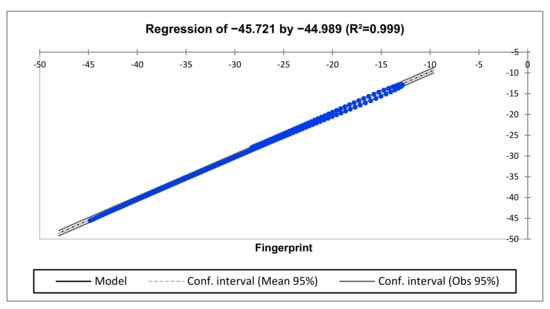
Figure 18.
Regression for H2-H1 vs. H3-H2 (lower-frequency region).
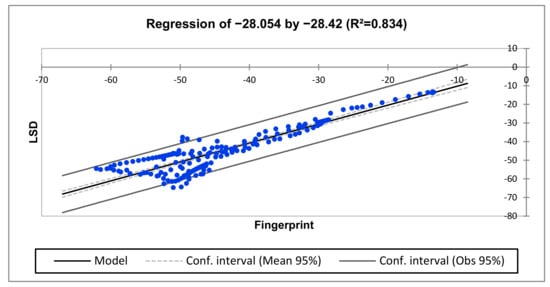
Figure 19.
Regression for H2-H1 vs. H3-H2 (medium-frequency region).
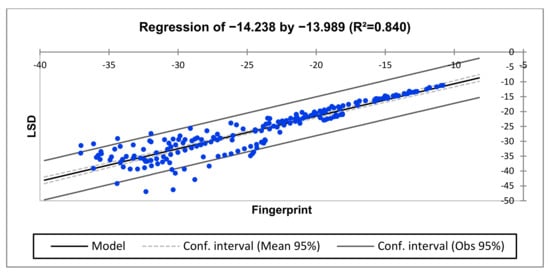
Figure 20.
Regression for H2-H1 vs. H3-H2 (high-frequency region).
Equation of the model: LSD = 0.465 + 1.021 × Fingerprint
Equation of the model: LSD = −5.834 × 10−2 + 1.017 × Fingerprint
Equation of the model: LSD = 0.281 + 1.093 × Fingerprint
The regression for comparing H2-H1 vs. H3-H2 is represented in Figure 21, Figure 22 and Figure 23 for the low-, middle- and higher-frequency regions. The middle- and higher-frequency regions reveal deformed and slightly deformed conditions, respectively.
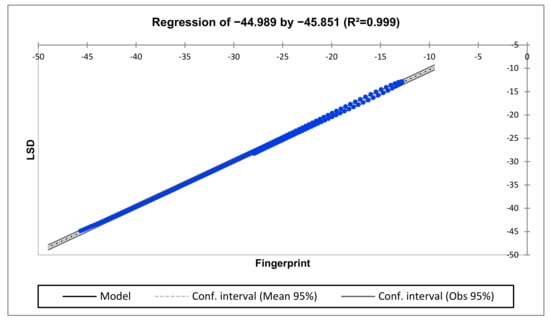
Figure 21.
Regression for H2-H1 vs. H3-H2 (lower-frequency region).
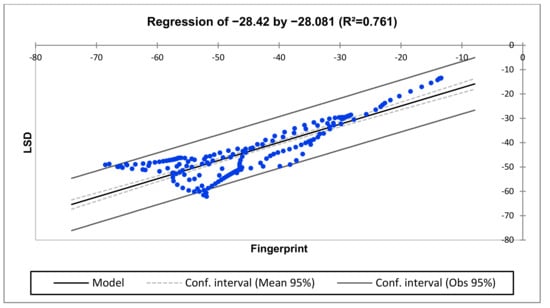
Figure 22.
Regression for H2-H1 vs. H3-H2 (medium-frequency region).
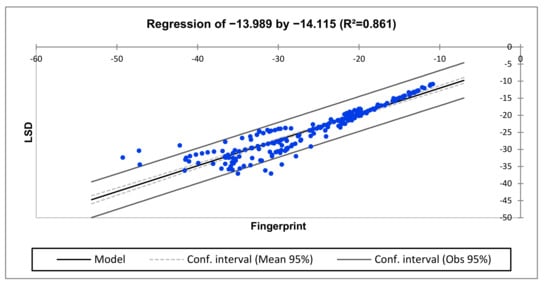
Figure 23.
Regression for H2-H1 vs. H3-H2 (high-frequency region).
Equation of the model: LSD = −0.560 + 0.976 × Fingerprint
Equation of the model: LSD = −9.952 + 0.748 × Fingerprint
Equation of the model: LSD = −4.460 + 0.758 × Fingerprint
The regression comparison between H3-H2 vs. H1-H3 is represented in Figure 24, Figure 25 and Figure 26. The middle-frequency region reveals a slight winding deformation.
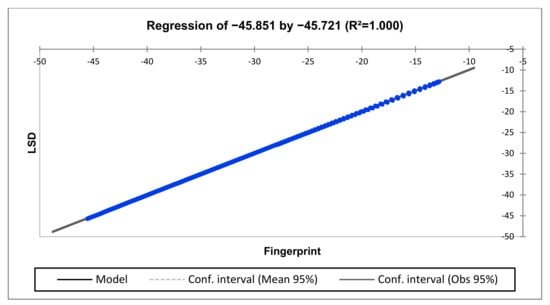
Figure 24.
Regression for H3-H2 vs. H1-H3 (lower-frequency region).
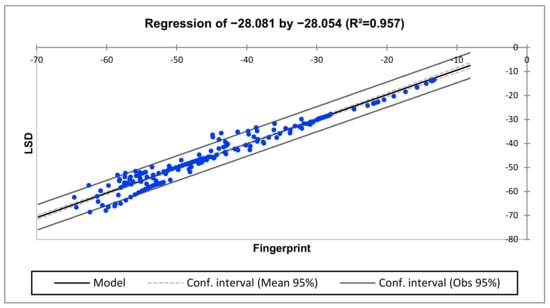
Figure 25.
Regression for H3-H2 vs. H1-H3 (medium-frequency region).
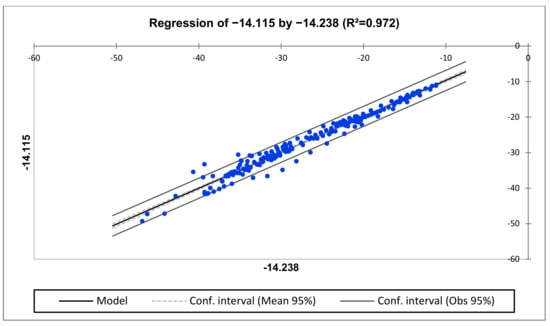
Figure 26.
Regression for H3-H2 vs. H1-H3 (High-frequency region).
Equation of the model: LSD = 7.653 × 10−2 + 1.003 × Fingerprint
Equation of the model: LSD = 0.809 + 1.024 × Fingerprint
Equation of the model: LSD = 0.457 + 1.0123 × Fingerprint
For Case IV, the equation of the model at each frequency region for all the compared phases indicates that when the fingerprint increases by one hertz, the LSD increases by 1.021, 1.017 and 1.0929 at lower-, medium- and high-frequency regions, respectively, in the range of variable fingerprint that is taken into account here, when the phases H1H3 and H2H1 are compared. A similar observation is made when comparing the H2H1 vs. H3H2 phases as well as the H3H2 vs. H1H3 phases, where the LSD increases by 0.976, 0.748 and 0.758 and 1.003, 1.024 and 1.1022, respectively. Here the obvious deformation is observed when comparing H2H1 vs. H3H2 phases. The CC and ASLE appear to agree with this assessment. Upon internal inspection, the winding was found to have a buckled winding deformation on H2-H1.
4. Conclusions
In this work, a novel regression analysis fault recognition algorithm (RAFRA) for computerised transformer winding condition monitoring is proposed. The algorithm is based on developing a regression model between the fingerprint and the latest FRA measurement data and numerical indicators for benchmarking.
The database was formulated in this work to discretise the measuring frequency into three sub-bands (low-, medium- and high-frequency sub-bands) to narrow the potential faults. It was done in this way since different frequency regions can be intrinsically linked to a physical fault consisting of FRA measurements from 70 mineral-oil-immersed power transformers of different designs, ratings and manufacturers that were physically inspected for various faults.
The validity of the numerical frequency segmentation algorithm was conclusively demonstrated by reviewing four practical case studies. Two key statistical indicators, viz., CC and ASLE, were used to assess the FRA data. It was realised that RAFRA had the highest overall precision, with most of the case studies properly diagnosed using the supplied database numerical frequency sub-bands, while CC and ASLE had satisfactory performance, with some of the case studies not correctly diagnosed.
The case studies comprised transformers with a range of winding faults as well as one with a healthy condition. The suggested method was shown to be sensitive enough to recognise and identify a wide range of winding faults. The results demonstrate that the proposed regression analysis algorithm can accurately assess the transformer winding condition and identify the fault type, thus also addressing the big hurdle of the FRA for commercial application, i.e., the reliable numerical evaluation of FRA results.
Author Contributions
B.A.T. formulated the regression analysis fault recognition algorithm (RAFRA), conceptualised numerical frequency discretisation methods, carried out the computations and prepared the article. A.F.N. and G.A.D. were responsible for editing the article. P.N.B. supervised and made final edits to the article. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank local manufacturers, utilities and municipalities for their contribution to the database.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ramesh, K.; Sushama, M. Inter-Turn Fault Detection in Power Transformer Using Fuzzy Logic. In Proceedings of the 2014 International Conference on Science Engineering and Management Research (ICSEMR), Chennai, India, 27–29 November 2014. [Google Scholar]
- Gouda, O.E.; El Dein, A.Z.; Moukhtar, I. Turn-to-earth fault modelling of power transformer based on symmetrical components. IET Gener. Transm. Distrib. 2013, 7, 709–716. [Google Scholar] [CrossRef]
- Afkar, H.; Vahedi, A. Detecting and locating tum to tum Fault on layer winding of distribution transformer. In Proceedings of the 5th IEEE Conference on Thermal Power Plants (lPGC2014), Shahid Beheshti University, Tehran, Iran, 10–11 June 2014; pp. 109–116. [Google Scholar]
- Patel, B.; Wang, Z.; Milanovic, J.; Jarman, P. Assessing transformer reliability using post-mortem data and health indices. In Proceedings of the 2014 International Conference on Condition Monitoring and Diagnosis (CMD), Jesu, Korea, 21–25 September 2014; pp. 472–475. [Google Scholar]
- Behjat, V. Diagnosing Shorted Turns on the Windings of Power Transformers Based Upon Online FRA Using Capacitive and Inductive Couplings. IEEE Trans. Power Deliv. 2011, 26, 2123–2133. [Google Scholar] [CrossRef]
- Tenbohlen, S. Transformer Reliability Survey; Technical Brochure 642 CIGRE; CIGRE: Paris, France, 2015. [Google Scholar]
- Tenbohlen, S.; Lapworth, M. Development and results of a worldwide transformer reliability survey. In Proceedings of the CIGRE SC A2 Colloquium, Shanghai, China, 20–25 September 2015. [Google Scholar]
- Ahn, H.M.; Lee, J.Y.; Kim, J.K.; Oh, Y.H.; Jung, S.Y.; Hahn, S.C. Finite-Element Analysis of Short-Circuit Electromagnetic Force in Power Transformer. IEEE Trans. Ind. Appl. 2011, 47, 1267–1272. [Google Scholar]
- Abu-Siada, A.; Hashemnia, N.; Islam, S.; Masoum, M.A. Understanding power transformer frequency response analysis signatures. IEEE Electr. Insul. Mag. 2013, 29, 48–56. [Google Scholar] [CrossRef]
- Dick, E.P.; Erven, C.C. Transformer Diagnostic Testing by Frequency Response Analysis. IEEE Trans. Power Appar. Syst. 1978, 6, 2144–2153. [Google Scholar] [CrossRef]
- Nyandeni, D.B.; Phoshoko, M.; Murray, R.; Thango, B.A. Transformer Oil Degradation on PV Plants—A Case Study. In Proceedings of the 8th South African Regional Conference (CIGRE), Johannesburg, South Africa, 14–17 November 2017. [Google Scholar]
- IEEE. IEEE Recommended Practice for Validation of Computational Electromagnetics Computer Modeling and Simulations. 2011. Available online: http://ieeexplore.ieee.org/document/5721917/ (accessed on 15 January 2022).
- Tahir, M.; Tenbohlen, S. Transformer Winding Condition Assessment Using Feedforward Artificial Neural Network and Frequency Response Measurements. Energies 2021, 14, 3227. [Google Scholar] [CrossRef]
- Zambrano, G.M.V.; Ferreira, A.C.; Caloba, L.P. Power transformer equivalent circuit identification by artificial neural network using frequency response analysis. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 6. [Google Scholar] [CrossRef]
- Singh, J.; Sood, Y.R.; Jarial, R.K. Novel method for detection of transformer winding faults using Sweep Frequency Response Analysis. In Proceedings of the Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007. [Google Scholar]
- Sathya, M.A. Prediction of Transformer Winding Displacement from Frequency Response Characteristics. In Proceedings of the 2013 IEEE 1st International Conference on Condition Assessment Techniques in Electrical Systems, Kolkata, India, 6–8 December 2013. [Google Scholar]
- Waters, M. The Short-Circuit Strength of Power Transformers; McDonald & Co., Ltd.: London, UK, 1966. [Google Scholar]
- Miroslav, G. Experimental Analysis of Short-Circuit Effects in Transformer Winding by Impact Test and SFRA. In Proceedings of the 2016 Diagnostic of Electrical Machines and Insulating Systems in Electrical Engineering (DEMISEE), Papradno, Slovakia, 20–22 June 2016. [Google Scholar]
- Rahman, M.A.A. The Effects of Short-Circuit and Inrush Currents on HTS Transformer Windings. IEEE Trans. Appl. Supercond. 2012, 22, 5500108. [Google Scholar] [CrossRef]
- Kulkarni, S.V.; Khaparde, S.A. Transformer Engineering Design and Practice; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Abdi, S.; Harid, N.; Safiddine, L.; Boubakeur, A.; Haddad, A. The Correlation of Transformer Oil Electrical Properties with Water Content Using a Regression Approach. Energies 2021, 14, 2089. [Google Scholar] [CrossRef]
- Tamus, Z.Á. Regression analysis to evaluate the reliability of insulation diagnostic methods. J. Electrost. 2013, 3, 564–567. [Google Scholar] [CrossRef]
- Gopalakrishna, S.; Kumar, K.; George, B.; Jayashankar, V. Design margin for short circuit withstand capability in large power transformer. In Proceedings of the 8th International Power Engineering, Singapore, 3–6 December 2007. [Google Scholar]
- Ghani, S.A.; Thayoob, Y.M.; Ghazali, Y.; Khiar, M. Evaluation of transformer core and winding conditions from SFRA measurement results using statistical techniques for distribution transformers. In Proceedings of the 2012 IEEE International Power Engineering and Optimization Conference, Melaka, Malaysia, 6–7 June 2012; pp. 448–453. [Google Scholar]
- Banaszak, S.; Szoka, W. Transformer Frequency Response Analysis With the Grouped Indices Method in End-to-End and Capacitive Inter-Winding Measurement Configurations. IEEE Trans. Power Deliv. 2020, 35, 571–579. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).