Modeling Cycle-to-Cycle Variations of a Spark-Ignited Gas Engine Using Artificial Flow Fields Generated by a Variational Autoencoder
Abstract
:1. Introduction
2. Materials and Methods
2.1. Engine Setup
2.2. CFD Simulation Setup
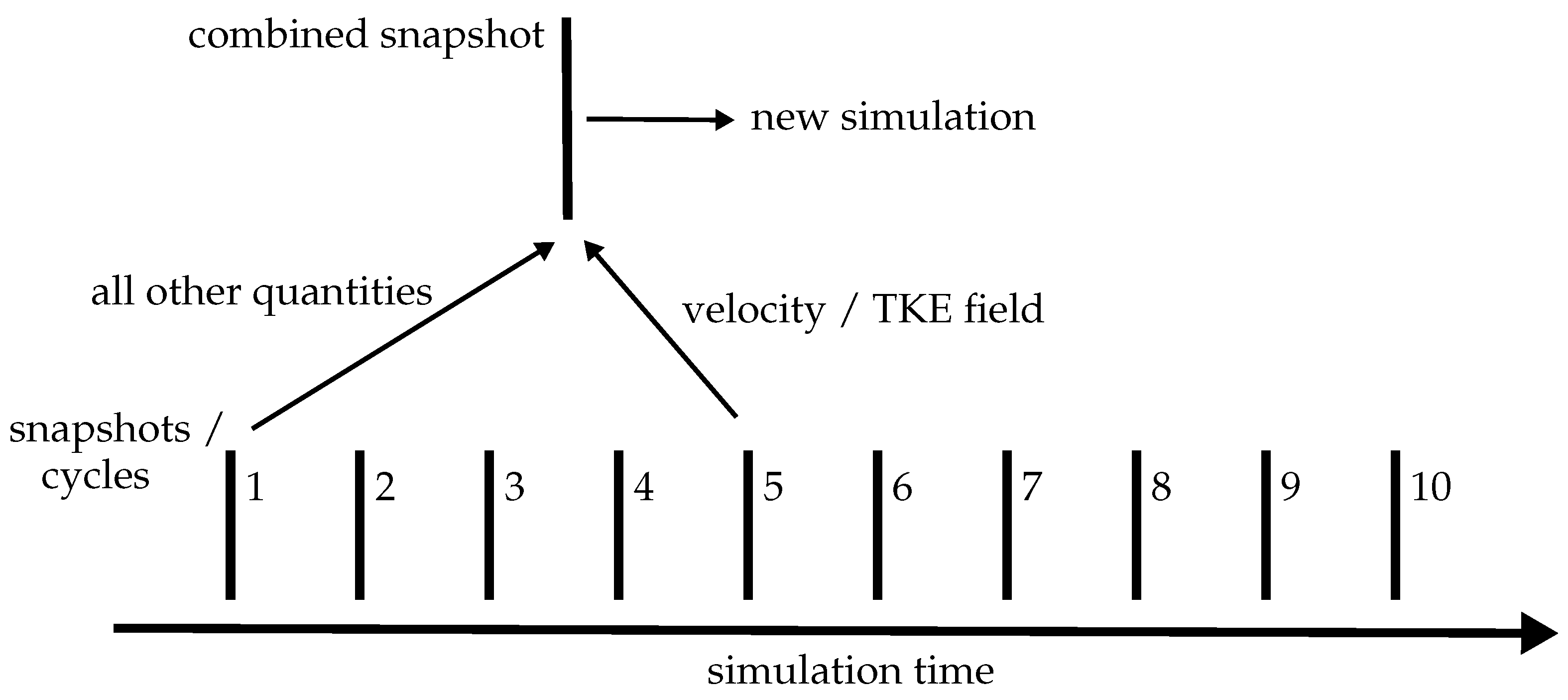
2.3. Multicycle Simulations
2.4. Variational Autoencoder
2.4.1. Principal Component Analysis and Latent Space Definition
2.4.2. Architecture
2.4.3. Data Preparation, Hyperparameters, and Training
2.5. Artificial Flow Field Generation
3. Results
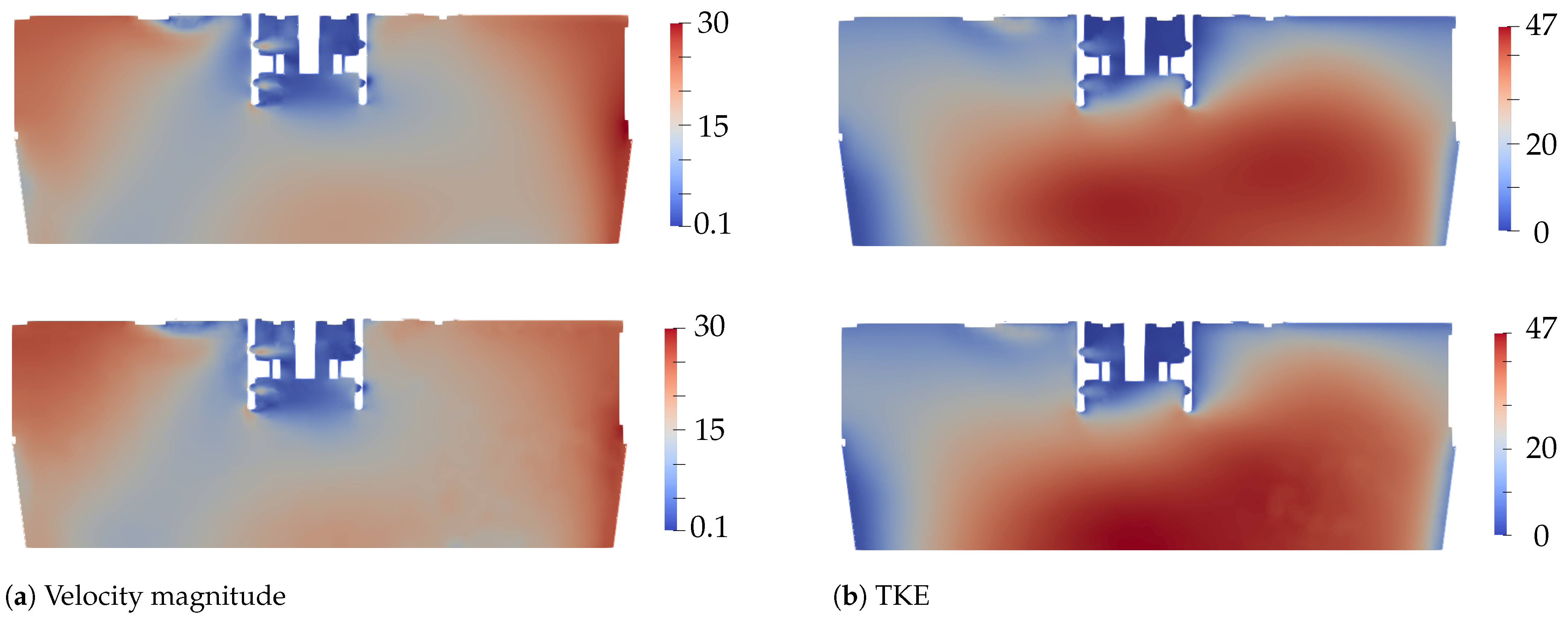
3.1. Model Validation
3.2. Artificial Cyclic Variations
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CoV | Coefficient of variation |
| CCV | Cycle-to-cycle variations |
| CFL | Courant–Friedrichs–Lewy |
| SI | Spark-ignited |
| RANS | Reynolds-averaged Navier–Stokes equations |
| CFD | Computational fluid dynamics |
| AMR | Adaptive mesh refinement |
| CAD | Crank angle degree |
| MFB | Mass fraction burned |
References
- Smallbone, A.; Jia, B.; Atkins, P.; Roskilly, A.P. The impact of disruptive powertrain technologies on energy consumption and carbon dioxide emissions from heavy-duty vehicles. Energy Convers. Manag. X 2020, 6, 100030. [Google Scholar] [CrossRef]
- Ni, P.; Wang, X.; Li, H. A review on regulations, current status, effects and reduction strategies of emissions for marine diesel engines. Fuel 2020, 279, 118477. [Google Scholar] [CrossRef]
- Guelpa, E.; Bischi, A.; Verda, V.; Chertkov, M.; Lund, H. Towards future infrastructures for sustainable multi-energy systems: A review. Energy 2019, 184, 2–21. [Google Scholar] [CrossRef]
- Young, M.B. Cyclic Dispersion in the Homogeneous-Charge Spark-Ignition Engine-A Literature Survey. SAE Trans. 1981, 49–73. [Google Scholar] [CrossRef]
- Ozdor, N.; Dulger, M.; Sher, E. Cyclic Variability in Spark Ignition Engines A Literature Survey. SAE Trans. 1994, 103, 1514–1552. [Google Scholar] [CrossRef]
- Maurya, R.K. Combustion Stability Analysis. In Reciprocating Engine Combustion Diagnostics: In-Cylinder Pressure Measurement and Analysis; Springer: Cham, Switzerland, 2019; pp. 361–459. [Google Scholar] [CrossRef]
- Matekunas, F.A. Modes and Measures of Cyclic Combustion Variability. SAE Trans. 1983, 1139–1156. [Google Scholar] [CrossRef]
- El-Adawy, M.; Heikal, M.R.; A. Aziz, A.R.; Adam, I.K.; Ismael, M.A.; Babiker, M.E.; Baharom, M.B.; Firmansyah; Abidin, E.Z.Z. On the Application of Proper Orthogonal Decomposition (POD) for In-Cylinder Flow Analysis. Energies 2018, 11, 2261. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Boggio, S.; Merola, S.; Teixeira Lacava, P.; Irimescu, A.; Curto-Risso, P. Effect of Fuel and Air Dilution on Syngas Combustion in an Optical SI Engine. Energies 2019, 12, 1566. [Google Scholar] [CrossRef] [Green Version]
- Johansson, B. Cycle to Cycle Variations in S.I. Engines-The Effects of Fluid Flow and Gas Composition in the Vicinity of the Spark Plug on Early Combustion. SAE Trans. 1986, 2281–2296. [Google Scholar] [CrossRef] [Green Version]
- Schiffmann, P. Root Causes of Cyclic Variability of Early Flame Kernels in Spark Ignited Engines. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2016. [Google Scholar]
- Schiffmann, P.; Reuss, D.L.; Sick, V. Empirical investigation of spark-ignited flame-initiation cycle-to-cycle variability in a homogeneous charge reciprocating engine. Int. J. Engine Res. 2018, 19, 491–508. [Google Scholar] [CrossRef]
- Lauer, T.; Frühhaber, J. Towards a Predictive Simulation of Turbulent Combustion?-An Assessment for Large Internal Combustion Engines. Energies 2021, 14, 43. [Google Scholar] [CrossRef]
- Vermorel, O.; Richard, S.; Colin, O.; Angelberger, C.; Benkenida, A.; Veynante, D. Towards the understanding of cyclic variability in a spark ignited engine using multi-cycle LES. Combust. Flame 2009, 156, 1525–1541. [Google Scholar] [CrossRef]
- Liu, K.; Haworth, D.C.; Yang, X.; Gopalakrishnan, V. Large-eddy simulation of motored flow in a two-valve piston engine: POD analysis and cycle-to-cycle variations. Flow Turbul. Combust. 2013, 91, 373–403. [Google Scholar] [CrossRef]
- Fontanesi, S.; d’Adamo, A.; Rutland, C. Large-Eddy simulation analysis of spark configuration effect on cycle-to-cycle variability of combustion and knock. Int. J. Engine Res. 2015, 16, 403–418. [Google Scholar] [CrossRef] [Green Version]
- Richard, S.; Dulbecco, A.; Angelberger, C.; Truffin, K. Invited Review: Development of a one-dimensional computational fluid dynamics modeling approach to predict cycle-to-cycle variability in spark-ignition engines based on physical understanding acquired from large-eddy simulation. Int. J. Engine Res. 2015, 16, 379–402. [Google Scholar] [CrossRef]
- He, C.; Kuenne, G.; Yildar, E.; van Oijen, J.; di Mare, F.; Sadiki, A.; Ding, C.P.; Baum, E.; Peterson, B.; Böhm, B.; et al. Evaluation of the flame propagation within an SI engine using flame imaging and LES. Combust. Theory Model. 2017, 21, 1080–1113. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Moiz, A.A.; Som, S.; Fogla, N.; Bybee, M.; Wahiduzzaman, S.; Mirzaeian, M.; Millo, F.; Kodavasal, J. Examining the role of flame topologies and in-cylinder flow fields on cyclic variability in spark-ignited engines using large-eddy simulation. Int. J. Engine Res. 2018, 19, 886–904. [Google Scholar] [CrossRef]
- Ameen, M.M.; Mirzaeian, M.; Millo, F.; Som, S. Numerical Prediction of Cyclic Variability in a Spark Ignition Engine Using a Parallel Large Eddy Simulation Approach. J. Energy Resour. Technol. 2018, 140, 052203. [Google Scholar] [CrossRef] [Green Version]
- Netzer, C.; Pasternak, M.; Seidel, L.; Ravet, F.; Mauss, F. Computationally efficient prediction of cycle-to-cycle variations in spark-ignition engines. Int. J. Engine Res. 2020, 21, 649–663. [Google Scholar] [CrossRef]
- Ameen, M.M.; Yang, X.; Kuo, T.W.; Som, S. Parallel methodology to capture cyclic variability in motored engines. Int. J. Engine Res. 2017, 18, 366–377. [Google Scholar] [CrossRef]
- Accelerating Computational Fluid Dynamics Simulations of Engine Knock Using a Concurrent Cycles Approach, Vol. ASME 2020 Internal Combustion Engine Division Fall Technical Conference, Internal Combustion Engine Division Fall Technical Conference, 2020, V001T06A002. Available online: http://xxx.lanl.gov/abs/https://asmedigitalcollection.asme.org/ICEF/proceedings-pdf/ICEF2020/84034/V001T06A002/6603631/v001t06a002-icef2020-2916.pdf (accessed on 26 January 2022).
- Scarcelli, R.; Richards, K.; Pomraning, E.; Senecal, P.K.; Wallner, T.; Sevik, J. Cycle-to-Cycle Variations in Multi-Cycle Engine RANS Simulations. In Proceedings of the SAE 2016 World Congress and Exhibition, Detroit, MI, USA, 12–14 April 2016. [Google Scholar] [CrossRef]
- Kingma, D.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Zemouri, R.; Lévesque, M.; Amyot, N.; Hudon, C.; Kokoko, O.; Tahan, S.A. Deep Convolutional Variational Autoencoder as a 2D-Visualization Tool for Partial Discharge Source Classification in Hydrogenerators. IEEE Access 2020, 8, 5438–5454. [Google Scholar] [CrossRef]
- Kopf, A.; Claassen, M. Latent representation learning in biology and translational medicine. Patterns 2021, 2, 100198. [Google Scholar] [CrossRef]
- Gößnitzer, C.; Givler, S. A New Method to Determine the Impact of Individual Field Quantities on Cycle-to-Cycle Variations in a Spark-Ignited Gas Engine. Energies 2021, 14, 4136. [Google Scholar] [CrossRef]
- Bourque, G.; Healy, D.; Curran, H.; Zinner, C.; Kalitan, D.; de Vries, J.; Aul, C.; Petersen, E. Ignition and Flame Speed Kinetics of Two Natural Gas Blends with High Levels of Heavier Hydrocarbons. J. Eng. Gas Turbines Power 2009, 132, 021504. [Google Scholar] [CrossRef]
- Kosmadakis, G.; Rakopoulos, D.; Arroyo, J.; Moreno, F.; Muñoz, M.; Rakopoulos, C. CFD-based method with an improved ignition model for estimating cyclic variability in a spark-ignition engine fueled with methane. Energy Convers. Manag. 2018, 174, 769–778. [Google Scholar] [CrossRef]
- Kosmadakis, G.M.; Rakopoulos, C.D. A Fast CFD-Based Methodology for Determining the Cyclic Variability and Its Effects on Performance and Emissions of Spark-Ignition Engines. Energies 2019, 12, 4131. [Google Scholar] [CrossRef] [Green Version]
- Kramer, M.A. Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 1991, 37, 233–243. [Google Scholar] [CrossRef]
- Gondara, L. Medical image denoising using convolutional denoising autoencoders. In Proceedings of the 2016 IEEE 16th international conference on data mining workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; pp. 241–246. [Google Scholar]
- Zhou, C.; Paffenroth, R.C. Anomaly detection with robust deep autoencoders. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 665–674. [Google Scholar]
- Wang, Y.; Yao, H.; Zhao, S. Auto-encoder based dimensionality reduction. Neurocomputing 2016, 184, 232–242. [Google Scholar] [CrossRef]
- Xing, C.; Ma, L.; Yang, X. Stacked denoise autoencoder based feature extraction and classification for hyperspectral images. J. Sens. 2016, 2016, 3632943. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Welling, M. An introduction to variational autoencoders. arXiv 2019, arXiv:1906.02691. [Google Scholar]
- Burgess, C.P.; Higgins, I.; Pal, A.; Matthey, L.; Watters, N.; Desjardins, G.; Lerchner, A. Understanding disentangling in beta-VAE. arXiv 2018, arXiv:1804.03599. [Google Scholar]
- Shao, H.; Lin, H.; Yang, Q.; Yao, S.; Zhao, H.; Abdelzaher, T. DynamicVAE: Decoupling Reconstruction Error and Disentangled Representation Learning. arXiv 2020, arXiv:2009.06795. [Google Scholar]
- Oja, E. Simplified neuron model as a principal component analyzer. J. Math. Biol. 1982, 15, 267–273. [Google Scholar] [CrossRef]
- Vajapeyam, S. Understanding Shannon’s Entropy metric for Information. arXiv 2014, arXiv:1405.2061. [Google Scholar]
- Du, T.Y. Dimensionality reduction techniques for visualizing morphometric data: Comparing principal component analysis to nonlinear methods. Evol. Biol. 2019, 46, 106–121. [Google Scholar] [CrossRef]
- Wang, J.; He, C.; Li, R.; Chen, H.; Zhai, C.; Zhang, M. Flow field prediction of supercritical airfoils via variational autoencoder based deep learning framework. Phys. Fluids 2021, 33, 086108. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Tipping, M.E.; Bishop, C.M. Probabilistic principal component analysis. J. R. Stat. Soc. Ser. B 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Kalchbrenner, N.; Grefenstette, E.; Blunsom, P. A convolutional neural network for modelling sentences. arXiv 2014, arXiv:1404.2188. [Google Scholar]
- Kefalas, A.; Ofner, A.B.; Pirker, G.; Posch, S.; Geiger, B.C.; Wimmer, A. Detection of knocking combustion using the continuous wavelet transformation and a convolutional neural network. Energies 2021, 14, 439. [Google Scholar] [CrossRef]
- Ofner, A.B.; Kefalas, A.; Posch, S.; Geiger, B.C. Knock Detection in Combustion Engine Time Series Using a Theory-Guided 1D Convolutional Neural Network Approach. IEEE/ASME Trans. Mechatron. 2022; in press. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]










| # of PCs | u | v | w | Mean | |
|---|---|---|---|---|---|
| 1 | 0.503 | 0.350 | 0.357 | 0.404 | 0.404 |
| 2 | 0.689 | 0.625 | 0.573 | 0.568 | 0.614 |
| 3 | 0.806 | 0.778 | 0.702 | 0.702 | 0.747 |
| 4 | 0.870 | 0.851 | 0.803 | 0.821 | 0.836 |
| 5 | 0.918 | 0.907 | 0.869 | 0.889 | 0.895 |
| 6 | 0.951 | 0.941 | 0.920 | 0.934 | 0.937 |
| 7 | 0.971 | 0.969 | 0.963 | 0.972 | 0.969 |
| 8 | 0.987 | 0.989 | 0.986 | 0.987 | 0.987 |
| 9 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| 10 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Posch, S.; Gößnitzer, C.; Ofner, A.B.; Pirker, G.; Wimmer, A. Modeling Cycle-to-Cycle Variations of a Spark-Ignited Gas Engine Using Artificial Flow Fields Generated by a Variational Autoencoder. Energies 2022, 15, 2325. https://doi.org/10.3390/en15072325
Posch S, Gößnitzer C, Ofner AB, Pirker G, Wimmer A. Modeling Cycle-to-Cycle Variations of a Spark-Ignited Gas Engine Using Artificial Flow Fields Generated by a Variational Autoencoder. Energies. 2022; 15(7):2325. https://doi.org/10.3390/en15072325
Chicago/Turabian StylePosch, Stefan, Clemens Gößnitzer, Andreas B. Ofner, Gerhard Pirker, and Andreas Wimmer. 2022. "Modeling Cycle-to-Cycle Variations of a Spark-Ignited Gas Engine Using Artificial Flow Fields Generated by a Variational Autoencoder" Energies 15, no. 7: 2325. https://doi.org/10.3390/en15072325
APA StylePosch, S., Gößnitzer, C., Ofner, A. B., Pirker, G., & Wimmer, A. (2022). Modeling Cycle-to-Cycle Variations of a Spark-Ignited Gas Engine Using Artificial Flow Fields Generated by a Variational Autoencoder. Energies, 15(7), 2325. https://doi.org/10.3390/en15072325






