Evaluation Methodology of Rotary Flow Dividers Used as Pressure Intensifiers with Creation of a New Pressure Multiplying Efficiency
Abstract
:1. Introduction
2. Evaluation Methodology of Pressure Multiplication
2.1. Definition of Pressure Multiplying Efficiency
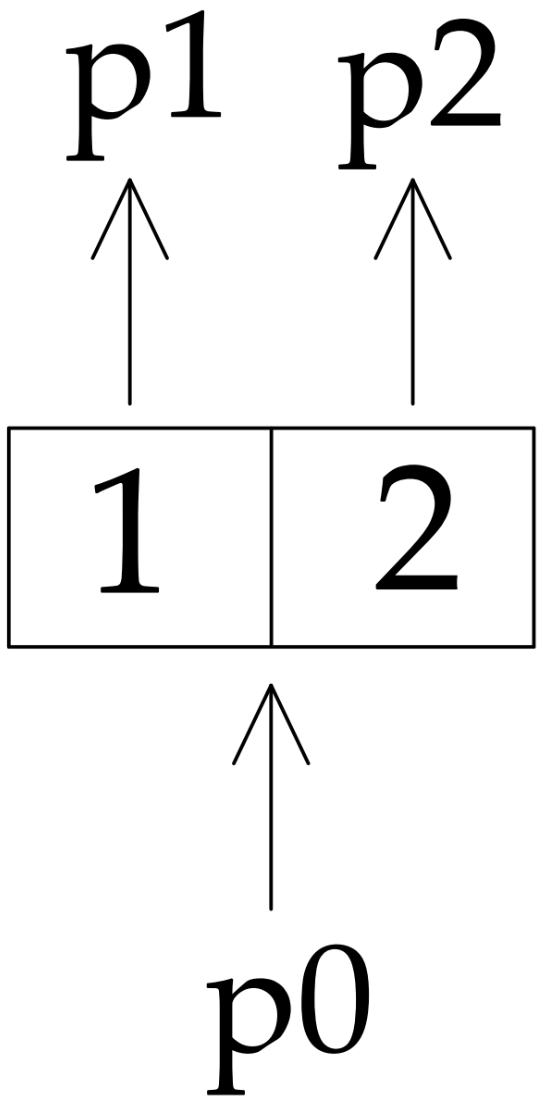
2.2. Two-Section Divider with Equal Section Volumes
2.3. N-Section Divider with Equal Section Volumes
2.4. N-Section Divider with Unequal Section Volumes
3. Evaluation Methodology of Flow Dividing Inaccuracy
3.1. N-Section Divider with Equal Section Volumes
3.2. N-Section Divider with Unequal Section Volumes
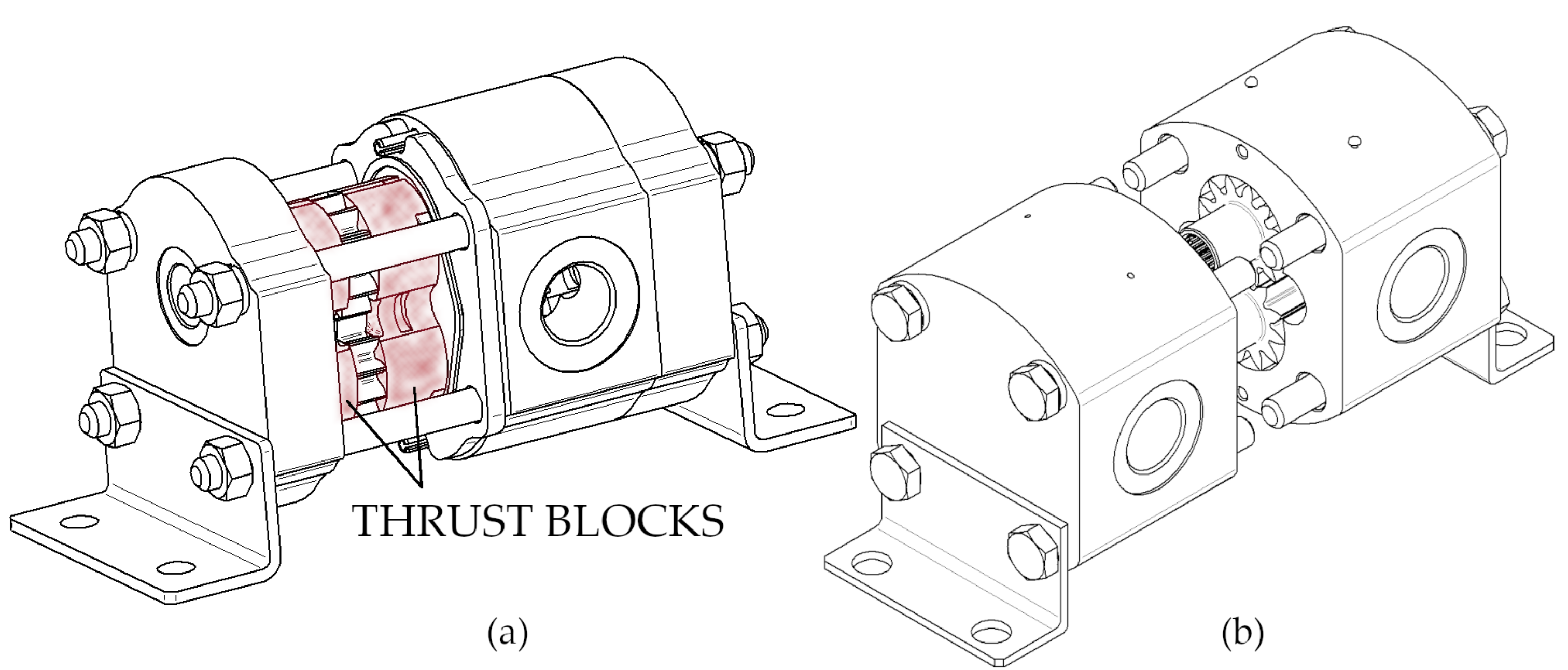
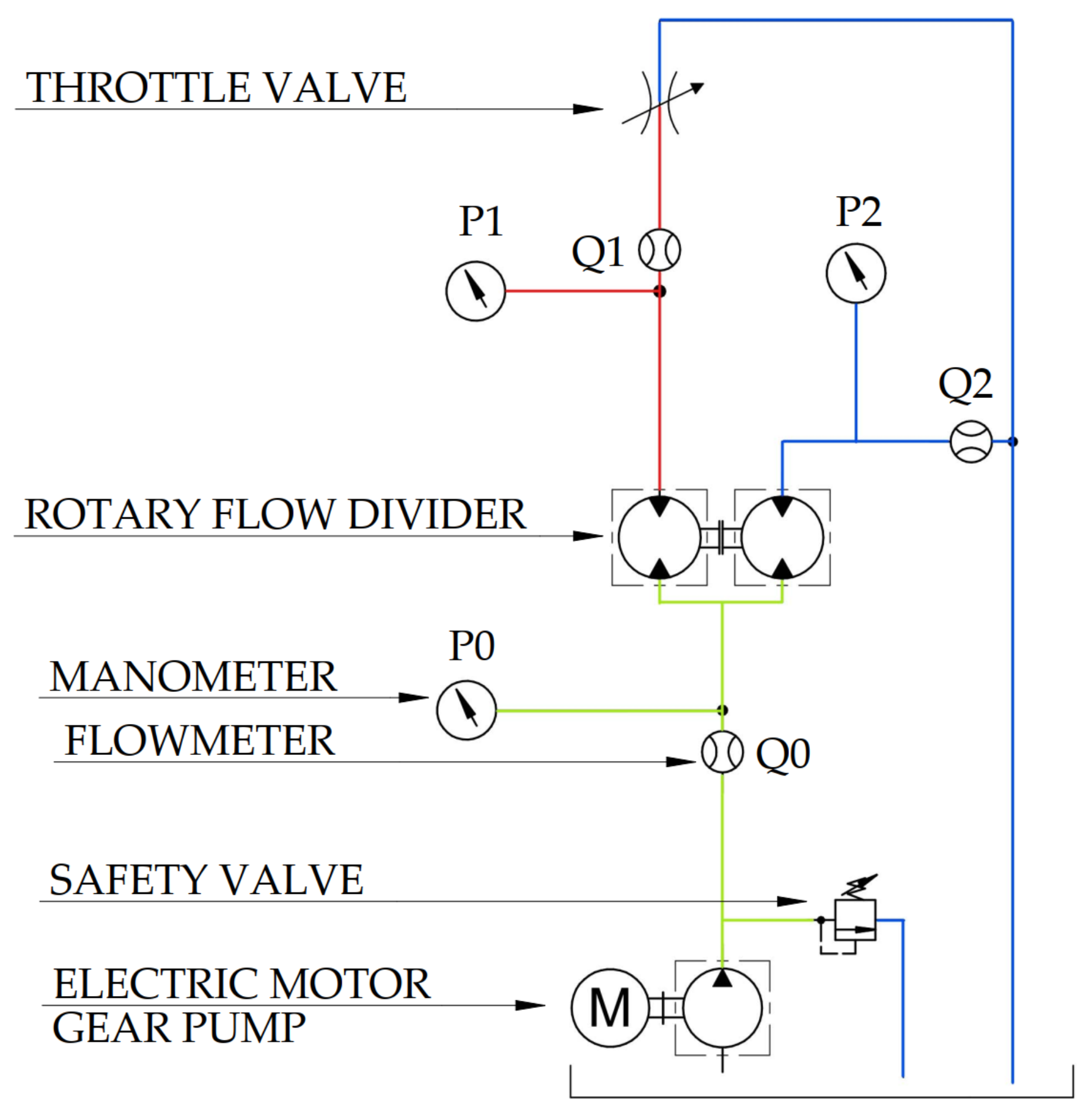
4. Experimental Comparison of Rotary Flow Dividers
4.1. Run of the Experiment
4.2. Results of Measured Data from the Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karassik, I.J.; Messina, J.P.; Cooper, P.; Heald, C.H.C. Pump Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 2001; ISBN 0-07-034032-3. [Google Scholar]
- Michael, P.W.; Khalid, H.; Wanke, T. An Investigation of External Gear Pump Efficiency and Stribeck Values; SAE Technical Paper Series; SAE: Warrendale, PA, USA, 2012. [Google Scholar]
- Borghi, M.; Zardin, B.; Specchia, E. External Gear Pump Volumetric Efficiency: Numerical and Experimental Analysis; SAE Technical Paper Series; SAE: Warrendale, PA, USA, 2009. [Google Scholar]
- Sedri, F.; Riasi, A. Investigation of leakage within an external gear pump with new decompression slots: Numerical and experimental study. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 224. [Google Scholar] [CrossRef]
- Manring, N.D.; Kasaragadda, S.B. The Theoretical Flow Ripple of an External Gear Pump. J. Dyn. Syst. Meas. Control 2003, 125, 396–404. [Google Scholar] [CrossRef]
- Liguori, A.; Armentani, E.; Bertocco, A.; Formato, A.; Pellegrino, A.; Villecco, F. Noise Reduction in Spur Gear Systems. Entropy 2020, 22, 1306. [Google Scholar] [CrossRef] [PubMed]
- Del Campo, D.; Castilla, R.; Raush, G.A.; Gamez Montero, P.J.; Codina, E. Numerical Analysis of External Gear Pumps Including Cavitation. J. Fluids Eng. 2012, 134. [Google Scholar] [CrossRef]
- Cao, Y.; Deng, Y.; Wang, Y. Evaluation on Influential Factors of Hydraulic Gear Pumps Wear Life Using FAHP. In Proceedings of the 3rd International Conference on Material, Mechanical and Manufacturing Engineering, Guangzhou, China, 27–28 June 2015. [Google Scholar]
- Castilla, R.; Gamez-Montero, P.J.; Del Campo, D.; Raush, G.; Garcia-Vilchez, M.; Codina, E. Three-Dimensional Numerical Simulation of an External Gear Pump With Decompression Slot and Meshing Contact Point. J. Fluids Eng. 2015, 137, 041105. [Google Scholar] [CrossRef]
- Houzeaux, G.; Codina, R. A finite element method for the solution of rotary pumps. Comput. Fluids 2007, 36, 667–679. [Google Scholar] [CrossRef]
- Ghazanfarian, J.; Ghanbari, D. Computational Fluid Dynamics Investigation of Turbulent Flow Inside a Rotary Double External Gear Pump. J. Fluids Eng. 2014, 137, 021101. [Google Scholar] [CrossRef]
- Castilla, R.; Gamez-Montero, P.J.; Ertürk, N.; Vernet, A.; Coussirat, M.; Codina, E. Numerical simulation of turbulent flow in the suction chamber of a gearpump using deforming mesh and mesh replacement. Int. J. Mech. Sci. 2010, 52, 1334–1342. [Google Scholar] [CrossRef]
- Flow Divider Circuits. Available online: https://www.hydraulicspneumatics.com/technologies/other-technologies/article/21883443/book-2-chapter-11-flow-divider-circuits (accessed on 3 June 2021).
- Flow Controls and Flow Dividers. Available online: https://www.hydraulicspneumatics.com/technologies/other-technologies/article/21883442/chapter-13-flow-controls-and-flow-dividers (accessed on 3 June 2021).
- Pressure Intensifier Circuits. Available online: https://www.hydraulicspneumatics.com/technologies/other-technologies/article/21884328/book-2-chapter-13-pressure-intensifier-circuits (accessed on 3 June 2021).
- Intensification Circuit Uses Rotary Flow Divider. Available online: https://www.hydraulicspneumatics.com/technologies/hydraulic-valves/article/21883446/intensification-circuit-uses-rotary-flow-divider (accessed on 3 June 2021).
- Flow Dividers. Available online: https://www.jihostroj.com/en/hydraulics/production-program/flow-dividers.htm (accessed on 26 January 2022).
- Gear Flow Dividers. Available online: https://www.casappa.com/en/c/downloads/category/2/ (accessed on 26 January 2022).
- Use a Vivoil Flow divider as Pressure Multipliers. Available online: https://www.vivoil.com/blog/use-a-vivoil-flow-divider-as-pressure-multipliers/ (accessed on 26 January 2022).
- Flow Divider Designs. Available online: https://www.jahns-hydraulik.de/PDF/kat_mtx-2801-gb.pdf (accessed on 26 January 2022).
- Booster-Intensifiers. Available online: https://www.powermotiontech.com/technologies/hydraulic-pumps-motors/article/21884313/boosterintensifiers (accessed on 26 January 2022).
- Latos, G.D. Remote Hydraulic Pressure Intensifier. U.S. Patent 5429036 A, 7 April 1995. [Google Scholar]
- Baatrup, J.V.; Esperson, C.H. Pressure Intensifier. U.S. Patent 7354252 B2, 8 April 2008. [Google Scholar]
- White, L.E. Pressure Intensifier for Repositioning Telescopic Plungers in Synchronized Telescopic Cylinders. U.S. Patent 5060762 A, 29 October 1991. [Google Scholar]
- Gill, S.D.; Roberts, T.J. Hydraulic Intensifiers. U.S. Patent 20090317267 A1, 24 December 2009. [Google Scholar]
- Nomura, K.; Kitamura, H.; Komatsu, S. Pressure Intensifying Apparatus for Hydraulic Cylinder. U.S. Patent 6581379 B2, 24 June 2003. [Google Scholar]
- Lopot, F.; Dub, M.; Flek, J.; Hadraba, D.; Havlíček, M.; Kučera, L.; Štoček, O.; Veselý, T.; Janáček, J. Gearbox Mechanical Efficiency Determination by Strain Gauges Direct Application. Appl. Sci. 2021, 11, 11150. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G.; Rajda, J. Analysis of the Energy Efficiency Improvement in a Load-Sensing Hydraulic System Built on the ISO Plate. Energies 2021, 14, 6735. [Google Scholar] [CrossRef]
- Stawinski, L.; Skowronska, J.; Kosucki, A. Energy Efficiency and Limitations of the Methods of Controlling the Hydraulic Cylinder Piston Rod under Various Load Conditions. Energies 2021, 14, 7973. [Google Scholar] [CrossRef]
- Vacca, A.; Guidetti, M. Modelling and experimental validation of external spur gear machines for fluid power applications. Simul. Model. Pr. Theory 2011, 19, 2007–2031. [Google Scholar] [CrossRef]
- Marinaro, G.; Frosina, E.; Senatore, A. A Numerical Analysis of an Innovative Flow Ripple Reduction Method for External Gear Pumps. Energies 2021, 14, 471. [Google Scholar] [CrossRef]
- Understand the Function of Hydraulic Components in Circuits: The Application of Pumps and Intensifiers. Available online: https://fluidpowerjournal.com/understand-the-function-of-hydraulic-components-in-circuits-the-application-of-pumps-and-intensifiers/ (accessed on 10 October 2021).
- Morgan, G.H. Hydraulic Intensification Circuit with Rotary Flow Devider and Bypass Valve. U.S. Patent 7000386B1, 14 February 2008. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hradecký, J.M.; Bubák, A.; Dub, M. Evaluation Methodology of Rotary Flow Dividers Used as Pressure Intensifiers with Creation of a New Pressure Multiplying Efficiency. Energies 2022, 15, 2293. https://doi.org/10.3390/en15062293
Hradecký JM, Bubák A, Dub M. Evaluation Methodology of Rotary Flow Dividers Used as Pressure Intensifiers with Creation of a New Pressure Multiplying Efficiency. Energies. 2022; 15(6):2293. https://doi.org/10.3390/en15062293
Chicago/Turabian StyleHradecký, Jakub Milan, Antonín Bubák, and Martin Dub. 2022. "Evaluation Methodology of Rotary Flow Dividers Used as Pressure Intensifiers with Creation of a New Pressure Multiplying Efficiency" Energies 15, no. 6: 2293. https://doi.org/10.3390/en15062293
APA StyleHradecký, J. M., Bubák, A., & Dub, M. (2022). Evaluation Methodology of Rotary Flow Dividers Used as Pressure Intensifiers with Creation of a New Pressure Multiplying Efficiency. Energies, 15(6), 2293. https://doi.org/10.3390/en15062293





