1. Introduction
The design and manufacture of hydraulic gear pumps are very important economic, technical and research requirements in the industrial and academic environments. These pumps have a big number of industry applications in fields such as automotive, naval, aerospace, consumer goods, medical, energy production, electronics, food preparation and preservation, etc.
The pumps must comply with very different functional requirements from the beneficiaries. Generally, these pumps drive a specific fluid identified by the flow and pressure, such as fuel transfer, recirculation of water in a cooling circuit, dosing of medical substances in various applications, mixing of additives, paints or chemicals, etc.
In this context, where the flow is very important, the paper [
1] presents a review of a few different methodologies that were used for the calculus and the simulation of the flow rates generated by gerotor, external gear and crescent pumps. Some ways of selecting the control volumes of the pumps are analyzed, and the main calculus parameters and relations are presented. The working principles and the industry applications of distributed models are also presented, and an important section refers to the evaluation methods of the required geometric quantities, such as analytical, numerical, CAD based.
The paper explains the leakages that may appear through the clearances that appear between the two gears and/or between a gear and the pump casing. These leakages appear due to the interactions between the pressurized fluid and the moving mechanical parts, and they should be taken into account.
Due to their known design simplicity, low-cost manufacturing, versatility and operational safety, these spur gear pumps are used in a large range of applications. On the market, there is a large number of constructive solutions of gear pumps, which can be identified by: pressure level (from low to high in several steps depending on the driven fluid), gear type (external, internal, bevel, straight, V-shaped), tooth profile (involute, most used in gear machinery, or cycloid, used for the most part in the elements of bulk impeller machines), pumping capacity (constant or variable) and number of rotors (bi- or multi-rotor).
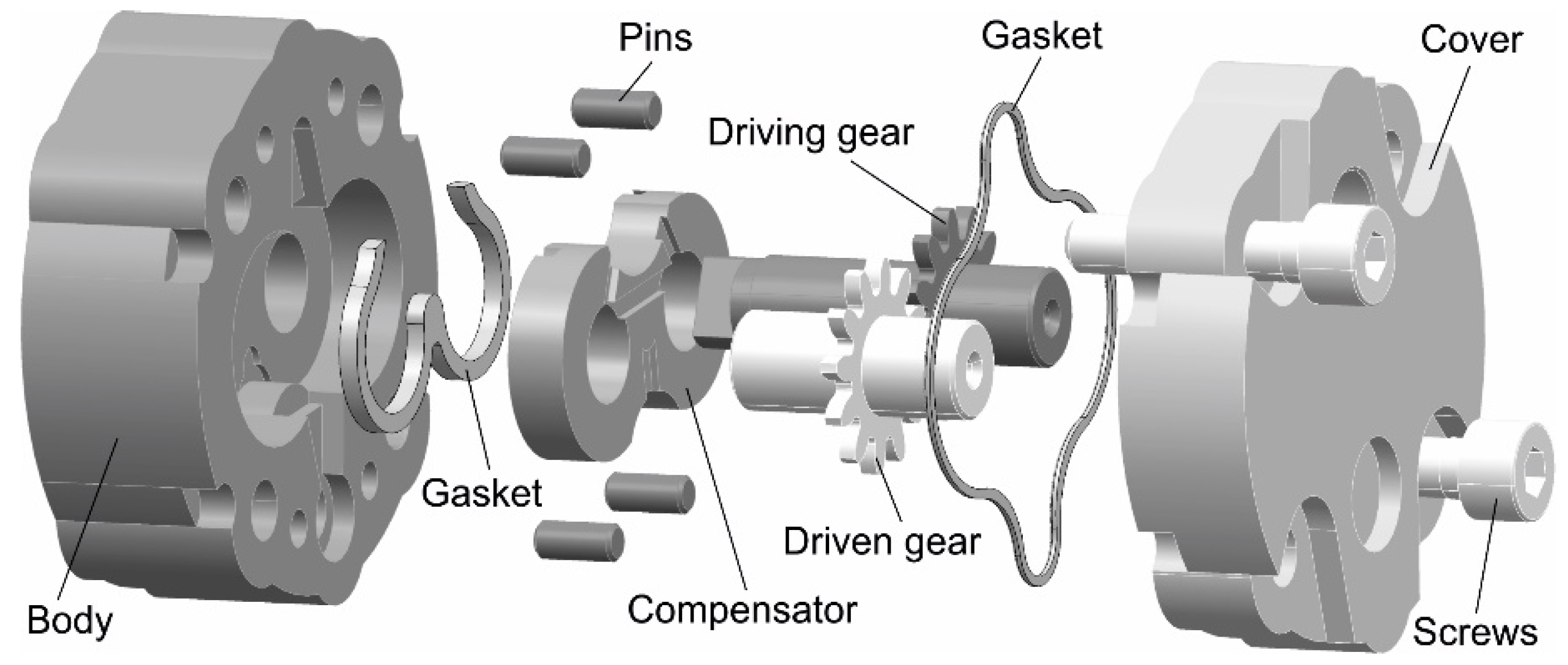
Gear pumps with straight external involute teeth [
2] are the most common types and are positive displacement pumps. These pumps contain rotors (either mounted on, or integrated with shafts), orientation pins, gaskets, screws, a body and a cover. Their volumes (the active cups) are composed of gaps between the teeth, successively passing through the inlet chamber; the fluid enters these gaps and is transferred to the hydraulic installation.
Using parametric design, a manufacturing company wishes to extend the range of production of these pumps through variation of dimensions of certain components and of their modular whole-pump assembly, so the resulting flow rates vary from 2 L/min to 22.52 L/min for the rotational speed of 3000 rev/min.
There is a different solution for small flow rates, where the pump has reduced overall dimensions and may be considered to be part of group 0—micropumps (with 1 cm3/rev).
Although the manufacturer produces a wide variety of pumps, this particular pump model to be assembled as a micropump is of interest in certain configurations.
In recent years, many research papers have focused on conceiving hydraulic gear pumps to increase operating pressures [
3,
4], to extend the manufacturing range [
4,
5], to improve the efficiency in operation [
6], to reduce pressure variations [
3,
7], the dynamic loads [
8,
9], weight [
10], vibrations [
11], etc.
In addition to their constructive and operational simplicity, low price and other positive features of the spur gear pumps, many problems are caused by the generation of an important vibration due to the fluctuation of the generated flow during the pump’s functioning [
12]. It is known that vibrations are one of the main sources of noise in most hydraulic systems, but they also produce mechanical failures, premature wear of moving components, leaks, etc. Therefore, many studies are focused on reducing the flowrate variation, as it is an important and continuous concern in the design process of hydraulic gear pumps.
Ref. [
11] contains an experimental study and numerical modal analysis for an external gear pump mounted on a test stand in a laboratory setup. Many research works on experimental modal analysis of hydraulic gear pumps focus on the modal frequencies in order to approve the model validation.
The pump components, its assembly and mounting in an installation come with some modeling problems, such as establishing the material properties of each component, the importance and use of the bolted joints, critical modeling of the boundary conditions linked to pump mounting. The authors experimentally observed and analyzed the vibration modes of a reference pump using the least-square complex exponential method with an emphasis on the characteristics of the mode shapes. More simple modeling strategies are created, proposed and confirmed by performing the analysis from the simplest level (a component) to the whole complex assembly.
The paper highlights that the pump casing does not show any important deformation, but it is close to the rigid body motion. Without increasing the 3D model complexity too much, the presented numerical approach offers a good accuracy with low error in modal frequencies of 6% and a good agreement in terms of mode shapes.
Additionally, Ref. [
11] discusses the vibration reduction strategy using the measured mode shapes and the proposed modeling approaches that can be useful for studying a large number of constructive solutions of external gear pumps, which may be of low model complexity but with a reasonable result accuracy.
2. Parametric Design and Optimization of the Pump
Usually, the new versions of pumps are, in fact, optimized models of the previous working solutions, with improved parametric design, optimizations based on tests and user experience.
Ref. [
13] presents the topic of external gear pumps to be used in several automotive applications because they are able to work at high rotational speed and low pressure. The authors present a parametrically designed model that has been developed with an extensive finite element analysis, the scope being to predict the pump’s dynamic behavior for gears and casing acceleration. Their model includes the most important phenomena that are involved in the pump operation and is validated after experimental tests and data gathering.
In their work, the authors establish an optimization process with three methodologies in order to reduce the level of pump vibration. The complex setup of the optimization process contains the objective of case accelerations, operational and geometrical input variables, the most important among those being oil viscosity, oil bulk modulus, radial clearance in the bearings.
The research and the optimization processes use simulations that are compared with a combined and complex analysis using the design of experiments (DOE), response surface modeling (RSM) and by applying algorithms in order to find the optimal variable combination. These are compared in terms of time efficiency and accuracy of the resulting solution. In addition, the authors proposed a design process to calculate and establish the manufacturing tolerances of the pump solution and evaluate their effect on its performance. The results offer important data, design perspectives and ideas that could be very difficult to obtain without these procedures.
In the current paper, for modeling and simulation of the proposed pump, the author chose CATIA v5 that can perform the pump model design, assembly and parameterization. This software also contains FEM and CAM simulation workbenches, an assembly of components, simulations of product kinematics, etc.
The modeling of components took advantage of 2D drawings offered by the pump manufacturer [
4], and different dimensions and patented [
14] manufacturing solutions were integrated, as well as ideas from the literature review, improvements made in the production workshops and input from technicians based on their experience. Different design solutions of pumps were available during 3D modeling to observe the constructive solutions, quality of the assemblies, etc. The company is persistently focused on its product lines improvement.
After surface examination, certain parts were observed to display failure of design and/or manufacturing (i.e., non-coaxiality, misalignment of certain areas, difficulty in mounting the pins and the compensator). The author created, assembled and parameterized the 3D model in CATIA v5 to identify and optimize the geometry in order to remove or reduce such defects. An important requirement from the manufacturing company was to preserve, where possible, the shape and outer dimensions of the semi-products/stocks as an important part of the technology process [
5].
The pump assembly design very much depends on the modeling accuracy of the two gears, in accordance with the imposed flow rate, the distance between shaft axes, the size and positions of the body pockets. The teeth flanks of the two gears are designed to have an involute profile, with corrected toothing according to the specific standards [
15]. The profile and flank line equations are used in parameterization to respect the position of the toothing line.
Drawing the involute tooth profile was a crucial step in the pump modeling and was followed by correct determination of the distance between the shafts, conforming to the methodology previously presented in detail in Refs. [
16,
17] and others. Each gear has 12 teeth and is manufactured in one piece with its shaft.
The modeling of the other components took into account the particularities of shape and position of the two gears, using drawings and measurements of the parts in the faculty control and calibration laboratories.
During the modeling process, multiple dimensions and constructive conditions were identified and transformed into parameters and later used to establish formulae for parametric design [
5,
15]. Some of these parameters are mentioned as follows: diameters and lengths of shafts, distance between their axes, position, shape and dimensions of the driving and supporting parts, diameters and positions of the support holes for the gear shafts, diameters and depths of the holes that contain the rotating gears and the compensator, etc. [
16,
18].
The compensator, also called the thrust block, is an essential pump component, and it was created using this parametric design so that its nominal diameters are defined to be equal to the diameters of the gears’ head circle and, consequently, equal to the diameters of the holes bored in the pump body. The holes’ diameters in the pump body where the gear shafts are mounted have the same values as these gear shafts, being fitted together using the same distances between axes. The lateral openings’ radii are also parameterized using discrete values, letting the hydraulic fluid lubricate the gear shafts’ bearings manufactured in the pump’s body and cover [
18].
The compensator has one of its faces in contact with the front surface of the gears; this face also contains lubrication channels. The other face has a groove for mounting the sealing gasket. Its dimensions were parameterized on discrete values, taking into account the diversity of gasket standard sizes the company uses in the series production.
Such exemplified conditions are set for all the components of the gear pump using large and various sets of formulae, which act as important constraints in pump parameterization.
Figure 1 shows a pump retired from service as an assembly (a) and (b) as separate parts (c) to observe its components and the worn areas.
Figure 2 features an expanded 3D model to identify each of the pump components.
After the geometric modeling is completed, the parametric design of the pump proceeds according to certain functional and dimensional constraints [
4]. The main parameter imposed by the manufacturing company and the parametric design goal is the pump’s flow rate, which is directly linked to one important characteristic of hydrostatic pumps: the geometric volume. This volume is expressed through Relation (1) [
19]:
thus z—the teeth number on each gear, b—gear width, in mm, A—the area of the profile between two successive teeth, in cm
2. Parameter A is determined by assisted drawing of the pump gear, then by measuring the respective area. Parametric-assisted design of the pump assembly leads to fast and accurate area determination.
This area A is geometrically and automatically calculated; its value depends on the specific gear parameters, such as modulus, number of teeth, and angle of gearing and correction coefficient. The teeth profile and gear features are confidential for every pump manufacturer. The profile area between two teeth decreases when teeth number increases. This determines the overall internal pump size.
Knowing the area A, it is possible to determine the volume between two consecutive teeth, as well as the pump’s geometric volume, noted as V
g. Using relation (2), the pump flow rate is:
where n—driving shaft rotational speed, in rev/min and η
v—volumetric efficiency, in %. For this pump, the manufacturer imposed n = 3000 rev/min to be the nominal rotational speed (but the pump has the capability of rotational speeds of n
min = 700 rev/min and n
max = 5000 rev/min). In conformity with the pump’s specifications, η
v = 93% [
4,
18].
The gear width is determined, so that the pump has a corresponding value of the geometric volume specific to the pump series HP05 [
4], currently in series production. Thus, in conformity with the manufacturing company’s technical data sheets, the first value of this parameter for the pump’s first constructive variant is 1.2 cm
3/rev. There are minimal dimensions imposed for the gear teeth and the compensator widths, which should not be less than 2.2 mm and 6 mm, respectively.
The manufacturing company requested an increase in this geometric volume without changing the external shape and size of the stock parts used to manufacture the body and the cover. An external supplier provided the stock parts. The focus was to increase the pump’s flow rate with the same type of pump and not by selecting the next pump model that differs in the sizes and shapes of its components. All the constructive variants/solutions have to be fitted in narrow spaces in various hydraulic installations. By parametric design and according to the imposed constraints, a calculation is possible in order to find the values that define the teeth, the compensator and body widths, depth of holes in the body where the gears and the compensator are mounted, etc.
When a user, placing an order via a web interface, changes the pump flow rate [
1,
10], the geometric parametric modeling of the body, gears and compensator is automatically updated by the various relations and one reaction written in Visual Basic. The user is aware at all times of the pump’s dimensions and its characteristics, whereas the manufacturing company has all the specifications for any customized order production.
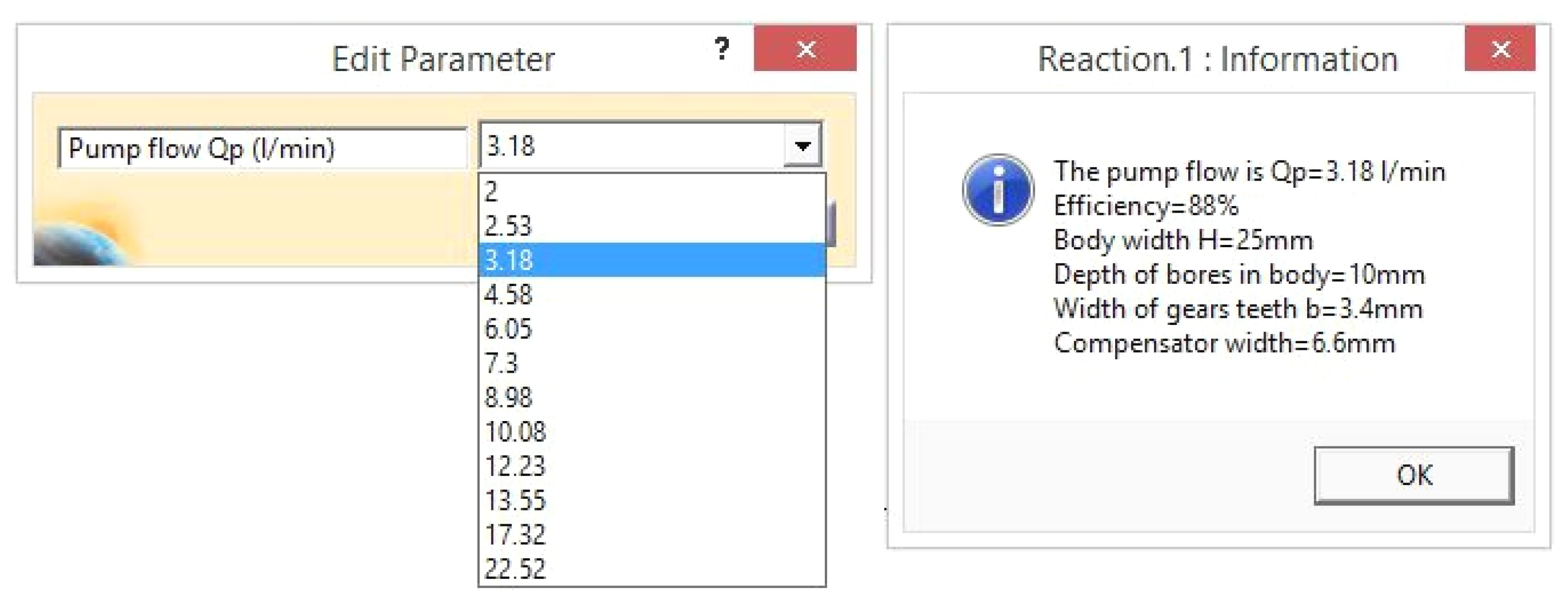
Table 1 identifies the parameters involved in the above-mentioned relations, based on one multi-value parameter for the pump flow rate depending on the constructive solution.
As an example, the user selects the flow rate from a list (
Figure 3), while the remaining parameters take discrete values, as shown in
Table 1.
This reaction written in Visual Basic using the CATIA v5 interface and presented in
Appendix A is based on these parameters organized into several sequences, in a conditioned manner, depending on the selected value of flow rate. To create the 3D models of the pump’s components, the author used the CATIA v5 capabilities of working with solid parts. Thus, each component is a solid part that needs many parameters to create its volume, the holes, pockets, etc. Some of these parameters were used in the Visual Basic code. Changing their values affects other parameters and thus the dimensions/shapes of the components. The code that generates the change of constructive parameters of the pump assembly contains a number of conditions that constantly check the required flow rate parameter values. The reaction works only in the CATIA v5 environment because it needs access to the pump parameters. Their names and relations that establish values are stored and managed within the program.
When a certain condition is met for the pump flow (the user has chosen a certain value from the list), the code sequence imposes new discrete values for the pump parameters and modifies the 3D models of the pump components. In
Appendix A, several sequences of the reaction code for specified values of the pump flow rate are briefly presented.
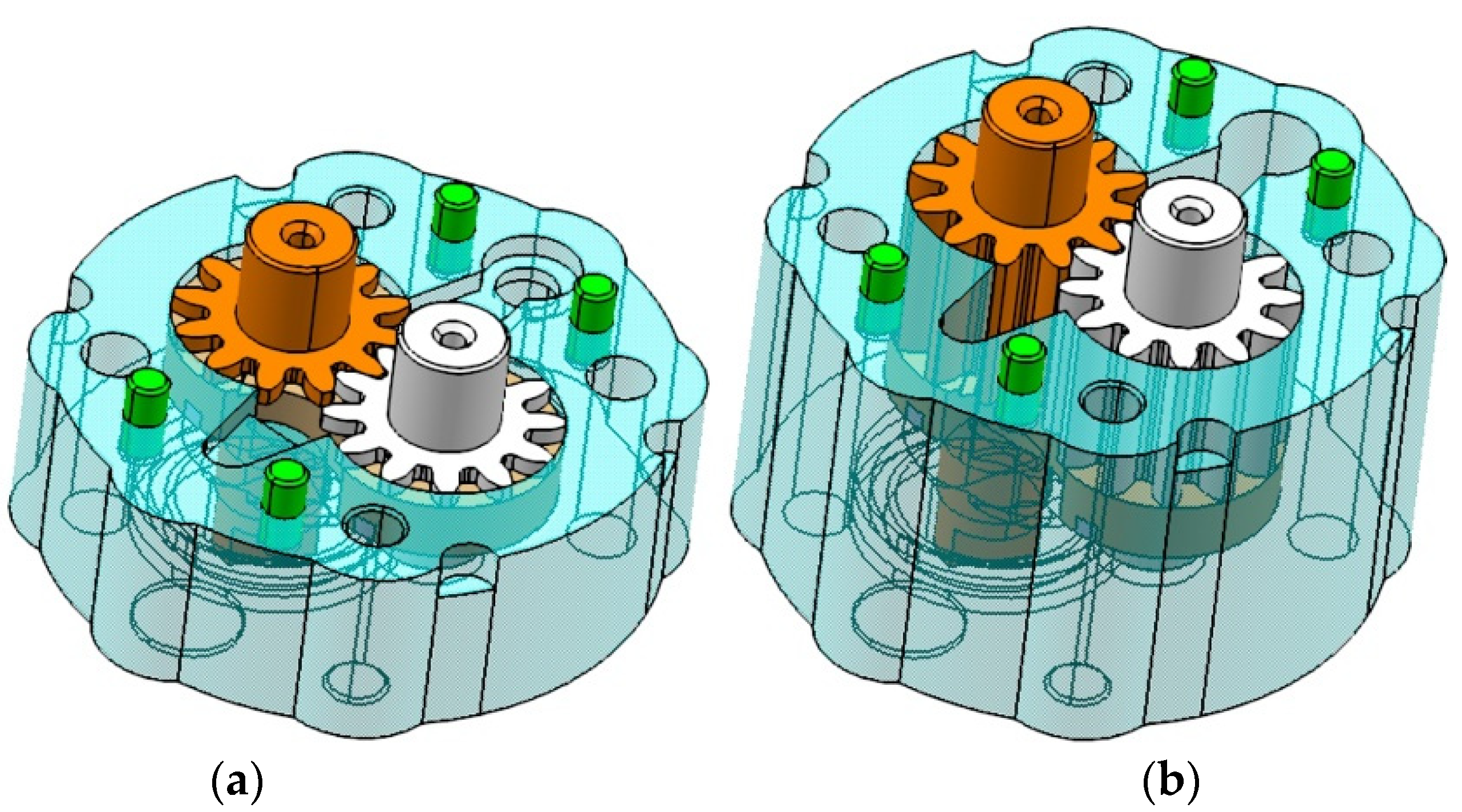
Figure 4 contains two of the twelve constructive variants of the parametrically designed pump, depending on flow rates, as follows: (a) Q
p = 2 L/min and (b) Q
p = 22.52 L/min.
Certain standard components of the assembly (i.e., cover, screws and gaskets) were not represented in the figure to simplify it and only to highlight how the parameterized components are changed.
The two models express the pump assembly parametric design possibilities when the modification criterion is the user’s required flow rate.
Figure 4 shows different widths of the bodies, compensators and gears, easily and correctly mounted in CATIA v5. In the pump assembly modeling phases, some improvements were identified and proposed to the company.
Figure 5 presents the components from two constructive variants of the same type of pump, after and before its improvement/redesign. The new pump body and cover use four pins for better cover orientation, whereas the previous solution had only two pins. The often incorrect cover mounting by the technicians after the application of maintenance and repair operations imposed this change.
An additional improvement is the hole diameter and its position relative to the outlet chamber. The new compensator has a slightly larger gasket channel, obtained directly during the casting phase, while the previous compensator was contour milled. Additionally, in the new compensator, a supplementary thin plastic gasket is added and mounted for a better sealing of the pump chambers. This plastic gasket holds the rubber gasket tightly inside the compensator, preventing movements and premature wears.
For each subfigure, the left side shows the new proposed solutions of the pump components, while the right side corresponds to the previous solutions, following the parameterization and design processes. Both solutions are still in production and testing stages.
3. Numerical Analysis of the Loads Applied on the Pump’s Spur Gear
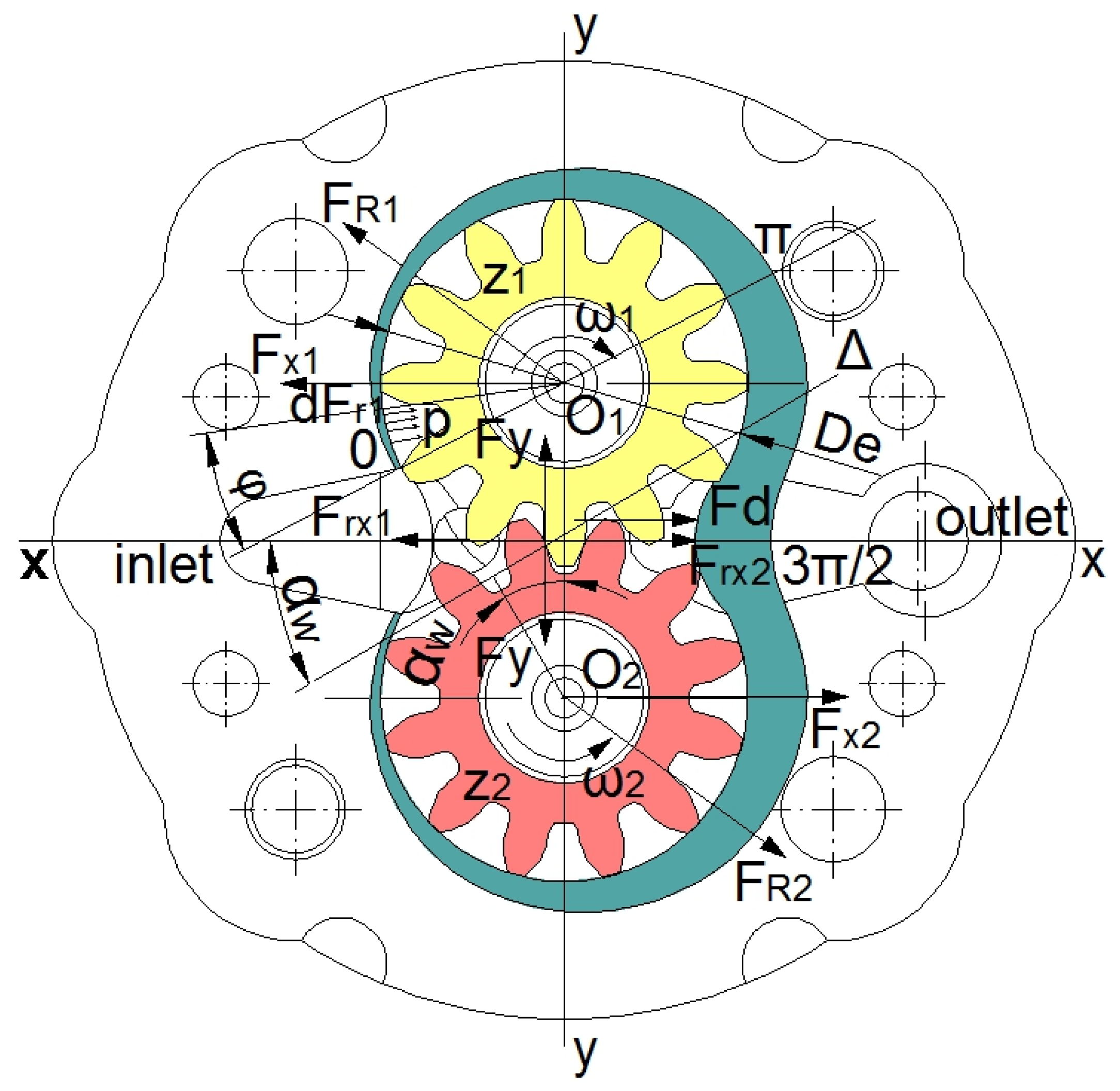
This step is important in order to understand the behavior of the external spur gear loaded with pressures and forces to simulate the real operating conditions, for every constructive solution. By mathematical computation, the loads and constraints applied in the pump assembly were determined.
A specific systematic methodology previously presented in Refs. [
5,
19] was applied to count the distribution of the loading forces that affect the gears, body, cover, shafts and their support bearings. These elements are loaded by the radial components of the pressure forces applied on gears and also by the gearing forces that correspond to the components of the pressure forces acting on teeth flanks [
5,
8,
9] in each teeth space between two consecutive teeth (
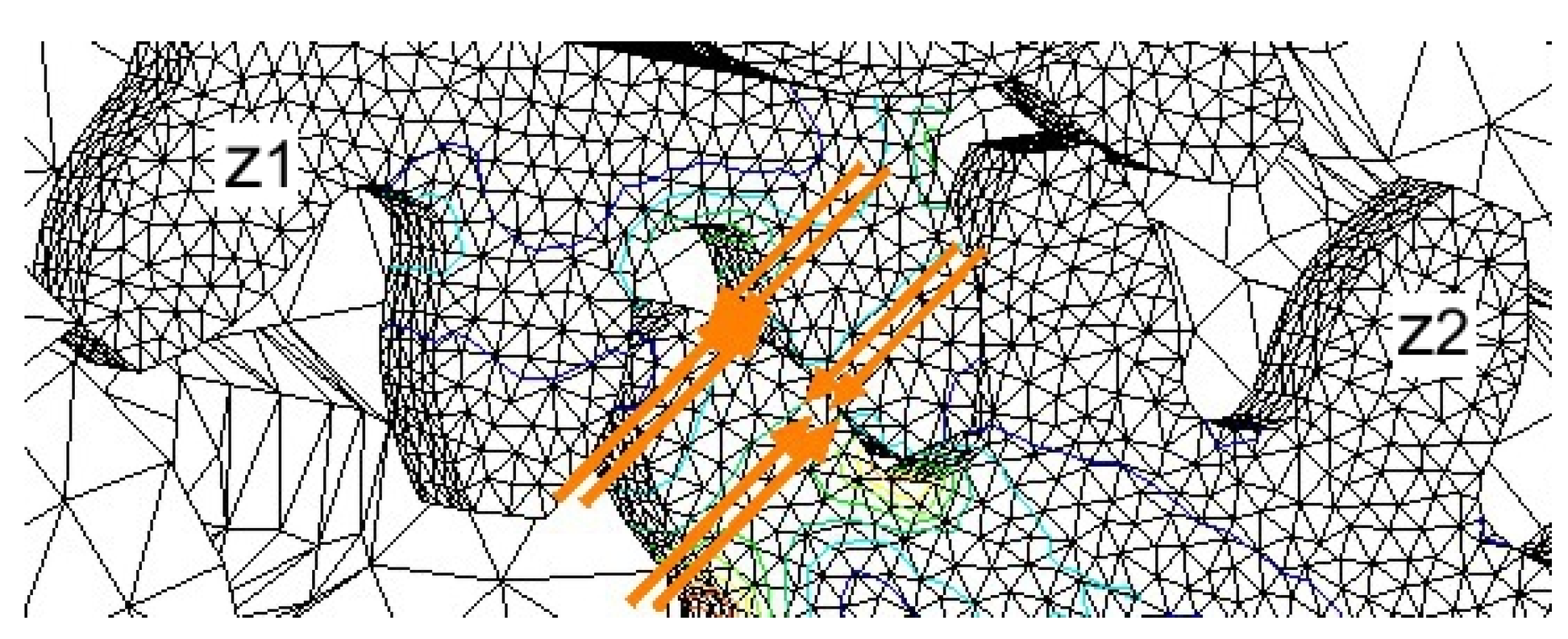
Figure 6).
In the addendum area of every tooth, a pressure distribution appears and operates. There are some very small variations of pressure along every tooth, and therefore, the radial pressure distribution is considered continuous.
The gearing forces oriented along the gearing line (marked with Δ) are decomposed in two directions: tangent and radial. The theory and practice considered that under nominal operating conditions, the pressure distribution has a parabolic shape [
19]. The radial clearance between the gears and the respective holes in the pump body has an influence on the flow rate and fluid discharge pressure.
Considering the directions of movement at the angular speed ω1 = ω2 of the two gears, the contact between any tooth of the driving gear z1 with the conjugate tooth of the driven gear z2 takes place at a point belonging to the gearing line Δ. At that moment, the pair of teeth cause a discharge of fluid into the outlet aperture of the pump.
Once the pair of teeth leave out the meshing area, the next pair of teeth follow in.
Applying the generated pressures on the peripheral surfaces of the gears creates a resisting torque that is counteracted by the engaging of the driving gear. This torque value gives the measure of the necessary driving power, by the relation (3):
where the parameters are indicated in §2, η
m is the hydro-mechanical efficiency (%), and η
t is the total efficiency (%). Because of the viscous friction losses that appear in the bearing couplings between the gear shafts and the compensator [
20]; of the viscous friction losses at the teeth tips within the gap between these tips and the pump’s internal casing; of the viscous friction losses generated within the gap between the gear’s lateral surface and the internal surfaces of the bushing blocks of the pump; and of the mechanical losses due to the gears meshing, in practice, the hydro-mechanical efficiency η
m is considered and applied.
Relation (4) determines the force acting on each tooth in the horizontal (x–x) direction because of the torque generated by the driving gear (z
1):
where M
a (N⋅mm) is the torque that has to be generated by the driving shaft, and D
w (mm) is the gear-rolling diameter. M
a may be calculated [
19] using relation (5):
where p—pressure (bar) generated within the pump (especially in the outlet chamber) while it is operating, b = λ⋅m—gears width (mm), λ—width coefficient, m—gear modulus (mm), z
1 = z
2—teeth numbers of the driving gear, also called pinion, and of the driven gear.
The values of the necessary powers and torques to run the pump are determined and presented for each parametric variant in
Table 2. The rolling diameters D
w12 [
4,
19] of the displaced spur gears are given by (6)
where ξ—specific displacement of the gear teeth profile. Therefore, the calculation formula of the force, which is applied on the teeth, is (7)
F
d—the tangent component of the generated force acting on the driving gear tooth z
1.
The fluid under pressure that fills the space between the teeth is a load in the radial direction (
Figure 6) for both gears. This pressure has a variation from the atmospheric pressure p
0 in the inlet chamber up to the nominal pressure p in the outlet chamber.
Considering an angular variation starting with the inlet chamber, φ ∈ (0…π), the pressure is rising, while for φ ∈ (π…3π/2),
Figure 6, it remains almost constant [
18].
Taking a point on the circumference of the driving gear z1, in the interval φ ∈ (0…π), the pressure generated in the pumped fluid to the outlet chamber is pgz1 = p⋅φ/π.
This pressure creates a radial elementary force dFr1, which acts on the outside radius circumference of the driving gear z1, in correspondence with the angle dφ.
This force can be calculated by relation (8):
The radial elementary force acting on the interval φ ∈ (π…3π/2) is (9):
The total radial force F
rx acting in the horizontal direction x–x on both gears results through relation (10).
Here, φ—the rotation angle of the driving gear z
1, D
e = D
e12—the outer diameter of gears, calculated by using formula (11).
It may be considered, due to the small diameter of the gears, that forces F
rx1, F
rx2 (
Figure 7) also act on the gear centers O
1 and O
2. The resulting forces F
R1 and F
R2 are considered to act on these centers as well.
The radial force acting on the driving shaft in the direction x–x is determined [
6,
8] by formula (12), while for the force applied on the driven shaft and in the same direction, relation (13) is used.
The resultant of the radial forces, relation (14), acting in the vertical direction (y–y) on the two gears becomes null (according to the radial distribution of pressures).
A radial rejecting force F
y acting in the same y–y direction results as a reaction of teeth in contact—relation (15).
As an example, the gear angle is α
w = 23
0, and the gear has displaced teeth [
8,
16].
Relations (16) and (17) calculate the resulting forces F
R1 and F
R2, which produce loads on the gear bearings:
To calculate the forces with the above formulae, the following values were used: p = 150 bar, m = 2 mm, ξ = 0.5 mm.
Table 2 contains the values of forces F
d, F
rx1, F
rx2, F
x1, F
x2, F
y, F
R1 and F
R2 determined for each constructive variant.
Analyzing the data presented in
Table 2, a proportional increase by 8–10 times the calculated values between the first and the last parameterized constructive variant of the pump may be observed.
4. Simulation with Finite Elements of the Spur Gear Loads
A FEM simulation model is applied for validating various variants of the pump product’s parameterized concept. The force values and the pressure distribution used were presented in
Table 2. Thus, crucial data are obtained and presented in this paragraph regarding the stresses and deformation distributions that appeared related to the pump assembly. Keeping the safety conditions to operate the pump, it is required that the computed stresses be lower than the critical ones. For most critical conditions (tensile strength, flow limit, elasticity limit, etc.), different safety coefficients can be chosen.
The yield strength of each material applied on the pump’s parts is defined as the maximum limit of the actual stresses under the safety conditions imposed by the safety coefficient admissible value. The yield strength value determines the change of the model (its geometry, mesh refining), of the restraints and/or the loads. The goal is to control and keep the deformations, if possible, in the elastic domain, respecting the safety coefficient imposed by the manufacturer after testing the pump in real conditions [
21].
The physical properties of the pump components’ materials are very important to be correctly implemented in the FEM analysis. The yield strength values crucially affect the simulations results computed in this analysis. According to the pump manufacturer, its body is made of an aluminum alloy AlSi9Cu3(Fe), yield strength R
m = 240 MPa, HBS 2.5/62.5 = 104, Si (9.75%), Fe (0.73%), Cu (3.04%), Ni (0.43%), Mg (0.3%), Zn (0.2%), Sn (0.18%), Ti (0.18%), Mn (0.08%) [
3]. The cover is made of AlSi6Cu4, yield strength R
m = 200 MPa, HBS 2.5/62.5 = 121 with the composition: Si (7.97%), Cu (5.12%), Mg (0.7%), Fe (0.53%), Mn (0.12%), Ni (0.01%), Zn (0.12%). These alloys are recommended for casting parts, having a very good machinability. For the gears and shafts, a steel alloy R
m = 350 MPa, HRC = 51 was considered, and for the assembly components (pins and screws), a quality carbon steel R
m = 250 MPa.
A good 3D model of the pump assembly should be followed by the discretization of the main components. Thus, a correct refining of the mesh for these components leads to a reduced error of the computations model, so the values resulted from FEA are close to the real ones [
3,
22]. In order to analyze the pump, a mesh of points and elements is defined in CATIA v5, with a good precision for the gears (size = 0.5 mm, sag = 0.2 mm, parabolic type). These components are the most stressed, also presenting a high interest for the proposed study.
FEM analysis also considers other components having the bearing role for the gear shafts: cover, body and compensator (size = 1.5 mm, sag = 1 mm, linear type). After the discretization and simulation computations are completed, the results for the gears present a much lower error rate than for the other components. All, however, are within the accepted limits of good practice related to such analyses [
9,
21].
Figure 8 shows the meshing solution for the gears and the pump’s body.
Physical constraints, such as Contact, Pressure, Fastened and Slider, were applied between the components of the gear pump, according to Refs. [
3,
7,
22].
An important stage in the analysis of the pump assembly is the application of virtual loads on certain surfaces of the components. These virtual loads (pressures and forces) replace and simulate the real loads that appear within the model during operation [
8].
According to the theoretical considerations and practice, the forces inside the pump assembly act on teeth and also on the pressures radially distributed in the gaps between the teeth. Other pressure loads affect the bearings, the plane surfaces of the cover and of the compensator. These loads determine the appearance of stresses and deformations inside the pump [
10,
22,
23].
The applied pressures for FEA are located in the gaps between the teeth (
Figure 8) for each gear. The pressure distribution starts from a value of 1.5 MPa going up to the value of 15 MPa (150 bar), which is the nominal pressure for pump operation according to the manufacturer’s specifications. The inlet chamber presents the lowest pressure, close to the atmospheric pressure p
0, and the highest value is found in the outlet chamber [
19]. Two forces of equal value but opposite direction F
d also act tangentially on the gearing teeth. Together with the forces created by the applied pressures (F
rx1 and F
rx2), the pump assembly is loaded with the resulting forces F
x1, F
x2, applied for FEA on the gearing teeth and on the gear shafts (
Figure 7).
Combining these forces with the reaction force of the gearing teeth, F
y, the resulting forces F
R1 and F
R2 (
Figure 7) are obtained. These forces stress the bearings of the driving and driven gears.
Figure 9 presents the loading applied on the two gear teeth in contact at a certain moment. The forces mentioned above create stresses in gears and shafts but also in other components of the pump: compensator, body, cover, pins and screws.
The finite elements analysis reveals that the teeth are most stressed when they reach the position where maximum pressure is applied on their flanks but also in the gearing area [
3,
6]. In addition, the deformation values of such areas are determined by the analysis. The maximum and the minimum stress values are possible to be located on every component of the pump and also the deformations and the rates of error for all 12 parameterized pump variants, according to
Table 3.
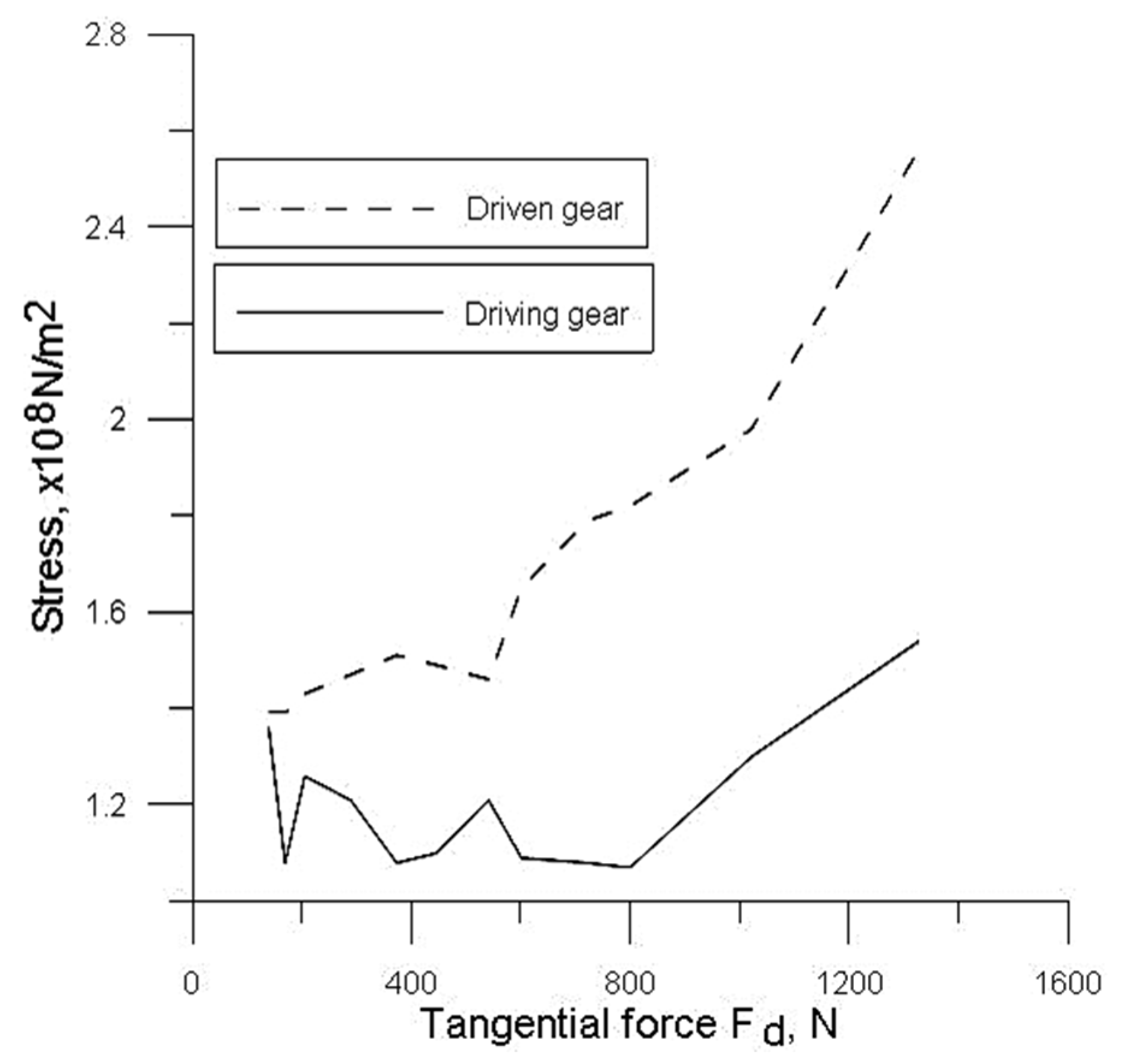
Maximum stresses appear for the last parameterized pump model (width of gear teeth b = 22.1 mm, tangential forces Fd = 1326 N).
The most loaded components are the gear teeth. The maximum stress (of 256 MPa) is obtained in the driven gear, in the last constructive variant. The stress is located at the teeth root [
17]. Additionally, the driving gear presents maximum stress (of 154 MPa) at the root of the teeth.
The maximum stress values identified in the gears do not exceed the yield strength value (350 MPa) of the gear steel. The deformations experienced by each gear model in the contact area are small (10.9 × 10−3 mm—driven gear, 5.7 × 10−3 mm—driving gear), insignificant for the proper pump assembly operation.
The error rates for the two gears discretized by finite elements of the parabolic type are within the 7–10% interval. These values are convenient and accepted for a FEM analysis of such an assembly [
21].
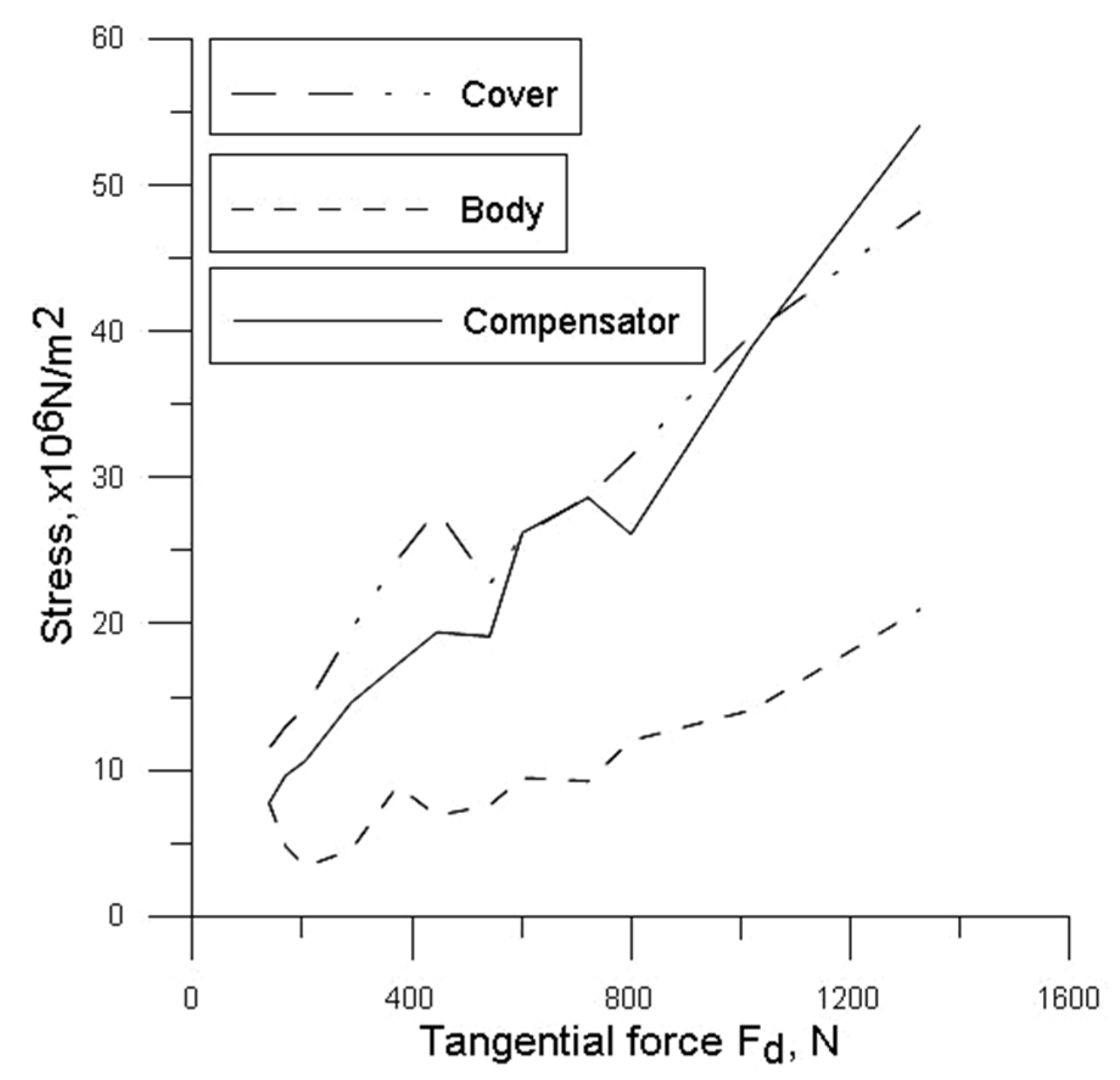
The compensator presents a maximum stress of 54 MPa, the body has a maximum stress of 21 MPa, while the cover has a maximum stress of 48.2 MPa.
The other pump components (pins, screws and gaskets) present various levels of stress, but their values are very low and do not influence its functioning. The good influence of those two supplementary pins, which stiffen the pump assembly, was observed.
It was also observed that the stress distribution is higher in the driven gear bearings (compensator and cover), in the gearing area and in the gaps between the teeth that contain the high pressures.
The stress values found in these components after analysis are smaller than the value of yield strength (260 MPa) of the aluminum alloy that they are made of.
Figure 10 and
Figure 11 present the evolution of stresses that occurred in the driving and driven gears and in the body, compensator and cover, according to the values of F
d forces applied on the teeth, for all the parameterized variants.
Knowing the simulation practices with FEM and analyzing all these results presented in tables, it can be concluded that the parameterized variants of the pump model meet the conditions for manufacturing [
24].
Figure 12 shows the maximum stress location in the main components of the analyzed pump for the third parameterized variant (
Table 3). The areas where the stress increases, as well the pressure distribution between the gear teeth, are graphically presented, together with the palette of values. In addition, the figure highlights how the meshing of the pump components was prepared. Thus, the finite elements mesh is denser on gears, which leads to lower (and better) error percentages.
If the error is relatively high in a particular area of interest, the analysis results will not be considered, and the 3D model must be refined and the calculation repeated. The purpose of refining the pump’s mesh [
11] is to achieve a rate of error as small as possible and, therefore, the least possible difference in pump assembly behavior under both virtual and real conditions.
To complete this study, many computation iterations were performed, which were required to obtain the imposed objectives regarding a low error percentage.
5. Concluding Remarks
The parametric design study, quick creation of twelve constructive variants of the gear pump product and finite element analysis of each assembly show that it is entirely possible to reach preliminary product validation, which is an important stage in product design optimization [
5], with significant impact on the process of establishing similar product ranges for future development.
The paper presented an applied methodology for the manufacture of a family of pumps, as well as for calculating the power and torque required for the electric drive motor, the forces involved in the operation of the pump, the dimensions of its components, etc. The dimensional parameters of the pump have discrete values resulting from successive calculations and tests, taking into account the semi-finished products available for the body and cover. The pump must supply certain flows according to requirements from the beneficiaries, and the sizing of its components especially takes into account the parameters that define the geometric volume.
The finite element analysis applied and performed on the parametric pump assembly provided the validation by simulation of all twelve identified solutions, as the maximum stress values were lower than the material yield strength of each component. The maximum values of displacements in all the parts were very low and would not lead to interference between the pump components nor to a leakage of the hydraulic fluid during operation.
After an optimal pump assembly re-modeling, corresponding to the third solution (which is already in production and testing), the weight increased from 546 g to 587 g.
The number of pump components increased for several reasons. For the new pump, a supplementary thin but rigid plastic gasket was added to the compensator for a better sealing of the pump chambers. This gasket also prevented the movement and premature wear of the rubber gasket, which was re-designed to have a slightly different shape to match the new shape of the larger channel of the compensator. Additionally, the higher number of pins was due to the increased stresses that appeared in the larger constructive versions of the pump but also the fact that, sometimes, the beneficiaries’ technicians incorrectly mounted the pump cover after completing the maintenance and repair operations.
The analysis presented in this paper did not consider the pressure pulsation, nor the hydraulic fluid temperature increase in the operating time, which also impacts the pump components’ loads. Further research might consist of fully testing the resulting prototype variants in experimental conditions to measure the real stress values, flows, temperatures, noise and vibrations. This validation should be the final product confirmation before a full series production.