Modeling of Thermal Traces Using Fractional Order, a Discrete, Memory-Efficient Model
Abstract
:1. Introduction
- Recalling of some elementary ideas and definitions from fractional calculus.
- The CFE-based method of solution of the FO state equation and its adaptation to solving of a scalar, initial problem.
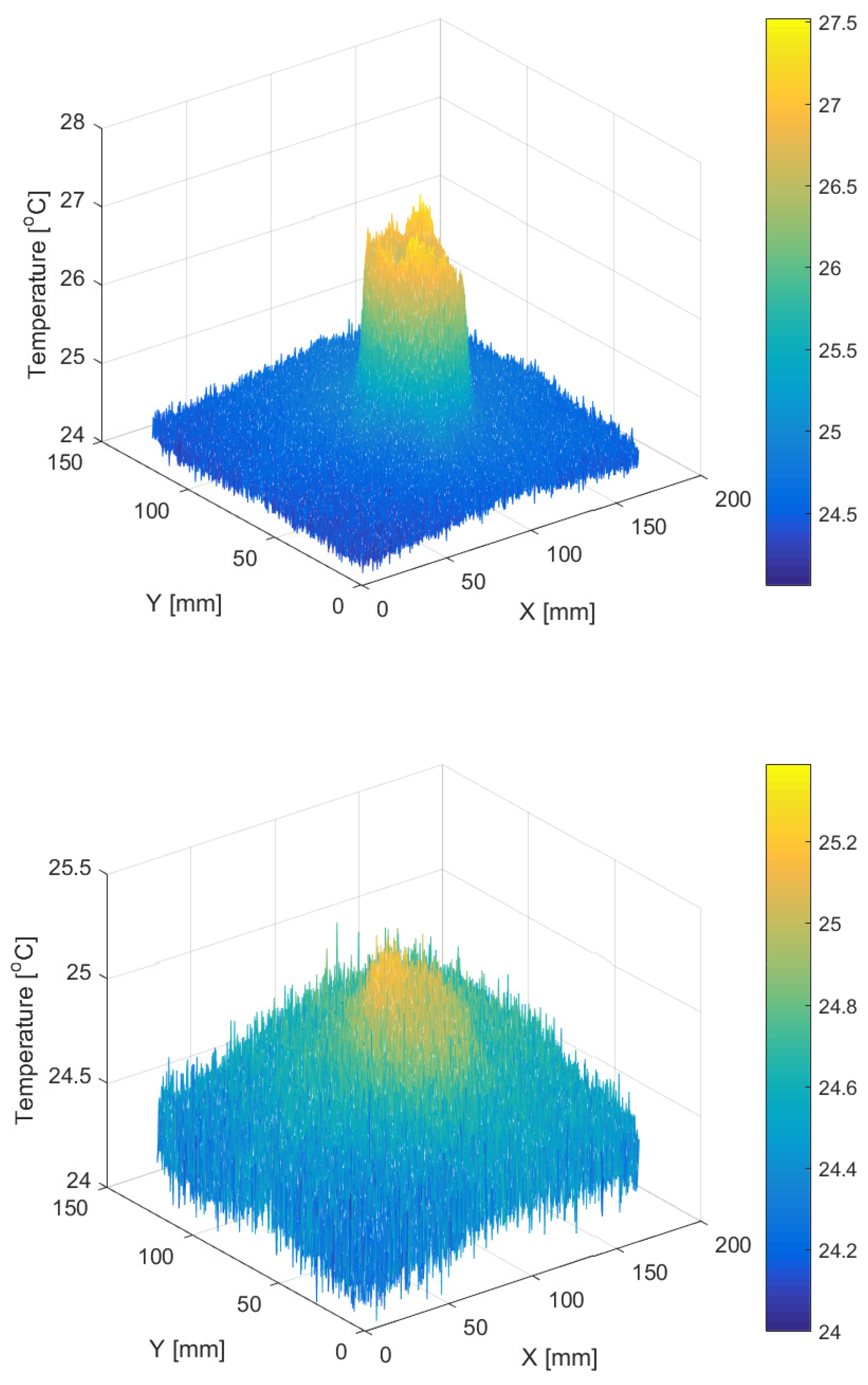
- The use of the proposed model for modeling of thermal traces on flat wooden surfaces.
- Experimental verification of results.
2. Preliminaries
2.1. Elementary Ideas
2.2. The CFE Approximation
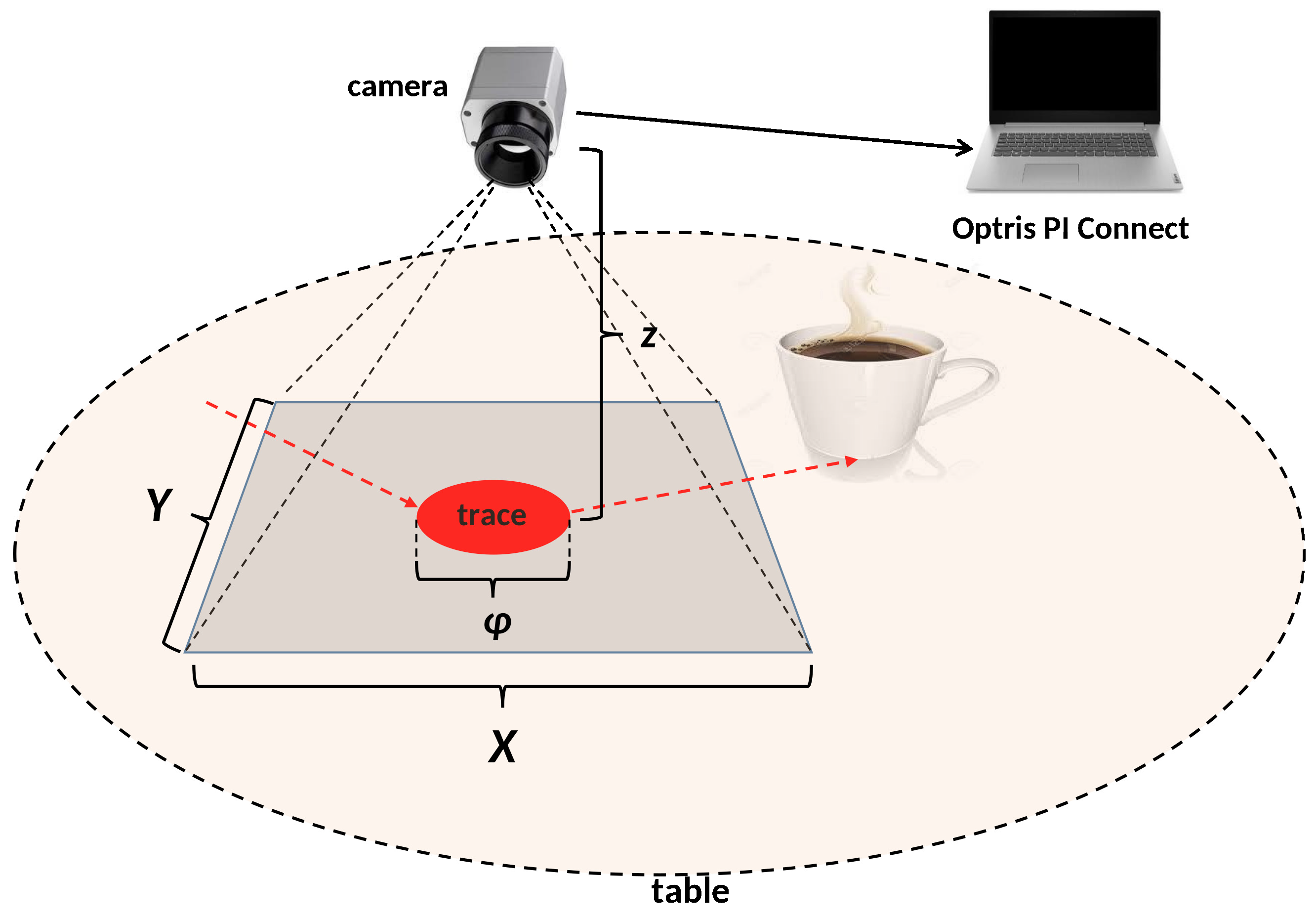
3. The Considered Heat System
4. Main Results
4.1. The Free, Scalar, IO State Equation
4.2. The Discrete, Free, Scalar, FO State Equation Using CFE Approximation
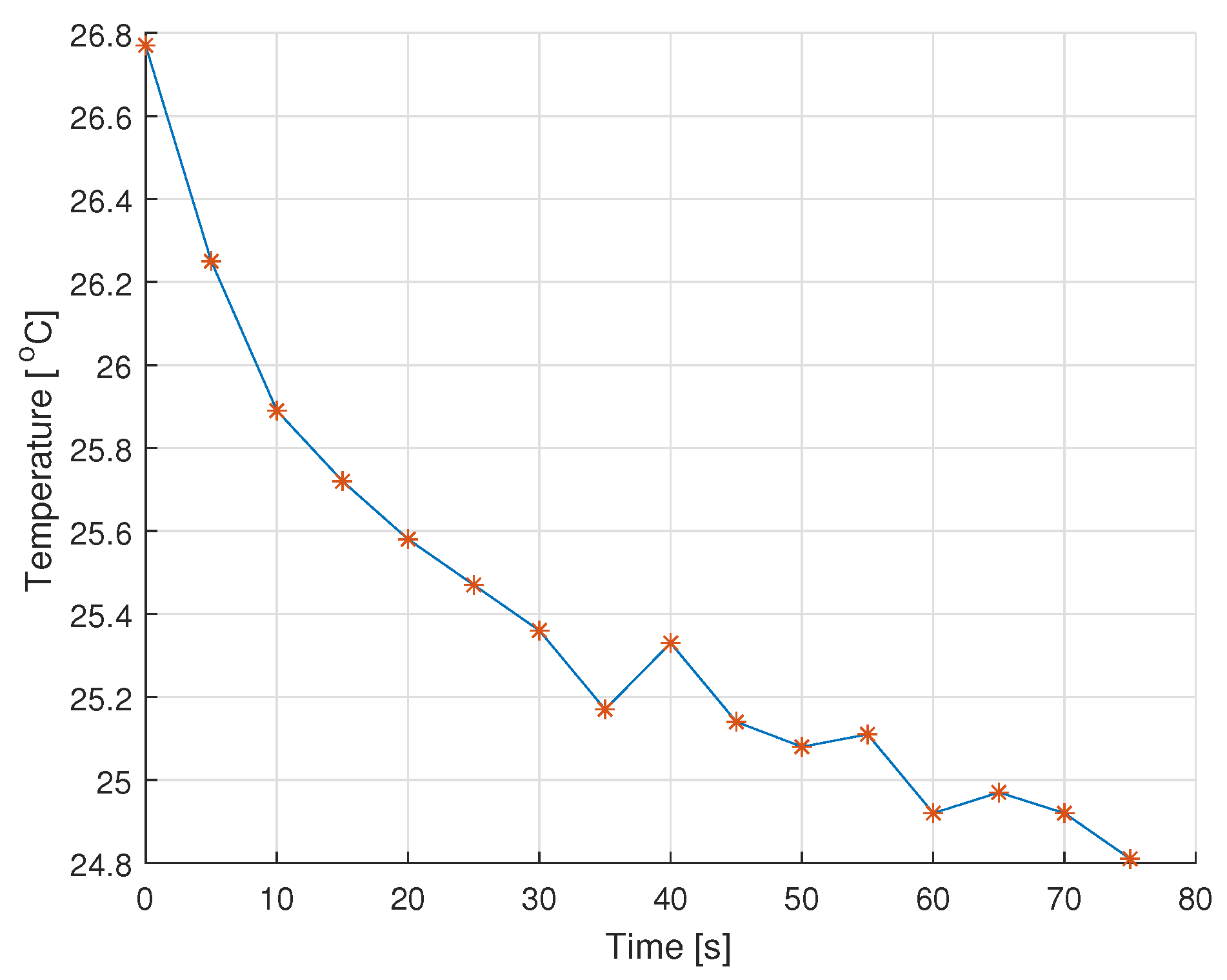
5. Experimental Verification of Results
6. Discussion of Results
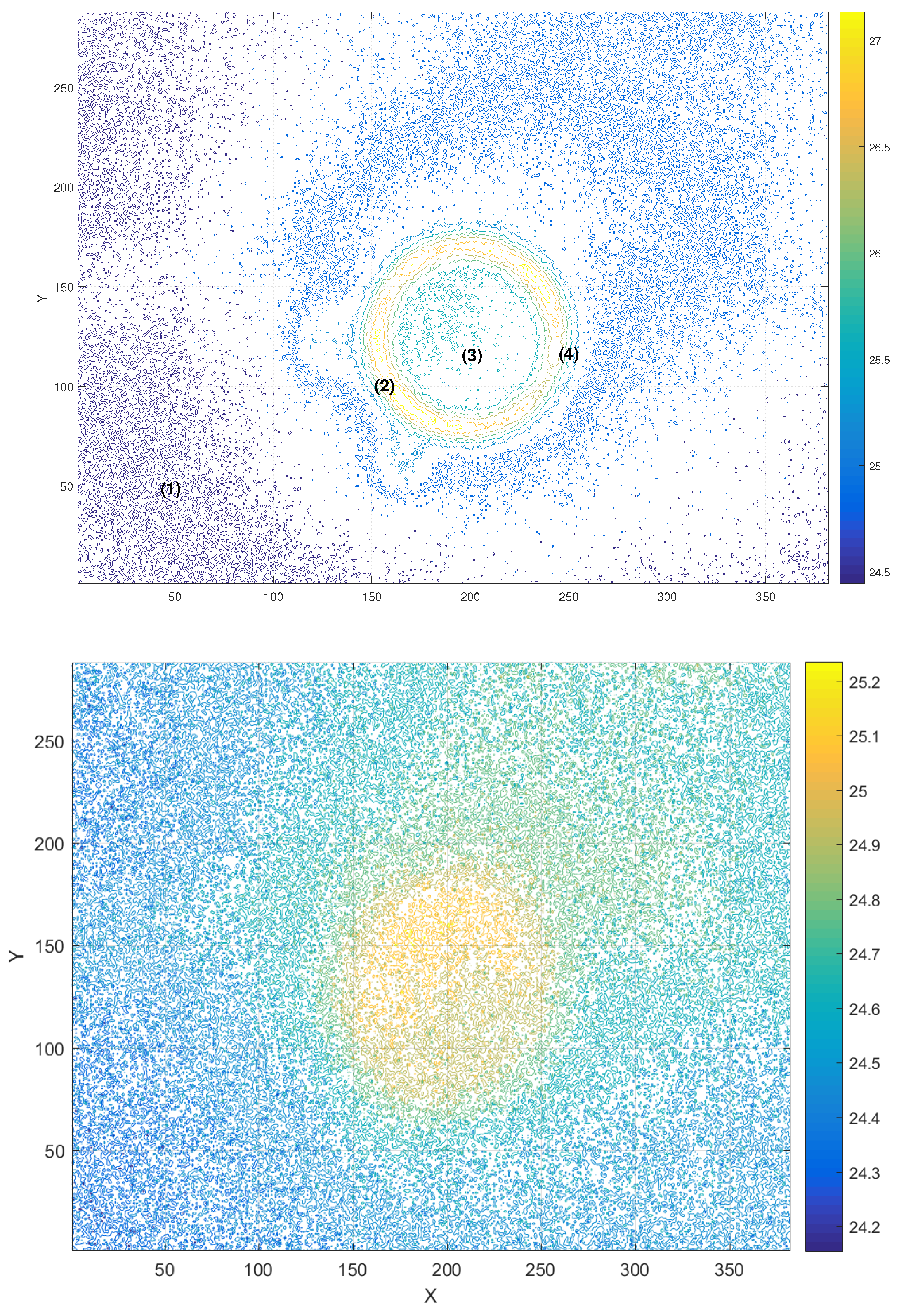
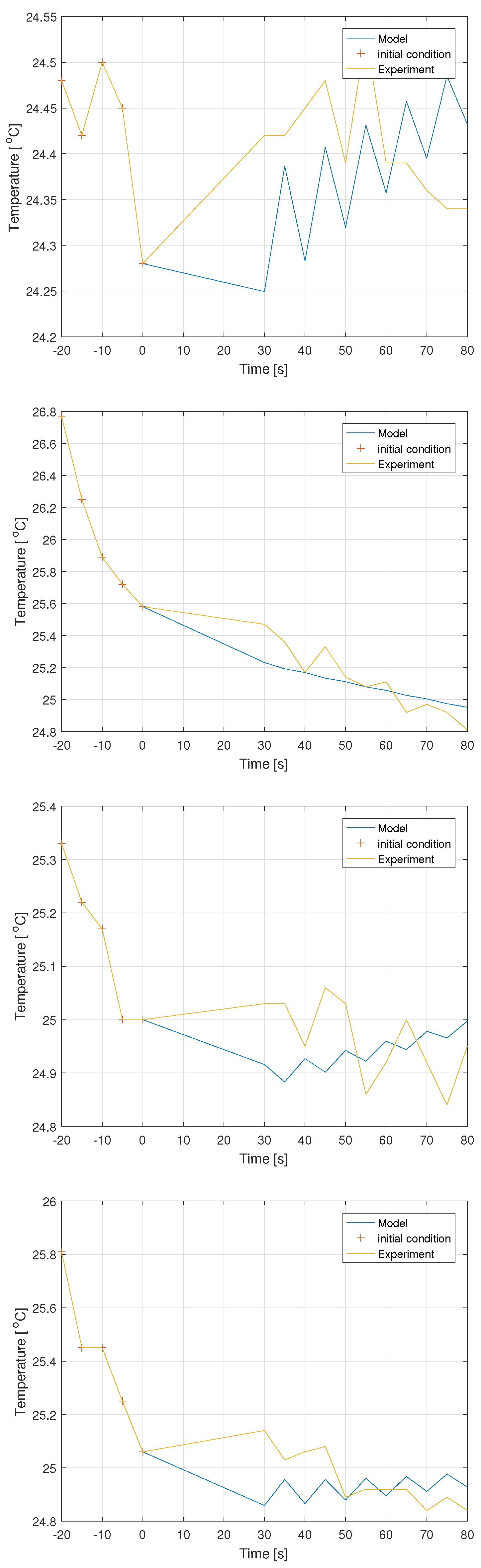
- The FO model is more accurate than the IO model in points (1)–(3). In point (4), the IO model is more accurate.
- The sense of use of the FO model, where the initial condition is given as a function, not as a single point is well illustrated by result for point (1). At this point, the use of the initial function allows to correct prediction of the behavior of the temperature in contrast to IO model, where the prediction was incorrect.
- For the IO model, values of time constant are significantly different for each point.
- For the FO model, the values of the parameters are very close for all the tested points of the modeled temperature field. This allows the conclusion that the proposed, simplified model correctly describes the real thermal process under consideration.
7. Final Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Suleman, M.; Lu, D.; He, J.; Farooq, U.; Hui, Y.; Rahman, J.U. Numerical investigation of Fractional HIV model Using Elzaki Projected Differential Transform Method. Fractals 2018, 26, 1850062. [Google Scholar] [CrossRef]
- Suleman, M.; Lu, D.; Rahman, J.U.; Anjum, N. Analytical Solution of Linear Fractionally Damped Oscillator by Elzaki Transformed Method. DJ J. Eng. Appl. Math. 2018, 4, 49–57. [Google Scholar] [CrossRef]
- Lu, D.; Suleman, M.; Ramzan, M.; Rahman, J.U. Numerical solutions of coupled nonlinear fractional KdV equations using He’s fractional calculus. Int. J. Mod. Phys. B 2021, 35, 2150023. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus for System Identification and Controls; Springer: Berlin, Germany, 2010. [Google Scholar]
- Dzieliński, A.; Sierociuk, D.; Sarwas, G. Some applications of fractional order calculus. Bull. Pol. Acad. Sci. Tech. Sci. 2010, 58, 583–592. [Google Scholar] [CrossRef] [Green Version]
- Dlugosz, M.; Skruch, P. The application of fractional-order models for thermal process modelling inside buildings. J. Build. Phys. 2016, 39, 440–451. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Gawin, E.; Mitkowski, W. Modeling heat distribution with the use of a non-integer order, state space model. Int. J. Appl. Math. Comput. Sci. 2016, 26, 749–756. [Google Scholar] [CrossRef] [Green Version]
- Oprzędkiewicz, K.; Gawin, E.; Mitkowski, W. Parameter identification for non integer order, state space models of heat plant. In Proceedings of the MMAR 2016: 21th international conference on Methods and Models in Automation and Robotics, Międzyzdroje, Poland, 29 August–1 September 2016; pp. 184–188. [Google Scholar]
- Oprzedkiewicz, K.; Stanislawski, R.; Gawin, E.; Mitkowski, W. A new algorithm for a CFE approximated solution of a discrete-time non integer-order state equation. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 429–437. [Google Scholar]
- Oprzędkiewicz, K.; Mitkowski, W.; Gawin, E. An accuracy estimation for a non integer order, discrete, state space model of heat transfer process. In Proceedings of the Automation 2017: Innovations in Automation, Robotics and Measurment Techniques, Warsaw, Poland, 15–17 March 2017; pp. 86–98. [Google Scholar]
- Oprzędkiewicz, K.; Mitkowski, W.; Gawin, E.; Dziedzic, K. The Caputo vs. Caputo-Fabrizio operators in modeling of heat transfer process. Bull. Pol. Acad. Sci. Tech. Sci. 2018, 66, 501–507. [Google Scholar]
- Oprzędkiewicz, K.; Gawin, E. The practical stability of the discrete, fractional order, state space model of the heat transfer process. Arch. Control Sci. 2018, 28, 463–482. [Google Scholar]
- Oprzędkiewicz, K.; Mitkowski, W. A memory efficient non integer order discrete time state space model of a heat transfer process. Int. J. Appl. Math. Comput. Sci. 2018, 28, 649–659. [Google Scholar] [CrossRef] [Green Version]
- Oprzędkiewicz, K.; Mitkowski, W.; Rosol, M. Fractional order model of the two dimensional heat transfer process. Energies 2021, 14, 6371. [Google Scholar] [CrossRef]
- Ryms, M.; Tesch, K.; Lewandowski, W. The use of thermal imaging camera to estimate velocity profiles based on temperature distribution in a free convection boundary layer. Int. J. Heat Mass Transf. 2021, 165, 120686. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method. Entropy 2019, 21, 597. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olsen-Kettle, L. Numerical Solution of Partial Differential Equations; The University of Queensland: Queensland, Australia, 2011. [Google Scholar]
- Al-Omari, S.K. A fractional Fourier integral operator and its extension to classes of function spaces. Adv. Differ. Equ. 2018, 2019, 195. [Google Scholar] [CrossRef]
- Berger, J.; Gasparin, S.; Mazuroski, W.; Mendes, N. An efficient two-dimensional heat transfer model for building envelopes. Numer. Heat Transf. Part A Appl. 2021, 79, 163–194. [Google Scholar] [CrossRef]
- Moitsheki, R.; Rowjee, A. Steady Heat Transfer through a Two-Dimensional Rectangular Straight Fin. Math. Probl. Eng. 2011, 2011, 826819. [Google Scholar] [CrossRef]
- Yang, L.; Sun, B.; Sun, X. Inversion of Thermal Conductivity in Two-Dimensional Unsteady-State Heat Transfer System Based on Finite Difference Method and Artificial Bee Colony. Appl. Sci. 2019, 9, 4824. [Google Scholar] [CrossRef] [Green Version]
- Kaczorek, T. Selected Problems of Fractional Systems Theory; Springer: Berlin, Germany, 2011. [Google Scholar]
- Ostalczyk, P. Discrete Fractional Calculus. Applications in Control and Image Processing; World Scientific: Hackensack, NJ, USA; London, UK; Singapore, 2016. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Mozyrska, D.; Pawluszewicz, E. Fractional discrete-time linear control systems with initialisation. Int. J. Control 2011, 1, 213–219. [Google Scholar] [CrossRef]
- Kaczorek, T. Singular fractional linear systems and electrical circuits. Int. J. Appl. Math. Comput. Sci. 2011, 21, 379–384. [Google Scholar] [CrossRef]
- Kaczorek, T.; Rogowski, K. Fractional Linear Systems and Electrical Circuits; Bialystok University of Technology: Bialystok, Poland, 2014. [Google Scholar]
- Kaczorek, T. Reduced-order fractional descriptor observers for a class of fractional descriptor continuous-time nonlinear systems. Int. J. Appl. Math. Comput. Sci. 2016, 26, 277–283. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.Q.; Moore, K.L. Discretization Schemes for Fractional-Order Differentiators and Integrators. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 263–269. [Google Scholar]
- Petras, I. Fractional order feedback control of a DC motor. J. Electr. Eng. 2009, 60, 117–128. [Google Scholar]
- Petras, I. 2009. Available online: http://people.tuke.sk/igor.podlubny/USU/matlab/petras/dfod2.m (accessed on 1 January 2022).
- Stanisławski, R.; Latawiec, K.; Łukaniszyn, M. A Comparative Analysis of Laguerre-Based Approximators to the Grünwald-Letnikov Fractional-Order Difference. Hindawi Publ. Corp. Math. Probl. Eng. 2015, 2015, 512104. [Google Scholar] [CrossRef]
- Dzieliński, A.; Sierociuk, D. Stability of Dicrete Fractional Order State-Space Systems. In Proceedings of the 2nd IFAC Workshop on Fractional Differentiation and its Applications, Porto, Portugal, 19–21 July 2006; pp. 505–510. [Google Scholar]


| Order L | ||
|---|---|---|
| L = 1 | ||
| L = 3 | ||
| L = 5 | ||
| No. | x | y | ||
|---|---|---|---|---|
| 1 | 50 | 50 | 17,959.12 | 0.0286 |
| 2 | 165 | 100 | 1721.28 | 0.0114 |
| 3 | 200 | 125 | 3486.51 | 0.0067 |
| 4 | 250 | 125 | 6455.36 | 0.0078 |
| No. | x | y | a | |||
|---|---|---|---|---|---|---|
| 1 | 50 | 50 | 0.4898 | 24.0387 | 1.1037 | 0.0072 |
| 2 | 165 | 100 | 0.4859 | 24.1231 | 1.1042 | 0.0102 |
| 3 | 200 | 125 | 0.4893 | 24.0492 | 1.1044 | 0.0061 |
| 4 | 250 | 125 | 0.4889 | 24.0538 | 1.1050 | 0.0102 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oprzędkiewicz, K.; Rosół, M.; Mitkowski, W. Modeling of Thermal Traces Using Fractional Order, a Discrete, Memory-Efficient Model. Energies 2022, 15, 2257. https://doi.org/10.3390/en15062257
Oprzędkiewicz K, Rosół M, Mitkowski W. Modeling of Thermal Traces Using Fractional Order, a Discrete, Memory-Efficient Model. Energies. 2022; 15(6):2257. https://doi.org/10.3390/en15062257
Chicago/Turabian StyleOprzędkiewicz, Krzysztof, Maciej Rosół, and Wojciech Mitkowski. 2022. "Modeling of Thermal Traces Using Fractional Order, a Discrete, Memory-Efficient Model" Energies 15, no. 6: 2257. https://doi.org/10.3390/en15062257
APA StyleOprzędkiewicz, K., Rosół, M., & Mitkowski, W. (2022). Modeling of Thermal Traces Using Fractional Order, a Discrete, Memory-Efficient Model. Energies, 15(6), 2257. https://doi.org/10.3390/en15062257







