A Versatile Model for Estimating the Fuel Consumption of a Wide Range of Transport Modes
Abstract
:1. Introduction
2. Literature Review
2.1. On-Road Transport Modes
2.2. Non-Road Transport Modes
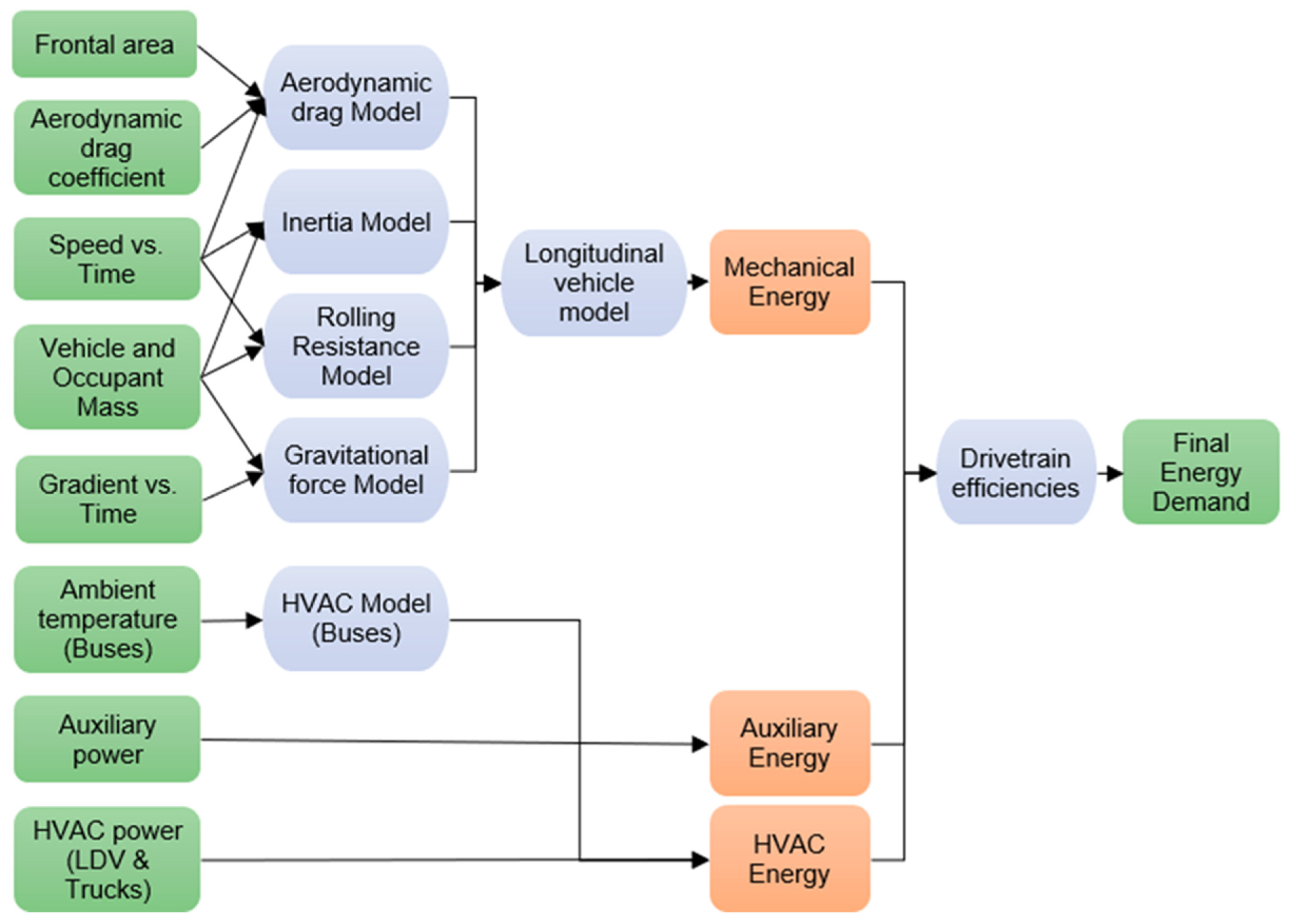
3. Methodology
- Aerodynamic friction;
- Rolling friction;
- Energy dissipated by braking.
- Traction mode—the engine is doing the work of moving the vehicle;
- Braking mode—the brakes are dissipating energy to slow down the vehicle;
- Coasting mode—the vehicle is moving under its own stored mechanical energy.
4. Data Preparation and Validation
4.1. On-Road Transport Modes
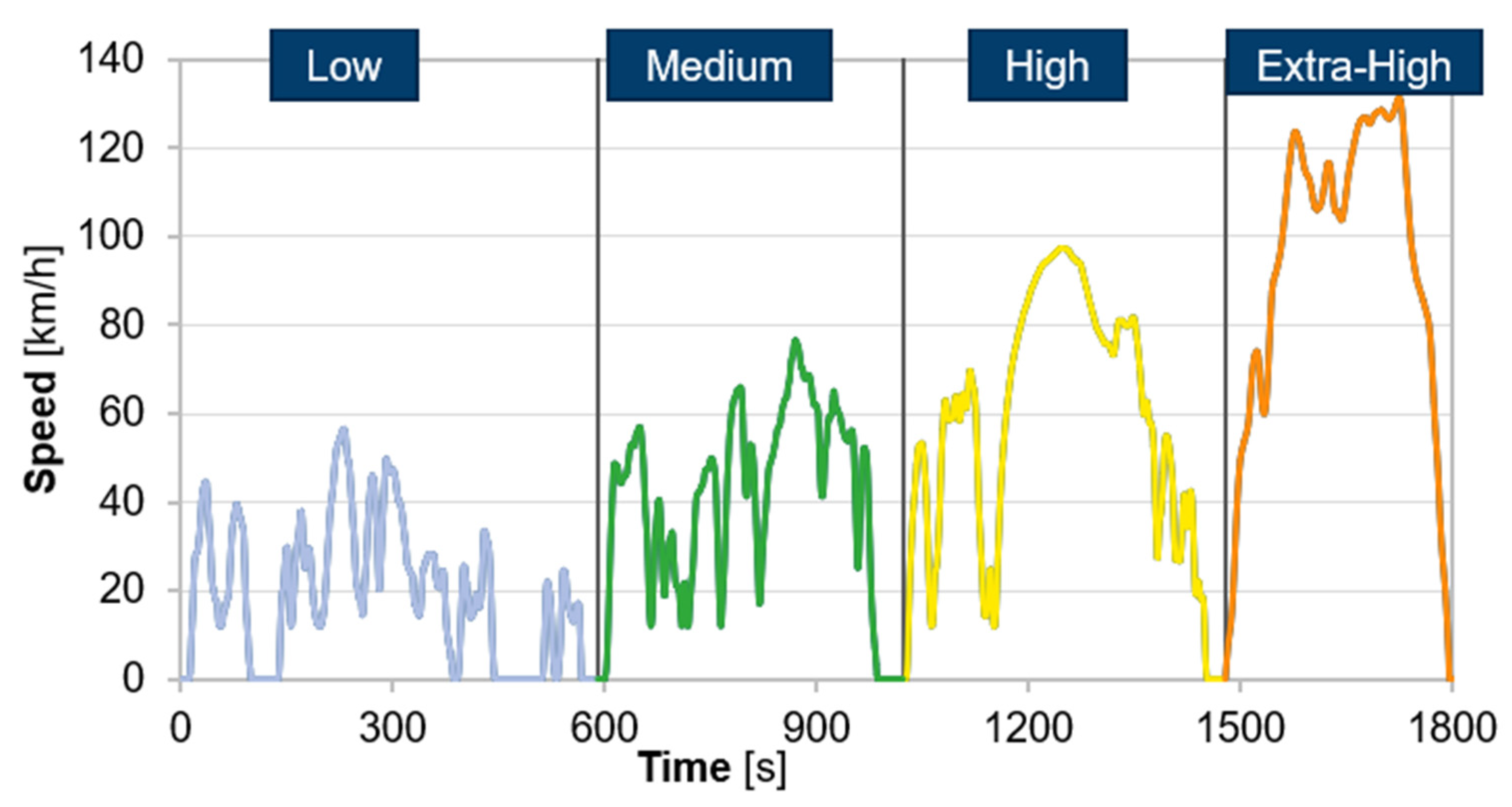
4.1.1. Standard Driving Cycles
4.1.2. Light-Duty Vehicles
4.1.3. Buses
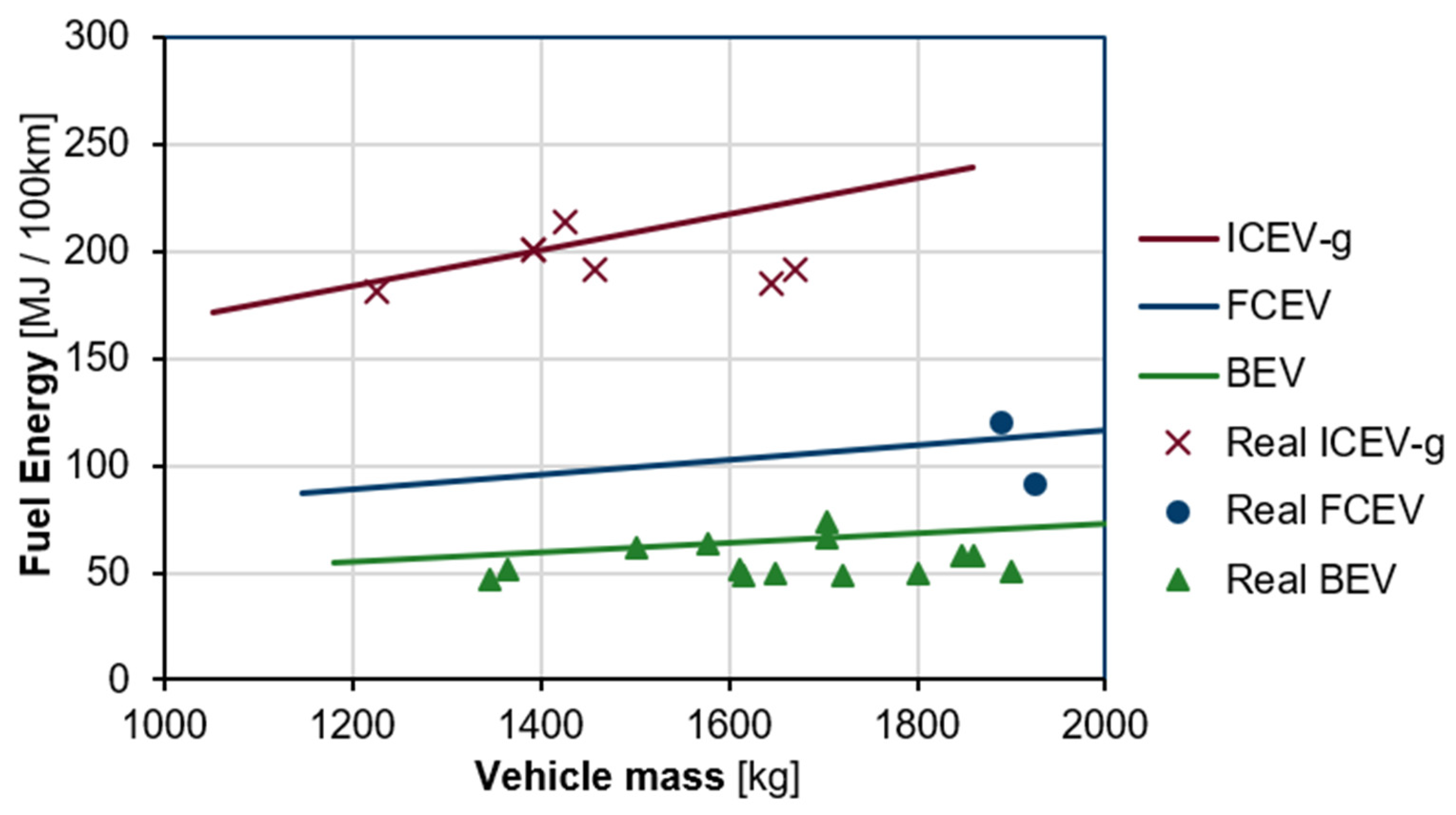
4.1.4. Validation
4.2. Non-Road Transport Modes
4.2.1. Airplanes
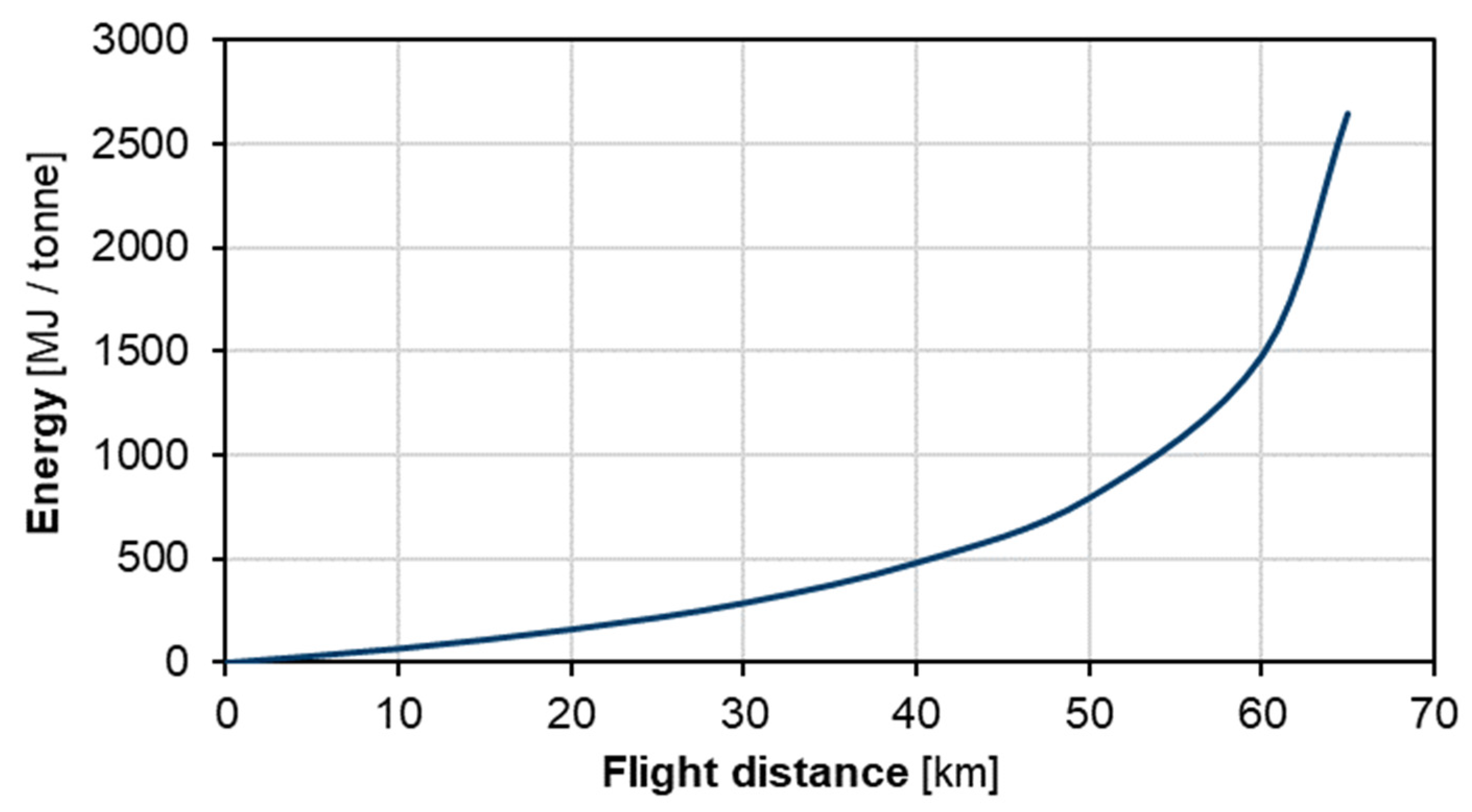
4.2.2. Unmanned Aviation
4.2.3. Trains
4.2.4. Ships
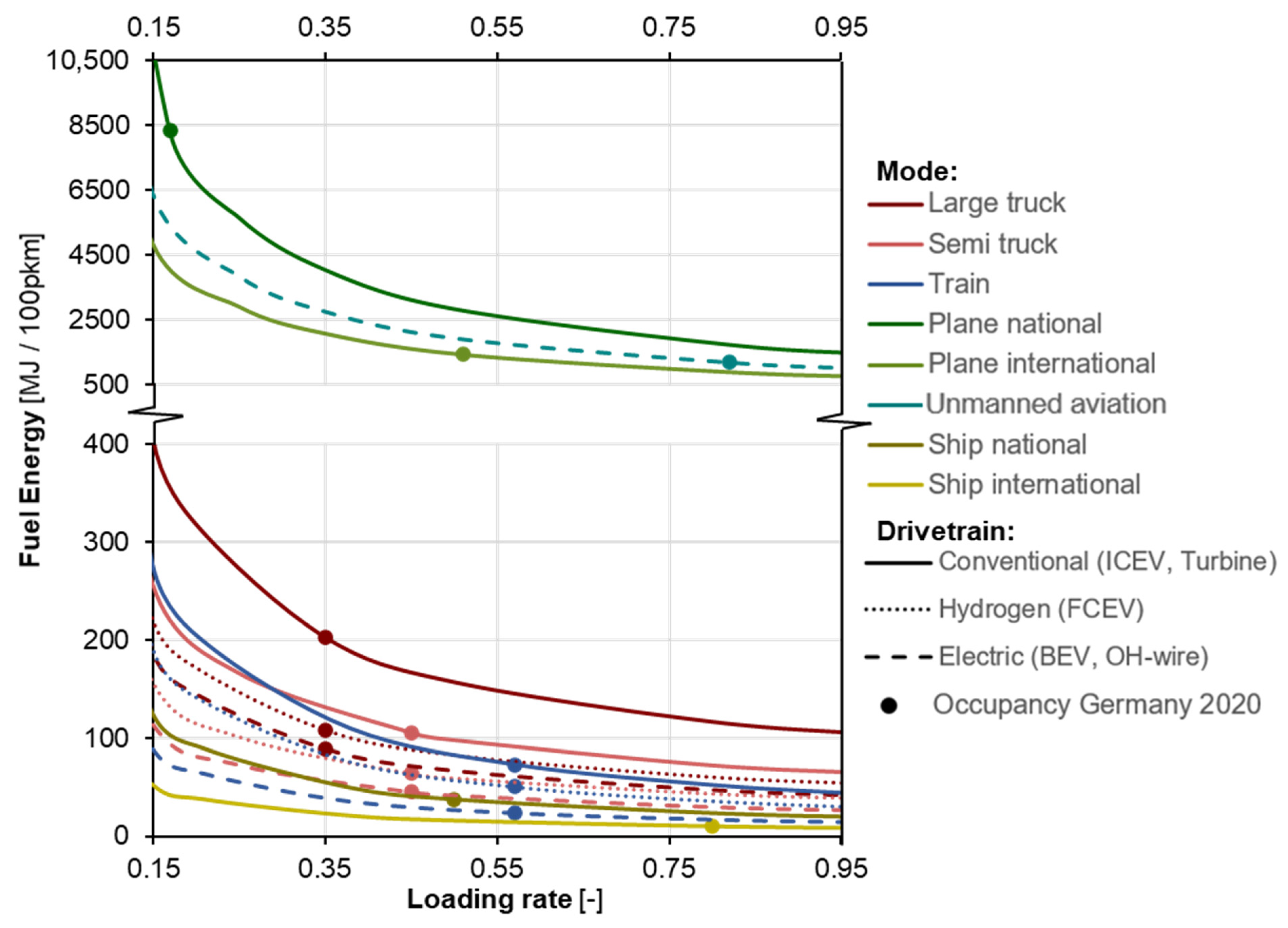
4.3. Occupancy and Loading Rates
5. Results and Discussion
5.1. Parameter Variation
5.2. Modal Analysis
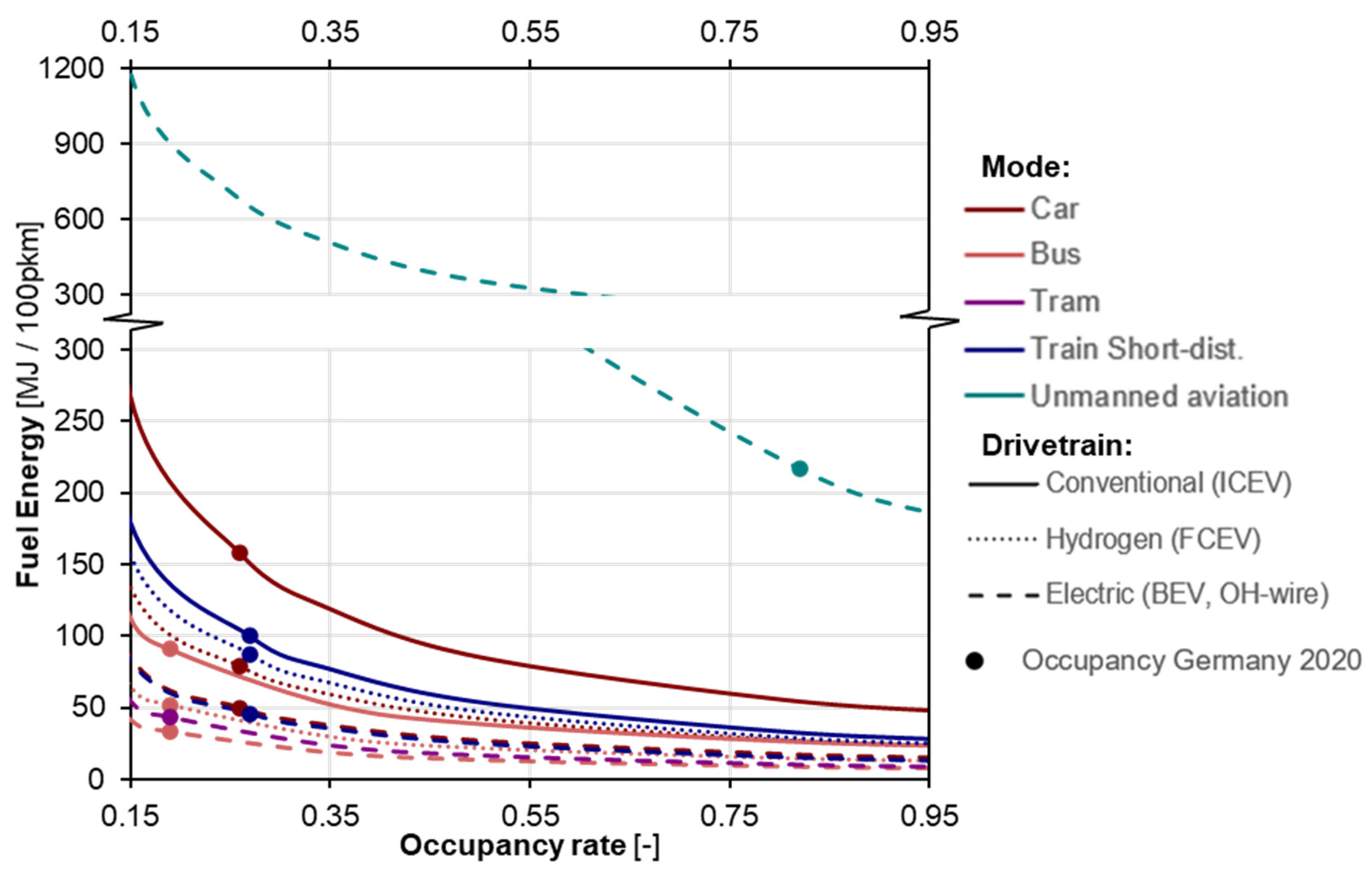
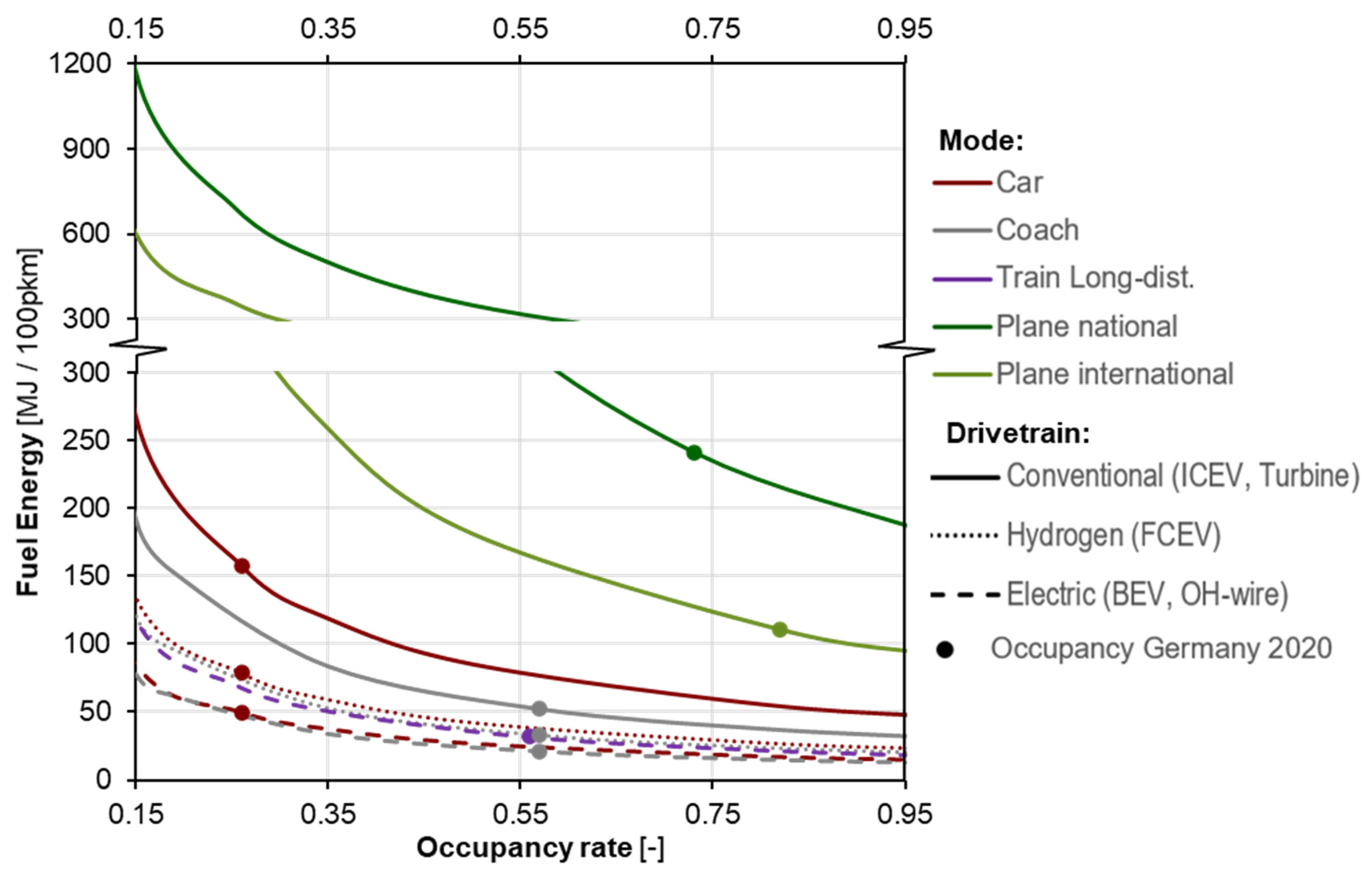
5.2.1. Passenger Modes
5.2.2. Freight Modes
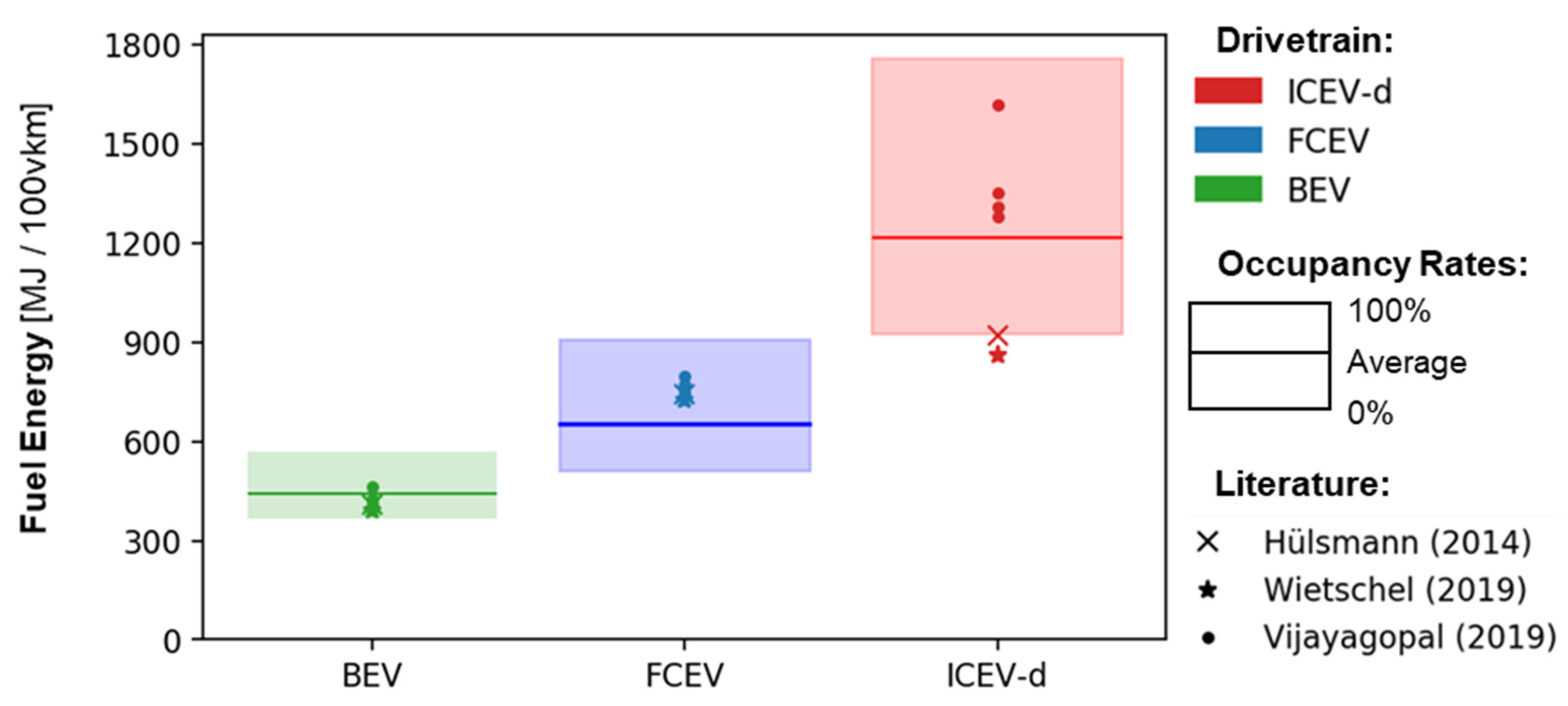
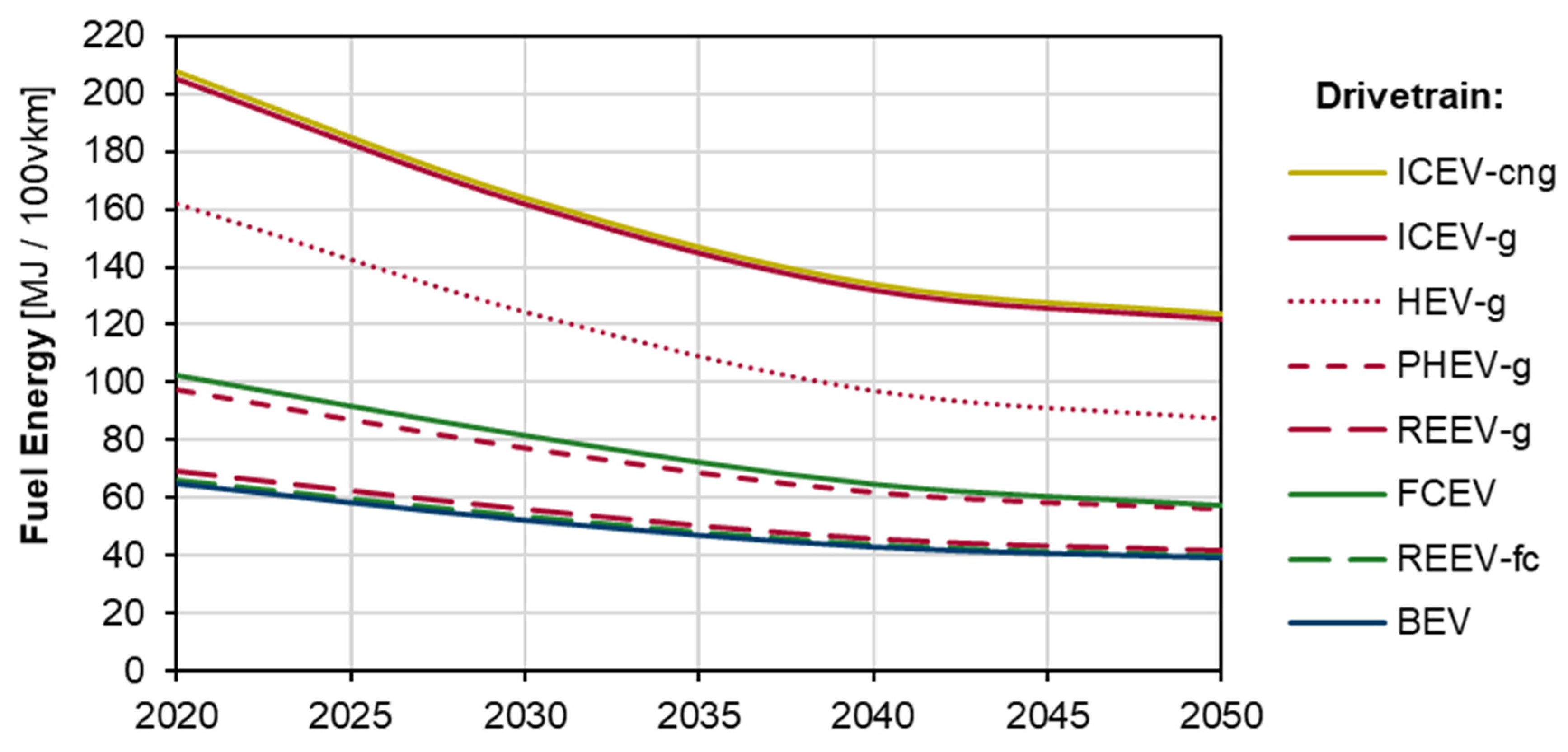
5.3. Drivetrain Analysis
5.4. Electric Share
5.5. Effects of the Driving Environment
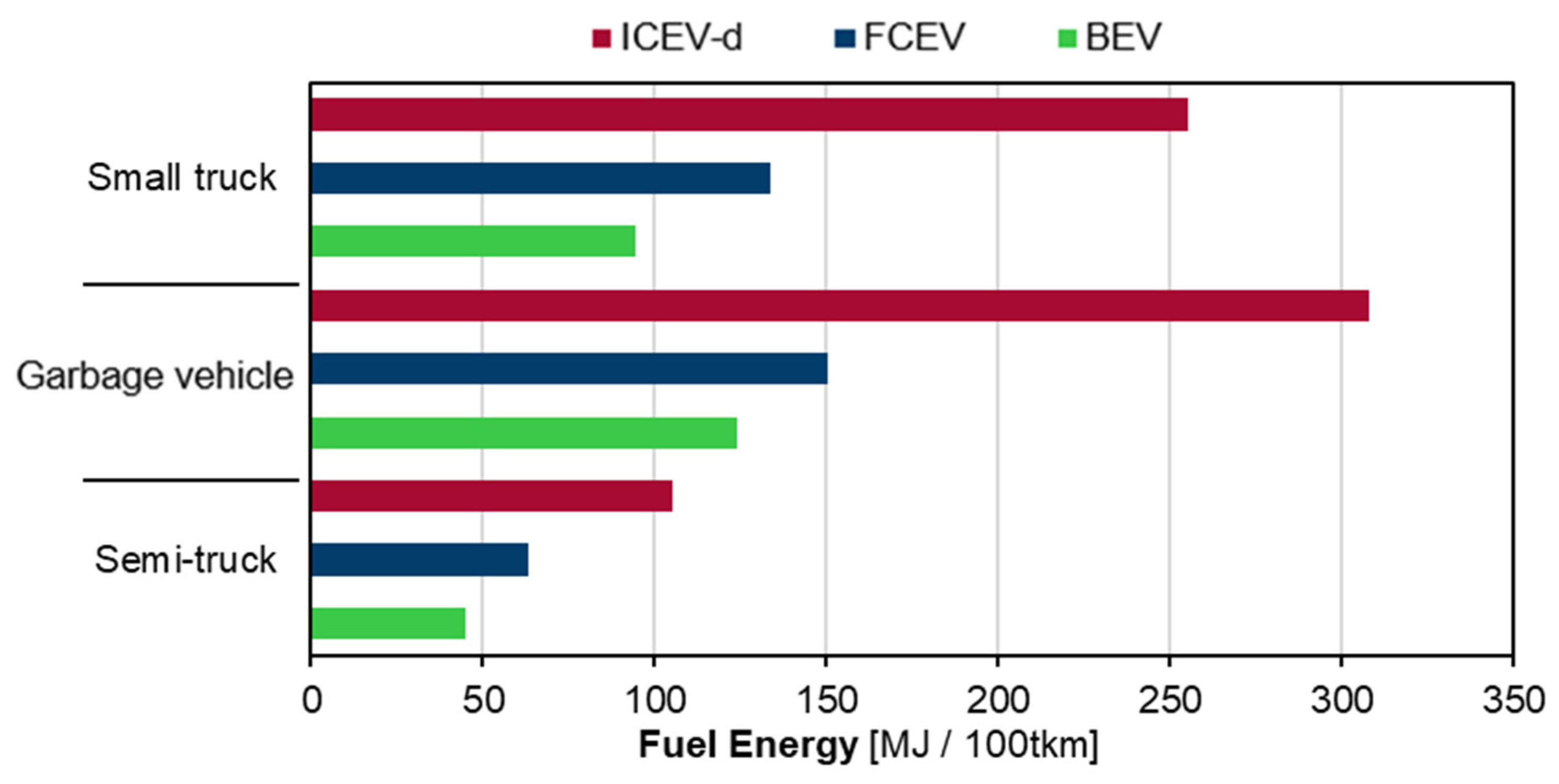
5.5.1. Trucks for Different Purposes
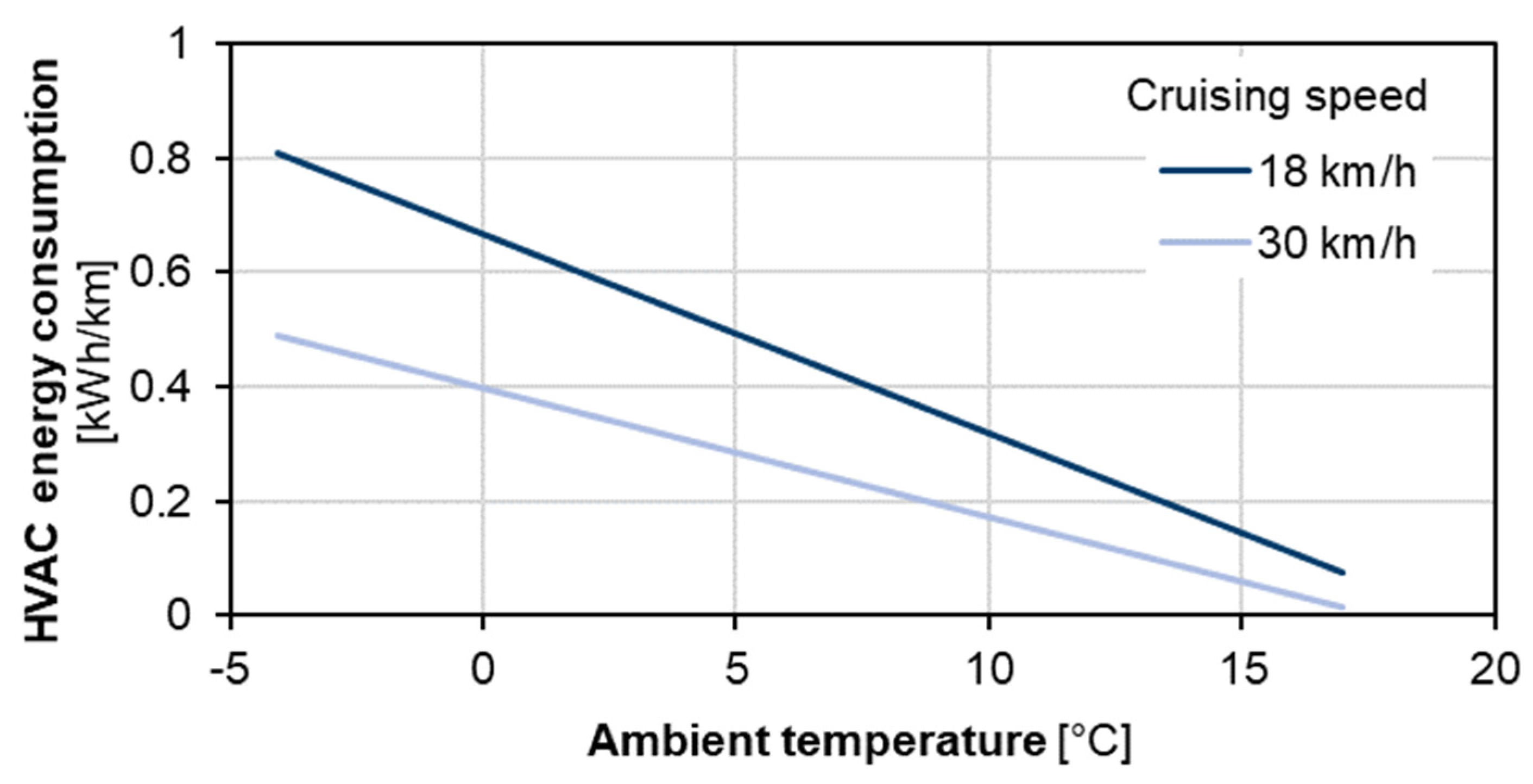
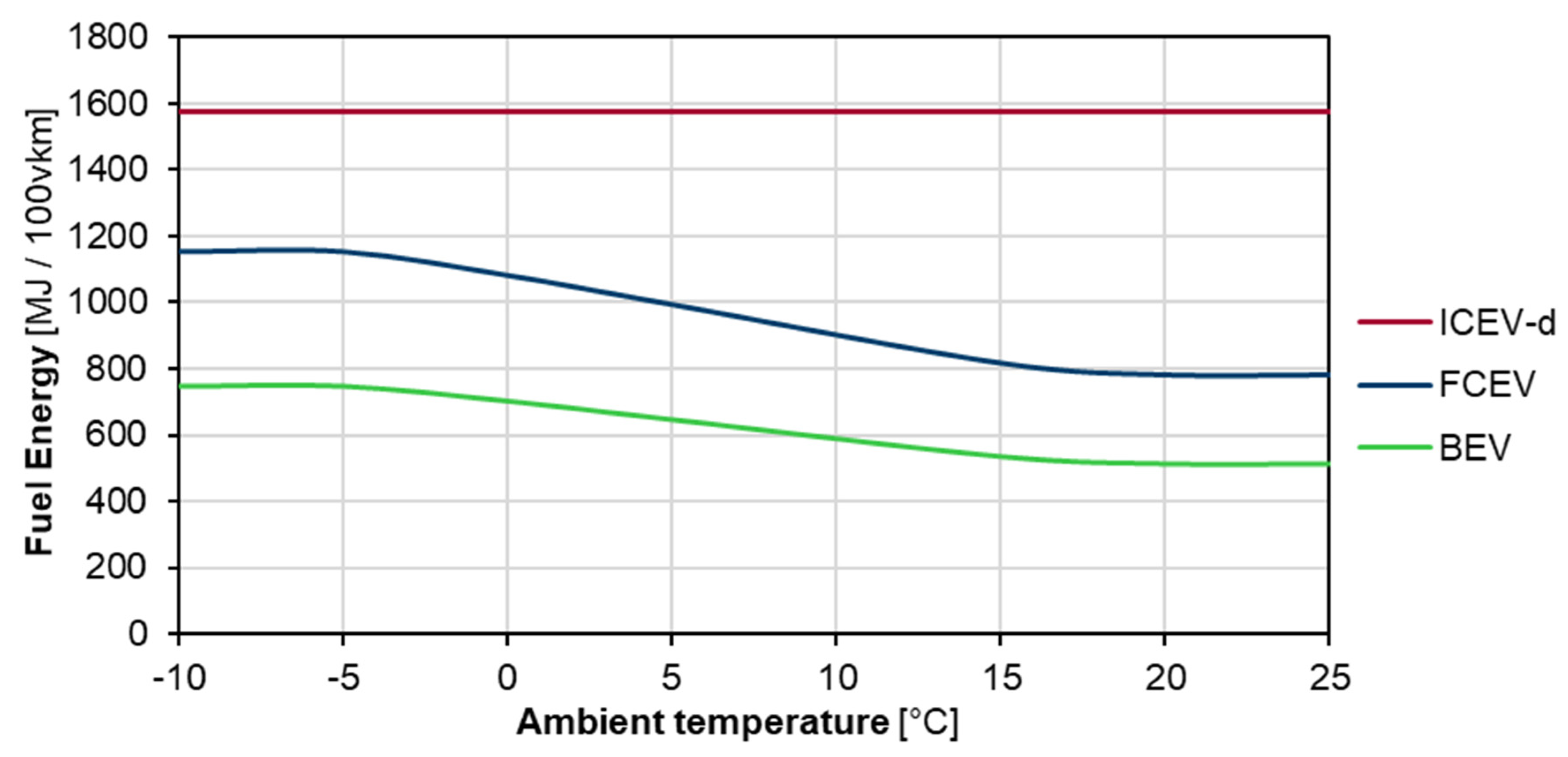
5.5.2. Effects of Ambient Temperature on Buses
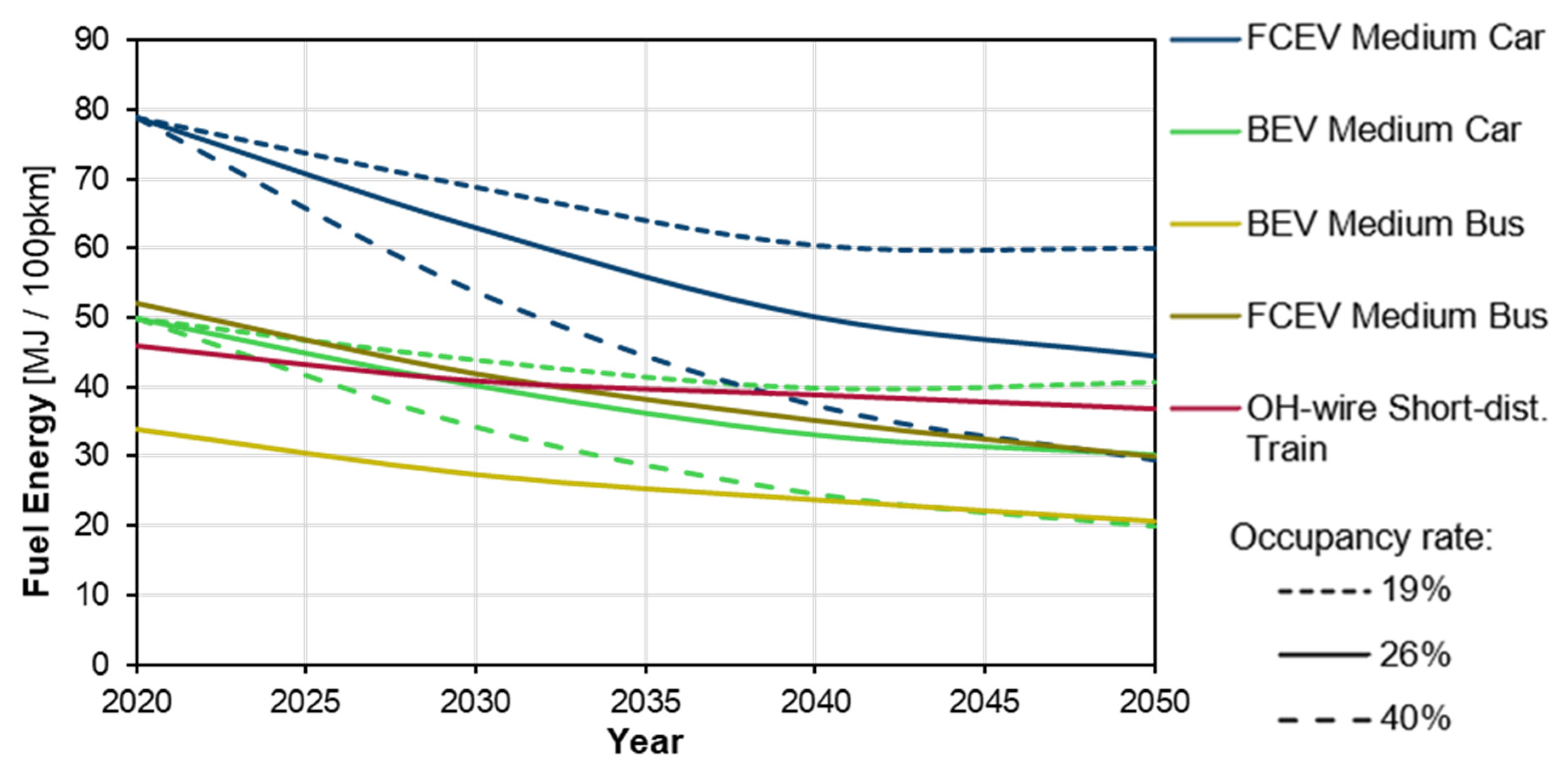
5.6. Change in Occupancy through 2050
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPBES. Summary for Policymakers of the Ipbes Global Assessment Report on Biodiversity and Ecosystem Services. 2019. Available online: https://ipbes.net/system/tdf/ipbes_global_assessment_report_summary_for_policymakers.pdf?file=1&type=node&id=35329 (accessed on 18 January 2022).
- Indicator: Greenhouse Gas Emissions|Umweltbundesamt. Available online: https://www.umweltbundesamt.de/en/indicator-greenhouse-gas-emissions#at-a-glance (accessed on 1 February 2021).
- Climate Change Act—Climate Neutrality by 2045. Available online: https://www.bundesregierung.de/breg-de/themen/klimaschutz/climate-change-act-2021-1913970 (accessed on 17 October 2021).
- Climate Action Plan 2050—Germany’s Long-Term Emission Development Strategy|BMU. The Federal Minister for the Environment, Nature Conservation, and Nuclear Safety; Available online: https://www.bmu.de/en/topics/climate-energy/climate/national-climate-policy/greenhouse-gas-neutral-germany-2050/ (accessed on 5 July 2020).
- Amelang, S. Germany commits additional €3 bln to ease green mobility transition in car industry. Clean Energy Wire 2020. Available online: https://www.cleanenergywire.org/news/germany-commits-additional-eu3-bln-ease-green-mobility-transition-car-industry (accessed on 14 December 2020).
- Jardin, P.; Esser, A.; Givone, S.; Eichenlaub, T.; Schleiffer, J.-E.; Rinderknecht, S. The Sensitivity in Consumption of Different Vehicle Drivetrain Concepts Under Varying Operating Conditions: A Simulative Data Driven Approach. Vehicles 2019, 1, 69–87. [Google Scholar] [CrossRef] [Green Version]
- Gao, D.W.; Mi, C.; Emadi, A. Modeling and Simulation of Electric and Hybrid Vehicles. Proc. IEEE 2007, 95, 729–745. [Google Scholar] [CrossRef]
- Fiori, C.; Ahn, K.; Rakha, H.A. Power-based electric vehicle energy consumption model: Model development and validation. Appl. Energy 2016, 168, 257–268. [Google Scholar] [CrossRef]
- Halbach, S.; Sharer, P.; Pagerit, S.; Rousseau, A.P.; Folkerts, C. Model architecture, methods, and interfaces for efficient math-based design and simulation of automotive control systems. SAE Tech. Pap. 2010, 2010, 20100241. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, F.; Mazlan, S.A.; Zamzuri, H.; Jamaluddin, H.; Hudha, K.; Short, M. Modelling and validation of the vehicle longitudinal model. Int. J. Automot. Mech. Eng. 2014, 10, 2042–2056. [Google Scholar] [CrossRef]
- Edwardes, W.; Rakha, H. Virginia tech comprehensive power-based fuel consumption model. Transp. Res. Rec. 2014, 2428, 1–9. [Google Scholar] [CrossRef]
- Edwardes, W.; Rakha, H. Modeling diesel and hybrid bus fuel consumption with Virginia Tech comprehensive power-based fuel consumption model: Model enhancements and calibration issues. Transp. Res. Rec. 2015, 2533, 100–108. [Google Scholar] [CrossRef]
- Park, S.; Rakha, H.; Ahn, K.; Moran, K. Virginia Tech Comprehensive Power-based Fuel Consumption Model (VT-CPFM): Model Validation and Calibration Considerations. Int. J. Transp. Sci. Technol. 2013, 2, 317–336. [Google Scholar] [CrossRef] [Green Version]
- Vagg, C.; Brace, C.J.; Akehurst, S.; Ash, L. Minimizing battery stress during hybrid electric vehicle control design: Real world considerations for model-based control development. In Proceedings of the 2013 9th IEEE Vehicle Power and Propulsion Conference IEEE VPPC 2013, Beijing, China, 15–18 October 2013; pp. 329–334. [Google Scholar] [CrossRef] [Green Version]
- Abousleiman, R.; Rawashdeh, O. Energy consumption model of an electric vehicle. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo, ITEC 2015, Dearborn, MI, USA, 14–17 June 2015. [Google Scholar] [CrossRef]
- Luin, B.; Petelin, S.; Al-Mansour, F. Microsimulation of electric vehicle energy consumption. Energy 2019, 174, 24–32. [Google Scholar] [CrossRef]
- Hayes, J.G.; Davis, K. Simplified electric vehicle powertrain model for range and energy consumption based on EPA Coast-down Parameters and Test Validation by Argonne national lab data on the Nissan leaf. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo Components, System Power Electron—From Technology to Bussiness Public Policy, ITEC 2014, Dearborn, MI, USA, 16–19 June 2014; Available online: https://ieeexplore.ieee.org/document/6861831 (accessed on 18 January 2022).
- Grube, T.; Stolten, D. The impact of drive cycles and auxiliary power on passenger car fuel economy. Energies 2018, 11, 1010. [Google Scholar] [CrossRef] [Green Version]
- Bielaczyc, P.; Szczotka, A.; Woodburn, J. The effect of a low ambient temperature on the cold-start emissions and fuel consumption of passenger cars. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2011, 225, 1253–1264. [Google Scholar] [CrossRef]
- Duarte, G.O.; Gonçalves, G.A.; Farias, T.L. Analysis of fuel consumption and pollutant emissions of regulated and alternative driving cycles based on real-world measurements. Transp. Res. Part D Transp. Environ. 2016, 44, 43–54. [Google Scholar] [CrossRef]
- Energy Statistics—An Overview Statistics Explained. Available online: https://ec.europa.eu/eurostat/statisticsexplained/ (accessed on 15 October 2020).
- Teter, J.; Le Feuvre, P.; Bains, P.; Re, L. IEA. Aviation, IEA, Paris. 2020. Available online: https://www.iea.org/reports/aviation (accessed on 14 February 2021).
- Burzlaff, M. Aircraft Fuel Consumption—Estimation and Visualization. Fuel Consum. 2017. [Google Scholar] [CrossRef]
- Park, Y.; O’Kelly, M.E. Fuel burn rates of commercial passenger aircraft: Variations by seat configuration and stage distance. J. Transp. Geogr. 2014, 41, 137–147. [Google Scholar] [CrossRef]
- Peeters, P.; Middel, J.; Hoolhorts, A. Fuel Efficiency of Commercial Aircraft: An Overview of Historical and Future Trends; National Aerospace Laboratory NLR: Amsterdam, The Netherlands, 2005; Available online: https://www.transportenvironment.org/sites/te/files/media/2005-12_nlr_aviation_fuel_efficiency.pdf (accessed on 18 January 2022).
- Kharina, A.; Rutherford, D. Fuel Efficiency Trends for New Commercial Jet Aircraft: 1960 to 2014; The International Council on Clean Transportation: Washington, DC, USA, 2015; Available online: https://theicct.org/wp-content/uploads/2021/06/ICCT_Aircraft-FE-Trends_20150902.pdf (accessed on 18 January 2022).
- Xu, J. Design Perspectives on Delivery Drones; RAND Corporation: Santa Monica, CA, USA, 2017. [Google Scholar] [CrossRef] [Green Version]
- Electric VTOL Aircraft for Urban Air Mobility: Bauhaus Luftfahrt. Available online: https://www.bauhaus-luftfahrt.net/en/research/systems-aircraft-technologies/electric-vtol-aircraft-for-urban-air-mobility/ (accessed on 28 September 2020).
- Zhang, H.; Jia, L.; Wang, L.; Xu, X. Energy consumption optimization of train operation for railway systems: Algorithm development and real-world case study. J. Clean. Prod. 2019, 214, 1024–1037. [Google Scholar] [CrossRef]
- Salvador, P.; Martínez, P.; Villalba, I.; Insa, R. Modelling energy consumption in diesel multiple units. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 1539–1548. [Google Scholar] [CrossRef]
- Wang, J.; Rakha, H.A. Electric train energy consumption modeling. Appl. Energy 2017, 193, 346–355. [Google Scholar] [CrossRef] [Green Version]
- Kee, K.-K.; Lau Simon, B.-Y.; Yong Renco, K.-H. Prediction of Ship Fuel Consumption and Speed Curve by Using Statistical Method. J. Comput. Sci. Comput. Math. 2018, 8, 19–24. [Google Scholar] [CrossRef] [Green Version]
- Jeon, M.; Noh, Y.; Shin, Y.; Lim, O.-K.; Lee, I.; Cho, D. Prediction of ship fuel consumption by using an artificial neural network. J. Mech. Sci. Technol. 2018, 32, 5785–5796. [Google Scholar] [CrossRef]
- Yang, L.; Chen, G.; Rytter, N.G.M.; Zhao, J.; Yang, D. A genetic algorithm-based grey-box model for ship fuel consumption prediction towards sustainable shipping. Ann. Oper. Res. 2019, 813, 13. [Google Scholar] [CrossRef]
- Germany—Countries & Regions—IEA. Available online: https://www.iea.org/countries/germany (accessed on 9 July 2020).
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems, 2nd ed.; Springer: Zürich, Switzerland, 2007; ISBN 9783540746911. [Google Scholar]
- Grube, T. Potentiale des Strommanagements zur Reduzierung des Spezifischen Energiebedarfs von Pkw; Technische Universität: Berlin, Germany, 2014. [Google Scholar]
- National Research Council of the National Academies. Transitions to Alternative Vehicles and Fuels; National Research Council of the National Academies: Washington, DC, USA, 2013. Available online: https://www.nap.edu/catalog/18264/transitions-to-alternative-vehicles-and-fuels (accessed on 18 January 2022). [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control, 1st ed.; Ling, F.F., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 9780387263960. [Google Scholar]
- Forward and Backward Euler Methods. Available online: https://web.mit.edu/10.001/Web/Course_Notes/Differential_Equations_Notes/node3.html (accessed on 16 September 2020).
- Barlow, T.J.; Latham, S.; Mccrae, I.S.; Boulter, P.G. A Reference Book of Driving Cycles for Use in the Measurement of Road Vehicle Emissions; Berkshire; 2009; Available online: https://trid.trb.org/view/909274 (accessed on 18 January 2022).
- Emission Test Cycles: WLTC. Available online: https://dieselnet.com/standards/cycles/wltp.php (accessed on 10 July 2020).
- Office for Official Publications of the European Communities L-2985 Luxembourg. Regulation (EEC) No 4064/89 Merger Procedure Article 6(1)(b); Office for Official Publications of the European Communities L-2985 Luxembourg: Brussels, Belgium, 1999. [Google Scholar]
- Islam, E.S.; Moawad, A.; Kim, N.; Rousseau, A. Energy Consumption and Cost Reduction of Future Light-Duty Vehicles through Advanced Vehicle Technologies: A Modeling Simulation Study Through 2050; Argonne National Lab.: Argonne, IL, USA, 2020. Available online: https://publications.anl.gov/anlpubs/2020/08/161542.pdf (accessed on 18 January 2022).
- Al-Samari, A. Study of emissions and fuel economy for parallel hybrid versus conventional vehicles on real world and standard driving cycles. Alex. Eng. J. 2017, 56, 721–726. [Google Scholar] [CrossRef]
- Spanoudakis, P.; Tsourveloudis, N.; Doitsidis, L.; Karapidakis, E. Experimental Research of Transmissions on Electric Vehicles’ Energy Consumption. Energies 2019, 12, 388. [Google Scholar] [CrossRef] [Green Version]
- Drivetrain Losses (Efficiency)—x-engineer.org. Available online: https://x-engineer.org/automotive-engineering/drivetrain/transmissions/drivetrain-losses-efficiency/ (accessed on 17 September 2020).
- Li, K.; Tseng, K.J. Energy efficiency of lithium-ion battery used as energy storage devices in micro-grid. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2015; pp. 5235–5240. [Google Scholar]
- Schimpe, M.; Naumann, M.; Truong, N.; Hesse, H.C.; Santhanagopalan, S.; Saxon, A.; Jossen, A. Energy efficiency evaluation of a stationary lithium-ion battery container storage system via electro-thermal modeling and detailed component analysis. Appl. Energy 2018, 210, 211–229. [Google Scholar] [CrossRef]
- Eftekhari, A. Energy efficiency: A critically important but neglected factor in battery research. Sustain. Energy Fuels 2017, 1, 2053–2060. [Google Scholar] [CrossRef]
- Trost, T. Erneuerbare Mobilität im Motorisierten Individualverkehr; Fraunhofer Verlag: Stuttgart, Germany, 2017; ISBN 9783839611296. [Google Scholar]
- Occupancy Rates—European Environment Agency. Available online: https://www.eea.europa.eu/publications/ENVISSUENo12/page029.html (accessed on 15 October 2020).
- Air—Density, Specific Weight and Thermal Expansion Coefficient at Varying Temperature and Constant Pressures. Available online: https://www.engineeringtoolbox.com/air-density-specific-weight-d_600.html?vA=15&units=C# (accessed on 17 September 2020).
- Berdowski, Z.; Broek-Serlé, F.N.; Jetten, J.T.; Kawabatta, Y.; Schoemaker, J.T.; Versteegh, R. Survey on Standard Weights of Passengers and Baggage Final Report. Available online: https://www.easa.europa.eu/system/files/dfu/WeightSurveyR20090095Final.pdf (accessed on 18 January 2022).
- Cox, B. Mobility and the Energy Transition: A Life Cycle Assessment of Swiss Passenger Transport Technologies Including Developments Until 2050. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2018. [Google Scholar] [CrossRef]
- Knote, T.; Haufe, B.; Saroch, L. Gefördert durch das Bundesministerium für Umwelt, Naturschutz, Bau und Reaktorsicherheit E-Bus-Standard «Ansätze zur Standardisierung und Zielkosten für Elektrobusse»; Fraunhofer IVI: Dresden, Germany, 2017. [Google Scholar]
- VW.com|Official Home of Volkswagen Cars & SUVs. Available online: https://www.vw.com/en.html (accessed on 12 May 2021).
- Electric Cars, Solar & Clean Energy|Tesla. Available online: https://www.tesla.com/ (accessed on 12 May 2021).
- Hülsmann, F.; Mottschall, M.; Hacker, F.; Kasten, P. Konventionelle und Alternative Fahrzeugtechnologien bei Pkw und Schweren Nutzfahrzeugen—Potenziale zur Minderung des Energieverbrauchs bis 2050; Öko-Institut: Freiburg, Germany, 2014; Available online: https://www.oeko.de/oekodoc/2105/2014-662-de.pdf (accessed on 18 January 2022).
- Dünnebeil, F.; Keller, H. Monitoring Emission Savings from Low Rolling Resistance Tire Labelling and Phase-Out Schemes; Institut für Energie- und Umweltforschung Heidelberg: Heidelberg, Germany, 2015; Volume 49, Available online: http://transferproject.org/wp-content/uploads/2014/10/TRANSfer_MRV-Blueprint_lower-tires_EU.pdf (accessed on 18 January 2022).
- Wietschel, M.; Moll, C.; Oberle, S.; Lux, B.; Sebastian, T.; Neuling, U.; Kaltschmitt, M.; Ashley-Belbin, N. Klimabilanz, Kosten und Potenziale Verschiedener Kraftstoffarten und Antriebssysteme für Pkw und Lkw; Fraunhofer ISI: Karlsruhe, Germany, 2019; Available online: https://www.isi.fraunhofer.de/content/dam/isi/dokumente/cce/2019/klimabilanz-kosten-potenziale-antriebe-pkw-lkw.pdf (accessed on 18 January 2022).
- Vijayagopal, R.; Prada, D.N.; Rousseau, A. Fuel Economy and Cost Estimates for Medium- and Heavy-Duty Trucks; Argonne National Lab.: Argonne, IL, USA, 2019. Available online: https://publications.anl.gov/anlpubs/2021/02/165815.pdf (accessed on 18 January 2022).
- Study on Air Traffic: Lufthansa Dominates the Skies over Germany. Available online: https://ga.de/ga-english/news/lufthansa-dominates-the-skies-over-germany_aid-43675911 (accessed on 13 September 2020).
- Germany: State of the Market|Routesonline. Available online: https://www.routesonline.com/news/29/breaking-news/283754/germany-state-of-the-market-/ (accessed on 13 September 2020).
- 1.A.3.a Aviation 2 LTO Emissions Calculator 2019—European Environment Agency. Available online: https://www.eea.europa.eu/publications/emep-eea-guidebook-2019/part-b-sectoral-guidance-chapters/1-energy/1-a-combustion/1-a-3-a-aviation-1-annex5-LTO/view (accessed on 13 September 2020).
- Energiewende Outlook: Transportation Sector. Available online: www.pwc.de/energy-transition (accessed on 10 September 2020).
- Kuminek, T. Energy consumption in tram transport. Logist. Transp. 2013, 18, 93–100. [Google Scholar]
- GEMIS Database—IINAS. Available online: http://iinas.org/database.html (accessed on 13 September 2020).
- Deutsche Bahn 2018 Integrated Report On Track towards a Better Railway; Deutsche Bahn: Berlin, Germany, 2019; Available online: https://ibir.deutschebahn.com/ib2018/fileadmin/PDF/IB18_e_web.pdf (accessed on 18 January 2022).
- Bründlinger, T.; König, J.E.; Frank, O.; Gründig, O.; Jugel, C.; Kraft, P.; Krieger, O.; Mischinger, S.; Prein, P.; Seidl, H.; et al. Dena-Leitstudie Integrierte Energiewende. Impulse für die Gestaltung des Energiesystems bis 2050. Deutche Energie-Agentur 2018. Available online: https://www.dena.de/fileadmin/dena/Dokumente/Pdf/9261_dena-Leitstudie_Integrierte_Energiewende_lang.pdf (accessed on 18 January 2022).
- International Shipping—Analysis—IEA. Available online: https://www.iea.org/reports/international-shipping (accessed on 15 October 2020).
- Allekotte, M.; Bergk, F.; Biemann, K.; Deregowski, C.; Knörr Ifeu, W.; Hans-Jörg-Althaus, H.; Sutter Infras, D.; Thomas Bergmann, Z. Ökologische Bewertung von Verkehrsarten. 2019. Available online: http://www.umweltbundesamt.de/publikationen (accessed on 13 September 2020).
- Facts & Figures. Available online: https://www.atag.org/facts-figures.html (accessed on 2 October 2020).
- Zimmer, W.; Von Waldenfels, R.; Cyganski, R.; Wolfermann, A.; Winkler, C.; Heinrichs, M.; Dünnebeil, F.; Fehrenbach, H.; Kämper, C.; Biemann, K.; et al. Endbericht Renewbility III; Öko-Institut: Berlin, Germany, 2016; Available online: https://elib.dlr.de/109486/1/__bafiler1_VF-BA_VF_Server_neu_Projekte_PJ_laufend_RNB3_2-Ergebnisse_21-Berichte_Renewbility-III_Endbericht.pdf (accessed on 18 January 2022).
- Emission Test Cycles: World Harmonized Vehicle Cycle (WHVC). Available online: https://dieselnet.com/standards/cycles/whvc.php (accessed on 16 September 2020).
- Emission Test Cycles: Neighborhood Refuse Truck Cycle. Available online: https://dieselnet.com/standards/cycles/neigh_refuse_truck.php (accessed on 26 September 2020).
- Harb, M.; Xiao, Y.; Circella, G.; Mokhtarian, P.L.; Walker, J.L. Projecting travelers into a world of self-driving vehicles: Estimating travel behavior implications via a naturalistic experiment. Transportation 2018, 45, 1671–1685. [Google Scholar] [CrossRef]
- Martinez, L.M.; Viegas, J.M. Assessing the impacts of deploying a shared self-driving urban mobility system: An agent-based model applied to the city of Lisbon, Portugal. Int. J. Transp. Sci. Technol. 2017, 6, 13–27. [Google Scholar] [CrossRef]
- Raposo, A.; Grosso, M.; Macías, F.; Galassi, E.; Krasenbrink, C.; Krause, A.; Levati, J.; Saveyn, A.; Thiel, B.; Ciuffo, C. An Analysis of Possible Socio-Economic Effects of a Cooperative, Connected and Automated Mobility (CCAM) in Europe; 2018; Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC111477 (accessed on 18 January 2022).





| Mode | EC Classification | (m2) | (-) | |||
|---|---|---|---|---|---|---|
| 2020 | 2030 | 2040 | 2050 | |||
| Small Car | A and B | 2.16 | 0.309 | 0.286 | 0.245 | 0.239 |
| Medium Car | C | 2.25 | 0.271 | 0.251 | 0.215 | 0.210 |
| Large Car | D | 2.21 | 0.262 | 0.242 | 0.208 | 0.203 |
| SUV | J | 2.45 | 0.327 | 0.302 | 0.259 | 0.253 |
| LCV | M | 3.17 | 0.349 | 0.322 | 0.276 | 0.270 |
| Drivetrain | 2020 | 2030 | 2040 | 2050 | Sources |
|---|---|---|---|---|---|
| ICEV-g | 0.26 | 0.31 | 0.34 | 0.36 | [44,46,47] |
| ICEV-d | 0.27 | 0.36 | 0.39 | 0.40 | [44,46,47] |
| HEV-g | 0.30 | 0.35 | 0.38 | 0.40 | [44,45,46,47] |
| HEV-d | 0.31 | 0.40 | 0.43 | 0.44 | [44,45,46,47] |
| PHEV-g | 0.30 | 0.35 | 0.38 | 0.40 | [44,45,46,47] |
| PHEV-d | 0.31 | 0.40 | 0.43 | 0.44 | [44,45,46,47] |
| PHEV-fc | 0.47 | 0.52 | 0.56 | 0.59 | [44,46,48,49,50] |
| REEV-g | 0.30 | 0.35 | 0.38 | 0.40 | [44,45,46,47] |
| REEV-d | 0.31 | 0.40 | 0.43 | 0.44 | [44,45,46,47] |
| REEV-fc | 0.47 | 0.52 | 0.56 | 0.59 | [44,46,48,49,50] |
| BEV | 0.75 | 0.81 | 0.85 | 0.87 | [44,46,48,49,50] |
| FCEV | 0.47 | 0.52 | 0.56 | 0.59 | [44,46,48,49,50] |
| ICEV-cng | 0.26 | 0.31 | 0.34 | 0.36 | [44,46,47] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan Ankur, A.; Kraus, S.; Grube, T.; Castro, R.; Stolten, D. A Versatile Model for Estimating the Fuel Consumption of a Wide Range of Transport Modes. Energies 2022, 15, 2232. https://doi.org/10.3390/en15062232
Khan Ankur A, Kraus S, Grube T, Castro R, Stolten D. A Versatile Model for Estimating the Fuel Consumption of a Wide Range of Transport Modes. Energies. 2022; 15(6):2232. https://doi.org/10.3390/en15062232
Chicago/Turabian StyleKhan Ankur, Atiquzzaman, Stefan Kraus, Thomas Grube, Rui Castro, and Detlef Stolten. 2022. "A Versatile Model for Estimating the Fuel Consumption of a Wide Range of Transport Modes" Energies 15, no. 6: 2232. https://doi.org/10.3390/en15062232
APA StyleKhan Ankur, A., Kraus, S., Grube, T., Castro, R., & Stolten, D. (2022). A Versatile Model for Estimating the Fuel Consumption of a Wide Range of Transport Modes. Energies, 15(6), 2232. https://doi.org/10.3390/en15062232








