Analysis of Circuit Parameters of New Graphene Partial Discharge Sensor Electrode Plate Based on Transmission Line Model
Abstract
:1. Introduction
2. Circuit Parameters
2.1. Resistive Properties of Graphene
2.1.1. Quantum Resistance
2.1.2. Contact Resistance
2.1.3. Scattering Resistance
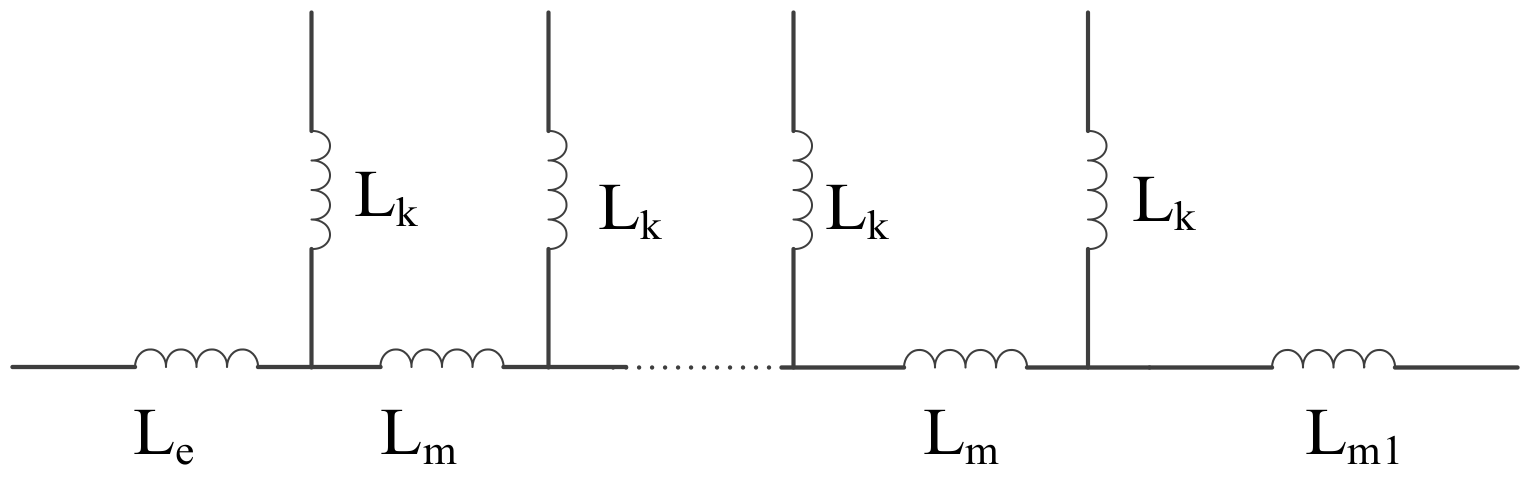
2.2. Inductive Properties of Graphene
2.2.1. Magnetoelectric Inductance
2.2.2. Dynamic Inductance
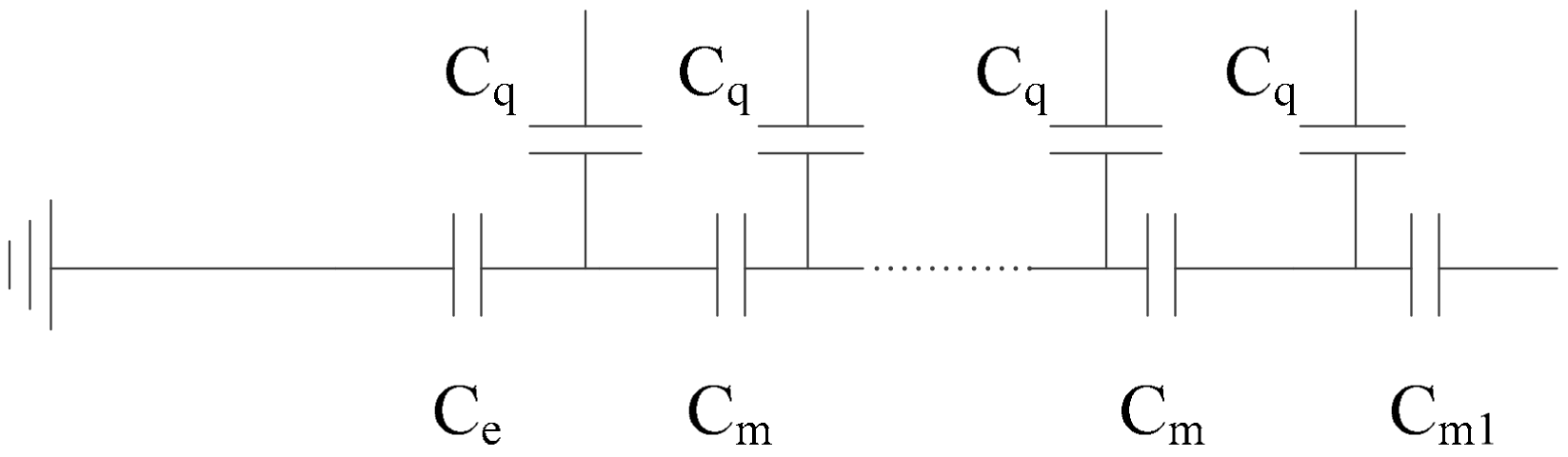
2.3. Capacitive Properties of Graphene
2.3.1. Electrostatic Capacitance
2.3.2. Quantum Capacitance
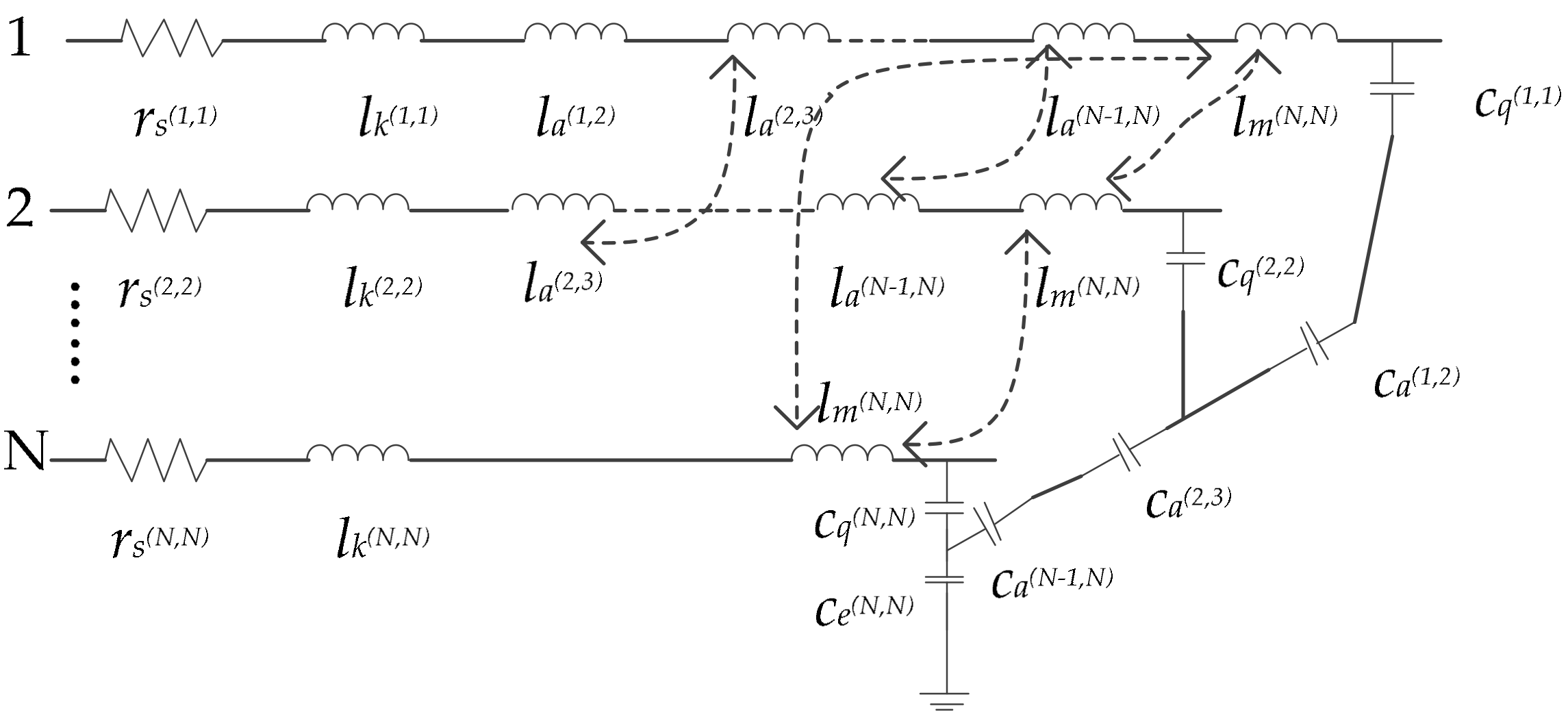
2.4. Circuit Parameters of Multilayer Graphene
2.4.1. Mutual Inductance
2.4.2. Mutual Capacitance
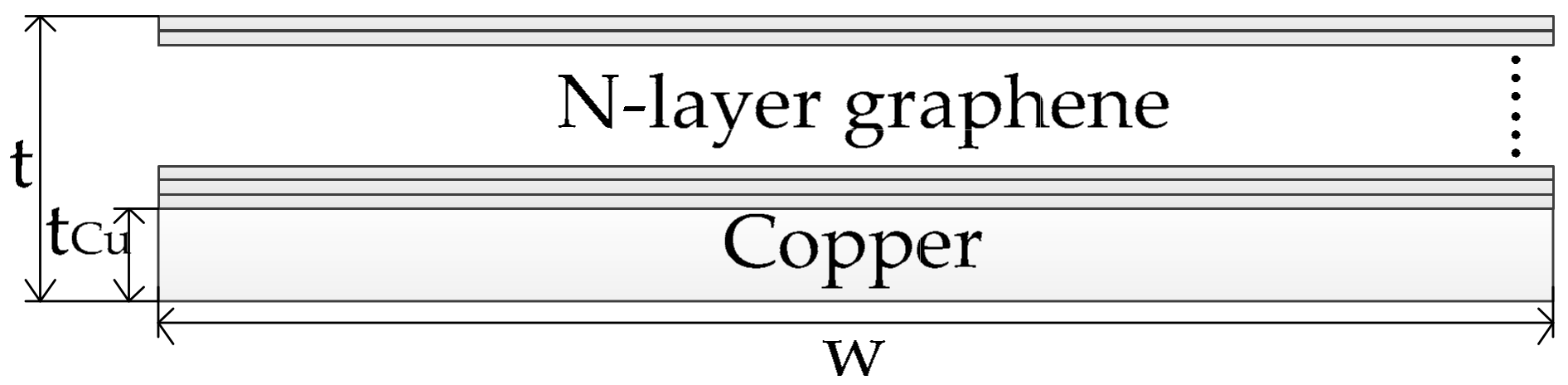
2.5. Characteristics of Copper
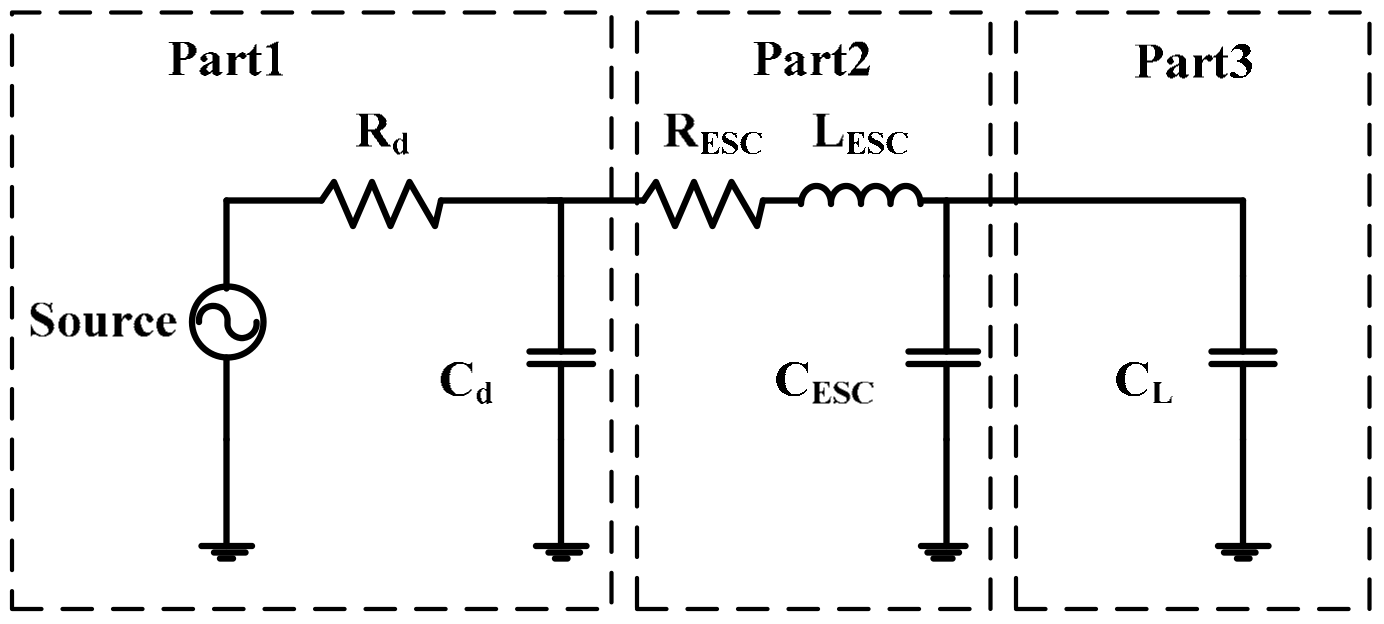
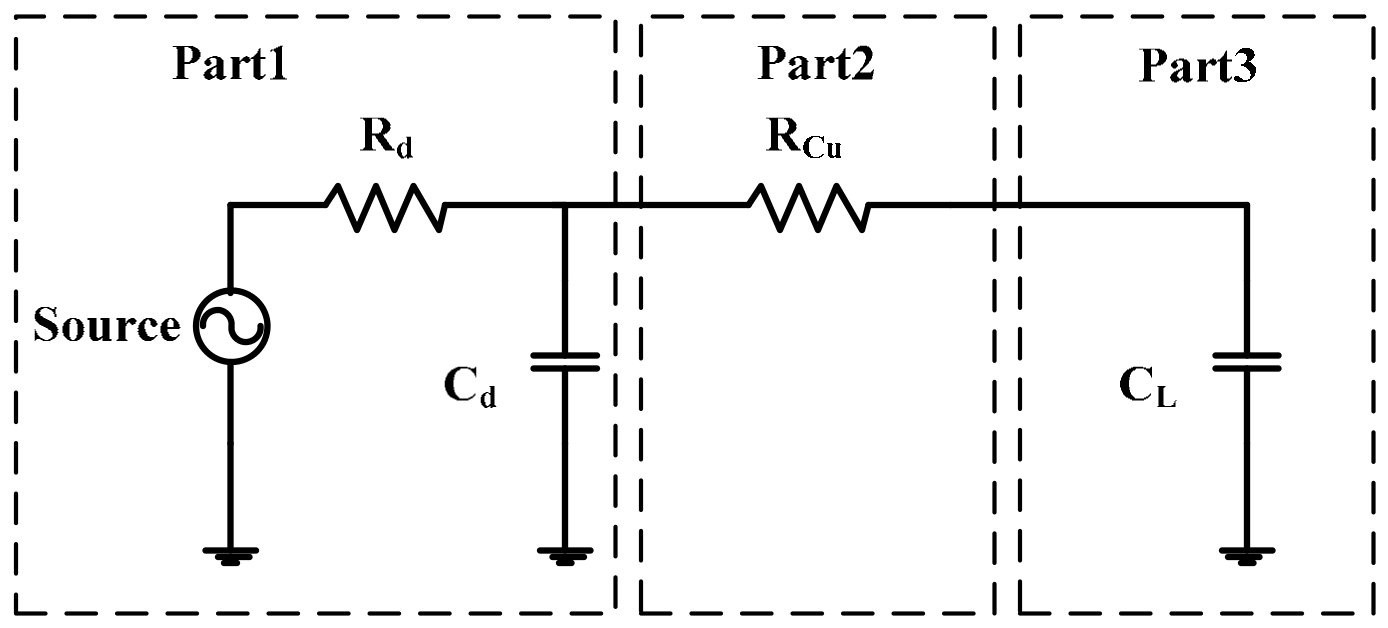
3. Circuit Parameters of Graphene Copper-Clad Electrode Plates
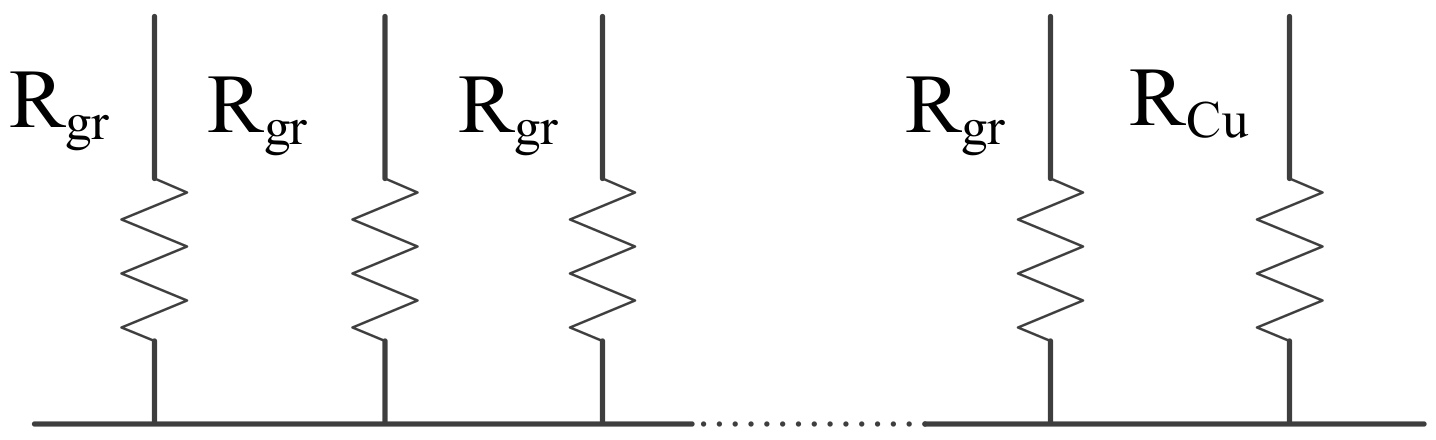
3.1. Resistance Characteristics
3.2. Inductance Characteristics
3.3. Capacitance Characteristics
4. Analysis of Influencing Factors
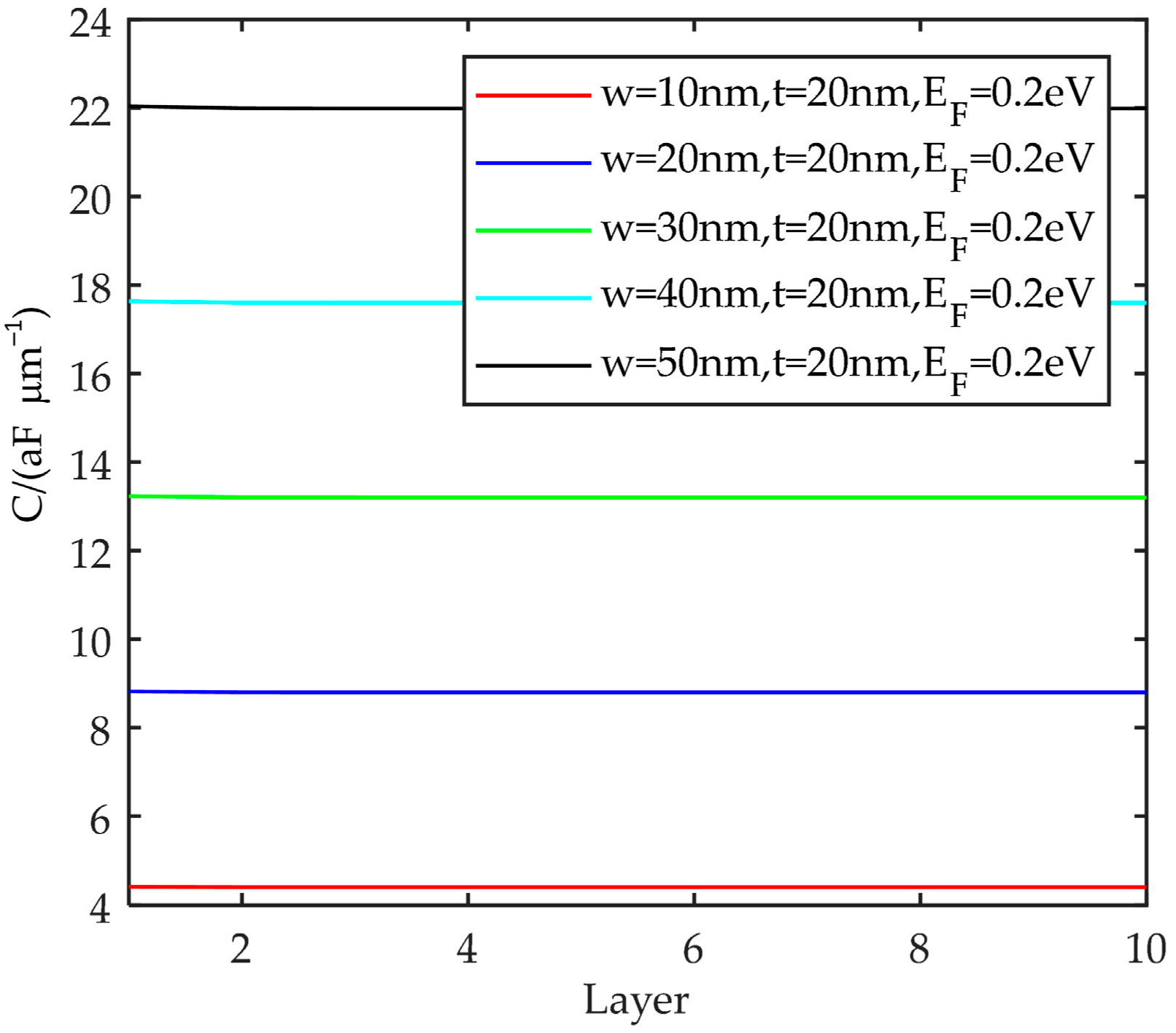
4.1. Width
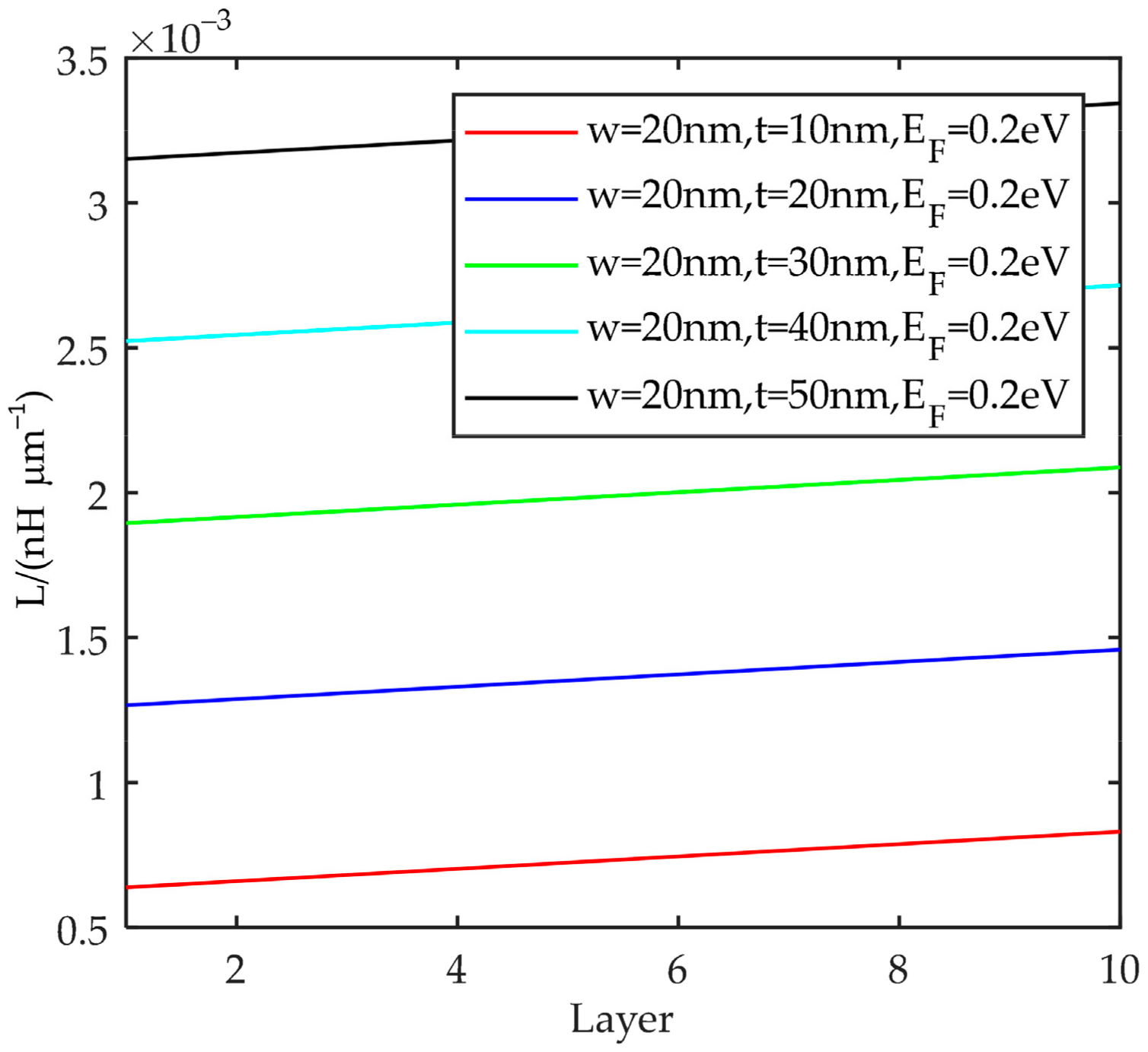
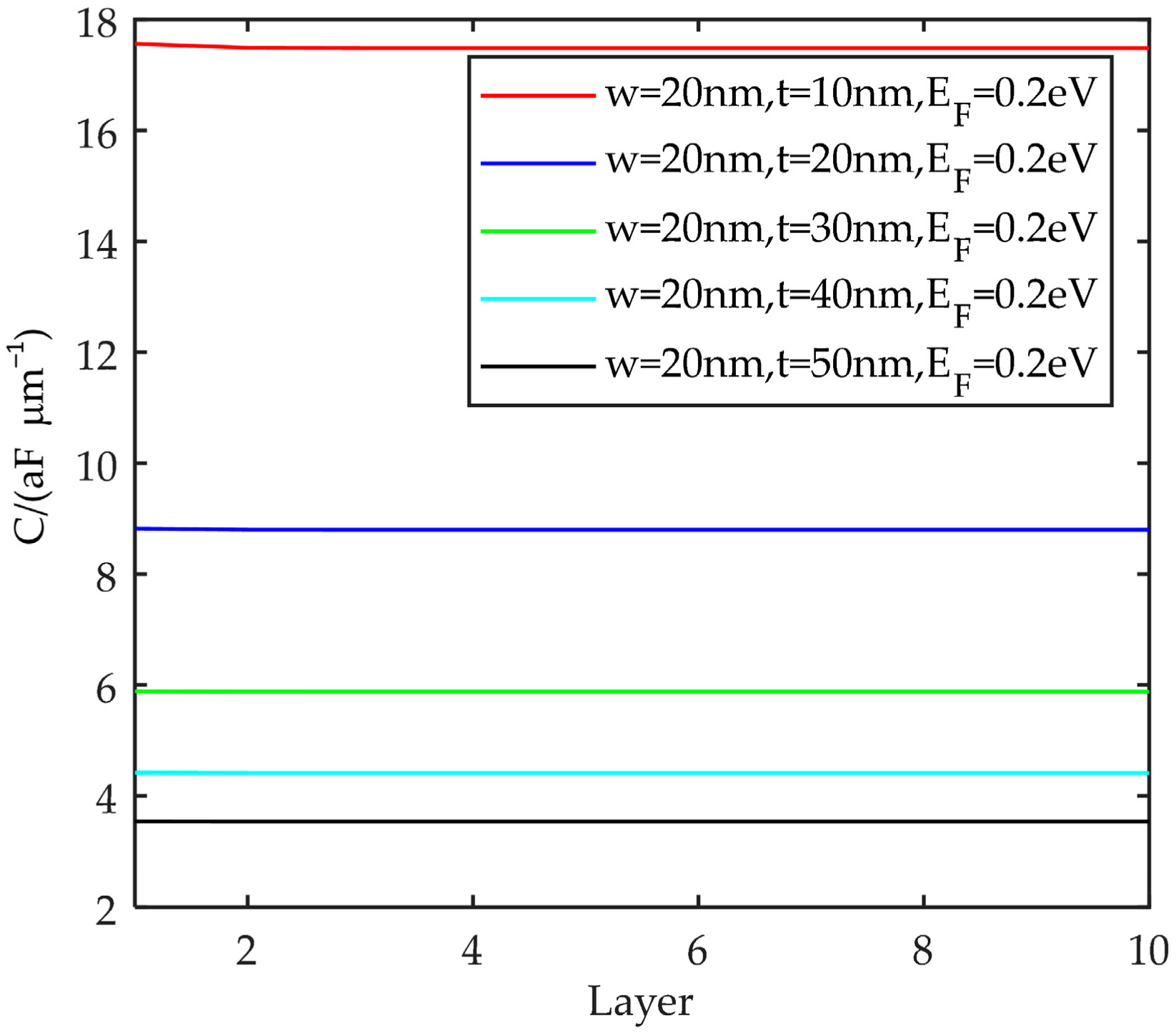
4.2. Thickness and Number of Layers
4.3. Fermi Energy Level
5. Computational Analysis
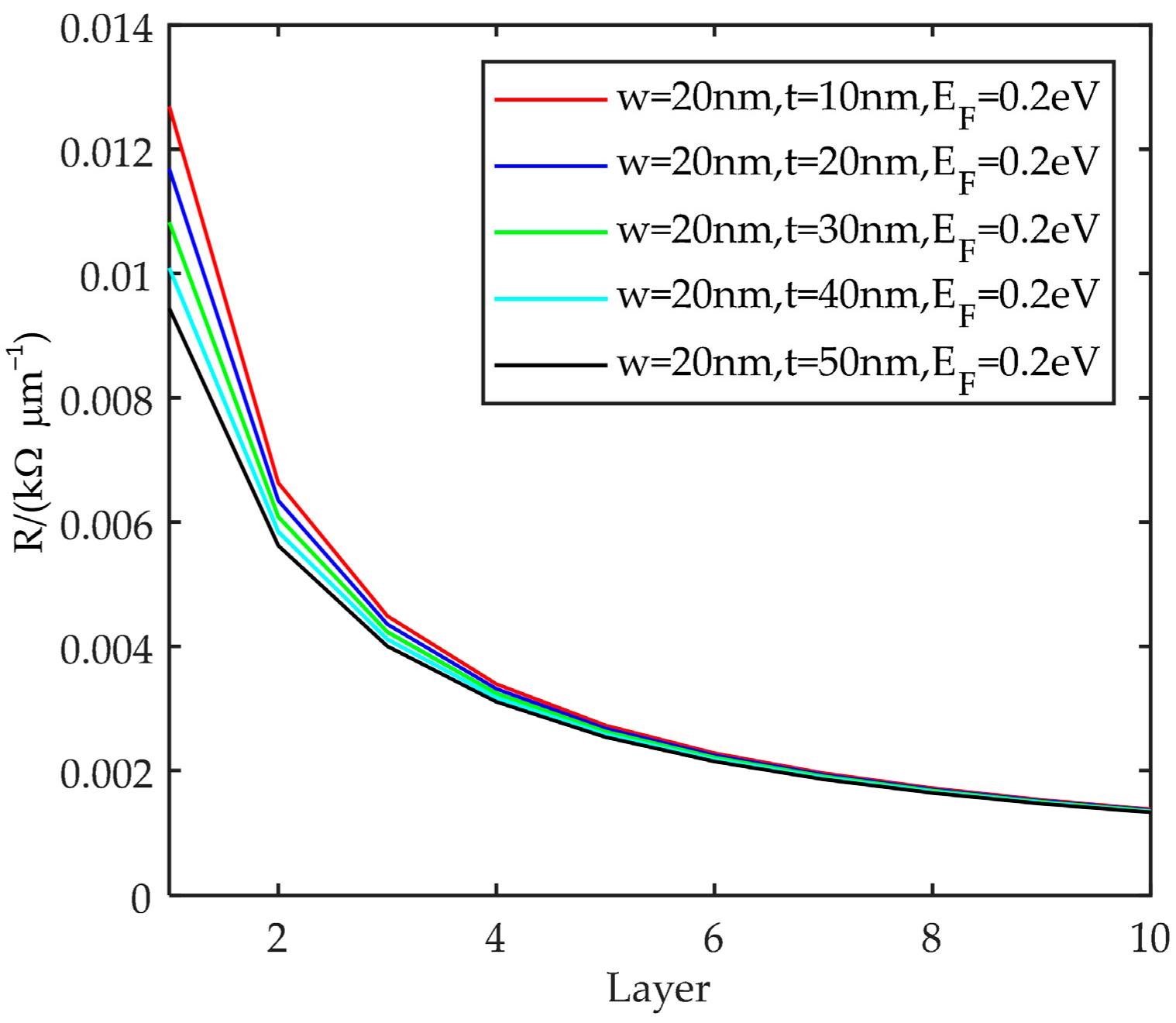
5.1. Resistance Characteristics
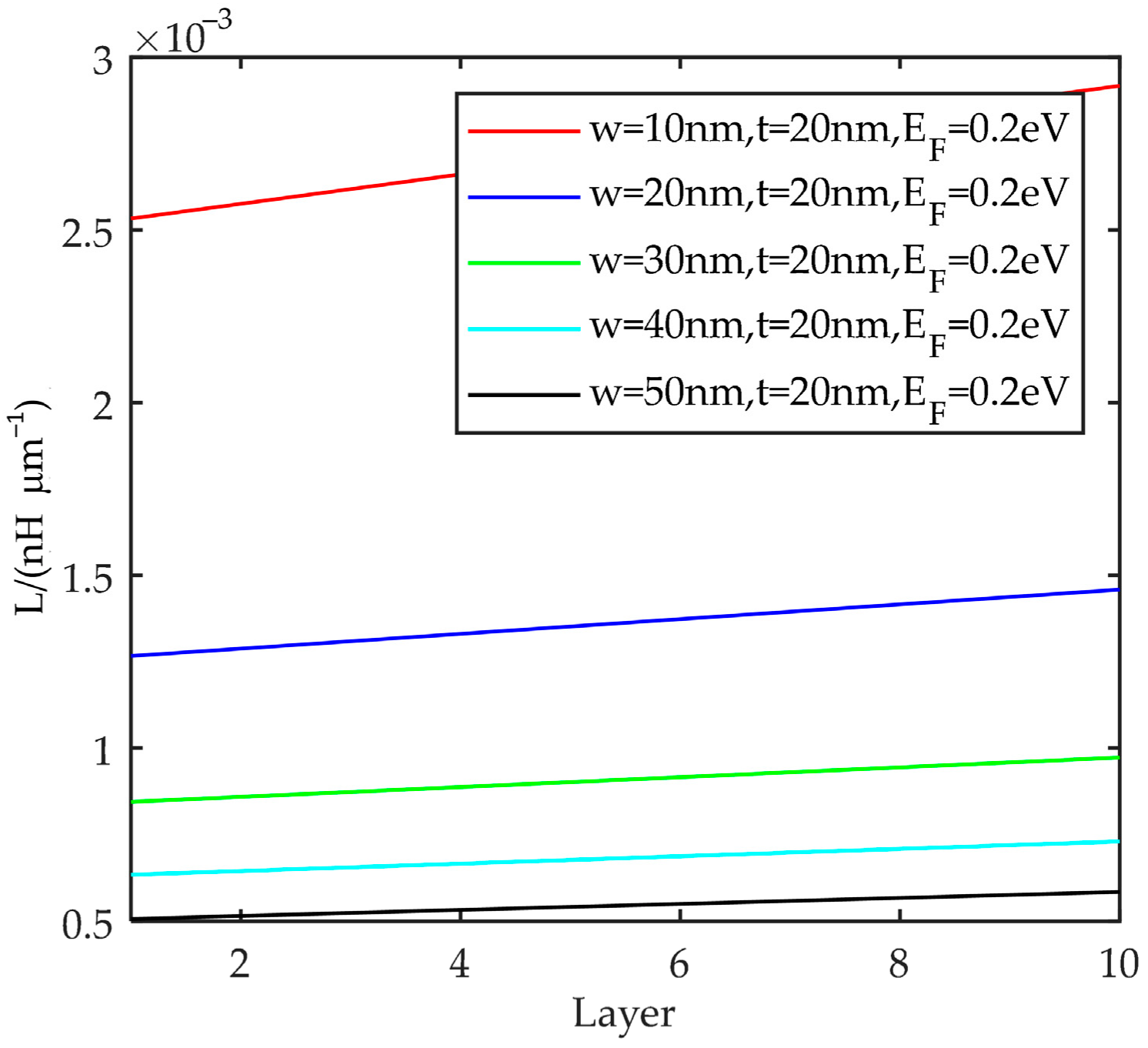
5.2. Inductance Characteristics
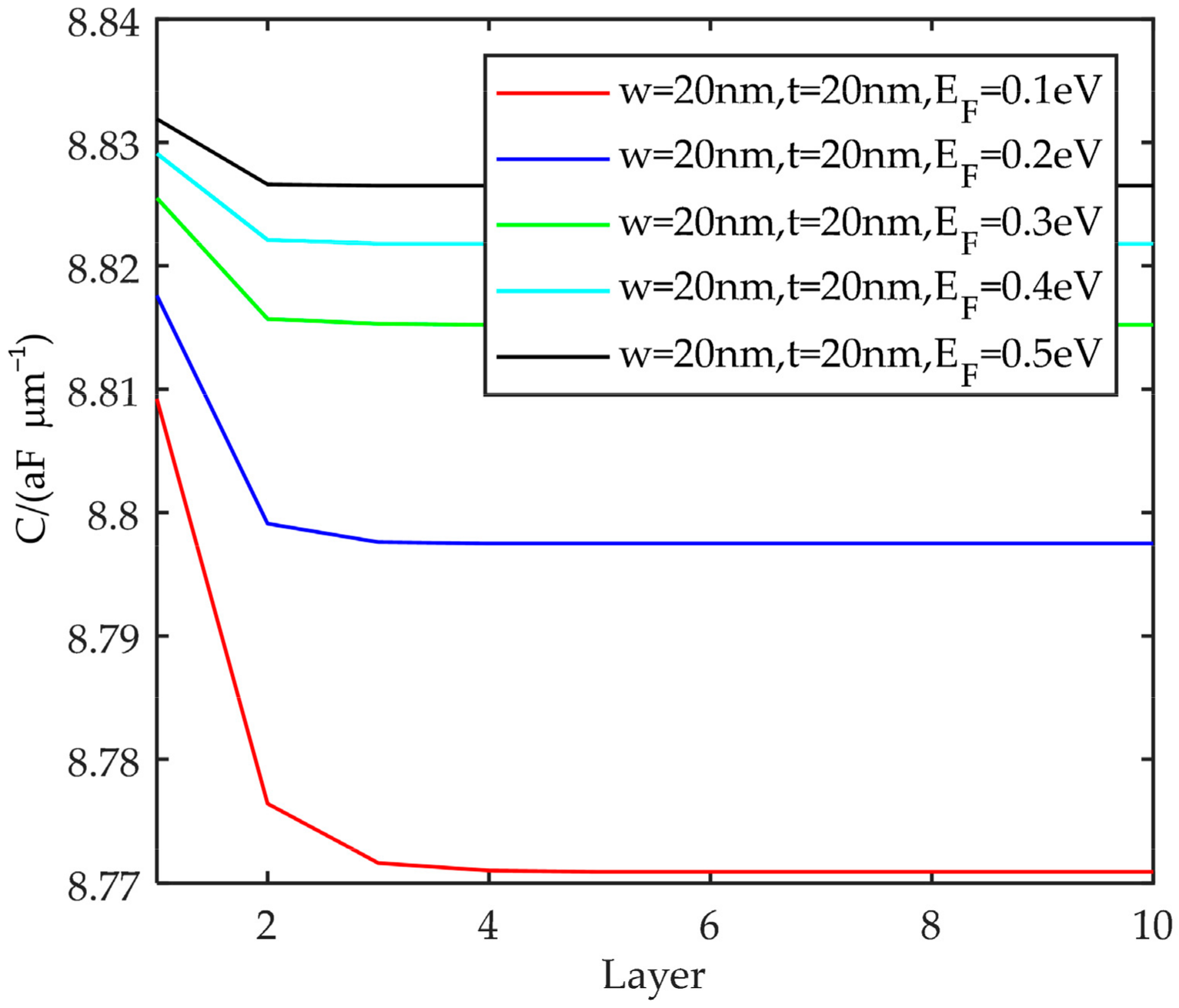
5.3. Capacitance Characteristics
6. Prediction Models of Circuit Parameter
6.1. Prediction Model of Resistance
6.2. Prediction Model of Inductance
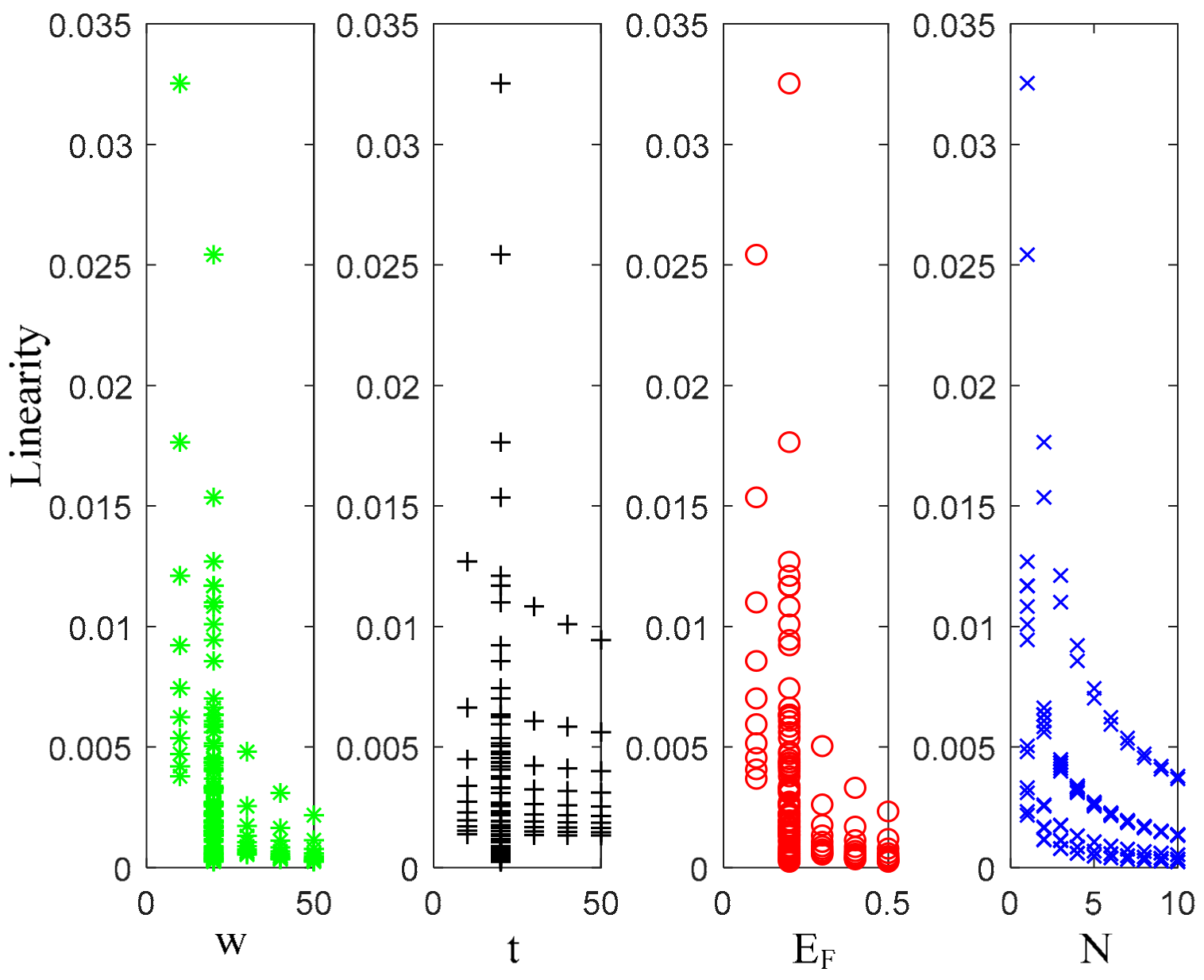
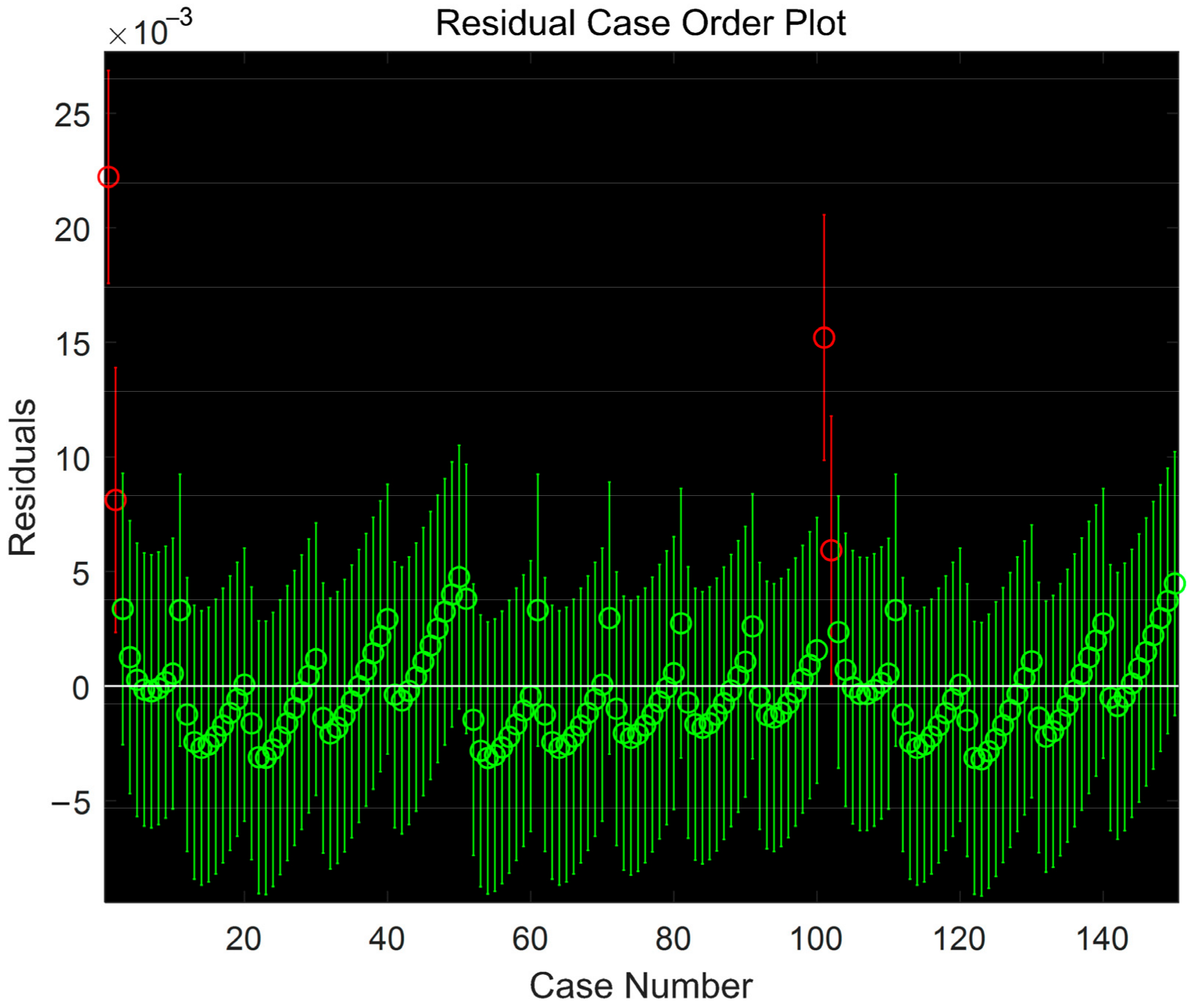
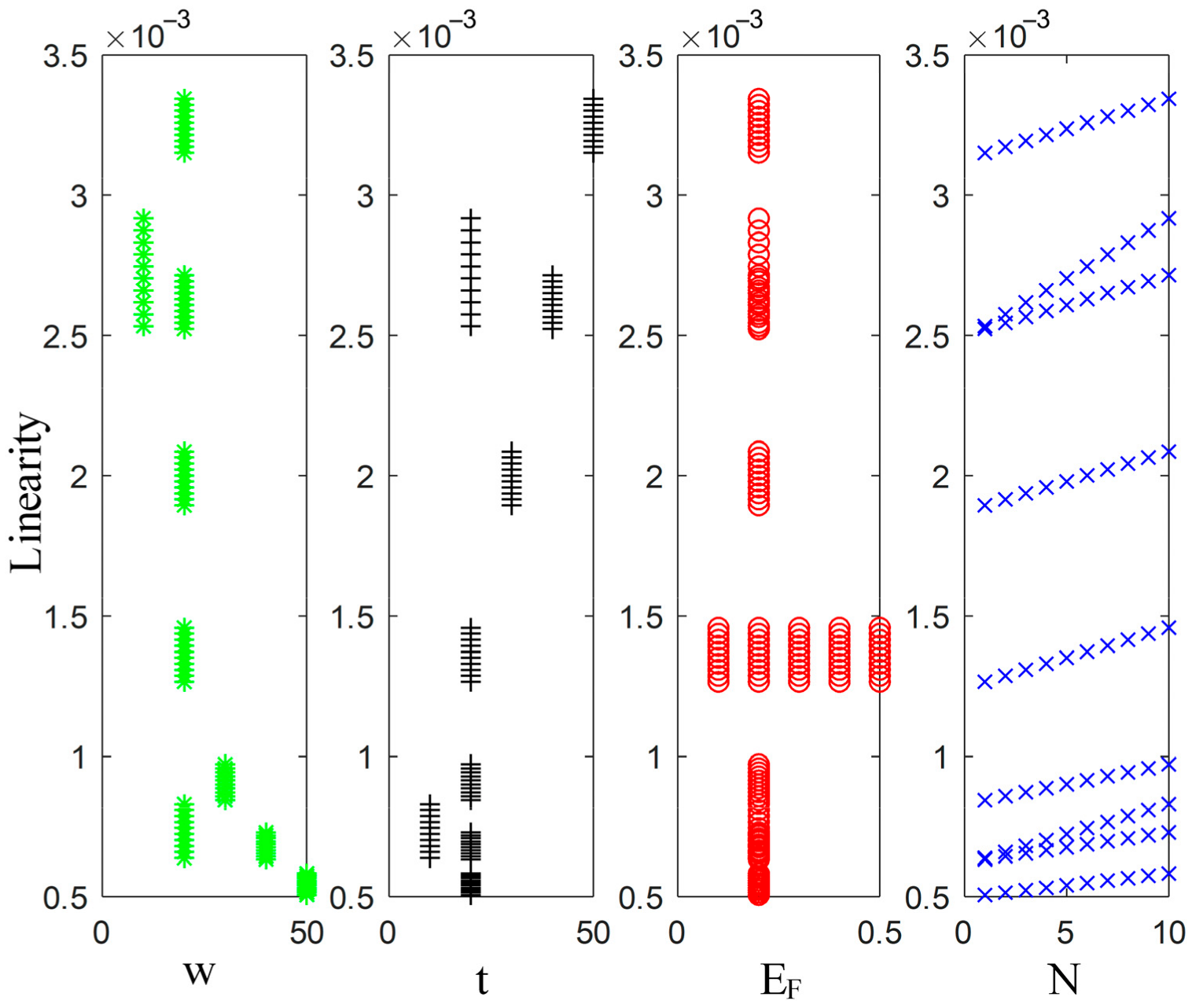
6.3. Prediction Model of Capacitance
7. Simulation and Experimental Analysis
7.1. Simulation Analysis
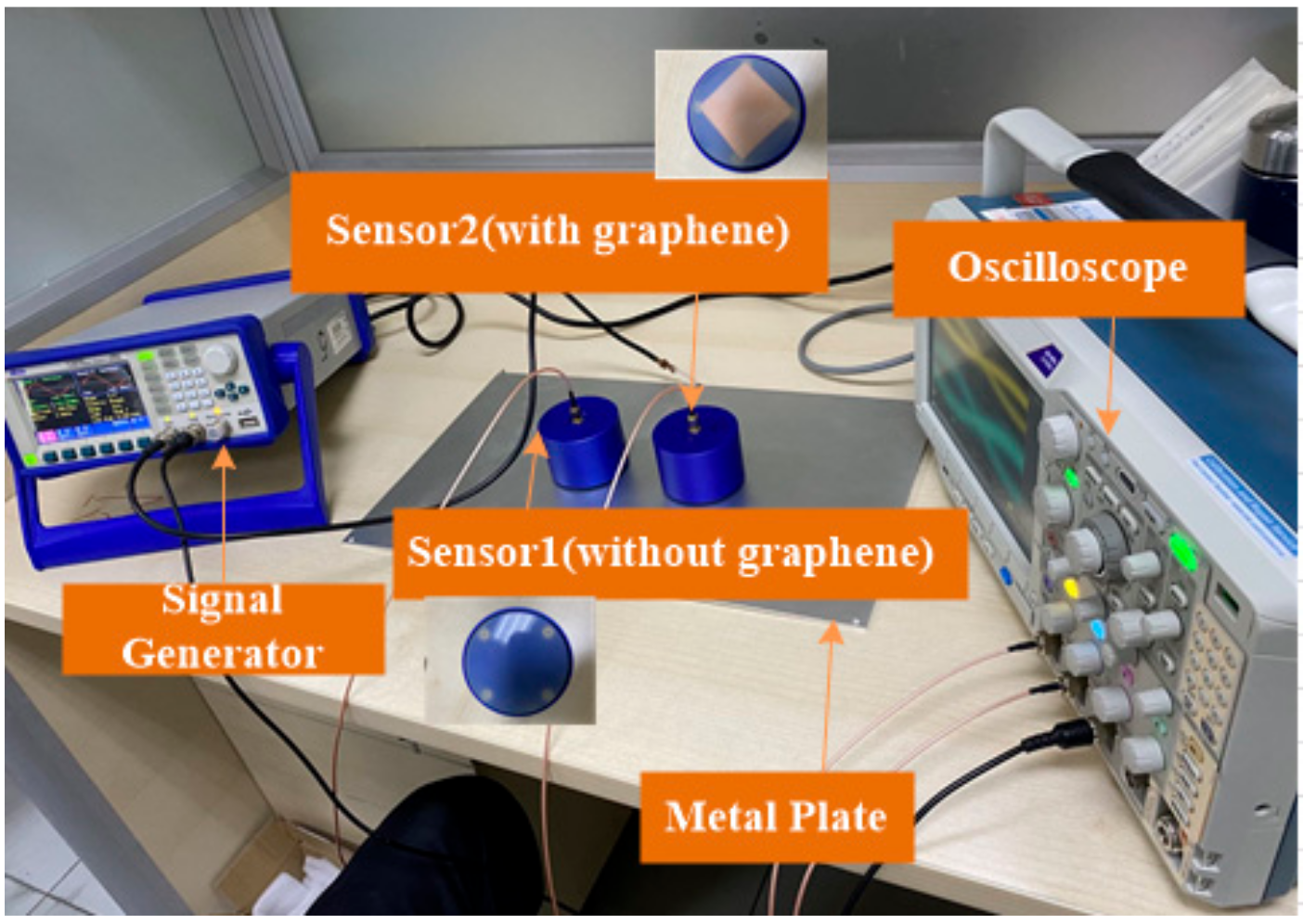
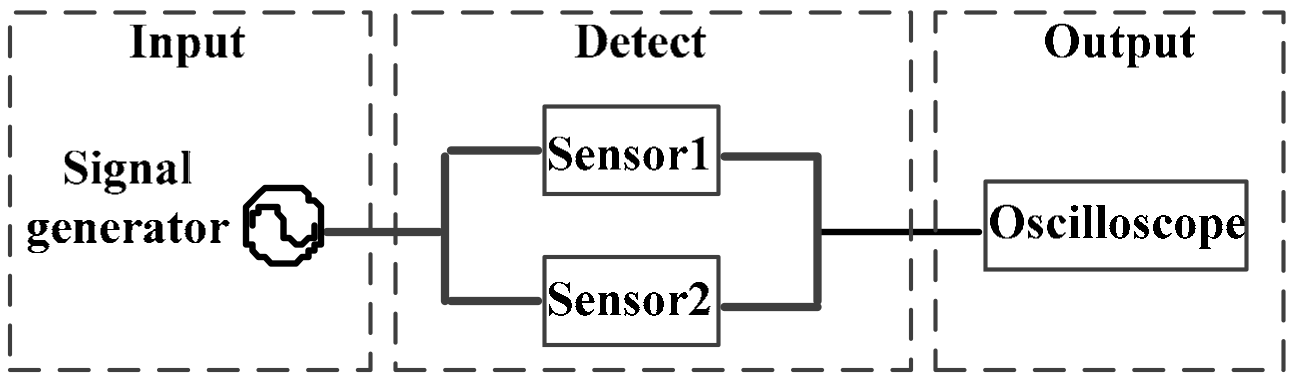
7.2. Experimental Analysis
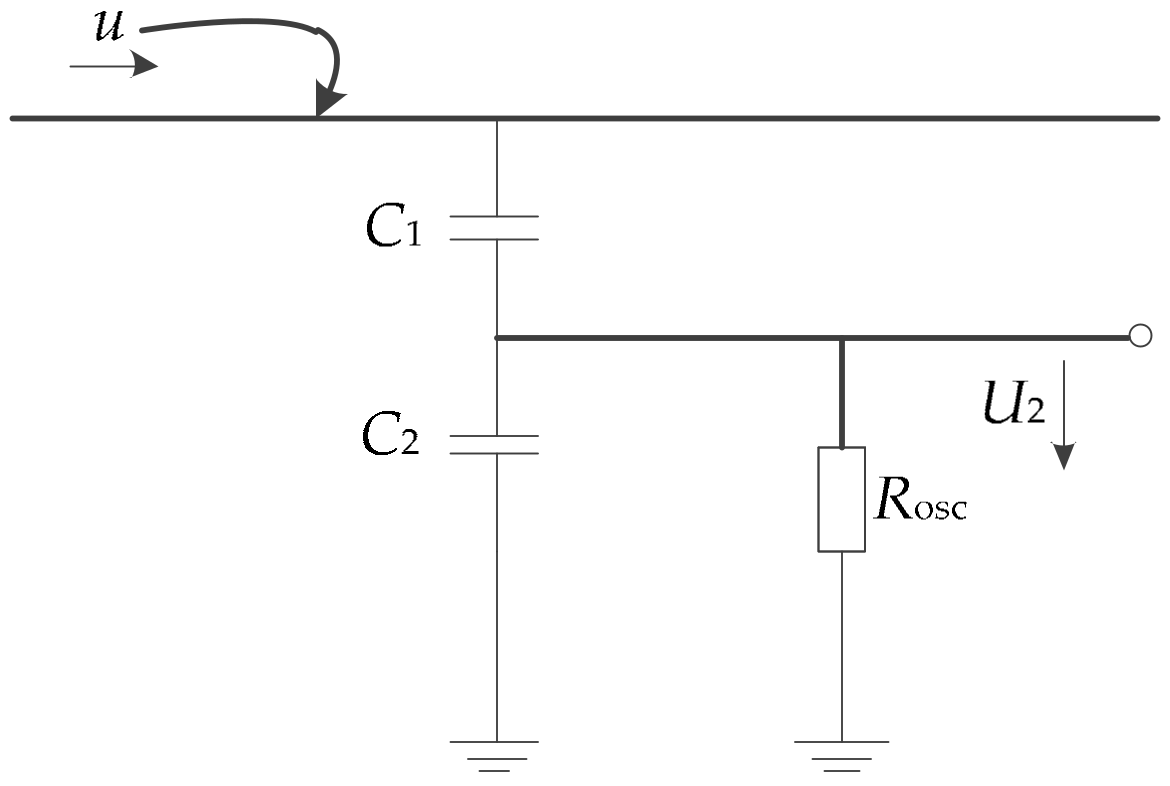
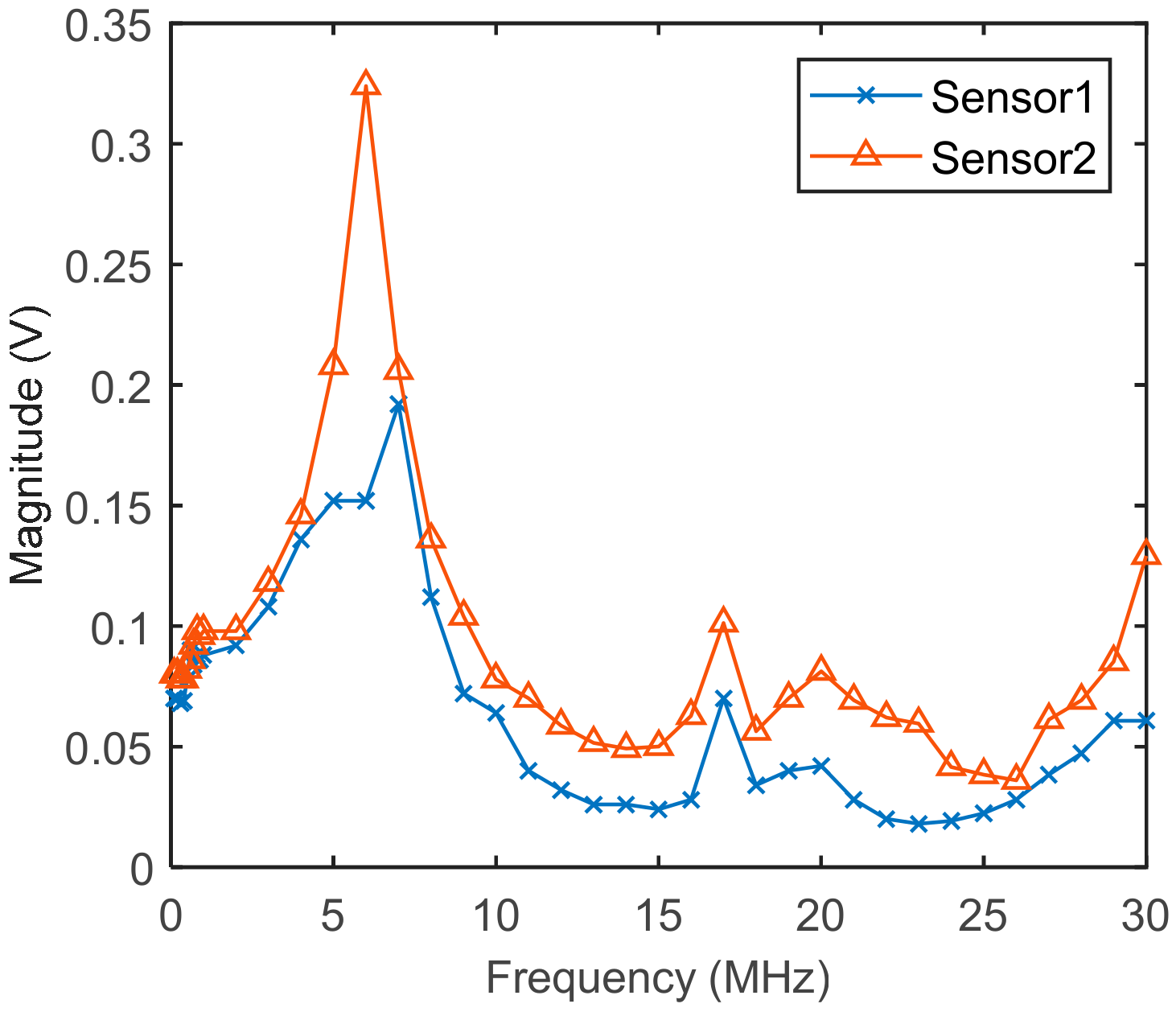
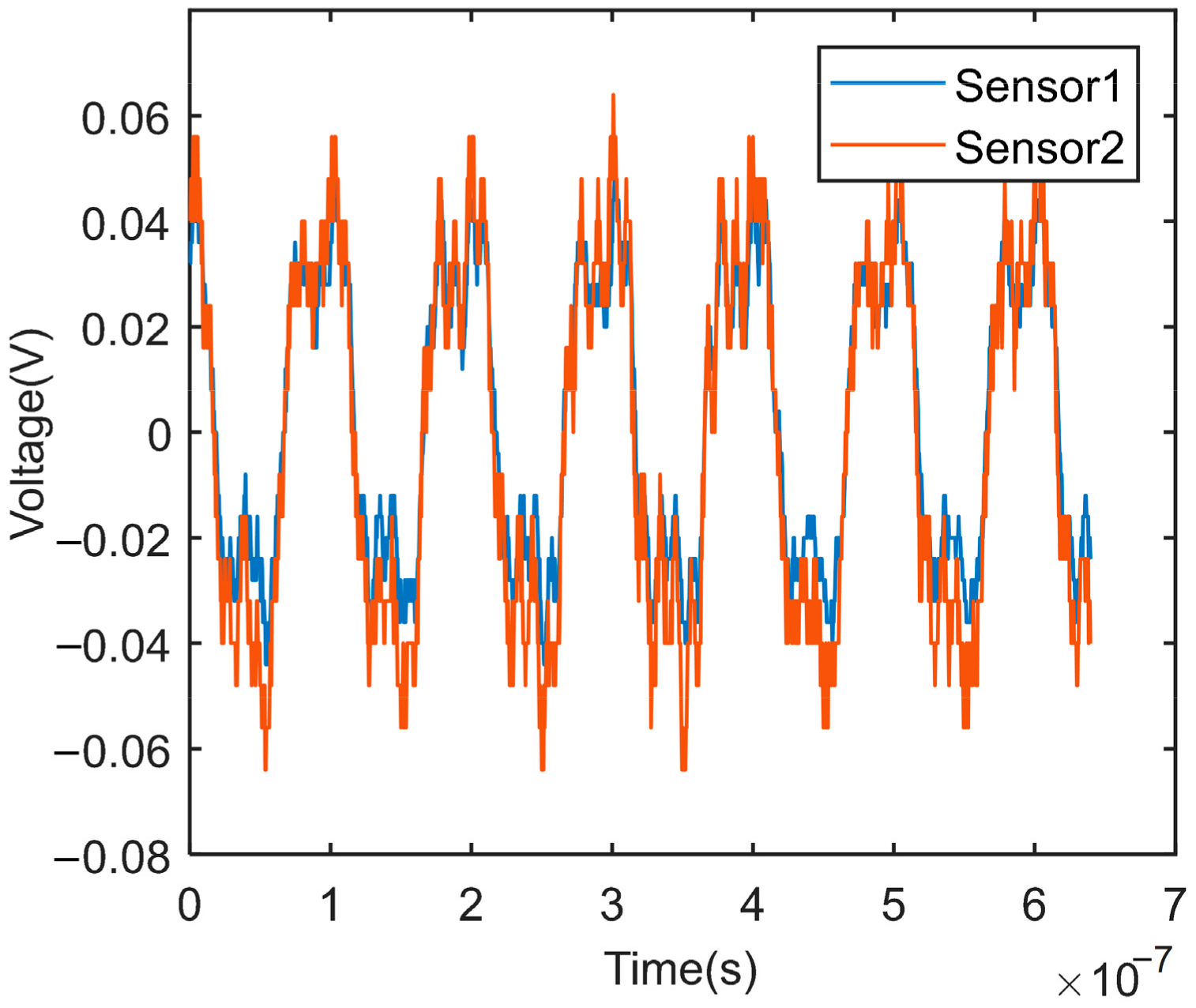
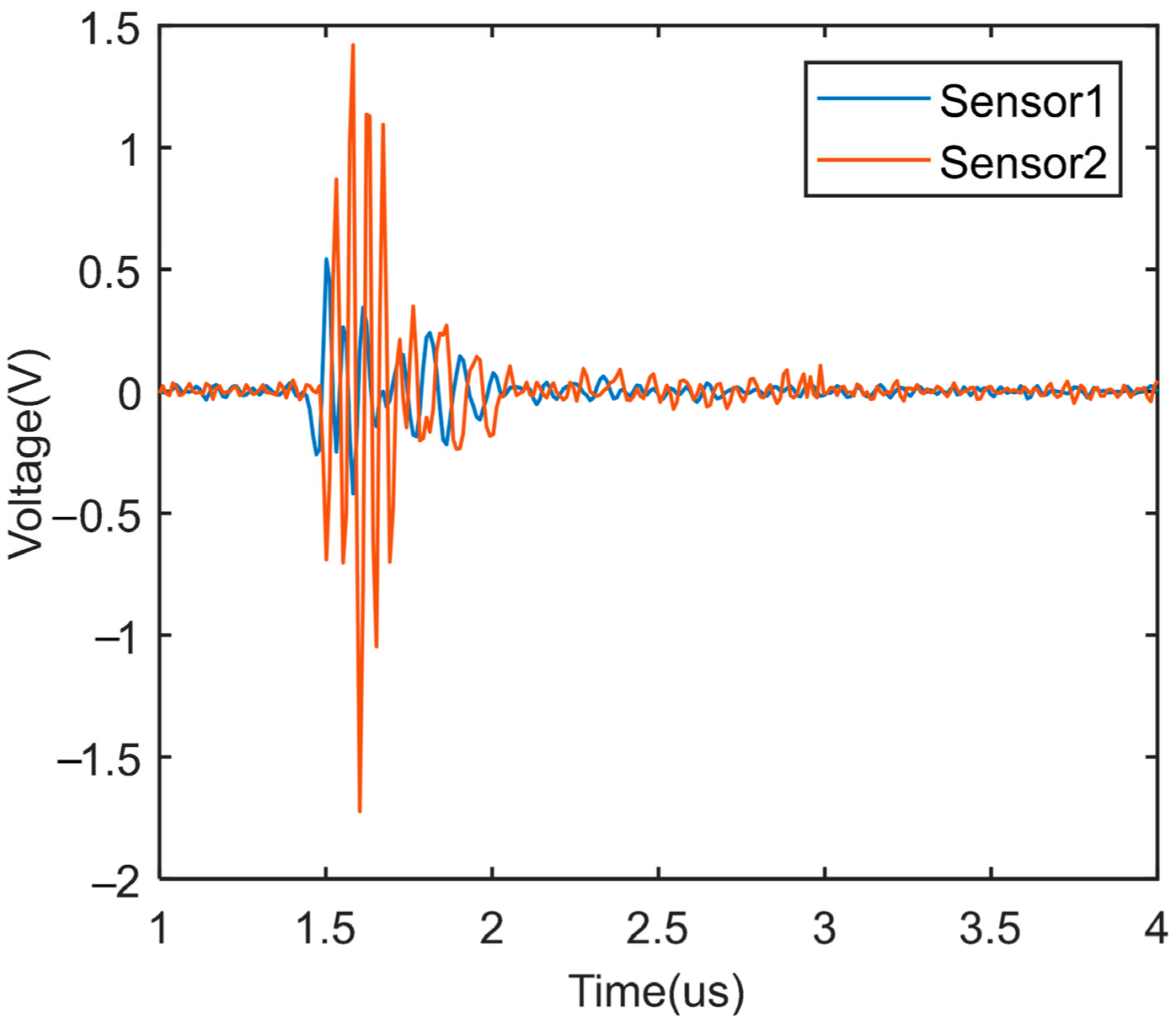
7.2.1. Experiment of Sensor Characteristics
7.2.2. Experiment of Partial Discharge Detection of Switchgear
8. Conclusions
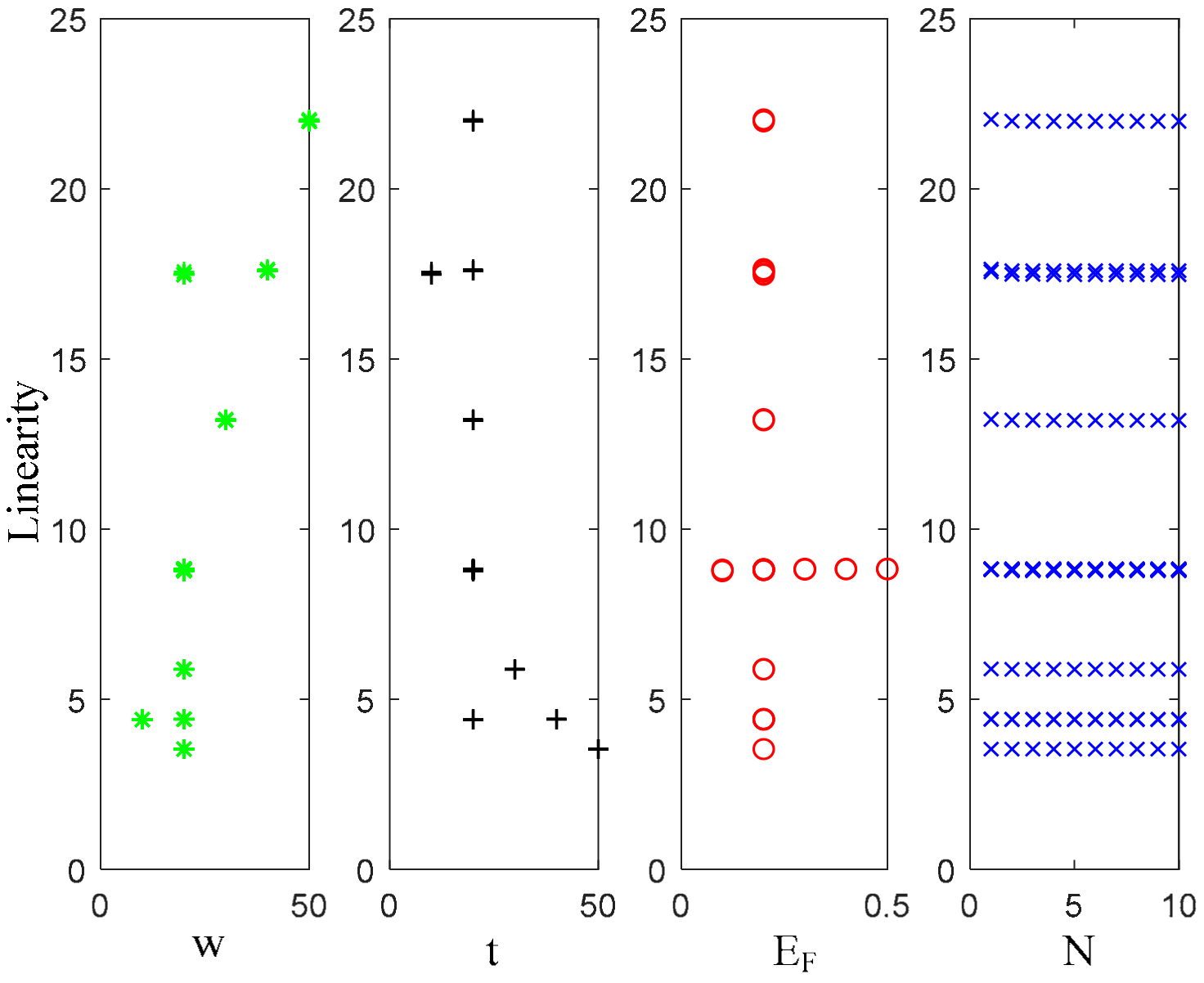
- Resistance gradually decreases with the increasing number of layers. The greater the width and Fermi energy level, the lower the equivalent resistance. The total thickness has less effect on the resistance;
- Inductance gradually increases with the number of layers, but the overall change is small. The greater the width, the lower the total inductance of the electrode plate, but the total thickness is the opposite. The Fermi energy level does not affect the inductance;
- Capacitance gradually decreases with the increase of the number of layers, but the trend is flat. With the increase of the width, the capacitance gradually increases. The thickness has the opposite effect on the capacitance. The Fermi energy level becomes larger, and the equivalent capacitance tends to increase.
- Multiple linear regression models based on the least-square method were established for three circuit parameters, which can further simplify the calculation of circuit parameters and provide a good fit of the data.
- Simulation and experimental results verify that the graphene PD sensor exhibits high gain characteristics compared to the traditional PD sensor.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.Y.; Mei, J.; Zheng, J.Y.; Mei, F. Research on a Multilayer Distributed Online Monitoring System of 10 kV High Voltage Switchgear. In Proceedings of the 2013 4th International Conference on Digital Manufacturing & Automation (ICDMA), Qingdao, China, 29–30 June 2013; pp. 1025–1028. [Google Scholar]
- Knezev, M.; Djekic, Z.; Kezunovic, M. Automated Circuit Breaker Monitoring. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting (PES), Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar]
- Ruan, W.-C.; Yao, Y.; Ouyang, X.-D.; Zeng, G.-W.; Su, C.; Xia, Z.-Q. Study on the reliability of 10kV uninterrupted maintenance outgoing switchgear under the condition of main device switching to the back-up device. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 1–4. [Google Scholar]
- Qian, Y.; Huang, W.; Li, D.; Zhang, H.; Liu, P.; Peng, Z. Optimization design of bushing of distribution switchgear equipment. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chengdu, China, 19–22 September 2016; pp. 1–4. [Google Scholar]
- Yao, Y. Study on Design of Main Busbar System of Large-current High-voltage Switchgear. In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 29–31 May 2020; pp. 12–15. [Google Scholar]
- Ji, Y.; Nie, Y.; Lin, X.; Qiu, H.; Wang, X.; Pan, J. Research on 3D Electric Field Distribution of 12 kV Switchgear Based on ANSYS. In Proceedings of the 2020 8th International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 7–10 December 2020; pp. 1–6. [Google Scholar]
- Zeng, X.; Li, H.; Lu, Y.; Chen, Y. Online monitoring of partial discharge in high voltage switchgear using a differential electric field sensor. In Proceedings of the 2017 IEEE Conference on Electrical Insulation and Dielectric Phenomenon (CEIDP), Fort Worth, TX, USA, 22–25 October 2017; pp. 385–388. [Google Scholar]
- Li, J.; Zhang, X.; Han, X.; Yao, X. A Partial Discharge Detection Method for SF6 Insulated Inverted Current Transformers Adopting Inner Shield Case as UHF Sensor. IEEE Trans. Power Deliv. 2018, 33, 3237–3239. [Google Scholar] [CrossRef]
- Li, Y.; Lu, F.; Xie, H.; Wang, Y. Study on ultrasonic generation mechanism of partial discharge. In Proceedings of the 2005 International Symposium on Electrical Insulating Materials (ISEIM), Kitakyushu, Japan, 5–9 June 2005; pp. 467–471. [Google Scholar]
- Rencheng, Z.; Li, X.; Liu, E.; Yang, J. Arithmetic and experiment research on ultrasonic detection of partial discharge for switchboard. In Proceedings of the 2011 IEEE International Conference on Computer Science and Automation Engineering (CSAE), Shanghai, China, 10–12 June 2011; pp. 330–334. [Google Scholar]
- Cullen, G.; Stewart, B.G.; Hepburn, D.M. Application of a radio frequency antenna technique for monitoring the speed, torque and internal fault conditions of A.C. and D.C. electric motors. In Proceedings of the 2004 IEEE Sensors for Industry Conference (ISA), New Orleans, LA, USA, 27–29 January 2004; pp. 50–54. [Google Scholar]
- Birlasekaran, S.; Leong, W.H. Comparison of Known PD Signals with the Developed and Commercial HFCT Sensors. IEEE Trans. Power Deliv. 2007, 22, 1581–1590. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Hou, F.; Ji, S.; Rehman, H.; Wu, X. Primary Differential Pulse Method for Partial-Discharge Detection of Oil-Immersed Inverted Current Transformers. IEEE Trans. Power Deliv. 2018, 33, 1492–1494. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, M.; Ren, M.; Wang, L.; Zhou, J. High bandwidth measurement of partial discharge current pulses based on the optimized needle-plate electrode system. In Proceedings of the 2016 International Conference on Condition Monitoring and Diagnosis (CMD), Xi’an, China, 25–28 September 2016; pp. 916–919. [Google Scholar]
- Davies, N.; Tian, Y.; Cheung, J.; Tang, Y.; Shiel, P. Non-intrusive partial discharge measurements of MV switchgears. In Proceedings of the 2008 International Conference on Condition Monitoring and Diagnosis, Beijing, China, 21–24 April 2008; pp. 385–388. [Google Scholar]
- Coenen, S.; Tenbohlen, S.; Markalous, S.M.; Strehl, T. Sensitivity of UHF PD measurements in power transformers. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1553–1558. [Google Scholar] [CrossRef]
- Zheng, Q.; Ma, G.; Jiang, J.; Li, C.; Zhan, H. A comparative study on partial discharge ultrasonic detection using fiber Bragg grating sensor and piezoelectric transducer. In Proceedings of the 2015 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Ann Arbor, MI, USA, 18–21 October 2015; pp. 282–285. [Google Scholar]
- Fujii, Y.; Cho, H.; Nakamura, Y. Highly sensitive partial discharge detection by TEV method under severe noise conditions. In Proceedings of the 2017 4th International Conference on Electric Power Equipment—Switching Technology (ICEPE-ST), Xi’an, China, 22–25 October 2017; pp. 783–786. [Google Scholar]
- Subramaniam, A.; Raman, S.J.; Panda, S.K. Comparison of Partial Discharge signal in a Three phase Transformer by UHF, TEV and HFCT sensors. In Proceedings of the 2021 1st International Conference on Power Electronics and Energy (ICPEE), Bhubaneswar, India, 2–3 January 2021; pp. 1–4. [Google Scholar]
- Wang, Z.; Shaygan, M.; Otto, M.; Schall, D.; Neumaier, D. Flexible Hall sensors based on graphene. Nanoscale 2016, 8, 7683–7687. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedman, A.L.; Robinson, J.T.; Perkins, F.K.; Campbell, P.M. Extraordinary magnetoresistance in shunted chemical vapor deposition grown graphene devices. Appl. Phys. Lett. 2011, 99, 022108. [Google Scholar] [CrossRef]
- Tamagnone, M.; Gómez-Díaz, J.S.; Mosig, J.R.; Perruisseau-Carrier, J. Reconfigurable terahertz plasmonic antenna concept using a graphene stack. Appl. Phys. Lett. 2012, 101, 214102. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Lu, W.B.; Liu, Z.G.; Zhang, A.Q. Graphene-Based Microwave Antennas with Reconfigurable Pattern. IEEE Trans. Antennas Propag. 2020, 68, 2504–2510. [Google Scholar] [CrossRef]
- Wang, X.C.; Zhao, W.S.; Hu, J.; Yin, W.Y. Reconfigurable terahertz leaky-wave antenna using graphene-based high-impedance surface. IEEE Trans. Nanotechnol. 2015, 14, 62–69. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, W.S.; Hu, J.; Yin, W.Y. Electrothermal Characterization of Multilevel Cu-Graphene Heterogeneous Interconnects in the Presence of an Electrostatic Discharge (ESD). IEEE Trans. Nanotechnol. 2015, 14, 205–209. [Google Scholar] [CrossRef]
- Koziel, S.; Leifsson, L.; Couckuyt, I.; Dhaene, T. Fourth order hybrid implicit and explicit FDTD method. Int. J. Numer. Model 2013, 26, 493–505. [Google Scholar] [CrossRef]
- Kumar, V.; Rakheja, S.; Naeemi, A. Modeling and optimization for multi-layer graphene nanoribbon conductors. In Proceedings of the 2011 IEEE International Interconnect Technology Conference (IITC), Dresden, Germany, 8–12 May 2011; pp. 1–3. [Google Scholar]
- Rostaminia, R.; Saniei, M.; Vakilian, M. Effects of transformer core modeling on Partial Discharge current pulses simulation accuracy. In Proceedings of the 2015 IEEE 11th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Sydney, Australia, 19–22 July 2015; pp. 664–667. [Google Scholar]
- Amin, E.M.; Karmakar, N.C. A Passive RF Sensor for Detecting Simultaneous Partial Discharge Signals Using Time-Frequency Analysis. IEEE Sens. J. 2016, 16, 2339–2348. [Google Scholar] [CrossRef]
- Cheng, Z.H.; Zhao, W.S.; Dong, L.X.; Wang, J.; Zhao, P.; Gao, H.; Wang, G.F. Investigation of Copper-Carbon Nanotube Composites as Global VLSI Interconnects. IEEE Trans. Nanotechnol. 2017, 16, 891–900. [Google Scholar] [CrossRef]
- Cheng, Z.H.; Zhao, W.S.; Wang, D.W.; Wang, J.; Dong, L.X.; Wang, G.F.; Yin, W.Y. Analysis of Cu-Graphene Interconnects. IEEE Access 2018, 6, 53499–53508. [Google Scholar] [CrossRef]
- Zhao, W.S.; Fu, K.; Wang, D.W.; Li, M.; Wang, G.; Yin, W.Y. Mini-review: Modeling and performance analysis of nanocarbon interconnects. Appl. Sci. 2019, 9, 2174. [Google Scholar] [CrossRef] [Green Version]
- Hu, Q.H.; Zhao, W.S.; Fu, K.; Wang, D.W.; Wang, G. Electrical modeling of carbon nanotube-based shielded through-silicon vias for three-dimensional integrated circuits. Int. J. Numer. Model. Electron. Netw. Devices Fields 2021, 34, e2842. [Google Scholar] [CrossRef]
- Kondo, D.; Nakano, H.; Zhou, B.; Akiko, I.; Hayashi, K.; Takahashi, M.; Sato, S.; Yokoyama, N. Sub-10-nm-wide intercalated multi-layer graphene interconnects with low resistivity. In Proceedings of the 2014 IEEE International Interconnect Technology Conference (IITC), San Jose, CA, USA, 20–23 May 2014; pp. 189–192. [Google Scholar]
- Sarto, M.S.; Tamburrano, A. Comparative analysis of TL models for multilayer graphene nanoribbon and multiwall carbon nanotube interconnects. In Proceedings of the 2010 IEEE International Symposium on Electromagnetic Compatibility (ISEMC), Fort Lauderdale, FL, USA, 25–30 July 2010; pp. 212–217. [Google Scholar]


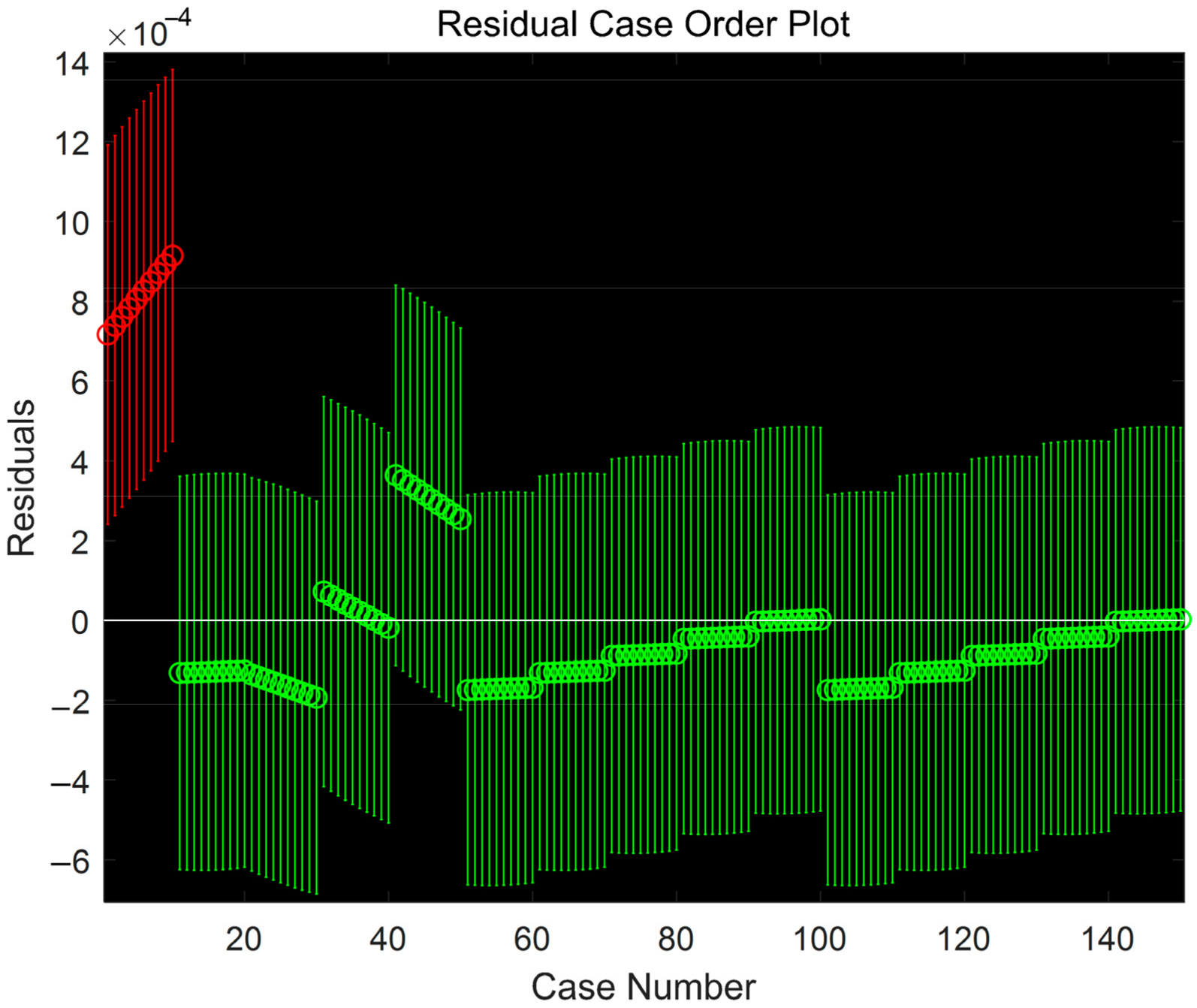
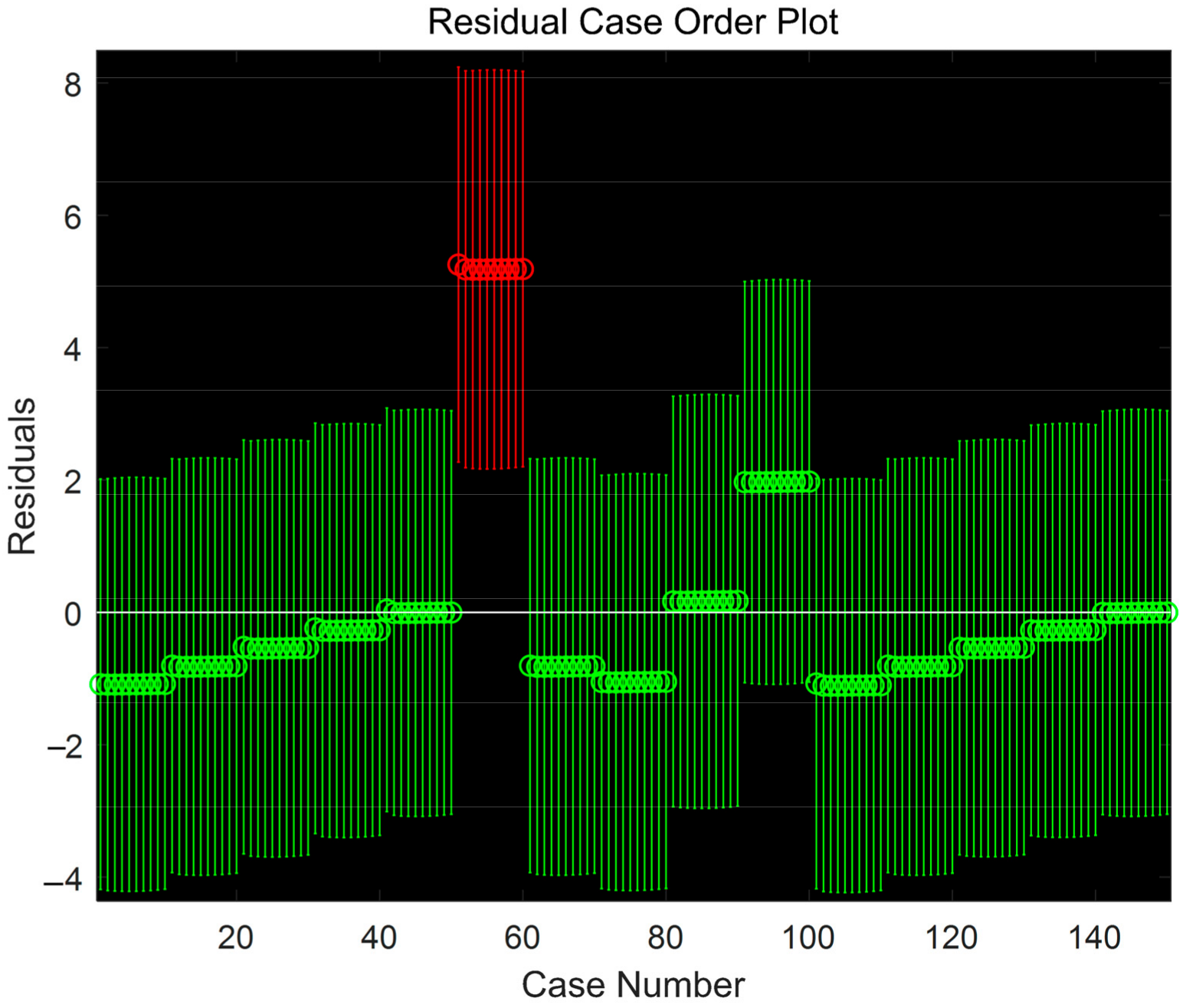



| Material | Resistivity | Carrier Mobility | Electrical Conductivity | Thermal Conductivity | Electron Transfer Capability |
|---|---|---|---|---|---|
| Graphene | 10−6 Ω/cm | 200,000 cm2V−1S−1 | high | high | good |
| Circuit Parameters | w | t | EF | N |
|---|---|---|---|---|
| Resistance | − | \ | − | − |
| Inductance | − | + | \ | + |
| Capacitance | + | − | + | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wu, Z. Analysis of Circuit Parameters of New Graphene Partial Discharge Sensor Electrode Plate Based on Transmission Line Model. Energies 2022, 15, 2169. https://doi.org/10.3390/en15062169
Zhang H, Wu Z. Analysis of Circuit Parameters of New Graphene Partial Discharge Sensor Electrode Plate Based on Transmission Line Model. Energies. 2022; 15(6):2169. https://doi.org/10.3390/en15062169
Chicago/Turabian StyleZhang, Huiyuan, and Zhensheng Wu. 2022. "Analysis of Circuit Parameters of New Graphene Partial Discharge Sensor Electrode Plate Based on Transmission Line Model" Energies 15, no. 6: 2169. https://doi.org/10.3390/en15062169
APA StyleZhang, H., & Wu, Z. (2022). Analysis of Circuit Parameters of New Graphene Partial Discharge Sensor Electrode Plate Based on Transmission Line Model. Energies, 15(6), 2169. https://doi.org/10.3390/en15062169






