Numerical Simulation of Heat Removal from a Window Slab Partition of a Radiative Coil Coating Oven
Abstract
1. Introduction
2. Physical Model
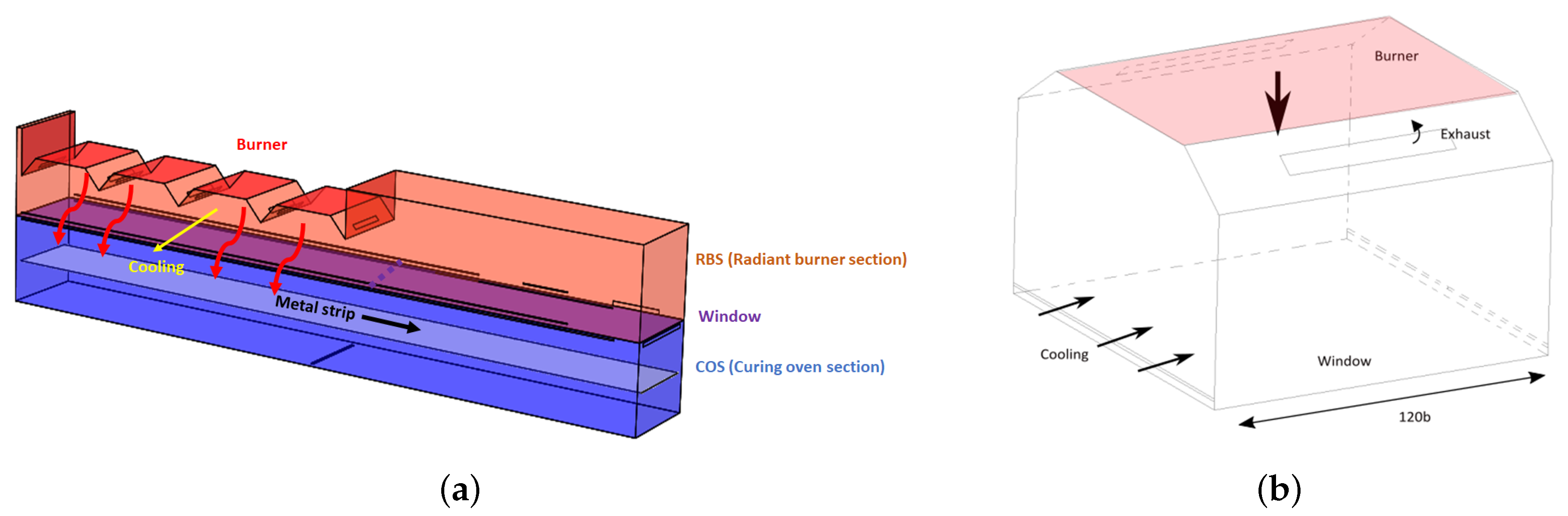
2.1. Oven Geometry
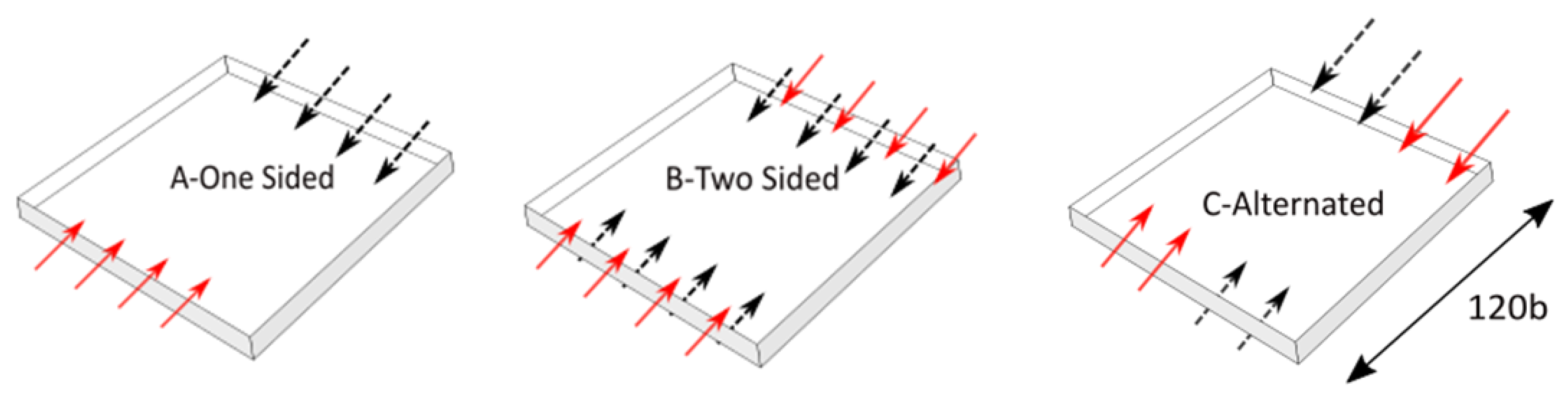
2.2. Window Wall Jet Cooling Schemes
3. Mathematical and Numerical Models
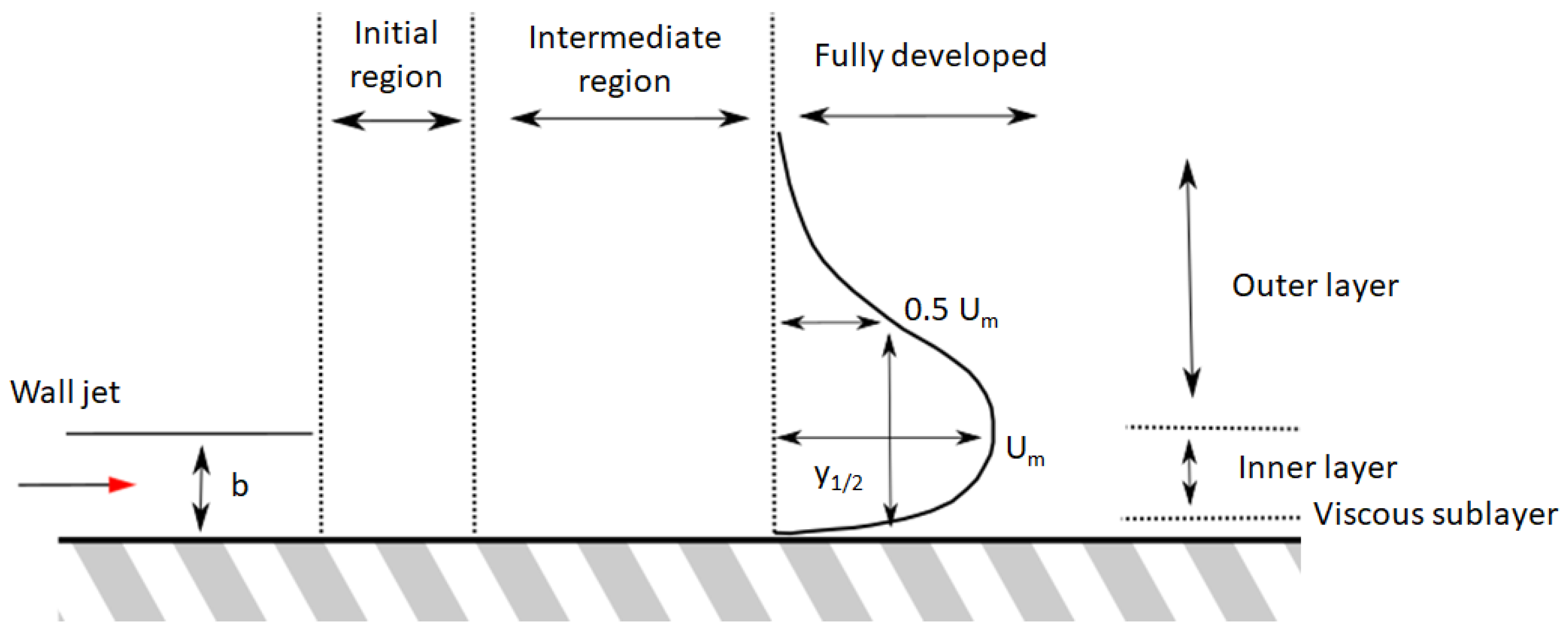
3.1. 3D Oven Model
- standard model with (i) standard wall function (WF), (ii) scalable WF, and (iii) non-equilibrium WF;
- realizable model with standard WF;
- low-Reynolds (i) Yang and Shih model, and (ii) AKN model;
- SST model; and
- Spalart-Allmaras (SA) model.
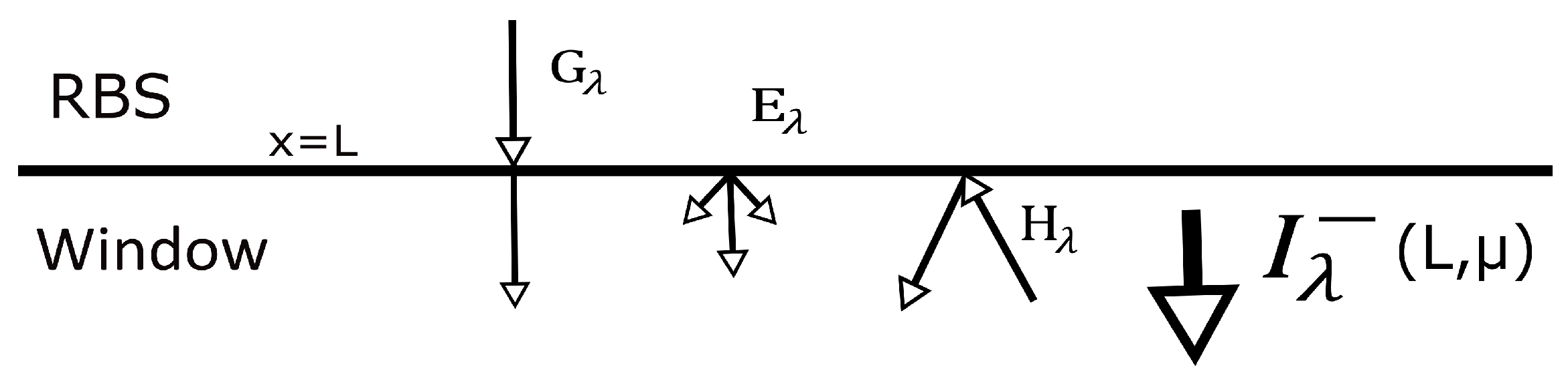
3.2. 1D Window Thermal Energy and Radiation Models
3.2.1. Thermal Model
3.2.2. Radiation Model
4. Results
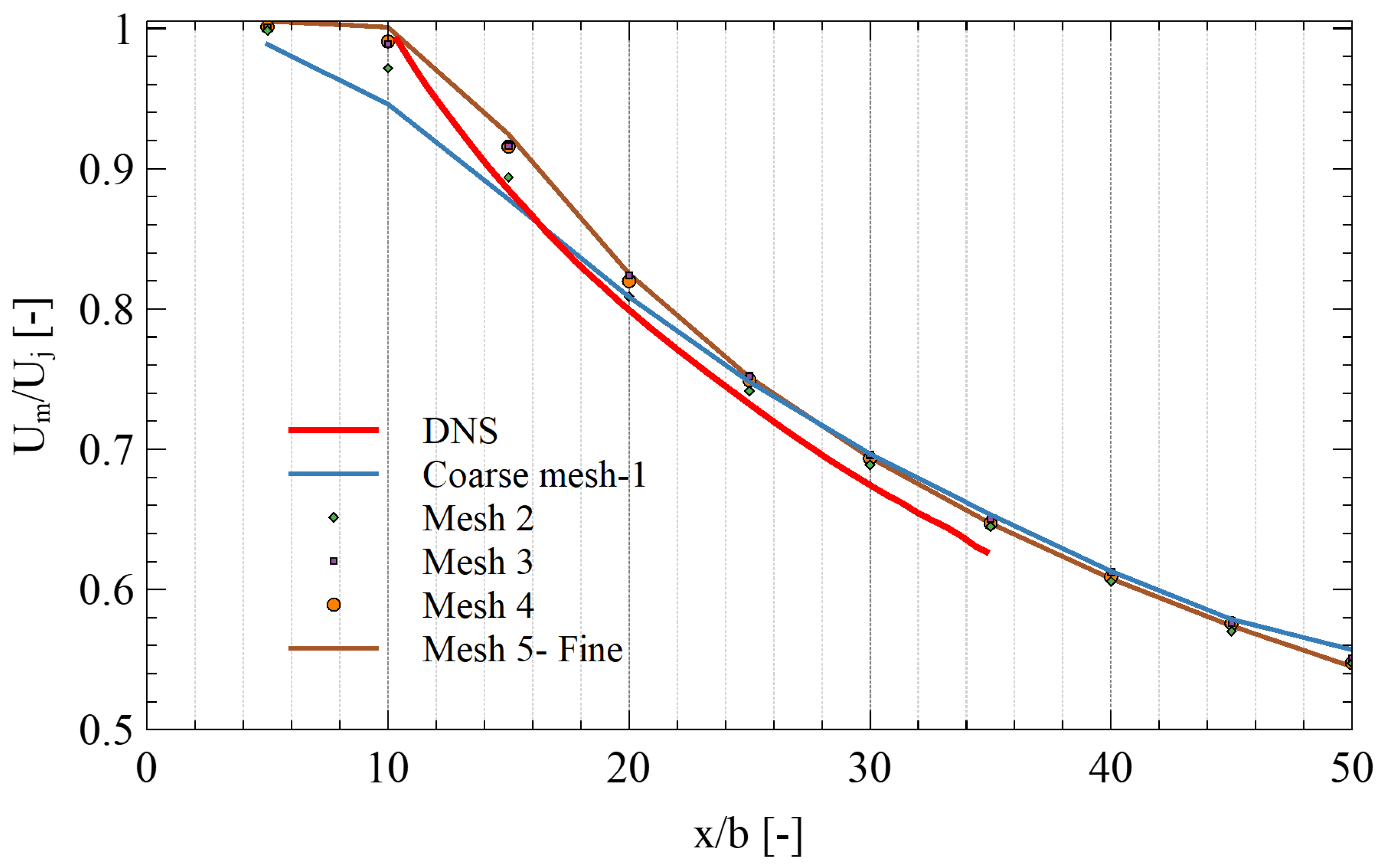
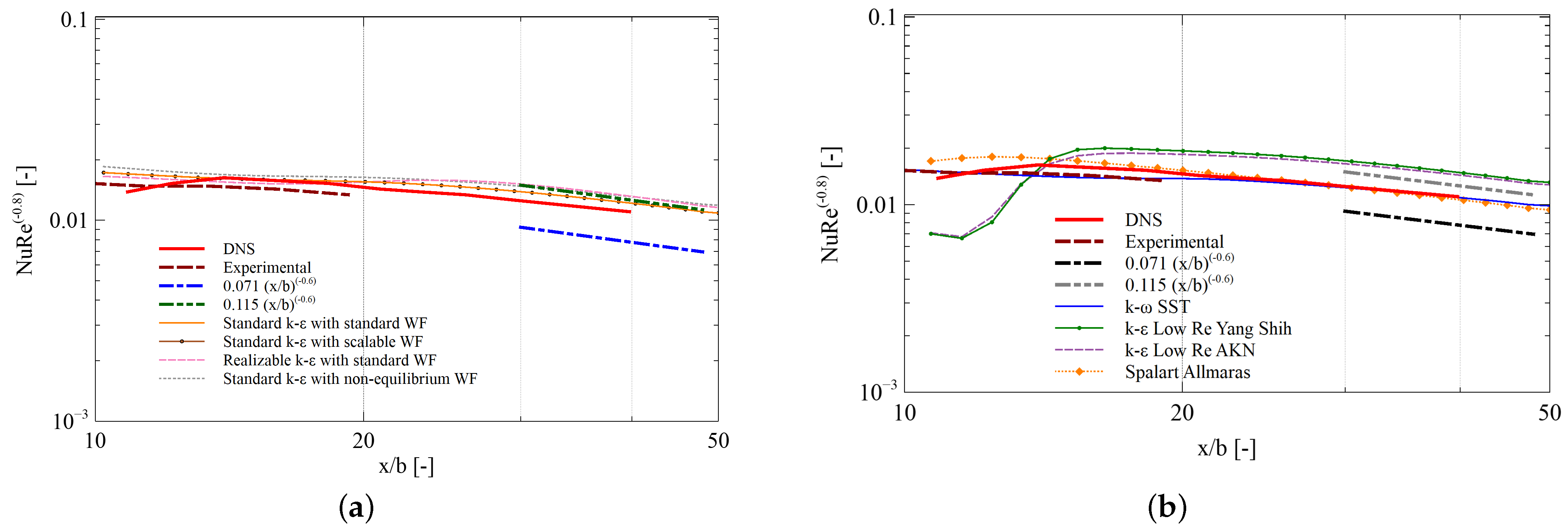
4.1. RANS Turbulence Model Selection—Comparison with Benchmark Results
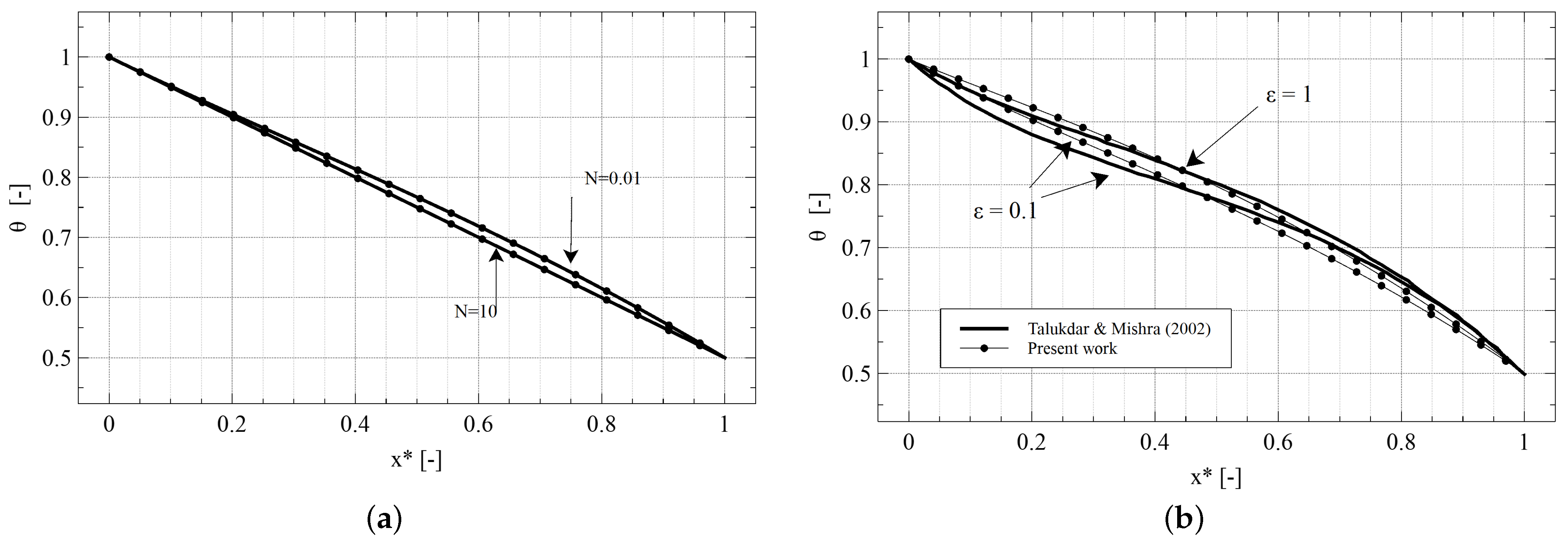
4.2. 1D Window Models Verification
4.3. Convective Heat Transfer Correlations
4.4. Parametric Studies on the Window Thermal Performance
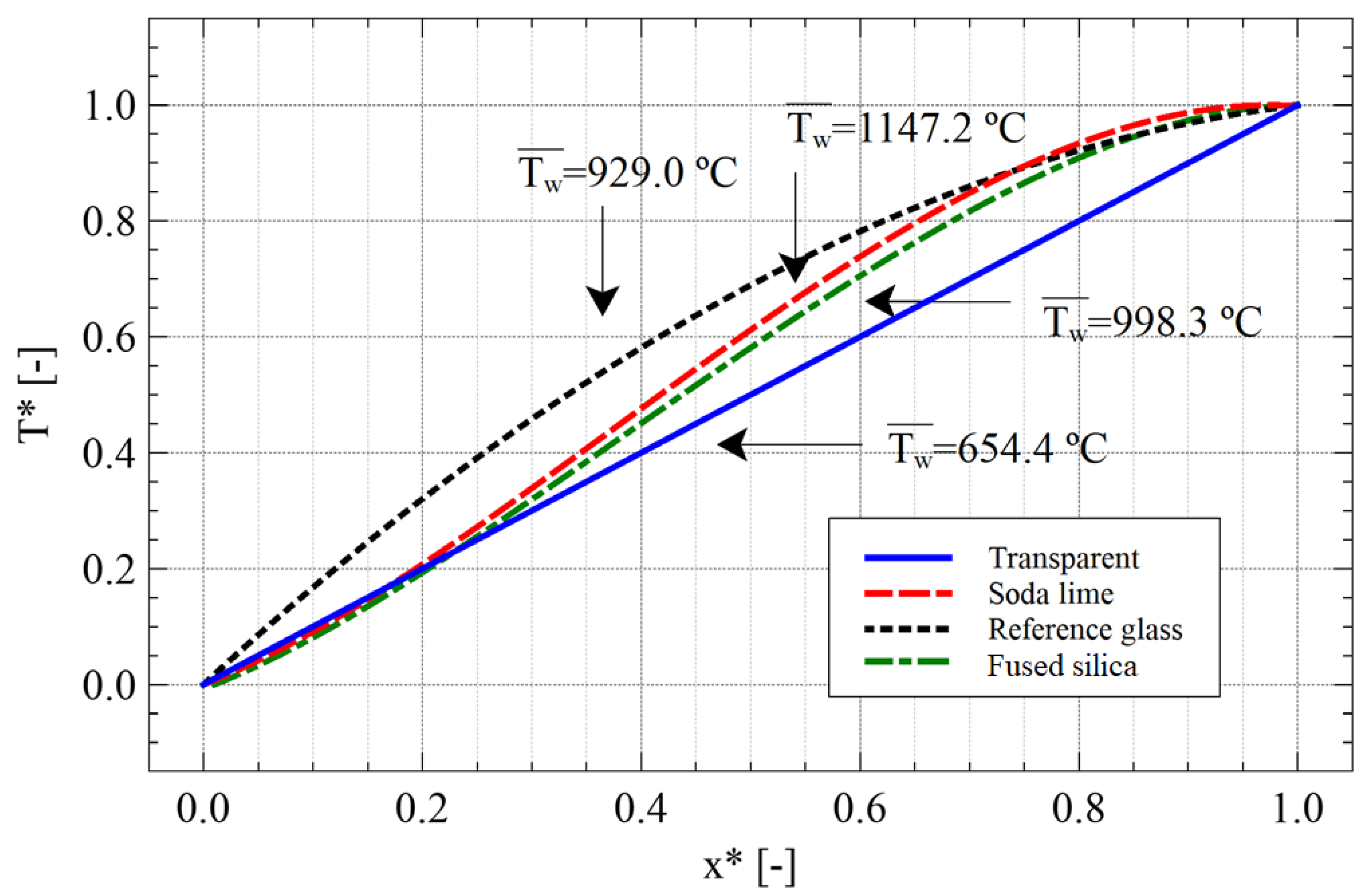
4.4.1. Glass Material—Radiative Properties
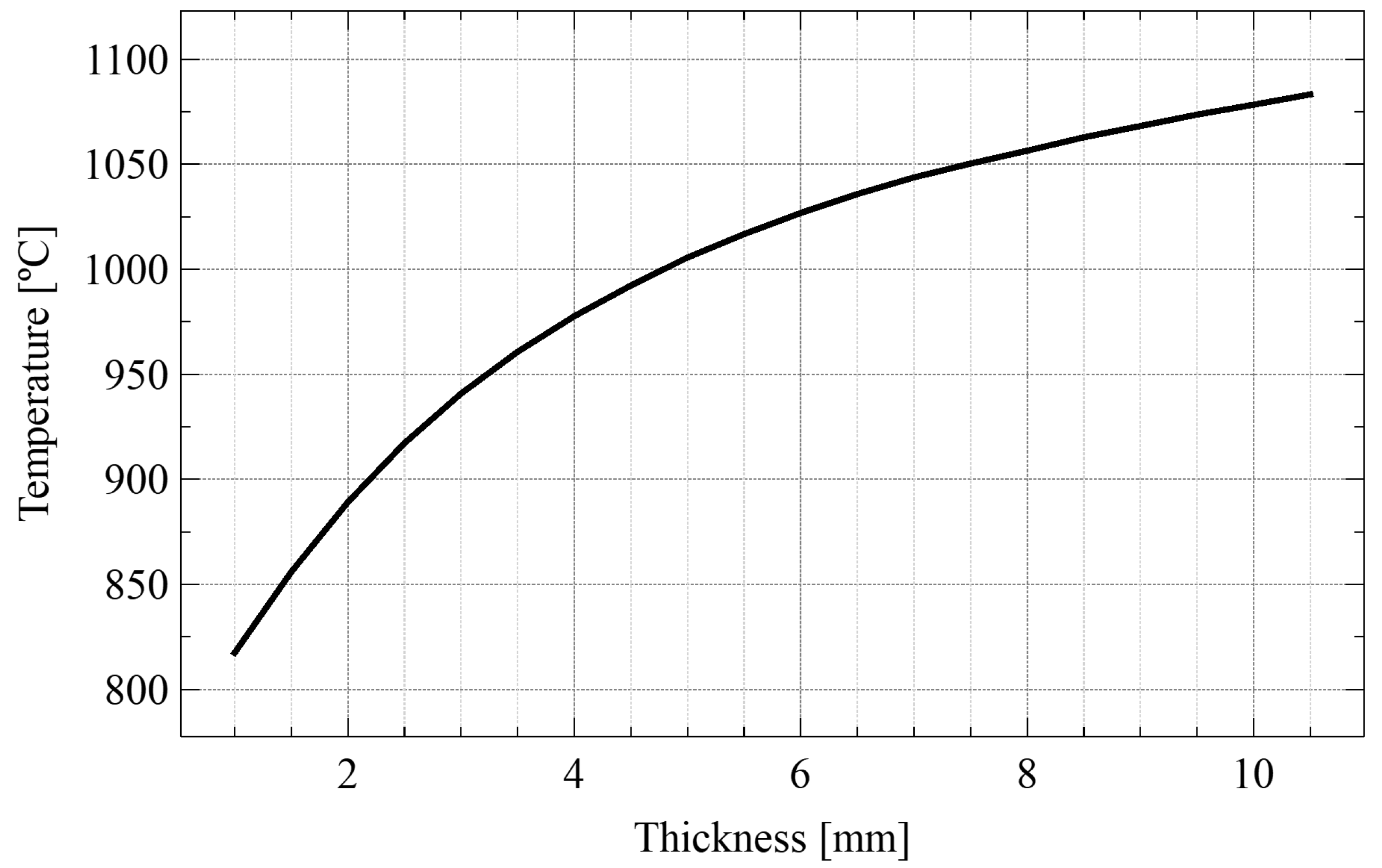
4.4.2. Window Thickness
4.4.3. Burner Radiation Efficiency
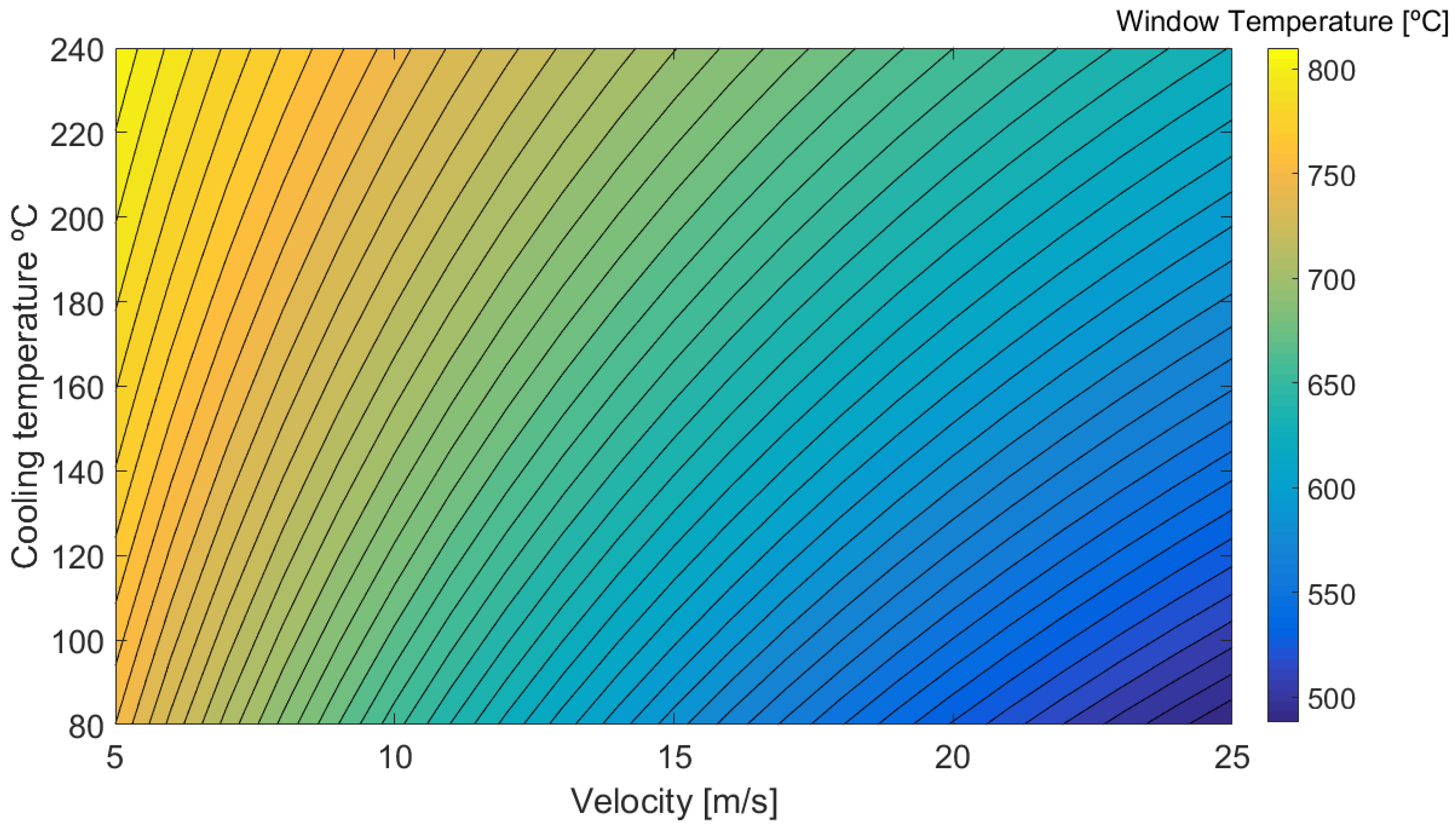
4.4.4. Cooling Gas Temperature and Velocity
4.5. 3D Full Oven
4.5.1. Operating Conditions
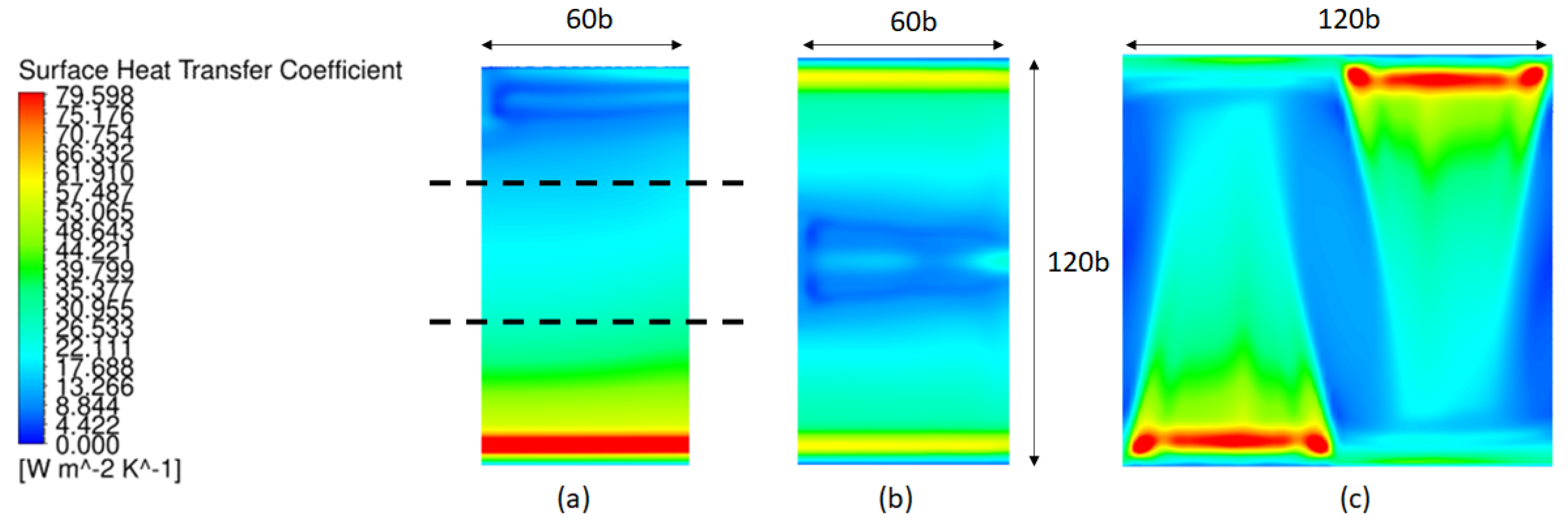
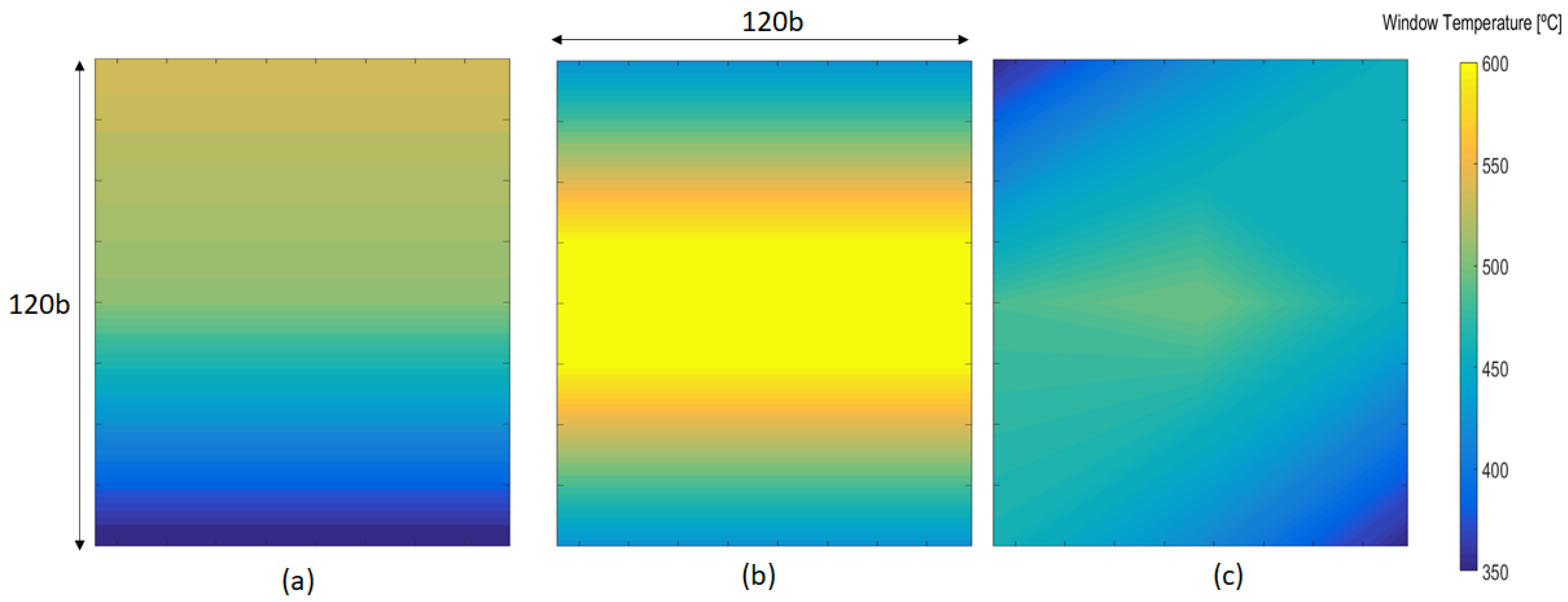
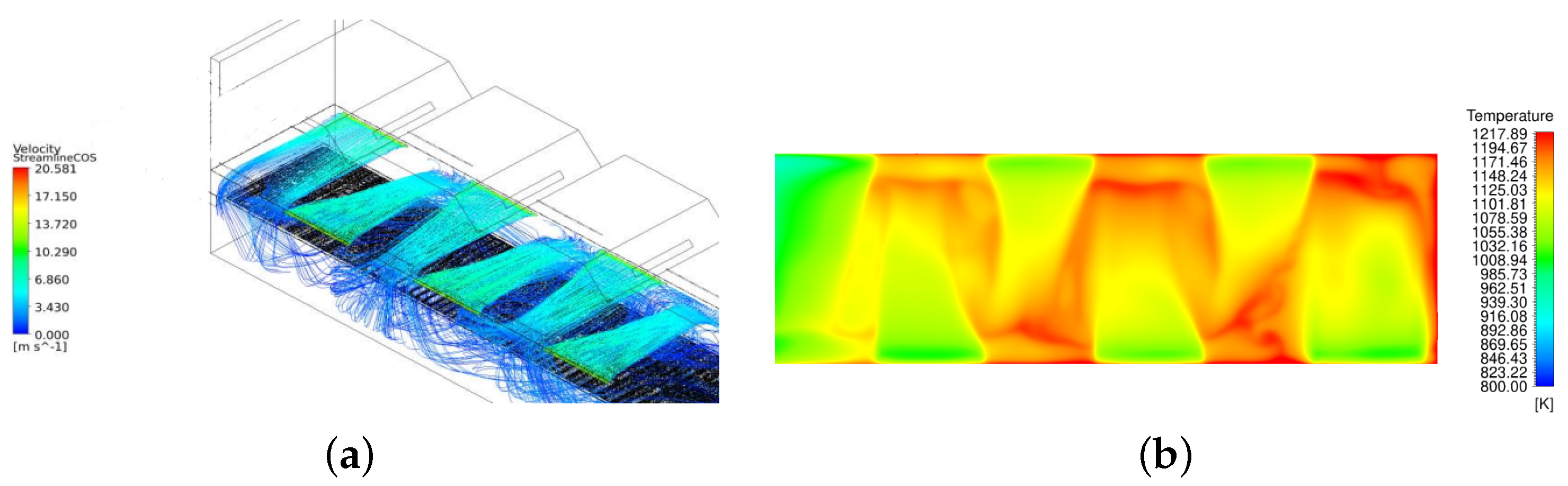
4.5.2. Hydrothermal Performance Characterization
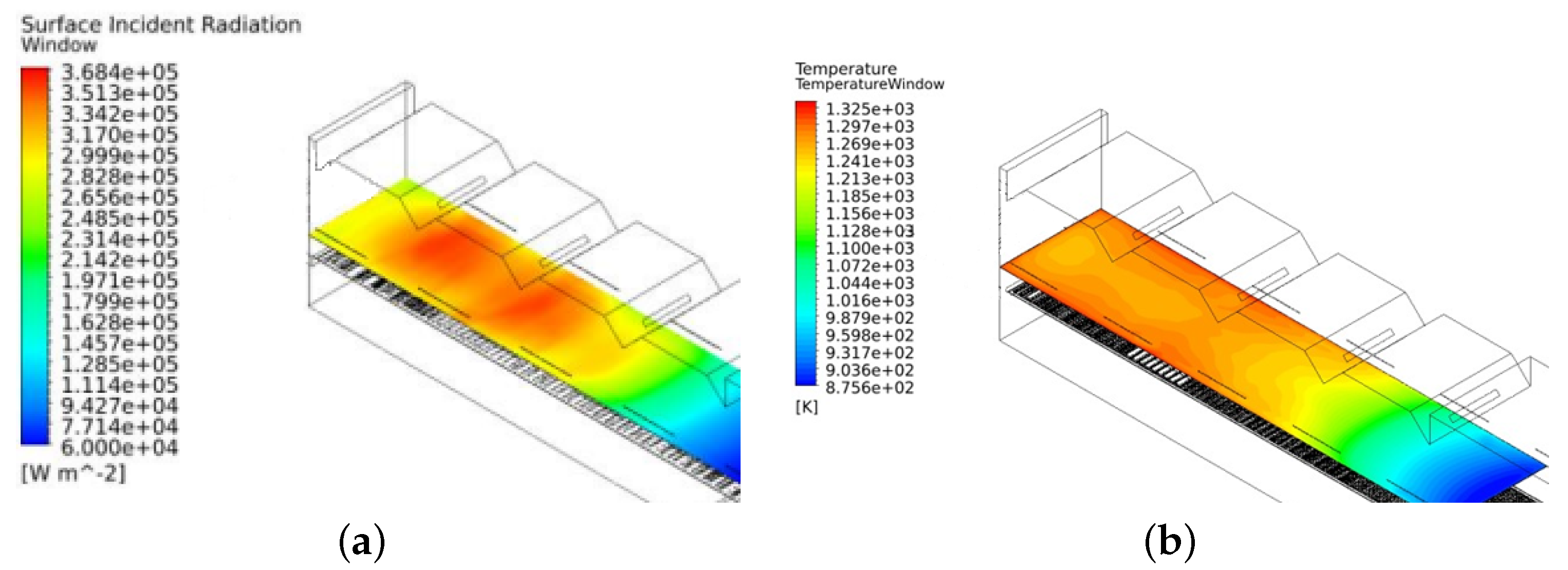
No Active Cooling
Cooling—COS
Cooling—RBS
4.5.3. Active Cooling Process Optimisation
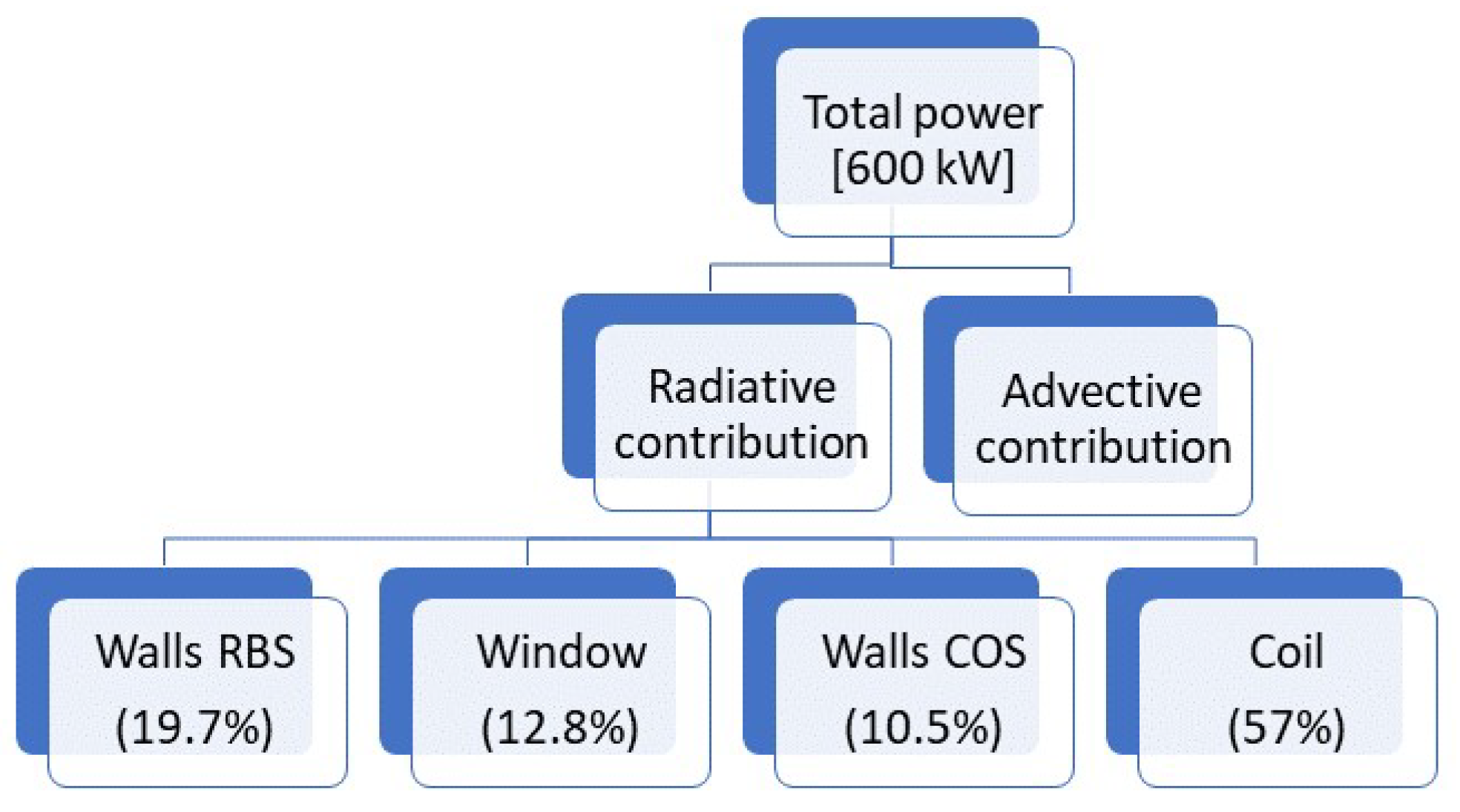
Global Energy Budget
Optimised Variables and Constraints
5. Conclusions
- Different turbulence RANS high- and low-Re models were validated to predict wall jets with heat transfer. The SST and SA turbulence models with low-Re modeling are recommended for satisfactory predictions of a quantity like the heat transfer coefficient. Numerical simulations in a simplified 3D model were performed to obtain the heat transfer correlations associated to the wall jet cooling.
- The previous information (heat transfer correlations) is integrated in the developed 1D/3D conduction-radiation model with discrete ordinates method to predict and analyse the thermal behaviour of the glass. The 1D model was verified and a parametric study was conducted to detect the influence of glass thickness, radiative properties, cooling jets conditions such as temperature, velocity, and arrangement strategies.
- Three different cooling strategies are analysed and compared. Cooling with opposite jets leads to less heat removed from the window and higher gradient of temperature due to the stagnation region at the middle of the glass plate and resulting fountain flow. There is no significant difference on the total heat removed from the window by considering cooling from one-side or in alternated scheme.
- The average glass temperature predicted by 1D/3D model is in satisfactory agreement with full 3D curing furnace numerical simulation results, identifying the high window temperature for the situation without cooling (889 °C/929 °C) and impact of cooling in COS (758 °C/830 °C). The results for 3D full numerical simulations with cooling inside RBS show as well, the 1D/3D model, a negligible difference between different cooling schemes (one-sided or alternated).
- The optimisation procedure based on the developed 1D/3D model leads to the cooling control conditions (minimum cooling power) for selected safety requirements (maximum window temperature and gradient of temperature). The demand of cooling power increases when there is a need of a lower maximum temperature. The optimisation shows that the use of the heat exchanger inside COS is more relevant for energetic purposes. The optimisation dictates Scheme C to be the best choice for the scheme of cooling, and Scheme A for °C.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Sander, J. Coil Coating; Vincentz Network: Hanover, Germany, 2014. [Google Scholar]
- Kolås, T.; Røyset, A.; Grandcolas, M.; Lacau, A. Solar energy materials and solar cells cool coatings with high near infrared transmittance for coil coated aluminium. Sol. Energy Mater. Sol. Cells 2019, 196, 94–104. [Google Scholar] [CrossRef]
- Joudi, A.; Svedung, H.; Cehlin, M.; Rönnelid, M. Reflective coatings for interior and exterior of buildings and improving thermal performance. Appl. Energy 2013, 103, 562–570. [Google Scholar] [CrossRef]
- Johansson, K.; Johansson, M. A model study on fatty acid methyl esters as reactive diluents in thermally cured coil coating systems. Prog. Org. Coat. 2006, 55, 382–387. [Google Scholar] [CrossRef]
- Gupta, G.; Pathak, S.; Khanna, A. Anticorrosion performance of eco-friendly silane primer for coil coating applications. Prog. Org. Coat. 2012, 74, 106–114. [Google Scholar] [CrossRef]
- Choi, J.W.; Chun, W.P.; Oh, S.H.; Lee, K.J.; Kim, S.I. Experimental studies on a combined near infrared (NIR) curing system with a convective oven. Prog. Org. Coat. 2016, 91, 39–49. [Google Scholar] [CrossRef]
- Mabbett, I.; Elvins, J.; Gowenlock, C.; Jones, P.; Worsley, D. Effects of highly absorbing pigments on near infrared cured polyester/melamine coil coatings. Prog. Org. Coat. 2013, 76, 1184–1190. [Google Scholar] [CrossRef]
- Mabbett, I.; Elvins, J.; Gowenlock, C.; Glover, C.; Jones, P.; Williams, G.; Worsley, D. Addition of carbon black NIR absorber to galvanised steel primer systems: Influence on NIR cure of polyester melamine topcoats and corrosion protection characteristics. Prog. Org. Coat. 2014, 77, 494–501. [Google Scholar] [CrossRef]
- Keramiotis, C.; Katoufa, M.; Vourliotakis, G.; Hatziapostolou, A.; Founti, M. Experimental investigation of a radiant porous burner performance with simulated natural gas, biogas and synthesis gas fuel blends. Fuel 2015, 158, 835–842. [Google Scholar] [CrossRef]
- Maznoy, A.; Kirdyashkin, A.; Pichugin, N.; Zambalov, S.; Petrov, D. Development of a new infrared heater based on an annular cylindrical radiant burner for direct heating applications. Energy 2020, 204, 117965. [Google Scholar] [CrossRef]
- Energy Efficient Coil Coating Process, European Project. Available online: https://www.spire2030.eu/ecco (accessed on 22 February 2022).
- Kim, K.M.; Moon, H.; Park, J.S.; Cho, H.H. Optimal design of impinging jets in an impingement/effusion cooling system. Energy 2014, 66, 839–848. [Google Scholar] [CrossRef]
- Cho, H.H.; Goldstein, R.J. Heat (Mass) Transfer and Film Cooling Effectiveness With Injection Through Discrete Holes: Part I—Within Holes and on the Back Surface. J. Turbomach. 1995, 117, 440–450. [Google Scholar] [CrossRef]
- Huber, A.M.; Viskanta, R. Effect of jet-jet spacing on convective heat transfer to confined, impinging arrays of axisymmetric air jets. Int. J. Heat Mass Transf. 1994, 37, 2859–2869. [Google Scholar] [CrossRef]
- Förthmann, E. On turbulent jet propagation (in German: Über turbulente Strahlausbreitung). Ingenieur-Archiv 1934, 5, 42–54. [Google Scholar] [CrossRef]
- Glauert, M.B. The wall jet. J. Fluid Mech. 1956, 1, 625. [Google Scholar] [CrossRef]
- Launder, B.E.; Rodi, W. The turbulent wall jet measurements and modeling. Annu. Rev. Fluid Mech. 1983, 15, 429–459. [Google Scholar] [CrossRef]
- George, W.K.; Abrahamsson, H.; Eriksson, J.; Karlsson, R.I.; Lofdahl, L.; Wosnik, M. A similarity theory for the turbulent plane wall jet without external stream. J. Fluid Mech. 2000, 425, 367–411. [Google Scholar] [CrossRef]
- Rostamy, N.; Bergstrom, D.J.; Deutscher, D.; Sumner, D.; Bugg, J.D. An experimental study of a plane turbulent wall jet using LDA. ICHMT Digit. Libr. 1998, 25, 50–60. [Google Scholar]
- Dejoan, A.; Leschziner, M.A. Large eddy simulation of a plane turbulent wall jet. Phys. Fluids 2005, 17, 025102. [Google Scholar] [CrossRef]
- Ahlman, D.; Brethouwer, G.; Johansson, A.V. Direct numerical simulation of a plane turbulent wall-jet including scalar mixing. Phys. Fluids 2007, 19, 065102. [Google Scholar] [CrossRef]
- Banyassady, R.; Piomelli, U. Interaction of inner and outer layers in plane and radial wall jets. J. Turbul. 2015, 16, 460–483. [Google Scholar] [CrossRef]
- Dakos, T.; Verriopoulos, C.A.; Gibson, M.M. Turbulent flow with heat transfer in plane and curved wall jets. J. Fluid Mech. 1984, 145, 339. [Google Scholar] [CrossRef]
- AbdulNour, R.S.; Willenborg, K.; McGrath, J.J.; Foss, J.F.; AbdulNour, B.S. Measurements of the convection heat transfer coefficient for a planar wall jet: Uniform temperature and uniform heat flux boundary conditions. Exp. Therm. Fluid Sci. 2000, 22, 123–131. [Google Scholar] [CrossRef]
- Godi, S.C.; Abraham, S.; Pattamatta, A.; Balaji, C. Evaluation of candidate strategies for the estimation of local heat transfer coefficient from wall jets. Exp. Heat Transf. 2020, 33, 40–63. [Google Scholar] [CrossRef]
- Godi, S.C.; Pattamatta, A.; Balaji, C. Heat transfer from a single and row of three dimensional wall jets—A combined experimental and numerical study. Int. J. Heat Mass Transf. 2020, 159, 119801. [Google Scholar] [CrossRef]
- Naqavi, I.Z.; Tyacke, J.C.; Tucker, P.G. A numerical study of a plane wall jet with heat transfer. Int. J. Heat Fluid Flow 2017, 63, 99–107. [Google Scholar] [CrossRef][Green Version]
- ANSYS Inc. ANSYS Fluent User’s Guide, Release 17.2; ANSYS Inc.: Canonsburg, PA, USA, 2016. [Google Scholar]
- Chen, Y.; Lei, D. Analysis and numerical simulation research of the heating process in the oven. J. Therm. Sci. 2016, 25, 454–459. [Google Scholar] [CrossRef]
- Al-Nasser, M.; Fayssal, I.; Moukalled, F. Numerical simulation of bread baking in a convection oven. Appl. Therm. Eng. 2021, 184, 116252. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2013; Volume 5317, pp. 724–746. [Google Scholar]
- Modest, M.F. Radiative Heat Transfer, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Rek, Z.; Rudolf, M.; Zun, I. Application of CFD simulation in the development of a new generation heating oven. Stroj. Vestn. 2012, 58, 134–144. [Google Scholar] [CrossRef]
- Fidalgo, M.F.; Mendes, M.A.; Pereira, J.M. An automated method for efficient multi-parametric analysis of porous radiant burner performance. Int. J. Therm. Sci. 2021, 163, 106851. [Google Scholar] [CrossRef]
- Abrahamsson, H.; Johansson, B.; Lofdahl, L. A turbulent plane two-dimensional wall-jet in a quiescent surrounding. Eur. J. Mech. B Fluids 1994, 13, 533–556. [Google Scholar]
- Nguyen, T.D.; Souad, H. PIV measurements in a turbulent wall jet over a backward-facing step in a three-dimensional, non-confined channel. Flow Meas. Instrum. 2015, 42, 26–39. [Google Scholar] [CrossRef]
- Nait Bouda, N.; Schiestel, R.; Amielh, M.; Rey, C.; Benabid, T. Experimental approach and numerical prediction of a turbulent wall jet over a backward facing step. Int. J. Heat Fluid Flow 2008, 29, 927–944. [Google Scholar] [CrossRef]
- Tsai, Y.; Hunt, J.; Nieuwstadt, F.; Westerweel, J.; Gunasekaran, B. Effect of Strong External Turbulence on a Wall Jet Boundary Layer. Flow Turbul. Combust. 2007, 79, 155–174. [Google Scholar] [CrossRef]
- Talukdar, P.; Mishra, S.C. Analysis of conduction-radiation problem in absorbing, emitting and anisotropically scattering media using the collapsed dimension method. Int. J. Heat Mass Transf. 2002, 45, 2159–2168. [Google Scholar] [CrossRef]
- Zuckerman, N.; Lior, N. Jet impingement heat transfer: Physics, correlations, and numerical modeling. Adv. Heat Transf. 2006, 39, 565–631. [Google Scholar]
- Martin, H. Heat and mass transfer between impinging gas jets and solid surfaces. Adv. Heat Transf. 1977, 13, 1–60. [Google Scholar]
- Rubin, M. Optical properties of soda lime silica glasses. Sol. Energy Mater. 1985, 12, 275–288. [Google Scholar] [CrossRef]
- Fraas, L.; Minkin, L.; Avery, J.; Ferguson, L.; Samaras, J. Spectral control development for thermophotovoltaics. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 0323–0327. [Google Scholar] [CrossRef]
- Johansson, P.S.; Anderson, H.I. Direct numerical simulation of two opposing wall jets. Phys. Fluids 2005, 17, 055109. [Google Scholar] [CrossRef]
- Arabia, S. A numerical study of the flow and heat- transfer characteristics of an impinging laminar slot-jet including crossflow effects. Int. J. Heat Mass Transf. 1992, 35, 2501–2513. [Google Scholar]
- The MathWorks Inc. Global Optimisation Toolbox; The MathWorks Inc.: Natick, MA, USA, 2020. [Google Scholar]


| RBS | COS | |||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| 0.0048 | 0.0058 | 0.0037 | 0.0077 | 0.0088 | 0.0087 | |
| 0.838 | 0.795 | 0.867 | 0.819 | 0.800 | 0.784 | |
| Design and Operating Conditions—Input Parameters | |||||||
|---|---|---|---|---|---|---|---|
| Modeling | Number of points | 100 | COS | Convection coefficient, [] | 10 | ||
| DO model | S4 | Surrounding temperature, [K] | 700 | ||||
| Burner | Radiative efficiency, [-] | 0.3 | Window | Number of wavelength bands | 3 | ||
| Emissivity, [-] | 0.9 | Wavelength range, [] | 0–5 | 5–6.3 | 6.3–25 | ||
| Gas temperature, [K] | 1340 | Spectral absorption coefficient, k [] | 7.2 | 228.9 | 973.7 | ||
| Gas velocity, [] | 1.975 | Spectral index of refraction, [-] | 1.69 | 1.58 | 1.31 | ||
| Coil | Surface temperature, [K] | 407.15 | Thickness, L [mm] | 2 | |||
| Emissivity, [-] | 0.31 | Thermal conductivity, [] | 8 | ||||
| Number of Bands | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| Wavelength range, | 0–25 | 0–5.7 | 5.7–25 | 0–5 | 5–6.3 | 6.3–25 |
| Absorption coeff., | 458.66 | 17.68 | 907.95 | 7.15 | 228.91 | 973.71 |
| Index of refraction, [-] | 1.51 | 1.68 | 1.34 | 1.69 | 1.58 | 1.31 |
| Avg window temp., [°C] | 931.0 | 982.8 | 889.2 | |||
| Radiative Efficiency, [-] | 0.3 | 0.4 | 0.5 |
|---|---|---|---|
| Burner surface temperature, [°C] | 1364 | 1477 | 1572 |
| Avg window temperature, [°C] | 889.2 | 967.7 | 1035.1 |
| Requirement | Optimised Variables | Objective Function | |||||
|---|---|---|---|---|---|---|---|
| [°C] | [°C] | [m/s] | [°C] | [m/s] | Scheme | Power [kW] | |
| 800 | 62 | 327 | 5.0 | 427 | 10.2 | A | 28.9 |
| 750 | 133 | 327 | 5.0 | 427 | 21.7 | C | 30.7 |
| 700 | 140 | 327 | 5.0 | 384 | 25.0 | C | 32.0 |
| 650 | 152 | 327 | 5.0 | 319 | 25.0 | C | 33.3 |
| 600 | 159 | 327 | 5.0 | 265 | 25.0 | C | 34.5 |
| 550 | 143 | 80 | 5.5 | 250 | 25.0 | C | 65.0 |
| 500 | 129 | 80 | 11.6 | 250 | 25.0 | C | 110.9 |
| 450 | 115 | 80 | 18.6 | 250 | 25.0 | C | 153.0 |
| 400 | Not feasible | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neno, R.J.F.; Dias, B.S.; Navalho, J.E.P.; Pereira, J.C.F. Numerical Simulation of Heat Removal from a Window Slab Partition of a Radiative Coil Coating Oven. Energies 2022, 15, 2080. https://doi.org/10.3390/en15062080
Neno RJF, Dias BS, Navalho JEP, Pereira JCF. Numerical Simulation of Heat Removal from a Window Slab Partition of a Radiative Coil Coating Oven. Energies. 2022; 15(6):2080. https://doi.org/10.3390/en15062080
Chicago/Turabian StyleNeno, Rodrigo J. F., Beatriz S. Dias, Jorge E. P. Navalho, and José C. F. Pereira. 2022. "Numerical Simulation of Heat Removal from a Window Slab Partition of a Radiative Coil Coating Oven" Energies 15, no. 6: 2080. https://doi.org/10.3390/en15062080
APA StyleNeno, R. J. F., Dias, B. S., Navalho, J. E. P., & Pereira, J. C. F. (2022). Numerical Simulation of Heat Removal from a Window Slab Partition of a Radiative Coil Coating Oven. Energies, 15(6), 2080. https://doi.org/10.3390/en15062080







