Next Article in Journal
Characterization of Two-Phase Flow from Pore-Scale Imaging Using Fractal Geometry under Water-Wet and Mixed-Wet Conditions
Previous Article in Journal
Certainty-Equivalence-Based Sensorless Robust Sliding Mode Control for Maximum Power Extraction of an Uncertain Photovoltaic System
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 15
Issue 6
10.3390/en15062043
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modulated Predictive Control to Improve the Steady-State Performance of NSI-Based Electrification Systems

by
Mustafa Gokdag
Department of Electrical-Electronics Engineering, Karabuk University, Karabuk 78050, Turkey
Energies 2022, 15(6), 2043; https://doi.org/10.3390/en15062043
Submission received: 26 January 2022 / Revised: 23 February 2022 / Accepted: 9 March 2022 / Published: 10 March 2022
(This article belongs to the Section F: Electrical Engineering)
Browse Figures
Versions Notes

Abstract

:
This paper presents a modulated model predictive control (M2PC) strategy for a nine-switch inverter (NSI) based electrification system to improve the steady-state performance. The model predictive control method has gained significant interest due to its straightforward structure. However, the traditional finite control set model predictive control (FCS-MPC) imposes a high computational burden that is problematic in practical applications. This prevents reaching the high sampling frequencies due to an excessive increase in algorithm run-time. Selecting a low sampling frequency causes an unpleasant distortion in the control variable or poor power quality. An M2PC method for the NSI is proposed in this work to remove this trade-off. One zero vector and two active vectors are selected by evaluating a cost function for each allowed switching state of the NSI. The duty cycles of these vectors are calculated by assessing the cost function employing current error terms. An optimized sequence of these vectors is applied to the system that operates with the fixed-modulation frequency. Thus, an improvement in power quality (reduced harmonics with a better spectral content) with a lower sampling frequency is achieved. The computational burden rate (CBR) on the processor is reduced. These enhancements were proved by simulation and experimental studies. The comparison work was conducted to highlight the advantages of the proposed method over the other techniques reported in the literature. The proposed M2PC method was verified on a lab-scale NSI prototype driving two induction machines. The machine torques and speeds are well regulated, and the quality of the stator current is improved.

1. Introduction

In power electronics applications, reduced count topologies have been receiving attention due to their compact structures [1]. Among these topologies, the nine-switch inverter (NSI) is a promising solution for various applications. The NSI has the capability of driving two three-phase ac loads using fewer switching devices. The key benefit of using reduced count topology such as NSI is a remarkable reduction in the power stage’s size, volume, and weight [2,3].
The NSI topology and its application were first introduced in [3]. Following the initial emergence of the NSI, some studies focused on developing appropriate control and modulation techniques for NSI [4,5,6,7,8,9,10,11]. Several other research groups investigated the improved modulation strategies that reduce the thermal stress of the NSI by taking into account conduction and switching losses [12,13,14,15]. Another research consideration was to derive the NSI topologies combined with impedance source networks to increase the inverter’s voltage utilization [16,17].
The NSI has been used as a core topology in various power energy conversion applications such as an integrated motor drive and battery charger [18], a DFIG based wind power system [19], and grid-connected hybrid ac/dc energy sources [20]. Apart from these applications, various control strategies for the NSI have been reported in the literature to control the two independent three-phase loads/machines or a single six-phase load [2,3,7,17,21,22,23,24,25,26]. These strategies are mostly combined versions of vector control and suitable pulse-width modulation (PWM) techniques. Among the control strategies for NSI-driven two separate three-phase loads, the model predictive control (MPC) method is a desirable feedback strategy to regulate multi-phase/load dynamics [27,28]. The MPC uses the explicit system model (including the converter and load models) to predict the control variables [29]. In ac drive applications, the control variables are usually electromechanical torque, rotor speed, and stator phase currents [30,31]. The MPC predicts the control variables for each feasible control input and assesses the multi-objective cost function. The control input that offers minimum cost value is picked and applied to the system. In general, the MPC method is a very promising control strategy in ac drive applications due to the ease of including control objectives, control constraints, and system limitations [32,33,34]. However, there are several drawbacks with the traditional finite control set (FCS) MPC method—poor steady-state performance and high computational burden. In particular, the FCS-MPC drastically suffers from poor steady-state performance due to the lack of a modulator stage, especially for systems with small electrical time constants requiring that high sampling frequency is mandatory to achieve acceptable power quality [35,36]. Since the MPC requires a high number of calculations using a system model, it becomes challenging for existing DSP technologies to complete these calculations at high sampling frequencies [37]. Moreover, the MPC produces the gate signals directly, and the system has a non-fixed switching frequency. The variable operating frequency causes variable switching harmonics with a wide-range frequency spectrum. In this case, shaping the frequency contents is not possible, resulting in uncontrolled harmonics and complicated filter designs. Therefore, the control variables (output variables) suffer from unwanted distortions and harmonics. Thus the steady-state performance of the traditional MPC is degraded due to the uncontrolled switching frequency [38,39]. Several strategies have been proposed to improve the steady-state performance, including a switching frequency control term in the cost function [40]. However, penalizing the switching effort in the objective function does not noticeably reduce the total of harmonic distortions (THD). The most common technique to attain a good steady-state performance is to reduce the sampling period. To reduce the sampling period effectively reduces the THD in control variables; however, the practical systems usually have a limitation on computational power. The sampling period must be long enough to cover the control algorithm execution time. Because of this, the energy conversion operation is not always possible with a lower sampling period [41].
The exciting strategy to improve the steady-state performance of the traditional MPC is to include the modulator in the closed-loop design. This strategy is called modulated model predictive control (M2PC), which considers the dedicated switching pattern to generate the gate pulses [42,43,44,45,46,47]. The M2PC operates under a fixed switching frequency, and the frequency harmonics are distributed around the switching frequency and its harmonics. Hence the unwanted variable frequency contents imposed by the variable system frequency are eliminated. The controlled switching frequency remarkably reduces the THD in control variables and enhances the steady-state characteristics. The essential advantage of the M2PC is that superior steady-state performance can be achieved even at a lower sampling frequency [39]. This is quite a vital point since a decent steady-state performance can be obtained without increasing the sampling frequency. In some practical applications, a sampling frequency constraint (limitation on the maximum value of the sampling frequency) has been considered. Hence, achieving steady-state goals at a lower sampling frequency is a good capability of the feedback strategies [48]. Various M2PC techniques have been reported for the ac drive applications in the literature. In [43], an M2PC technique that utilizes virtual voltage vectors to reduce the low-order harmonics in the phase currents has been proposed for a five-phase voltage source inverter (VSI). The interesting implementation of the M2PC method with optimal switching time and reduced complexity [46] has been proposed for a neutral point clamped (NPC) three-phase inverter. Another research paper [47] investigated a modulated-type predictive control that uses optimal two voltage vectors and associated duty cycles to reduce the phase current THD. In [49], a modulated predictive current control with properly adopted space-vector PWM technique was presented to control an asymmetrical dual three-phase induction motor driven by a six-phase VSI. Although the reported strategies are useful for traditional topologies such as VSI and NPC, no M2PC type strategy has been presented to control the NSI topology.
Motivated from the above discussion, a novel M2PC strategy is proposed in this paper to generate the required gate signals for the NSI in order to regulate the dynamics of two induction motors. Essentially, the proposed method can be used for any energy conversion system employing the NSI as far as the system model is available. The proposed method reduces the undesired harmonics and offers better steady-state performance even at a lower sampling frequency. The stator current THD is noticeably reduced to improve the power quality. The independent induction motors are controlled under different loading conditions, and the demanded torque and speed profiles are maintained. The primary benefit of the proposed method is that steady-state torque ripple and stator current THD are reduced. The torque ripples degrade the mechanical performance of the induction motors and negatively affect the rotor speed. Due to these unpleasant aspects, improving the reference trajectory tracking performance is crucial for a better energy conversion process. The main contributions of the paper are summarized as follows:
  • A novel M2PC method is proposed to control two induction motors fed by a nine-switch inverter. The proposed strategy effectively controls the independent motors and provides a robust operation without undesired interactions.
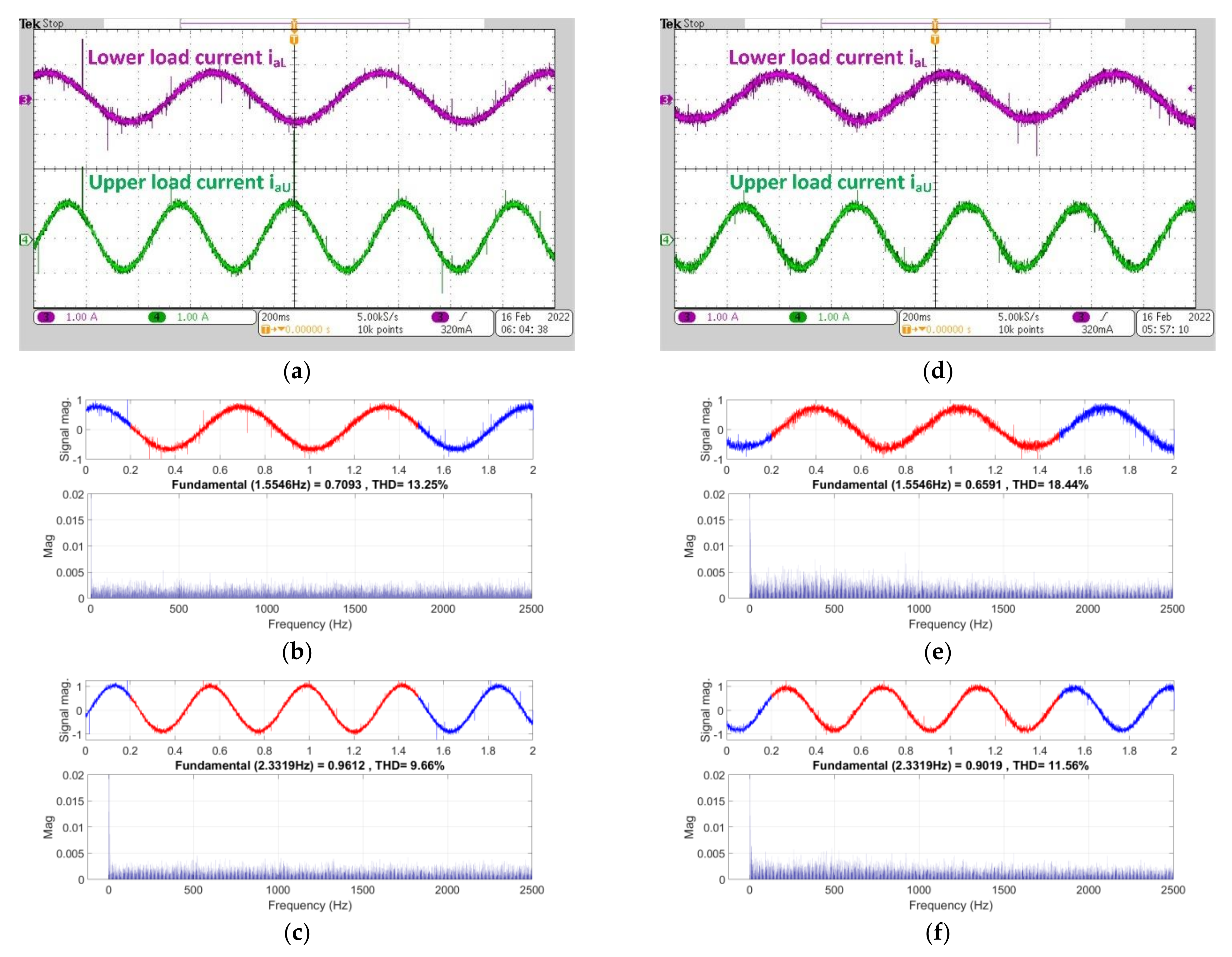
  • The steady-state performance is significantly improved by reducing the stator current THD and the torque ripple. The problem with the steady-state performance of the MPC strategy is solved by the proposed method without increasing the sampling frequency, and the stator current THD is reduced approximately by 50% at low current levels. The THD reduction in stator current also decreases the associated losses. The torque ripple is reduced by 25% under steady-state conditions.
  • The proposed method is then experimentally validated using a real hardware NSI prototype. The mathematical framework of the proposed method is proved under different real test scenarios. Different experimental cases are considered to demonstrate the effectiveness of the proposed method. Furthermore, comprehensive comparison works are performed between the proposed method and the traditional MPC strategy. Quantitative comparison results are provided to prove the advantages of the proposed method over the conventional MPC.

2. Nine-Switch Inverter Basics

The Nine Switch Inverter (NSI) was built by merging two VSIs to decrease the number of required switching devices by 25% compared to the conventional system (two parallel inverters). Using fewer switching devices in the power stage design increases the effective power density. The NSI can drive two independent three-phase loads or a single six-phase load (with galvanically isolated two three-phase windings), see Figure 1. The NSI consists of three switches in each leg, and the middle switches S4, S5, and S6 are shared by the upper and lower load stages [3]. During operation, only two switches in each leg of the NSI are allowed to conduct simultaneously, and this constraint can be defined as:
S i + S i + 3 + S i + 6 = 2   with   i ∈ 1 , 2 , 3
Thus, short-circuiting of the dc bus is prevented while the current continuity of the inductive loads is guaranteed. So, there are three possible switching states for each leg and a total of 27 allowed switching states for NSI, as listed in Table 1. According to Table 1, the switching states of NSI can be divided into three groups. While Group I is the group with zero vectors for both load stages, Group II has zero vectors for one of the loads and active vectors for the other, while Group III consists of active vectors for both loads [9].
The transition between the input and output quantities of the NSI is performed via the matrices given in (2) and (3):
T U = S 1 S 2 S 3
T L = 1 − S 7 1 − S 8 1 − S 9
The NSI leg voltages for the upper and lower load stages can be defined as:
V U = V D C T U T
V L = V D C T L T
where V U = V a U V b U V c U T , V L = V a L V b L V c L T . The three-phase load voltages for a balanced system can be calculated by using (6) and (7):
V a U n V b U n V c U n = V D C 3 T U T = V D C 3 2 − 1 − 1     − 1 2 − 1     − 1 − 1 2 S 1 S 2 S 3
V a L n ′ V b L n ′ V c L n ′ = V D C 3 T L T = V D C 3 2 − 1 − 1     − 1 2 − 1     − 1 − 1 2 1 − S 7 1 − S 8 1 − S 9

3. Induction Machine Model

3.1. Dynamic Model of the Induction Machine

The dynamic model of an induction machine in the d-q reference frame, that rotates with a synchronous angular speed of ω g and an instantaneous angle of θ with respect to the fixed-frame, can be defined with the set of Equations (8)–(13) [50]. Here, the electrical state variables are direct (d) and quadrature (q) axis stator current components and d–q axis rotor flux components. The dynamic model of the current components can be defined as:
d i s d d t = − L r R s + L m 2 τ r σ L s L r i s d + ω g i s q + L m τ r σ L s L r Ψ r d + v s d σ L s + L m σ L s L r ω r Ψ r q
d i s q d t = − L r R s + L m 2 τ r σ L s L r i s q − ω g i s d + L m τ r σ L s L r Ψ r q + v s q σ L s − L m σ L s L r ω r Ψ r d
where stator, rotor, and mutual inductances are denoted with Ls, Lr, and Lm, respectively, the stator and rotor winding resistances are designated with Rs and Rr, the term τ r = L r / R r is the rotor time constant, and the leakage constant is calculated by σ = L r L s − L m 2 / L r L s . The electrical angular speed, ω r , is calculated by ω r = p ω m in rad/s where p is the number of pole pairs, ω m is the mechanical angular speed of the rotor.
The dynamic model of the rotor flux is defined as:
d Ψ r d d t = L m τ r i s d − Ψ r d τ r + ω g − ω r Ψ r q
d Ψ r q d t = L m τ r i s q − Ψ r q τ r − ω g − ω r Ψ r d
The rotor electrical angular speed modelling the mechanical dynamic is given by:
d ω r d t = 3 2 p L m J L r Ψ r d i s q − Ψ r q i s d − B J ω r − T L J
where TL and B designate the load torque and the friction factor, respectively, and the inertia is symbolized with J. The angle of the synchronously rotating frame, θ, is defined as:
d θ d t = ω g

3.2. Discrete-Time Model of the Induction Machine

The model predictive control requires the system model in the discrete-time domain. The Forward Euler discretization technique defined by (14) can be applied to obtain discrete-time expressions of continuous differential equations [51,52].
d β t d t = β k + 1 − β k T s
where TS implies the sampling period and the time duration between the two consecutive samplings. The discrete-time domain model of the stator current components is obtained as in (15) and (16):
i s d k + 1 = 1 − L r R s + L m 2 τ r σ L s L r T s i s d k + T s ω g k i s q k + L m τ r σ L s L r Ψ r d k + T s L m σ L s L r ω r k Ψ r q k + v s d k σ L s
i s q k + 1 = 1 − L r R s + L m 2 τ r σ L s L r T s i s q k + T s − ω g k i s d k + L m τ r σ L s L r Ψ r q k − T s L m σ L s L r ω r k Ψ r d k − v s q k σ L s
The discrete-time model to estimate rotor flux components is obtained as in (17) and (18):
Ψ r d k = Ψ r d k − 1 1 − T s τ r + T s L m τ r i s d k − 1 + ω g k − 1 − ω r k − 1 Ψ r q k − 1
Ψ r q k = Ψ r q k − 1 1 − T s τ r + T s L m τ r i s q k − 1 − ω g k − 1 − ω r k − 1 Ψ r d k − 1
The discrete-time models for the angle of the synchronously rotating frame θ(k) with respect to fixed-frame and the synchronous angular speed ωg(k − 1) are obtained as in (19) and (20) respectively.
θ k = θ k − 1 + T s ω g k − 1
ω g k − 1 = L m τ r Ψ r d i s q k − 1 + ω r k − 1 = L m τ r Ψ r d ∗ i s q k − 1 + ω r k − 1

4. Control Strategy

The schematic representation of the overall control strategy is shown in Figure 2. The IFOC is adopted to generate the reference signals for the IM’s speed and torque regulation, and it operates as an outer loop. The proposed M2PC method is cascaded to IFOC to generate the required gate signals and serves as an inner loop.

4.1. Reference Generation in Indirect Field-Oriented Control of IM

One of the vector control-based methods used in machine drivers is field orientation. In this technique, the electromagnetic torque of a three-phase ac motor can be regulated similar to the control of a separately excited dc motor. However, for an induction machine, it is necessary to take into account the slip between the magnetic fields of the stator and rotor, which varies with the load torque. The stator current is split into two current components, i.e., torque- and flux-producing components, to achieve a similar torque control strategy to that of a dc motor. If the rotor flux vector is aligned with the d-axis of the reference frame, then Ψ r q = 0 is achieved for the steady-state. Thus, the torque expression (21) becomes more straightforward, and the electrical variables slowly change [53].
T e = 3 2 p L m L r Ψ r d i s q − Ψ r q i s d
In order to convert the stator currents measured in the fixed reference frame into the variables in the synchronously rotating reference frame, the angle between these two frames must be found. Aligning the rotor flux with d-axis yields Ψ r q = d Ψ r q / d t = 0 for the steady-state. By replacing these terms in (11) with zero, the slip angular frequency ω s l is obtained as in (22). This slip is considered as in (20) to estimate the synchronous angular speed ω g k − 1 . Then, the Ψ r q   asymptotically reaches zero.
ω s l = ω g − ω r = L m τ r Ψ r d i s q
Replacing the Ψ r q with zero in (10) yields (23) for the steady-state, and the field orientation is attained.
Ψ r d = L m i s d
Therefore, the magnetizing current component i s d regulates the rotor flux. Even though the reference value of Ψ r d ∗ , which is set as a constant, is substituted in Equations (20) and (22) instead of the instantaneous value of Ψ r d , the rotor flux can be aligned with the d-axis. Then, the reference for the magnetizing current component is calculated by:
i s d ∗ = Ψ r d ∗ L m
In this case, like that of a separately excited dc motor, the torque term becomes in proportion to the torque current component, i s q , as in (25).
T e = K t i s q
where K t is the torque constant and K t = 3 2 p L m Ψ r d ∗ L r . The reference torque value T e ∗ in speed control applications can be generated from the speed error using a proportional-integral (PI) compensator. Then, the torque current reference, i s q ∗ is calculated by (26).
i s q ∗ = T e ∗ / K t

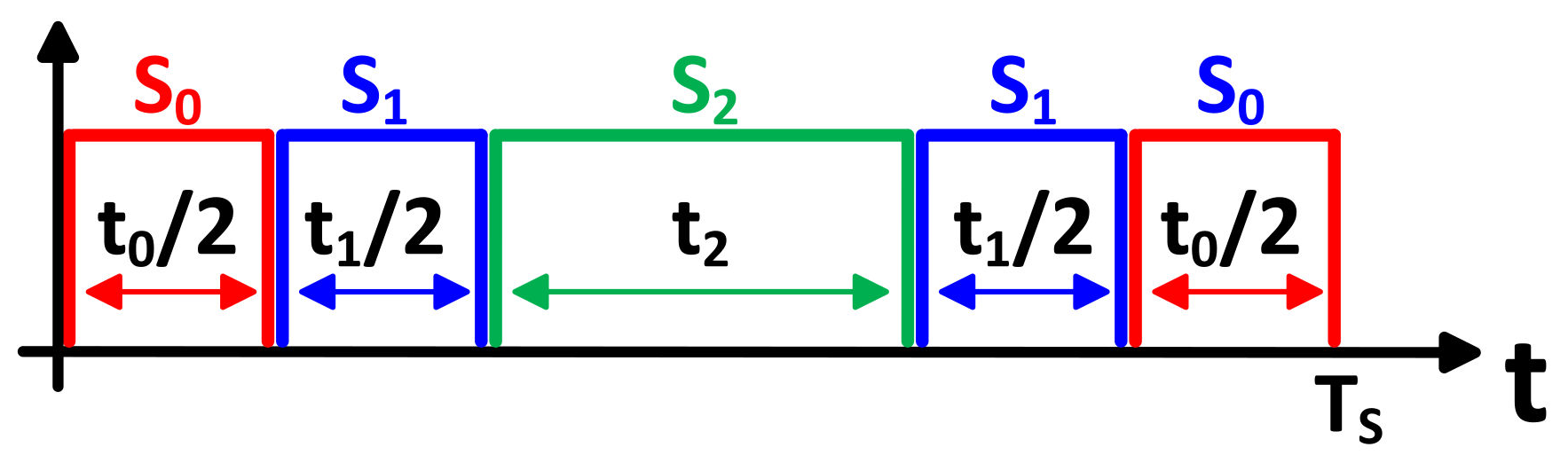
4.2. Proposed Modulated Model Predictive Control of NSI

The proposed modulated model predictive control operates as follows: the controller samples the stator currents, dc bus voltage, and mechanical speeds. First, the stator currents measured in the abc frame are converted into the d-q frame variables. Then, the future values of the d-q frame currents are predicted for each candidate switching vector of the NSI by using (15) and (16). The errors, which are the difference between the reference values and the predicted currents, are evaluated in the cost function (27). Since the cost function employs the variables in the same order of magnitude, there is no need for a weighting factor to control the different objectives properly.
g = ∑ j = d , q i s j _ u p ∗ − i s j _ u p 2 + ∑ j = d , q i s j _ l o w ∗ − i s j _ l o w 2
In modulation techniques like the space-vector strategy developed for the voltage-source inverter, specific switching vectors (two active vectors + one zero vector) are applied to synthesize the sinusoidal voltage/current during the switching period. In this study, a modulated model predictive control strategy is proposed for the NSI. In Algorithm 1, the procedure to select the optimum switching vectors used during the one switching cycle is summarized. Accordingly, one of the zero vectors from Group I of Table 1 is selected as the zero vector, S0. Since the switching states of Group I produce the same voltages, thus the same cost, for the load stages, the index of ‘for loop’ is started from 3 to eliminate the repeatedly calculated same cost. Hence, the cost calculated according to (27) is stored as g0. The vectors that provide the lowest two costs from the remaining vectors sw4–sw27 are considered g1 and g2, and the corresponding switching vectors are kept as S1 and S2. As can be observed from Algorithm 1, there is no need to determine the sector of the space vector by optimizing an additional cost function. The proposed technique differs from traditional M2PC methods with this feature. The next step is to calculate the duty cycles d 0 , d 1 , and d 2 for each of these switching states S0, S1, and S2. The sum of the duty cycles over a single switching cycle must be equal to 1 as stated by (28).
d 0 + d 1 + d 2 = 1
Algorithm 1 The routine for selecting the best two switching states and calculating the associated duty cycles
 1: for i = 3:27
 2:  calculate cost: Equation (27)
 3:  if (i = = 3) then
 4:   g0 = cost
 5:  else
 6:   if (cost < g1) then
 7:    g2 = g1
 8:    g1 = cost
 9:    index_of_g2 = index_of_g1
10:   index_of_g1 = i
11:  elseif (cost < g2) then
12:   g2 = cost
13:   index_of_g2 = i
14:  end if
15:   end if
16: end for
17: calculate duty cycles; d0, d1, d2: Equation (30)
18: S0 = [1 1 1; 0 0 0; 1 1 1]
19: S1 = sw (:, :, index_of_g1)
20: S2 = sw (:, :, index_of_g2)
21: if (sum(abs(S0−S1)) > sum(abs(S0−S2))) then
22:   temp_1 = S1
23:   S1 = S2
24:   S2 = temp_1
25:   temp_2 = d1
26:   d1 = d2
27:   d2 = temp_2
28: end if
Their allocation over the switching cycle is determined as the reciprocal of the corresponding cost by (29):
d 0 = k g 0   , d 1 = k g 1   , d 2 = k g 2
Simultaneously solving (28) and (29) yields (30), which allows calculation of the associated duty cycle for each vector.
d 0 = T s g 1 g 2 g 0 g 1 + g 0 g 2 + g 1 g 2 d 1 = T s g 0 g 2 g 0 g 1 + g 0 g 2 + g 1 g 2 d 2 = T s g 0 g 1 g 0 g 1 + g 0 g 2 + g 1 g 2
To complete the proposed modulated model predictive approach, there is a need for an optimized switching vector sequence. With a proper algorithm, the number of switches that change their states simultaneously can be reduced. Thus, this decreases the EMI radiation due to high dv/dt and di/dt at the switched nodes. The routine to determine the optimum switching sequence is shown between rows 18–28 of Algorithm 1. For this aim, the switching state sw3 is stored as S0, and it is the only zero vector allowed in Group I. Then, S1 and S2 are compared with S0, and the vector with the minimum number of state changes for the switches is kept as S1. So, the other one is held as S2. The allocation of the switching states over the switching cycle and the optimum switching sequence is shown in Figure 3. When Table 1 is closely inspected, the states between sw16 and sw21, which have the on-state condition for the whole middle switches and require more switching to change their state, can be removed from the switching state table to optimize the switching sequence further. Accordingly, the proposed modulation strategy can also be operated with a reduced number of switching states, and the computational burden on the processor can be reduced.

5. Comparison with Other Control Strategies

The proposed control strategy was compared with hysteresis-based [21], predictive torque control (PTC) [27], and FCS-MPC [31] techniques regarding the total harmonic distortion in stator currents, torque variance, and execution time. All methods were simulated in Simulink with the parameters listed in Table 2.
The sampling time TS is selected as 100 μs for all methods to make a fair comparison. Accordingly, the modulation frequency for the proposed method is 10 kHz. Table 3 tabulates the THD values for the upper and lower load stages for two test scenarios. The upper motor speed reference is 40 rad/s in these scenarios, while the lower motor speed reference is 25 rad/s. Each motor operates with a no-loading condition (0 N·m) for scenario I. The magnitude of the fundamental current component for the upper motor is 1.37 A @ 12.866 Hz. The magnitude of the fundamental current component for the lower motor is 1.37 A @ 8.055 Hz. For scenario II, the upper motor operates with a load torque of 3 N·m and the lower motor operates with a load torque of 4 N·m, and the magnitude of the fundamental current component for the upper motor is 2.22 A @ 14.928 Hz, the magnitude of the fundamental current component for the lower motor is 2.66 A @ 10.880 Hz. According to Table 3, the proposed M2PC method significantly reduces THD values compared to other methods.
Each method’s controller block execution time is measured with the “Run and Time” menu in Matlab. The increment in the execution time for the proposed method is acceptable to decrease the THD values. The execution times reported in the table are the run time measured in Matlab for a single loop of each algorithm. These are used to compare fairly each algorithm’s computational burden and are not actual execution times for the code blocks that implement the algorithms on a real DSP or FPGA.
To better show their performance in terms of computational burden, the figure of merit “Computational Burden Rate (CBR)” can be defined as:
CBR = execution   time sampling   period
The proposed method can be compared with the FCS-MPC technique in CBR. For this aim, the sampling frequency of the FCS-MPC can be increased until it provides similar performance in THD compared to the proposed method. Accordingly, the CBR for the proposed method is less than that of the FCS-MPC, as listed in Table 4.
To prove the improved steady-state performance of the proposed M2PC method, it was compared with the FCS-MPC in torque ripples. The upper motor’s electromagnetic torque is plotted in Figure 4 for both control methods, and it is observed that the ripple in the torque is less for the M2PC. It can also be concluded from Figure 4 that the transient responses for both techniques are similar as they follow the same trajectories during the start-up and load step transitions.
Figure 5 compares the spectral content of the stator currents of the lower motor for scenario II when the NSI is controlled with both M2PC and FCS-MPC methods. The M2PC has a spectral content with reduced order of magnitudes since it is a strategy with a fixed modulation frequency. In comparison, FCS-MPC has a significant spectral content covering broadband since it is a strategy without a modulator stage and operates with a variable frequency operation. As a result, the EMI problems are reduced, and the required filter designs are much simpler for the proposed modulated technique.
The traditional FCS-MPC employs only one voltage vector during the sampling period and results in large current ripple and variable switching frequency since the same voltage vector can be applied during the consecutive sampling periods. Conversely, the proposed method considers the switching sequence of three voltage vectors during each sampling period. Therefore, an average voltage vector is achieved for the proposed strategy. The use of an average voltage vector offers a reduction in current ripple, also resulting in torque ripple. The other problem of the variable switching frequency operation of the FCS-MPC is that the spectral harmonic is randomly distributed. Hence, estimating the harmonic contents in the frequency spectrum is quite challenging, and selecting the filter parameter is not a trivial task. On the other hand, the proposed method uses the modulator to generate the gate signals. Therefore, the major parts of the harmonic content are located on the order of the switching frequency and its harmonics. Because of all these reasons, the estimation of the filter parameter is much easier for the proposed control technique, and the benefit of using a modulator is fully exploited [39].

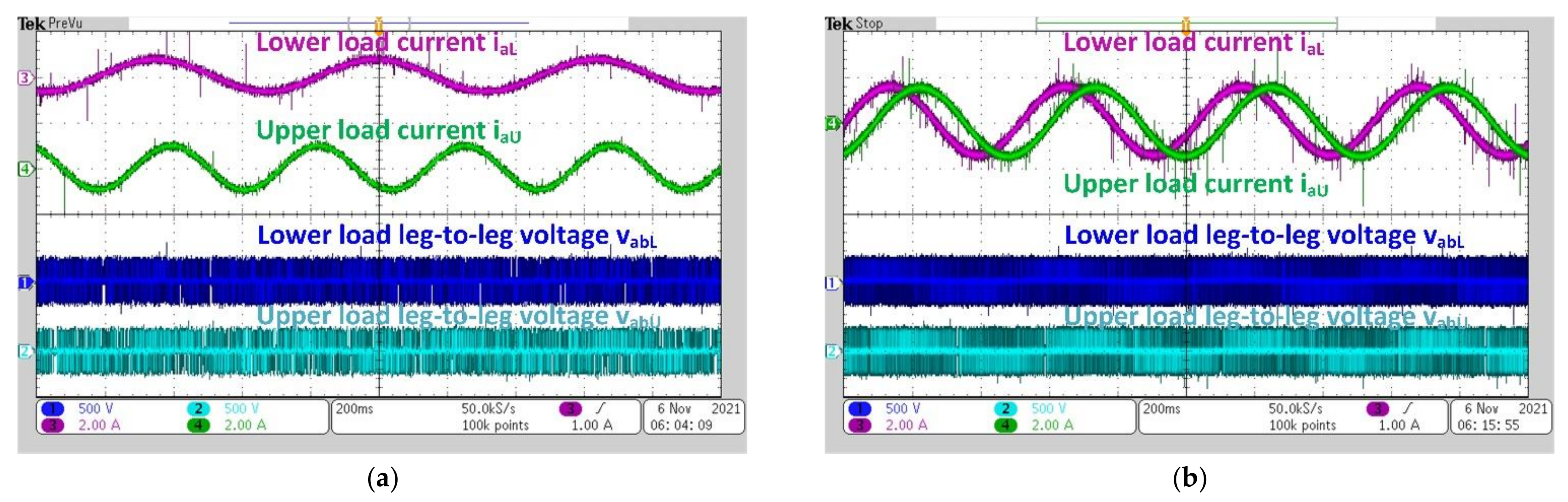
6. Experimental Results

In this section, experimental results are presented to show that the proposed control strategy successfully achieves the independent operation of two induction machines driven by NSI. The test bench built in the laboratory is shown in Figure 6, and the system parameters are tabulated in Table 2. In the test bench, the separately excited compound dc machines, whose shafts are mechanically coupled to IMs, are used to test the proposed control strategy under different loading conditions. The incremental encoders with 5000 ppr are also coupled to the shafts of the IMs to measure the rotor mechanical speeds. The proposed M2PC method, covering the whole process from reading the speeds of IMs and ADCs (for measuring the currents and the dc bus voltage) to generating the required gate signals, is embedded into the Altera Cyclone IV FPGA (Terasic DE0-Nano Board).
The proposed M2PC method is first tested to observe its potency to synthesize the sinusoidal currents. Figure 7a shows the phase currents (iaU and iaL) with different frequencies for both output stages, whereas Figure 7b shows the phase currents (iaU and iaL) when they are forced to have the same frequency with a phase displacement of 60°. The leg-to-leg voltages (vabU and vabL) are also shown in Figure 7 for consistency. It can be concluded from the results in Figure 7 that the proposed M2PC can be used to drive both the two three-phase loads independently and a single symmetric/asymmetric six-phase load.
Figure 8 presents the oscilloscope screenshots showing the experimentally measured one-phase current waveforms of the lower and upper load stages for the cases where the NSI is controlled with the proposed M2PC method and conventional FCS-MPC. Both techniques are operated with a sampling period of 100 μs. THD values and spectral contents of the currents obtained for both methods are also compared in Figure 8. The proposed modulated-based technique reduces the THD values and spectral content compared to FCS-MPC.
The proposed method was also experimentally verified in terms of speed reference tracking performance regarding the start-up and applied speed reference ramp transitions. Both machines’ speeds (ωm_U and ωm_L) and stator currents (iaU and iaL) are measured and recorded through a digital oscilloscope. Figure 9a presents the measured waveforms for start-up transition. In this test, the speed references of both machines are initially set to 0 rad/s. Afterwards, a user-defined button is used to initiate the operation. Then the reference speeds, which are driven to the controller’s comparator blocks, reach their final values with a ramp function having a slope of 10 rad/s per 1 s. The upper machine speed reference is set to 25 rad/s while the lower machine is set to 40 rad/s. According to the waveforms in Figure 9a, each machine follows its speed reference, and the stator currents for both machines are synthesized to correspond to their speed profiles. Figure 9b presents the experimental waveforms when the reference speeds are varied with a ramp function having a slope of 10 rad/s per 0.2 s. In this test scenario, a user-defined button triggers the speed reference transition from 25 rad/s to 35 rad/s for the upper machine and from 40 rad/s to 20 rad/s for the lower machine. As observed from Figure 9, each machine tracks its speed profile without any interaction between them.
The proposed controller is also tested under incremental load torque steps. Figure 10a presents the experimental waveforms when both IMs are loaded at the same time instant. In this test, the upper machine speed reference is set to 25 rad/s, with 40 rad/s for the lower machine. As observed from Figure 10a, the speed waveforms have deviations from their reference trajectories at the time instant of the load torque step. Subsequently, the outer loop compensates the speed error and increases the reference for the torque-current component i s q ∗ to meet the new torque demand. To investigate the response of the proposed control strategy to the asymmetric loading, one of the IM is exposed to the torque load step while the other one is not. According to the results presented in Figure 10b,c, the proposed controller can independently regulate both the machines’ speeds and torques without cross-coupling and unwanted interaction.

7. Conclusions

In this study, a modulated model predictive control is proposed for the first-time for the NSI to improve the steady-state performance. Driving the two separate IMs with NSI was chosen as a case study to verify the proposed approach. Indeed, the proposed M2PC approach can be applied to any energy conversion system employing NSI as far as the discrete-time model of the system can be derived. The comparative simulation results for NSI driven two IMs prove that the proposed M2PC reduces the THD in stator currents and ripples in the electromagnetic torque of the machine compared to other methods. Moreover, the modulated approach allows the controller to operate with lower sampling frequencies. Thus, the computational burden rate (CBR) on the processor, which must be completed within a particular sampling period, is reduced. Especially for energy conversion systems with lower electrical time constants (systems with lower inductive characteristics), the M2PC is not an option but a necessity since the synthesized sinusoidal currents require very challenging sampling periods (around 10–20 μs) to obtain acceptable THD levels. The M2PC also provides a spectral content with reduced order of magnitudes for stator current compared to the FCS-MPC technique, and the required filter design becomes simpler. The proposed M2PC was experimentally verified on a lab-scale NSI prototype, and the experimental results prove that the independent operation of two separate IMs can be achieved with the proposed M2PC.

Funding

This research received no external funding.

Acknowledgments

The proposed modulated predictive control strategy was experimentally verified using the hardware prototype developed under the Grant 117E769 which was supported by The Scientific and Technological Research Council of Turkey (TUBITAK). The author also wishes to thank Ozan Gulbudak who was project coordinator while developing the above-mentioned project.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Sathik, J.; Aleem, S.H.E.A.; Shalchi Alishah, R.; Almakhles, D.; Bertilsson, K.; Bhaskar, M.S.; Fernandez Savier, G.; Dhandapani, K. A Multilevel Inverter Topology Using Diode Half-Bridge Circuit with Reduced Power Component. Energies 2021, 14, 7249. [Google Scholar] [CrossRef]
  2. Kominami, T.; Fujimoto, Y. Inverter with Reduced Switching-Device Count for Independent AC Motor Control. In Proceedings of the IECON 2007—33rd Annual Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 5–8 November 2007; pp. 1559–1564. [Google Scholar]
  3. Kominami, T.; Fujimoto, Y. A Novel Nine-Switch Inverter for Independent Control of Two Three-Phase Loads. In Proceedings of the 2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 23–27 September 2007; pp. 2346–2350. [Google Scholar]
  4. Dabour, S.M.; Abdel-Khalik, A.S.; Ahmed, S.; Massoud, A.M. A Family of Discontinuous PWM Strategies for Quasi Z-Source Nine-Switch Inverters. IEEE Access 2021, 9, 169161–169176. [Google Scholar] [CrossRef]
  5. Pan, L.; Zhang, J.; Zhang, J.; Pang, Y.; Wang, B.; Wang, K.; Xu, D. A Novel Space-Vector Modulation Method for Nine-Switch Converter. IEEE Trans. Power Electron. 2020, 35, 1789–1804. [Google Scholar] [CrossRef]
  6. Li, X.; Qu, L.; Zhang, B.; Zhang, G.; Liao, H. A Simplified Modulation Strategy of Nine-Switch Inverter to Cut Off Half of Switching Modes. IEEE Access 2018, 6, 7254–7261. [Google Scholar] [CrossRef]
  7. Goyal, G.N.; Aware, M.V. Speed sensorless control of multiple induction motor drives with single nine switch inverter. In Proceedings of the 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), Chennai, India, 1–2 August 2017; pp. 3639–3644. [Google Scholar]
  8. Jarutus, N.; Kumsuwan, Y. A Carrier-Based Phase-Shift Space Vector Modulation Strategy for a Nine-Switch Inverter. IEEE Trans. Power Electron. 2017, 32, 3425–3441. [Google Scholar] [CrossRef]
  9. Dehghan, S.M.; Amiri, A.; Mohamadian, M.; Andersen, M.A.E. Modular space-vector pulse-width modulation for nine-switch converters. IET Power Electron. 2013, 6, 457–467. [Google Scholar] [CrossRef] [Green Version]
  10. Gao, F.; Zhang, L.; Li, D.; Loh, P.C.; Tang, Y.; Gao, H. Optimal Pulsewidth Modulation of Nine-Switch Converter. IEEE Trans. Power Electron. 2010, 25, 2331–2343. [Google Scholar] [CrossRef]
  11. Dehnavi, S.M.D.; Mohamadian, M.; Yazdian, A.; Ashrafzadeh, F. Space Vectors Modulation for Nine-Switch Converters. IEEE Trans. Power Electron. 2010, 25, 1488–1496. [Google Scholar] [CrossRef]
  12. Ali, K.; Das, P.; Panda, S.K. A Special Application Criterion of the Nine-Switch Converter with Reduced Conduction Loss. IEEE Trans. Ind. Electron. 2018, 65, 2853–2862. [Google Scholar] [CrossRef]
  13. de Andrade, F.C.; Bradaschia, F.; Limongi, L.R.; Cavalcanti, M.C. A Reduced Switching Loss Technique Based on Generalized Scalar PWM for Nine-Switch Inverters. IEEE Trans. Ind. Electron. 2018, 65, 38–48. [Google Scholar] [CrossRef]
  14. Qin, Z.; Loh, P.C.; Blaabjerg, F. Application Criteria for Nine-Switch Power Conversion Systems with Improved Thermal Performance. IEEE Trans. Power Electron. 2015, 30, 4608–4620. [Google Scholar] [CrossRef]
  15. Qin, Z.; Loh, P.C.; Bahman, A.S.; Blaabjerg, F. Evaluation of current stresses in nine-switch energy conversion systems. IET Power Electron. 2014, 7, 2877–2886. [Google Scholar] [CrossRef]
  16. Dehghan, S.M.; Mohamadian, M.; Yazdian, A. Hybrid Electric Vehicle Based on Bidirectional Z-Source Nine-Switch Inverter. IEEE Trans. Veh. Technol. 2010, 59, 2641–2653. [Google Scholar] [CrossRef]
  17. Pinjala, M.K.; Bhimasingu, R. Improving the DC-Link Utilization of Nine-Switch Boost Inverter Suitable for Six-Phase Induction Motor. IEEE Trans. Transp. Electrif. 2020, 6, 1177–1187. [Google Scholar] [CrossRef]
  18. Diab, M.S.; Elserougi, A.A.; Abdel-Khalik, A.S.; Massoud, A.M.; Ahmed, S. A Nine-Switch-Converter-Based Integrated Motor Drive and Battery Charger System for EVs Using Symmetrical Six-Phase Machines. IEEE Trans. Ind. Electron. 2016, 63, 5326–5335. [Google Scholar] [CrossRef]
  19. Wen, G.; Chen, Y.; Zhong, Z.; Kang, Y. Dynamic Voltage and Current Assignment Strategies of Nine-Switch-Converter-Based DFIG Wind Power System for Low-Voltage Ride-Through (LVRT) Under Symmetrical Grid Voltage Dip. IEEE Trans. Ind. Appl. 2016, 52, 3422–3434. [Google Scholar] [CrossRef]
  20. Liu, X.; Loh, P.C.; Wang, P.; Blaabjerg, F. A Direct Power Conversion Topology for Grid Integration of Hybrid AC/DC Energy Resources. IEEE Trans. Ind. Electron. 2013, 60, 5696–5707. [Google Scholar] [CrossRef]
  21. Gulbudak, O.; Gokdag, M. Dual-Hysteresis Band Control of Nine-Switch Inverter to Control Two Induction Motors. IEEE Trans. Energy Convers. 2021, 1. [Google Scholar] [CrossRef]
  22. Abbache, M.A.; Tabbache, B.; Douida, S.; Benbouzid, M. Direct torque control scheme for nine switches inverter fed two induction motors-based more electric vehicle powertrains. Int. Trans. Electr. Energy Syst. 2021, 31, e13175. [Google Scholar] [CrossRef]
  23. Wei, J.; Zhang, T.; Shi, L.; Zhou, B. Dual-Stator Doubly Salient Electromagnetic Motor Driving System Utilizing a Nine-Switch Converter. IEEE Trans. Ind. Appl. 2019, 55, 1550–1560. [Google Scholar] [CrossRef]
  24. Reusser, C.A. Full-electric ship propulsion, based on a dual nine-switch inverter topology for dual three-phase induction motor drive. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Busan, Korea, 1–4 June 2016; pp. 1–6. [Google Scholar]
  25. dos Santos, E.C.; Jacobina, C.B.; da Silva, O.I. Six-phase machine drive system with nine-switch converter. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 4204–4209. [Google Scholar]
  26. Oka, K.; Matsuse, K. A nine-switch inverter for driving two AC motors independently. IEEJ Trans. Electr. Electron. Eng. 2007, 2, 94–96. [Google Scholar] [CrossRef]
  27. Gulbudak, O.; Gokdag, M. Finite control set model predictive control approach of nine switch inverter-based drive systems: Design, analysis, and validation. ISA Trans. 2021, 110, 283–304. [Google Scholar] [CrossRef]
  28. Barrero, F.; Arahal, M.R.; Gregor, R.; Toral, S.; Durán, M.J. A proof of concept study of predictive current control for VSI-driven asymmetrical dual three-phase AC machines. IEEE Trans. Ind. Electron. 2009, 56, 1937–1954. [Google Scholar] [CrossRef]
  29. Wang, F.; Mei, X.; Rodriguez, J.; Kennel, R. Model predictive control for electrical drive systems-an overview. CES Trans. Electr. Mach. Syst. 2020, 1, 219–230. [Google Scholar] [CrossRef]
  30. Elmorshedy, M.F.; Xu, W.; El-Sousy, F.F.M.; Islam, M.R.; Ahmed, A.A. Recent Achievements in Model Predictive Control Techniques for Industrial Motor: A Comprehensive State-of-the-Art. IEEE Access 2021, 9, 58170–58191. [Google Scholar] [CrossRef]
  31. Gokdag, M.; Gulbudak, O. Dual-model predictive control of two independent induction motors driven by a SiC nine-switch inverter. Int. J. Electron. 2021, 1–19. [Google Scholar] [CrossRef]
  32. Zhang, Y.; Xia, B.; Yang, H.; Rodriguez, J. Overview of model predictive control for induction motor drives. Chin. J. Electr. Eng. 2019, 2, 62–76. [Google Scholar] [CrossRef]
  33. Reyes Dreke, V.D.; Lazar, M. Long-Horizon Nonlinear Model Predictive Control of Modular Multilevel Converters. Energies 2022, 15, 1376. [Google Scholar] [CrossRef]
  34. Chen, G.-J.; Liu, Y.-H.; Cheng, Y.-S.; Pai, H.-Y. A Novel Optimal Charging Algorithm for Lithium-Ion Batteries Based on Model Predictive Control. Energies 2021, 14, 2238. [Google Scholar] [CrossRef]
  35. Vazquez, S.; Acuna, P.; Aguilera, R.P.; Pou, J.; Leon, J.I.; Franquelo, L.G. DC-Link Voltage-Balancing Strategy Based on Optimal Switching Sequence Model Predictive Control for Single-Phase H-NPC Converters. IEEE Trans. Ind. Electron. 2020, 67, 7410–7420. [Google Scholar] [CrossRef]
  36. Zhang, K.; Fan, M.; Yang, Y.; Chen, R.; Zhu, Z.; Garcia, C.; Rodriguez, J. Tolerant Sequential Model Predictive Direct Torque Control of Permanent Magnet Synchronous Machine Drives. IEEE Trans. Transp. Electrif. 2020, 6, 1167–1176. [Google Scholar] [CrossRef]
  37. Sankar, D.; Syamala, L.; Chembathu Ayyappan, B.; Kallarackal, M. FPGA-Based Cost-Effective and Resource Optimized Solution of Predictive Direct Current Control for Power Converters. Energies 2021, 14, 7669. [Google Scholar] [CrossRef]
  38. Zheng, C.; Dragicevic, T.; Majmunovic, B.; Blaabjerg, F. Constrained Modulated Model-Predictive Control of an LC -Filtered Voltage-Source Converter. IEEE Trans. Power Electron. 2020, 35, 1967–1977. [Google Scholar] [CrossRef]
  39. Zucuni, J.P.; Carnielutti, F.; Pinheiro, H.; Norambuena, M.; Rodriguez, J. Cost Function Design for Stability Assessment of Modulated Model Predictive Control. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Virtual, 7–11 September 2020; pp. P.1–P.9. [Google Scholar]
  40. Aguirre, M.; Kouro, S.; Rojas, C.A.; Vazquez, S. Enhanced Switching Frequency Control in FCS-MPC for Power Converters. IEEE Trans. Ind. Electron. 2021, 68, 2470–2479. [Google Scholar] [CrossRef]
  41. Yang, Y.; Wen, H.; Fan, M.; Xie, M.; Peng, S.; Norambuena, M.; Rodriguez, J. Computation-Efficient Model Predictive Control With Common-Mode Voltage Elimination for Five-Level ANPC Converters. IEEE Trans. Transp. Electrif. 2020, 6, 970–984. [Google Scholar] [CrossRef]
  42. Mora, A.; Cardenas-Dobson, R.; Aguilera, R.P.; Angulo, A.; Donoso, F.; Rodriguez, J. Computationally Efficient Cascaded Optimal Switching Sequence MPC for Grid-Connected Three-Level NPC Converters. IEEE Trans. Power Electron. 2019, 34, 12464–12475. [Google Scholar] [CrossRef]
  43. Song, W.; Xue, C.; Wu, X.; Yu, B. Modulated Finite-Control-Set Model Predictive Current Control for Five-Phase Voltage-Source Inverter. IEEE Trans. Transp. Electrif. 2021, 7, 718–729. [Google Scholar] [CrossRef]
  44. Yaramasu, V.; Milev, K.; Dekka, A.; Rivera, M.; Rodriguez, J.; Rojas, F. Modulated Model Predictive Current Control of a Four-Leg Inverter. In Proceedings of the 2020 11th Power Electronics, Drive Systems, and Technologies Conference, Tehran, Iran, 4–6 February 2020. [Google Scholar]
  45. Garcia, C.; Rodriguez, J.; Odhano, S.; Zanchetta, P.; Davari, S.A. Modulated Model Predictive Speed Control for PMSM Drives. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference, Nottingham, UK, 7–9 November 2018. [Google Scholar] [CrossRef]
  46. Wang, Q.; Yu, H.; Li, C.; Lang, X.; Yeoh, S.S.; Yang, T.; Rivera, M.; Bozhko, S.; Wheeler, P. A Low-Complexity Optimal Switching Time-Modulated Model-Predictive Control for PMSM with Three-Level NPC Converter. IEEE Trans. Transp. Electrif. 2020, 6, 1188–1198. [Google Scholar] [CrossRef]
  47. Liu, Y.; Cheng, S.; Zhao, Y.; Liu, J.; Li, Y. Optimal two-vector combination-based model predictive current control with compensation for PMSM drives. Int. J. Electron. 2019, 106, 880–894. [Google Scholar] [CrossRef]
  48. Ayala, M.; Doval-Gandoy, J.; Rodas, J.; Gonzalez, O.; Gregor, R.; Rivera, M. A Novel Modulated Model Predictive Control Applied to Six-Phase Induction Motor Drives. IEEE Trans. Ind. Electron. 2021, 68, 3672–3682. [Google Scholar] [CrossRef]
  49. Gregor, R.; Barrero, F.; Toral, S.L.; Durán, M.J.; Arahal, M.R.; Prieto, J.; Mora, J.L. Predictive-space vector PWM current control method for asymmetrical dual three-phase induction motor drives. IET Electr. Power Appl. 2010, 4, 26. [Google Scholar] [CrossRef] [Green Version]
  50. Jabłoński, M.; Borkowski, P. Correction Mechanism for Balancing Driving Torques in an Opencast Mining Stacker with an Induction Motor and Converter Drive System. Energies 2022, 15, 1282. [Google Scholar] [CrossRef]
  51. González, E.; Sanchis, J.; García-Nieto, S.; Salcedo, J. A Comparative Study of Stochastic Model Predictive Controllers. Electronics 2020, 9, 2078. [Google Scholar] [CrossRef]
  52. Calderón, A.J.; Vivas, F.J.; Segura, F.; Andújar, J.M. Integration of a Multi-Stack Fuel Cell System in Microgrids: A Solution Based on Model Predictive Control. Energies 2020, 13, 4924. [Google Scholar] [CrossRef]
  53. Sevinç, A. Speed Sensorless Control of Induction Motors; University of Bristol: Bristol, UK, 2001. [Google Scholar]
Energies 15 02043 g001 550
Figure 1. Nine-switch inverter-based electrification system.
Figure 1. Nine-switch inverter-based electrification system.
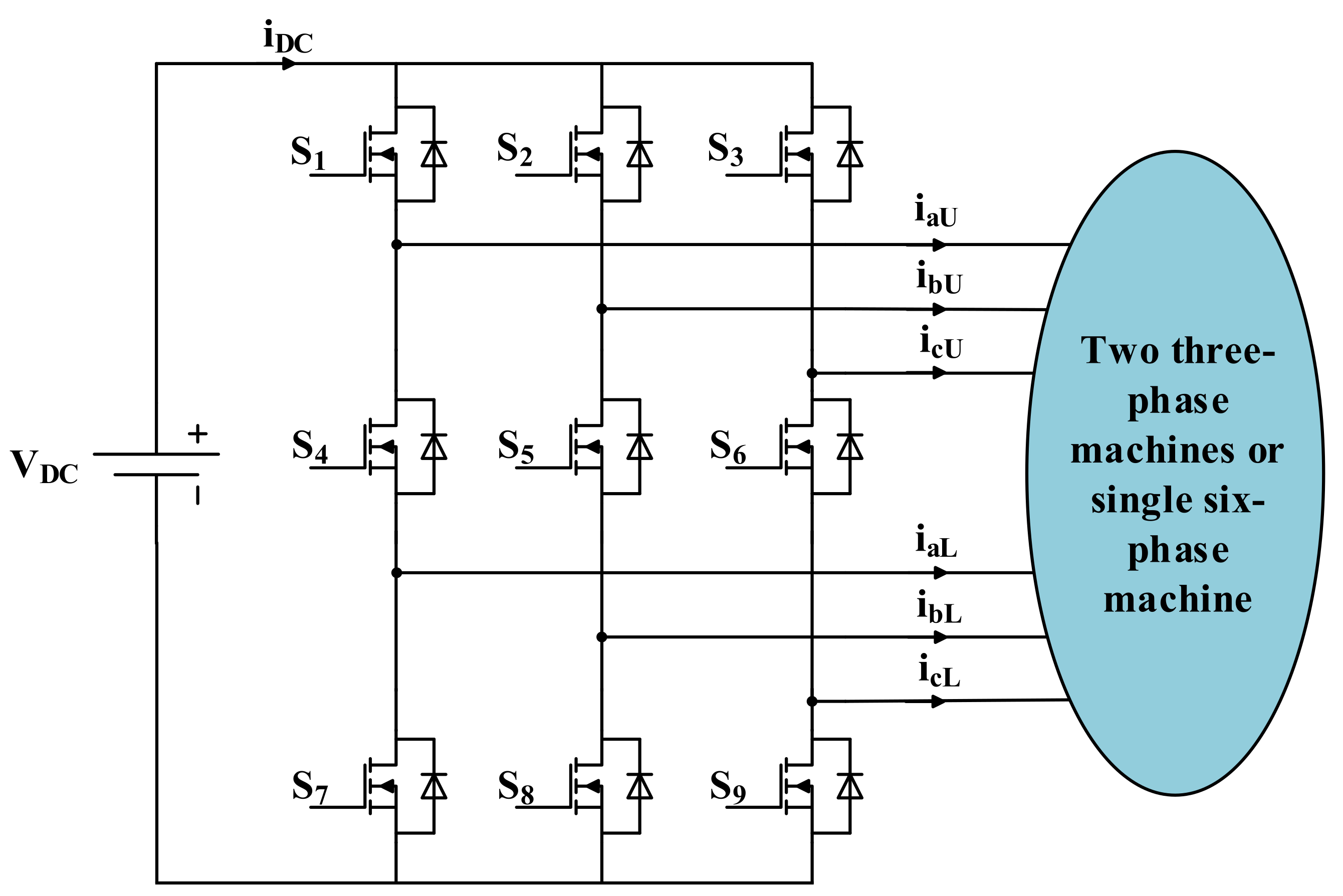
Energies 15 02043 g001
Energies 15 02043 g002 550
Figure 2. The scheme for proposed IFOC based M2PC of the NSI drive system. An FPGA (Altera Cyclone IV) is used to accomplish the proposed control.
Figure 2. The scheme for proposed IFOC based M2PC of the NSI drive system. An FPGA (Altera Cyclone IV) is used to accomplish the proposed control.
Energies 15 02043 g002
Energies 15 02043 g003 550
Figure 3. The allocation of the switching period between the associated switching vectors.
Figure 3. The allocation of the switching period between the associated switching vectors.
Energies 15 02043 g003
Energies 15 02043 g004 550
Figure 4. The comparison of oscillations in the electromagnetic torque for both control methods.
Figure 4. The comparison of oscillations in the electromagnetic torque for both control methods.
Energies 15 02043 g004
Energies 15 02043 g005 550
Figure 5. Comparing the spectral content of stator currents: (a) M2PC; (b) FCS-MPC.
Figure 5. Comparing the spectral content of stator currents: (a) M2PC; (b) FCS-MPC.
Energies 15 02043 g005
Energies 15 02043 g006 550
Figure 6. Overview of the experimental test bench.
Figure 6. Overview of the experimental test bench.
Energies 15 02043 g006
Energies 15 02043 g007 550
Figure 7. Stator currents (iaU and iaL) and leg-to-leg voltages (vabU and vabL) for both output stages. Scope channel 1: Leg-to-leg voltage vabL of the lower stage. Scope channel 2: Leg-to-leg voltage vabU of the upper stage. Scope channel 3: Phase current, iaL, of the lower stage. Scope channel 4: Phase current, iaU, of the upper stage. The current scale is 2 A per division. The voltage scale is 500 V per division. (a) stator current waveforms at different frequencies for both outputs; (b) stator current waveforms for the symmetrical six-phase reference with a phase displacement of 60°.
Figure 7. Stator currents (iaU and iaL) and leg-to-leg voltages (vabU and vabL) for both output stages. Scope channel 1: Leg-to-leg voltage vabL of the lower stage. Scope channel 2: Leg-to-leg voltage vabU of the upper stage. Scope channel 3: Phase current, iaL, of the lower stage. Scope channel 4: Phase current, iaU, of the upper stage. The current scale is 2 A per division. The voltage scale is 500 V per division. (a) stator current waveforms at different frequencies for both outputs; (b) stator current waveforms for the symmetrical six-phase reference with a phase displacement of 60°.
Energies 15 02043 g007
Energies 15 02043 g008 550
Figure 8. Comparison of the experimental current waveforms, THD results, and current spectrums for two control strategies: the left column is for the M2PC, the right column is for the FCS-MPC. (a) Experimental current waveforms for M2PC. (b) THD value and spectrum of the iaL for M2PC. (c) THD value and spectrum of the iaU for M2PC. (d) Experimental current waveforms for FCS-MPC. (e) THD value and spectrum of the iaL for FCS-MPC. (f) THD value and spectrum of the iaU for FCS-MPC.
Figure 8. Comparison of the experimental current waveforms, THD results, and current spectrums for two control strategies: the left column is for the M2PC, the right column is for the FCS-MPC. (a) Experimental current waveforms for M2PC. (b) THD value and spectrum of the iaL for M2PC. (c) THD value and spectrum of the iaU for M2PC. (d) Experimental current waveforms for FCS-MPC. (e) THD value and spectrum of the iaL for FCS-MPC. (f) THD value and spectrum of the iaU for FCS-MPC.
Energies 15 02043 g008
Energies 15 02043 g009 550
Figure 9. Experimental waveforms for speeds (ωm_U and ωm_L) and one-phase stator current (iaU and iaL) for each machine. Scope channel 1: Upper machine speed, ωm_L. Scope channel 2: Lower machine speed, ωm_U. Scope channel 3: Lower machine stator current, iaL. Scope channel 4: Upper machine stator current, iaU. The speed scale is 20 rad/s per division. The current scale is 2 A per division. (a) during start-up transient. (b) during the speed references the machines are varied with a ramp function having a slope of 10 rad/s per 0.2 s.
Figure 9. Experimental waveforms for speeds (ωm_U and ωm_L) and one-phase stator current (iaU and iaL) for each machine. Scope channel 1: Upper machine speed, ωm_L. Scope channel 2: Lower machine speed, ωm_U. Scope channel 3: Lower machine stator current, iaL. Scope channel 4: Upper machine stator current, iaU. The speed scale is 20 rad/s per division. The current scale is 2 A per division. (a) during start-up transient. (b) during the speed references the machines are varied with a ramp function having a slope of 10 rad/s per 0.2 s.
Energies 15 02043 g009
Energies 15 02043 g010 550
Figure 10. Experimental waveforms for speeds (ωm_U and ωm_L) and one-phase stator currents (iaU and iaL) for each machine under the applied torque steps. Scope channel 1: Lower machine speed, ωm_L, is 40 rad/s. Scope channel 2: Upper machine speed, ωm_U, is 25 rad/s. Scope channel 3: Lower machine stator current, iaL. Scope channel 4: Upper machine stator current, iaU. The speed scale is 20 rad/s per division. The current scale is 2 A per division. (a) Torque steps of 2 N·m and 1.25 N·m are applied to the lower and upper machines, respectively. (b) A torque step of 2 N·m is applied to the lower machine while the upper machine is operated under a fixed torque of 1.25 N·m. (c) A torque step of 1.25 N·m is applied to the upper machine while the lower machine is operated under a fixed torque of 2 N·m.
Figure 10. Experimental waveforms for speeds (ωm_U and ωm_L) and one-phase stator currents (iaU and iaL) for each machine under the applied torque steps. Scope channel 1: Lower machine speed, ωm_L, is 40 rad/s. Scope channel 2: Upper machine speed, ωm_U, is 25 rad/s. Scope channel 3: Lower machine stator current, iaL. Scope channel 4: Upper machine stator current, iaU. The speed scale is 20 rad/s per division. The current scale is 2 A per division. (a) Torque steps of 2 N·m and 1.25 N·m are applied to the lower and upper machines, respectively. (b) A torque step of 2 N·m is applied to the lower machine while the upper machine is operated under a fixed torque of 1.25 N·m. (c) A torque step of 1.25 N·m is applied to the upper machine while the lower machine is operated under a fixed torque of 2 N·m.
Energies 15 02043 g010
Table
Table 1. NSI Switching Vectors.
Table 1. NSI Switching Vectors.
GroupStatesNSI Switch Position *VaUnVbUnVcUnVaLn’VbLn’VcLn’
Isw1[1 1 1; 1 1 1; 0 0 0]000000
sw2[0 0 0; 1 1 1; 1 1 1]000000
sw3[1 1 1; 0 0 0; 1 1 1]000000
IIsw4[1 0 0; 0 1 1; 1 1 1](2/3) VDC(−1/3) VDC(−1/3) VDC000
sw5[1 1 0; 0 0 1; 1 1 1](1/3) VDC(1/3) VDC(−2/3) VDC000
sw6[0 1 0; 1 0 1; 1 1 1](−1/3) VDC(2/3) VDC(−1/3) VDC000
sw7[0 1 1; 1 0 0; 1 1 1](−2/3) VDC(1/3) VDC(1/3)VDC000
sw8[0 0 1; 1 1 0; 1 1 1](−1/3) VDC(−1/3) VDC(2/3) VDC000
sw9[1 0 1; 0 1 0; 1 1 1](1/3) VDC(−2/3) VDC(1/3) VDC000
sw10[1 1 1; 1 0 0; 0 1 1]000(2/3) VDC(−1/3) VDC(−1/3) VDC
sw11[1 1 1; 1 1 0; 0 0 1]000(1/3) VDC(1/3) VDC(−2/3) VDC
sw12[1 1 1; 0 1 0; 1 0 1]000(−1/3) VDC(2/3) VDC(−1/3) VDC
sw13[1 1 1; 0 1 1; 1 0 0]000(−2/3) VDC(1/3) VDC(1/3) VDC
sw14[1 1 1; 0 0 1; 1 1 0]000(−1/3) VDC(−1/3) VDC(2/3) VDC
sw15[1 1 1; 1 0 1; 0 1 0]000(1/3) VDC(−2/3) VDC(1/3) VDC
IIIsw16[1 0 0; 1 1 1; 0 1 1](2/3) VDC(−1/3) VDC(−1/3) VDC(2/3) VDC(−1/3) VDC(−1/3) VDC
sw17[1 1 0; 1 1 1; 0 0 1](1/3) VDC(1/3) VDC(−2/3) VDC(1/3) VDC(1/3) VDC(−2/3) VDC
sw18[0 1 0; 1 1 1; 1 0 1](−1/3) VDC(2/3) VDC(−1/3) VDC(−1/3) VDC(2/3) VDC(−1/3) VDC
sw19[0 1 1; 1 1 1; 1 0 0](−2/3) VDC(1/3) VDC(1/3) VDC(−2/3) VDC(1/3) VDC(1/3) VDC
sw20[0 0 1; 1 1 1; 1 1 0](−1/3) VDC(−1/3) VDC(2/3) VDC(−1/3) VDC(−1/3) VDC(2/3) VDC
sw21[1 0 1; 1 1 1; 0 1 0](1/3) VDC(−2/3) VDC(1/3) VDC(1/3) VDC(−2/3) VDC(1/3) VDC
sw22[1 1 0; 1 0 1; 0 1 1](1/3) VDC(1/3) VDC(−2/3) VDC(2/3) VDC(−1/3) VDC(−1/3) VDC
sw23[1 1 0; 0 1 1; 1 0 1](1/3) VDC(1/3) VDC(−2/3) VDC(−1/3) VDC(2/3) VDC(−1/3) VDC
sw24[0 1 1; 1 1 0; 1 0 1](−2/3) VDC(1/3) VDC(1/3) VDC(−1/3) VDC(2/3) VDC(−1/3) VDC
sw25[0 1 1; 1 0 1; 1 1 0](−2/3) VDC(1/3) VDC(1/3) VDC(−1/3) VDC(−1/3) VDC(2/3) VDC
sw26[1 0 1; 0 1 1; 1 1 0](1/3) VDC(−2/3) VDC(1/3) VDC(−1/3) VDC(−1/3) VDC(2/3) VDC
sw27[1 0 1; 1 1 0; 0 1 1](1/3) VDC(−2/3) VDC(1/3) VDC(2/3) VDC(−1/3) VDC(−1/3) VDC
* NSI switch position = [S1 S2 S3; S4 S5 S6; S7 S8 S9].
Table
Table 2. System parameters.
Table 2. System parameters.
DescriptionParameterValue
stator inductanceLs452.3 mH
rotor inductanceLr452.3 mH
mutual inductanceLm442.2 mH
pole pairp2
stator resistanceRs3.9190 Ω
rotor resistanceRr4.9618 Ω
friction factorB0.002985 N·m·s
inertiaJ0.0131 kg·m2
stator flux referenceΨ*s0.61 Wb.
dc-link voltageVDC250 V
sampling period of the inner loopTs100 µs
PI parameterKp1
PI parameterKi16
PI controller discretization periodTs_PI5 ms
Table
Table 3. Comparison results between different control strategies.
Table 3. Comparison results between different control strategies.
Compared Quantity →
Control Strategy↓		Scenario IScenario IIExecution
Time
THD% for Upper LoadTHD% for Lower LoadTHD% for Upper LoadTHD% for Lower Load
Proposed Method6.796.795.995.25202.4 μs
FCS-MPC18.4419.6411.669.63165.7 μs
PTC18.9820.1011.399.79170.1 μs
Hysteresis22.7623.1514.4812.7067.66 μs
Table
Table 4. Comparison results in terms of the computational burden.
Table 4. Comparison results in terms of the computational burden.
Compared
Quantity→
Control
Strategy↓		Scenario IScenario IISampling PeriodExecution
Time		CBR
THD% for Upper LoadTHD% for Lower LoadTHD% for Upper LoadTHD% for Lower Load
Proposed Method6.796.795.995.25100 μs202.4 μs2.2024
FCS-MPC7.508.034.594.3740 μs165.7 μs4.1430
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Gokdag, M. Modulated Predictive Control to Improve the Steady-State Performance of NSI-Based Electrification Systems. Energies 2022, 15, 2043. https://doi.org/10.3390/en15062043

AMA Style

Gokdag M. Modulated Predictive Control to Improve the Steady-State Performance of NSI-Based Electrification Systems. Energies. 2022; 15(6):2043. https://doi.org/10.3390/en15062043

Chicago/Turabian Style

Gokdag, Mustafa. 2022. "Modulated Predictive Control to Improve the Steady-State Performance of NSI-Based Electrification Systems" Energies 15, no. 6: 2043. https://doi.org/10.3390/en15062043

APA Style

Gokdag, M. (2022). Modulated Predictive Control to Improve the Steady-State Performance of NSI-Based Electrification Systems. Energies, 15(6), 2043. https://doi.org/10.3390/en15062043

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop