A Novel Agent-Based Power Management Scheme for Smart Multiple-Microgrid Distribution Systems

Abstract

In this work, a novel agent-based day-ahead power management scheme is proposed for multiple-microgrid distribution systems with the intent of reducing operational costs and improving system resilience. The proposed power sharing algorithm executes within each microgrid (MG) locally, and the neighboring MGs cooperate via a multi-agent system cooperation scheme, established to model the communication among the agents. The power management for each agent is modeled as a multi-objective optimization problem (MOP) including two objectives: maximizing load coverage and minimizing the operating costs. The proposed MOP is solved using the Nondominated Sorting Genetic Algorithm (NSGA-II), where a set of Pareto optimal solutions is obtained for each agent through the NSGA-II. The final solution is obtained using an Analytical Hierarchical Process. The effectiveness of the proposed scheme is evaluated using a benchmark 4-MG distribution system. It is shown that the proposed power management scheme and the cooperation of agents lead to a higher overall system resilience and lower operation costs during extreme events.

1. Introduction

With the frequent occurrence of extreme events and their severe impact on the existing grid architecture, the need for improving the resilience of the grid has also grown. Power system resilience is defined as the ability to withstand the High Impact Low Probability (HILP) events, such as wildfires and hurricanes, and continue to energize at least the critical loads and quickly recover from any interruptions caused by the extreme events [1]. The HILP events can cause severe damages throughout the power grid and may lead to cascading outages and blackouts [2]. Traditional power systems are more prone to failure during extreme events due to their centralized and interconnected structure, and enormous size. As a result, failure of one component may lead to cascading failures and finally wide-spread outage or blackout of the entire system [3]. Furthermore, maintaining grid reliability is challenging due to the load growth and integration of intermittent renewable energies. One of the promising solutions to the above-mentioned challenges is to form autonomous multiple-microgrid-based distribution systems with peer-to-peer communication and power sharing ability among the microgrids (MGs) [4]. During an extreme event, an MG can be islanded and operated independently using its own resources in order to prevent the propagation of the impact of the extreme event through the whole network [5]. Moreover, networked MGs can cooperate to ensure that all their critical loads are supplied [6]. Such control schemes can reduce the total curtailed load, ensure uninterrupted supply of the critical loads, such as hospitals and data centers, and improve the overall resilience of the system [7].

The growing use of distributed energy resources (DERs) demonstrates the necessity of distributed control in the MG-based architecture [3]. Indeed, distributed control algorithms can overcome three major issues that can occur in a centralized control architecture: (1) there is a huge computational burden associated with centralized control algorithms and decision-making processes, specifically in larger systems; (2) failure of the central controller could result in losing the control of the entire network; (3) maintaining the data privacy and ownership regulations are prone to being violated since all the information has to be gathered in one single node. On the other hand, establishing a decentralized control scheme is a robust solution for tackling these issues. In our proposed scheme, each MG processes its own information locally and shares only the necessary data with its neighboring MGs. Moreover, during an extreme event, the MGs can communicate with each other on a plug-and-play basis in such a way that if an MG is severely affected by an extreme event, it can be islanded from the grid to avoid propagation of the fault(s).

The agent-based MG power management problem has been explored and solved using a variety of optimization frameworks. In [3], a power management scheme is introduced by locating fair solutions on the Pareto frontier using the Nash Bargaining system. The objectives for each agent are formulated to maximize the efficiency, profit, and utility of power consumption. In [8], the energy trading between multiple MGs is formulated as a distributed optimization problem and solved using an iterative subgradient-based algorithm to minimize operation cost. Reference [9] proposes a multiple-MG-based power management scheme through a common interface to offer ancillary services, black start capability, and for improving stability of the system. The power management of a multiple-MG system is modeled as a bi-level optimization problem in [10]. Reference [11] proposes a two-layer optimization model to improve stability and security for multi-MG systems. Optimal solutions are found using a bilateral bidding and trading strategy. The scheduling method encourages the MGs to share power rather than importing power from the main utility. A robust power flow control strategy between multiple interconnected MGs is presented in [12] with a focus on frequency stabilization. A bi-level power management scheme is proposed in [13], where the energy trading (upper layer) is formed as a mixed integer quadratic programming and the MG energy production (lower layer) is formed as a robust optimization model.

Reference [14] utilizes an agent-based platform to establish autonomy, proactivity, and social communication among the interconnected MGs. This work, however, focuses on a plug-and-play-based secondary regulation control system rather than the day-ahead component-wise scheduling. Reference [15] proposes a peer-to-peer voltage control strategy through dual decomposition and linearization. The voltage control problem is formulated as a decentralized constrained optimization and the voltage deviation is minimized with the help of a peer-to-peer communication protocol. A prosumer-based peer-to-peer energy trading platform is developed in [16]. In this platform, the individual users shift their tasks between a producer and a consumer, based on the situation. The overall objective is to establish an efficient utilization of local resources and minimize the transfer of energy with other areas. References [17,18] propose using the Java Agent Development Environment (JADE) to facilitate the power management of agent-based systems. Indeed, JADE is an application platform for developing agent-based communication protocol. Reference [18] used a decentralized power management approach to enhance the system self-healing. However, these references did not consider any energy storage systems (ESSs). JADE is a highly capable system that enables the formation of agents with easy plug-and-play operation that can lead to robust solutions. Reference [19] proposes a hybrid multi-agent system (MAS) using electric vehicles (EVs). The hybrid system combines centralized and distributed control to improve efficiency and system resilience. However, in this reference, the proposed MAS does not protect data privacy; all the information is distributed through the whole system. In [20], a resilient and extreme-event-aware planning framework was proposed for MGs to ensure maximum load coverage during a prolonged period of extreme event. Reference [21] developed a demand and congestion management strategy during extreme events and contingency focusing on home appliances and available electric vehicles. Different indices such as consumer convenience and demand rebound are considered in this study.

In this paper, we propose a novel distributed power management scheme for multiple-MG distribution systems in order to improve the overall system resiliency and reduce the operating costs. For this purpose, an agent is assigned to each MG’s controllable components. The role of each agent is to solve its own multi-objective problem (MOP) and to communicate with its neighboring agents to create a set of optimal solutions that lie on the Pareto front. Each MG determines a set of optimal solutions that improves the overall system resiliency while simultaneously minimizing operating costs. It should be noted that since the PV output power is essentially free, it is utilized whenever available; it is not included in the optimization process.

The main contributions of this work are as follows:

(1)

Formulization of a unique MOP that encourages each agent to find an optimal solution that will result in lower overall operating costs.

(2)

Establishing a reciprocal communication and negotiation between local agents and neighboring MGs.

(3)

Protecting data privacy as each MG does not share its local information with other MGs.

The paper is structured as follows: Section 2 describes the proposed methodology and problem formulation. Section 3 presents the benchmark multiple-MG test system and describes the solution approach. The proposed power management scheme through the modeling and simulation of an agent-based multiple-MG system that is impacted by an extreme event is presented in Section 4. Finally, Section 5 concludes the paper with the final remarks on the advantages and the applicability of the proposed approach.

2. Methodology

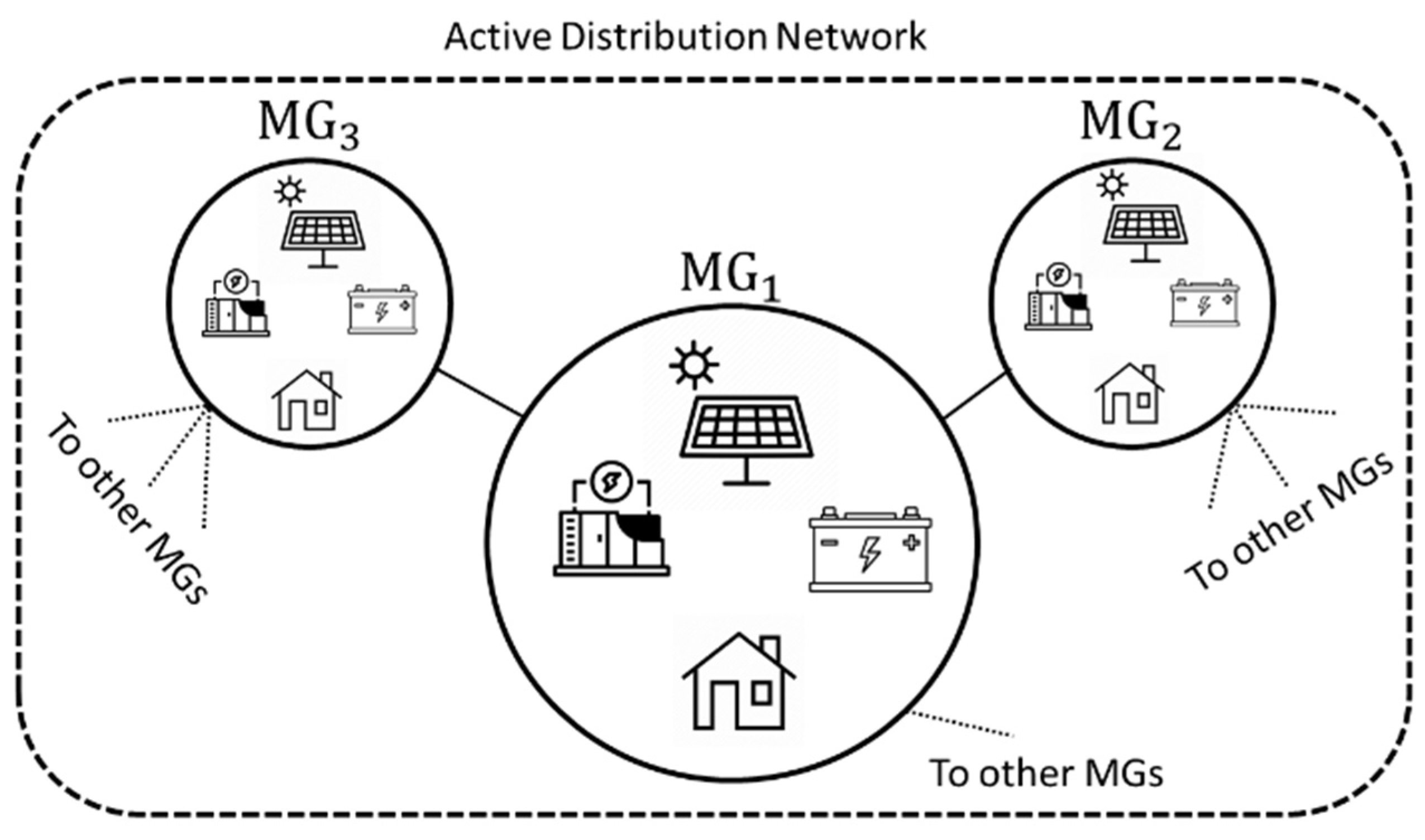
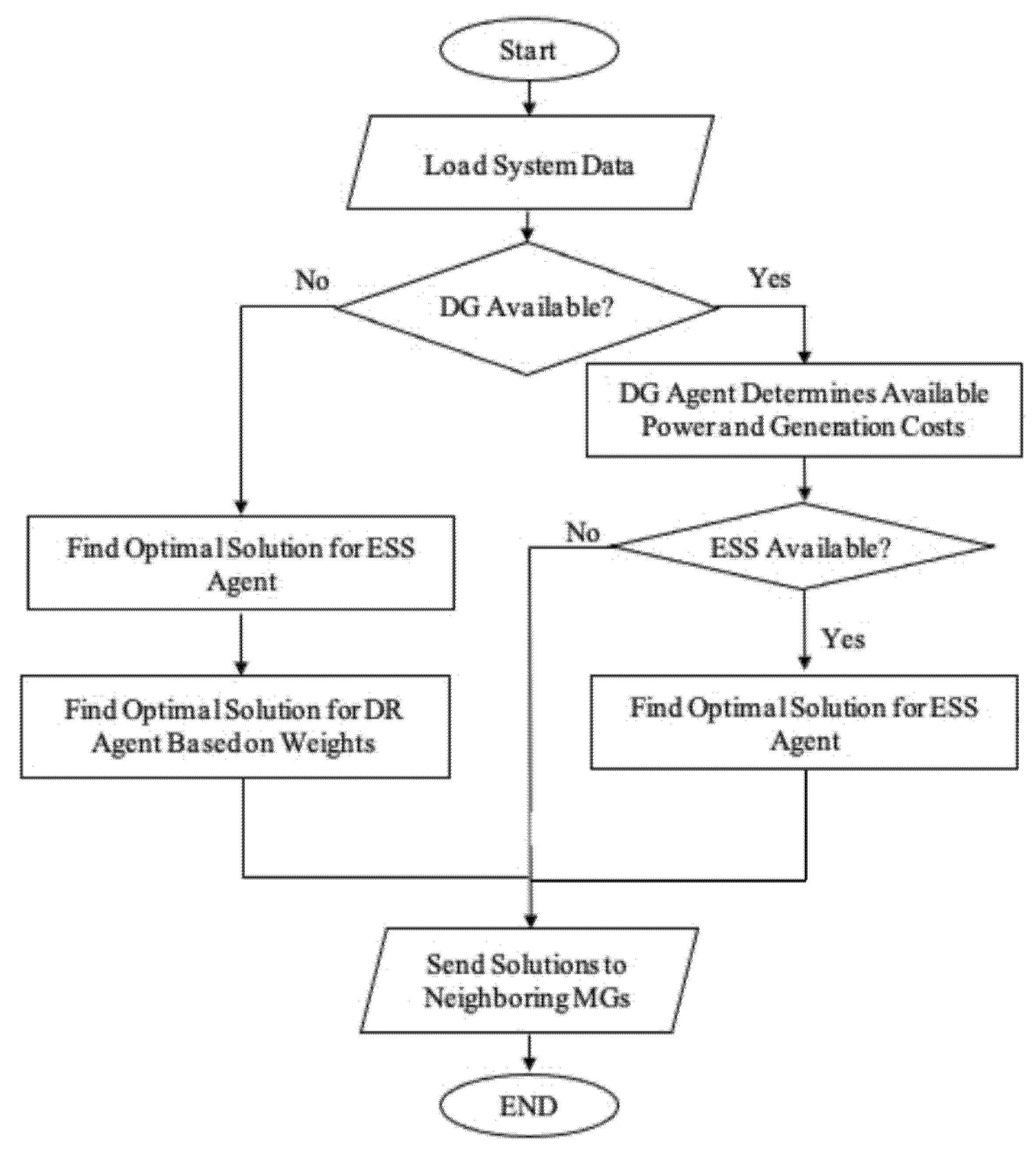
The general framework for the multiple-MG active distribution system is shown in Figure 1, where a distribution grid is divided into several MGs. Each MG has its own resources, and under normal conditions supply–demand balance is maintained within the MG. During an extreme event, each MG isolates from the rest of the grid and operates in island mode. Furthermore, the main priority within each MG is to supply the critical loads within the MG. In other words, MGs have the ability to control their own components, such as Distributed Generation (DG) units, ESSs, and controllable loads facilitated by Demand Response (DR).

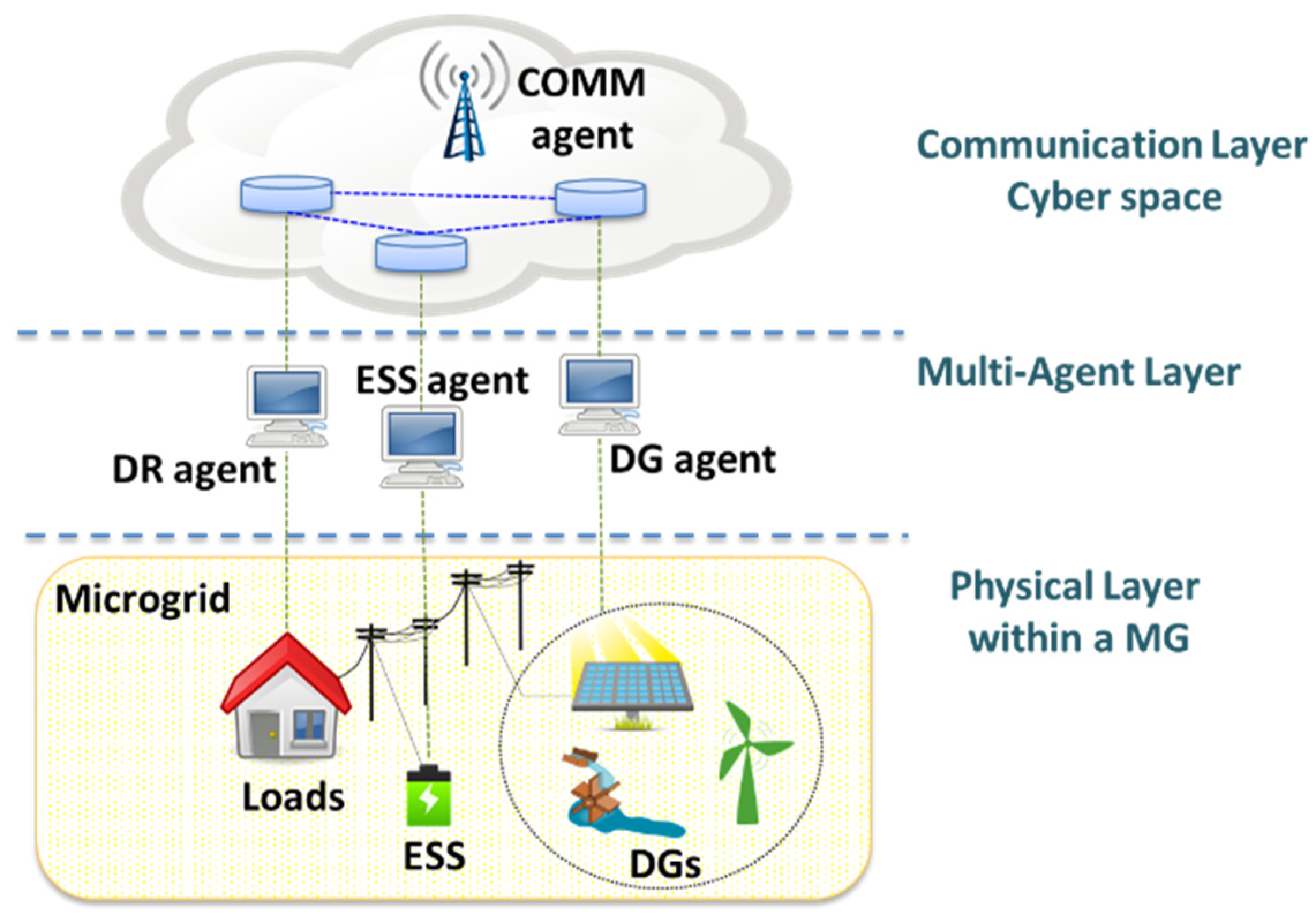
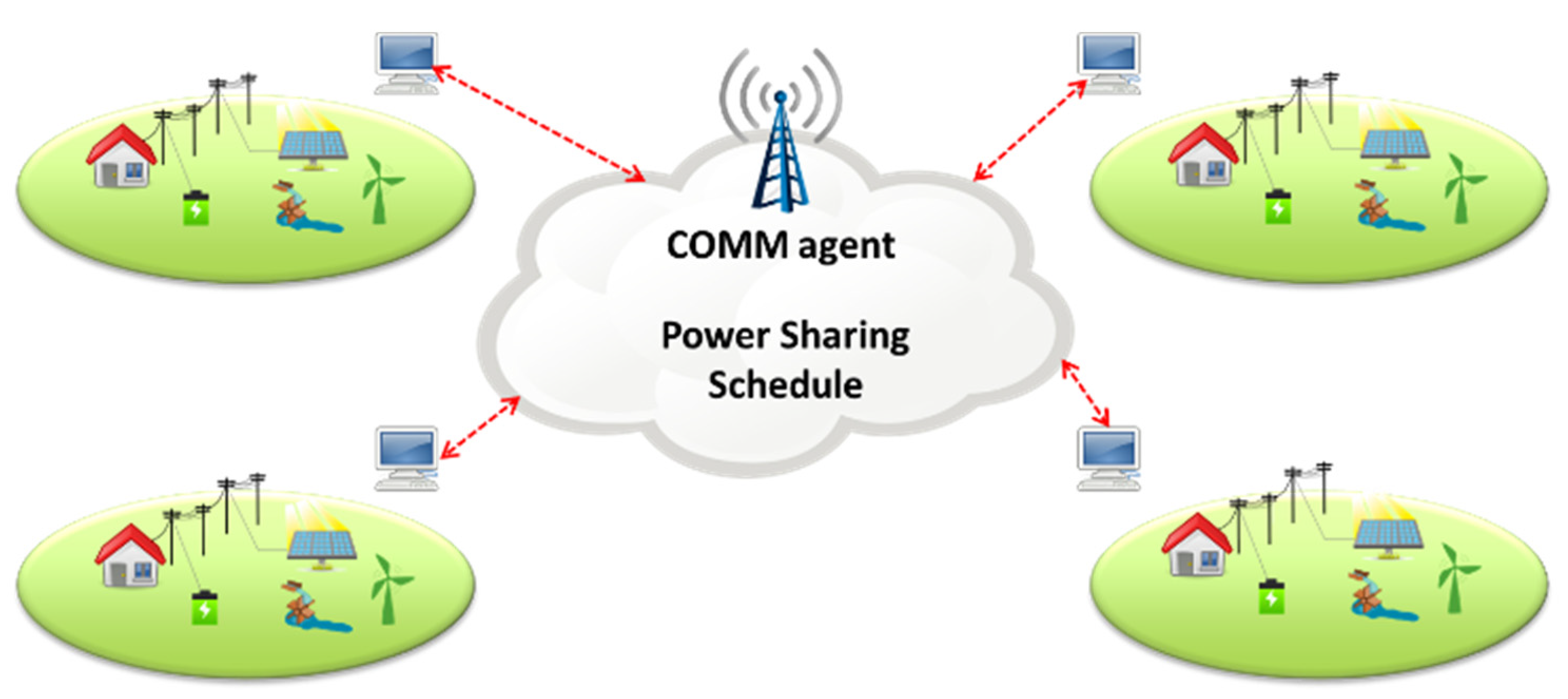
The general framework of the proposed agent-based active power management approach is shown in Figure 2. The scheme is visualized in three different layers: (1) The physical layer, which includes the actual components of the MG (loads, DGs, ESSs, etc.). (2) The multi-agent layer, where the local agents are located. One agent is assigned to each controllable component of the MG, i.e., the DG agent, ESS agent, and DR agent. (3) The communication layer, where the MG can communicate with other MGs. To model the peer-to-peer communication, a communication agent (COMM) is assigned to each MG, as shown in Figure 3. These COMM agents allow the MGs to communicate with each other in order to facilitate a power sharing scheme. The analytical formulation of the different agents and the problem formulation are presented below.

2.1. ESS Agent

An agent is assigned to the ESS(s) within each MG, which is used as a backup source for emergency situations and can be charged and be prepared if an extreme event is forecasted. The objective of the ESS agent depends on the state of the MG. During an extreme event where the MG is disconnected from the main grid, the ESS agent creates a discharge scheme to maximize load coverage that is biased towards more expensive hours of generation. A weighting system is formulated based on the total cost for an MG to supply all loads at each hour. The ESS agent plays a key role in minimizing the overall operating costs by reducing the operation of synchronous generators (SGs) during the most expensive hours. The cost of operating the SGs at each hour for independent MGs is calculated by (1).

$$C_{SG}\left(t\right)=\alpha \ast P_{SG}{}^2\left(t\right)+\beta \ast P_{SG}\left(t\right)+\gamma$$

(1)

where $\alpha$, $\beta$, and $\gamma$ are constant cost coefficients and $P_{SG}\left(t\right)$ is the SG’s power generation at time t. In this paper, they are considered as 0.008, 6.3, and 180, respectively.

Before an extreme event, ESS is fully charged, and during the extreme event, it is discharged in order to minimize the power deficiency within the MG.

When the healthy MGs reconnect, the ESS in each MG supplies its available power during the most expensive hours to minimize power import from its neighboring MGs, therefore minimizing the MG’s operation costs. The cost at each hour is determined by solving an economic dispatch problem formulated by (2).

$$\begin{gathered} \min C_{total}\left(t\right)={\displaystyle \sum }{C}_i\left(P_i\left(t\right)\right) \\ s.t. P_L\left(t\right)={\displaystyle \sum }{P}_{SG}\left(t\right) \\ {P}_{SG}\left(t\right)\le P_{i,available}\left(t\right) \end{gathered}$$

(2)

where $C_i$ is the MG’s hourly cost and $P_i\left(t\right)$ is the imported power from the neighboring MGs at each hour. $P_L\left(t\right)$ is the local MG’s total load and $P_{i,available}\left(t\right)$ is the neighboring MG’s available power at time t. Solving the optimization problem, it will determine the required power from each neighboring MG with the objective to minimize the hourly costs. A cost weighting function is defined for the generation cost at each hour, as shown in (3).

$$w\left(t\right)=\frac{C_{min}}{C\left(t\right)}$$

(3)

where $C_{min}$ and $C\left(t\right)$ are the minimum hourly generation cost and generation cost at each hour, respectively. At each hour, the weighting function $\left(w_0\right)$ can range from $0$ to 1; where $w_0=0$ corresponds to the most expensive hour and $w_0=$ 1 corresponds to the least expensive hour.

Depending on the available resources within an MG during an extreme event, two objectives are considered. Generally, the ESS reserves its charge for emergency cases, and it only supplies critical loads. Therefore, the first objective function is given for ESS as follows.

$$Ob{j}_{ESS,1}={{\displaystyle \sum }}_{t=t_1}^{t_2}{\left(P_{L_{crit}}\left(t\right)-P_{ESS}\left(t\right)\right)}^2\times w\left(t\right)$$

(4)

where $t_1$ and $t_2$ are the forecasted times when the extreme event starts and ends. $P_{ESS}\left(t\right)$ is the charge/discharge power of ESS, and $P_{L_{crit}}\left(t\right)$ is the amount of critical load in the MG at the time step t.

If the MG does not have adequate power supply to cover all its loads during the extreme event, the ESS agent creates a discharge scheme that tries to supply critical loads at all hours of the extreme event. The objective function for this case is formulated by (5).

$$Ob{j}_{ESS,2}={{\displaystyle \sum }}_{t=t_1}^{t_2}{\left(SE\left(t\right)-P_{ESS}\left(t\right)-SE\left(t+1\right)\right)}^2$$

(5)

where $SE\left(t\right)$ is the stored energy in the ESS at time t. The following constraints, (6)–(9), are considered for the ESS agent to ensure it operates within its power limits and energy capacity.

$$P_{ESS}^{min}\le P_{ESS}\left(t\right)\le P_{ESS}^{max}$$

(6)

$$S{E}_{ESS}^{min}\le S{E}_{ESS}\left(t\right)\le S{E}_{ESS}^{max}$$

(7)

$$\left|SE\left(t\right)-SE\left(t+1\right)\right|\le P_{ESS}^{max}\times \mathsf{\Delta }t$$

(8)

$${{\displaystyle \sum }}_{t=t_2}^{t_3}{P}_{ESS}\left(t\right)\le \left(S{E}^{max}-S{E}^{min}\right)$$

(9)

2.2. DR Agent

A DR agent is assigned to the controllable loads within each MG. This agent is responsible for managing load curtailments to find a balance between customer discomfort costs associated with curtailing of noncritical loads, generation costs associated with importing power from the neighboring MGs, and load coverage. In the case of an extreme event, the DR agent determines the level of curtailment of the price-sensitive controllable loads. Three objective functions are considered for the DR agent, as shown in (10)–(12). The first objective, (10), is to minimize the customer discomfort cost, expressed as a quadratic nonlinear function of the curtailed power, to show the exponential increase in the customers discomfort with increasing load curtailment. The second objective is to minimize the power import (and therefore its cost), and the third objective is to minimize the load curtailment.

$$Ob{j}_{DR,1}=m\times P_c{(t)}^2+c\times P_c\left(t\right)$$

(10)

$$Ob{j}_{DR,2}={{\displaystyle \sum }}_{t=1}^N\left\{\alpha \ast P_{import}{\left(t\right)}^2+\beta \ast P_{import}\left(t\right)+\gamma \right\}$$

(11)

$$Ob{j}_{DR,3}={(P_L\left(t\right)-P_{import}\left(t\right))}^2$$

(12)

where $P_c\left(t\right)$ is the amount of curtailed power, $P_L\left(t\right)$ is the local load power, and $P_{import}\left(t\right)$ is the power imported from the grid at hour t. m and c are constant cost coefficients associated with customer discomfort costs and $\alpha$, $\beta$, and $\gamma$ are constant cost coefficients associated with importing power from the grid.

The curtailed power is bound by the constraints in (13), which do not let an MG curtail loads below a critical threshold $\left(P_{L_{crit}}\left(t\right)\right)$.

$$P_c\left(t\right)\le P_L\left(t\right)-P_{L_{crit}}\left(t\right)$$

(13)

2.3. DG Agent

The DG agent represents the synchronous generators in the MGs and sets their output power as per the local electricity demand and the requested power from the neighboring areas. For this purpose, cost coefficients α, β, and γ are generated for each DG to provide the cost of exported power to the neighboring MGs that suffer from lack of energy. The first objective is the Mean Squared Error (MSE) between the generation and the amount of power to be supplied (i.e., the summation of the output power of the DR agent and the power exported to the other MGs), and the second objective is to minimize the generation cost. The two objectives are given in (14)–(15).

$$Ob{j}_{DG,1}={\displaystyle \sum }_t{\left(P_{DG}\left(t\right)-\left(P_L\left(t\right)-P_c\left(t\right)\right)+P_{exp}\left(t\right)\right)}^2$$

(14)

$$Ob{j}_{DG,2}=\alpha \ast P_{DG}{\left(t\right)}^2+\beta \ast P_{DG}\left(t\right)+\gamma$$

(15)

$P_{DG}\left(t\right)$ is the DG power output, and $P_{exp}\left(t\right)$ is the amount of power that an MG provides to the neighbor MG, which is proportional to the power requested by the affected MG.

The control variable of the DG agents is their output power, which is limited by the maximum and minimum generating limits of each DG, i.e., $P_{DG}^{min}$ and $P_{DG}^{max}$, as given in (16).

$$P_{DG}^{min}\le P_{DG}\left(t\right)\le P_{DG}^{max}$$

(16)

$P_{DG}\left(t\right)$, must be within its ramping limit. This constraint is given in (17).

$$\left|P_{DG}\left(t\right)-P_{DG}\left(t-1\right)\right|\le \rho \times \mathsf{\Delta }t$$

(17)

where $\rho$ is the generation rate constant representing the ramp-up and ramp-down limits between two consecutive time steps, $\mathsf{\Delta }t$.

It should be noted that the operation cost of the DGs is a function of their power output and duration of operation. Batteries do not directly change the operating cost of the DGs. However, batteries, and specifically the power management scheme, can affect the total operational cost of the MGs by scheduling appropriate amount of power import from the neighboring MGs and charging/discharging cycles of the ESSs.

2.4. COMM Agent

Each MG has a communication agent (COMM), which maintains peer-to-peer communication with its neighboring MGs to facilitate energy exchange and create a power sharing scheme. However, the COMM agents do not share their internal information with each other to ensure privacy of data. The only data shared among the MGs are the maximum available power that can be exported/imported as well as the information on common boundary buses, such as bus voltage and power limits. The COMM agent collects information from the other agents in the MG, such as their available power and generation costs and the information from the DR agent.

2.5. Problem Formulation

The proposed power management algorithm is expressed as a multi-objective constrained optimization problem. The Nondominated Sorting Genetic Algorithm (NSGA-II) is used to find a set of global minima for multiple, nonlinear objective functions. NSGA-II is one type of multi-objective evolutionary algorithm, which finds a set of solutions to the multi-objective problems with an elitist nondominating sort-based approach, ensuring population diversity preservation [22]. The sets of solutions obtained by NSGA-II are Pareto optimal, meaning they have a ‘fair’ balance between the different objectives. In this approach, a parent population is defined among each generation based on the fitness of each individual. A child population is created from the parent population using binary tournament selection, crossover, and mutation. The parent–children combined population is sorted as per their rank of nondomination, whereas each member of the population is evaluated using the objective functions and the crowding distances. More detail about this approach is given in [22]. In this algorithm, the usage of crowding distance as a measure of fitness ensures preservation of diversity. Meanwhile, the inclusion of the fittest chromosomes from the previous generation in the next generation reassures higher fitness properties (elitism).

While the overall objectives include maximizing the load coverage and minimizing the operating cost, these objectives may be contradictory of each other and therefore a set of fair tradeoff solutions is obtained. The extent and weightage of the tradeoff for each objective can be defined by the MG operator to reach either lower operational costs or minimum load curtailments.

3. Test System and the Solution Approach

3.1. Test System

The effectiveness of the proposed algorithm is evaluated using a modified 4-MG benchmark system [23], shown in Figure 4. A normally closed switch exists on the tie-lines between the MGs, giving the MGs the ability to import and export power. Hourly load data were taken from [23] considering a monsoon weekday. Only solar PV was considered in the modified benchmark, and the hourly PV profile was also generated from [23] considering a cloudy day during week 23–24. The total MVA capacity of the onsite SG and MWh capacity of the ESS units for each MG are given in

Table 1. MG Generation and storage power capacity.

MG	SG (MVA)	ESS (MWh)
1	15	10
2	6	12
3	6	12.4
4	4	12

.

A 24-h power management simulation is performed on each MG using parallel processing with a time step of 1 h.

The set of solutions found lie on a three-dimensional Pareto front as shown in Figure 5. The set of Pareto optimal solutions is highlighted in blue, while the set of all feasible solutions is shown in black.

3.2. Extreme Event

An extreme event is forecasted at hour 2, which prompts the ESS to begin charging in order to be prepared for the extreme event that occurs at hour 8 and lasts until hour 20, during which time the utility grid is projected to black out. As a result of the extreme event, the whole network is disconnected from the grid, and each MG is operating in islanded mode. At the same time, the generator in MG3 is considered out of service, causing a shortage of available power in that MG. Therefore, the MG3’s only available resources are its ESS and solar PV power production.

3.3. The Agent-Based Solution Process

In the case of an extreme event, the solution process initiates with each DG agent determining its available generation and the generation costs, based on the local data. The ESS agent in each MG creates an optimal solution based on the output of the DG agent and the required power to supply the critical loads.

The DG agent will then respond to the solution of the ESS agent by reassessing its available generation. If the DG agent is down, for example, in MG3, the solution process initiates with the ESS agent. After the ESS agent has reached an optimal solution, the DR agent will create a set of optimal solutions. It is up to the operator to select a solution set from the DR agent based on the weight of importance assigned to customer discomfort and the cost of power import. Finally, the solutions are sent to the neighboring MGs to reconnect and effectively create an optimal power sharing scheme. The flow chart for the power management process is shown in Figure 6.

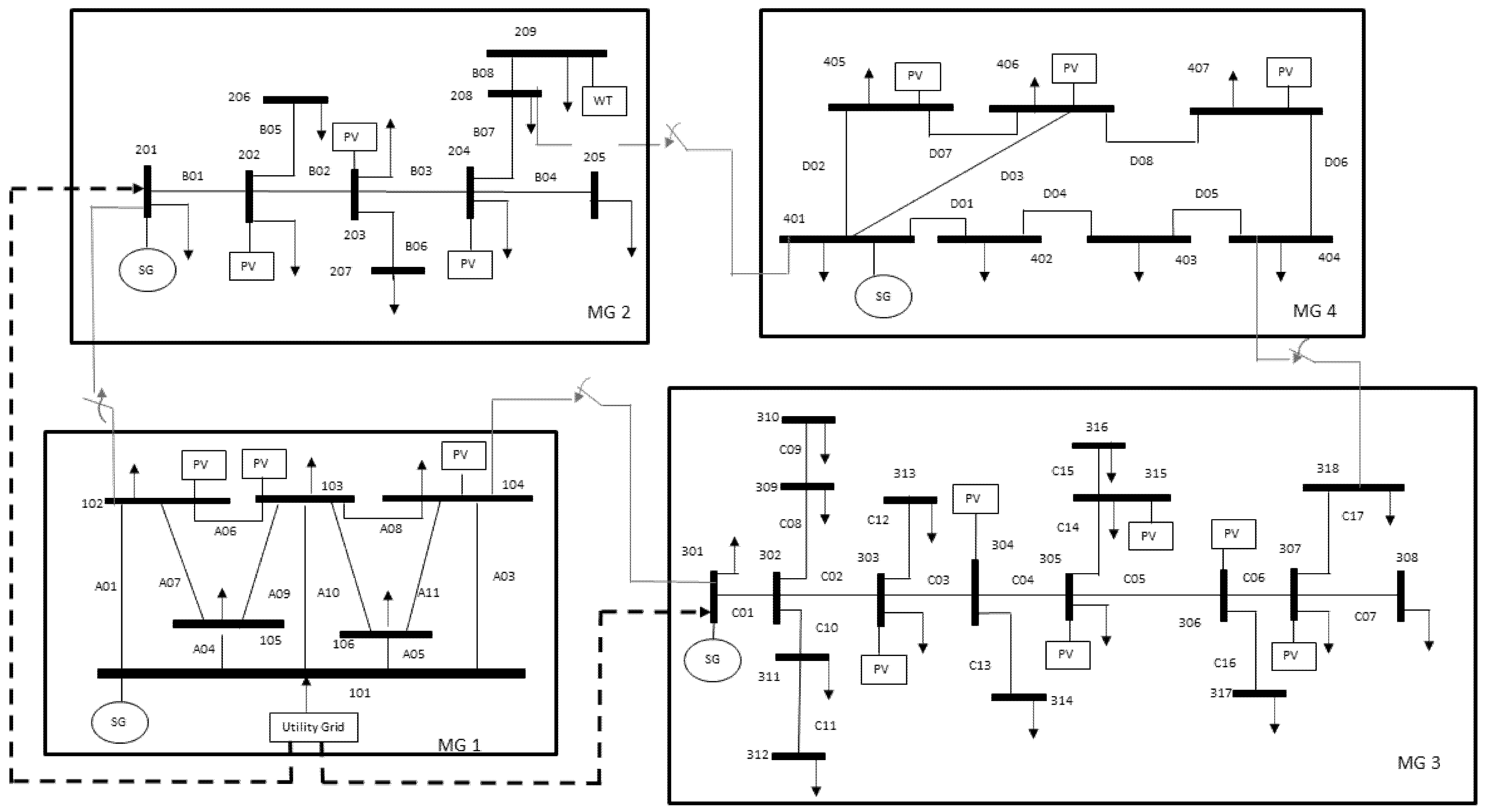
4. Simulation Results

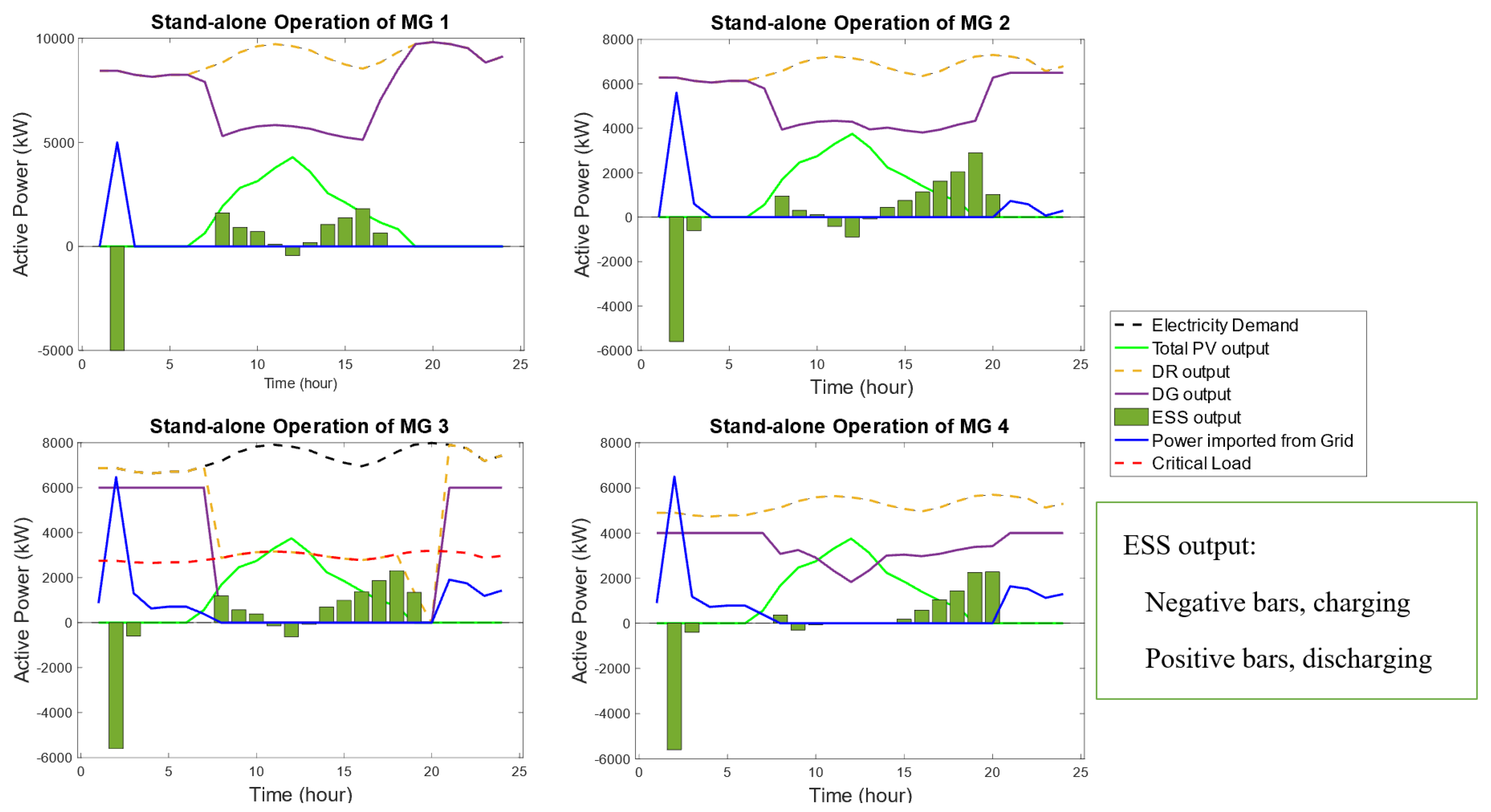
Figure 7 shows the simulation results for the four interconnected MGs without power sharing. An extreme event is forecasted at hour 2, to start at hour 8. From hour 2, all the MGs start importing power from the grid to charge their ESS in preparation for the extreme event. Once the extreme event occurs at hour 8, the interconnected MGs disconnect from the main grid and operate in standalone mode. The impact of the extreme event is minimal on the healthy MGs 1, 2, and 4, as they can supply their own demand. However, because of the coincidental loss of conventional generation in MG3, it forces the DR agent to drastically curtail loads. The noncritical loads of MG3 are curtailed and its available resources are able to supply all its critical loads except for the last two hours of the extreme event. During the last hour of the extreme event, all loads are curtailed in MG3, causing a complete blackout. Therefore, the overall system resiliency is compromised.

Due to the poor resilience of the system, the need for a power sharing scheme is evident. The results of the MG power sharing solution, based on minimizing the overall operating costs of MG3, are depicted in Figure 8. By importing power from its neighboring MGs during the extreme event, the curtailed load in MG3 is significantly reduced from 82.97% of the total load, to 31.57%; thus, the system resiliency has improved.

Furthermore, by conducting the MOP and the proposed power sharing scheme, MG3 is able to find optimal solutions that reduce its operating costs during the extreme event. The final solution is selected to reduce the overall operating costs.

Table 2. Weighted Power Request Options (MG3).

Weights (Gc, Dc)	Load Curtailed (%)	Total Generator Cost (USD)	Total Customer Discomfort Cost (USD)	Operating Cost (USD)
1.0, 0.0	60.00	5115	11,114	16,229
0.6, 0.4	47.81	7243	7432	14,675
0.5, 0.5	31.58	10,352	3565	13,917
0.4, 0.6	20.37	12,618	1694	14,312
0.3, 0.7	11.74	14,464	711	15,175
0.2, 0.8	4.96	15,928	214	16,142
0.1, 0.9	0.04	16,993	1	16,994
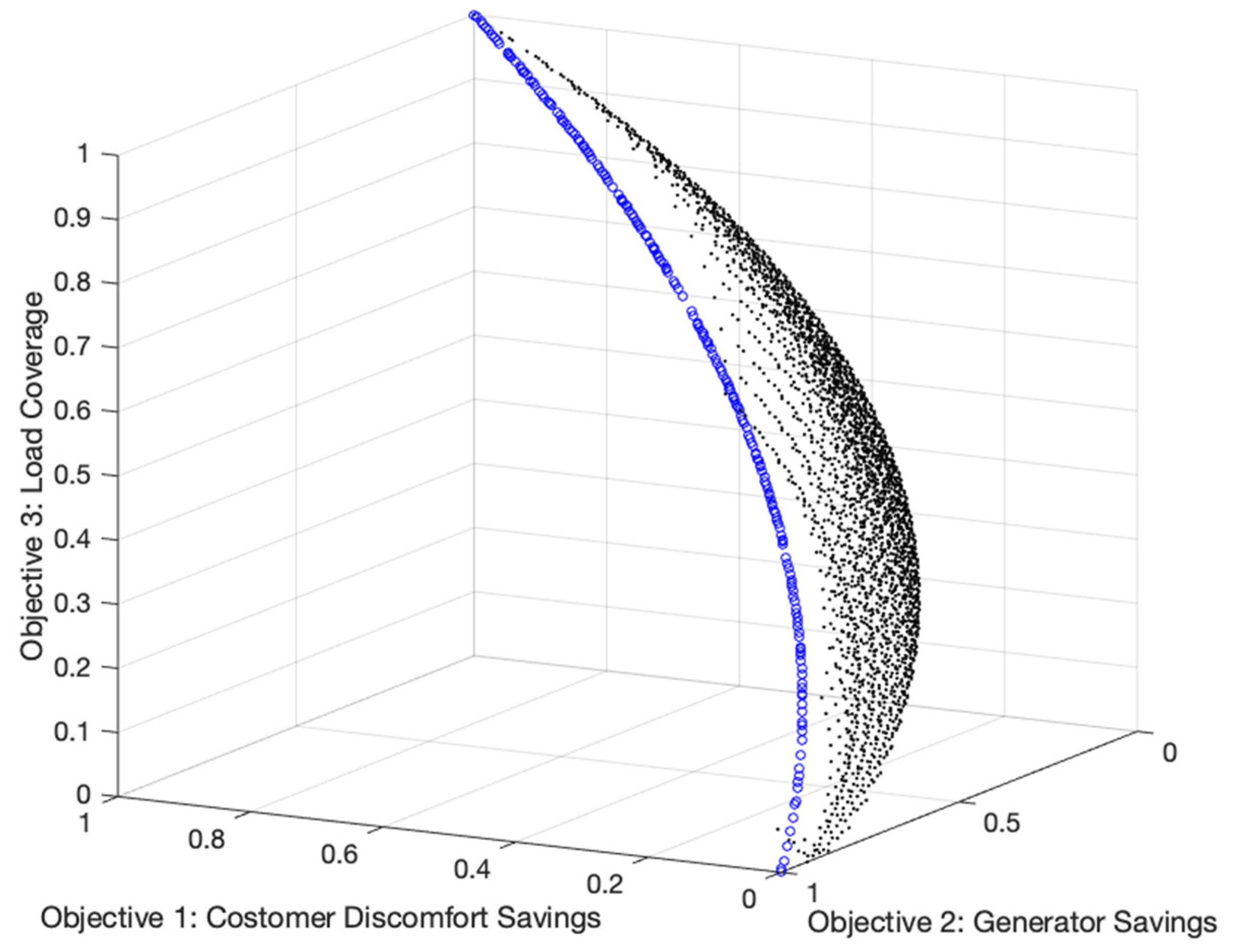
0.0, 1.0	0	17,006	0	17,006

shows the operating cost, customer discomfort cost, generation cost, and percent load curtailment for different weight factors (Gc and Dc). Dc is the weight factor associated with the load curtailment and customer discomfort, and Gc is the weight factor associated with the total operational cost. The weight values for the minimum operating cost of MG3 are highlighted. However, the operator of MG3 could select a desired tradeoff solution, for example, a set of weight values that may result in reduced load curtailment, but with an increase in the operating cost. All weighted solutions for MG3 are presented in Figure 9.

5. Conclusions

In this paper, a resilient agent-based power management scheme involving active power sharing and cooperation between multiple MGs in an MG-based distribution system has been proposed with the intent to improve system resiliency and reduce operating costs. The neighboring MGs communicate with each other on a peer-to-peer communication basis through their communication agents while protecting their privacy of ownership by limiting the shared information only to the requested power and total generation capacities. It is shown that the overall system prepares for an upcoming extreme event in a fully decentralized and agent-based approach.

The optimal solutions of these agents exist in the solution space containing an infinite number of possible solutions for the 24-h simulation horizon. To find those solutions, an evolutionary multi-objective solver algorithm, NSGA-II, is used to find the Pareto front, and the final solution is selected from the Pareto front.

A benchmark power system model consisting of four MGs is used to evaluate the effectiveness of the proposed method. Simulation results show that using the proposed approach during the occurrence of an extreme event, even with the grid blackout and possible unit failure in the system, the MGs can survive by helping each other when necessary. It is shown that by using the proposed method the system resiliency is improved and the operating costs are reduced, thus reinforcing the proposed power management scheme.