The Estimation of Lightning Impulses Superimposed onto Pre-Stressed DC Breakdown Voltages Using the Leader Propagation Method
Abstract
1. Introduction
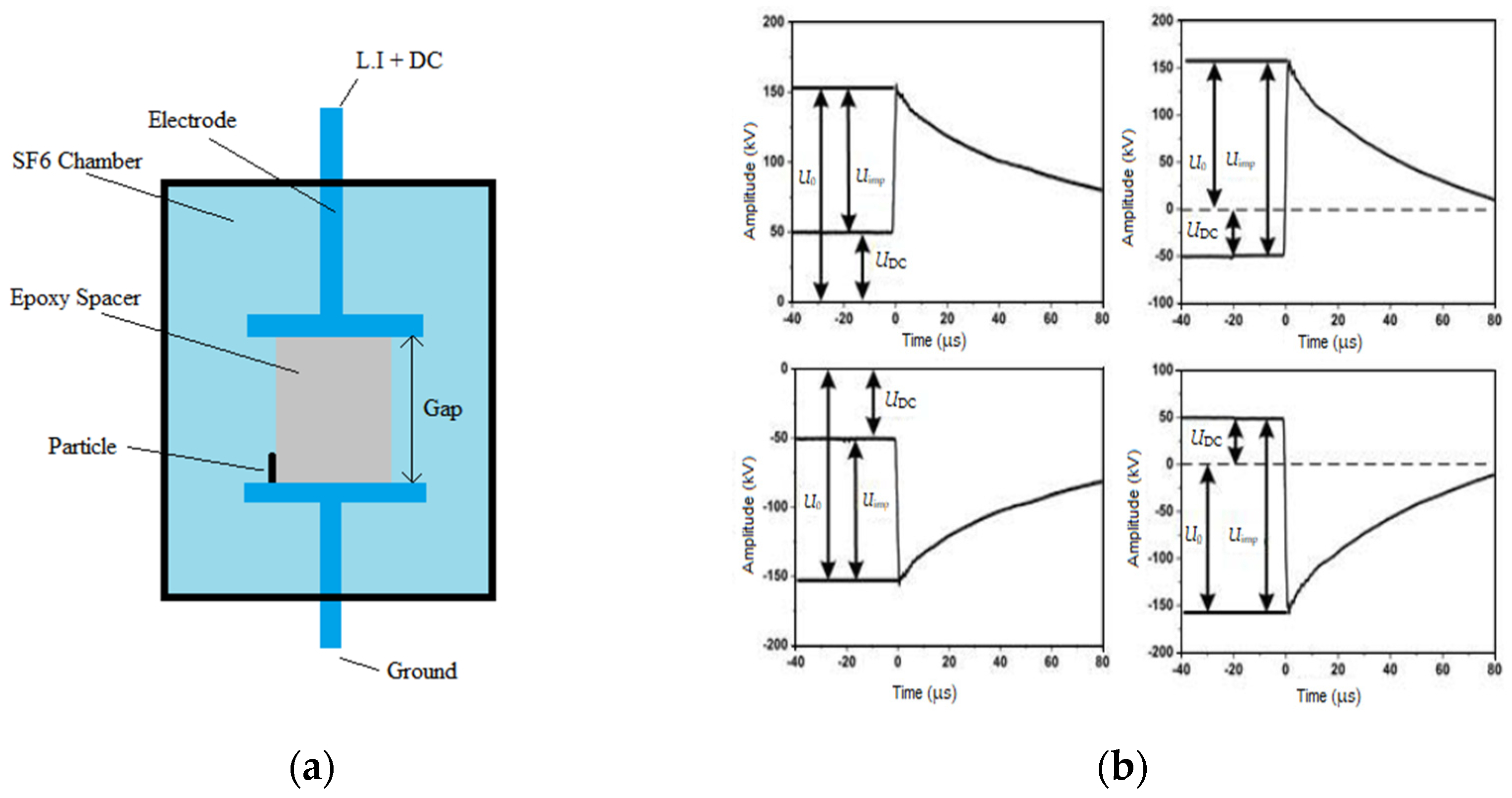
2. Simulation Model Setup
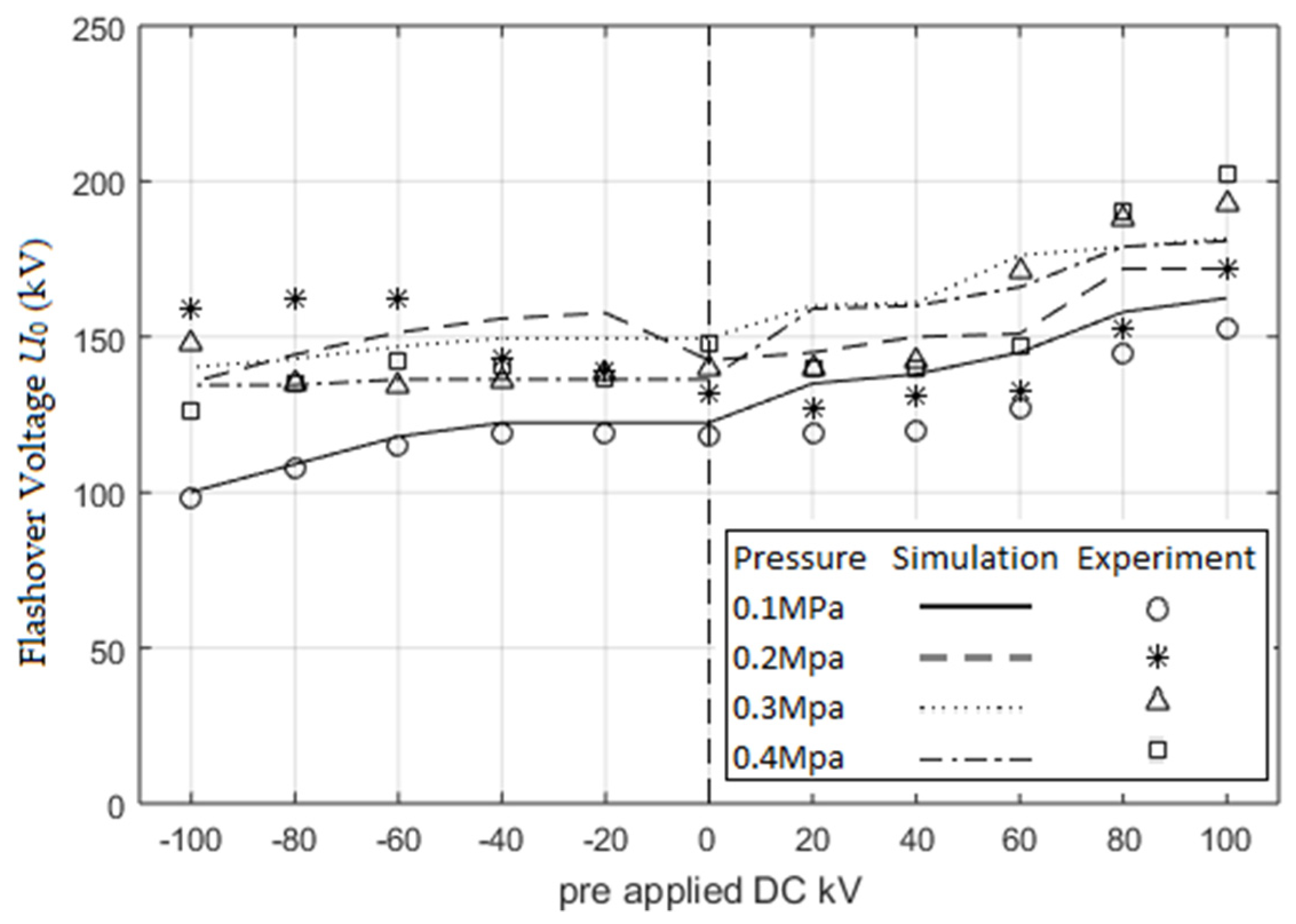
- Case 1 (i.e., gas gap with contaminating particle): A pair of plain electrodes (with a gap length of D = 50 mm) with particles (with a particle length of L = 10 mm) but without spacers. The simulations were conducted with the gap filled with SF6 gas at different pressure values of 0.1 MPa, 0.2 MPa, 0.3 MPa, and 0.4 MPa. LI voltages were superimposed onto pre-stressed DC voltages to the HV electrode;
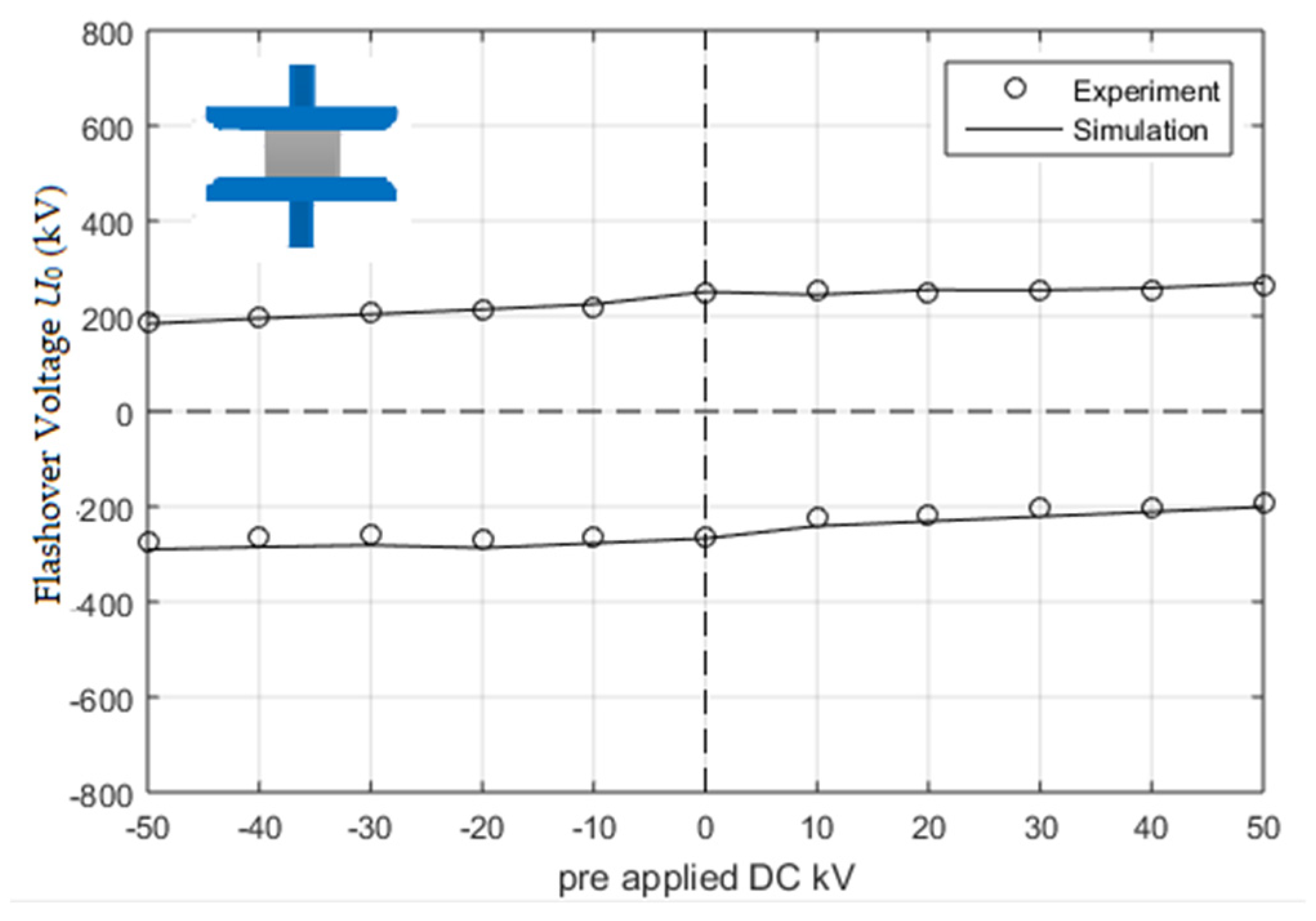
- Case 2 (i.e., gas gap with a spacer without contaminating particles): A pair of plain electrode gaps (with a gap length of D = 15 mm) without particles but with a spacer (εr = 5.93). The simulations were conducted with the gap filled with SF6 gas at a pressure value of 0.4 MPa. LI voltages were superimposed onto pre-stressed DC voltages to the HV electrode;
- Case 3 (i.e., gas gap with a spacer and contaminating particles): Aair of plain electrode gaps (with a gap length of D = 15 mm) with particles (particle length L = 3 mm) and with a spacer (εr = 5.93). These simulations were also conducted with the gap filled with SF6 gas at a pressure value of 0.4 MPa. LI voltages were superimposed onto pre-stressed DC voltages to the HV electrode.
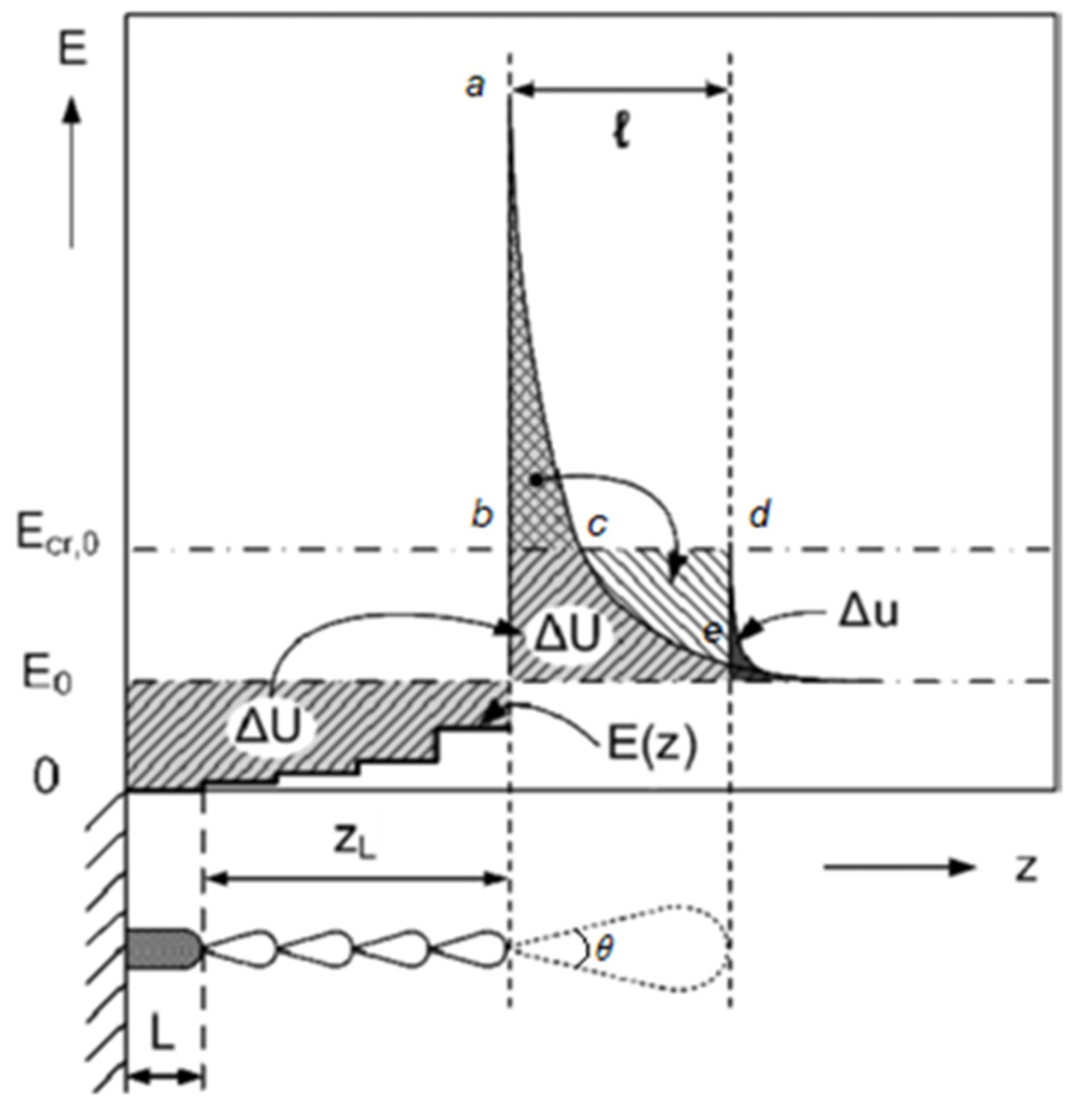
3. Mathematical Model
3.1. Case 1: A Gas Gap without a Spacer
3.2. Case 2 (i.e., a Gas Gap with a Spacer and without Particles) and Case 3 (i.e., a Gas Gap with a Spacer and with Particles)
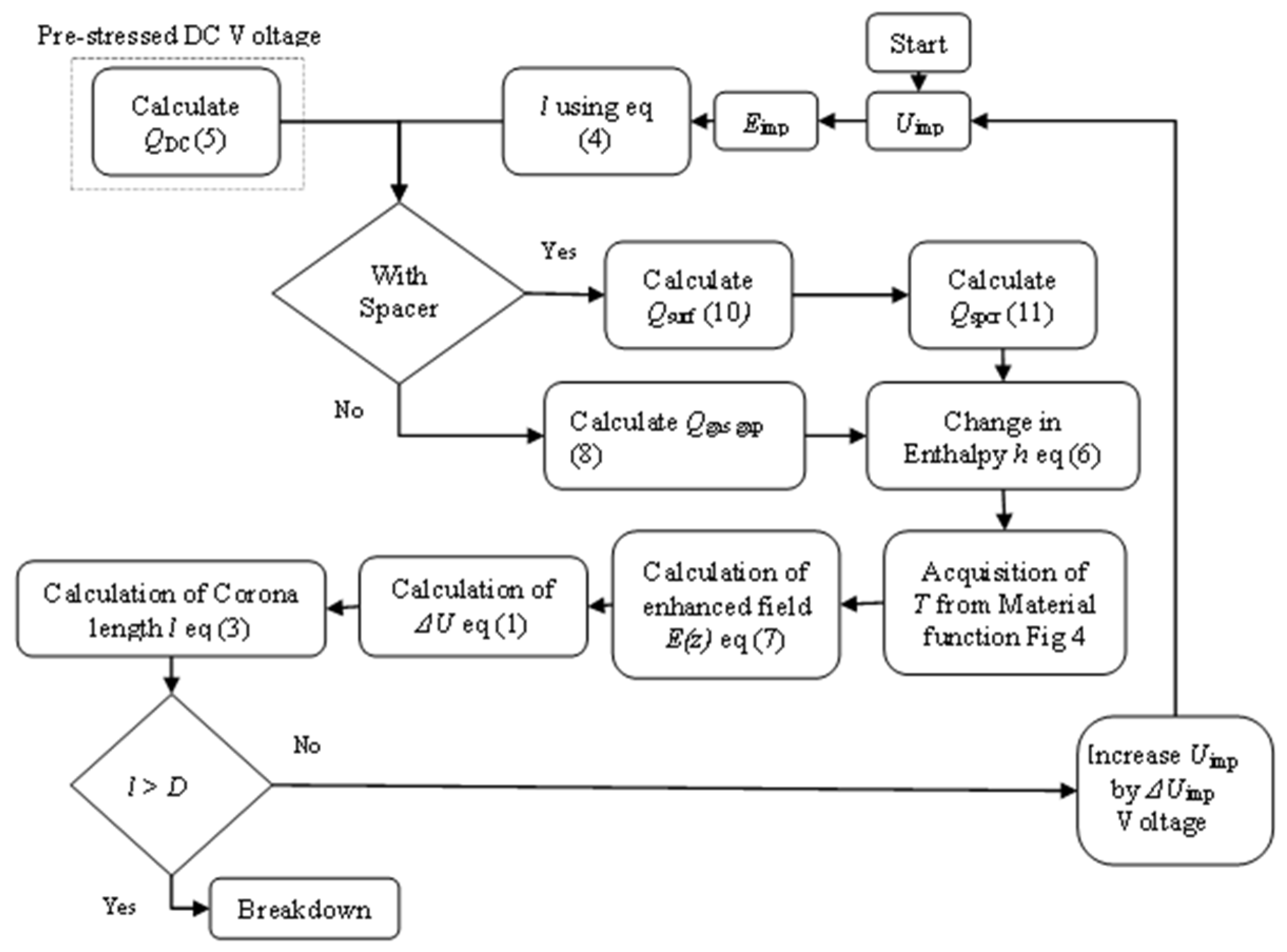
4. Simulation Flowchart
5. Results and Discussion
5.1. Case 1: The Gas Gap without a Spacer
5.2. Case 2: A Gas Gap with a Spacer and without Particles
5.3. Case 3: A Gas Gap with a Spacer and with Particles
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Laghari, J.R.; Qureshi, A.H. Surface Flashover of Spacer in Compressed Gas Insulated Systems. IEEE Trans. EI 1981, 16, 373–387. [Google Scholar] [CrossRef]
- Hara, M.; Adachi, K.; Tobata, H.; Akazaki, M. Particle Initiated Breakdown Characteristics of Conical Insulator in N2 Gas and N2/O2 Mixture under DC Voltage. IEEE Trans. EI 1987, 22, 431–438. [Google Scholar]
- Haseqawa, T.; Fujiwara, T.; Ooi, H.; Yanabu, S.; Ayogi, H.; Kanno, Y. The Influence of Charging of GIS Epoxy Insulator on DC/Impulse Superimposed Breakdown Characteristics. Gaseous Dielectric VII; Springer: Boston, MA, USA, 1994; pp. 511–517. [Google Scholar]
- Sarathi, R.; Krishnamurthi, M. Breakdown Characteristics of a Short Air Gap with Conducting Particle under Composite Voltages. Gaseous Dielectric VIII; Springer: Boston, MA, USA, 1998; pp. 411–416. [Google Scholar]
- Okabe, S.; Okada, T.; Yuasa, S.; Utsami, T.; Endo, F.; Saitoh, K. Effect of DC Pre-stress on Dielectric Characteristics of an Insulator in SF6 Gas. In Proceedings of the 12th international symposium on high voltage engineering, Bangalore, India, 20–24 August 2001; pp. 351–354. [Google Scholar]
- Sakai, K.; Tsuru, S.; Abella, D.L.; Hara, M. Conducting Particle Motion and Particle Initiated Breakdown in DC Electric Field between Diverging Conducting Plates in Atmospheric Air. IEEE Trans. EI 1999, 6, 43–50. [Google Scholar] [CrossRef]
- Khan, Y.; Sakai, K.; Lee, E.K.; Suehiro, J.; Hara, M. Motion Behavior and Deactivation Method of Free-conducting Particle around Spacer between Diverging Air Gap. IEEE Trans. EI 2003, 10, 444–457. [Google Scholar]
- Khan, Y.; Oda, A.; Okabe, S.; Suehiro, J.; Hara, M. Wire Particle Motion Behavior and Breakdown Characteristics around Different Shaped Spacers within Diverging Air Gap. IWHV 2003, 1, 89–94. [Google Scholar] [CrossRef][Green Version]
- Khan, Y.; Lee, E.K.; Oda, A.; Sakai, k.; Zhang, Q.; Okabe, S.; Suehiro, J.; Hara, M. Characteristics of Corona and Surface Flashover Triggered by Free-conducting Particle around Simple Shaped Spacer under DC Voltage. Proc. Jpn. Korea Jt. Sypo. EDHVE 2001, 1, 101–104. [Google Scholar]
- Cherukupalli, S.E.; Tsurta, K.; Srivastava, K.D. Mechanism of pre-breakdown spacer charging in non-uniform field under unidirectional voltages. IEEE Trans. Electr. Insul. 1990, 25, 642–654. [Google Scholar] [CrossRef]
- Nakanishi, K.; Yoshida, A.; Arahata, Y.; Shibuya, Y. Surface charge on epoxy spacer at DC stress in compressed SF 6 gas. IEEE Trans. Power App. Syst. 1983, 102, 3919–3927. [Google Scholar] [CrossRef]
- Zhu, F.; Fouracre, R.A.; Farish, O. Investigations of surface charging of DC insulator spacers. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena—CEIDP’ 96, Millbrae, CA, USA, 23–23 October 1996; pp. 149–152. [Google Scholar]
- Nitta, T.; Nakanishi, K. Charge accumulation on insulating spacers for HVDC GIS. IEEE Trans. Elctr. Insul. 1991, 26, 418–427. [Google Scholar] [CrossRef]
- Sato, S.; Zaengl, S.W.; Knecht, A. A numerical analysis of accumulated surface charge on DC epoxy resin spacer. IEEE Trans. Electr. Insul. 1987, 22, 333–340. [Google Scholar] [CrossRef]
- Okabe, S.; Ueta, G.; Utsumi, T.; Nukaga, J. Insulation characteristics of GIS insulators under lightning impulse with DC voltage superimposed. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3269–3277. [Google Scholar] [CrossRef]
- Cooke, C.M. Charging of insulator surfaces by ionization and transport in gases. IEEE Trans. Electr. Insul. 1982, 17, 172–178. [Google Scholar] [CrossRef]
- Ren, M.; Dong, M.; Xiao, Z.G.; Qiu, A.C. Partial discharge pulses at artificial protrusions in SF6 under negative IEC 60060-3 standard impulses. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 273–283. [Google Scholar] [CrossRef]
- Zhao, X.F.; Yao, X.; Guo, Z. Partial discharge characteristics and mechanism in voids at impulse voltage. IET Proc. Meas. Sci. Technol. 2011, 22, 035704. [Google Scholar] [CrossRef]
- Zhang, L.; Han, X.T.; Li, X.J.H. Partial discharge detection and analysis of needle-plane defect in SF6 under negative oscillating lightning impulse voltage based on UHF method. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 296–303. [Google Scholar] [CrossRef]
- Ren, M.; Dong, M.; Liu, Y.; Miao, J.; Qiu, A. Partial discharges in SF6 gas filled void under standard oscillating lightning and switching impulses in uniform and non-uniform background fields. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 138–147. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, Q.; You, H.; Wu, Z.; Wen, T.; Guo, C.; Wang, G.; Gao, C. Study on insulation characteristics of GIS under combined voltage of DC and lightning impulse. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 893–900. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, Q.; Wu, Z.; Wen, T.; Guo, C.; Du, Q.; Wang, G.; Gao, C. Study on flashover characteristics of insulators in SF6 under combined voltage of DC and lightning impulse. In Proceedings of the 2017 IEEE Electrical Insulation Conference (EIC), Baltimore, MD, USA, 11–14 June 2017; pp. 62–65. [Google Scholar]
- Ma, J.; Zhang, Q.; Wu, Z.; Guo, C.; Wen, T.; Wang, G.; Gao, C. Breakdown characteristics of particle-contaminated HVDC GIL under superimposed voltage of DC and impulse. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 1439–1447. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, H.Y.; Lu, S.J.; Li, C.R. Insulation Characteristics of SF6/N2-Filled GIS Spacers under Lightning Impulse with DC Voltage Superimposed. In Proceedings of the 2018 IEEE 2nd International Conference on Dielectrics (ICD), Budapest, Hungary, 1–5 July 2018; pp. 1–4. [Google Scholar]
- Ma, G.; Zhou, H.; Wang, Y.; Zhang, H.; Lu, S.; Tu, Y.; Wang, J.; Li, C. Flashover behavior of cone-type spacers with inhomogeneous temperature distribution in SF6/N2-filled DC-GIL under lightning impulse with DC voltage superimposed. CSEE J. Power Energy Syst. 2020, 6, 427–433. [Google Scholar]
- Zhou, H.Y.; Ma, G.M.; Wang, Y.; Li, C.R.; Tu, Y.P.; Ye, S.P.; Zhang, B.; Guo, X.F.; Yan, X.L. Surface charge accumulation on 500kV cone-type GIS spacer under residual DC voltage. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 1230–1237. [Google Scholar] [CrossRef]
- Tenbohlen, S.; Schroder, G. The influence of surface charge on lightning impulse breakdown of spacers in SF6. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 241–246. [Google Scholar] [CrossRef]
- Imano, A.M. The influence of the dielectric strength of the N 2 /SF 6-insulation by conducting particle on the spacer surface. IEEE Trans. Dielectr. Electr. Insul. 2003, 10, 483–490. [Google Scholar] [CrossRef]
- Qi, B.; Li, C.R.; Hao, Z.; Geng, B.B. Surface discharge initiated by immobilized metallic particles attached to gas insulated substation insulators: Process and features. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 792–800. [Google Scholar] [CrossRef]
- Jun, X.; Chalmers, I.D. The influence of surface charge upon flashover of particle-contaminated insulators in SF6 under impulse-voltage conditions. J. Phys. D 1997, 30, 1055–1063. [Google Scholar] [CrossRef]
- Siodla, K.; Kuffel, E.; Fujinami, H. Breakdown of SF/sub 6/ in non-uniform field gaps under combined DC fast oscillating impulse and standard lightning impulse voltages. IEEE Trans. Electr. Insul. 1993, 28, 253–260. [Google Scholar] [CrossRef]
- Seeger, M.; Niemeyer, L.; Bujotzek, M. Leader propagation in uniform background fields in SF6. J. Phys. D Appl. Phys. 2009, 42, 185205. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M.; Pitaevskii, L.P. Electrodynamics of Continuous Media. In Landau and Lifshitz Course of Theoretical Physics, 2nd ed.; Elsevier/Butterworth-Heinemann: Amsterdam, The Netherlands; Volume 8.
- Niemeyer, L.; Ullrich, L.; Wiegart, N. The mechanism of leader breakdown in electronegative gases. IEEE Trans. Electr. Insul. 1989, 24, 309–324. [Google Scholar] [CrossRef]
- Seeger, M.; Niemeyer, L.; Bujotzek, M. Partial discharges and breakdown in SF6 at protrusions in uniform background fields. J. Phys. D Appl. Phys. 2008, 41, 185204. [Google Scholar] [CrossRef]
- Speckhofer, G.; Gilles, R.; Smith, W.; Bures, M. A consistent set of thermodynamic properties and transport coefficients for high temperature plasmas. In Proceedings of the 14th International Symposium on Plasma Chemistry (ISPC-14), Prague, Czech Republic, 2–6 August 1999; Volume 1, pp. 269–274. [Google Scholar]
- Gallimberti, I.; Wiegart, N. Streamer and leader formation in SF6 and SF6 mixtures under positive impulse conditions: II. Streamer to leader transition. J. Phys. D Appl. Phys. 1986, 19, 2363–2379. [Google Scholar] [CrossRef]
- Gallimberti, I.; Ullrich, L.; Wiegart, N. Experimental investigation of the streamer to leader transition in SF6 under negative polarity Gaseous Dielctrics V. In Proceedings of the Fifth International Symposium on Gaseous Dielectrics, Knoxville, TN, USA, 3–7 May 1987; pp. 126–133. [Google Scholar]
- Iwabuchi, H.; Matsuoka, S.; Kumada, A.; Hidaka, K.; Hoshina, Y.; Yasuoka, T.; Takei, M. Influence of tiny metal particles on charge accumulation phenomena of GIS model spacer in high-pressure SF6 gas. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 1895–1901. [Google Scholar]



| Notation | Description | Value | Unit |
|---|---|---|---|
| L | Particle length | 3, 10 | mm |
| D | Gap distance | 15, 50 | mm |
| εr | Spacer permittivity | 5.93 | - |
| Ecr,0 | Critical electric field | 90 | kV/cm−1 |
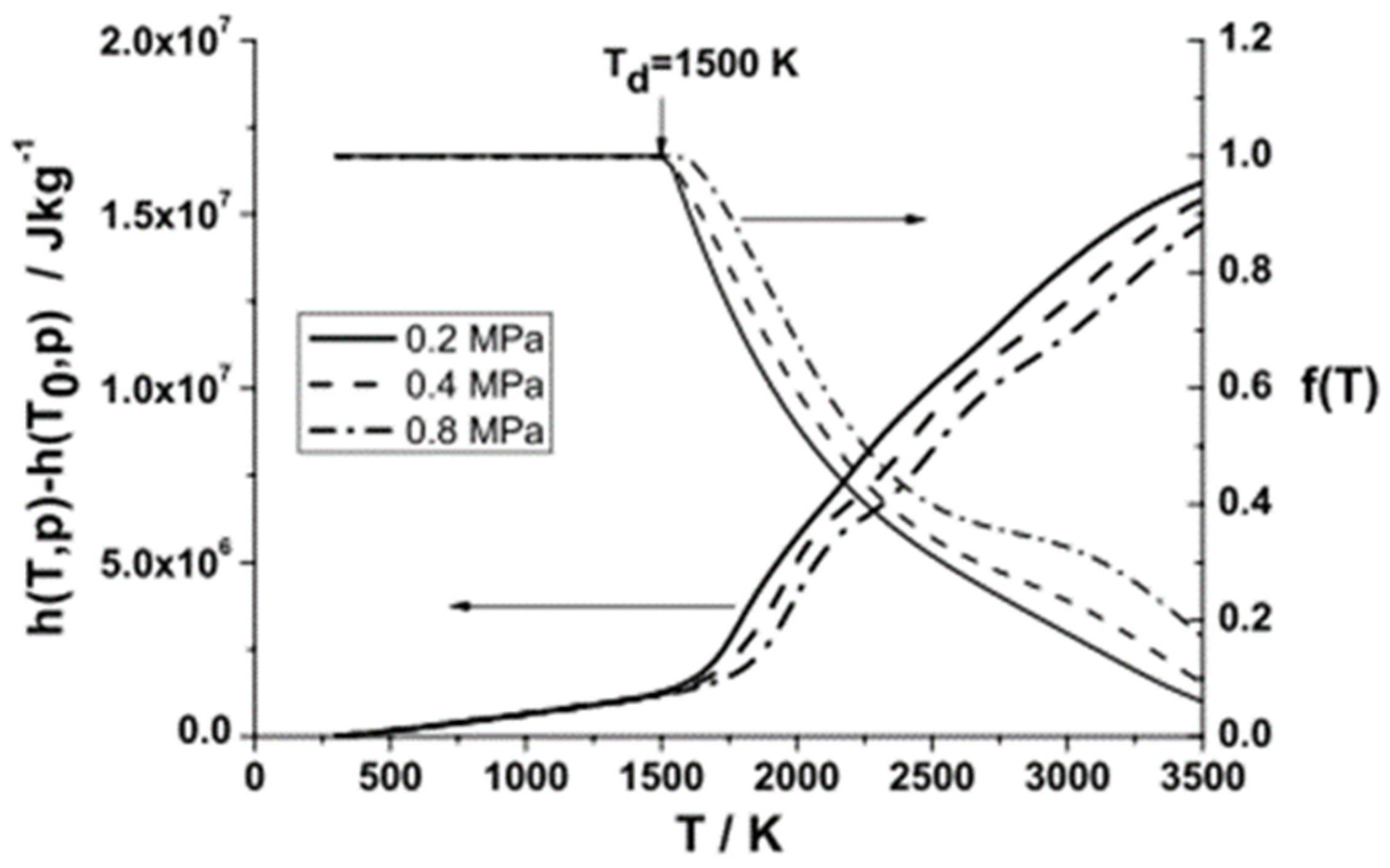
| CΔh | Material constant of SF6 | 4.8 × 105 | Vm2kg−1 |
| Cs | Polarity constant | 2+, 3− | - |
| f(T) | Thermal dissociation function | 0 to 1 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meer, R.; Khan, Y.; Wani, N.R.; Al-Arainy, A.A. The Estimation of Lightning Impulses Superimposed onto Pre-Stressed DC Breakdown Voltages Using the Leader Propagation Method. Energies 2022, 15, 1708. https://doi.org/10.3390/en15051708
Meer R, Khan Y, Wani NR, Al-Arainy AA. The Estimation of Lightning Impulses Superimposed onto Pre-Stressed DC Breakdown Voltages Using the Leader Propagation Method. Energies. 2022; 15(5):1708. https://doi.org/10.3390/en15051708
Chicago/Turabian StyleMeer, Rashed, Yasin Khan, Nissar Rasool Wani, and Abdulrahman Ali Al-Arainy. 2022. "The Estimation of Lightning Impulses Superimposed onto Pre-Stressed DC Breakdown Voltages Using the Leader Propagation Method" Energies 15, no. 5: 1708. https://doi.org/10.3390/en15051708
APA StyleMeer, R., Khan, Y., Wani, N. R., & Al-Arainy, A. A. (2022). The Estimation of Lightning Impulses Superimposed onto Pre-Stressed DC Breakdown Voltages Using the Leader Propagation Method. Energies, 15(5), 1708. https://doi.org/10.3390/en15051708







