LambertW Function to Extract Physical Parameters of a Schottky Barrier Diode from Its I–V Characteristics
Abstract
:1. Introduction
- Optimization methods: these include vertical optimization [18,19], lateral optimization [20] and differential evolution [21]. These methods employ the entire range of the voltage to simultaneously extract all the physical parameters. Nevertheless, they do not take into account the effect of the shunt resistance. Moreover, they require high computation loads and they also require the introduction of initial values.
2. Basic Equations
3. Extraction Methods
3.1. Dynamical Conductance
3.2. Integral Method
3.3. FindFit Function
4. Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Maeda, T.; Takagi, S.; Ohnishi, T.; Lippmaa, M. Sulfur passivation of Ge (001) surfaces and its effects on Schottky barrier contact. Mater. Sci. Semicond. Process. 2006, 9, 706–710. [Google Scholar] [CrossRef]
- Aydoǧan, Ş.; Incekara, Ü.; Deniz, A.R.; Türüt, A. Extraction of electronic parameters of Schottky diode based on an organic Indigotindisulfonate Sodium (IS). Solid State Commun. 2010, 1592–1596. [Google Scholar] [CrossRef]
- Rhoderick, E.H.; Williams, R.H. Metal-Semiconductor Contacts, 2nd ed.; Clarendon Press: Oxford, UK; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
- Missoum, I.; Ocak, Y.S.; Benhaliliba, M.; Benouis, C.E.; Chaker, A. Microelectronic properties of organic Schottky diodes based on MgPc for solar cell applications. Synth. Met. 2010, 214, 76–81. [Google Scholar] [CrossRef]
- Gupta, R.K.; Singh, R.A. Fabrication and characteristics of Schottky diode based on composite organic semiconductors. Compos. Sci. Technol. 2010, 65, 677–681. [Google Scholar] [CrossRef]
- Keskin, B.; Denktaş, C.; Altındal, A.; Avcıata, U.; Gül, A. Synthesis of Ni(II) porphyrazine peripherally octa-substituted with the 4-tert-butylbenzylthio moiety and electronic properties of the Al/Ni(II)Pz/p-Si Schottky barrier diode. Polyhedron 2012, 38, 121–125. [Google Scholar] [CrossRef]
- Peumans, P.; Forrest, S.R. Very high efficiency double heterostructure copper phthalocyanine/C60 photovoltaic cells. Appl. Phys. 2001, 79, 126–128. [Google Scholar] [CrossRef]
- Kim, D.Y.; So, F.; Gao, Y. Aluminum phthalocyanine chloride/C60 organic photovoltaic cells with high open-circuit voltage. Sol. Energ. Mater. Sol. Cells 2009, 93, 1688–1691. [Google Scholar] [CrossRef]
- Pekdemir, F.; Kurnalı, S.; Şengül, A.; Altındal, A.; Özkaya, A.R.; Salih, B.; Bekaroglu, Ö. A conformationally stressed novel ball-type perylenediimide appended zinc(II)phthalocyanine hybrid: Spectro- electrochemical, electrocolorimetric and photovoltaic properties. Dalton Trans. 2009, 44, 158–166. [Google Scholar] [CrossRef]
- Rella, R.; Siciliano, P.; Manno, D.; Serra, A.; Taurino, A.; Tepore, A.; Valli, L.; Zocco, A. Gas-sensing properties of multilayers of two new macrocyclic copper complexes. Sens. Actuators B Chem. 1977, 44, 585–589. [Google Scholar] [CrossRef]
- Şahin, S.; Altun, A.; Altındal, A.; Odabaş, Z. Synthesis of novel azo-bridged phthalocyanines and their toluene vapour sensing properties. Sens. Actuators B Chem. 2015, 206, 601–608. [Google Scholar] [CrossRef]
- Chen, Y.; Hanack, M.; Blau, W.J.; Dini, D.; Liu, Y.; Lin, Y.; Bai, J. Soluble axially substituted phthalocyanines: Synthesis and nonlinear optical response. J. Mater. Sci. 2006, 41, 2169–2185. [Google Scholar] [CrossRef]
- Sze, S.M. Physics of Semiconductor Devices, 2nd ed.; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Norde, H. A modified forward I-V plot for Schottky diodes with high series resistance. J. Appl. Phys. 1979, 50, 5052–5053. [Google Scholar] [CrossRef]
- Cheung, S.K.; Cheung, N.W. Extraction of Schottky diode parameters from forward current-voltage characteristics. Appl. Phys. Lett. 1986, 49, 85–87. [Google Scholar] [CrossRef]
- Werner, J.H. Schottky barrier and pn-junctionI/V plots—Small signal evaluation. Appl. Phys. A 1988, 47, 291–300. [Google Scholar] [CrossRef]
- Werner, J.H.; Guttler, J.H. Barrier Inhomogeneities at Schottky Contacts. J. Appl. Phys. 1991, 69, 1522–1533. [Google Scholar] [CrossRef]
- Osvald, J.; Dobročka, E. Generalized approach to the parameter extraction from I-V characteristics of Schottky diodes. Semicond. Sci. Technol. 1996, 11, 1198–1202. [Google Scholar] [CrossRef]
- Garcia Sanchez, F.J.; Ortiz-Conde, A.; Salcedo, J.A.; Liou, J.J.; Yue, Y. Extraction of the bulk-charge effect parameter in MOSFETs. In Proceedings of the 2000 22nd International Conference on Microelectronics, Nis, Yugoslavia, 14–17 May 2000. [Google Scholar]
- Ortiz-Conde, A.; Thomson, Y.M.J.; Santos, E.; Liou, J.J.; García Sànchez, F.J.; Lei, M.; Finol, J.; Layman, P. Direct extraction of semiconductor device parameters using lateral optimization method. Solid-State Electron. 1999, 43, 845–848. [Google Scholar] [CrossRef]
- Wang, K.; Ye, M. Parameter determination of Schottky-barrier diode model using differential evolution. Solid-State Electron. 2009, 53, 234–240. [Google Scholar] [CrossRef]
- Oruç, Ç.; Altındal, A. Comparative study of I–V methods to extract Au/FePc/p-Si Schottky barrier diode parameters. Appl. Phys. A 2018, 124, 1–8. [Google Scholar] [CrossRef]
- Banwell, T.C.; Jayakumar, A. Exact analytical solution for current flow through diode with series resistance. Electron. Lett. 2000, 36, 291–292. [Google Scholar] [CrossRef]
- Jain, A.; Kapoor, A. Exact analytical solutions of the parameters of real solar cells using Lambert W-function. Sol. Energy Mater. Sol. Cells 2004, 81, 269–277. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W Function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Mathematica 5.0, Copyright; Wolfram Research Inc.: Champaign, IL, USA, 2014.
- Dawidowski, W.; Ściana, B.; Zborowska-Lindert, I.; Mikolášek, M.; Bielak, K.; Badura, M.; Pucicki, D.; Radziewicz, D.; Kovác, J.; Tłaczał, M. The influence of top electrode of InGaAsN/GaAs solar cell on their electrical parameters extracted from illuminated I–V characteristics. Solid-State Electron. 2016, 120, 13–18. [Google Scholar] [CrossRef]
- Seon, Y.; Kim, J.; Kim, S.; Jeon, J. Analytical Current-Voltage Model for Gate-All-Around Transistor with Poly-Crystalline Silicon Channel. Electronics 2019, 8, 988. [Google Scholar] [CrossRef] [Green Version]
- Steinvall, O. Laser system range calculations and the Lambert W function. Appl. Opt. 2009, 48, B1–B7. [Google Scholar] [CrossRef]
- Lian, Y.; Lan, D.; Xing, S.; Guo, B.; Lai, R.; Zhao, B.; Friend, R.H.; Di, D. Ultralow-voltage operation of light-emitting diodes. arXiv 2021, arXiv:2108.01549. [Google Scholar]
- Zaimi, M.; El Achouby, H.; Ibral, A.; Assaid, E.M. Determining combined effects of solar radiation and panel junction temperature on all model-parameters to forecast peak power and photovoltaic yield of solar panel under non-standard conditions. Solar Energy 2019, 191, 341–359. [Google Scholar] [CrossRef]
- El Achouby, H.; Zaimi, M.; Ibral, A.; Assaid, E.M. New analytical approach for modelling effects of temperature and irradiance on physical parameters of photovoltaic solar module. Energy Convers. Manag. 2018, 177, 258–271. [Google Scholar] [CrossRef]
- Stone, R.J. Improved statistical procedure for the evaluation of solar radiation estimation models. Solar Energy 1993, 51, 289–291. [Google Scholar] [CrossRef]
- Aazou, S.; Ibral, A.; White, M.S.; Kaltenbrunner, M.; Głowacki, E.D.; Egbe, D.A.M.; Sariçiftçi, N.S.; Assaid, E.M. Organic bulk heterojunction solar cells based on P3HT and Anthracene- Containing PPE-PPV: Fabrication, Characterization and Modeling. J. Optoelectron. Adv. M 2013, 13, 395–404. [Google Scholar]
- White, M.S.; Kaltenbrunner, M.; Głowacki, E.D.; Gutnichenko, K.; Kettlgruber, G.; Graz, I.; Aazou, S.; Ulbricht, C.; Egbe, D.A.; Miron, M.C.; et al. Ultrathin, highly flexible and stretchable PLEDs. Nat. Photonics 2013, 7, 211–216. [Google Scholar] [CrossRef]
- Jung, W.; Guziewicz, M. Schottky diode parameters extraction using Lambert W function. Mater. Sci. Eng. B 2009, 165, 57–59. [Google Scholar] [CrossRef]
- Kumar, V.; Maan A., S.; Akhtar, J. Barrier height inhomogeneities induced anomaly in thermal sensitivity of Ni/4H-SiC Schottky diode temperature sensor. J. Vac. Sci. Technol. B 2014, 32, 041203. [Google Scholar] [CrossRef]
- Kumar, V.; Verma, J.; Maan A., S.; Akhtar, J. Epitaxial 4H-SiC based Schottky diode temperature sensors in ultra-low current range. Vacuum 2020, 182, 109590. [Google Scholar] [CrossRef]
- Aydin, M.; Akkılıç, K.; Kılıçoǧlu, T. The importance of the series resistance in calculating the characteristic parameters of the Schottky contacts. Appl. Surf. Sci. 2006, 253, 1304–1309. [Google Scholar] [CrossRef]
- Türüt, A.; Bati, B.; Kökçe, A.; Saǧlam, M.; Yalçin, N. The bias-dependence change of barrier height of Schottky diodes under forward bias by including the series resistance effect. Phys. Scr. 1996, 53, 118–122. [Google Scholar] [CrossRef]
- Ortiz-conde, A.; Garcia Sànchez, F.J.; Muci, J. New method to extract the model parameters of solar cells from the explicit analytic solutions of their illuminated I–V characteristics. Sol. Energy Mater. Sol. Cells 2006, 90, 352–361. [Google Scholar] [CrossRef]
- Brent, R.P. Algorithms for Minimization without Derivatives; Dover: New York, NY, USA, 2002. [Google Scholar]
- Fonash, S.J. Solar Cell Device Physics, 2nd ed.; Academic Press: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Castañer, L.; Silvestre, S. Modelling Photovoltaic Systems Using PSpice; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Brousse, B. Réalisation et Caractérisation de Cellule Photovoltaïque Organique Obtenues par Dépôt Physique. Ph.D. Thesis, Université de Limoges, Limoges, France, 2004. [Google Scholar]
- Available online: www.pveducation.org (accessed on 21 May 2019).
- Boudjemline, S.A. Réalisation et Caractérisation des Cellules Photovoltaïques Plastiques. Ph.D. Thesis, Université d’Angers, Angers, France, 2004. [Google Scholar]
- Steadman, J.W. Chapter Section III: Electronics; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
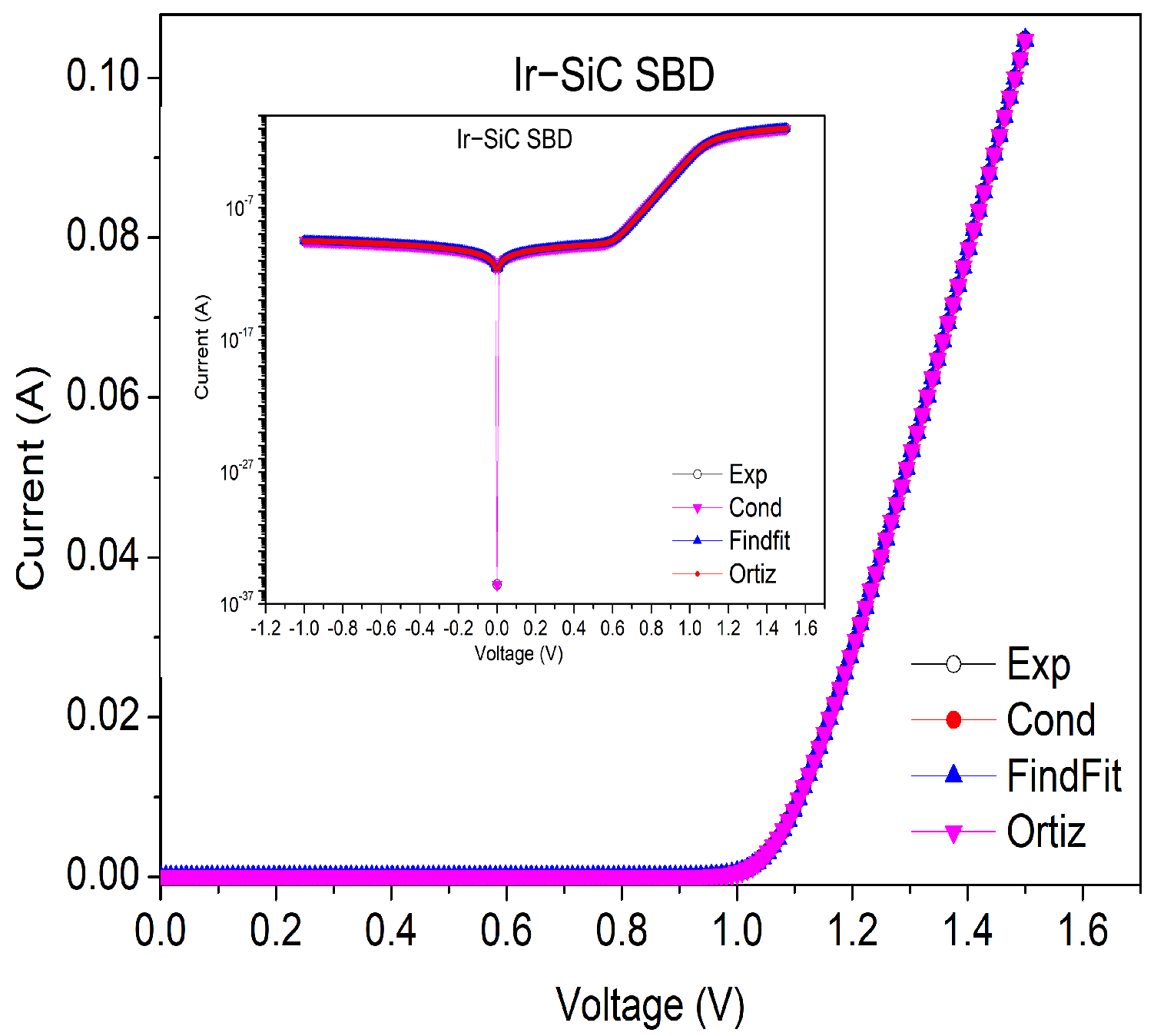
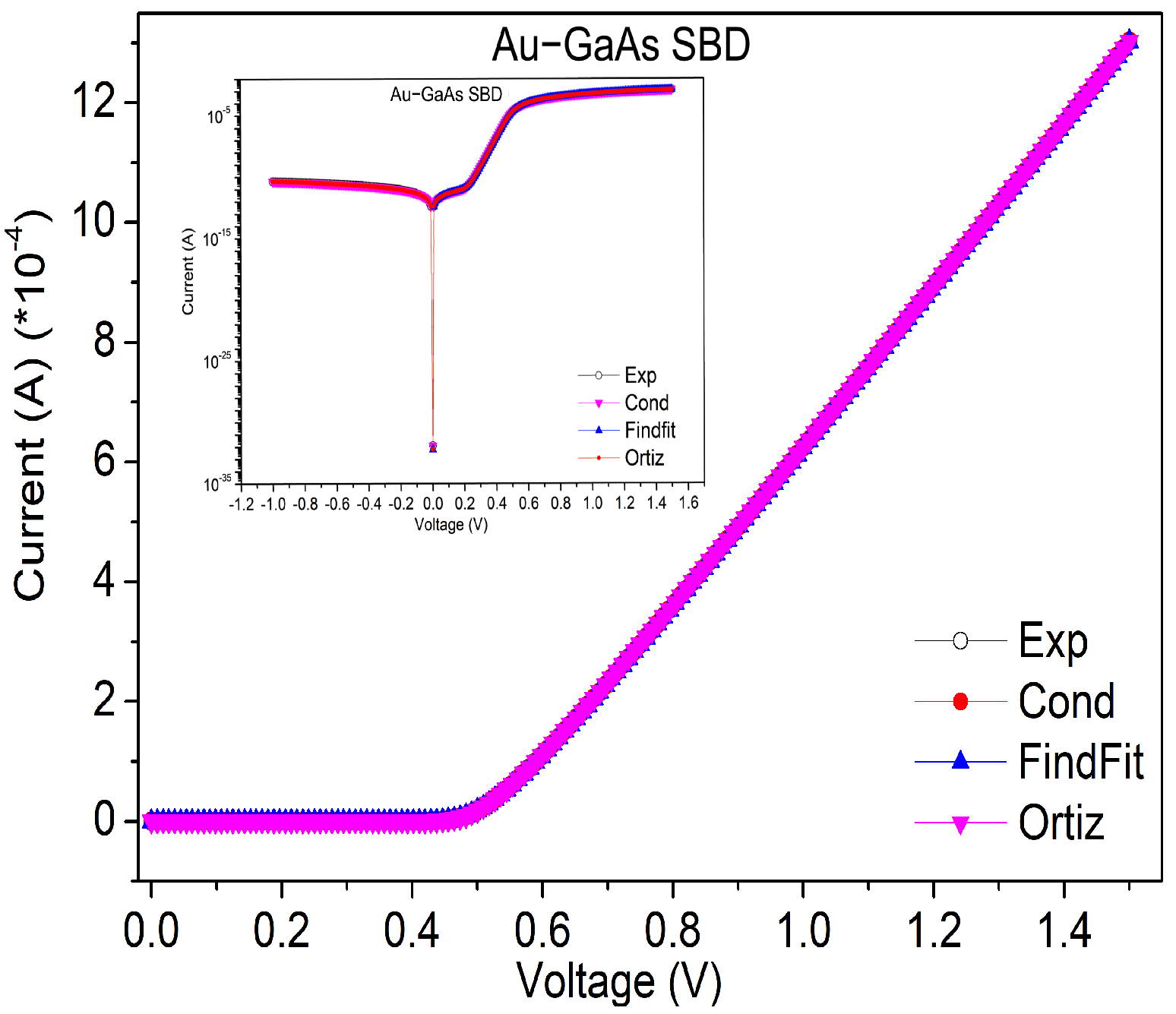


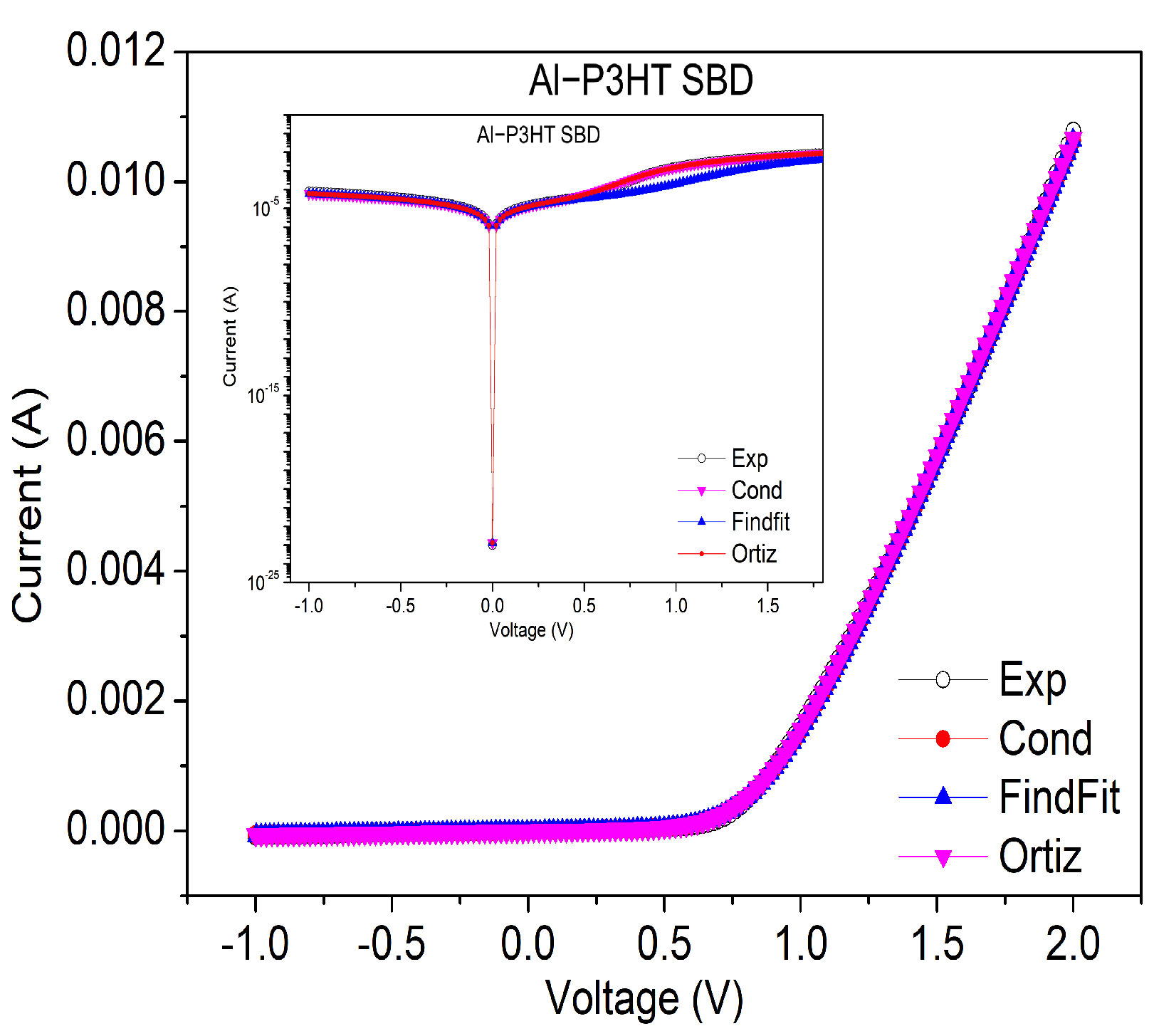

| Conductance | Integral | FindFit | |
|---|---|---|---|
| A) | |||
| 1.02 | |||
| 3.48 | 3.48 | ||
| Conductance | Integral | FindFit | |
|---|---|---|---|
| A) | |||
| 718 | 718 | 719 | |
| Conductance | Integral | FindFit | |
|---|---|---|---|
| A) | 8 | 8 | |
| 91 | 91 | 91 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aazou, S.; White, M.S.; Kaltenbrunner, M.; Sekkat, Z.; Egbe, D.A.M.; Assaid, E.M. LambertW Function to Extract Physical Parameters of a Schottky Barrier Diode from Its I–V Characteristics. Energies 2022, 15, 1667. https://doi.org/10.3390/en15051667
Aazou S, White MS, Kaltenbrunner M, Sekkat Z, Egbe DAM, Assaid EM. LambertW Function to Extract Physical Parameters of a Schottky Barrier Diode from Its I–V Characteristics. Energies. 2022; 15(5):1667. https://doi.org/10.3390/en15051667
Chicago/Turabian StyleAazou, Safae, Matthew Schuette White, Martin Kaltenbrunner, Zouheir Sekkat, Daniel Ayuk Mbi Egbe, and El Mahdi Assaid. 2022. "LambertW Function to Extract Physical Parameters of a Schottky Barrier Diode from Its I–V Characteristics" Energies 15, no. 5: 1667. https://doi.org/10.3390/en15051667
APA StyleAazou, S., White, M. S., Kaltenbrunner, M., Sekkat, Z., Egbe, D. A. M., & Assaid, E. M. (2022). LambertW Function to Extract Physical Parameters of a Schottky Barrier Diode from Its I–V Characteristics. Energies, 15(5), 1667. https://doi.org/10.3390/en15051667







