Influence of a Central Jet on Isothermal and Reacting Swirling Flow in a Model Combustion Chamber
Abstract
:1. Introduction
2. Experimental Setup and Flow Regimes
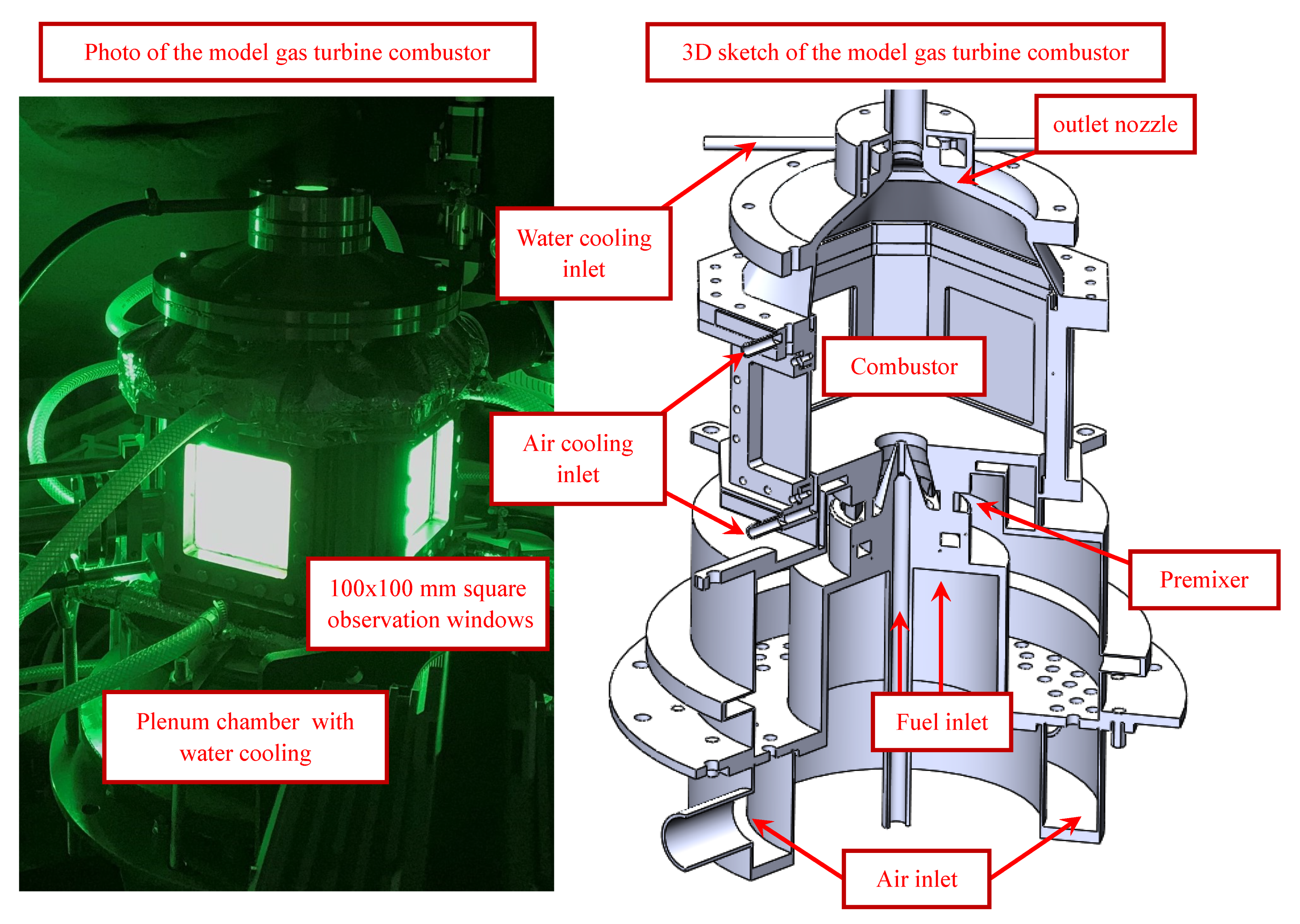
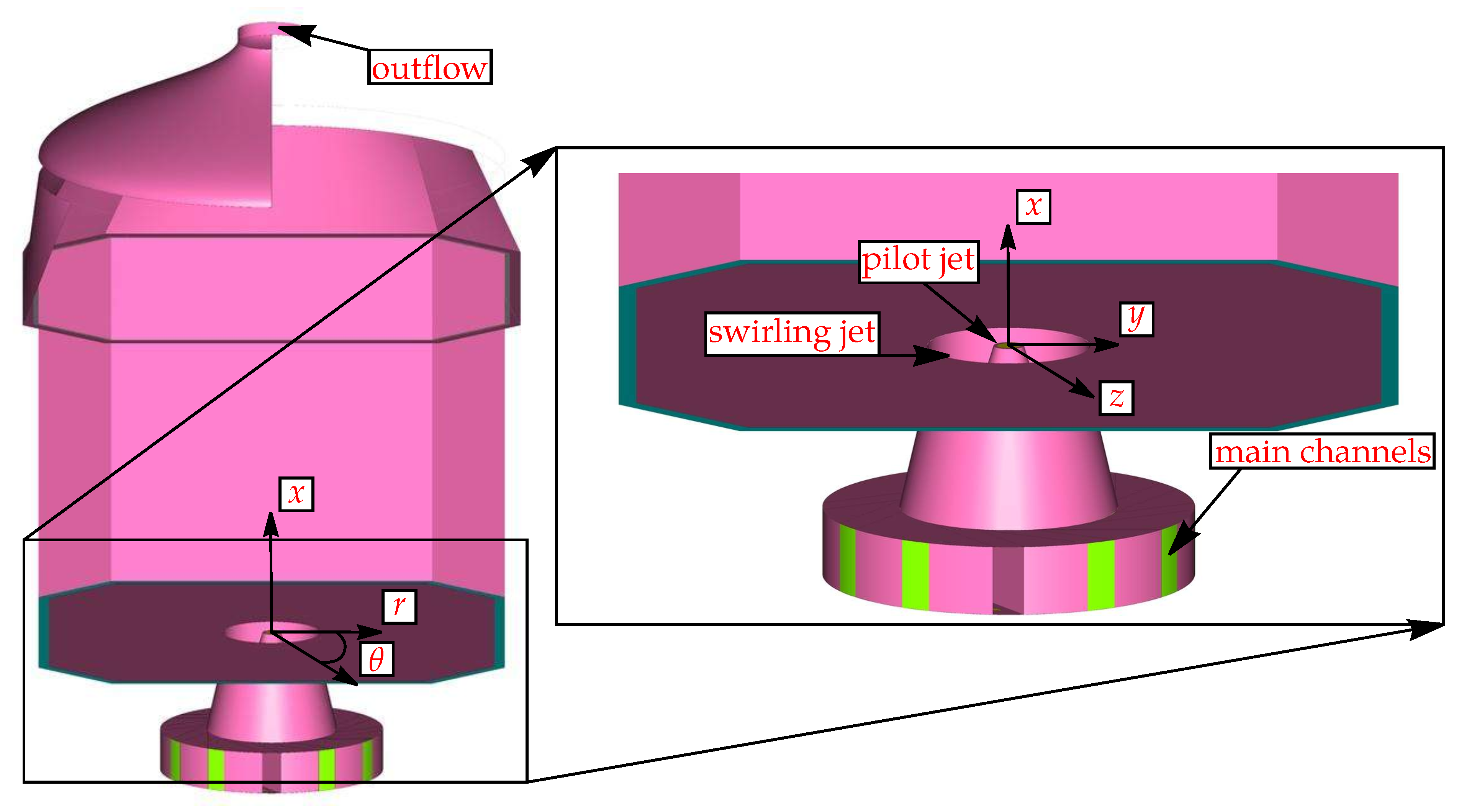
2.1. Combustor
2.2. PIV Measurements
3. Computational Details
4. Results
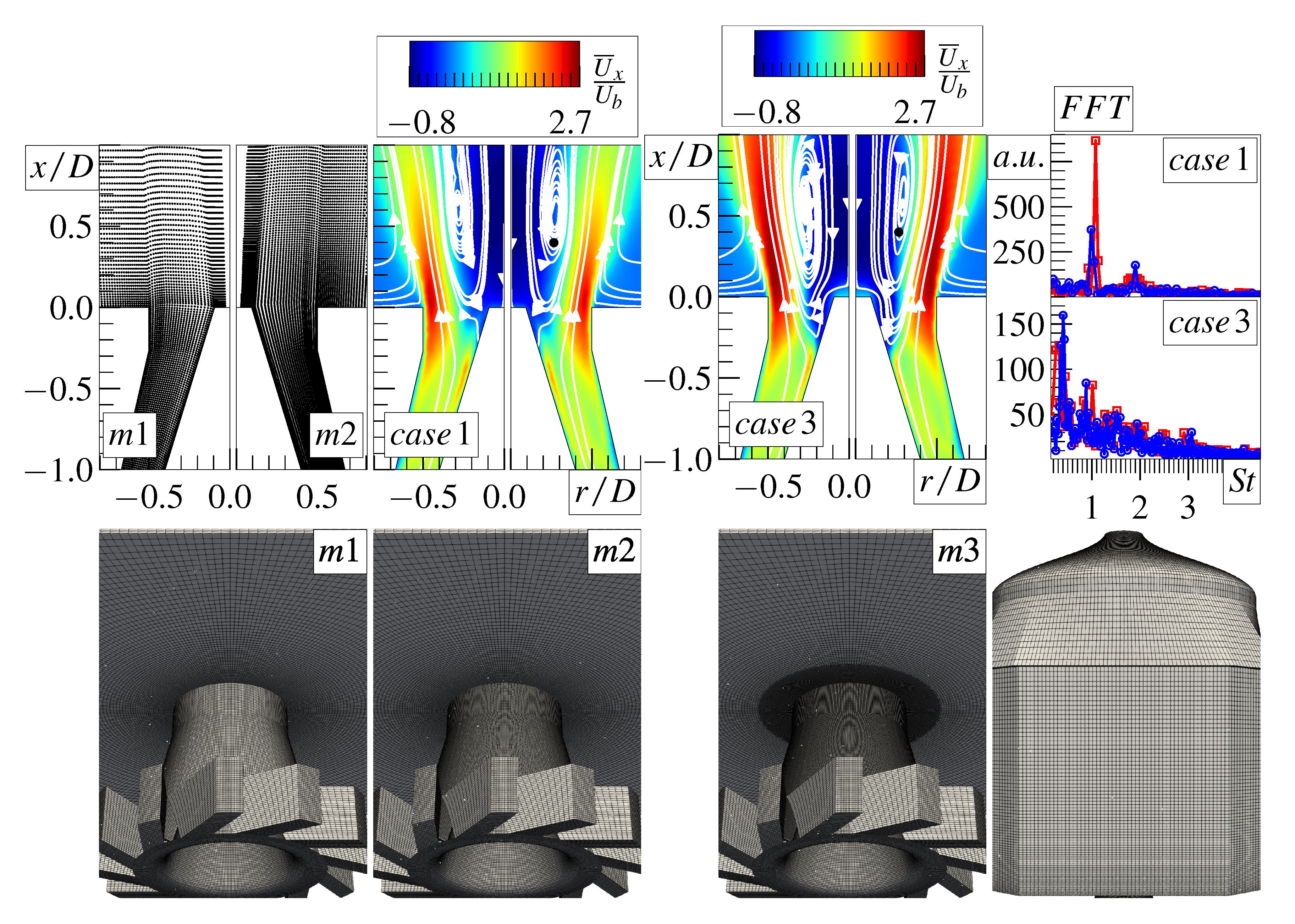
4.1. Mesh Convergence
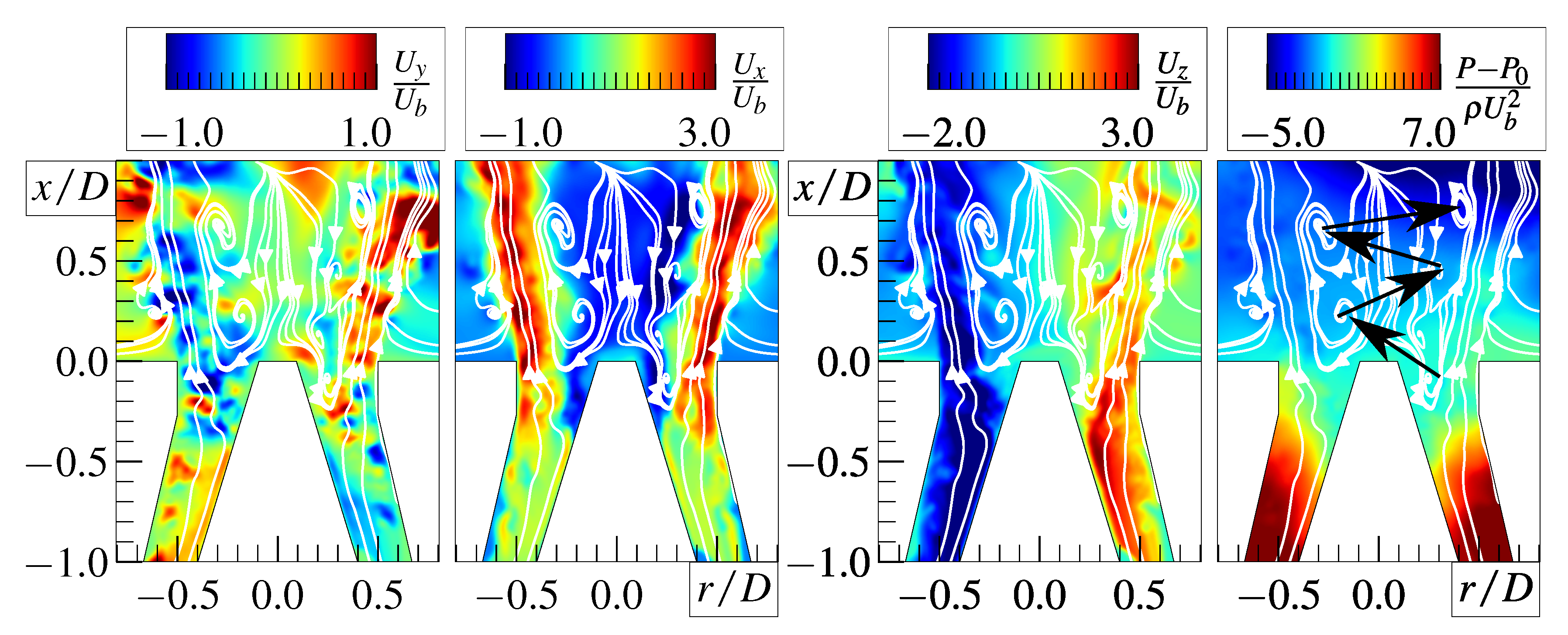
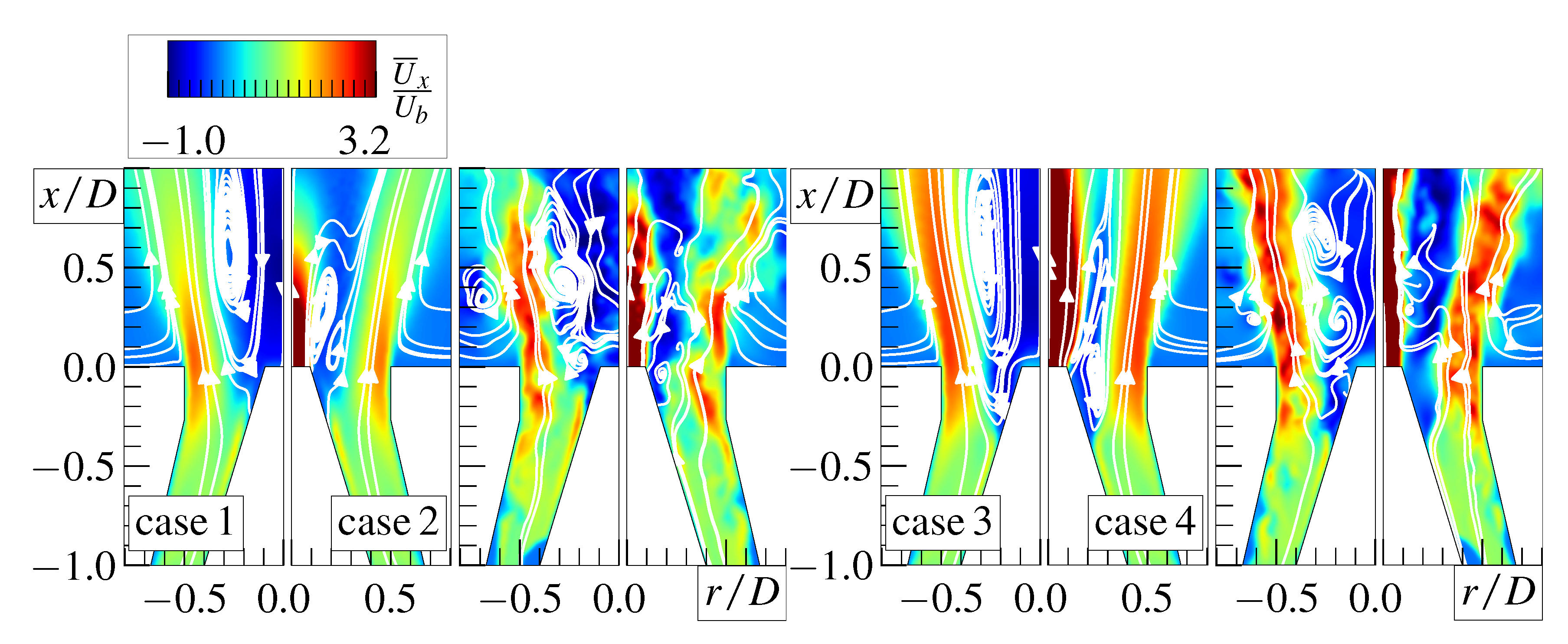
4.2. No Central Jet
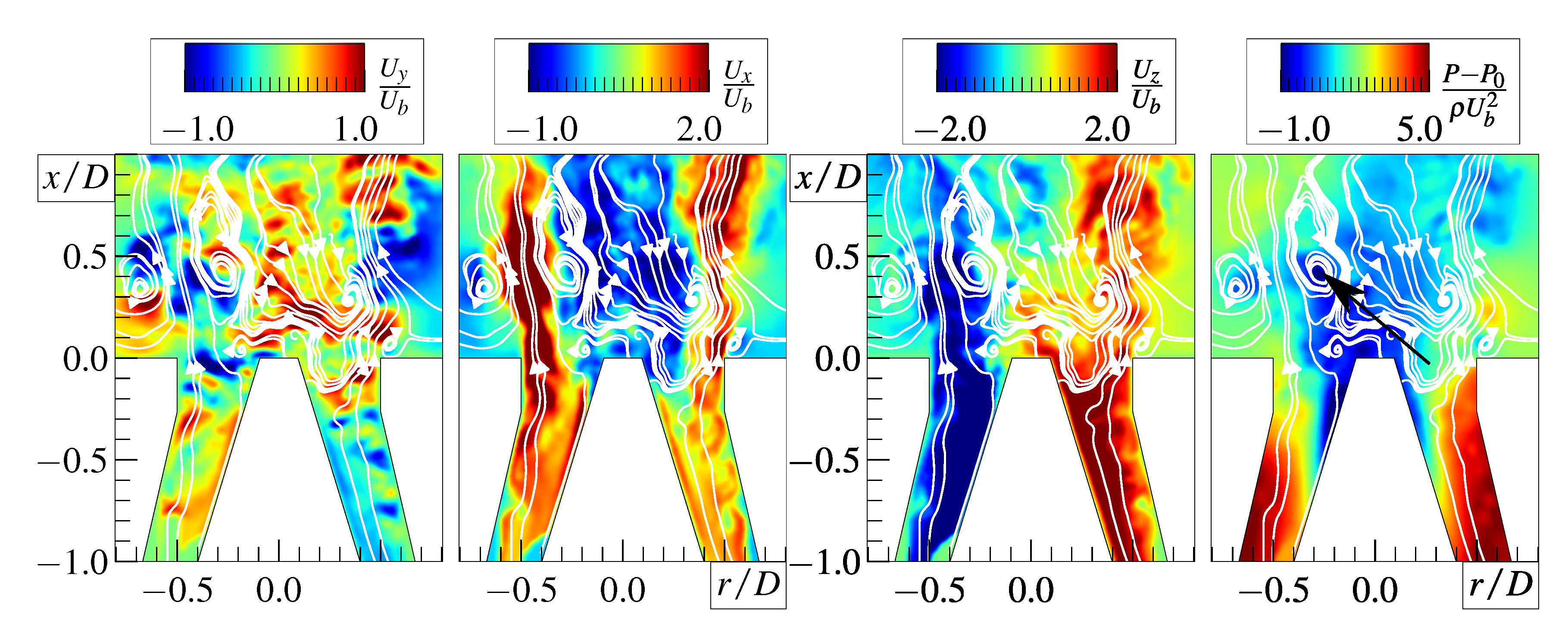
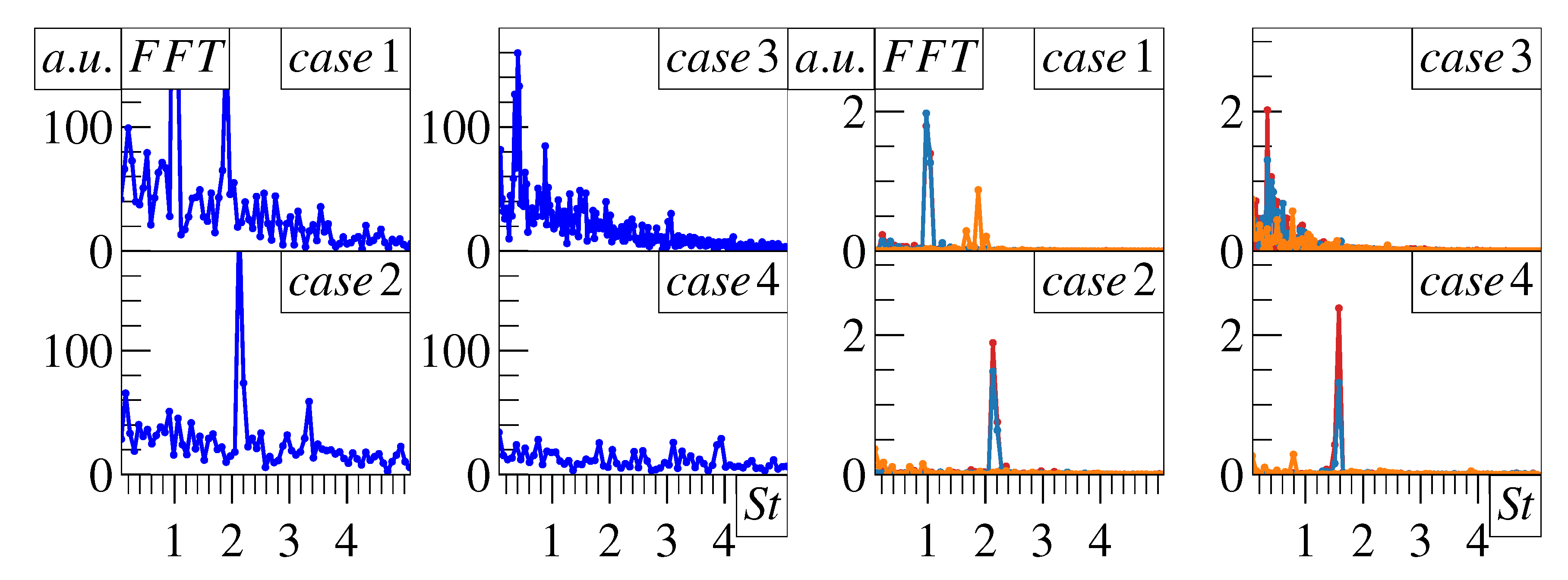
4.3. Central Jet Effect
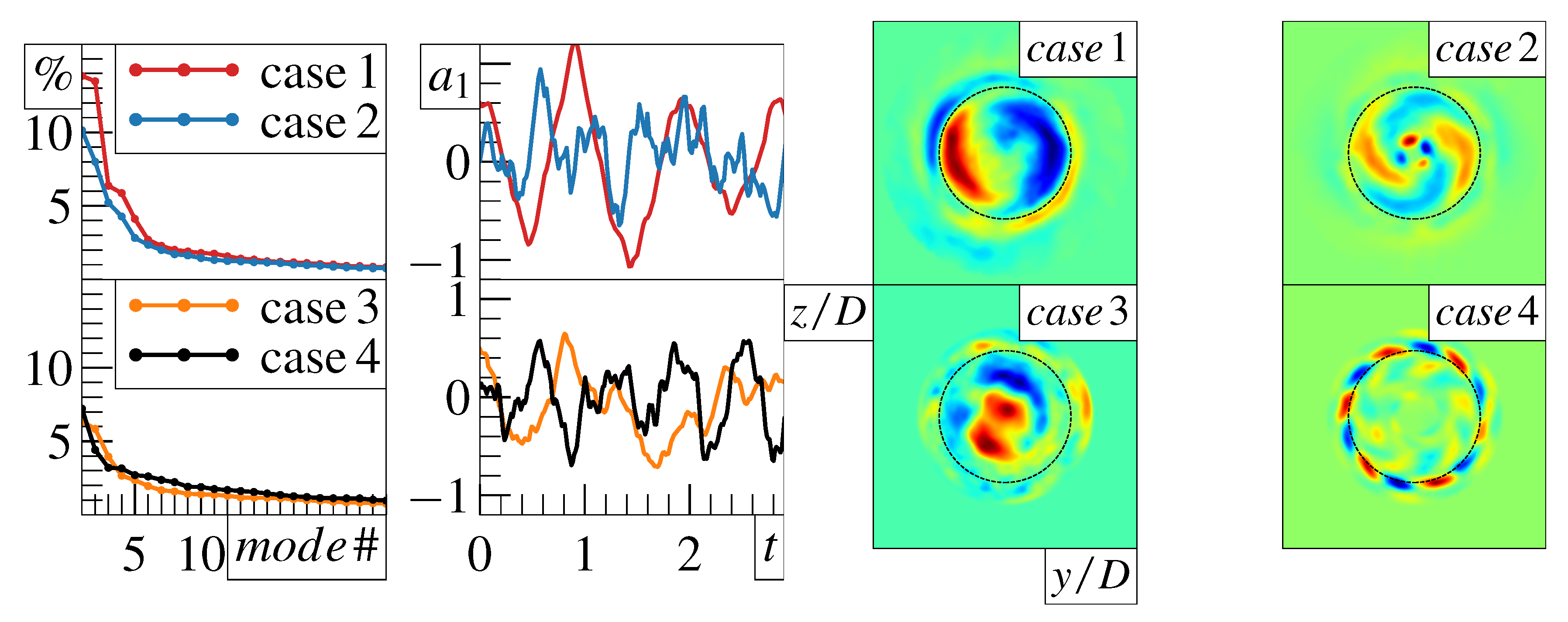
4.4. Proper Orthogonal Decomposition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PVC | Precessing vortex core |
| LES | Large-eddy simulation |
| PIV | Partice image velocimetry |
| PLIF | Planar laser-induced fluorescence |
| FGM | Flamelet-generated manifold |
| POD | Proper orthogonal decomposition |
| (r, , x) | Cylindrical coordiante system components |
| (x, y, z) | Cartesian coordiante system components |
| D | diameter of the swirler nozzle |
| dynamic viscosity | |
| turbulent viscosity | |
| f | frequency in Hz |
| bulk velocity calculated through the swirler nozzle | |
| bulk velocity calculated through the pilot nozzle | |
| St | Strouhal number |
| volumetric flow rate for air supplied in the air channel | |
| volumetric flow rate for fuel supplied in the pilot nozzle | |
| density | |
| velocity component | |
| p | pressure |
| progress variable | |
| Z | mixture fraction |
| time-averaged velocity component | |
| Favre-averaged velocity component | |
| subgrid-scale stresses tensor | |
| Schmidt number | |
| m | POD mode |
| energy in m POD mode |
References
- Gupta, A.; Lilley, D.; Syred, N. Swirl Flows; Abacus Press: Tunbridge Wells, UK, 1984. [Google Scholar]
- Weber, R.; Dugué, J. Combustion accelerated swirling flows in high confinements. Prog. Energy Combust. Sci. 1992, 18, 349–367. [Google Scholar] [CrossRef]
- Tacina, R. Combustor technology for future aircraft. In Proceedings of the 26th Joint Propulsion Conference, Orlando, FL, USA, 16–18 July 1990; p. 2400. [Google Scholar]
- Correa, S.M. Power generation and aeropropulsion gas turbines: From combustion science to combustion technology. Symp. Int. Combust. 1998, 27, 1793–1807. [Google Scholar] [CrossRef]
- Lefebvre, A. Gas Turbine Combustion, 2nd ed.; Taylor & Francis: Philadelphia, PA, USA, 1999. [Google Scholar]
- Dunn-Rankin, D. Lean Combustion: Technology and Control; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Lieuwen, T.; Torres, H.; Johnson, C.; Zinn, B. A mechanism of combustion instability in lean premixed gas turbine combustors. J. Eng. Gas Turbines Power 2001, 123, 182–189. [Google Scholar] [CrossRef]
- Billant, P.; Chomaz, J.M.; Huerre, P. Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 1998, 376, 183–219. [Google Scholar] [CrossRef] [Green Version]
- Lucca-Negro, O.; O’doherty, T. Vortex breakdown: A review. Prog. Energy Combust. Sci. 2001, 27, 431–481. [Google Scholar] [CrossRef]
- Syred, N. A review of oscillation mechanisms and the role of the precessing vortex core (PVC) in swirl combustion systems. Prog. Energy Combust. Sci. 2006, 32, 93–161. [Google Scholar] [CrossRef]
- Ruith, M.; Chen, P.; Meiburg, E.; Maxworthy, T. Three-dimensional vortex breakdown in swirling jets and wakes: Direct numerical simulation. J. Fluid Mech. 2003, 486, 331–378. [Google Scholar] [CrossRef] [Green Version]
- Akhmetov, D.; Nikulin, V.; Petrov, V. Experimental study of self-oscillations developing in a swirling-jet flow. Fluid Dyn. 2004, 39, 406–413. [Google Scholar] [CrossRef]
- Oberleithner, K.; Sieber, M.; Nayeri, C.N.; Paschereit, C.O.; Petz, C.; Hege, H.C.; Noack, B.R.; Wygnanski, I. Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: Stability analysis and empirical mode construction. J. Fluid Mech. 2011, 679, 383–414. [Google Scholar] [CrossRef] [Green Version]
- Oberleithner, K.; Paschereit, C.O.; Seele, R.; Wygnanski, I. Formation of turbulent vortex breakdown: Intermittency, criticality, and global instability. AIAA J. 2012, 50, 1437–1452. [Google Scholar] [CrossRef]
- Cala, C.; Fernandes, E.; Heitor, M.; Shtork, S. Coherent structures in unsteady swirling jet flow. Exp. Fluids 2006, 40, 267–276. [Google Scholar] [CrossRef]
- Alekseenko, S.; Dulin, V.; Kozorezov, Y.S.; Markovich, D. Effect of high-amplitude forcing on turbulent combustion intensity and vortex core precession in a strongly swirling lifted propane/air flame. Combust. Sci. Technol. 2012, 184, 1862–1890. [Google Scholar] [CrossRef]
- Oberleithner, K.; Paschereit, C.O.; Wygnanski, I. On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 2014, 741, 156–199. [Google Scholar] [CrossRef] [Green Version]
- McManus, K.; Poinsot, T.; Candel, S.M. A review of active control of combustion instabilities. Prog. Energy Combust. Sci. 1993, 19, 1–29. [Google Scholar] [CrossRef]
- Lieuwen, T.C. Unsteady Combustor Physics; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Moeck, J.P.; Bourgouin, J.F.; Durox, D.; Schuller, T.; Candel, S. Nonlinear interaction between a precessing vortex core and acoustic oscillations in a turbulent swirling flame. Combust. Flame 2012, 159, 2650–2668. [Google Scholar] [CrossRef]
- Oberleithner, K.; Schimek, S.; Paschereit, C.O. Shear flow instabilities in swirl-stabilized combustors and their impact on the amplitude dependent flame response: A linear stability analysis. Combust. Flame 2015, 162, 86–99. [Google Scholar] [CrossRef]
- Terhaar, S.; Ćosić, B.; Paschereit, C.; Oberleithner, K. Suppression and excitation of the precessing vortex core by acoustic velocity fluctuations: An experimental and analytical study. Combust. Flame 2016, 172, 234–251. [Google Scholar] [CrossRef]
- Ghani, A.; Poinsot, T.; Gicquel, L.; Müller, J.D. LES study of transverse acoustic instabilities in a swirled kerosene/air combustion chamber. Flow Turbul. Combust. 2016, 96, 207–226. [Google Scholar] [CrossRef] [Green Version]
- Stöhr, M.; Arndt, C.M.; Meier, W. Transient effects of fuel–air mixing in a partially-premixed turbulent swirl flame. Proc. Combust. Inst. 2015, 35, 3327–3335. [Google Scholar] [CrossRef] [Green Version]
- Terhaar, S.; Krüger, O.; Paschereit, C.O. Flow field and flame dynamics of swirling methane and hydrogen flames at dry and steam diluted conditions. J. Eng. Gas Turbines Power 2015, 137, 041503. [Google Scholar] [CrossRef]
- Reynolds, W.; Alonso, J.; Fatica, M. Aircraft gas turbine engine simulations. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 3698. [Google Scholar]
- Stricker, W.P. Measurement of Temperature in Laboratory Flames and Practical Devices; Taylor and Francis: New York, NY, USA, 2002. [Google Scholar]
- Meier, W.; Duan, X.R.; Weigand, P.; Lehmann, B. Temperatur-Messungen in turbulenten Drallflammen: Thermoelemente im Vergleich zu Laser-Raman-Streuung. Gas Wärme Int. 2004, 53, 153–158. [Google Scholar]
- Stöhr, M.; Sadanandan, R.; Meier, W. Experimental study of unsteady flame structures of an oscillating swirl flame in a gas turbine model combustor. Proc. Combust. Inst. 2009, 32, 2925–2932. [Google Scholar] [CrossRef]
- Boxx, I.; Stöhr, M.; Carter, C.; Meier, W. Temporally resolved planar measurements of transient phenomena in a partially pre-mixed swirl flame in a gas turbine model combustor. Combust. Flame 2010, 157, 1510–1525. [Google Scholar] [CrossRef] [Green Version]
- Midgley, K.; Spencer, A.; McGuirk, J. Unsteady flow structures in radial swirler fed fuel injectors. J. Eng. Gas Turbines Power 2005, 127, 755–764. [Google Scholar] [CrossRef]
- Spencer, A.; McGuirk, J.; Midgley, K. Vortex breakdown in swirling fuel injector flows. J. Eng. Gas Turbines Power 2008, 130, 021503. [Google Scholar] [CrossRef]
- Kim, W.W.; Menon, S.; Mongia, H.C. Large-eddy simulation of a gas turbine combustor flow. Combust. Sci. Technol. 1999, 143, 25–62. [Google Scholar] [CrossRef]
- Selle, L.; Lartigue, G.; Poinsot, T.; Koch, R.; Schildmacher, K.U.; Krebs, W.; Prade, B.; Kaufmann, P.; Veynante, D. Compressible large eddy simulation of turbulent combustion in complex geometry on unstructured meshes. Combust. Flame 2004, 137, 489–505. [Google Scholar] [CrossRef]
- Duwig, C.; Fuchs, L. Large eddy simulation of vortex breakdown/flame interaction. Phys. Fluids 2007, 19, 075103. [Google Scholar] [CrossRef]
- Dunham, D.; Spencer, A.; McGuirk, J.; Dianat, M. Comparison of URANS and LES CFD methodologies for air swirl fuel injectors. Turbo Expo Power Land Sea Air 2008, 43130, 187–196. [Google Scholar]
- Moureau, V.; Domingo, P.; Vervisch, L. From large-eddy simulation to direct numerical simulation of a lean premixed swirl flame: Filtered laminar flame-pdf modeling. Combust. Flame 2011, 158, 1340–1357. [Google Scholar] [CrossRef]
- Paschereit, C.O.; Gutmark, E.; Weisenstein, W. Structure and control of thermoacoustic instabilities in a gas-turbine combustor. Combust. Sci. Technol. 1998, 138, 213–232. [Google Scholar] [CrossRef]
- Paschereit, C.O.; Gutmark, E.; Weisenstein, W. Coherent structures in swirling flows and their role in acoustic combustion control. Phys. Fluids 1999, 11, 2667–2678. [Google Scholar] [CrossRef]
- Paschereit, C.O.; Gutmark, E.; Weisenstein, W. Excitation of thermoacoustic instabilities by interaction of acoustics and unstable swirling flow. AIAA J. 2000, 38, 1025–1034. [Google Scholar] [CrossRef]
- Külsheimer, C.; Büchner, H. Combustion dynamics of turbulent swirling flames. Combust. Flame 2002, 131, 70–84. [Google Scholar] [CrossRef]
- Balachandran, R.; Ayoola, B.; Kaminski, C.; Dowling, A.; Mastorakos, E. Experimental investigation of the nonlinear response of turbulent premixed flames to imposed inlet velocity oscillations. Combust. Flame 2005, 143, 37–55. [Google Scholar] [CrossRef]
- Bellows, B.D.; Neumeier, Y.; Lieuwen, T. Forced response of a swirling, premixed flame to flow disturbances. J. Propuls. Power 2006, 22, 1075–1084. [Google Scholar] [CrossRef]
- Bellows, B.D.; Bobba, M.K.; Forte, A.; Seitzman, J.M.; Lieuwen, T. Flame transfer function saturation mechanisms in a swirl-stabilized combustor. Proc. Combust. Inst. 2007, 31, 3181–3188. [Google Scholar] [CrossRef]
- Giauque, A.; SELLE, L.; Gicquel, L.; Poinsot, T.; Buechner, H.; Kaufmann, P.; Krebs, W. System identification of a large-scale swirled partially premixed combustor using LES and measurements. J. Turbul. 2005, 6, N21. [Google Scholar] [CrossRef]
- Kang, D.; Culick, F.; Ratner, A. Combustion dynamics of a low-swirl combustor. Combust. Flame 2007, 151, 412–425. [Google Scholar] [CrossRef]
- Lacarelle, A.; Faustmann, T.; Greenblatt, D.; Paschereit, C.; Lehmann, O.; Luchtenburg, D.; Noack, B. Spatiotemporal characterization of a conical swirler flow field under strong forcing. J. Eng. Gas Turbines Power 2009, 131, 031504. [Google Scholar] [CrossRef] [Green Version]
- Ayoola, B.; Hartung, G.; Armitage, C.; Hult, J.; Cant, R.; Kaminski, C. Temperature response of turbulent premixed flames to inlet velocity oscillations. Exp. Fluids 2009, 46, 27–41. [Google Scholar] [CrossRef]
- Thumuluru, S.K.; Lieuwen, T. Characterization of acoustically forced swirl flame dynamics. Proc. Combust. Inst. 2009, 32, 2893–2900. [Google Scholar] [CrossRef]
- Kim, K.T.; Lee, J.G.; Quay, B.; Santavicca, D. Response of partially premixed flames to acoustic velocity and equivalence ratio perturbations. Combust. Flame 2010, 157, 1731–1744. [Google Scholar] [CrossRef]
- Kim, K.T.; Hochgreb, S. The nonlinear heat release response of stratified lean-premixed flames to acoustic velocity oscillations. Combust. Flame 2011, 158, 2482–2499. [Google Scholar] [CrossRef]
- Palies, P.; Durox, D.; Schuller, T.; Candel, S. The combined dynamics of swirler and turbulent premixed swirling flames. Combust. Flame 2010, 157, 1698–1717. [Google Scholar] [CrossRef]
- Palies, P.; Schuller, T.; Durox, D.; Gicquel, L.; Candel, S. Acoustically perturbed turbulent premixed swirling flames. Phys. Fluids 2011, 23, 037101. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.T.; Santavicca, D. Generalization of turbulent swirl flame transfer functions in gas turbine combustors. Combust. Sci. Technol. 2013, 185, 999–1015. [Google Scholar] [CrossRef]
- Sharaborin, D.K.; Savitskii, A.G.; Bakharev, G.Y.; Lobasov, A.S.; Chikishev, L.M.; Dulin, V.M. PIV/PLIF investigation of unsteady turbulent flow and mixing behind a model gas turbine combustor. Exp. Fluids 2021, 62, 1–19. [Google Scholar] [CrossRef]
- Janus, B.; Dreizler, A.; Janicka, J. Experimental study on stabilization of lifted swirl flames in a model GT combustor. Flow Turbul. Combust. 2005, 75, 293–315. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.; Kompenhans, J.; Werely, S. Particle Image Velocimetry. A Practical Guide, 2nd ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Alekseenko, S.; Dulin, V.; Kozorezov, Y.; Markovich, D.; Shtork, S.; Tokarev, M. Flow structure of swirling turbulent propane flames. Flow Turbul. Combust. 2011, 87, 569–595. [Google Scholar] [CrossRef]
- Dulin, V.; Lobasov, A.; Chikishev, L.; Markovich, D.; Hanjalic, K. On impact of helical structures on stabilization of swirling flames with vortex breakdown. Flow Turbul. Combust. 2019, 103, 887–911. [Google Scholar] [CrossRef]
- Markovich, D.; Dulin, V.; Abdurakipov, S.; Kozinkin, L.; Tokarev, M.; Hanjalić, K. Helical modes in low- and high-swirl jets measured by tomographic PIV. J. Turbul. 2016, 17, 678–698. [Google Scholar] [CrossRef]
- Lobasov, A.; Alekseenko, S.; Markovich, D.; Dulin, V. Mass and momentum transport in the near field of swirling turbulent jets. Effect of swirl rate. Int. J. Heat Fluid Flow 2020, 83, 108539. [Google Scholar] [CrossRef]
- Scarano, F. Iterative image deformation methods in PIV. Meas. Sci. Technol. 2001, 13, R1. [Google Scholar] [CrossRef]
- Soloff, S.M.; Adrian, R.J.; Liu, Z.C. Distortion compensation for generalized stereoscopic particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1441. [Google Scholar] [CrossRef]
- Coudert, S.; Schon, J. Back-projection algorithm with misalignment corrections for 2D3C stereoscopic piv. Meas. Sci. Technol. 2001, 12, 1371–1381. [Google Scholar] [CrossRef]
- van Oijen, J.; de Goey, L. Modelling of premixed laminar flames using flamelet-generated manifolds. Combust. Sci. Technol. 2000, 161, 113–137. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Huang, X.; Roekaerts, D. Large Eddy Simulation of CO2 diluted oxy-fuel spray flames. Fuel 2017, 201, 165–175. [Google Scholar] [CrossRef]
- Ma, L. Computational Modeling of Turbulent Spray Combustion. Doctoral Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Cantera (an Open-Source Suite of Tools for Problems Involving Chemical Kinetics, Thermodynamics, and Transport Processes) Home Page. Available online: https://cantera.org/ (accessed on 9 February 2022).
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.; et al. GRI-Mech (an Optimized Detailed Chemical Reaction Mechanism Capable of the Best Representation of Natural Gas Flames and Ignition). Home Page. Available online: http://combustion.berkeley.edu/gri-mech/ (accessed on 9 February 2022).
- OpenFOAM (Free, Open Source CFD Software with an Extensive Range of Features to Solve Anything from Complex Fluid Flows Involving Chemical Reactions, Turbulence and Heat Transfer, to Acoustics, Solid Mechanics and Electromagnetics) Home Page. 2004. Available online: http://www.openfoam.com (accessed on 9 February 2022).
- Holmes, P.; Lumley, J.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Mullyadzhanov, R.; Abdurakipov, S.; Hanjalic, K. Helical structures in the near field of a turbulent pipe jet. Flow Turbul. Combust. 2017, 98, 367. [Google Scholar] [CrossRef]
- Mullyadzhanov, R.; Sandberg, R.; Abdurakipov, S.; George, W.; Hanjalić, K. Propagating helical waves as a building block of round turbulent jets. Phys. Rev. Fluids 2018, 3, 062601. [Google Scholar] [CrossRef] [Green Version]
- Sirovich, L. Turbulence and the dynamics of coherent structures, I. Coherent structures. Q. Appl. Math. 1987, 45, 561. [Google Scholar] [CrossRef] [Green Version]
- Vanierschot, M.; Muller, J.; Sieber, M.; Percin, M.; van Oudheusden, B.; Oberleithner, K. Single-and double-helix vortex breakdown as two dominant global modes in turbulent swirling jet flow. J. Fluid Mech. 2020, 883, A31. [Google Scholar] [CrossRef]



| Case | Type | ||||||
|---|---|---|---|---|---|---|---|
| Case 1 | 398 | 0 | 4.82 | 0 | 0 | 0 | isothermal |
| Case 2 | 398 | 0 | 4.82 | 29.2 | 0 | 17.18 | isothermal |
| Case 3 | 398 | 10.8 | 4.9 | 0 | 3.2 | 1.91 | reacting |
| Case 4 | 398 | 10.8 | 4.9 | 26.0 | 3.2 | 17.18 | reacting |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palkin, E.V.; Hrebtov, M.Y.; Slastnaya, D.A.; Mullyadzhanov, R.I.; Vervisch, L.; Sharaborin, D.K.; Lobasov, A.S.; Dulin, V.M. Influence of a Central Jet on Isothermal and Reacting Swirling Flow in a Model Combustion Chamber. Energies 2022, 15, 1615. https://doi.org/10.3390/en15051615
Palkin EV, Hrebtov MY, Slastnaya DA, Mullyadzhanov RI, Vervisch L, Sharaborin DK, Lobasov AS, Dulin VM. Influence of a Central Jet on Isothermal and Reacting Swirling Flow in a Model Combustion Chamber. Energies. 2022; 15(5):1615. https://doi.org/10.3390/en15051615
Chicago/Turabian StylePalkin, Egor V., Mikhail Yu. Hrebtov, Darya A. Slastnaya, Rustam I. Mullyadzhanov, Luc Vervisch, Dmitriy K. Sharaborin, Aleksei S. Lobasov, and Vladimir M. Dulin. 2022. "Influence of a Central Jet on Isothermal and Reacting Swirling Flow in a Model Combustion Chamber" Energies 15, no. 5: 1615. https://doi.org/10.3390/en15051615
APA StylePalkin, E. V., Hrebtov, M. Y., Slastnaya, D. A., Mullyadzhanov, R. I., Vervisch, L., Sharaborin, D. K., Lobasov, A. S., & Dulin, V. M. (2022). Influence of a Central Jet on Isothermal and Reacting Swirling Flow in a Model Combustion Chamber. Energies, 15(5), 1615. https://doi.org/10.3390/en15051615







