Predicting Gasoline Vehicle Fuel Consumption in Energy and Environmental Impact Based on Machine Learning and Multidimensional Big Data

Abstract

The underestimation of fuel consumption impacts various aspects. In the vehicle market, manufacturers often advertise fuel economy for marketing. In fact, the fuel consumption reference value provided by the manufacturer is quite different from the real-world fuel consumption of the vehicles. The divergence between reference fuel consumption and real-world fuel consumption also has negative effect on the aspects of policy and environment. In order to effectively promote the sustainable development of transport, it is urged to recognize the real-world fuel consumption of vehicles. The gaps in previous studies includes small sample size, single data dimension, and lack of feature weight evaluation. To fill the research gap, in this study, we conduct a comparative analysis through building five regression models to forecast the real-world fuel consumption rate of light-duty gasoline vehicles in China based on big data from the perspectives of vehicle factors, environment factors, and driving behavior factors. Results show that the random forest regression model performs best among the five candidate models, with a mean absolute error of 0.630 L/100 km, a mean absolute percentage error of 7.5%, a mean squared error of 0.805, an R squared of 0.776, and a 10-fold cross-validation score of 0.791. Further, we capture the most important features affecting fuel consumption among the 25 factors from the above three perspectives. According to the relative weight of each factor in the most optimal model, the three most important factors are brake and accelerator habits, engine power, and the fuel economy consciousness of vehicle owners in sequence.

1. Introduction

Real-world fuel consumption has been underestimated [1] and the underestimation has severe impact on various aspects. In terms of the environment, transportation is one of the industries most responsible for decreasing fossil fuel consumption and environmental pollution. According to the new round of investigation into fine particle sources in Beijing, mobile sources, especially vehicles, have replaced coal combustion to become the primary source of PM 2.5 [2]. Furthermore, it becomes hard to assess current and plan future policy to fulfill the promise of carbon peak and carbon neutrality [3]. In terms of industry, goals set to be achieved through the introduction of new technologies such as lightweight materials now seem to achievable solely through traditional methods, thus adversely affecting innovation. In addition, manufacturers often advertise fuel economy for marketing in the vehicle market, while the fuel consumption reference value provided by the manufacturer is quite different from the real-world vehicles fuel consumption. Therefore, to effectively promote the sustainable development of transport, it is urged to recognize the real-world fuel consumption of vehicles [1].

At present, the main reference fuel consumption of vehicles is provided by the Ministry of Industry and Information Technology (MIIT) of China, which is measured by indirect measurement method as follows. For light vehicles (maximum total quality is not more than 3.5 tons of vehicles), the vehicle is in the experimental stage, the actual driving speed is simulated and loaded on the road, and the carbon dioxide, carbon monoxide and hydrocarbon emissions are measured according to New European Driving Cycle (NEDC) working conditions. Then, the fuel consumption is derived from the measurement based on carbon mass balance in the exhaust gas [4].

On 20 February 2021, The State Administration for Market Regulation and the Standardization Administration approved and released the mandatory national standard of Fuel Consumption Limits for Passenger Vehicles (GB 19578-2021) organized by the MIIT, which was formally implemented on July 1. It is proposed that before 2025, the test conditions of traditional energy passenger vehicles and plug-in hybrid passenger vehicles will be switched from NEDC to WLTC (Worldwide Harmonized Light Vehicles Test Cycle) [5]. The change of operating conditions will affect the comprehensive fuel consumption of vehicles, which means that the NEDC standard will fully withdraw from MIIT. Compared with the NEDC working condition in the 1970s, the WLTC test condition officially completed in 2015 was more stringent [4]. The maximum speed, average speed, maximum acceleration and deceleration, acceleration and deceleration range, and test time are significantly improved; as a result, it could better reflect the actual driving situation.

However, a series of studies have identified that the reference fuel consumption is widely different from the real-world fuel consumption. Liu et al. (2018) found a gap between the test results under the NEDC working conditions and the real-world driving situation in China in terms of fuel consumption is approximately 30% [6]. Duarte et al.‘s study (2016) presents that fuel consumption is 23.9 ± 16.8% higher than certification values in average [7]. Even in the WLTC operating environment, there are a number of studies that reveal a wide discrepancy between the reference consumption information and the actual case [8,9,10].

Studies have identified the factors that cause the widespread divergence between the reference fuel consumption rate and the actual fuel consumption rate [11]. The main cause is the operation under off-cycle conditions. Since the operating conditions, the driving behavior of vehicle owner, and other external factors are various in the real life, no matter how accurately the test protocol is designed, it is scarcely possible to precisely predict the real-world fuel consumption.

Machine learning is popular in solving the prediction problems of complex systems such as fuel consumption prediction. By making the model learn the training set, it is possible for the model to show a better prediction effect on the test set [12]. There have been a large number of studies on fuel consumption prediction with machine learning models, which tend to focus on a single aspect of factors that affect fuel consumption prediction, involving vehicle factors [13], driving behavior factors [14], road conditions factors [15], weather factors [16], and so on. However, fuel consumption is affected by many factors, and it can hardly make accurate prediction only by focusing on a single dimension. In this case, due to the limitation of data acquisition, there is a lack of fuel consumption prediction research based on multi-dimensional factor data.

In addition, a model was considered good as long as it could predict correctly in the past, and there was not much focus on which variables led to the higher accuracy of the final results. Therefore, it seems that machine learning models are black-boxes that make precise predictions while not being able to understand the logic behind those predictions. Fuel consumption forecasting, in this case, becomes a complicated black-box problem as a result of the asymmetric information. There is a need of attempt to unlock the black box and help to understand the models better, including revealing the most important feature in the model and how much influence each feature has on the results of the model’s prediction.

In this paper, we extract data from the BearOil app, which is a well-known vehicle owner service app, with 7 million installed users, over 1.2 million monthly active owners, and more than 30 billion kilometers of mass test total mileage. At the same time, we take vehicle factors such as vehicle brand, engine power, and engine displacement; driving behavior factors such as usual driving speed, driving skills, brake and accelerator habits, fuel economy awareness, and car use frequency; and environmental factors such as temperature, wind speed, and precipitation into consideration. Above all, we aim to predict the real-world fuel consumption in sustainable transport based on multidimensional data and obtain more accurate predicted fuel consumption value through a machine learning method. Moreover, we focus on identifying the most important factors that affect the real-world consumption rate.

The rest of the paper is organized as follows. In Section 2, we review the related literature. In Section 3, we discuss the data source, the extraction factors in the aspect of real-world fuel consumption rate, the driving behavior, and the environment. Section 4 describes the criteria of model selection and the architecture of models. Then, we present the results which include the prediction results and the optimal model, as well as evaluating the most important factors. In Section 5, we analyze the most important features and in Section 6, we present the conclusions.

2. Literature Review

2.1. Fuel Consumption Forecasting Models

The fuel consumption prediction model can be divided into white-box model and black-box model. White-box model mainly refers to the mathematical or physical framework to predict fuel consumption which requires scholars to have a comprehensive and through understanding of the model and related knowledge. In contrast, the black-box model only uses input-output data and lacks physics in the model structure [17].

A typical white-box model in this field includes a mean value phenomenological model constructed by Heywood (2018) based on knowledge on internal combustion engine which consists of an intake system, a delivery system, a torque production system, and an exhaust system [18]. In general, the prediction of fuel consumption using the white-box model poses a high requirement on the understanding of the entire engine system. In addition, there are a large number of parameters involved, even some of the parameters are unavailable. Therefore, white-box is not practical for forecasting fuel consumption although it is transparent.

A class of outstanding black-box models are predictive models based on machine learning methods. They are completely data-driven and have no requirement on physical explanation. All coefficients are determined based on big data using multiple regression methods. The accuracy of the black-box model is always satisfied. However, the coefficients lack interpretability. Additionally, collecting such large amounts of data for the black-box model requires huge labor and time.

2.2. Machine Learning-Based Fuel Consumption Prediction

In the research on fuel consumption prediction, the use of a machine learning model is the main trend worthy of attention in recent years. Parlak et al. (2006) [19] adopt a back propagation learning algorithm to predict specific fuel consumption and exhaust temperature of a diesel engine for various injection timings. The comparison between the model results and the experimental results showed a high consistence. Togun and Baysec (2010) [20] present a genetic programming (GP)-based model to predict the torque and brake specific fuel consumption of a gasoline engine according to spark advance, throttle position, and engine speed, and find that the proposed GP models show satisfactory accuracy. Silva et al. (2006) [21] selected EcoGest, CMEM, and ADVISOR to simulate a sample of 14 urban trips for two 1999 Ford Taurus vehicles, which achieved a relatively high confidence to predict the fuel consumption. Based on 1750 records, Ziolkowski et al. (2021) [22] selected the Multi-Layer Perceptron 22-10-3 network to predict the fuel consumption and reached satisfactory MAPE for 6–10%. Similar studies used artificial neural network (ANN) model conducted by Togun and Baysec (2010) [23] in 81 data sets, Jahirul et al. (2009) [24] and Hjellvik and Maria (2019) [25] also suggest that ANN is very efficient for predicting fuel consumption. Syahputra (2016) [26] presented the application of neuro-fuzzy method for prediction of fuel consumption which shows a training RMSE of 2.767. Yao et al. (2020) [27] used back propagation neural network, support vector regression, and random forests to predict vehicle fuel consumption based on the mobile phone terminals and on-board diagnostic system installed in taxis riving behavior data. Results show that all three models are accurate with an absolute relative error less than 10%. Also focusing on driver-related factors, Ping et al. [28] developed a deep learning-based model as a predictor of the fuel consumption associated with driving behavior under the dynamic driving conditions. In terms of data, increasing big data-driven studies which focus on the topic of fuel consumption rate prediction extract data from the BearOil app [2,29,30,31,32].

2.3. Factors Related to Fuel Consumption Prediction

Studies have identified a series of important factors that affect vehicle fuel consumption. Zhou et al. (2016) [17] summarizes that the main factors affecting fuel consumption are travel-related, weather-related, vehicle-related, roadway-related, and driver-related factors.

In terms of travel-related factors, Ahn and Rakha (2008) [33] demonstrate that utilizing a slower arterial route could save energy but incur additional travel time. Greenwood et al.’s study (2007) [34] recommend that it is important to include information on the level of congestion in the driving patterns to get more accurate emission predictions.

In the aspect of weather, studies show that fuel consumption is higher at −30 °C than at 20 °C [35] and rises with the thermal load. He et al. (2016) [36] prove that the best strategy to reach fuel economy is to limit the acceleration if the combined effect of the road grade, rolling resistance, and wind is small. Test results also show that the fuel consumption is related to the inlet humidity [37].

According to Sriwilai et al. (2016) [38], engine size and type are related to energy consumption in Thailand. A similar conclusion based on an analytical approach was drawn by Ben et al. (2013) [39]. In addition, vehicle speed and acceleration are widely regarded as intuitive variables that have a significant effect on fuel consumption [40,41,42].

A number of scholars suggest the effect of road grade on fuel consumption by comparing flat routes and hilly routes [43,44,45]. Specifically, Renouf (1979) [46] addresses that increased energy requirements can be up to 9% due to a low-radius curve.

Driver-related factors refer to driver behavior and aggressiveness [17]. Sanchez et al. (2006) [47] identified that aggressive driving consumes more fuel than calm driving. Moreover, a study conducted by Mierlo et al. (2004) [14] based on on-road test demonstrated that fuel consumption could be reduced by up to 25% if drivers changed the driving style according to instruction.

Above all, the prediction formula based on physics often differs greatly from the actual case of fuel consumption. Meanwhile, existing studies which build machine learning models lack large-scale data; a small dataset means that there is no guarantee that the prediction model can be widely applied to a large number of car models under different conditions. Moreover, existing studies tend to focus on a single dimension, that is, choosing only the vehicle-related factors, the environment-related factors, or the driving behavior-related factors to predict the fuel consumption. However, fuel consumption prediction is complex work with a number of unknown features; there is a lack of related research that combines multi-dimensional information.

In addition, even though there are studies with various indicators, the weights are not assessed, which is still asymmetric in information, and thus is weakly interpretable. To open the black box, obtain accurate predictions, and expand the applicability of predictions, it is necessary to comprehensively assess the impact of factors and try to capture the most important features to provide meaningful recommendations for vehicle owners, industries, and government.

To fill the above research gap, we construct machine learning models based on big data in the aspects of the car models, the environment conditions, and driving behavior information to describe the driving reality as much as possible to predict the fuel consumption. Then, we comprehensively assess the impact of factors to open the so-called black box and try to capture the features that influence the fuel consumption in the sustainable transport. In this paper, we propose five models including linear regression, naïve Bayes regression, neural network regression, random forest regression, and LightGBM models. Each of them is helpful to improve the accuracy of the prediction after training on big data. The prediction results are compared to identify the optimal model. To clarify the scope of the study, our study focuses on gasoline vehicles as they are the most common road traffic vehicles in real life.

3. Materials and Methods

3.1. Data

We obtained data from three resources: the real-world fuel consumption rate recorded by vehicle owners in the BearOil app, results of a questionnaire survey on driving behavior of vehicle owners, and the monthly information of the climate and road grade in cities of China.

To generate the real-world fuel consumption rate, firstly, each time the vehicle owners refuel, they record the time, the mileage, the liters of fuel, and the payment via the BearOil app. They then mark whether the oil tank is full or not and update the record. The liters of oil added between two adjacent records marked as filled is the fuel consumption during the trip. We get the average fuel consumption rate by weighted averaging the fuel consumption of all trips of the vehicle owner with the mileage as the weight. Next, according to the average fuel consumption of different owners of the same car model, the samples with obvious errors are eliminated and the remaining samples are taken as valid samples.

The driving behavior questionnaire contains 20 questions from seven dimensions: gender, age, driving speed, driving skills, driving habits, fuel economy awareness, and car use frequency. We assign values to each option and calculate the score of each vehicle owner in each dimension. After processing the driving behavior questionnaire data, we matched driving behavior with the corresponding fuel consumption data on user ID and the external environmental data, including temperature, win speed, pressure, humidity, precipitation, sunshine, road grade, etc., based on the city and date information of the vehicle owners. Finally, we take the mean of the average fuel consumption of those with the same driving behavior, driving the same car model, and in the same external environment.

3.1.1. Fuel Consumption Data and Vehicle Factors

About 1.7 million records reported by gasoline vehicle owners in 315 cities of China during 2013 and 2017 were extracted from the BearOil app in this study. Examples of the records are shown in

Table 1. Example of row records from BearOil app.

Feature	Record 0	Record 1	Record 2	Record 3
User ID	02194194	70192504	40468960	74150957
City	Dali	Yangshan	Tianjin	Wuhan
Time	March 2013	March 2014	March 2015	March 2016
Brand Name	FORTHING	BYD	TOYOTA	HAVAL
Series Name	JOYEAR	BYD G6	E’Z	HAVAL H2
Version Year	2010	2012	2014	2016
Engine	1.5 L/120 ps/L4	2.0 L/140 ps/L4	1.8 L/140 ps/L4	1.5 T/150 ps/L4
Gearbox	MT-5	MT-5	E-CVT	AMT-6
refConsumption (L/100 km)	7.2	8.3	7.4	9
realConsumption (L/100 km)	6.4	9.1	8.9	8.2

. Only the last eight digits of the user number (User ID) are displayed for privacy reasons.

The User ID is the unique ID of a user in the BearOil app and each User ID corresponds to multiple samples. Multiple records of one user are the user’s fuel consumption information at different dates and in different cities.

Vehicle information is also given in the records which includes the vehicle brand, series, version, engine, and gearbox. The engine parameters consist of displacement engine power and the number of cylinders. The gearbox parameters show the type of transmission. MT is short for manual transmission, AT is short for automatic transmission, AMT is short for automated manual transmission, CVT is short for continuously variable transmission, DSG is short for direct shift gearbox, and so on.

The reference fuel consumption rate (Ref Consumption) of each car model is provided by the MIIT of China under the second stage of the NEDC working condition. The distribution of actual and reference fuel consumption is displayed in

Table 2. Distribution of fuel consumption rates.

		Engine Displacement (ED)
		ED ≤ 0.8 L	0.8 L < ED ≤ 1.6 L	1.6 L < ED ≤ 2.5 L	2.5 L < ED ≤ 4.0 L	ED > 4.0 L
Standard deviation	Ref Consumption (L/100 km)	0.486	0.778	1.211	1.270	0.582
	Real Consumption (L/100 km)	1.021	1.512	2.115	2.306	2.245
Min	Ref Consumption (L/100 km)	5.700	1.600	2.000	7.600	11.100
	Real Consumption (L/100 km)	4.429	0.829	1.350	6.278	12.352
Max	Ref Consumption (L/100 km)	6.700	9.800	12.300	15.700	13.200
	Real Consumption (L/100 km)	10.815	16.915	20.379	20.675	20.214
P25	Ref Consumption (L/100 km)	5.700	5.900	7.100	9.900	13.200
	Real Consumption (L/100 km)	5.082	6.846	8.207	11.029	14.119
Median	Ref Consumption (L/100 km)	6.700	6.400	7.800	10.400	13.200
	Real Consumption (L/100 km)	5.454	7.738	9.501	12.657	15.655
Mean	Ref Consumption (L/100 km)	6.301	6.459	7.794	10.608	13.038
	Real Consumption (L/100 km)	5.728	7.888	9.598	12.701	15.773
P75	Ref Consumption (L/100 km)	6.700	6.900	8.600	11.000	13.200
	Real Consumption (L/100 km)	5.974	8.774	10.889	14.178	17.059
Observation		113	116,302	53,788	866	13

according to displacement. It shows that most of the samples are with displacement coverages of 0.8–2.5 L. The reference fuel consumption rate of vehicles with displacement coverages of 0.8–1.6 L is 6.459 while the corresponding real-world consumption rate is 7.888. In addition, the reference fuel consumption rate of vehicles with displacement coverages of 1.6–2.5 L is 7.794 while the corresponding real-world consumption rate is 9.598. In a sum, the discrepancy between reference value and the real value suggests that the reference fuel consumption rate is often a poor estimation.

To clarify our research objectives again, our objective is to predict the average real-world fuel consumption rate of a given gasoline vehicle model under certain climate conditions and certain driving behaviors of the vehicle owner. Therefore, the real-world fuel consumption rate of users in the same city, the same month, and with the same driving behavior is averaged.

Gasoline vehicles with different brands, engine, and transmission are significantly different in fuel consumption rate. The above parameters are related to the vehicle series information. However, too many dimensions will be generated in the one-hot coding stage if the vehicle series is encoded as the input. As a result, we chose engine power, displacement, the number of cylinders, and gearbox type as the model input. Moreover, although the reference value provided by MIIT cannot be used as a direct estimate of the actual fuel consumption rate, we can still use the reference value to reduce the error caused by the abnormal real fuel consumption rate. Therefore, we incorporate the reference fuel consumption rate in our models.

3.1.2. Driving Behavior Factors

Driving behavior data were collected from questionnaires. We asked nearly 25,000 users in BearOil app to fill out the questionnaires about their driving behavior. Our questionnaire contains 20 questions from seven dimensions: gender, age, driving speed, driving skills, driving habits, fuel economy awareness, and car use frequency. The scoring for each dimension is shown below.

In the gender dimension, options are 0 for males and 1 for females; in the age dimension, integers 1 to 4 are assigned to four different age groups, with older people scoring higher. The questions of the remaining five dimensions are shown in

Table 3. Questions of the driving behavior questionnaire.

Dimensions	Questions
Car use frequency	Q1. Do you drive when the trip is less than 5 km? Q2. Do you always consider alternatives such as buses, subways, or bicycles instead of driving by yourself?
Fuel economy consciousness	Q1. Do you avoid using equipment that increases fuel consumption such as air conditioners and high-power car appliances as much as possible? Q2. Are you used to leaving anything such as sneakers, ball bags, and spare barbecue oil in the trunk? Q3. What is your attitude towards the maintenance, tire pressure, and car deposition condition of your car? Q4. Will you turn off the engine if the expected idle time is more than 3 min? Q5. Would you consider finding out the reason and adjusting your driving habits if you knew you were getting more gas mileage than your friends? Q6. Will you pay attention to the traffic situation to avoid possible traffic jams in advance?
Driving skill	Q1. What do you think of your parking skills? Q2. What do you think of your driving skills?
Driving speed	Q1. Do you overspeed a lot on the highway? Q2. What is your general approach in the traffic?Q3. What is the average speed of your driving?
Driving habit	Q1. What is your general strategy for intersection with red traffic light? Q2. What kind of road conditions have you been driving with in the past year? Q3. Do you tend to pedal to the ground when starting or accelerating? Q4. How do you drive when you find that you have to slow down in the 100 m ahead on the road? Q5. Imagine that you are driving, the green light is on, and the road ahead is empty, while one kilometer away is the destination where you have to pull over; how do you drive?

.

The total score of the two questions in the dimension of car use frequency ranges from 2 to 8. When the vehicle owner chose the option representing the lower frequency in Q1, and the option representing the higher frequency in Q2, the score would be higher. That is, the higher the score is, the lower the car use frequency is. The fuel economy consciousness dimension includes six questions, with a total score ranges from 6 to 28. When the vehicle owner has a greater willingness to avoid using fuel consumption equipment in Q1, has fewer behaviors in reality as shown in Q2, pays more attention to the situation mentioned in Q3, Q5, Q6, and has a greater likelihood to turn off the engine in the given situation in Q4, the score would be higher. That is, a higher score indicates stronger fuel economy consciousness. The driving skills dimension includes two questions on a scale of 2 to 8 and higher score indicates better driving skills (Q2) and parking skills (Q1) the user thinks he or she is. There are 3 questions in the driving speed dimension, scoring between 3 to 13. Vehicle owners score higher when they are more likely to speed on the highway (Q1), more likely to race ahead of other cars in traffic (Q2), and drive at a higher average speed (Q3). The driving habits dimension consists of 5 questions, with a total score of 5 to 19. When the vehicle owner is more likely to avoid pedaling down or slamming on the brakes in the case of Q1, Q3, Q4, and Q5, and chose less stop-go, more unblocked road in the past year, the vehicle owner is seen as having better driving habits, as a result, the score is higher.

Table 4. Age and gender distribution.

	Age
Gender	18–25	26–35	36–45	45+	Total
Male	3035	14,360	4910	1270	23,575
Female	85	361	104	24	574
Total	3120	14,721	5014	1294	24,149

shows the age and gender distribution of the users who filled in the questionnaire and descriptive statistics of scores in the other dimensions are shown in

Table 5. Descriptive statistics of scores.

Dimensions	Min	Max	P50	Mean
Car frequency	2.0	8.0	5.0	4.7
Fuel economy consciousness	6.0	28.0	20.0	19.6
Driving skill	2.0	8.0	6.0	5.7
Driving speed	3.0	13.0	9.0	9.3
Driving habit	6.0	19.0	16.0	15.9

.

3.1.3. Environment Factors

Environment factors include climate factors and road grade. Information on climate factors was extracted from the meteorological departments of the provincial regions in China. We extracted data on temperature, wind speed, air pressure, precipitation, sunlight, and so on during the period from 2013 to 2017. Road grade data were sourced from the research carried out by Gao et al. (2020) [48], specifically, splicing the Map of China based on Shuttle Radar Topography Mission (SRTM) Global Digital Elevation Model, and then connected with the administrative boundary data of China at the county level. Next, the administrative boundary of the county was cut out, and the road grade of each grid in the region was calculated. Finally, the average value, minimum value, maximum value, and standard difference of road grade in each region are obtained. We selected the average road grade of each county in this study.

Each piece of climate data consists of a regional station number and monthly weather information. Climate information varies greatly in regions during the observation period so that it should not be ignored when predicting the real-world fuel consumption rate of vehicles. Since the climate of a certain city during a certain month is almost in a fixed pattern, we averaged each climate factor in each month of different cities. Specifically, number 1 was assigned to north wind and the number increased by 1 for every 22.5 degrees clockwise for the wind direction factor. Additionally, if the wind speed does not reach 0.2 m/s, it is considered calm and the number 17 is assigned. In total, wind direction categories consist of numbers successively from 1 to 17.

It is worth noting that strong correlation between climate features often leads to multicollinearity, so we conducted a correlation coefficient test on the input climate features. For the feature pairs with correlation coefficient above 0.8, we eliminated one of them. Finally, the environment factors selected in this study are shown in

Table 6. Selected environment factors.

Environment Factors	Unit
Average pressure	0.1 hPa
Average temperature	0.1 °C
Average temperature anomaly	0.1 °C
Mean relative humidity	1%
Average wind speed	0.1 m/s
Maximum wind direction	azimuth
Extreme maximum wind direction	azimuth
Average precipitation	0.1 mm
Daily precipitation ≥ 0.1 mm days	1 day
Sunshine time	0.1 h
Road grade	°

.

We matched the real-world fuel consumption rate with the corresponding driving behavior information and climate information by User ID, city, and date, and combined them to be used as input variables in our models.

3.2. Model Selection and Criteria

The selection of the input factors is described in the above section and in this section, we introduce the model selection procedure.

Firstly, fuel consumption forecast is a continuous variable forecast, where regression models should be applied. In addition to the pursuit of accuracy of fuel consumption prediction, our research also aims to identify the most important factors affecting fuel consumption to strengthen the interpretability of each model. In this case, linear regression, also as the fastest and the most typical regression prediction algorithm, is suitable. However, maximum likelihood estimation of linear regression only considers the maximization of likelihood function. From the perspective of Bayes’ theorem, maximum posterior estimation treats parameter values as random variables, therefore, Naïve Bayes regression was selected.

Moreover, linear regression cannot capture a nonlinear relationship. As a result, we selected neural network regression and decision tree regression, which are widely used in nonlinear relationship prediction. It should be noted that decision tree regression is often not accurate since it is prone to over-fitting. Low bias and high variance often occur in a tree with deep depth and there are two ways commonly used to improve decision tree regression, namely bagging and boosting.

Random forest regression averages multiple decision trees based on bagging algorithm and can significantly reduce variance to improve overfitting. A typical example of an improved decision tree regression based on boosting is the GBDT model. Compared with the traditional GBDT model, XGBoost model adds regular terms in the cost function to control the complexity of the model, and it allows column sampling to prevent overfitting. LightGBM, as an improvement of XGBoost model, which takes up less memory and reduces complexity of data segmentation, has shown high prediction speed in many studies.

Above all, we selected linear regression, naïve Bayes regression, neural network regression, random forest regression, and LightGBM in this paper.

The architecture of the models are as follows. There are 64 neurons in the input layer of the neural network model. The activation function is set as max(0,x) to follow the common practice [49]. While the number of neurons is 64 according to the geometric pyramid rule proposed by Masters in the hidden layer [50], and the activation function is set as max(0,x). To reduce overfitting [51], the input matrix is processed with L2 regularization and the output matrix is processed with L1 regularization while the value of lambda is set as 0.05. There is one neuron in the third layer. At the same time, we selected RMSprop as the optimizer [52], MSE as the loss function, and MAE as the metric function [53,54]. For the random forest regression, the number of estimators is set as 20 which is the setting that achieves best performance through multiple tests. For better accuracy [55], we set 25 leaf nodes in the LightGBM model with the learning rate of 0.01 and the number of iterations of 5000.

The rules for model comparison include the mean absolute error (MAE), mean absolute percentage error (MAPE), mean squared error (MSE), R squared (R²), cross-validation scores and the calculation formula of MAE, MAPE, MSE, and R² are shown below.

$$\mathrm{MAE}=\frac{1}{\mathrm{n}}{\displaystyle \sum }_{i=1}^n\left|y_i-y_i^{\prime }\right|$$

(1)

$$\mathrm{MAPE}=\frac{1}{\mathrm{n}}{\displaystyle \sum }_{i=1}^n\frac{\left|y_i-y_i^{\prime }\right|}{y_i}$$

(2)

$$\mathrm{MSE}=\frac{1}{\mathrm{n}}{\displaystyle \sum }_{i=1}^n{\left(y_i-y_i^{\prime }\right)}^2$$

(3)

$${\mathrm{R}}^2=1-\frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-y_i^{\prime }\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\overline{y_i}\right)}^2}$$

(4)

where $y_{\mathrm{i}}$ refers to the true value, $y_{\mathrm{i}}^{\prime }$ refers to the predicted value, and $\overline{y_{\mathrm{i}}}$ refers to the mean actual value. The smaller the value of MAE, MAPE, and MSE, the larger the value of R² and cross-validation score, the smaller the error between the predicted and the actual value, which also indicates the better performance.

4. Results

4.1. Training and Test Results

Row data include 1,335,232 records from 24,149 gasoline vehicle owners during the period from 2004 to 2019. In the process of data preprocessing, 10,708 records with missing values and 355,185 records outside the observation period were removed, leaving 969,339 records. Next, we excluded detected fuel consumption outliers and 773,469 data records remained in this stage. Finally, we averaged the fuel consumption of vehicle owners with the same vehicle model and with same driving behaviors. The ultimate dataset contains 171,089 pieces of data.

After merging the environment factors, we divided the dataset into training sets and test sets in a ratio of 7 to 3, which is a common practice for predicting the performance of vehicle engines with machine learning models. In

Table 7. Result of each regression model.

Model	Training Data				Testing Data
	MAE	MAPE	MSE	R2	MAE	MAPE	MSE	R2
RefConsumption	1.650	24.2%	4.276	−2.234	1.654	24.2%	4.322	−2.288
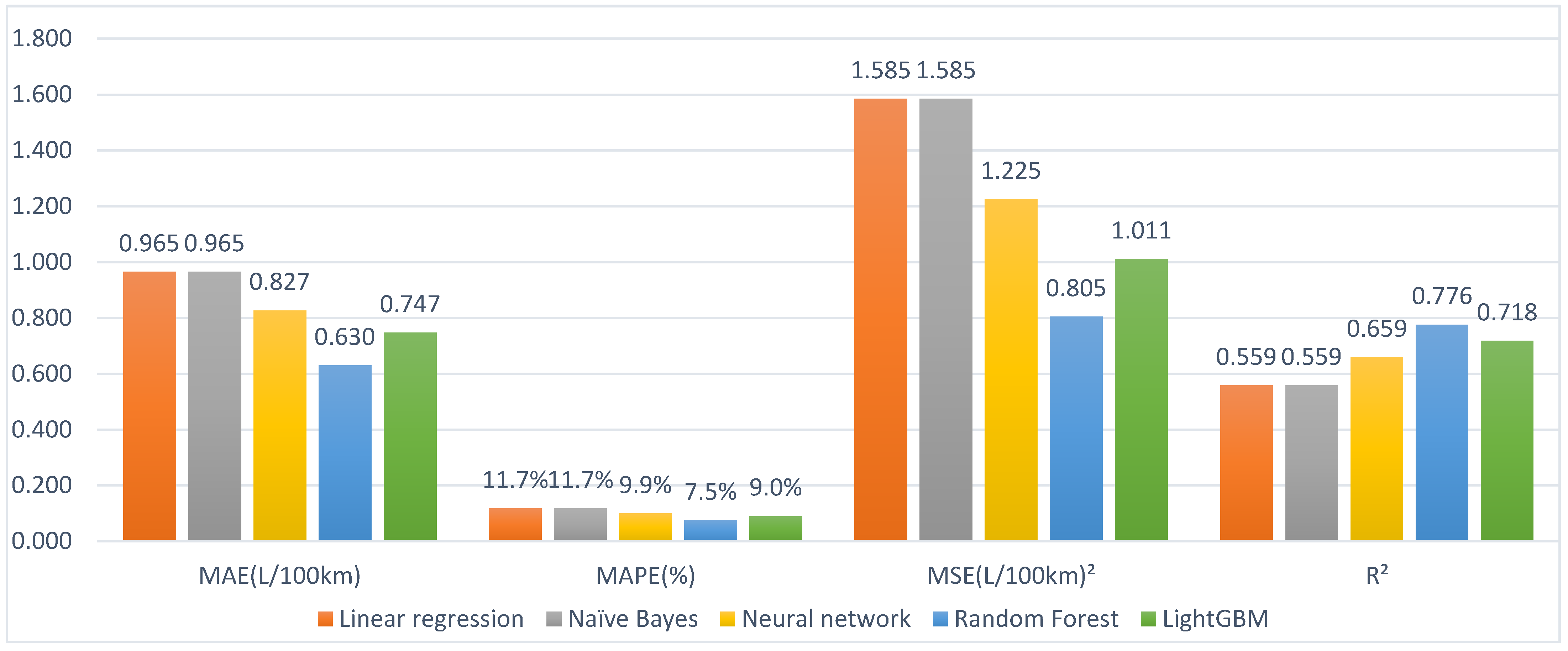
Linear regression	0.959	11.7%	1.550	0.558	0.965	11.7%	1.585	0.559
Naïve Bayes	0.959	11.7%	1.550	0.558	0.965	11.7%	1.585	0.559
Neural network	0.800	9.6%	1.146	0.674	0.827	9.9%	1.225	0.659
Random forest	0.245	2.9%	0.127	0.964	0.630	7.5%	0.805	0.776
LightGBM	0.701	8.5%	1.876	0.750	0.747	9.0%	1.011	0.718

, refConsumption refers to the reference fuel consumption value provided by MIIT. It can be seen that there is a large gap between the reference fuel consumption rate value and the actual case. Table 7 also presents errors of the training and testing process of each proposed model.

In

Table 8. Average predicted results.

Model		Engine Displacement (ED)
		ED ≤ 0.8 L	0.8 L < ED ≤ 1.6 L	1.6 L < ED ≤ 2.5 L	2.5 L < ED ≤ 4.0 L	ED > 4.0 L
Linear regression	Predicted value	7.258	7.813	8.868	10.187	14.853
	Deviation 1	26.413%	0.225%	0.164%	3.396%	4.566%
Naïve Bayes	Predicted value	7.257	7.813	8.868	10.188	14.854
	Deviation	26.401%	0.225%	0.164%	3.401%	4.561%
Neural network	Predicted value	6.019	7.969	9.015	9.900	14.822
	Deviation	2.726%	1.485%	1.596%	1.730%	8.557%
Random forest	Predicted value	5.851	7.851	8.872	9.874	15.690
	Deviation	0.138%	0.025%	0.014%	0.222%	1.979%
LightGBM	Predicted value	5.743	7.842	8.872	12.491	15.721
	Deviation	1.975%	0.140%	0.137%	0.345%	3.013%

¹ $\mathrm{Deviation}=\frac{\left|Predictedvalue-Realvalue\right|}{Realvalue}\times 100$.

, we present average prediction results of 10 runs of 5 proposed model by displacement distribution, referring to the practice by Liu et al. (2018) [6] and Zeng et al. (2021) [32]. The displacement range is divided according to Chinese national standard GB3730.1-88. Clearly, random forest regression show the best prediction validation in vehicles in all engine displacement ranges.

4.2. Models Comparison

Figure 1 shows the mean absolute error (MAE) between the model prediction values and the actual values. MAE from the reference consumption rate provided by the MIIT is 1.654 L/100 km, while MAE from our models including vehicle factors and environment factors is all below 1 L/100 km. Among the five models, MAE of the random forest regression model (0.630 L/100 km) is the lowest.

While MAE is the absolute value of the prediction error, it may not sufficiently capture how much the deviation is relative to the actual value. For this reason, we also calculated the mean absolute percentage error (MAPE). The reference fuel consumption rate is deviated greatly from the actual case since the MAPE between them is approximately 24.2%. Under this standard, the best prediction model is still random forest regression, which is more accurate with a MAPE of 7.5%. Results show that our proposed regression model could be applied into practice for prediction and revision.

In addition, in order to avoid the impact of sample size on the model performance, we selected the mean square errors (MSE) as comparison criteria as well. According to Figure 1, results reveal that MSE of the random forest regression is the smallest. Again, this proves that random forest is the best model among all the candidate models.

R², on the other hand, can measure the extent to which independent variables explain dependent variables. Moreover, unlike the comparison criteria above, R² has clear upper and lower limits. As shown in Figure 1, the reference fuel consumption rate is not explanatory to the actual case, while random forest regression reaches the largest R² value. It indicates that the independent variables in the random forest regression explain 77.6% of the variation in the dependent variable.

Since the training dataset and test dataset are selected randomly, regression results may have random fluctuations, we then applied the 10-fold cross-validation to assess the performance of five regression models. The scoring function of 10-fold cross-validation is R². The scores of the models each time are shown in Figure 2 and the average scores of the 10-fold cross-validation are shown in

Table 9. Average scores of the 10-fold cross-validation.

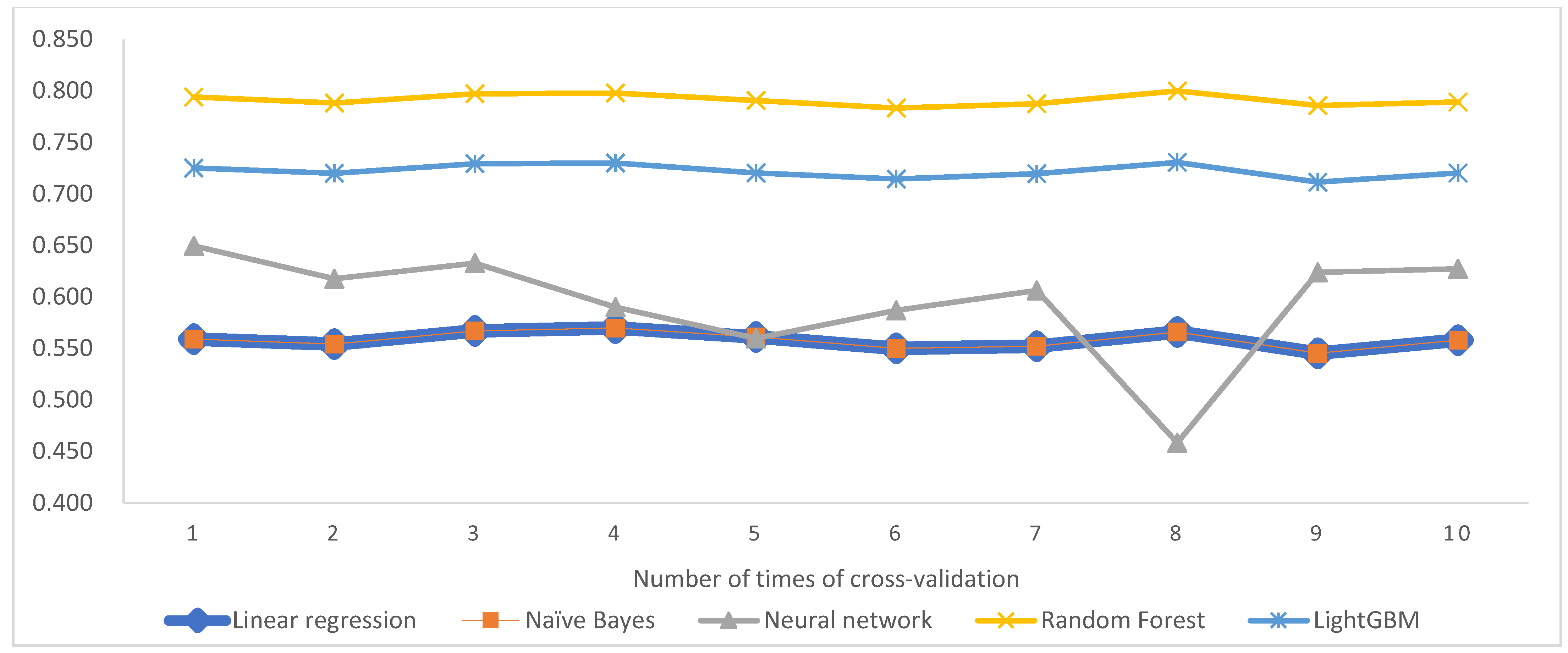
Model	Average Cross Validation Score
Linear regression	0.5583183
Naïve Bayes	0.5583183
Neural network	0.5952532
Random forest	0.7913839
LightGBM	0.7221006

. Figure 2 indicates that linear regression and naïve Bayes regression show similar accuracy since the corresponding two lines are overlapping. Clearly, random forest regression performs the best with the highest line in Figure 2 and the largest value in Table 9.

The above results indicate that the prediction errors of the actual fuel consumption rate based on the data of vehicle factors, driving behaviors, and environment factors are far lower than that of the reference fuel consumption rate. Specifically, the MAPE value is decreased by 16.7% by random forest regression, which is the optimal model with the best performance. Results show that the proposed prediction model can be put into practice for providing more precise estimates of the fuel consumption rate in the real-world applications.

5. Discussion

Comparison analysis indicates that the random forest regression achieved the best performance. Therefore, we estimated the weight of input parameters in random forest regression, and the result is shown in Figure 3.

According to Figure 3, reference fuel consumption rate is the parameter with the highest weight, which indicates that it could be a basis for the fuel consumption prediction.

Among all the factors, the driving behavior-related factors weigh the heaviest and have the greatest influence on fuel consumption. Specifically, driving habit dimension in this study focuses on two aspects, that is, whether there are frequently stop-and-go driving and whether the vehicle owners often brake sharply or press the accelerator hard. Previous studies have revealed that stop-and-go driving and slam on the brake behavior are wasteful for fuel [56]. Evans (1978) also recommended that drivers anticipate conditions ahead to minimize braking since previous extracted energy would be unproductively dissipated when there is a braking [57]. The second most important factor in this regard is fuel economy consciousness. In this study, six questions were set to score the fuel economy consciousness of gasoline vehicle owners. The result is in line with common sense, that is, the more fuel economy consciousness vehicle owners have, the more they avoid excess power consumption during driving and the more they care about the condition of the car, the less gasoline they consume. This is followed by car use frequency and driving skills, which indicates that the frequency of vehicle use, the driving and parking skills of car owners in daily life are also closely related to car fuel consumption. In addition, driving speed is recognized as having effects on fuel consumption. Haworth and Symmons (2001) also suggest that driving speed is positively related to fuel consumption [58] and research highlights that the optimum fuel economy cruising speeds range between 40 and 50 km/h [59].

Engine power is the second important factor among all the related factors with a weight of more than 0.05. It has been widely acknowledged that more horsepower implies more fuel consumption [60]. The following is brand name with a weight of 0.028. In the reality, some manufacturers carry out brand marketing with the slogan of fuel saving. For example, Japanese cars have always been known for fuel economy, and Honda and Toyota are the typical brands of fuel economy [61]. Gearbox type is also seen as an important vehicle-related factor when predicting the fuel consumption with a weight of 0.022.

Moreover, in the aspect of environmental factors, air pressure was identified as the most important environmental factor in this study, with a weight of 0.027. Air pressure affects fuel consumption by directly affecting tire pressure. When tire pressure is relatively large, fuel consumption is considered to be lower [62]. Air temperature also affects fuel consumption through tire pressure [63], and its weight in this study is 0.018. Average wind speed and road grade are the second and third most important environmental factors, respectively. The higher the average wind speed is, the greater the air resistance is, and the greater the road grade is, the more gasoline the car consumes [64].

Above all, in this section we conducted a comparative analysis of the factors from aspects of vehicle attribution, driving behavior, and environment to capture the factors that influence the fuel consumption value and found that, among all the factors, the driving behavior factors that have the greatest impact on the real-world fuel consumption rate are engine power and brand name. The driving behavior factors that have the greatest impact are driving habit, fuel economy consciousness, car use frequency, and driving skills. The environment factors that have the greatest impact are average pressure, average wind speed, road grade, and average temperature.

6. Conclusions

The prediction of fuel consumption is a black-box problem with asymmetric information. In China, the fuel consumption information mainly comes from the reference values provide by Ministry of Industry and Information Technology of the People’s Republic of China. However, the real-world fuel consumption is greater than the reference value in most situations. The underestimation of fuel consumption brings negative effect in multiple aspects of policy, industry, and market.

Since machine learning models have been widely applied to prediction problems in the field of engine performance, we utilized five regression models, namely, linear regression, naïve Bayes regression, neural network regression, random forest regression, and LightGBM models, to forecast the real-world fuel consumption rate of light-duty vehicles, and capture the important features that influence fuel consumption, based on big data from the aspects of vehicle factors, environment factors, and driving behavior factors in this paper.

After training and testing, results show that the mean absolute error, mean absolute percentage error, mean squared error, R squared, and 10-fold cross-validation values between the prediction values and the actual fuel consumption rate are far better than the reference value. The comparison analysis of the different models suggest that the random forest regression model performs best among the 5 proposed models under all the criteria with a mean absolute error of 0.630 L/100 km, a mean absolute percentage error of 7.5%, a mean squared error of 0.805, an R squared of 0.776, and a 10-fold cross-validation score of 0.791, respectively.

Finally, we assess the weight of 25 different factors and capture the priority order of each factor. Clearly, the three most important factors affecting fuel consumption are brake and accelerator habits, engine power, and the fuel economy consciousness of vehicle owners in sequence, according to the relative weight of each factor in the random forest model. For a vehicle owner who is not a BearOil app user, the real fuel consumption of the vehicle can be predicted according to reference fuel consumption and related feature information based on our model. Research results provide a meaningful reference for consumers, manufacturers, and related government departments.