Extended Application and Experimental Verification of a New Erosive Burning Model Coupled Heat Transfer between Gas and Grain Based on a Star-Grain Solid Rocket Motor

Abstract

The estimation of erosive burning is of great importance for the internal ballistics computation of a solid rocket motor (SRM) with a large aspect ratio. Because of the variety of parameters affecting erosive burning, most of the erosive burning models developed in earlier years usually contain unknown constants that need to be identified by a trial-and-error procedure for each SRM. Based on an SRM with a cylindrical grain, a new erosive burning model, which coupled the heat transfer between the gas and grain, was proven to be effective previously. To expand the scope of application of this model, in this paper, earlier and new erosive burning models were used in the transient one-dimensional internal ballistics computation, to obtain the internal ballistics for a star-grain SRM. A comparison between the computational and experimental results indicated that both the earlier and new erosive burning models can obtain results with good accuracy for a star-grain SRM. The paper shows that with no constants to be identified, the Ma model is easy to use and has the potential to predict the erosive burning rate before a firing test.

1. Introduction

To obtain good performance, a large aspect ratio is often used in different SRMs. In these SRMs, the augmentation of the burning rate, due to erosive burning, may affect the internal ballistics dramatically, and can sometimes even cause catastrophic consequences. For decades, many models on erosive burning have been proposed. In the simplest models [1,2,3,4], it is considered that there is a linear relationship between the erosive burning ratio (the ratio between the total burning rate and normal burning rate) and a key variable, such as velocity, Mach number, mass flux through the port, and so on. The erosive burning rate can be written as follows:

$$\epsilon \left(z\right)=\{\begin{array}{ll}1,& z<z^{\ast }\\ 1+k_z\left(z-z^{\ast }\right),& z\ge z^{\ast }\end{array}$$

(1)

where k_z and z* are two constants that vary with the propellants and SRMs. When such a model is used for internal ballistics computation, the two constants need to be identified by a trial-and-error procedure. Another erosive burning model, the L-R model [5], is a very popular model, modified and used by many researchers [6,7,8,9,10]. In the L-R model, the erosive burning rate is assumed to be proportional to the heat transfer coefficient at the propellant surface. During the estimation of the heat transfer coefficient, two unknown constants are introduced. As in the linear relationship model, the constants also make the L-R model inconvenient to implement.

To overcome the obstacle induced by the unknown constants, Mukunda [11,12] proposed a universal model. In Mukunda’s model, the two constants were determined by comparing the model with plenty of experimental data. Mukunda’s model was validated by Ref [13]. Now, this model has received more and more attention. Slvan [14] carried out ignition simulation based on Mukunda’s model, and obtained results with good agreement with the experiments. Ropia [15] used Mukunda’s model in an SRM with a cluster of seven grains. Greatrix [16] compared the results from Mukunda’s model to some classical studies, and indicated that the roughness of the propellant surface should also be considered. Ma and coauthors [17] proposed another erosive burning model. By evaluating the heat flux using the heat transfer model of Gnielinski [18], the model of Ma released all the unknown constants, making it another universal model to estimate the erosive burning rate.

The computation of internal ballistics involves the numerical computation procedure of the histories of different parameters in the solid rocket motors (SRMs). With internal ballistics computation, a number of tests and experiments can be reduced dramatically, as well as the time and financial expenses. In addition, the numerical computation of internal ballistics can reveal, or explain, some characteristics of SRMs that are difficult to measure directly. With the development of computer technology and numerical methodologies, two-dimensional (2D) and three-dimensional (3D) computations are now popular for the evaluation of internal ballistics [19,20,21]. Yet, because of their efficiency and acceptable accuracy, one-dimensional (1D) models are still vastly used and developed [8,9,10,22,23,24]. Thus, in this paper, a 1D model is used to compute the internal ballistics.

The ignition model plays an important role in the internal ballistics computation of SRMs. A popular and simple ignition model used by many researchers assumes that the propellant begins to burn once the propellant surface reaches a critical temperature [22]. To evaluate the temperature of the propellant surface, two methods can be used. In the first method, a 1D solid domain, perpendicular to the propellant surface, is initially created. Then, numerical 1D heat transfer computation, using the finite element method or finite volume method, can be carried out to evaluate the surface temperature. This method can obtain the propellant surface temperature history for each fluid cell of the 1D fluid domain with quite good accuracy. Yet, because of the great difference between the temperatures of the ignition gas and the propellant surface, the temperature gradient at the surface is very large. Thus, this method requires a very small mesh size to obtain credible results. Since the 1D heat transfer computation should be conducted for each corresponding fluid cell, this method would require huge computing resources. In the other method, the temperature at the propellant surface is expressed as a function of time. Based on this, an ordinary differential equation (ODE) is established, and the Runge–Kutta method is all that is needed to compute the surface temperature. This makes the method very efficient and widely used [8,25].

In this paper, the code the authors developed in Ref. [17] is extended to a star-grain SRM, with a large aspect ratio, to obtain the internal ballistics results. The Ma model and Mukunda model are used for erosive burning evaluation. The computational results met the experimental results well. This validates the two universal erosive burning models and the code, and proves that the Ma model has the potential to predict internal ballistics before a firing test of real SRMs.

2. Models

In this paper, a transient 1D CFD program was implemented on a star-grain SRM, with the erosive burning considered. The main assumptions used in this paper are listed below:

(1)

All the variables at the same cross section are assumed to be uniform (1D assumption).

(2)

The chemical reaction is ignored. Once the propellant is ignited, the surface is treated as a surface where combustion gas flows directly into the fluid domain.

(3)

The combustion gas is assumed to be a perfect gas of a single species.

(4)

The ignition gas has the same properties as the combustion gas, but a lower temperature.

(5)

The velocity of the combustion gas generated from the grain is vertical to the axis of SRM.

2.1. Governing Equations

The typical control volume of the 1D domain is depicted in Figure 1. Based on the Reynolds transport theorem, the governing equations, consisting of the three conservation laws for mass, momentum and energy, can be derived, and are listed below:

$$\frac{\partial }{\partial t}\left(\rho A_p\right)+\frac{\partial }{\partial x}\left(\rho u{A}_p\right)={\rho }_{p}rs$$

(2)

$$\frac{\partial }{\partial t}\left(\rho u{A}_p\right)+\frac{\partial }{\partial x}\left(\rho u^2{A}_p\right)=-A_p\frac{\partial p}{\partial x}$$

(3)

$$\frac{\partial }{\partial t}\left(\rho A_p\left(C_{v}T+\frac{u^2}{2}\right)\right)+\frac{\partial }{\partial x}\left(\rho u{A}_p\left(C_{p}T+\frac{u^2}{2}\right)\right)={\rho }_{p}rs{C}_p{T}_f$$

(4)

In addition to these equations, the following state equation is also needed:

$$p=\rho RT$$

(5)

2.2. Erosive Burning

In this paper, two different erosive burning models are used for comparison purposes. The first is the Ma model [17]. In this model, the total burning rate comprises the following two components: the normal burning rate and the erosive burning rate. The normal burning rate refers to the burning rate when the velocity of gas flow is low. The erosive burning rate is assumed to be proportional to the heat flux at the propellant surface. The total burning rate can be written as follows:

$$r=a{p}^n+\frac{(T_{\infty }-T_s)}{{\rho }_p{C}_{p,p}(T_s-T_i)}h$$

(6)

In Equation (6), h is the heat transfer coefficient at the propellant surface. Considering the effect of transpiration flow, h can be computed using the following expression:

$$\frac{h}{h_0}=\frac{{\beta }_{th}}{\exp \left({\beta }_{th}\right)-1}$$

(7)

where ${\beta }_{th}=\rho v_g{C}_p/h_0={\rho }_{p}r{C}_p/h_0$, and h₀ denotes the heat transfer coefficient without transpiration, computed by the Gnielinski correlation [18]. The burning rate r appears in Equation (7), thus it should be computed iteratively.

The second erosive burning model used for comparison in this paper is Mukunda’s model [11]. In Mukunda’s model, the erosive burning ratio is computed by the following correlation:

$$\frac{r}{r_0}=\{\begin{array}{l}1,\hspace{0.17em}g<g_{th}\\ 1+K_1\left(g^{0.8}-g_{th}^{0.8}\right),\hspace{0.17em}g>g_{th}\end{array}$$

(8)

where $g=g_0{\left({\mathrm{Re}}_0/1000\right)}^{-0.125}$, $g_0=G/{\rho }_p{r}_0$, and ${\mathrm{Re}}_0={\rho }_p{r}_0{D}_h/\mu$. The value of the two constants $K_1=0.023$ and $g_{th}=35$ are determined in Ref. [11], by a trial-and-error procedure with plenty of experimental data.

Using the erosive burning model, the burning rate r is computed for each cell during the computation.

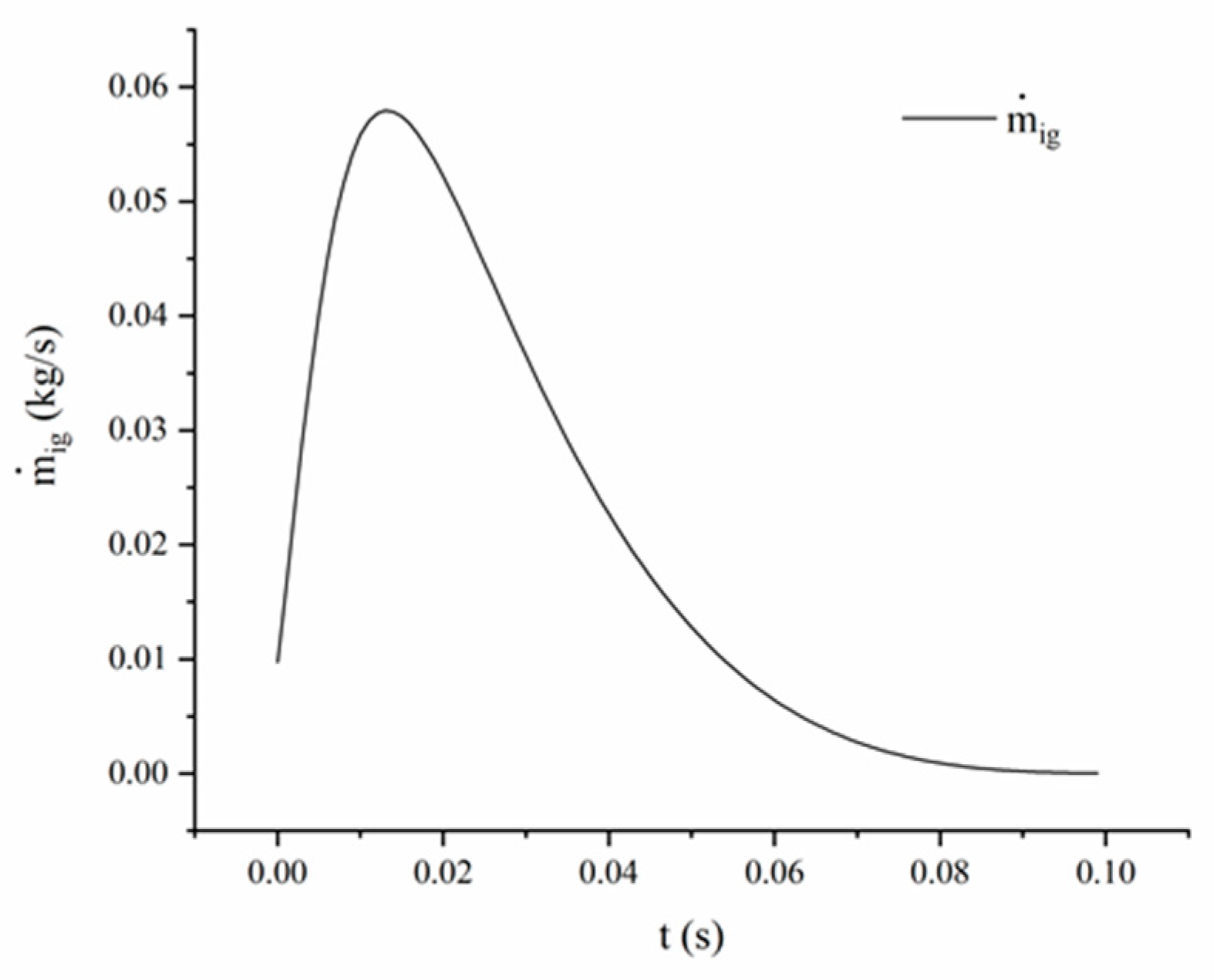
2.3. Ignition Model

The ignition criterion used in this paper is the critical-temperature model. This model is the simplest ignition model and has been vastly used [8,22,23,24]. In this model, the details of complex chemical reactions are ignored. The propellant begins to burn once the surface temperature reaches a critical value (ignition temperature). To evaluate the surface temperature before the ignition, the same equation as that in Ref. [8] was used, which is as follows:

$$\frac{d{T}_s}{dt}=\frac{4\alpha h^2{\left(T-T_s\right)}^3}{3{\lambda }^2\left(T_s-T_i\right)\left(2T-T_s-T_i\right)}$$

(9)

Equation (9) provides a relationship between surface temperature and time. During the computation described in this paper, at each time step, the propellant surface temperature for each fluid cell is computed using the fourth-order Runge–Kutta method. Once the ignition temperature is reached, the propellant of the corresponding fluid cell begins to burn. The sources of mass, momentum and energy for the corresponding fluid cell are then computed according to the burning rate and burning area.

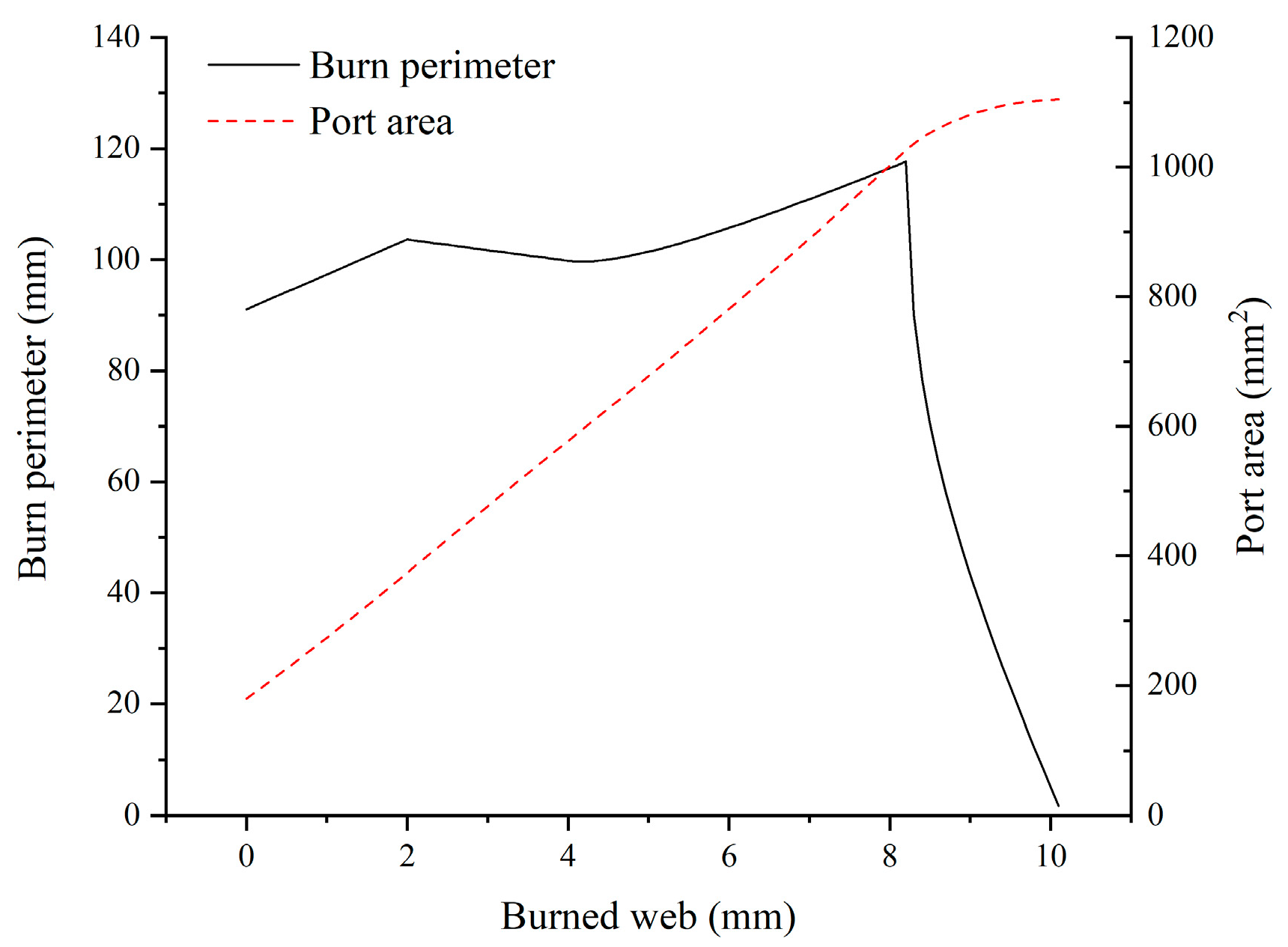
2.4. Geometric Correlations

The SRM studied in this paper uses a star grain. For this kind of grain, the burn perimeter s and the port area A_p can be analytically expressed as functions of the burned web e [26,27]. Figure 2 depicts a schematic for the star section. In Figure 2, D stands for the outer diameter of the grain. The points of the star are represented by n. Th web of the grain is denoted as e₁. The angle between the two adjacent star edges is θ. The transition arc has a radius r, and the radius of the arc at the star tip is r₁. For simplicity, the characteristic length of the grain l is defined as $l=D/2-\left(e_1+r\right)$, and y is defined as $y=\left(e+r\right)/l$. At the moment when the star edge disappears, the burned web is denoted as $e^{\ast }$, and the value of the corresponding y is $y^{\ast }=\left(e^{\ast }+r\right)/l$.

For the star grain with an arc at the star tip, the burning process of the grain can be divided into four stages. Different expressions for the burn perimeter s and port area A_p in different stages are given as follows [26,27]:

In the first stage, the arc at the star tip holds ($0\le e\le r_1$).

$$\frac{s}{l}=2n\left[\frac{\sin \epsilon \frac{\pi }{n}}{\sin \frac{\theta }{2}}+\left(1-\epsilon \right)\frac{\pi }{n}+\frac{r+r_1}{l}\left(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-\cot \frac{\theta }{2}\right)-\frac{r_1-e}{l}\frac{\pi }{n}\right]$$

(10)

$$\begin{array}{l}\frac{A_p}{l^2}=n\left[\left(1-\epsilon \right)\frac{\pi }{n}+\sin \epsilon \frac{\pi }{n}\left(\cos \epsilon \frac{\pi }{n}-\sin \epsilon \frac{\pi }{n}\cot \frac{\theta }{2}\right)\right]\hspace{0.17em}+2ny\left[\frac{\sin \epsilon \frac{\pi }{n}}{\sin \frac{\theta }{2}}+\left(1-\epsilon \right)\frac{\pi }{n}\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+n{y}^2\left(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-\cot \frac{\theta }{2}\right)+n{\left(\frac{r_1-e}{l}\right)}^2\left(\frac{\theta }{2}-\cot \frac{\theta }{2}-\frac{\pi }{2}\right)\end{array}$$

(11)

In the second stage, the arc at the star tip has burned out, and the star edge holds ($r_1<e\le e^{\ast }$).

$$\frac{s}{l}=2n\left[\frac{\sin \epsilon \frac{\pi }{n}}{\sin \frac{\theta }{2}}+\left(1-\epsilon \right)\frac{\pi }{n}+y\left(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-\cot \frac{\theta }{2}\right)\right]$$

(12)

$$\begin{array}{l}\frac{A_p}{l^2}=n\left[\left(1-\epsilon \right)\frac{\pi }{n}+\sin \epsilon \frac{\pi }{n}\left(\cos \epsilon \frac{\pi }{n}-\sin \epsilon \frac{\pi }{n}\cot \frac{\theta }{2}\right)\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+2ny\left[\frac{\sin \epsilon \frac{\pi }{n}}{\sin \frac{\theta }{2}}+\left(1-\epsilon \right)\frac{\pi }{n}\right]+n{y}^2\left(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-\cot \frac{\theta }{2}\right)\end{array}$$

(13)

In the third stage, the star edge has burned out, and the transition arc holds ($e^{\ast }<e\le e_1$).

$$\frac{s}{l}=2n\left\{\left(1-\epsilon \right)\frac{\pi }{n}+y\left[\frac{\pi }{n}+\arcsin \left(\frac{\sin \epsilon \frac{\pi }{n}}{y}\right)\right]\right\}$$

(14)

$$\frac{A_p}{l^2}=n\left\{\begin{array}{l}{\left(1+y\right)}^2\left(1-\epsilon \right)\frac{\pi }{n}+\sin \epsilon \frac{\pi }{n}\left(\sqrt{y^2-{\sin }^2\epsilon \frac{\pi }{n}}+\cos \epsilon \frac{\pi }{n}\right)\\ {+\mathrm{y}}^2\left[\epsilon \frac{\pi }{n}+\arcsin \left(\frac{\sin \epsilon \frac{\pi }{n}}{y}\right)\right]\end{array}\right\}$$

(15)

In the fourth stage, only the sliver remains ($e_1<e\le e_f$, where $e_f=\sqrt{l^2+{\left(\frac{D}{2}\right)}^2-Dl\cos \epsilon \frac{\pi }{n}}-r$).

$$s=2nR\left(\epsilon \frac{\pi }{n}-\arcsin \frac{D}{4R_C}+\arcsin \frac{l\sin \epsilon \frac{\pi }{n}}{e+r}\right)$$

(16)

$$A_p=n\left\{\begin{array}{l}{\left(\frac{D}{2}\right)}^2\left(\frac{\pi }{n}\left(1-\epsilon \right)+\arcsin \frac{e+r}{2R_C}\right)+R^2\left(\epsilon \frac{\pi }{n}-\arcsin \frac{D}{4R_C}+\arcsin \frac{l\sin \epsilon \frac{\pi }{n}}{e+r}\right)\\ +l\sin \epsilon \frac{\pi }{n}\left(l\cos \epsilon \frac{\pi }{n}+\sqrt{{\left(e+r\right)}^2-{\left(l\sin \epsilon \frac{\pi }{n}\right)}^2}\right)-l\frac{e+r}{2R_C}\frac{D}{2}\end{array}\right\}$$

(17)

where R_C is the radius of the circumcircle of the triangle OO’A, $R_C=\frac{l\left(e+r\right)D/2}{4\sqrt{m\left(m-l\right)\left(m-\left(e+r\right)\right)\left(m-D/2\right)}}$, and $m=\left(l+\left(e+r\right)+D/2\right)/2$.

In each time step of the internal ballistics computation, the burned web e is updated for each fluid cell, according to whether the propellant of the cell is ignited. Then, geometric evaluation is implemented, providing the correct values of burn perimeter s and port area A_p needed to solve Equations (1)–(3).

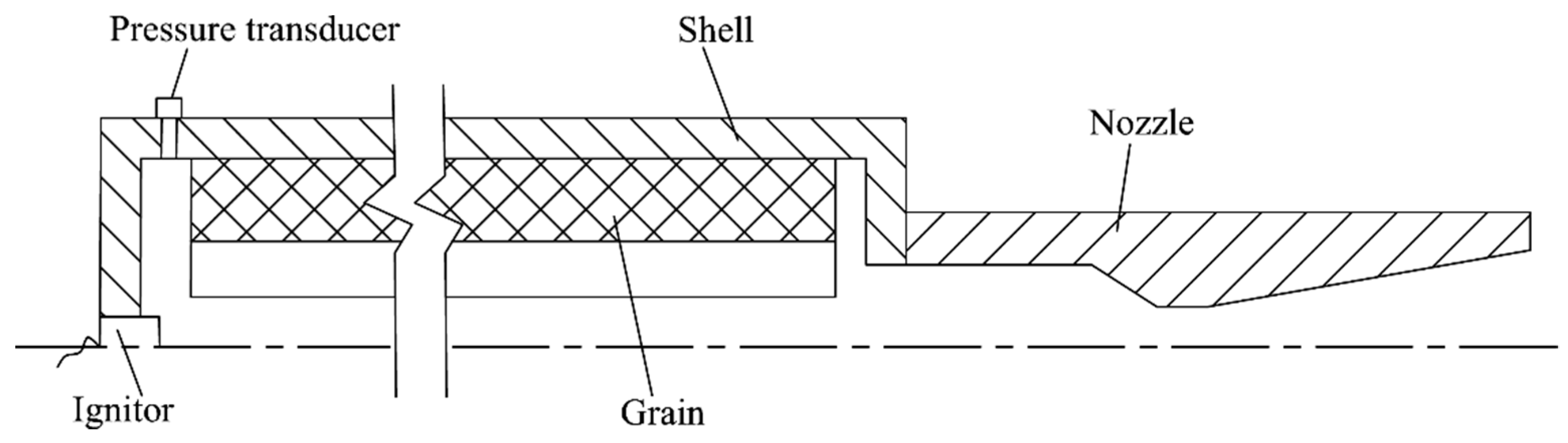
3. Numerical Procedure

The governing equations are solved using the finite volume method (FVM). The code used in this paper evolved from the code developed by the authors in Ref. [17], to accommodate the star grain in the SRM studied in this paper. During the computation, the SRM is divided into a cluster of 1D cells, from the head end of the combustion chamber down to the exit of the nozzle. The SIMPLE algorithm is used to decouple velocity and pressure. A TVD category scheme, the MUSCL scheme, is used for the discretization of convection term. More details can be found in [28]. For each cell in the fluid domain, the temperature of the propellant surface before ignition is computed by solving Equation (9), using the fourth-order Runge–Kutta method. After ignition, the geometric computation is carried out for the burn perimeter and port area. Since erosive burning plays an important role in the operation of SRMs with a large aspect ratio, as the SRM studied in this paper, erosive burning is considered in the code. The total burning rate at each cell of the 1D domain is computed using the erosive burning model, to obtain the mass source and energy source caused by combustion of the propellant grain. For comparison purposes, different erosive burning rate models, the Ma model and Mukunda model, are used.

Grid independence is guaranteed for both the space and time fields, with a uniform 1D mesh grid (size 0.5 mm and time step 10⁻⁶ s). At the head end, when the igniter works, a mass flow rate inlet condition is implemented. The mass flow rate history of the igniter is shown in Figure 3. Once the ignition mass flow drops to zero, an adiabatic wall condition is implemented at the head end. For the nozzle exit, a pressure outlet condition is implemented until the velocity of sound is approached. After that, a supersonic outlet condition is implemented, with all the variables at the boundary extrapolated from the interior cells.

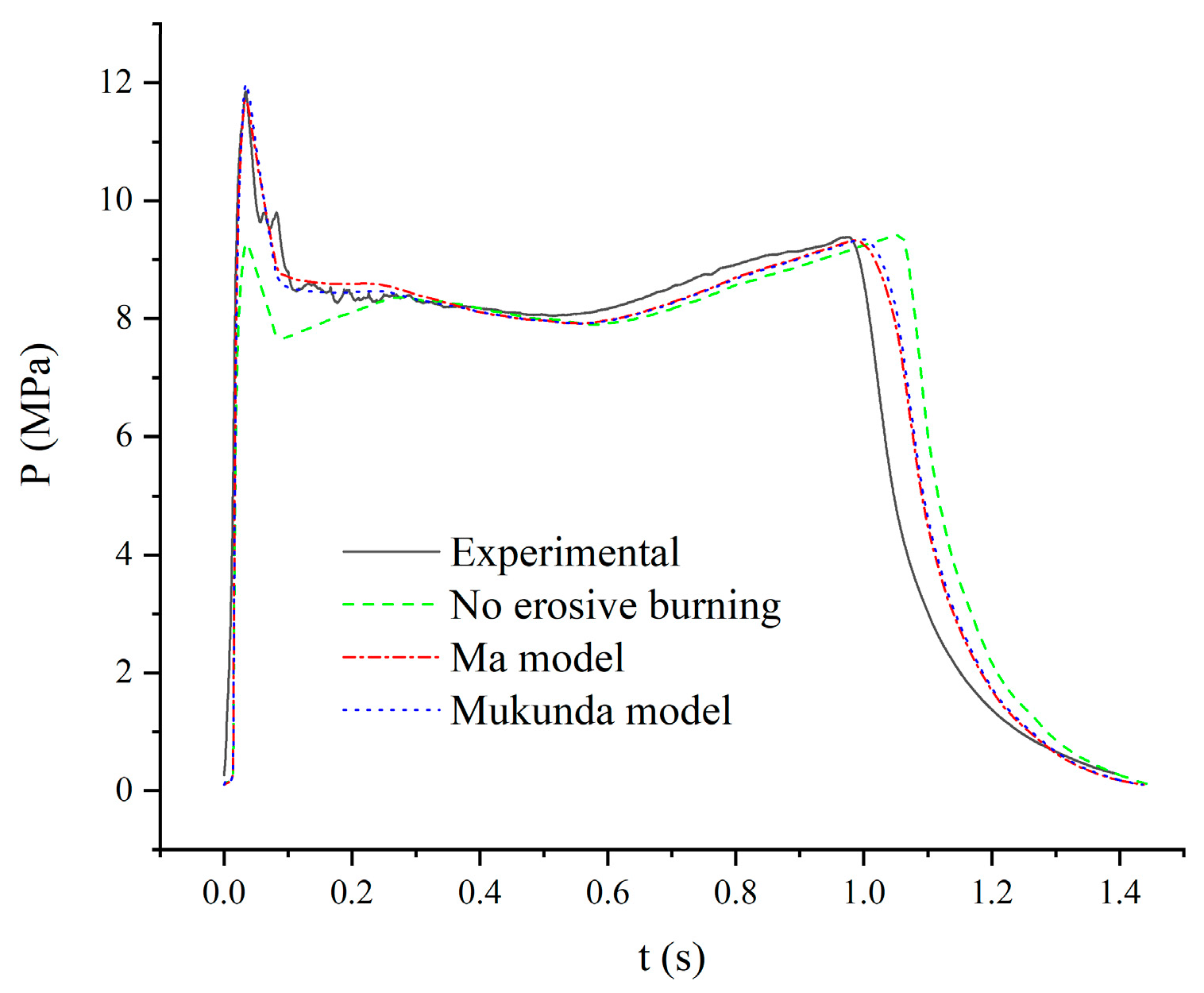
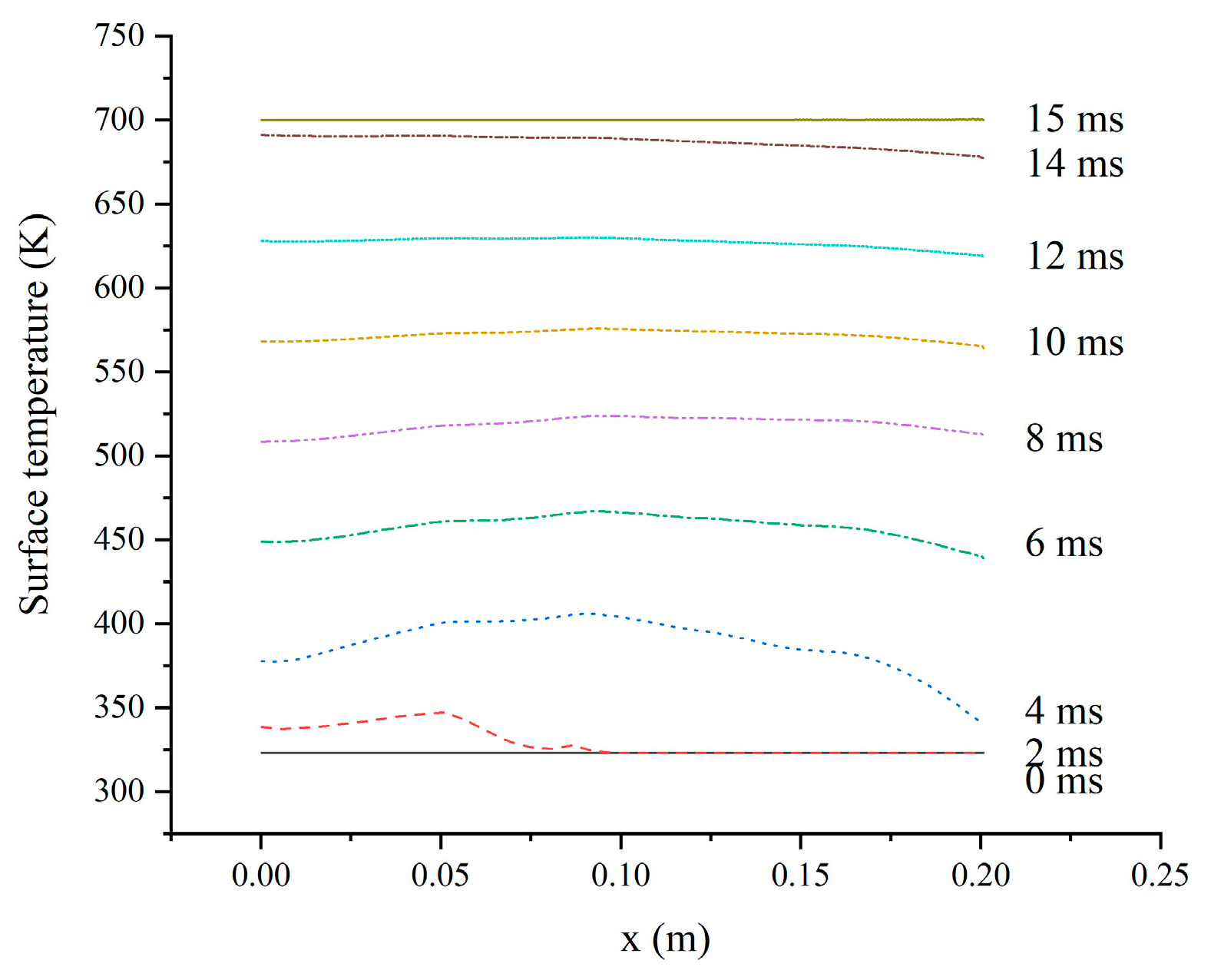
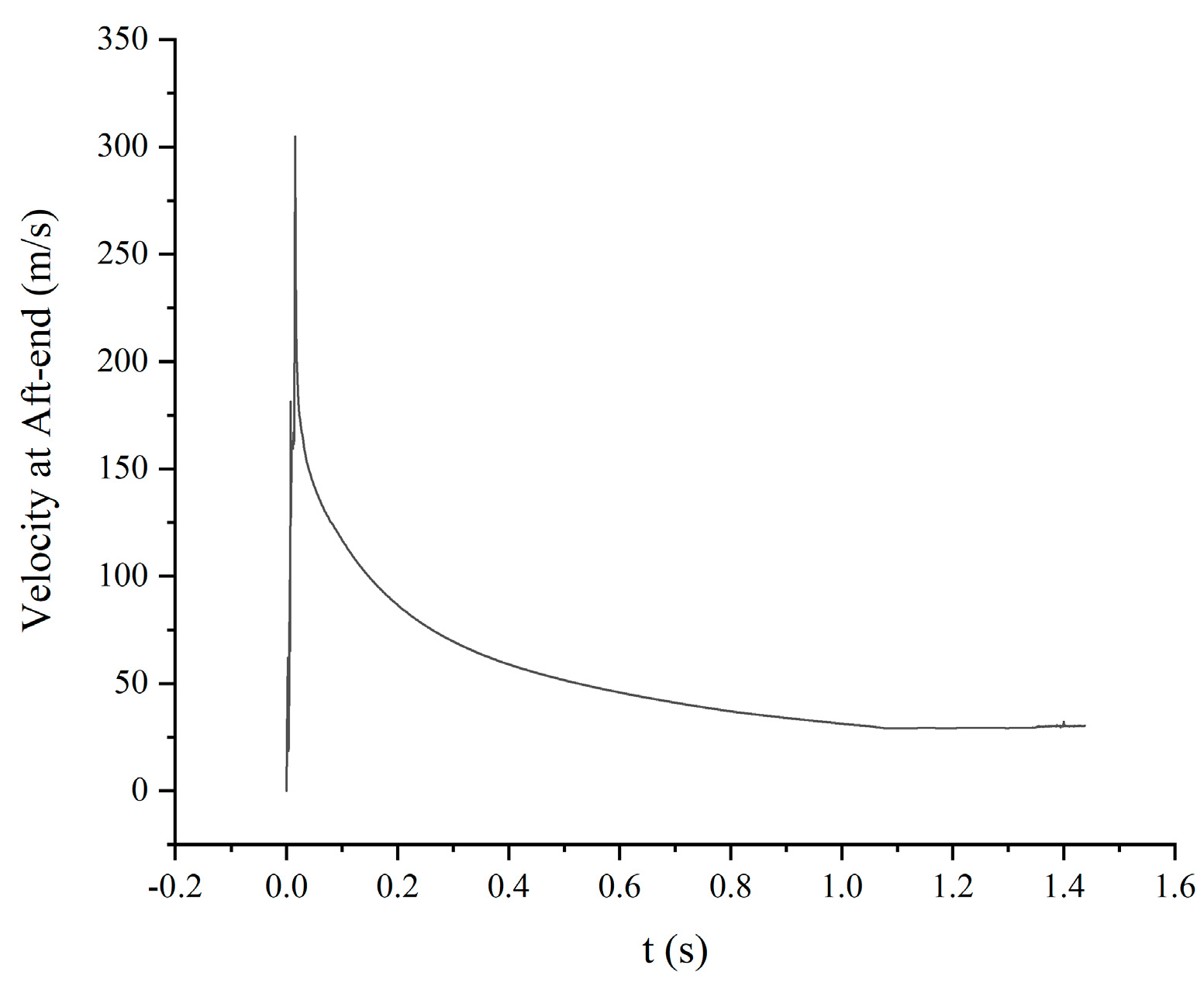
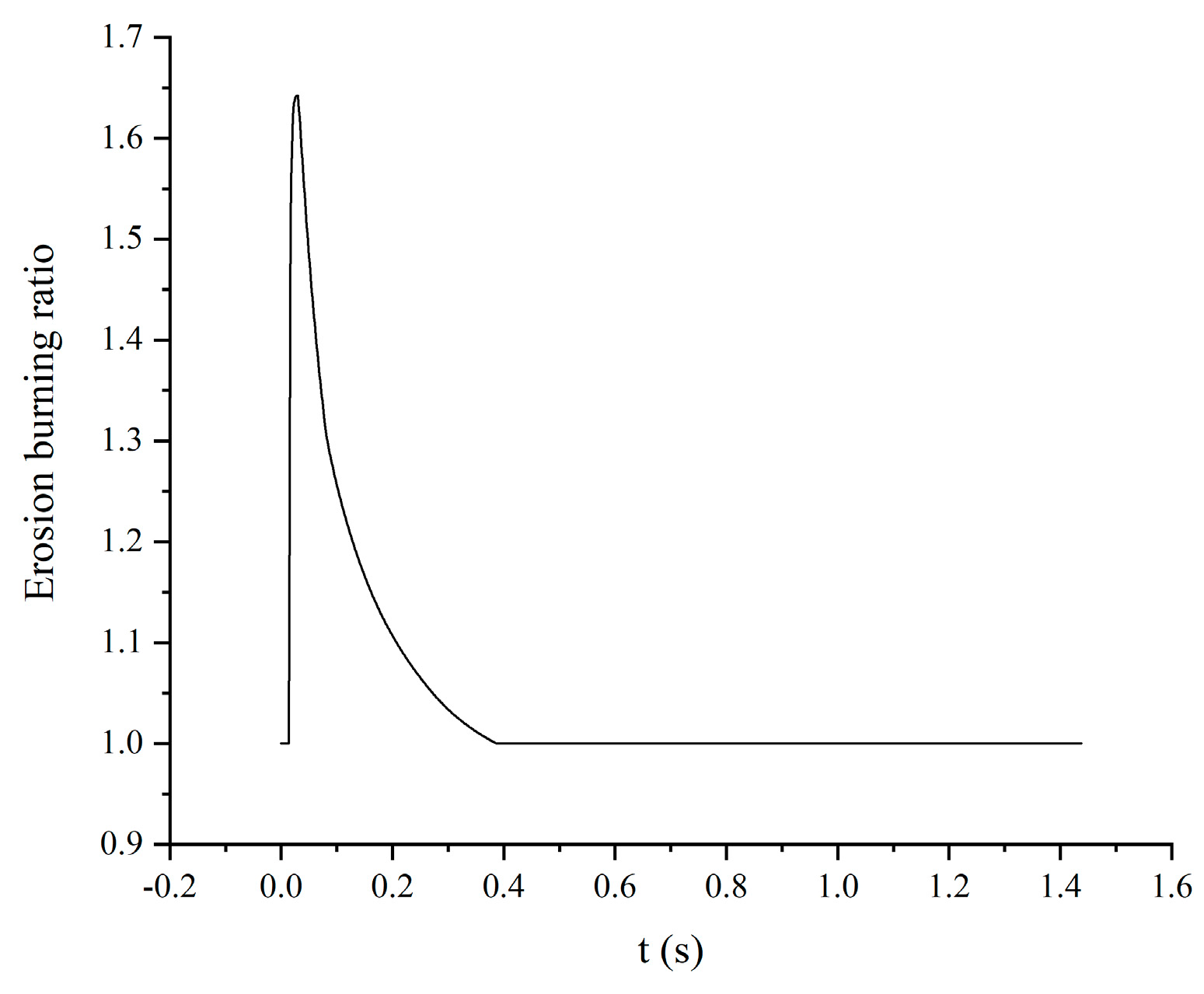
4. Results and Analysis

Figure 4 depicts the schematic of the SRM studied in this paper. The SRM has a six-pointed star grain, with a length of 201.5 mm and outer diameter of 37.5 mm. The diameter of the nozzle throat is 8 mm. A composite propellant, comprising 83% AP, 12% HTPB and 5% Al, was used. The properties of the combustion gas were computed using the Chemical Equilibrium with Applications (CEA) package [29]. More details of the SRM can be found in [30].

The igniter was mounted at the head end of the SRM. The mass flow rate of the igniter is shown in Figure 3. It is worth noting that, besides this study, the firing test was also used to evaluate the SRM’s performance at a high initial temperature. So, the SRM was fired after being kept at 50 °C for 48 h.

Using Equations (9)–(16), the burn perimeter and the port area, as functions of the burned web, were computed. The results are shown in Figure 5. The burn perimeter increases in the first stage, until the arcs at the star tips burn out. Then, in the second stage, it decreases slightly. After the star edges burn out, the third stage begins, and the burn perimeter increases to the maximum value. When the burned web reaches e₁, the regression procedure enters the fourth stage, in which the sliver burns and the burn perimeter quickly reduces to zero. The port area increases at a relatively steady rate until the fourth stage. In the fourth stage, the rate of increment becomes smaller and smaller. After all the propellant burns out, the port area reaches the maximum value (determined by the inner diameter of the SRM’s combustion chamber).

The pressure history results of computations with different erosive burning treatments are shown in Figure 6, along with the experimental data. When erosive burning is not considered, the computed pressure history was mainly controlled by the burn perimeter. After ignition, the pressure experiences a small peak, then increases to the maximum value just before the tail off. The trend is similar to the burn perimeter curve shown in Figure 5. Because of the erosive burning, the experiment gives a very different curve. The pressure peak at the early stage, just after ignition, is much higher than that of the computational results when erosive burning is not considered. In this stage, because of the small port area, the gas velocity in the port is very high, leading to severe erosive burning, which, in turn, brings a much higher burning rate (especially near the aft end of the grain) and pressure. As the propellant burns, the port area increases, and the erosive burning becomes weaker and weaker. Thus, the pressure drops, even when the burning area increases, until the end of the first stage. From then on, the erosive burning becomes so weak that the experimental data are not significantly different from the non-erosion results, except for the earlier transitions between different stages and the longer tail off stage.

With erosive burning considered using the two erosive burning models, the computational results meet the experimental data well. As shown in Figure 6, both the Ma model and Mukunda model obtain good results. The time and value of the pressure peak, just after the ignition, are well computed. The value of the ignition peak pressure in the experimental data is 11.85 MPa. The value of the Ma model is 11.71 MPa, 1.2% lower, and of the Mukunda model, it is 11.98 MPa, 1.1% higher. After the ignition, both the erosive burning models predict the pressure drop during the first stage of propellant burning. The results of the Ma model are a little higher than those of the experimental data, with a relative error of about 4.0%. The Mukunda model gives better results, and the relative error is about 1.0%. In the second and third stage of propellant burning, the pressure curves, predicted by the two different models, are very close. Compared with the experiment, the relative errors of both models are within 4.0%. Because of the relatively higher erosive burning predicted by the Ma model in the first stage, the burned web of the Ma model is a little larger than that of the Mukunda model, leading to slightly higher pressure and earlier transitions between different stages, as well as an earlier tail off stage.

For the ignition analysis, the temperature distributions of the propellant surface at different times before the whole grain is ignited are shown in Figure 7. It can be observed that, as the igniter begins to work, the ignition gas flows into the combustion chamber and raises the propellant surface gradually. Because of the small size of the SRM and the high gas velocity, the temperature values from the head end to the aft end are close. The whole propellant should be ignited in 14 ms to 15 ms, from the head end to the aft end.

Figure 8 depicts the velocity of the aft end of the grain as a function of time. At the beginning of the operation of the SRM, due to the ignition gas and combustion gas from the propellant grain, the velocity of the aft end rises rapidly and reaches the maximum value (304 m/s) at 0.015 s. Afterwards, the velocity drops gradually. The drop is caused by the increase in the area ratio between the port at the aft end of the grain and the throat of the nozzle. The Erosive burning ratio shows a similar trend as the velocity, as Figure 9 depicts. Once the aft end of the grain begins to burn, the erosive burning ratio increases. The maximum value of 1.64 is reached at 0.029 s. The maximum erosive burning ratio does not appear at the same time as the velocity does, indicating that the velocity is not the only factor that affects the erosive burning. During the ignition of the SRM, the temperature, pressure and other parameters changed violently. These factors, together with velocity, determine the erosive burning. After 0.029 s, the erosive burning ratio at the aft end drops gradually as the port area grows. At about 0.36 s, the erosive burning ratio at the aft end of the grain is lower than 1.01. The effect of erosive burning on the internal ballistics becomes negligibly small. The results of the velocity and erosive burning ratio can explain the pressure history in Figure 6, and validate the erosive burning model and the CFD program used in this paper.

The port area results at different times are shown in Figure 10. At the beginning, all the sections have the same port area. After the ignition, the grain at the rear end of the combustion chamber has a larger burning rate because of the erosive burning, leading to quicker regression. Thus, different port area values at different positions can be observed at 0.2 s. As the port area increases gradually, the erosive burning becomes weaker and weaker, and then disappears, after which the propellant regresses at the local normal burning rate. Since the pressure is the only parameter to affect the normal burning rate, and the pressure drop from the head end to the aft end is small during this period, the values of the burning rate at different positions are close. This situation lasts until about 1.0 s, when the transition from the third stage to the fourth stage occurs, and the tail off begins (see Figure 6). After that, the burn perimeter near the aft end becomes much smaller, causing the pressure to drop in the whole SRM. Therefore, the regression of the whole grain becomes slower and slower after 1.0 s. At 1.4 s, the grain at the rear end (behind about 0.18 m) has burned out completely. The pressure continues to drop, until the whole grain burns out.

From the port area history, we can observe the erosive burning’s effect on the internal ballistics of an SRM. At the beginning of the SRM operation, erosive burning raises the burning rate near the aft end of the SRM, and combines with the ignition gas results in a pressure peak in the SRM. Despite the fact that the erosive burning disappears quickly after ignition of the grain, as the port area increases and gas velocity decreases in the port, its effect lasts to the very end of the SRM operation. Erosive burning changes the original relationship between the burning area and burned web in parallel regression, and makes the burning area history become more complex and difficult to predict, and, thus, increases the difficulty of evaluating the internal ballistics. When the grain begins to burn out, the grain near the aft end will burn out first, leading to an earlier and gentler tail off stage. Besides the pressure and thruster deviation from the design intent, the long tail off stage would let the aft end part of the shell (or thermal insulation layer) be exposed to combustion gas, introducing a hidden danger to the whole SRM.

5. Conclusions

In this paper, a transient 1D CFD computation model is implemented to evaluate the internal ballistics for a star-grain SRM. In the computation, ignition and erosive burning are the two main elements considered. A critical temperature model is used for ignition simulation. Two different universal models, the Ma model and Mukunda model, are used for the erosive burning evaluation. Combined with the geometric computations for a star-shaped grain, both the models lead to results that have good agreement with the experimental data. The port area shows that, although the erosive burning only occurs at the beginning of the SRM’s operation, its effect can last until the tail off stage. This paper validates the two erosive burning rate models, indicating that the Ma model could be a promising universal erosive burning model. The research can also be used for convenient and quick internal ballistics predictions for star-grain SRMs, and, with suitable modifications, for SRMs of other categories.