Effect of Chordwise Struts and Misaligned Flow on the Aerodynamic Performance of a Leading-Edge Inflatable Wing
Abstract
:1. Introduction
2. Methodology
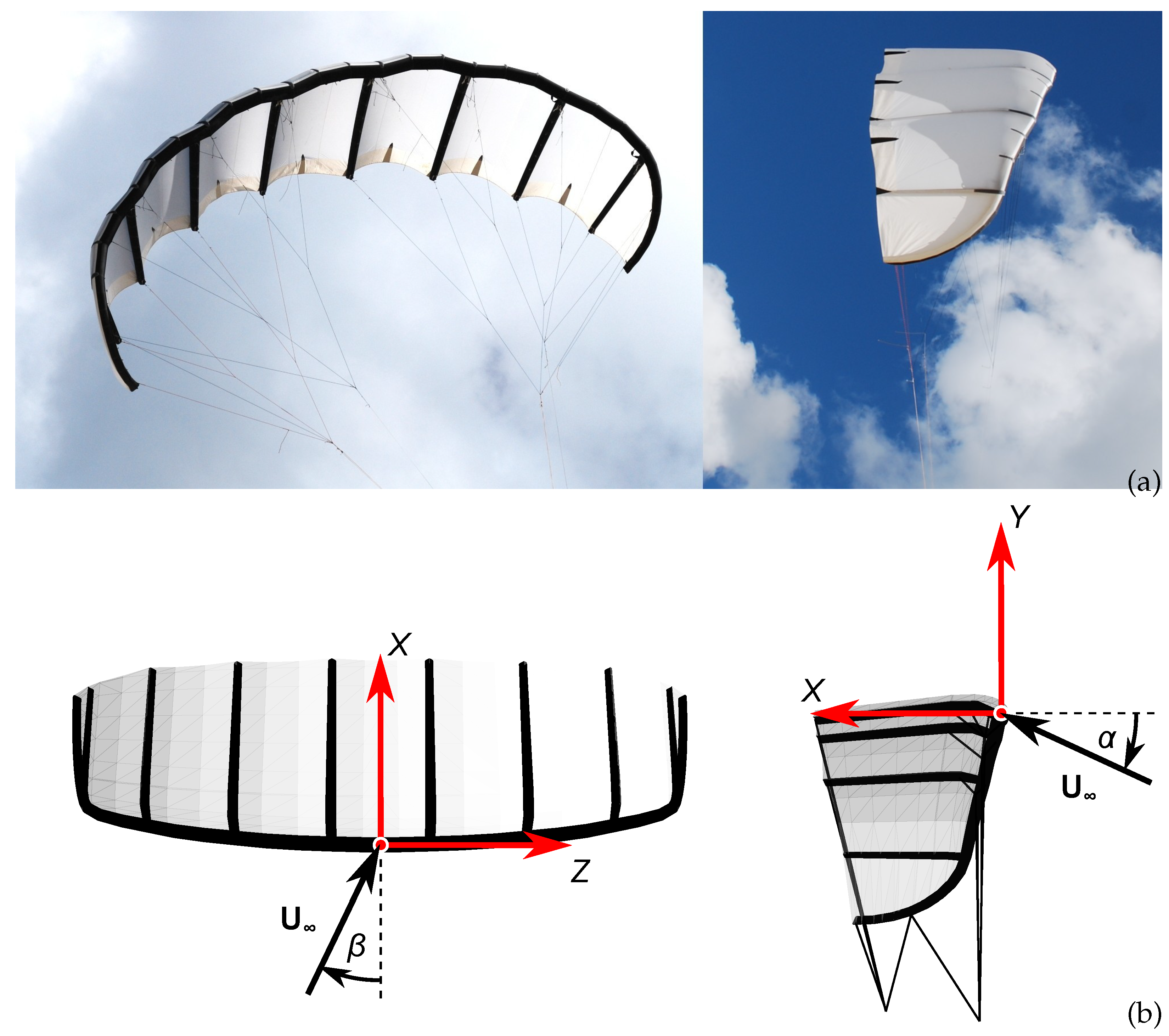
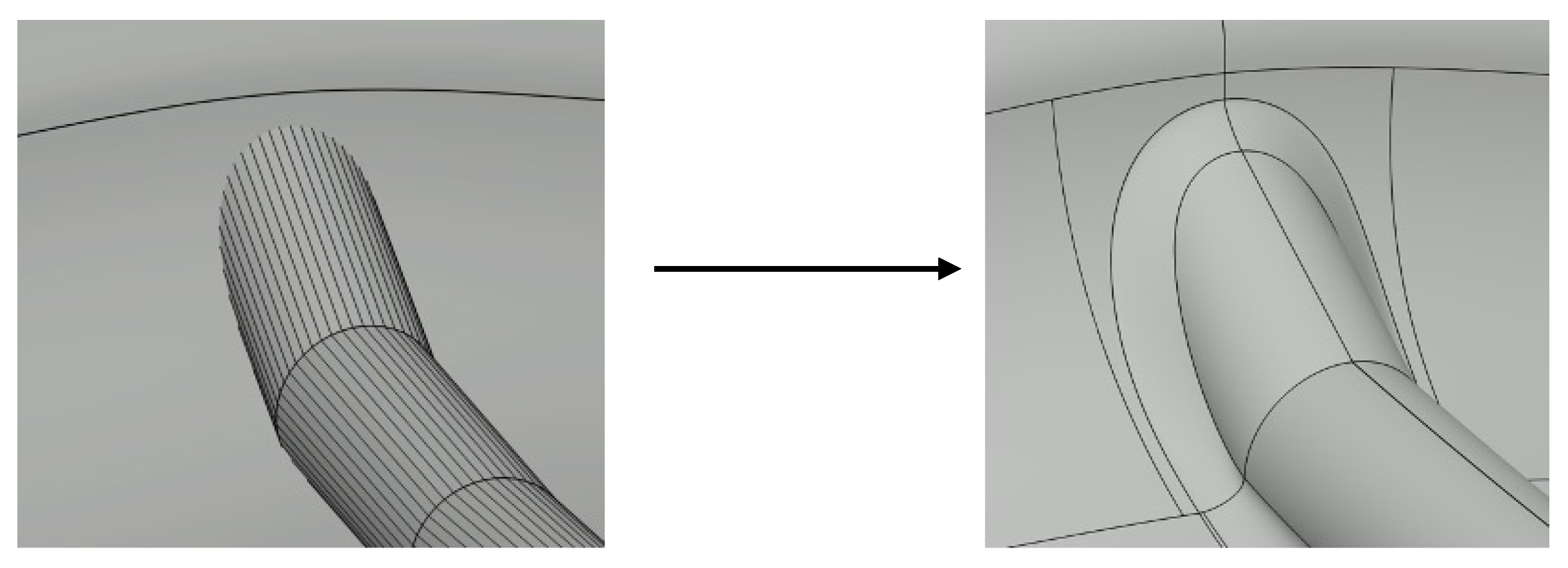
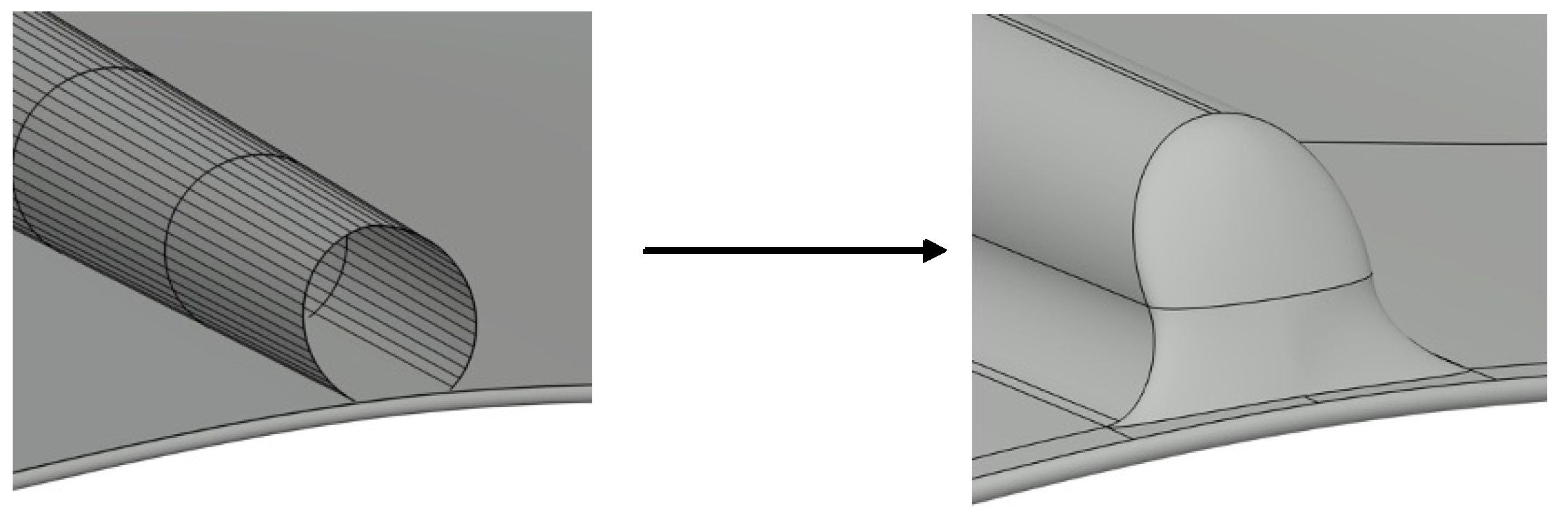
2.1. Geometric Model of the Wing
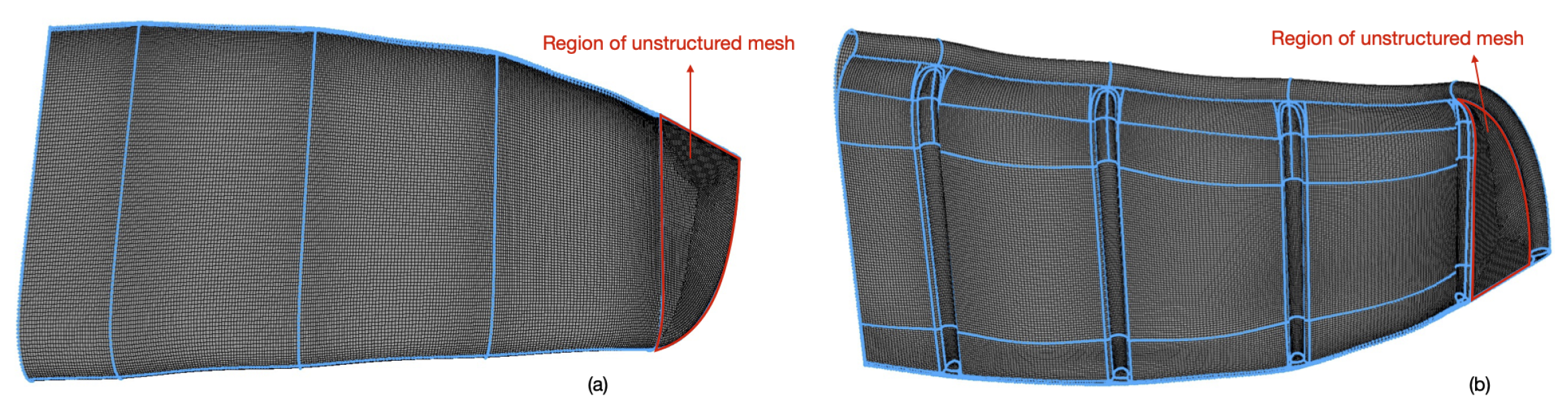
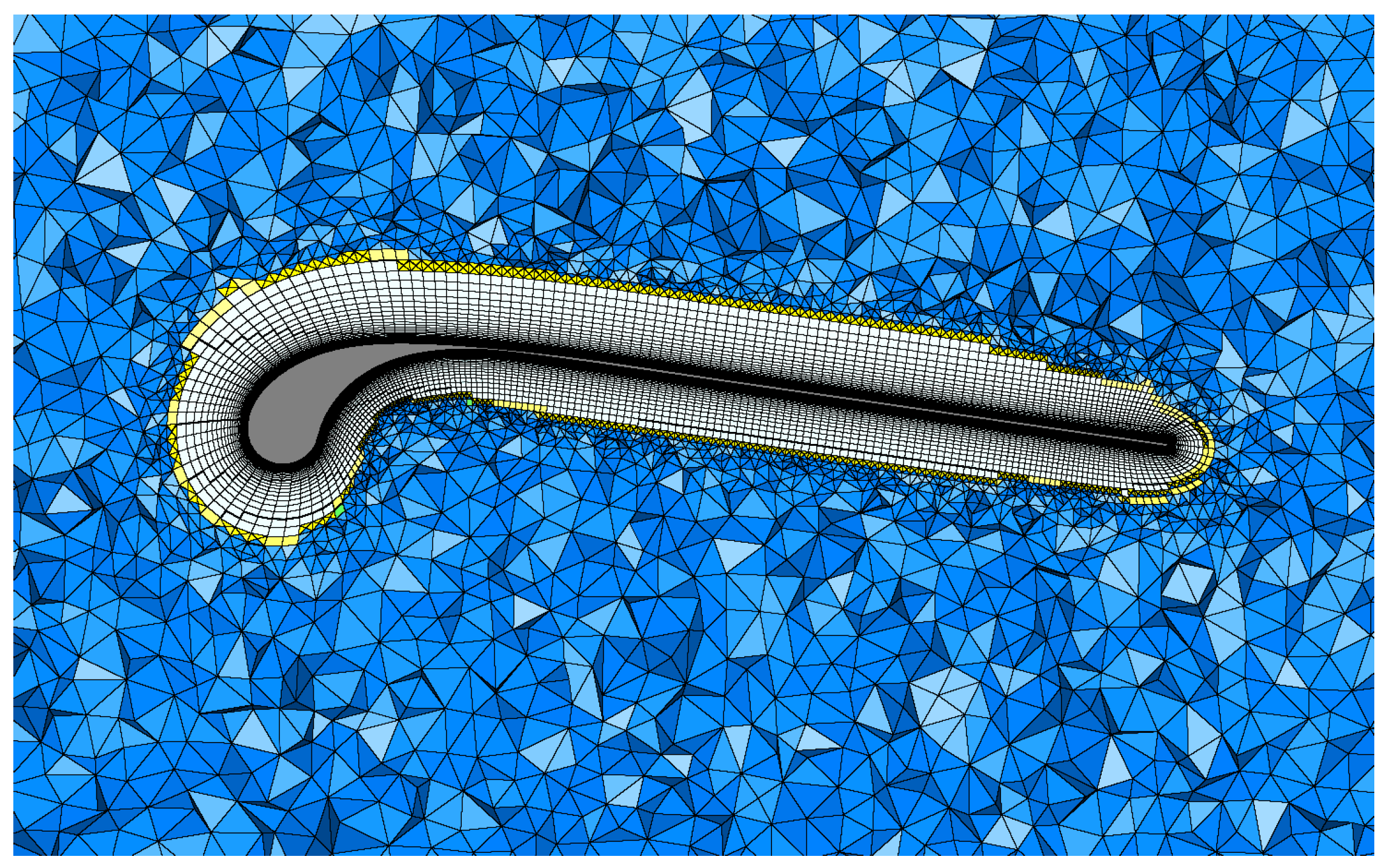
2.2. Meshing of the Wing Geometry
2.3. Fluid Dynamic Solver
3. Results
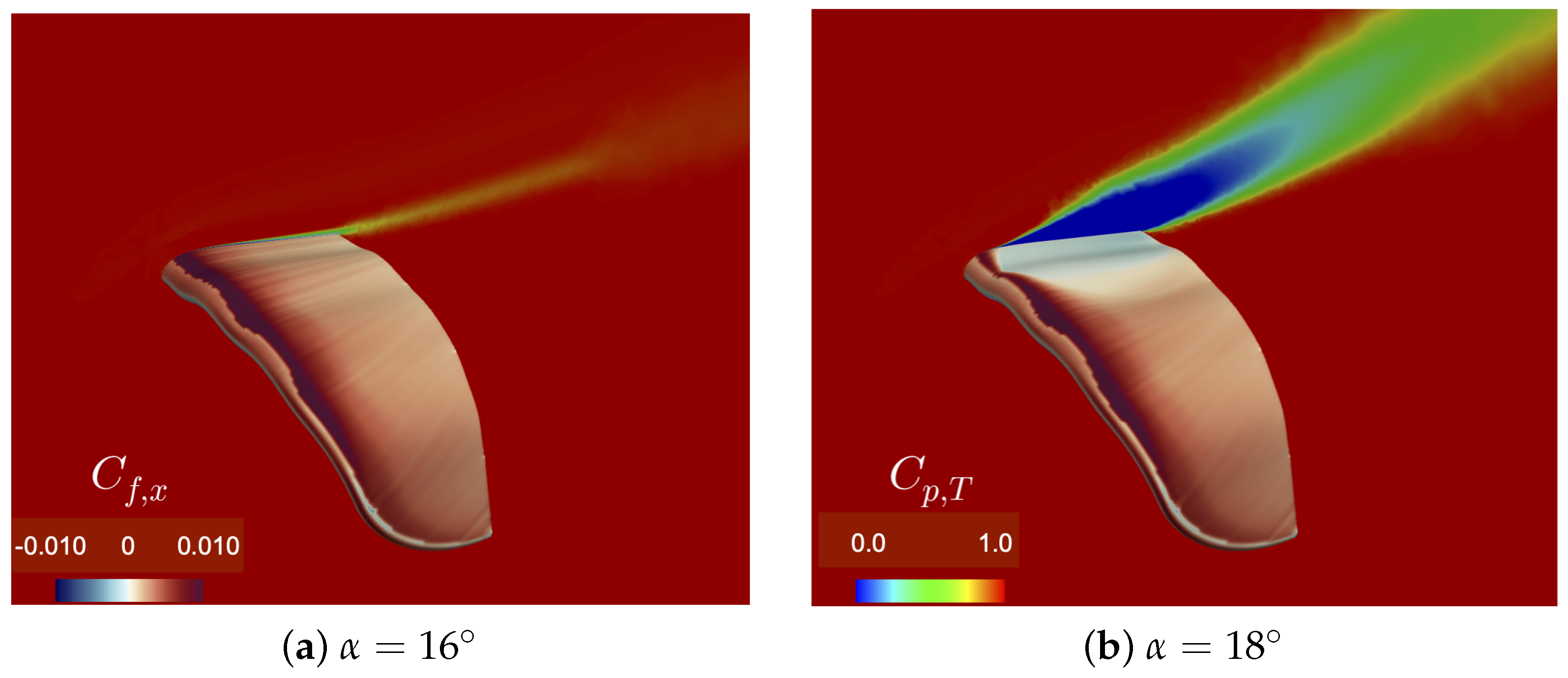
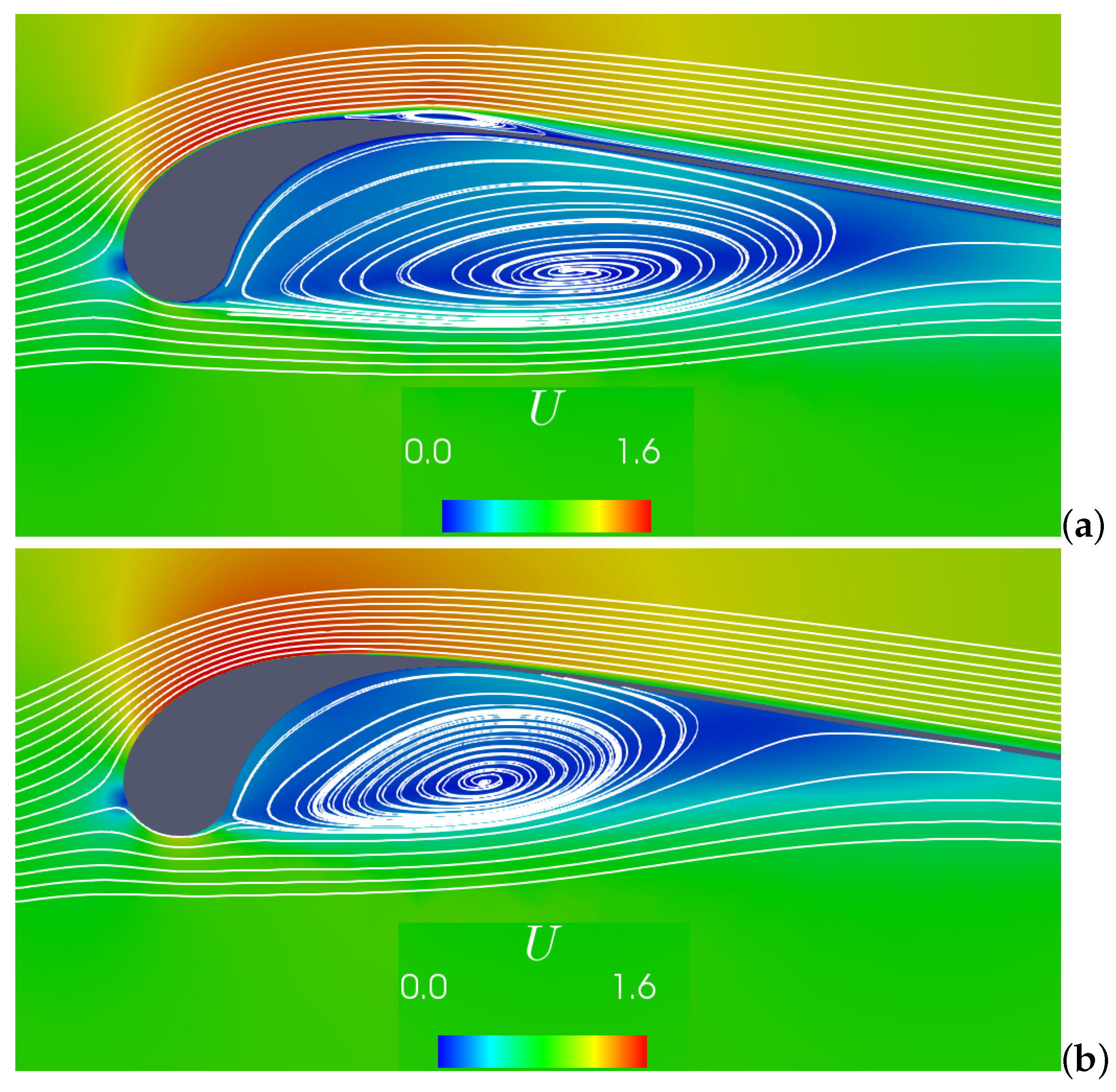
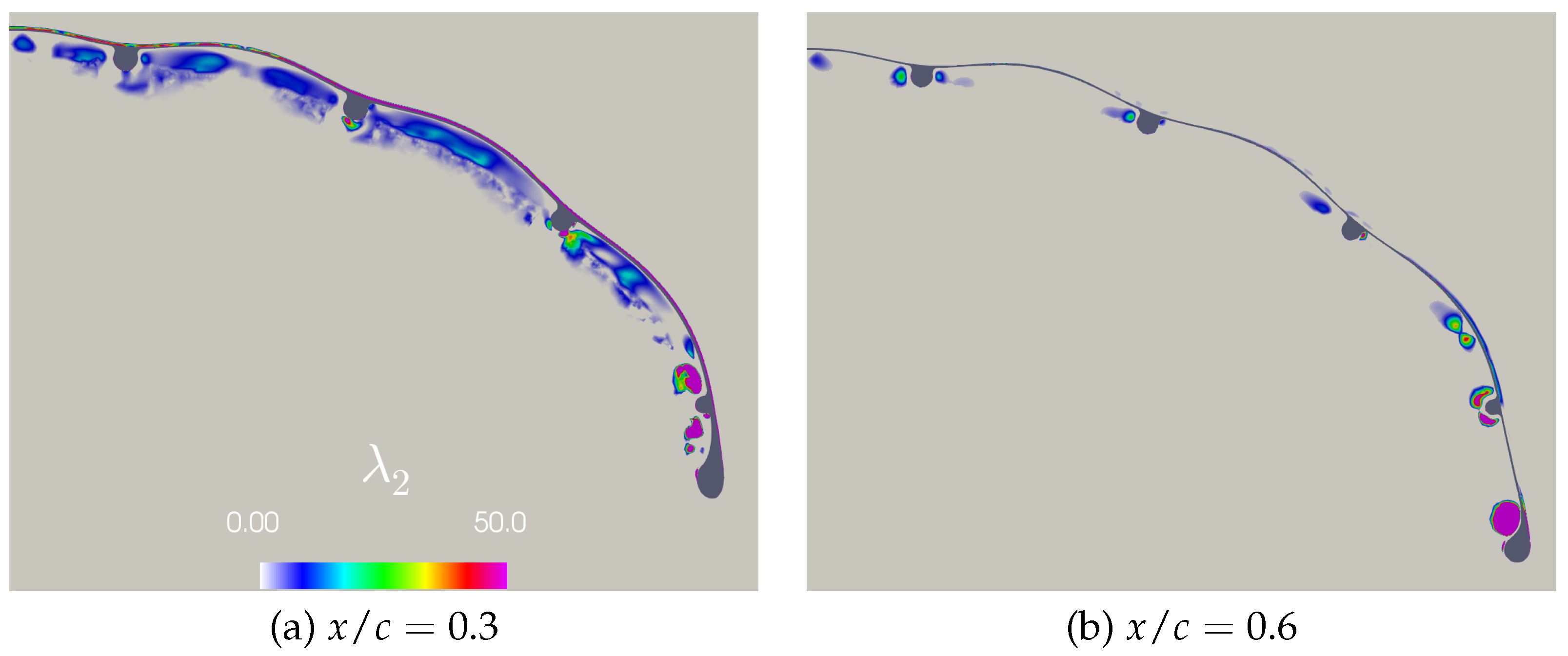
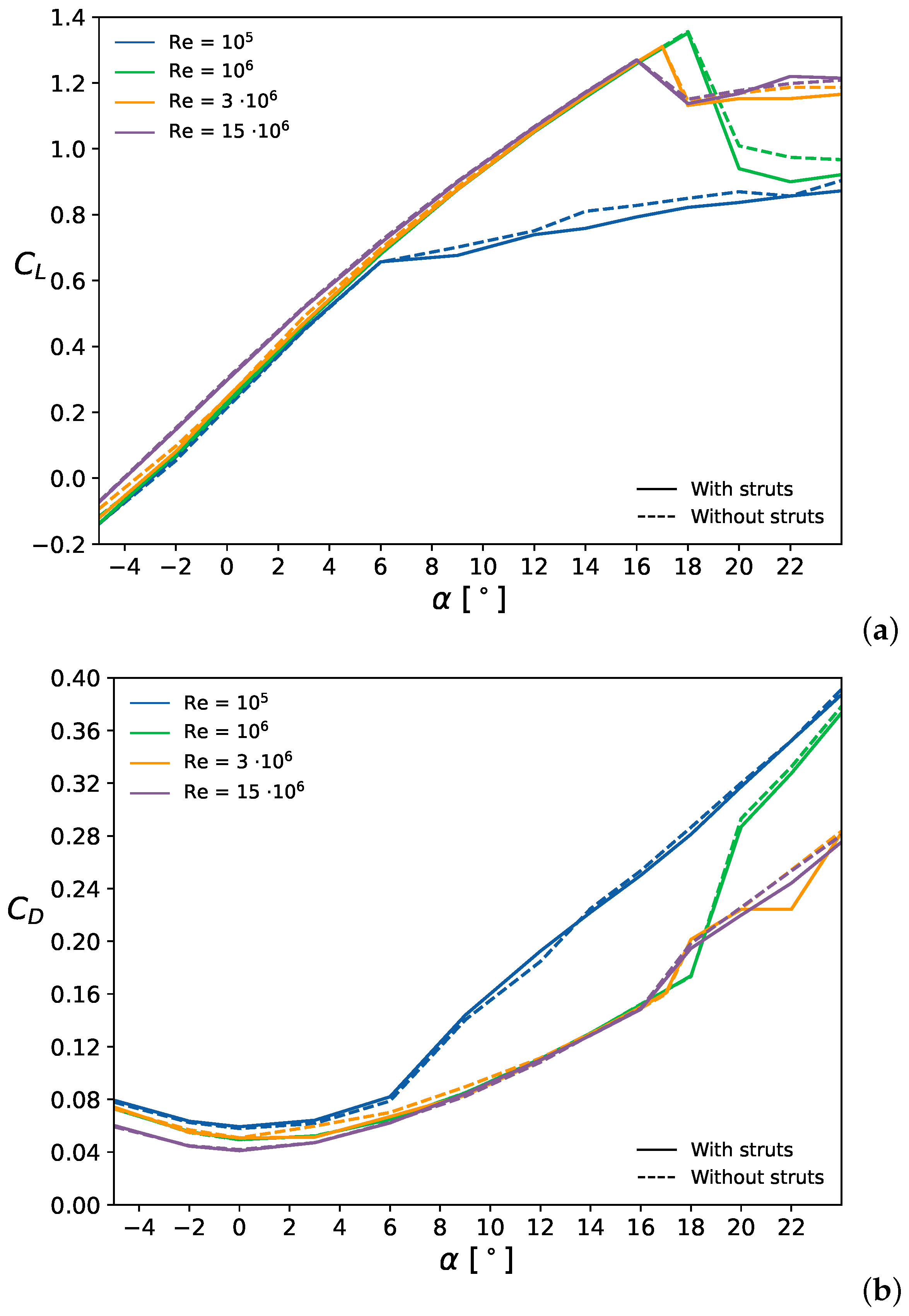
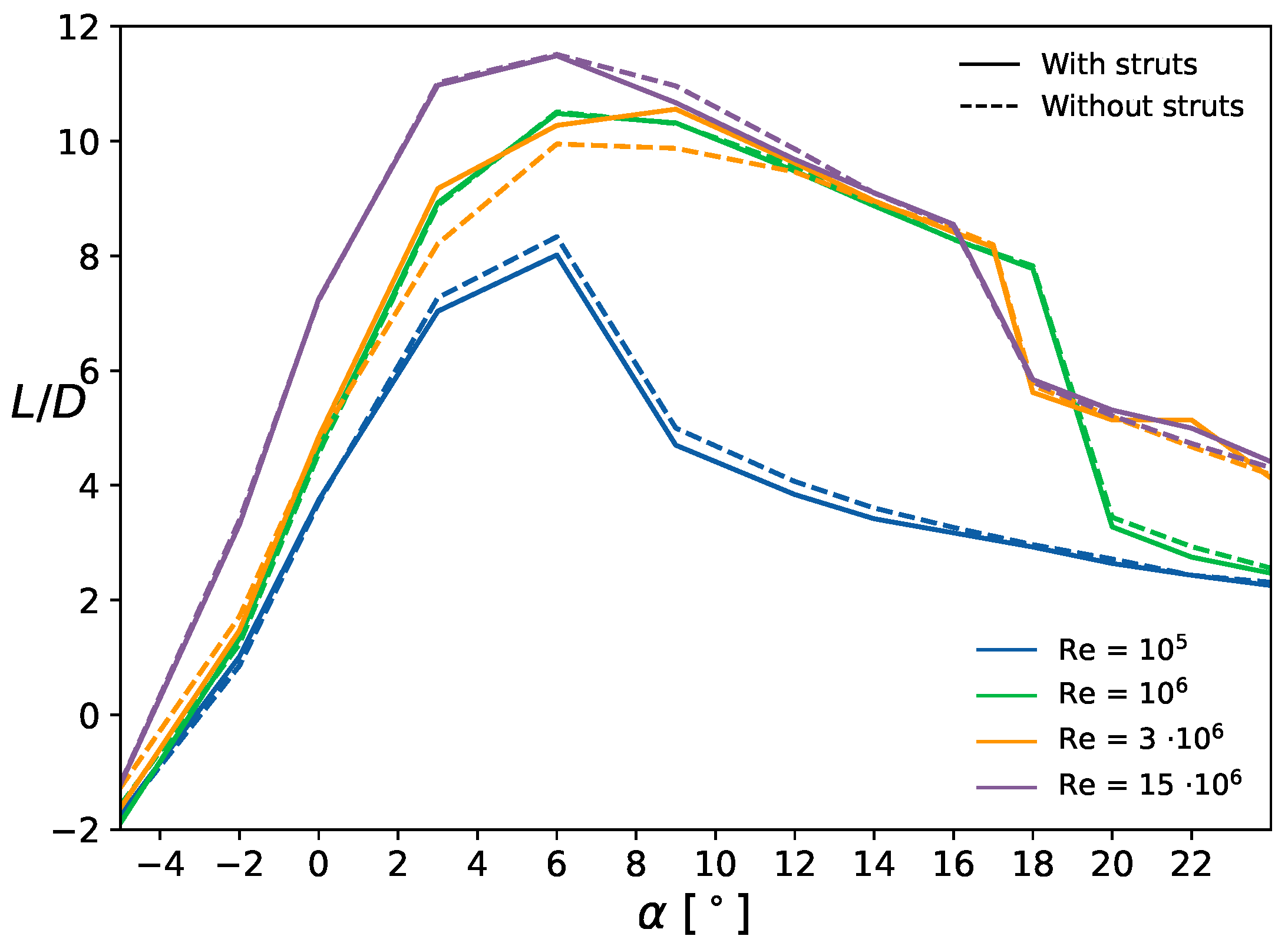
3.1. Aerodynamics without Side-Slip
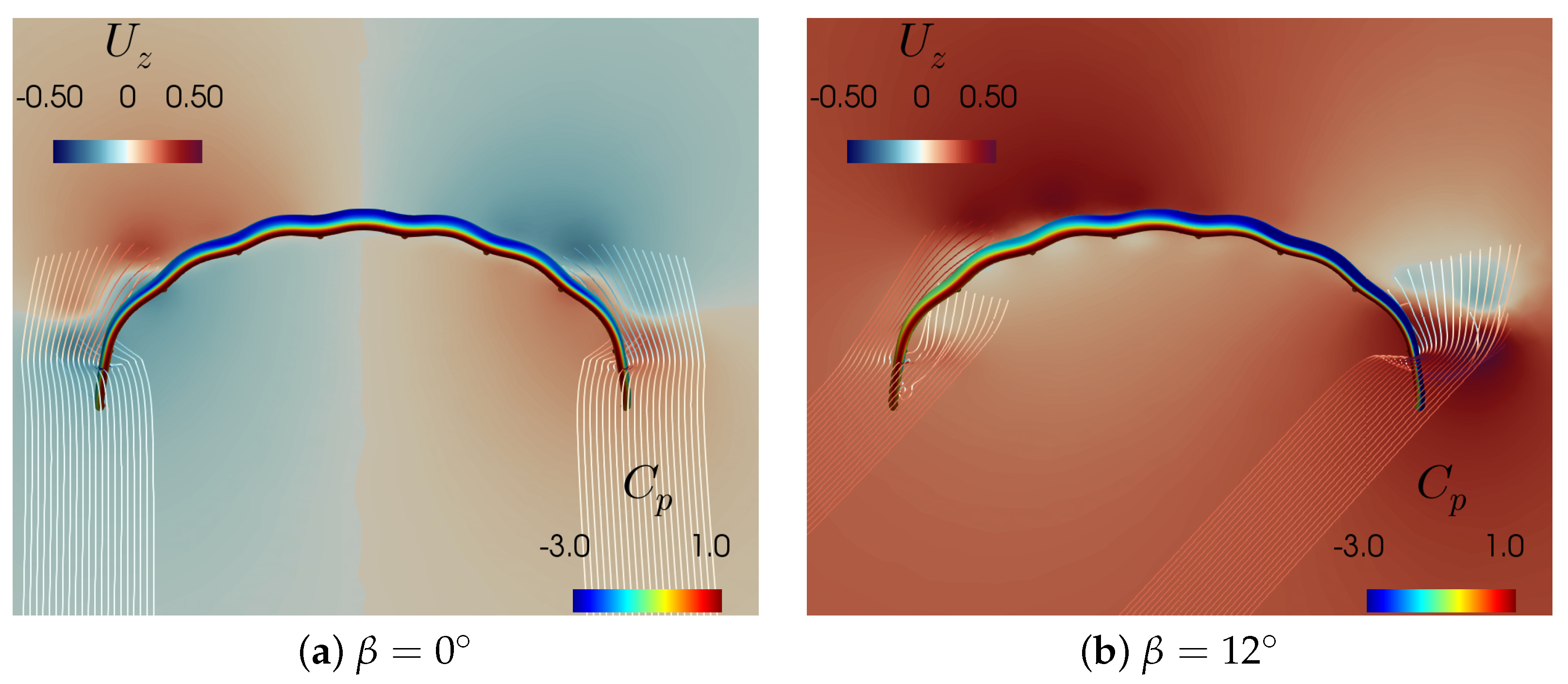
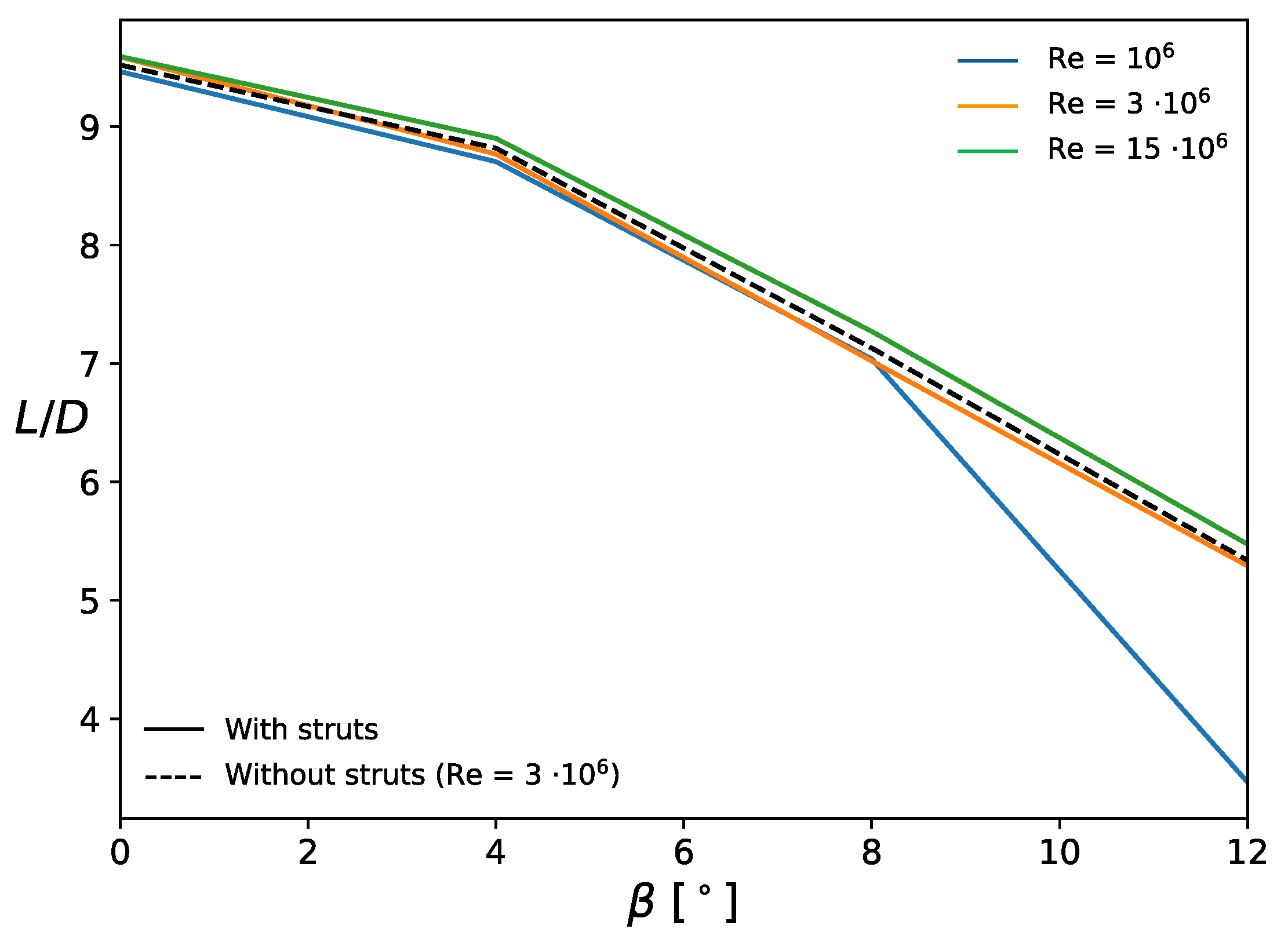
3.2. Aerodynamics with Side-Slip
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- IRENA. Future of Wind—Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects (A Global Energy Transformation Paper); Technical report; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- IRENA. Global Energy Transformation: A Roadmap to 2050, 2019th ed.; Technical Report; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- IRENA. Offshore Renewables: An Action Agenda for Deployment; Technical Report; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2021. [Google Scholar]
- Van der Vlugt, R.; Peschel, J.; Schmehl, R. Design and Experimental Characterization of a Pumping Kite Power System. In Airborne Wind Energy; Ahrens, U., Diehl, M., Schmehl, R., Eds.; Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 23; pp. 403–425. [Google Scholar] [CrossRef]
- Oehler, J.; Schmehl, R. Aerodynamic Characterization of a Soft Kite by in Situ Flow Measurement. Wind Energy Sci. 2019, 4, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Oehler, J.; van Reijen, M.; Schmehl, R. Experimental investigation of soft kite performance during turning maneuvers. J. Phys. Conf. Ser. 2018, 1037. [Google Scholar] [CrossRef]
- Van der Vlugt, R.; Bley, A.; Schmehl, R.; Noom, M. Quasi-Steady Model of a Pumping Kite Power System. Renew. Energy 2019, 131, 83–99. [Google Scholar] [CrossRef]
- Borobia-Moreno, R.; Ramiro-Rebollo, D.; Schmehl, R.; Sánchez-Arriaga, G. Identification of Kite Aerodynamic Characteristics Using the Estimation Before Modeling Technique. Wind Energy 2021, 24, 596–608. [Google Scholar] [CrossRef]
- Schmidt, E.; De Lellis Costa de Oliveira, M.; Saraiva da Silva, R.; Fagiano, L.; Trofino Neto, A. In-Flight Estimation of the Aerodynamics of Tethered Wings for Airborne Wind Energy. IEEE Trans. Control Syst. Technol. 2020, 28, 1309–1322. [Google Scholar] [CrossRef] [Green Version]
- Wood, T.A.; Hesse, H.; Smith, R.S. Predictive Control of Autonomous Kites in Tow Test Experiments. IEEE Control Syst. Lett. 2017, 1, 110–115. [Google Scholar] [CrossRef]
- Hummel, J.; Göhlich, D.; Schmehl, R. Automatic Measurement and Characterization of the Dynamic Measurands of Tethered Flexible Wings. Wind Energy Sci. 2019, 4, 41–55. [Google Scholar] [CrossRef] [Green Version]
- Rushdi, M.A.; Rushdi, A.A.; Dief, T.N.; Halawa, A.M.; Yoshida, S.; Schmehl, R. Power Prediction of Airborne Wind Energy Systems Using Multivariate Machine Learning. Energies 2020, 13, 2367. [Google Scholar] [CrossRef]
- Leloup, R.; Roncin, K.; Bles, G.; Leroux, J.B.; Jochum, C.; Parlier, Y. Estimation of the Lift-to-Drag Ratio Using the Lifting Line Method: Application to a Leading Edge Inflatable Kite. In Airborne Wind Energy; Ahrens, U., Diehl, M., Schmehl, R., Eds.; Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 19; pp. 339–355. [Google Scholar] [CrossRef]
- Duport, C. Modeling with Consideration of the Fluid-Structure Interaction of the Behavior under Load of a Kite for Auxiliary Traction of Ships. Ph.D. Thesis, ENSTA Bretagne, Brest, France, 2018. [Google Scholar]
- Gaunaa, M.; Paralta Carqueija, P.F.; Réthoré, P.E.M.; Sørensen, N.N. A Computationally Efficient Method for Determining the Aerodynamic Performance of Kites for Wind Energy Applications. In Proceedings of the European Wind Energy Association Conference, Brussels, Belgium, 14–17 March 2011; EWEA: Brussels, Belgium, 2011. [Google Scholar]
- Breukels, J. An Engineering Methodology for Kite Design. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2011. [Google Scholar]
- Leuthold, R.C. Multiple-Wake Vortex Lattice Method for Membrane-Wing Kites. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- Folkersma, M.; Schmehl, R.; Viré, A. Flow transition modeling on two-dimensional circular leading edge airfoils. Wind Energy 2019, 22, 908–921. [Google Scholar] [CrossRef] [PubMed]
- Demkowicz, P. Numerical Analysis of the Flow Past a Leading Edge Inflatable Kite Wing Using a Correlation-Based Transition Model. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Viré, A.; Demkowicz, P.; Folkersma, M.; Roullier, A.; Schmehl, R. Reynolds-Averaged Navier-Stokes Simulations of the Flow Past a Leading Edge Inflatable Wing for Airborne Wind Energy Applications. J. Phys. Conf. Ser. 2020, 1618, 032007. [Google Scholar] [CrossRef]
- Schelbergen, M.; Schmehl, R. Validation of the Quasi-Steady Performance Model for Pumping Airborne Wind Energy Systems. J. Phys. Conf. Ser. 2020, 1618, 032003. [Google Scholar] [CrossRef]
- Vermillion, C.; Cobb, M.; Fagiano, L.; Leuthold, R.; Diehl, M.; Smith, R.S.; Wood, T.A.; Rapp, S.; Schmehl, R.; Olinger, D.; et al. Electricity in the Air: Insights From Two Decades of Advanced Control Research and Experimental Flight Testing of Airborne Wind Energy Systems. Annu. Rev. Control 2021, 52, 330–357. [Google Scholar] [CrossRef]
- Lebesque, G. Steady-State RANS Simulation of a Leading Edge Inflatable Wing with Chordwise Struts. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2020. [Google Scholar]
- Menter, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Langtry, R.; Menter, F. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Jonard, S. In-Flight Measurement of Kite Deformations with Inertial Sensors. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2021. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viré, A.; Lebesque, G.; Folkersma, M.; Schmehl, R. Effect of Chordwise Struts and Misaligned Flow on the Aerodynamic Performance of a Leading-Edge Inflatable Wing. Energies 2022, 15, 1450. https://doi.org/10.3390/en15041450
Viré A, Lebesque G, Folkersma M, Schmehl R. Effect of Chordwise Struts and Misaligned Flow on the Aerodynamic Performance of a Leading-Edge Inflatable Wing. Energies. 2022; 15(4):1450. https://doi.org/10.3390/en15041450
Chicago/Turabian StyleViré, Axelle, Geert Lebesque, Mikko Folkersma, and Roland Schmehl. 2022. "Effect of Chordwise Struts and Misaligned Flow on the Aerodynamic Performance of a Leading-Edge Inflatable Wing" Energies 15, no. 4: 1450. https://doi.org/10.3390/en15041450
APA StyleViré, A., Lebesque, G., Folkersma, M., & Schmehl, R. (2022). Effect of Chordwise Struts and Misaligned Flow on the Aerodynamic Performance of a Leading-Edge Inflatable Wing. Energies, 15(4), 1450. https://doi.org/10.3390/en15041450






