Hedging Wind Power Risk Exposure through Weather Derivatives
Abstract
:1. Introduction
2. Fundamental Power Model and Wind Speed
2.1. Fundamental Power Model: SMaPS
- i.
- The load process ;
- ii.
- The short-term process ;
- iii.
- The long-term process ;
- iv.
- (Logarithmic) price load curve, abbreviated as PLC, ;
- v.
- The average relative availability of power plants
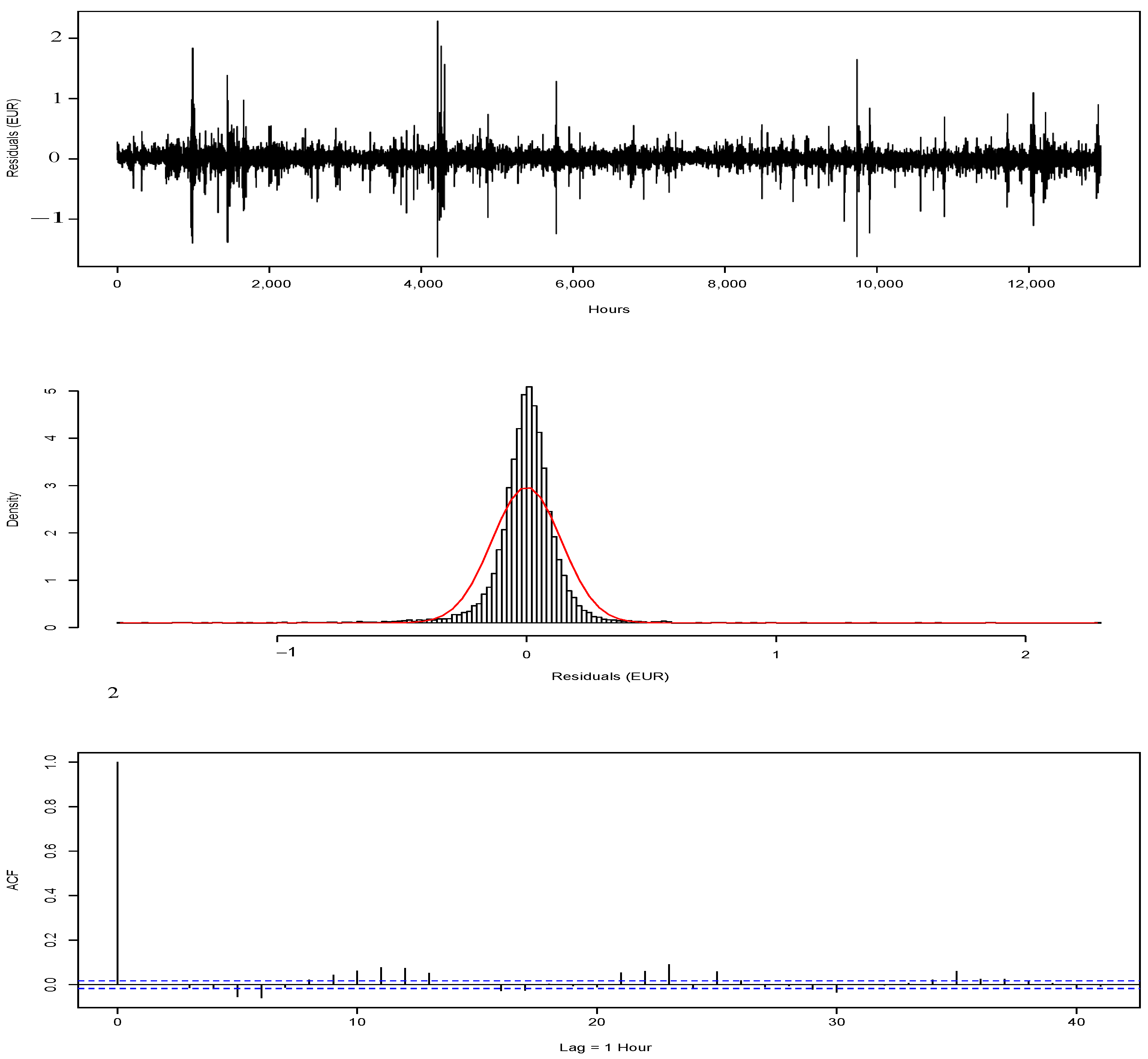
2.2. Statistical Analysis, Model Selection, and Model Fit: Short-Term Stochastic Process
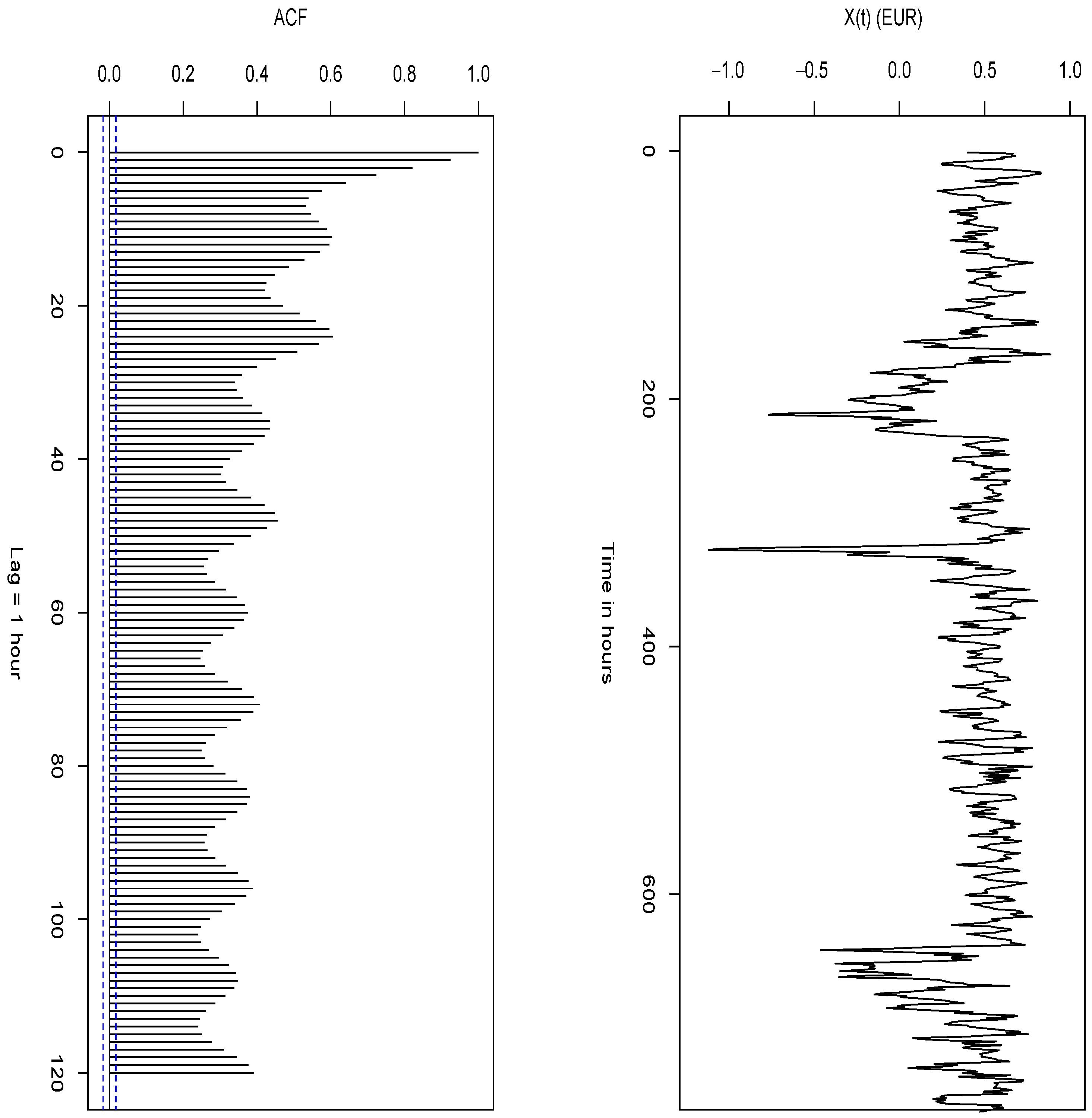
2.3. The Long-Term Process
Long-Term Component Calibration
- The SARIMA variance;
- The probability distribution.
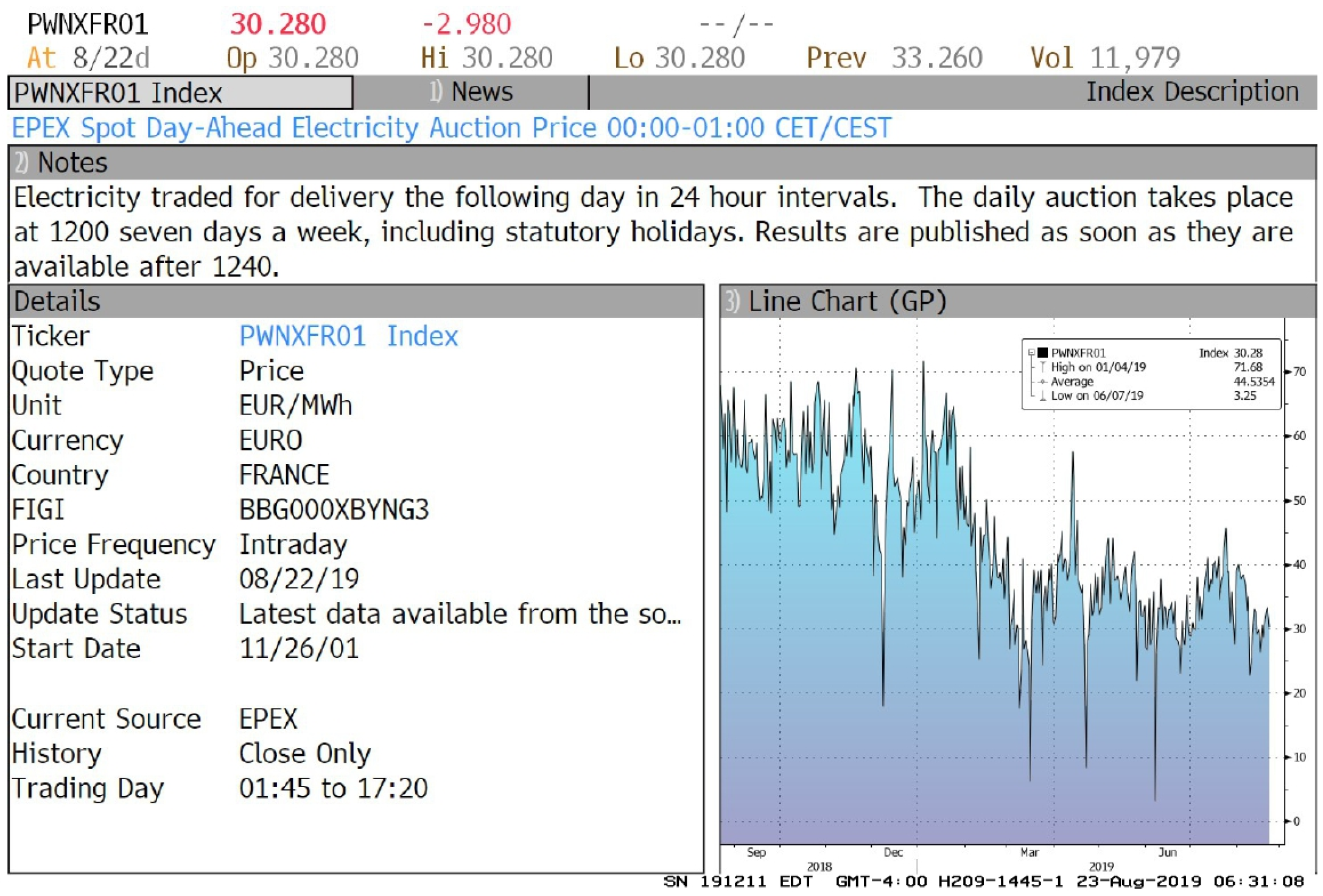
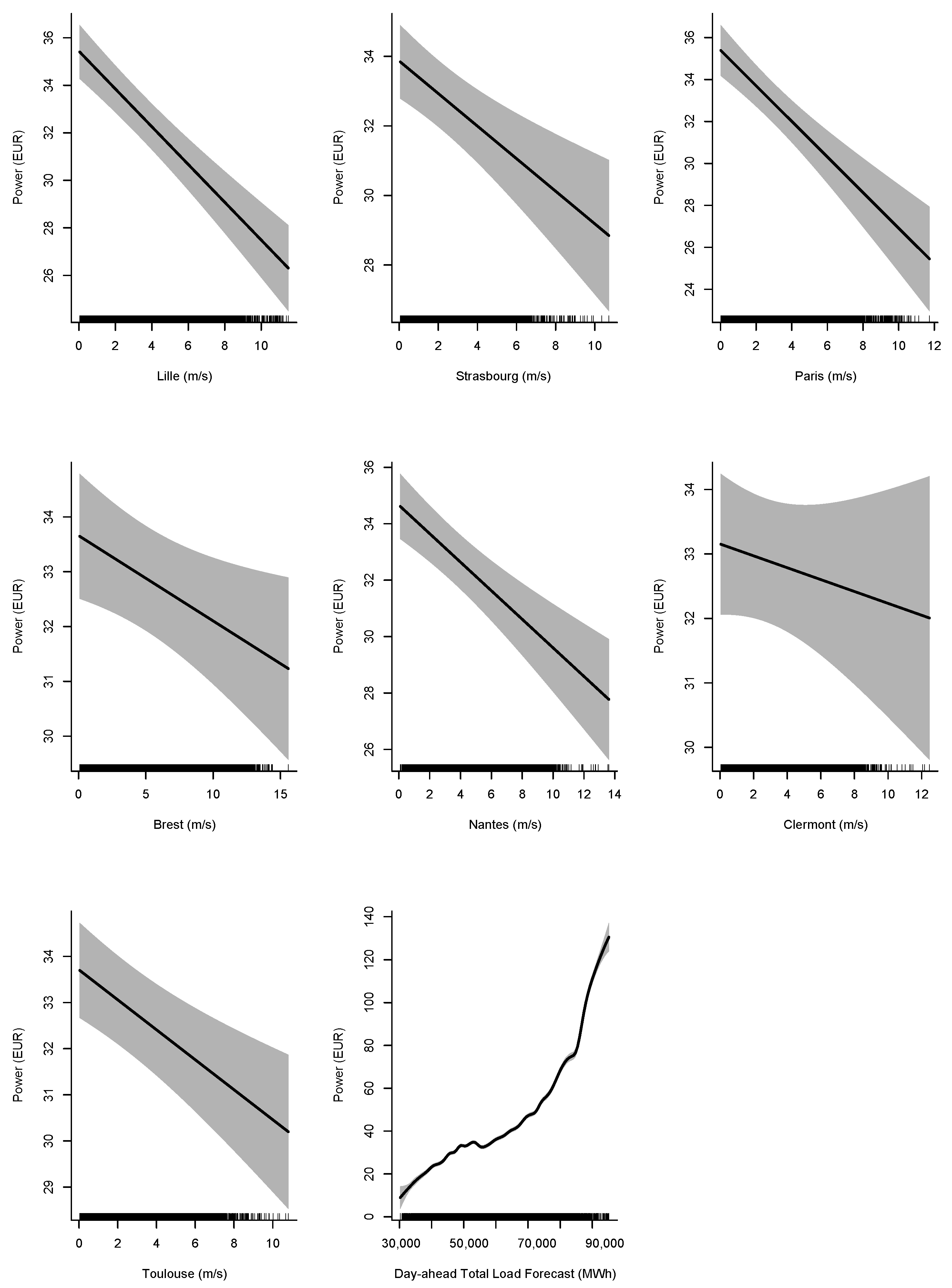
2.4. Statistical Relationship between Wind Speed and the EPEX Spot Day-Ahead Electricity Auction Price in France
3. Industrial Portfolio and Modification of Weather Risk Exposure Using Weather Derivatives
3.1. The Wind-Energy-Powered Park Module
- Hub height of the turbine: 95 m.;
- Rated power of the turbine: 2 MW;
- Cut-in wind speed: 4 m/s;
- Rated wind speed: 13 m/s;
- Cut-out wind speed: 25 m/s.
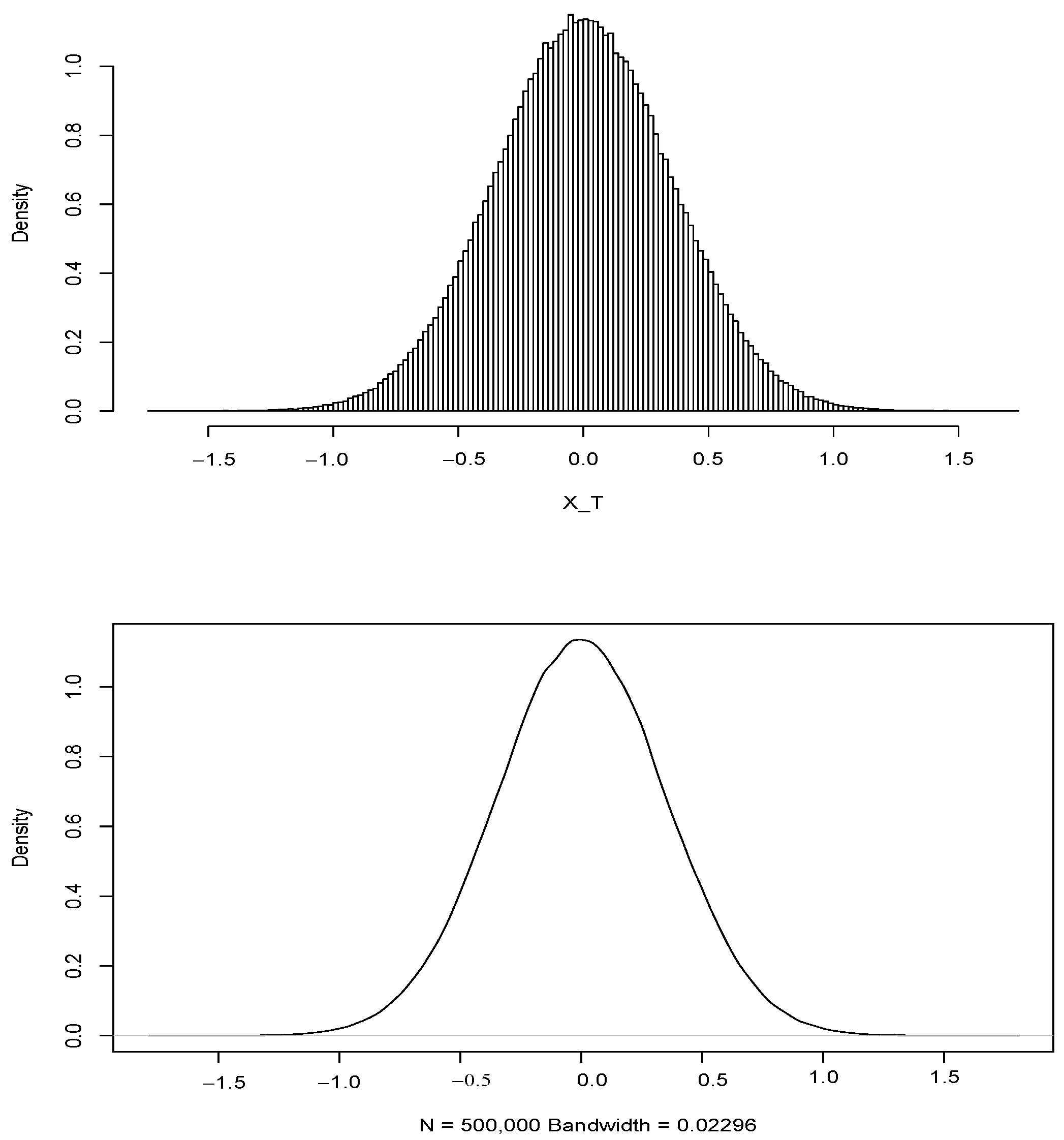
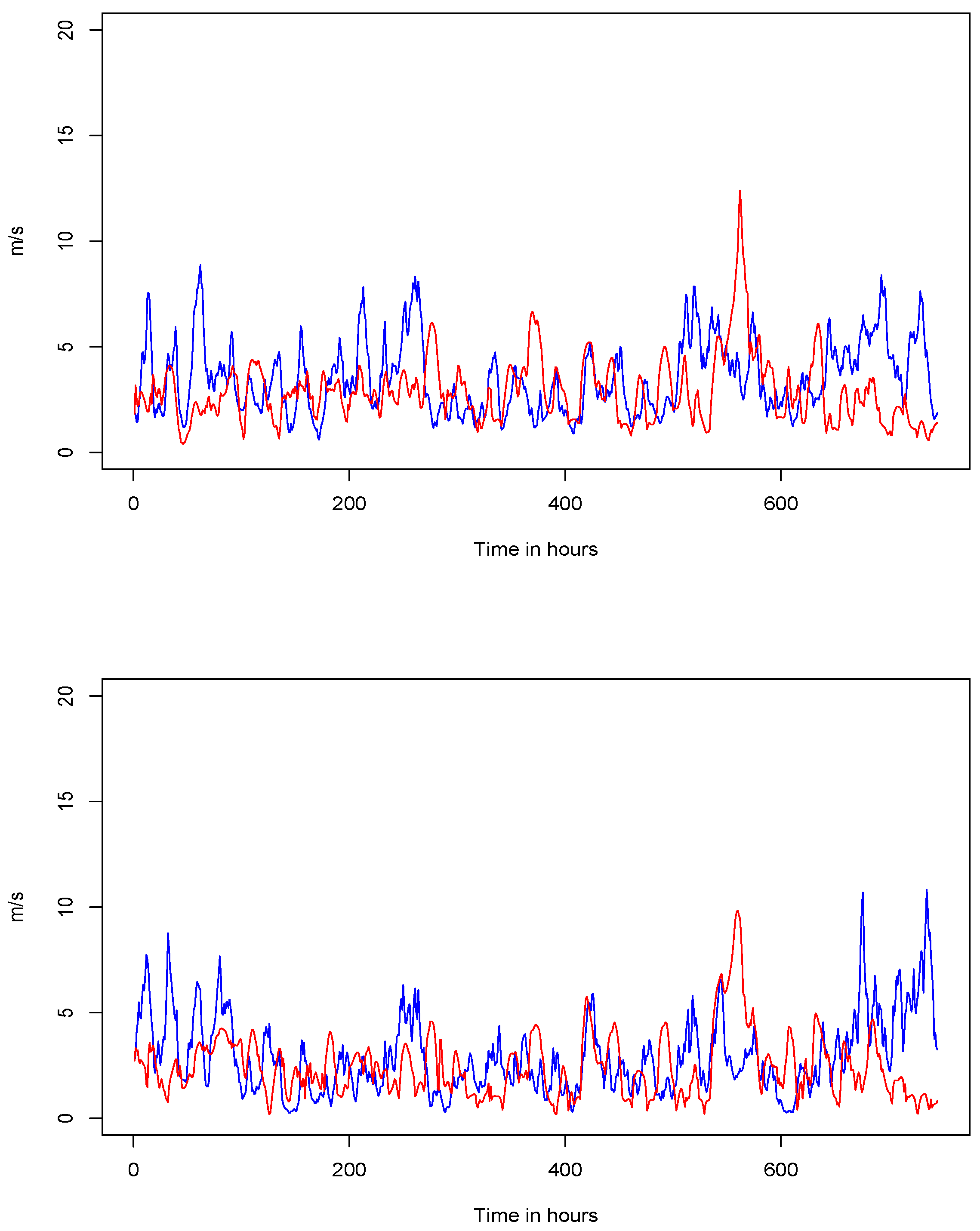
Wind Speed Stochastic Modeling
3.2. Earnings-at-Risk and Wind Sensitivity
3.3. Scenario Approach for Wind Sensitivity
4. Validation of the Delta Hedging Strategy Performance
4.1. Contract Issuing Phase
4.2. The Hedging Strategy and Its Impact on Risk Measures
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| spot price of electricity | |
| energy load process | |
| short-term process for the SMaPS model | |
| long-term process for the SMaPS model | |
| price load curve | |
| average relative availability of power plants (not used) | |
| backward shift operator | |
| typical white noise | |
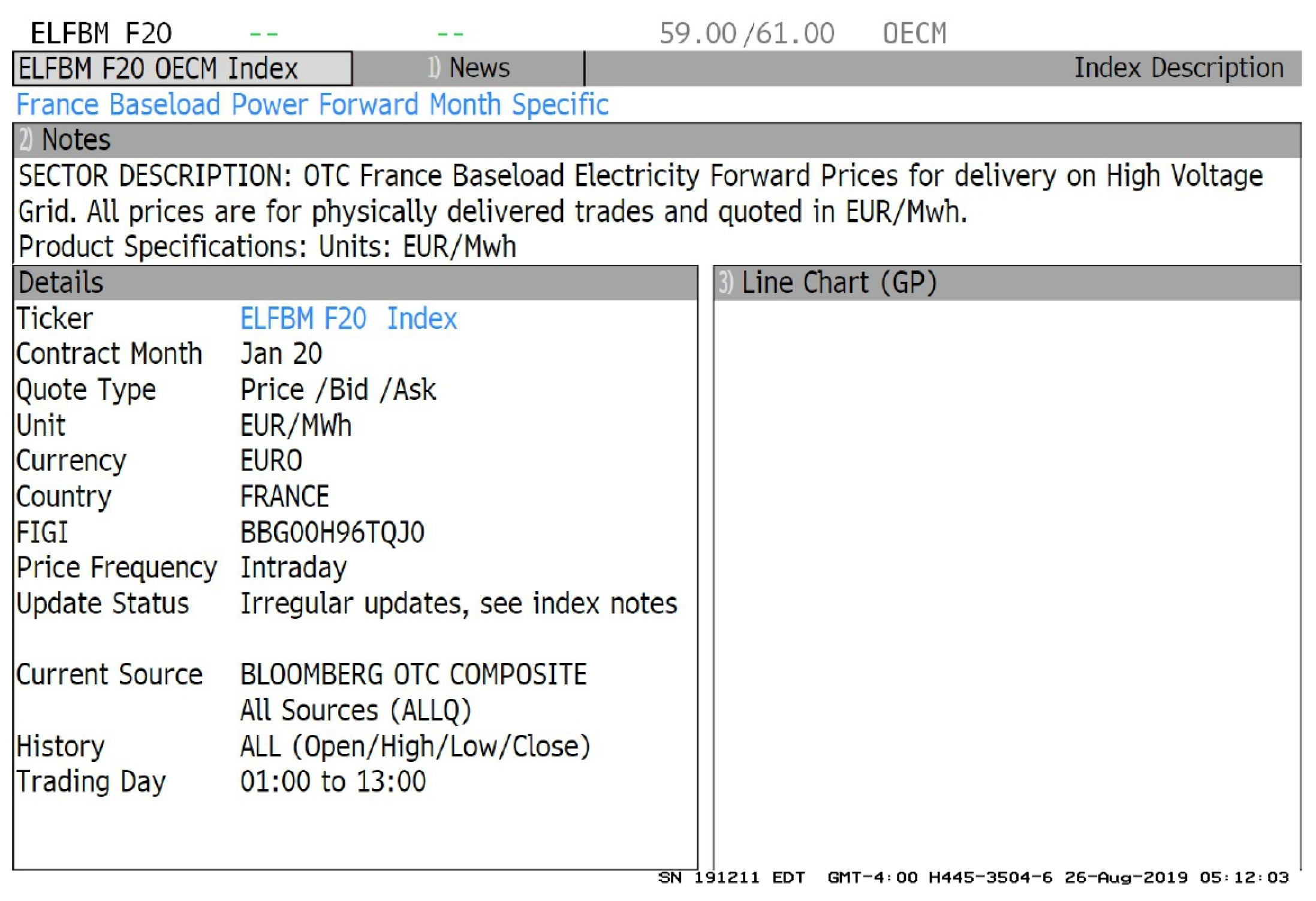
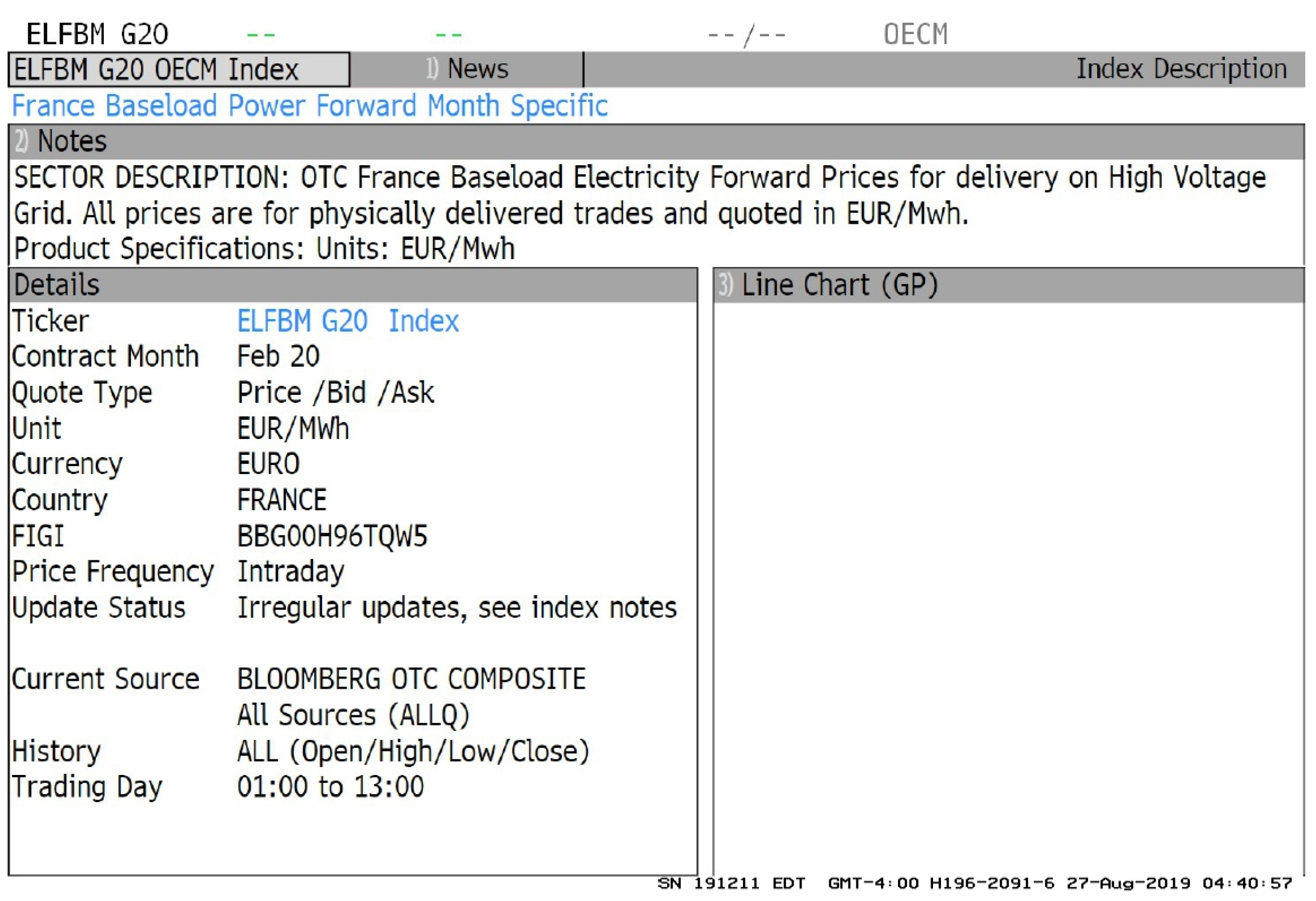
| futures price, at time t, of a contract that foresees delivery of 1 MWh at time | |
| wind speed at time i for station z | |
| aggregate revenue of the power company | |
| energy produced by wind plant | |
| power curve | |
| NPV of the industrial portfolio | |
| installed capacity of a wind plant | |
| earnings-at-risk | |
| , () | exposure to wind risk |
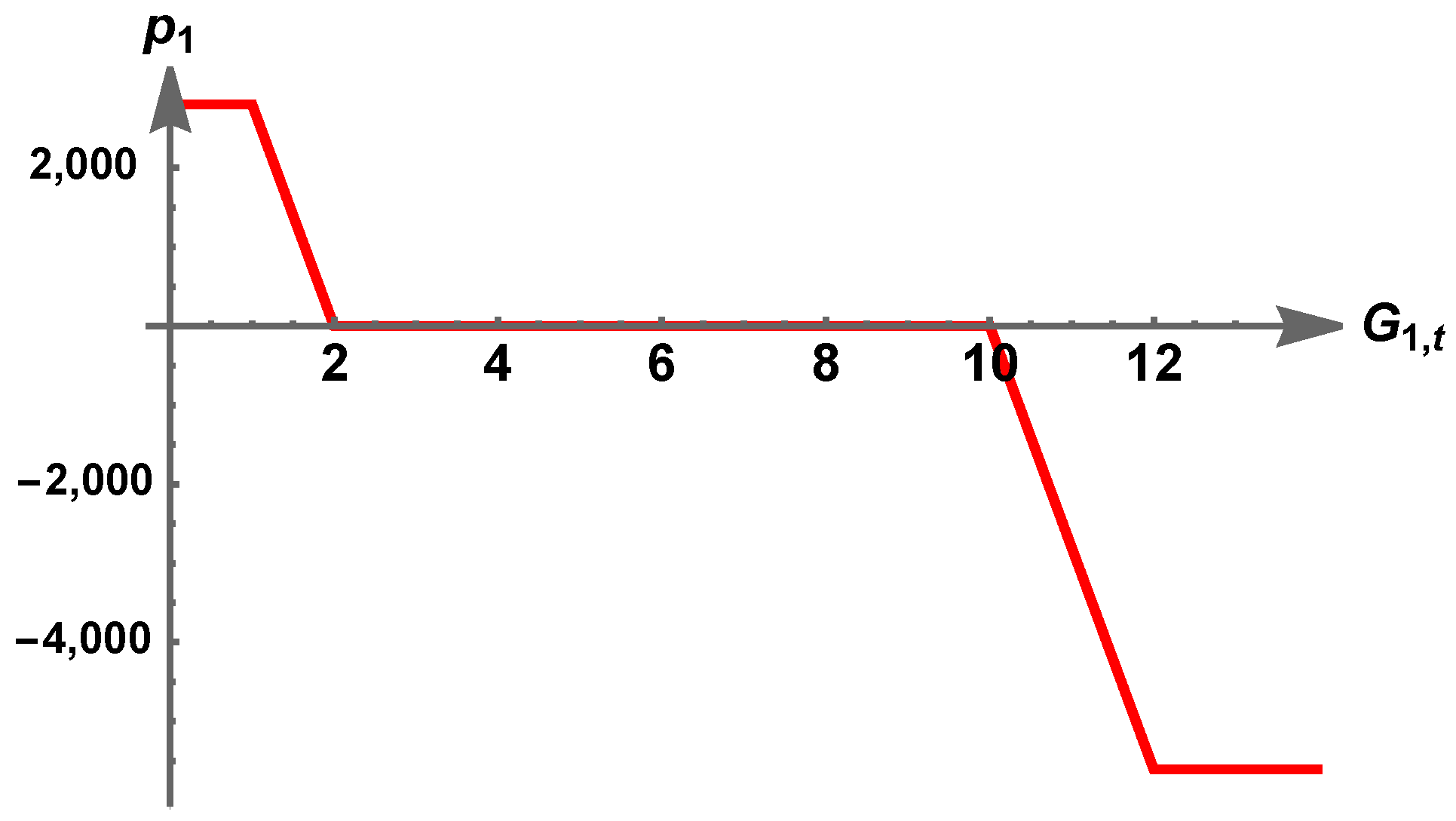
| pay-off of a long collar | |
| coverage cost in t of the structured contract |
References
- Muller, A.; Grandi, M. Weather Derivatives: A Risk Management Tool for Weather-sensitive Industries. Geneva Pap. Risk Insur. 2000, 25, 273–287. [Google Scholar] [CrossRef]
- Pérez-Gonzalez, F.; Yun, H. Risk Management and Firm Value: Evidence from Weather Derivatives. J. Financ. 2013, LXVIII, 2143–2176. [Google Scholar] [CrossRef]
- Salgueiro, A.M.; Tarrazon-Rodon, M.A. Weather derivatives to mitigate meteorological risks in tourism management: An empirical application to celebrations of Comunidad Valenciana (Spain). Tour. Econ. 2021, 27, 591–613. [Google Scholar] [CrossRef]
- Stulec, I.; Petljak, K.; Bakovic, T. Effectiveness of weather derivatives as a hedge against the weather risk in agriculture. Agric. Econ.-Czech. 2016, 62, 356–362. [Google Scholar] [CrossRef] [Green Version]
- Dawkins, L.C. Weather and Climate Related Sensitivities and Risks in a Highly Renewable UK Energy System: A Literature Review; Crown Copyright, Met Office, Exeter (UK): London, UK, 2019. [Google Scholar]
- Alexandridis, A.K.; Zapranis, A.D. Weather Derivatives, Modeling and Pricing Weather-Related Risk; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-6070-1. [Google Scholar]
- Burger, M.; Klar, B.; Muller, A.; Schindlmayr, G. A spot market model for pricing derivatives in electricity markets. Quant. Financ. 2004, 4, 109–122. [Google Scholar] [CrossRef]
- Jewson, S.; Brix, A. Weather Derivative Valuation: The Meteorological, Statistical, Financial and Mathematical Foundations; Cambridge University Press: Cambridge, UK, 2005; p. 392. [Google Scholar]
- Roncoroni, A.; Fusai, G.; Cummins, M. Handbook of Multi-Commodity Markets and Products: Structuring, Trading and Risk Management; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015; pp. 255–277. [Google Scholar]
- Alaton, P.; Djehiche, B.; Stillberger, D. On Modelling and Pricing Weather Derivatives. Appl. Math. Financ. 2002, 9, 1–20. [Google Scholar] [CrossRef]
- Cui, K.; Swishchuk, A. Applications of Weather Derivatives in Energy Market. J. Energy Mark. 2015, 8, 59–76. [Google Scholar] [CrossRef]
- Fernandes, G.; Lima Gomes, L.; Teixeira Brandão, L.E. Mitigating Hydrological Risk with Energy Derivatives. Energy Econ. 2019, 81, 528–535. [Google Scholar] [CrossRef]
- Barucci, E.; La Bua, G.; Marazzina, D. On relative performance, remuneration and risk taking of asset managers. Ann. Financ. 2018, 14, 517–545. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.; Oren, S.S. A multi-period equilibrium pricing model of weather derivatives. Energy Syst. 2010, 1, 3–30. [Google Scholar] [CrossRef] [Green Version]
- Bressan, G.M.; Romagnoli, S. Climate risks and weather derivatives: A copula-based pricing model. J. Financ. Stab. 2021, 54, 100877. [Google Scholar] [CrossRef]
- Kanamura, T.; Homann, L.; Prokopczuk, M. Pricing analysis of wind power derivatives for renewable energy risk management. Appl. Energy 2021, 304, 117827. [Google Scholar] [CrossRef]
- Benth, F.E.; Lange, N.; Myklebust, T.A. Pricing and hedging quanto options in energy markets. J. Energy Mark. 2015, 8, 1–35. [Google Scholar] [CrossRef]
- Benth, F.E.; Di Persio, L.; Lavagnini, S. Stochastic modeling of wind derivatives in energy markets. Risks 2018, 6, 56. [Google Scholar] [CrossRef] [Green Version]
- Caporin, M.; Preś, J.; Torro, H. Model based Monte Carlo pricing of energy and temperature Quanto options. Energy Econ. 2012, 34, 1700–1712. [Google Scholar] [CrossRef] [Green Version]
- Benth, F.E.; Ibrahim, N.A. Stochastic modeling of photovoltaic power generation and electricity prices. J. Energy Mark. 2017, 10, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez, Y.E.; Pérez-Uribe, M.A.; Contreras, J. Wind Put Barrier Options Pricing Based on the Nordix Index. Energies 2020, 14, 1177. [Google Scholar] [CrossRef]
- Kaufmann, J.; Kienscherf, P.A.; Ketter, W. Modeling and Managing Joint Price and Volumetric Risk for Volatile Electricity Portfolios. Energies 2020, 13, 3578. [Google Scholar] [CrossRef]
- Wieczorek-Kosmala, M. Weather Risk Management in Energy Sector: The Polish Case. Energies 2020, 13, 945. [Google Scholar] [CrossRef] [Green Version]
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 1991; p. 580. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting, 2nd ed.; Springer: New York, NY, USA, 2002; p. 437. [Google Scholar]
- Cont, R.; Tankov, P. Financial Modelling with Jump Processes; CRC Press LLC: Boca Raton, FL, USA, 2004; p. 528. [Google Scholar]
- Engle, R.F.; Granger, C.W.J.; Rice, J.; Weiss, A. Semiparametric Estimates of the Relation between Weather and Electricity Sales. J. Am. Stat. Assoc. 1986, 81, 310–320. [Google Scholar] [CrossRef]
- Craven, P.; Wahba, G. Smoothing noisy data with spline functions: Estimating the correct degree of smoothing by the method of generalized cross-validation. Numer. Math. 1979, 31, 377–403. [Google Scholar] [CrossRef]
- D’Amico, G.; Petroni, F.; Prattico, F. Wind speed prediction for wind farm applications by Extreme Value Theory and Copulas. J. Wind. Eng. Ind. Aerodyn. 2015, 145, 229–236. [Google Scholar] [CrossRef]
- Burger, M.; Graeber, B.; Schindlmayr, G. Managing Energy Risk. A Practical Guide for Risk Management in Power, Gas and Other Energy Markets; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; p. 439. [Google Scholar]
- McLeod, A.I.; Yu, H.; Krougly, Z. Algorithms for Linear Time Series Analysis: With R Package. J. Stat. Softw. 2007, 23, 1–26. [Google Scholar] [CrossRef] [Green Version]
- De Felice, M.; Moriconi, F. Una Nuova Finanza D’Impresa; Il Mulino: Bologna, Italy, 2011; Volume 196. [Google Scholar]



| Indicator | Value |
|---|---|
| log-likelihood function | 7172.87 |
| AIC | −14,335.74 |
| mean error (ME) | −8.32 × 10 |
| root mean square error (RMSE) | 0.138999 |
| mean absolute error (MAE) | 0.08493454 |
| mean percentage error (MPE) | 0.58% |
| mean absolute percentage error (MAPE) | 2.40% |
| mean absolute scaled error (MASE) | 0.4164696 |
| Weather Station | Latitude | Longitude | Altitude | Correlation (%) |
|---|---|---|---|---|
| LILLE | 50.567 | 3.1 | 52 | −10.66 |
| STRASBOURG | 48.549 | 7.633 | 153 | −4.38 |
| PARIS | 48.7167 | 2.3844 | 89 | −8.64 |
| BREST | 48.449 | −4.416 | 99 | −3.16 |
| NANTES | 47.15 | −1.6088 | 27 | −6.38 |
| BORDEAUX | 44.833 | −0.699 | 49 | −2.70 |
| CLERMONT | 45.783 | 3.167 | 332 | −7.19 |
| LYON | 45.733 | 5.083 | 240 | 0.83 |
| TOULOUSE | 43.633 | 1.366 | 152 | −3.96 |
| Weather Station | Coefficients (EUR/m/s) | Standard Error (m/s) | Ratio | p-Value |
|---|---|---|---|---|
| Lille | −0.79460 | 0.09339 | −8.5080 | 0.0000 |
| Strasbourg | −0.46830 | 0.11260 | −4.1580 | 0.0000 |
| Paris | −0.84810 | 0.12960 | −6.5440 | 0.0000 |
| Brest | −0.15570 | 0.06401 | −2.4330 | 0.0150 |
| Nantes | −0.50610 | 0.09472 | −5.3430 | 0.0000 |
| Clermont | −0.09214 | 0.10110 | −0.9114 | 0.3621 |
| Toulouse | −0.32470 | 0.08145 | −3.9860 | 0.0001 |
| Nantes Wind Speed Box–Cox Transformed | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1lmodel | SARIMA (3,0,1)(2,0,0) | |||||||
| Coefficients: | ||||||||
| ar1 | ar2 | ar1 | ma1 | sar1 | sar2 | mean | ||
| 1.1741 | 0.6337 | −0.2947 | 0.7379 | 0.1847 | 0.1367 | 1.2876 | ||
| (s.e.) 0.0060 | 0.0025 | 0.0026 | 0.0025 | 0.0061 | 0.0061 | 0.0307 | ||
| Measures of goodness of fit | ||||||||
| ME | RMSE | MAE | MSE | MAPE | MASE | |||
| 2.18 × 10 | 0.1750 | 0.1165 | 0.0306 | 0.50% | 0.1751 | |||
| Paris Wind Speed Box–Cox Transformed | |||||
|---|---|---|---|---|---|
| model: | SARIMAX (2,0,0)(2,0,0) | ||||
| coeff. | |||||
| ar1 | ar2 | sar1 | sar2 | ||
| est. | 1.1741 | −0.2651 | 0.1728 | 0.1276 | |
| s.d. | 0.0060 | 0.0059 | 0.0062 | 0.0061 | |
| Measures of goodness of fit | |||||
| ME | RMSE | MAE | MSE | MAPE | MASE |
| 2.47 × 10 | 0.2126 | 0.1427 | 0.0452 | 1.31% | 0.2438 |
| Exogenous: Nantes wind speed time series Box–Cox transformed (linear regression fitting) | |||||
| est. | s.d. | t-value | Pr(>|t|) | ||
| intercept | 0.1567 | 0.0074 | 21.27 | <2 × 10 *** | |
| Nantes | 0.6191 | 0.0049 | 125.93 | <2 × 10 *** | |
| Hour | Wind Park “Nantes” | Wind Park “Paris” | SMaPS | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i | Scenario: (MWh) | Scenario: (MWh) | Scenario: (EUR) | Scenario: (EUR) | Scenario: (EUR) | Scenario: (EUR) | Scenario: (EUR) | |||||||||||
| 1 | j | N | 1 | j | N | 1 | j | N | 1 | j | N | 1 | N | 1 | N | 1 | N | |
| 1 | 0 | … | 0 | 0 | … | 0 | 29.59 | … | 33.32 | 2124.52 | … | 2168.11 | 0 | 0 | 0 | 0 | 2124 | 2168 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 19 | 0 | … | 0 | 60.7 | … | 0 | 38.26 | … | 13.11 | 2450.82 | … | 0 | 0 | 2767.15 | 2321 | 0 | 4773 | 2767 |
| 20 | 0 | … | 0 | 0 | … | 0 | 38.09 | … | 13.08 | 1810.56 | … | 0 | 0 | 2450.47 | 0 | 0 | 1810 | 2451 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | |
| 81 | 0 | … | 341.4 | 2.5 | … | 0 | 104.68 | … | 75.72 | 2009.13 | … | 0 | 0 | 3413.70 | 259 | 25,747 | 2268 | 29,272 |
| 82 | 0 | … | 289.9 | 0 | … | 0 | 78.74 | … | 82.65 | 1546.86 | … | 0 | 0 | 2737.33 | 0 | 23,959 | 1546 | 26,697 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 2391 | 2000 | … | 14.7 | 1298.6 | … | 0 | 12.07 | … | 19.78 | −3982.38 | … | 0 | 0 | 3439.49 | 33,230 | 291.77 | 29,247 | 3731 |
| 2392 | 2000 | … | 35.8 | 1549.3 | … | 3.6 | 10.83 | … | 21.94 | −5607.96 | … | 0 | 0 | 0 | 38,456 | 863.96 | 32,848 | 863 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 2500 | 0 | … | 560.6 | 0 | … | 1018.4 | 18.60 | … | 25.78 | 0 | … | 0 | 562.85 | 0 | 0 | 40,712 | 563 | 40,713 |
| 2501 | 0 | … | 230.9 | 0 | … | 560.9 | 20.97 | … | 25.57 | 2054.52 | … | 0 | 867.13 | 0 | 0 | 20,244 | 2922 | 20,245 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 5135 | 0 | … | 153.7 | 0 | … | 358.2 | 15.16 | … | 17.96 | 1415.26 | … | 0 | 3489.54 | 0 | 0 | 9193 | 4905 | 9194 |
| kEur | kEur | kEur | kEur | kEur | mlnEur | mlnEur | mlnEur | mlnEur | ||||||||||
| Tot | 1726.00 | … | 2167.56 | 4594.57 | 5026.07 | 36,533 | 34,243 | 42,540 | 41,437 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masala, G.; Micocci, M.; Rizk, A. Hedging Wind Power Risk Exposure through Weather Derivatives. Energies 2022, 15, 1343. https://doi.org/10.3390/en15041343
Masala G, Micocci M, Rizk A. Hedging Wind Power Risk Exposure through Weather Derivatives. Energies. 2022; 15(4):1343. https://doi.org/10.3390/en15041343
Chicago/Turabian StyleMasala, Giovanni, Marco Micocci, and Andrea Rizk. 2022. "Hedging Wind Power Risk Exposure through Weather Derivatives" Energies 15, no. 4: 1343. https://doi.org/10.3390/en15041343
APA StyleMasala, G., Micocci, M., & Rizk, A. (2022). Hedging Wind Power Risk Exposure through Weather Derivatives. Energies, 15(4), 1343. https://doi.org/10.3390/en15041343






