Research on Capacity Allocation Optimization of Commercial Virtual Power Plant (CVPP)
Abstract
:1. Introduction
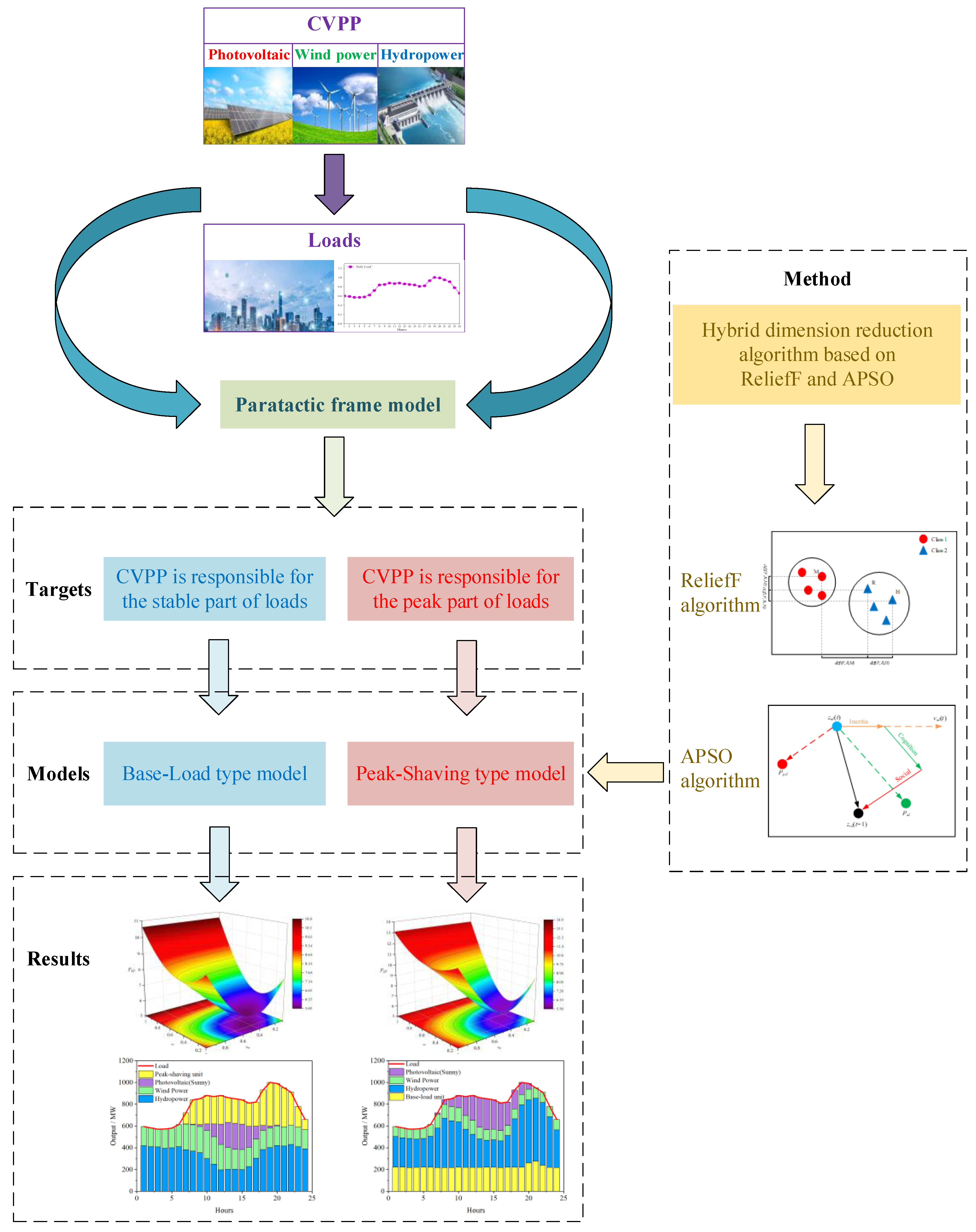
2. Method
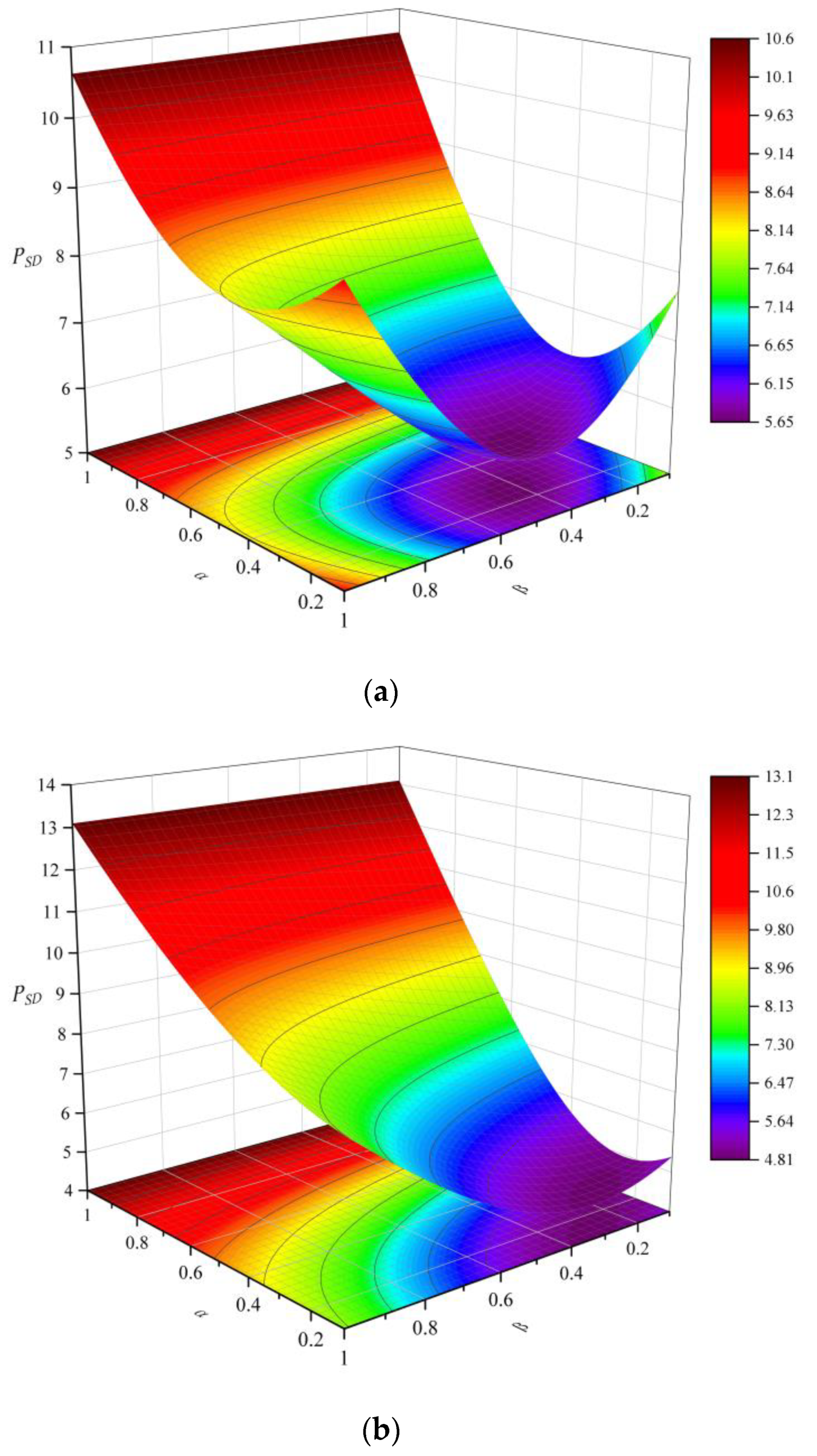
2.1. CVPP Capacity Allocation Modeling
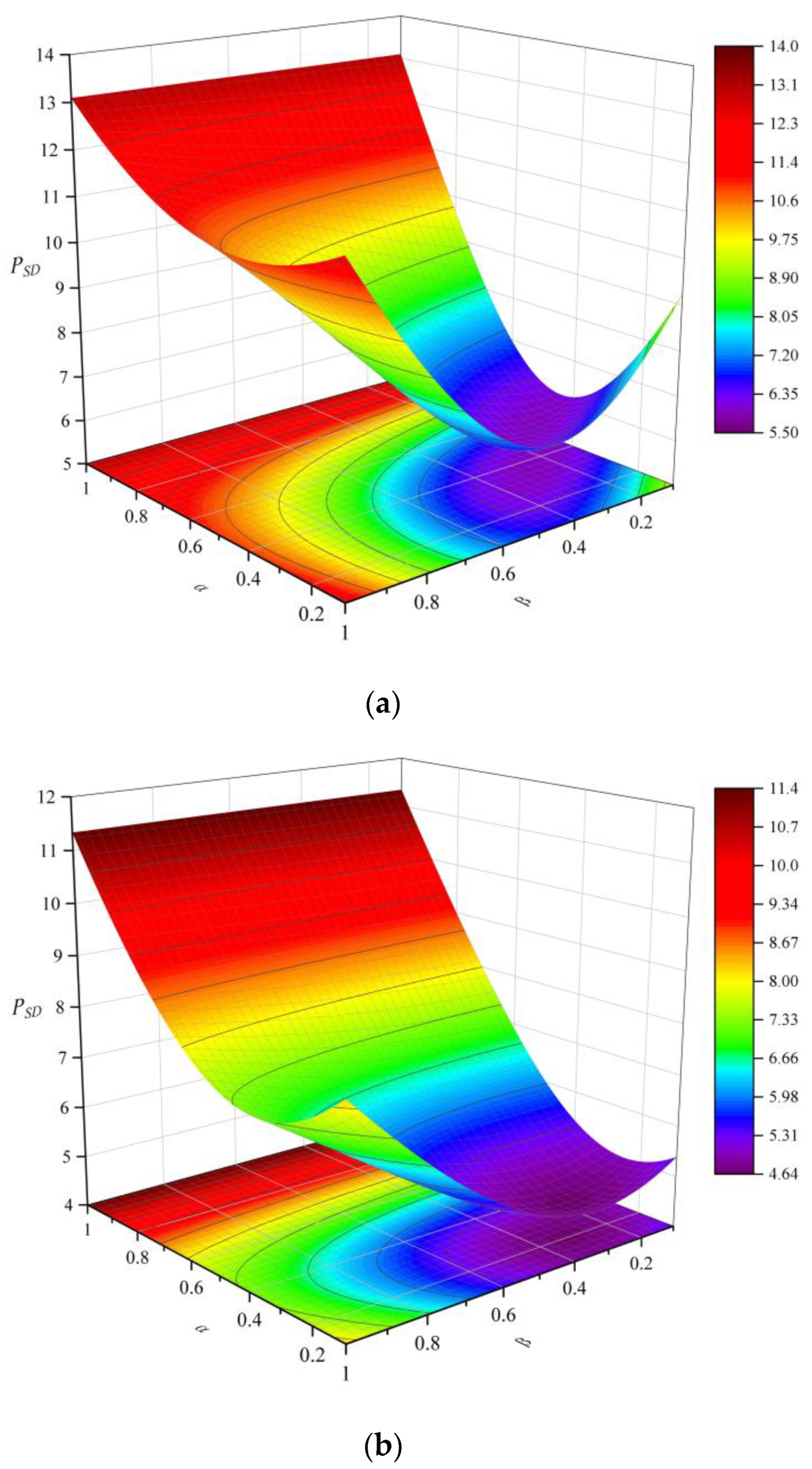
2.1.1. Base Load Type
2.1.2. Peak Shaving Type
2.2. Power Modeling
- (1)
- Wind power model
- (2)
- Photovoltaic model
- (3)
- Hydropower model
2.3. Hybrid Algorithm Based on ReliefF and APSO
2.3.1. APSO Algorithm
2.3.2. ReliefF Algorithm
- (1)
- Calculate SAHit, the distance between R and NearHit on each feature A.
- (2)
- Calculate SAMiss, the distance between R and NearMiss on each feature A.
- (3)
- Compare the two distances SAHit and SAMiss. If SAHit is greater than SAMiss, each feature of the A is helpful to distinguish the same kind and different kinds. If SAHit is less than SAMiss, each feature of the A hurts, distinguishing the same class and different classes and reduces the weight of the feature.
- (4)
- Repeat the above process m times to gain the average weight of each feature, as is shown in Formula (19)
2.3.3. ReliefF–APSO Hybrid Algorithm
- (1)
- The given data set is normalized by Z-score before training;
- (2)
- Using the Formula (19) to extract the features of the ReliefF algorithm and take the first d features with relatively large weight as the training set and test set of APSO, d = 100;
- (3)
- Generate population, set the number of particles N, set each particle as a random number vector within (−1, 1), and set the number of neurons and hidden layer nodes. In the experiment, N takes 20;
- (4)
- Initialize the speed and position variables of APSO, and set the individual optimal position and group optimal position of the population;
- (5)
- Calculate the fitness value of each particle;
- (6)
- Update the position and velocity of the adaptive particle swarm according to Formulas (17) and (18);
- (7)
- Judge whether the maximum number of iterations is reached. If so, stop the iteration. Otherwise, turn to step (5) and continue the iteration.
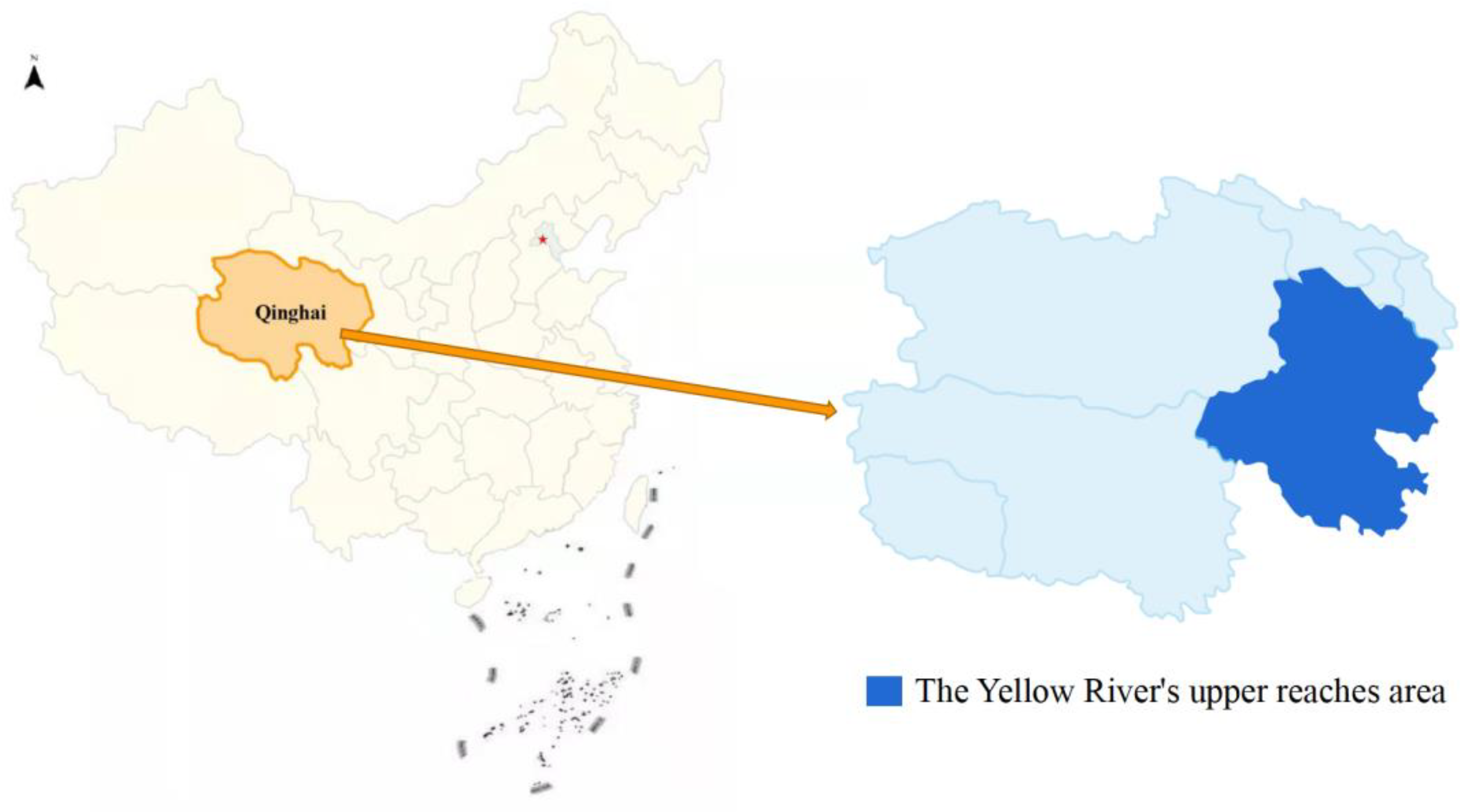
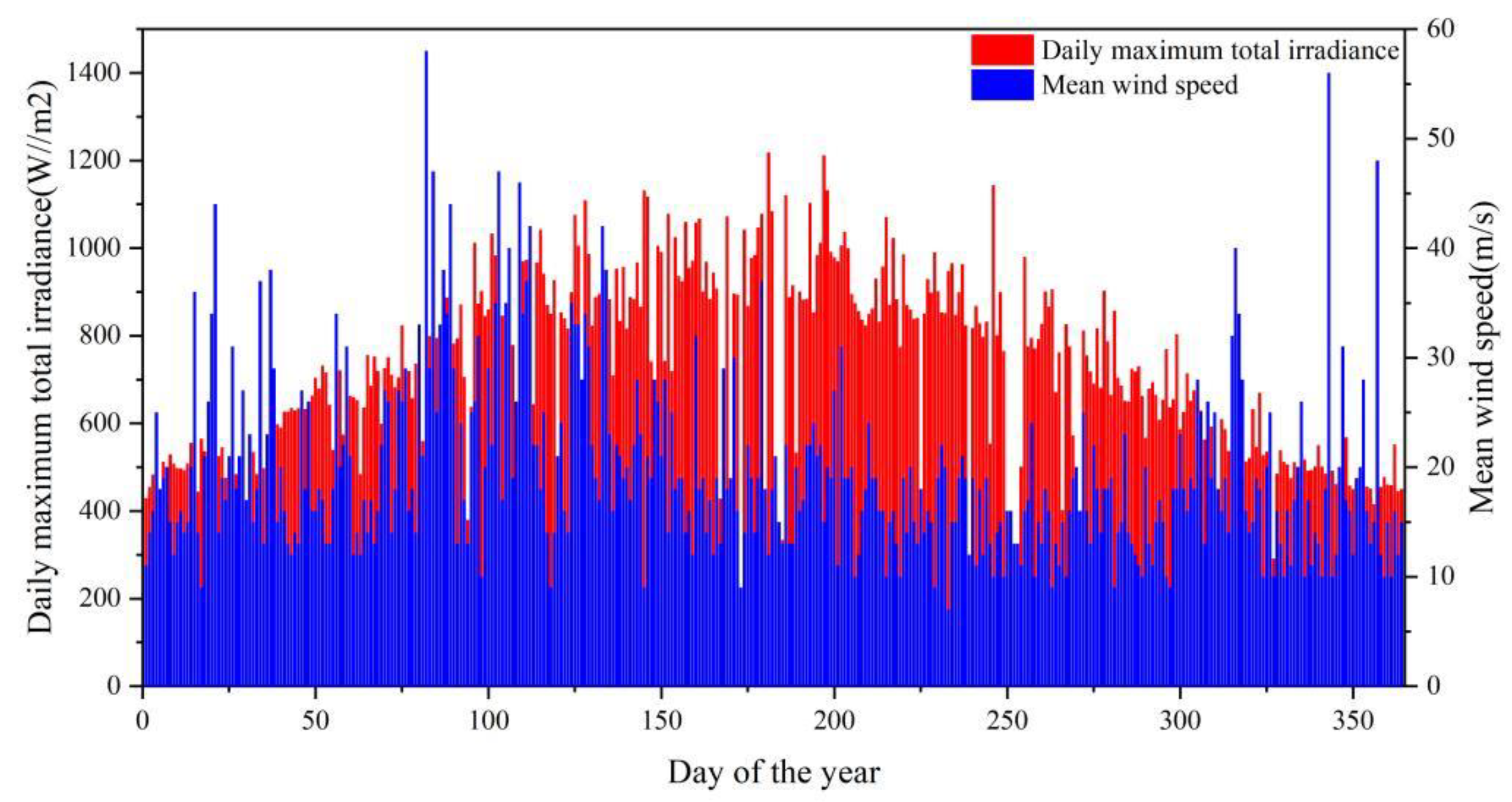
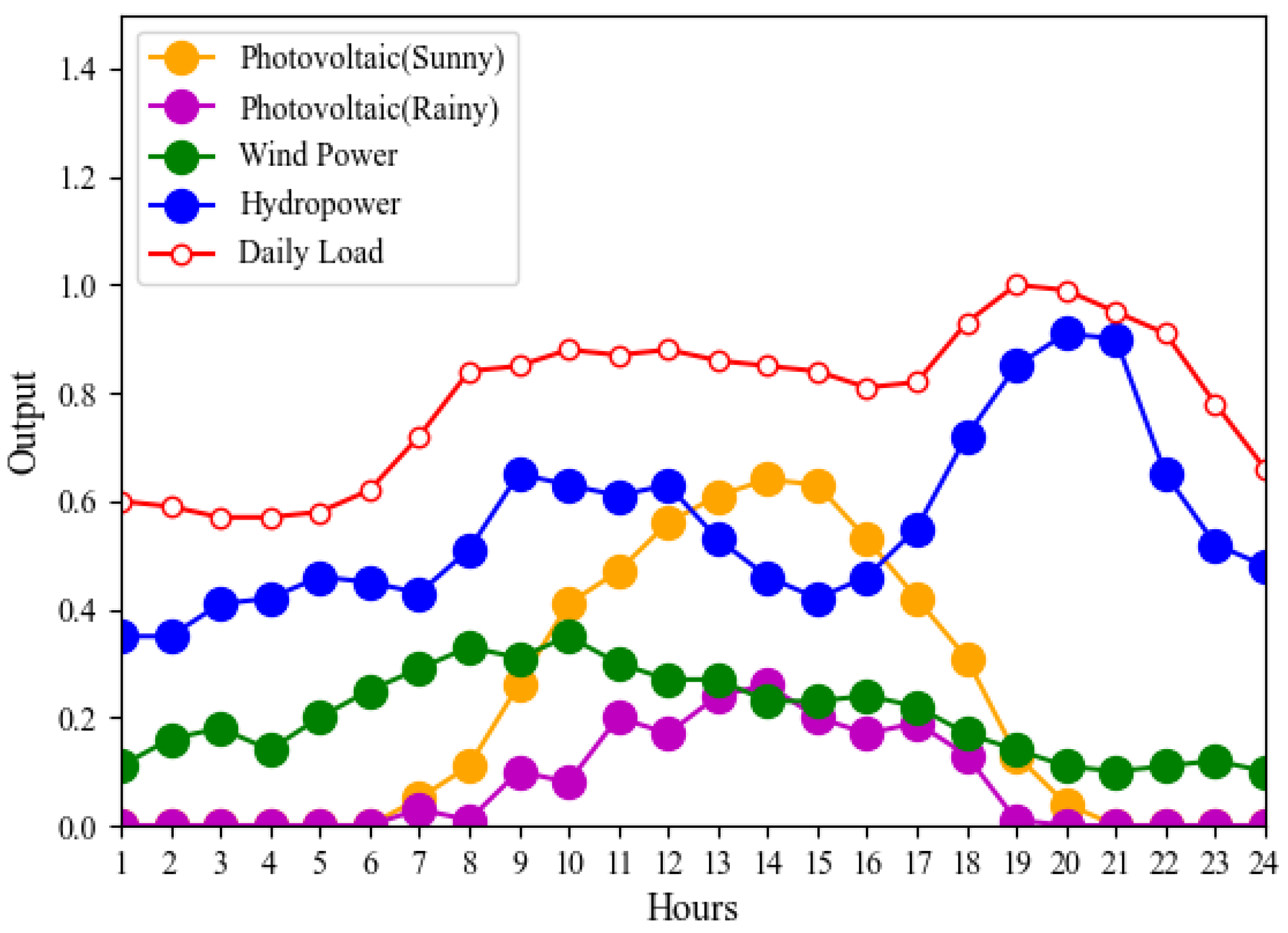
3. Case Study
4. Results and Discussion
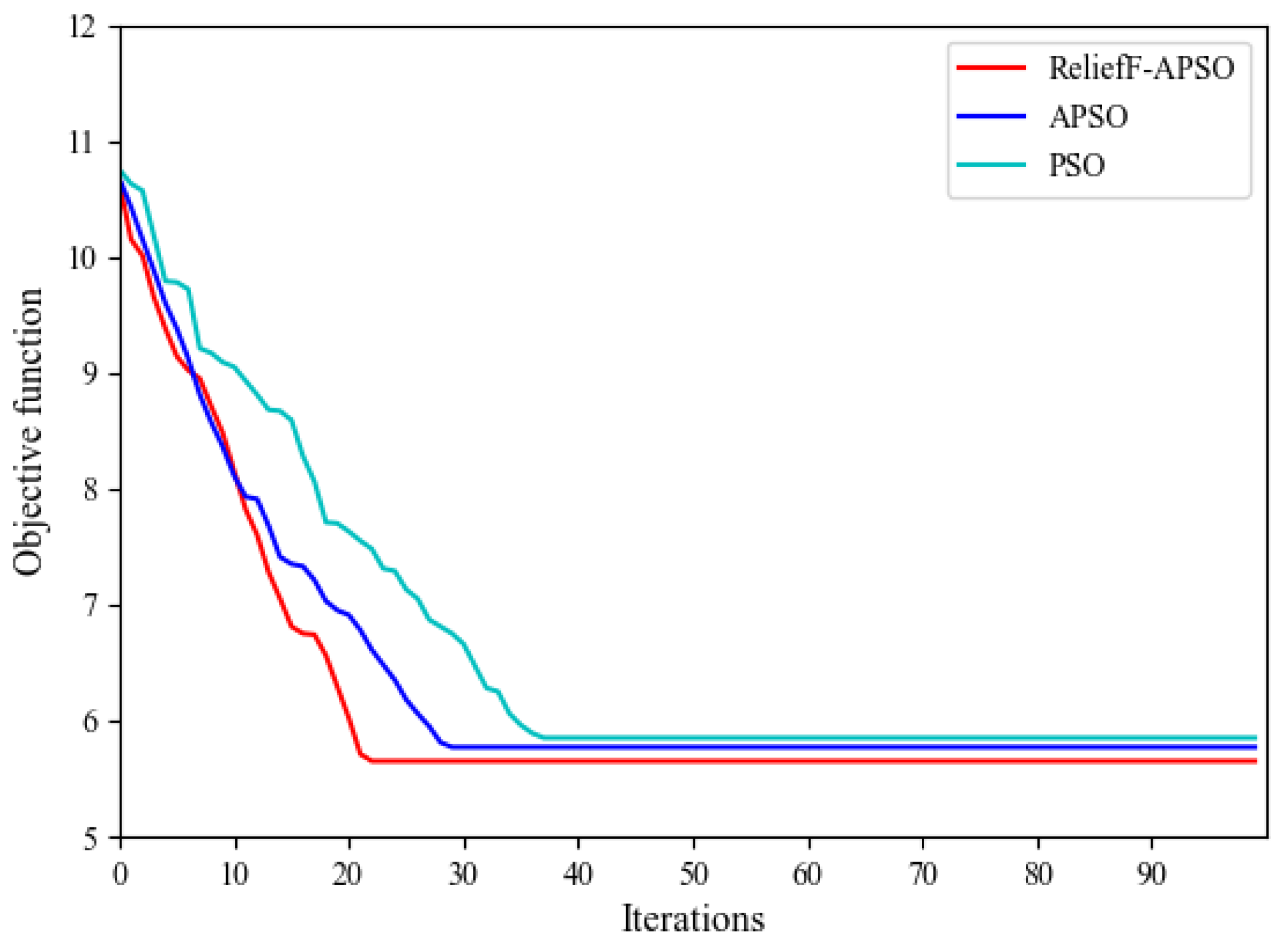
4.1. Comparative Analysis of ReliefF–APSO Hybrid Algorithm, APSO, and PSO
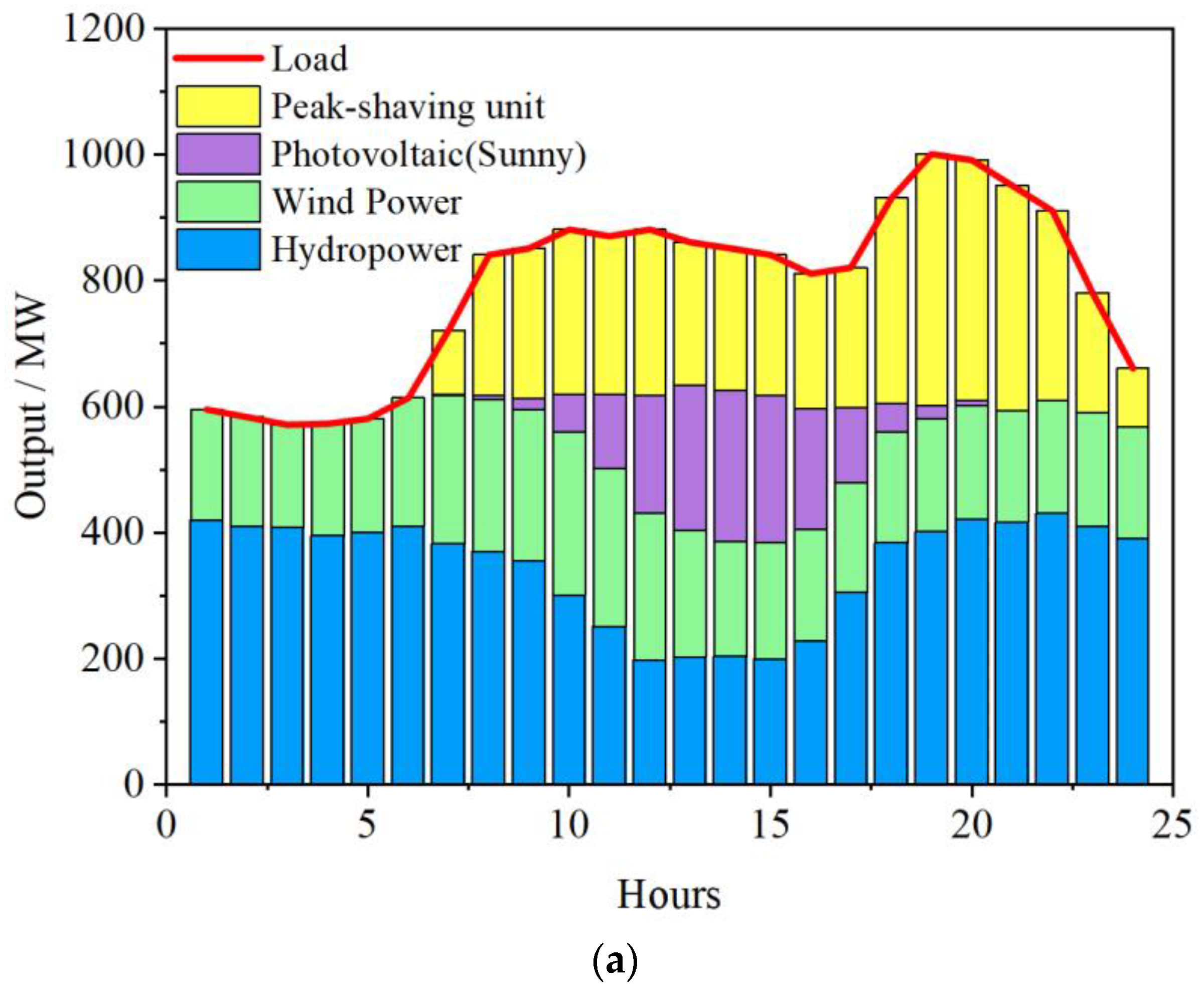
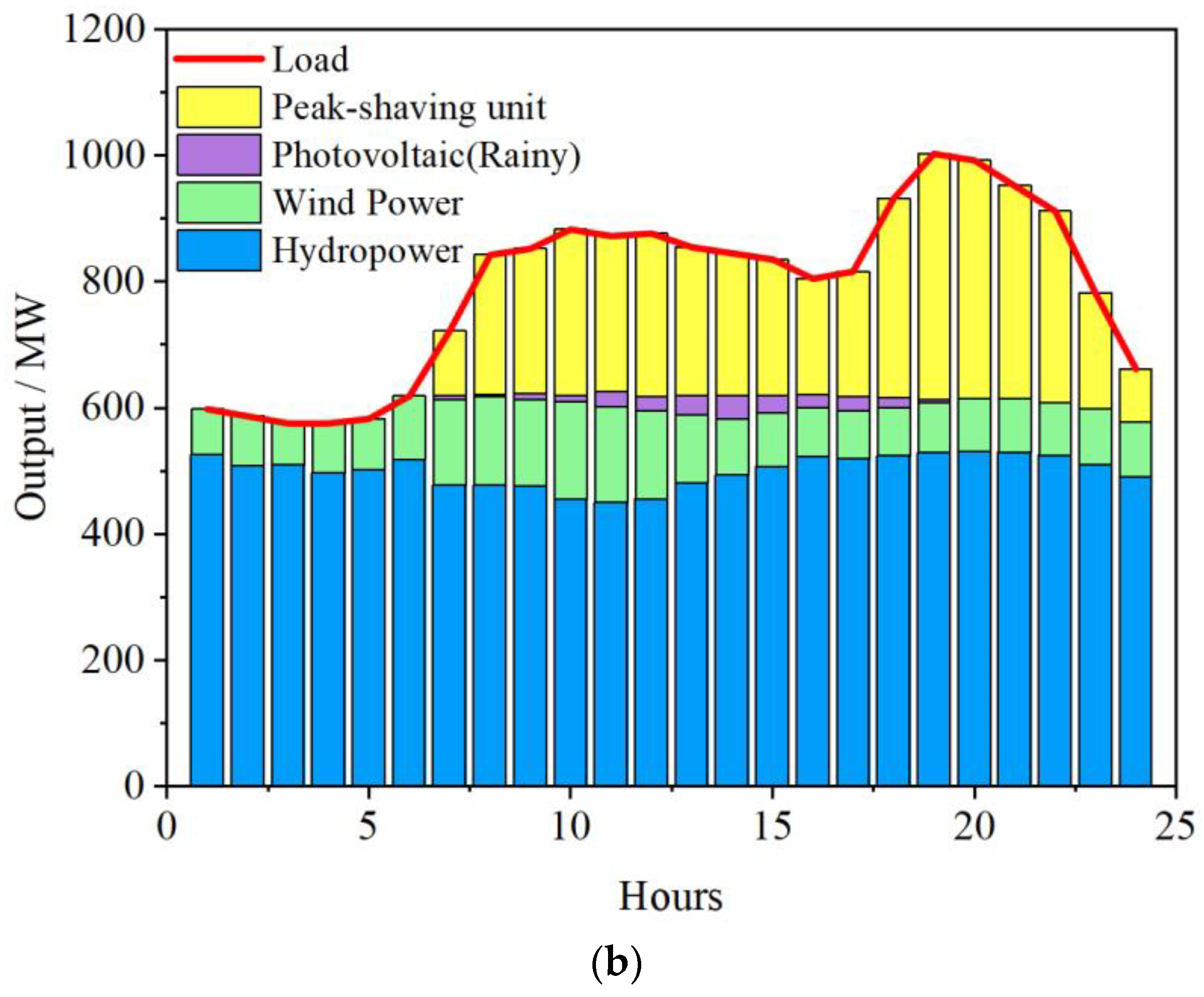
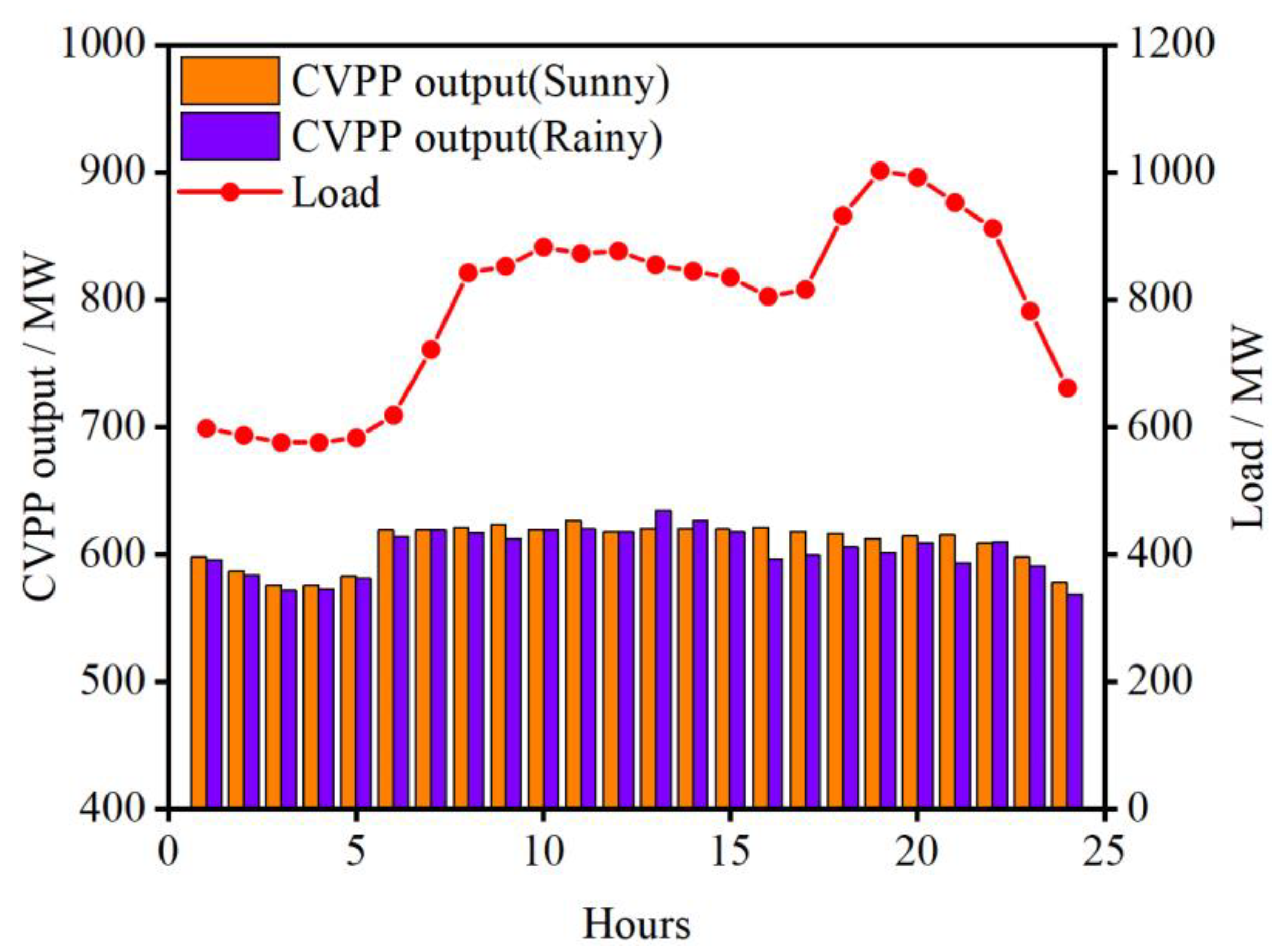
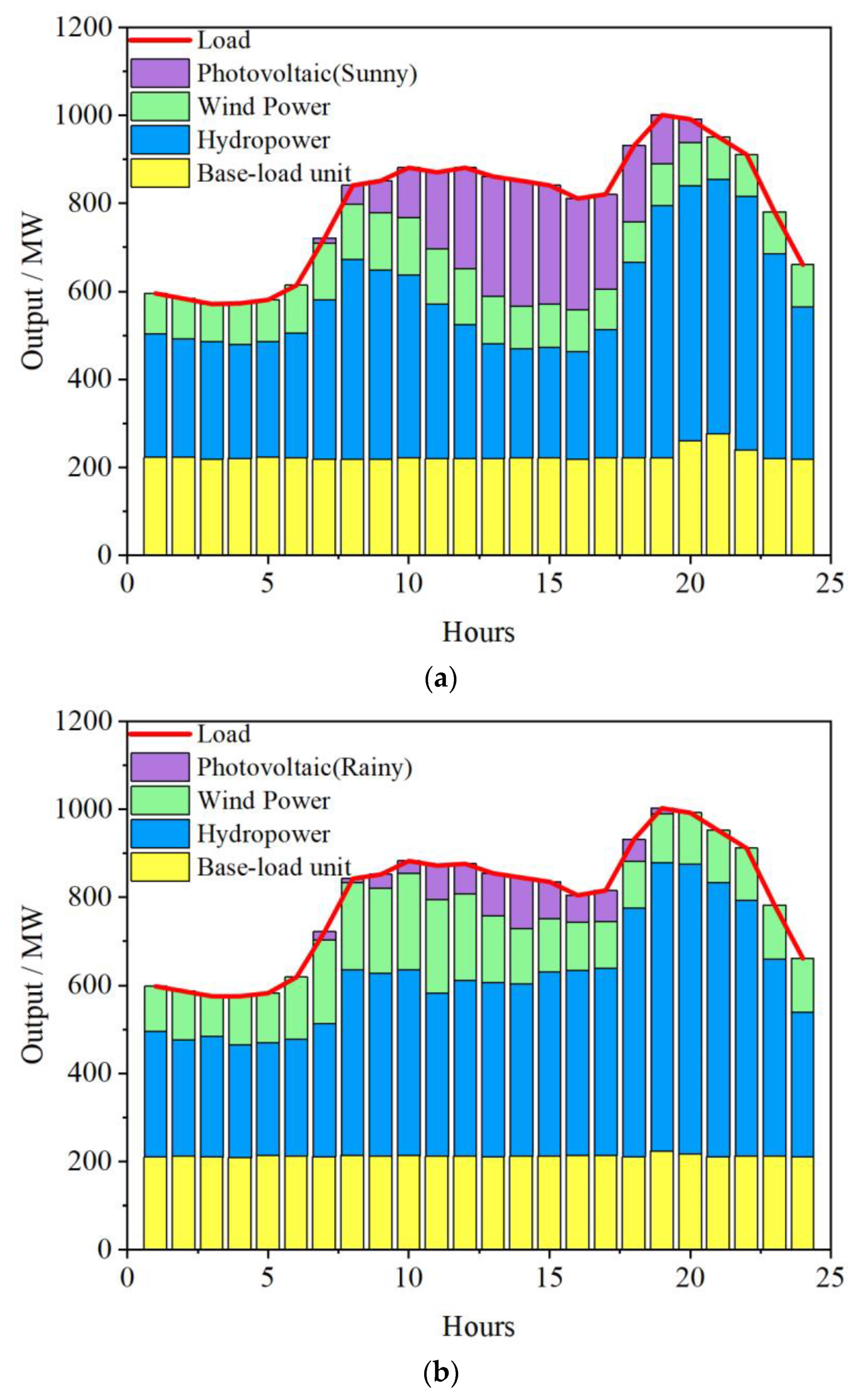
4.2. Base load Type Operation Model
4.3. Peak shaving Type Operation Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shafiekhani, M.; Ahmadi, A.; Homaee, O.; Shafie-khah, M.; Catalão, J.P. Optimal bidding strategy of a renewable-based virtual power plant including wind and solar units and dispatchable loads. Energy 2022, 239, 122379. [Google Scholar] [CrossRef]
- Rouzbahani, H.M.; Karimipour, H.; Lei, L. A review on virtual power plant for energy management. Sustain. Energy Technol. Assess. 2021, 47, 101370. [Google Scholar] [CrossRef]
- Naval, N.; Yusta, J.M. Virtual power plant models and electricity markets—A review. Renew. Sustain. Energy Rev. 2021, 149, 111393. [Google Scholar] [CrossRef]
- Kieny, C.; Berseneff, B.; Hadjsaid, N.; Besanger, Y.; Maire, J. On the concept and the interest of virtual power plant: Some results from the European project FENIX. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Foroughi, M.; Pasban, A.; Moeini-Aghtaie, M.; Fayaz-Heidari, A. A bi-level model for optimal bidding of a multi-carrier technical virtual power plant in energy markets. Electr. Power Energy Syst. 2021, 125, 106397. [Google Scholar] [CrossRef]
- Elgamal, A.H.; Kocher-Oberlehner, G.; Robu, V.; Andoni, M. Optimization of a multiple-scale renewable energy-based virtual power plant in the UK. Appl. Energy 2019, 256, 113973. [Google Scholar] [CrossRef]
- Papaefthymiou, S.V.; Papathanassiou, S.A. Optimum sizing of wind-pumped-storage hybrid power stations in island systems. Renew. Energy 2014, 64, 187–196. [Google Scholar] [CrossRef]
- Peik-Herfeh, M.; Seifi, H.; Sheikh-El-Eslami, M.K. Decision making of a virtual power plant under uncertainties for bidding in a day-ahead market using point estimate method. Int. J. Electr. Power Energy Syst. 2013, 44, 88–98. [Google Scholar] [CrossRef]
- Pandžić, H.; Kuzle, I.; Capuder, T. Virtual power plant mid-term dispatch optimization. Appl. Energy 2013, 10, 134–141. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L.; Yusta-Loyo, J.M.; Domínguez-Navarro, J.A.; Ramírez-Rosado, I.J.; Lujano, J.; Aso, I. Multi-objective optimization minimizing cost and life cycle emissions of stand-alone PV–wind–diesel systems with batteries storage. Appl. Energy 2011, 88, 4033–4041. [Google Scholar] [CrossRef]
- Olamaei, J.; Nazari, M.E.; Bahravar, S. Economic environmental unit commitment for integrated CCHP-thermal-heat only system with considerations for valve-point effect based on a heuristic optimization algorithm. Energy 2018, 159, 737–750. [Google Scholar] [CrossRef]
- Li, J.; Sang, C. Discussion on optimal planning and operation framework for integrated energy system. Electr. Power Constr. 2015, 36, 41–48. [Google Scholar] [CrossRef]
- Shunping, J.; Shoupeng, W.; Fang, F. Game theoretical analysis on capacity configuration for microgrid based on multi-agent system. Electr. Power Energy Syst. 2021, 125, 106485. [Google Scholar] [CrossRef]
- Fang, F.; Zhongyan, Z.; Shunping, J.; Shiyan, H. Two-Layer Game Theoretic Microgrid Capacity Optimization Considering Uncertainty of Renewable Energy. IEEE Syst. J. 2021, 15, 4260–4271. [Google Scholar] [CrossRef]
- Xue, M.; Zhao, B.; Zhang, X.; Jiang, Q. Integrated plan andevaluation of grid connected microgrid. Autom. Electr. Power Syst. 2015, 39, 6–13. [Google Scholar] [CrossRef]
- Yuan, C.; Liu, G.; Wang, Z.; Chen, X.; Illindala, M.S. Economic power capacity design of distributed energy resources for reliable community microgrids. Energy Procedia 2017, 142, 2561–2567. [Google Scholar] [CrossRef]
- Jing, Z.; Luo, Z. An IGDT model for capacity configuration optimization of island microgrid. Energy Procedia 2019, 158, 2774–2779. [Google Scholar] [CrossRef]
- Zhang, X.; Shahidehpour, M.; Alabdulwahab, A.S.; Abusorrah, A. Security-constrained co-optimization planning of electricity and natural gas transportation infrastructures. IEEE Trans. Power Syst. 2015, 30, 2984–2993. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M. A novel method for optimal DG units capacity and location in microgrids. Int. J. Electr. Power Energy Syst. 2016, 75, 36–44. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, Z.; Lin, H.C.; Li, S. Power Capacity Optimization in a Photovoltaics-Based Microgrid Using the Improved Artificial Bee Colony Algorithm. Applies Sci. 2020, 10, 2990. [Google Scholar] [CrossRef]
- Javadi, M.A.; Hoseinzadeh, S.; Ghasemiasl, R.; Heyns, P.S.; Chamkha, A.J. Sensitivity analysis of combined cycle parameters on exergy, economic, and environmental of a power plant. J. Therm. Anal. Calorim. 2019, 139, 519–525. [Google Scholar] [CrossRef]
- Maraver, D.; Sin, A.; Sebastián, F.; Royo, J. Environmental assessment of CCHP (combined cooling heating and power) systems based on biomass combustion in comparison to conventional generation. Energy 2013, 57, 17–23. [Google Scholar] [CrossRef]
- Xiao, H.; Pei, W.; Dong, Z.; Kong, L. Bi-level planning for integrated energy systems incorporating demand response and energy storage under uncertain environments using novel meta model. CSEE J. Power Energy Syst. 2018, 4, 155–167. [Google Scholar] [CrossRef]
- Ju, L.; Tan, Q.; Lu, Y.; Tan, Z.; Zhang, Y.; Tan, Q. A CVaR-robust-based multi-objective optimization model and three-stage solution algorithm for a virtual power plant considering uncertainties and carbon emission allowances. Int. J. Electr. Power Energy Syst. 2019, 107, 628–643. [Google Scholar] [CrossRef]
- Nosratabadi, S.M.; Hooshmand, R.A.; Gholipour, E. A comprehensive review on microgrid and virtual power plant concepts employed for distributed energy resources scheduling in power systems. Renew. Sustain. Energy Rev. 2017, 67, 341–363. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, M.; Wang, P.; Gu, J.; Zheng, W.; Dong, Y. Bi-stage stochastic model for optimal capacity and electric cooling ratio of CCHPs—A case study for a hotel. Energy Build. 2019, 194, 113–122. [Google Scholar] [CrossRef]
- Sharafi, M.; ELMekkawy, T.Y. Multi-objective optimal design of hybrid renewable energy systems using PSO-simulation based approach. Renew. Energy 2014, 68, 67–79. [Google Scholar] [CrossRef]
- Das, P.; Das, B.K.; Rahman, M.; Hassan, R. Evaluating the prospect of utilizing excess energy and creating employments from a hybrid energy system meeting electricity and freshwater demands using multi-objective evolutionary algorithms. Energy 2022, 238, 121860. [Google Scholar] [CrossRef]
- Wang, X.; Chen, L.; Chen, Q.; Mei, Y.; Wang, H. Model and Analysis of Integrating Wind and PV Power in Remote and Core Areas with Small Hydropower and Pumped Hydropower Storage. Energies 2018, 11, 3459. [Google Scholar] [CrossRef] [Green Version]
- Heide, D.; Von Bremen, L.; Greiner, M.; Hoffmann, C.; Speckmann, M.; Bofinger, S. Seasonal optimal mix of wind and solar power in a future, highly renewable Europe. Renew. Energy 2010, 35, 2483–2489. [Google Scholar] [CrossRef]
- Sasikumar, C.; Manokar, A.M.; Vimala, M.; Winston, D.P.; Kabeel, A.E.; Sathyamurthy, R.; Chamkha, A.J. Experimental studies on passive inclined solar panel absorber solar still. J. Therm. Anal. Calorim. 2019, 139, 3649–3660. [Google Scholar] [CrossRef]
- Manokar, A.M.; Vimala, M.; Sathyamurthy, R.; Kabeel, A.E.; Winston, D.P.; Chamkha, A.J. Enhancement of potable water production from an inclined photovoltaic panel absorber solar still by integrating with flat-plate collector. Environ. Dev. Sustain. 2020, 22, 4145–4167. [Google Scholar] [CrossRef]
- Ming, B.; Liu, P.; Guo, S.; Zhang, X.; Feng, M.; Wang, X. Optimizing utility-scale photovoltaic power generation for integration into a hydropower reservoir by incorporating long- and short-term operational decisions. Appl. Energy 2017, 204, 432–445. [Google Scholar] [CrossRef]
- Wang, S.; Jia, R.; Shi, X.; An, Y.; Huang, Q.; Guo, P.; Luo, C. Hybrid time-scale optimal scheduling considering multi-energy complementary characteristic. IEEE Access 2021, 9, 94087–94098. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Zaman, F.; Guerrero, J.M. Energy scheduling of community microgrid with battery cost using particle swarm optimisation. Appl. Energy 2019, 254, 113723. [Google Scholar] [CrossRef]
- Anand, H.; Ramasubbu, R. A real time pricing strategy for remote micro-grid with economic emission dispatch and stochastic renewable energy sources. Renew. Energy 2018, 127, 779–789. [Google Scholar] [CrossRef]
- Wen, X.; Xu, Z. Wind turbine fault diagnosis based on ReliefF-PCA and DNN. Expert Syst. Appl. 2021, 178, 115016. [Google Scholar] [CrossRef]
- Fang, W.; Huang, Q.; Huang, S.; Yang, J.; Meng, E.; Li, Y. Optimal sizing of utility-scale photovoltaic power generation complementarily operating with hydropower: A case study of the world’s largest hydro-photovoltaic plant. Energy Convers. Manag. 2017, 136, 161–172. [Google Scholar] [CrossRef]
- Du, C.; Wang, X.; Wang, X.; Shao, C. A Block-Based Medium-Long Term Energy Transaction Method. IEEE Trans. Power Syst. 2016, 31, 4155–4156. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Jia, R.; Shi, X.; Luo, C.; An, Y.; Huang, Q.; Guo, P.; Wang, X.; Lei, X. Research on Capacity Allocation Optimization of Commercial Virtual Power Plant (CVPP). Energies 2022, 15, 1303. https://doi.org/10.3390/en15041303
Wang S, Jia R, Shi X, Luo C, An Y, Huang Q, Guo P, Wang X, Lei X. Research on Capacity Allocation Optimization of Commercial Virtual Power Plant (CVPP). Energies. 2022; 15(4):1303. https://doi.org/10.3390/en15041303
Chicago/Turabian StyleWang, Songkai, Rong Jia, Xiaoyu Shi, Chang Luo, Yuan An, Qiang Huang, Pengcheng Guo, Xueyan Wang, and Xuewen Lei. 2022. "Research on Capacity Allocation Optimization of Commercial Virtual Power Plant (CVPP)" Energies 15, no. 4: 1303. https://doi.org/10.3390/en15041303
APA StyleWang, S., Jia, R., Shi, X., Luo, C., An, Y., Huang, Q., Guo, P., Wang, X., & Lei, X. (2022). Research on Capacity Allocation Optimization of Commercial Virtual Power Plant (CVPP). Energies, 15(4), 1303. https://doi.org/10.3390/en15041303






