A Novel Hybrid Chaotic Jaya and Sequential Quadratic Programming Method for Robust Design of Power System Stabilizers and Static VAR Compensator
Abstract
:1. Introduction
1.1. Research Background and Literature Review
1.2. Paper Contribution and Layout
- The CJaya-SQP is a novel and alternative metaheuristic algorithm for continuous optimization which redesigned the conventional Jaya by combining chaos theory, chaotic local search strategy and SQP technique. To the best of our knowledge, the Jaya algorithm is combined with the SQP method for the first time.
- The performance of the proposed CJaya-SQP technique is investigated on 17 benchmark functions and it is compared with various optimization algorithms, including the conventional Jaya, DE, PSO, ABC, IWO and FA.
- The CJaya-SQP provides the highest performance in terms of solution accuracy, convergence speed and robustness, with the highest success rate.
- A new method based on the real power loss sensitivity approach is proposed to find the optimal location of SVC in electric power systems.
- A novel methodology is proposed for optimal design of PSSs and SVC controllers in order to alleviate power system stability problems and to mitigate low frequency oscillations.
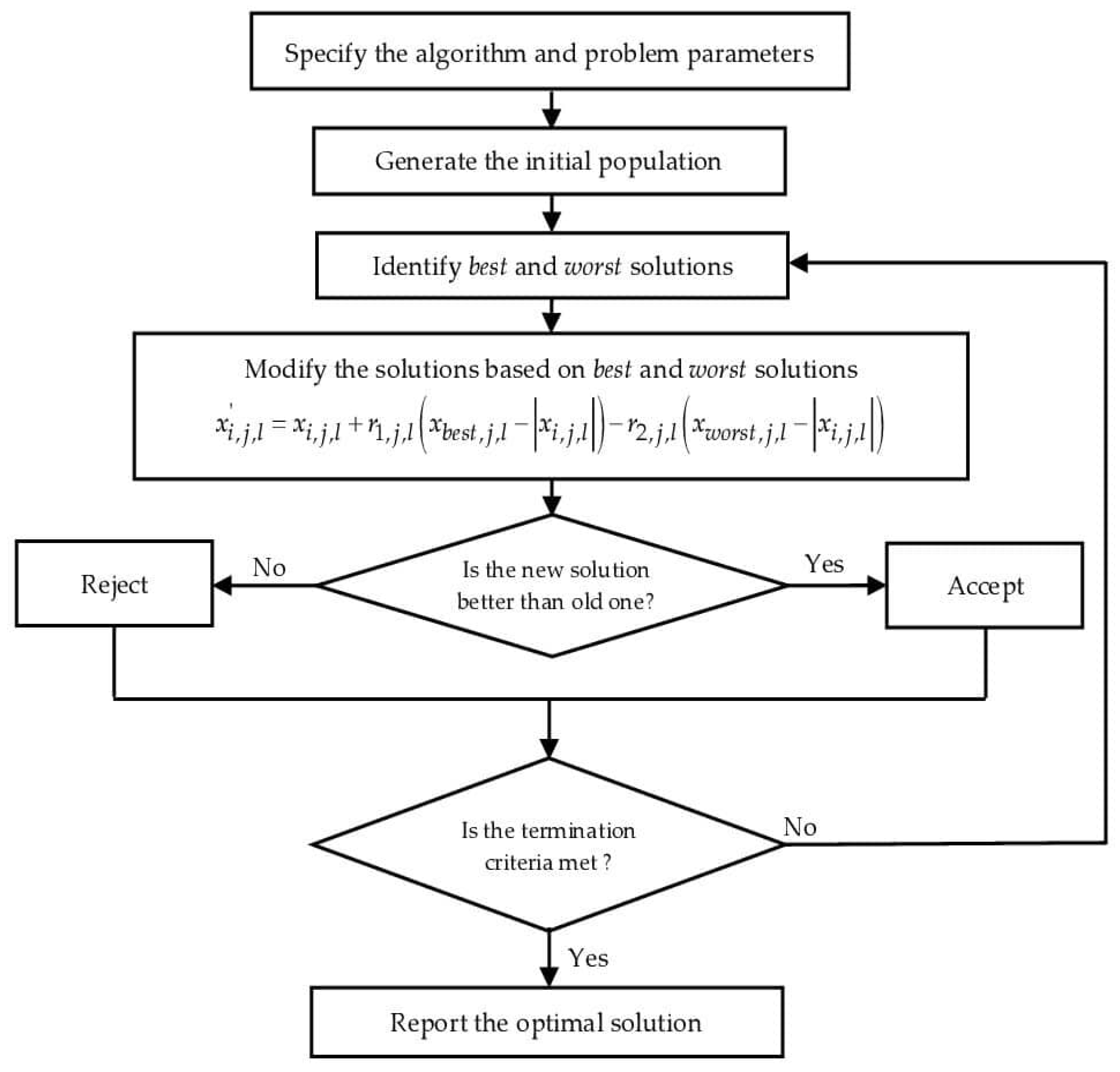
2. The Original Jaya Algorithm
3. The Hybrid CJaya-SQP Method
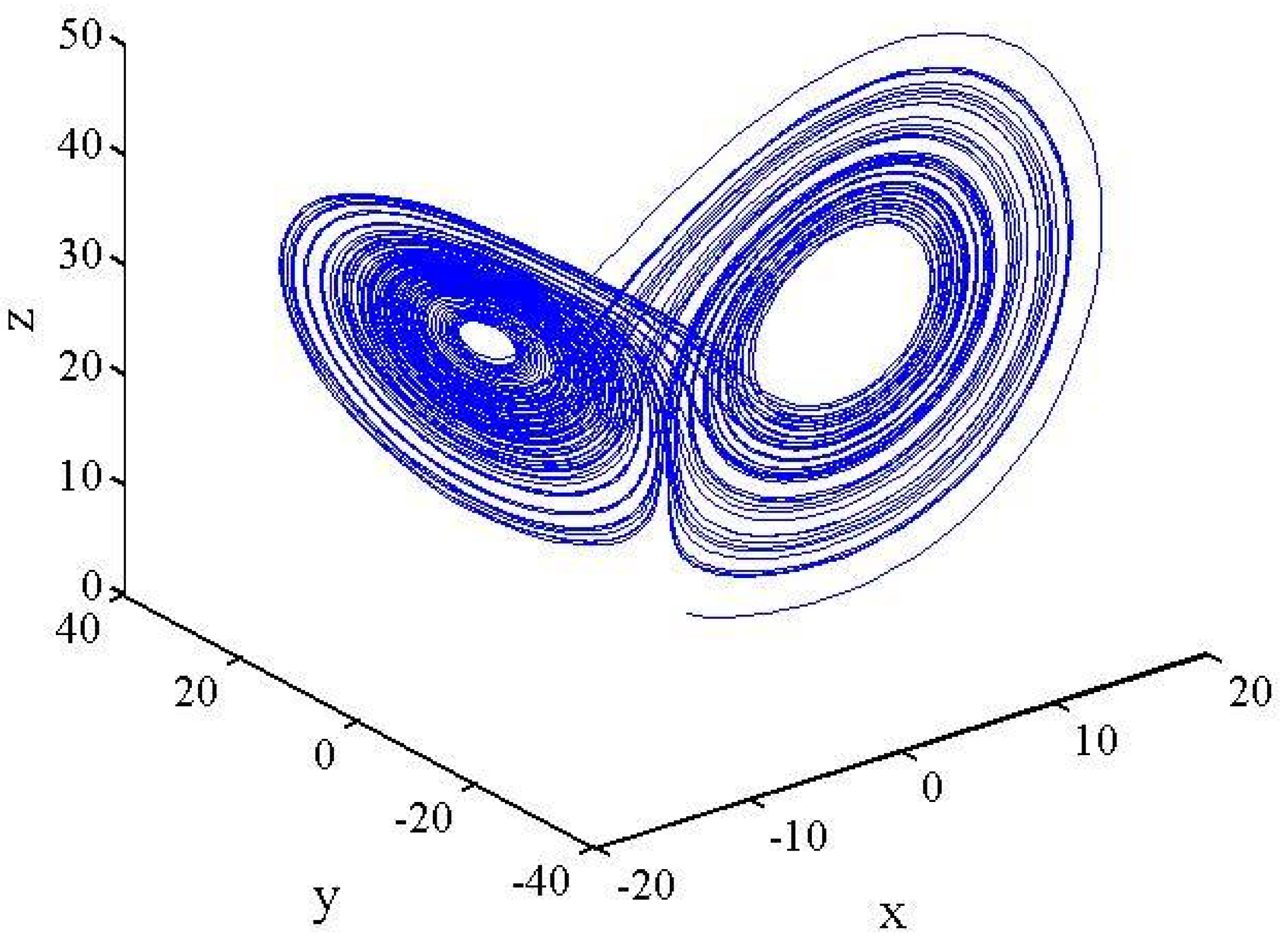
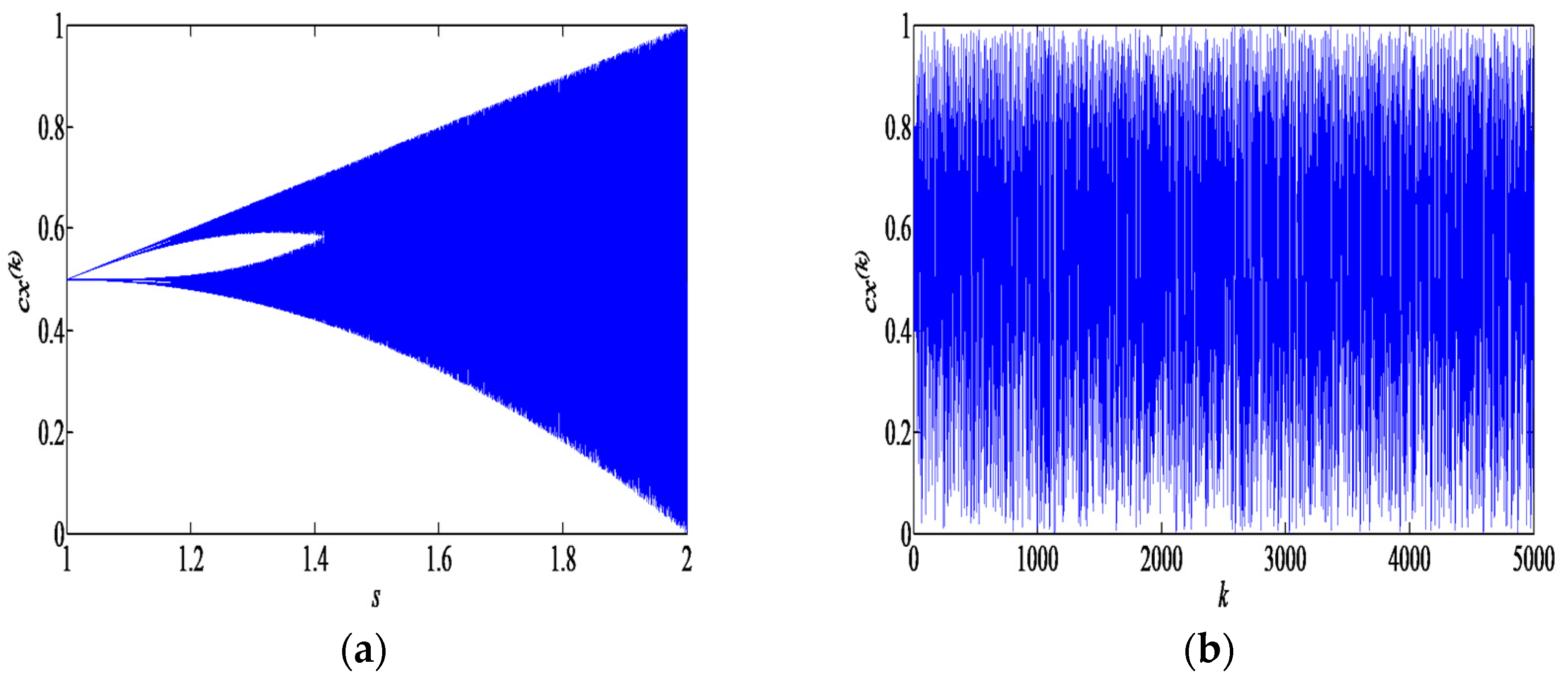
3.1. Chaotic Map
3.2. Original Jaya with Chaos
3.3. Chaotic Local Search Method (CLS)
3.4. Sequential Quadratic Programming (SQP)
- Update the Hessian of the Lagrangian function;
- Solve the QP sub-problem;
- Calculate a line search and merit function.
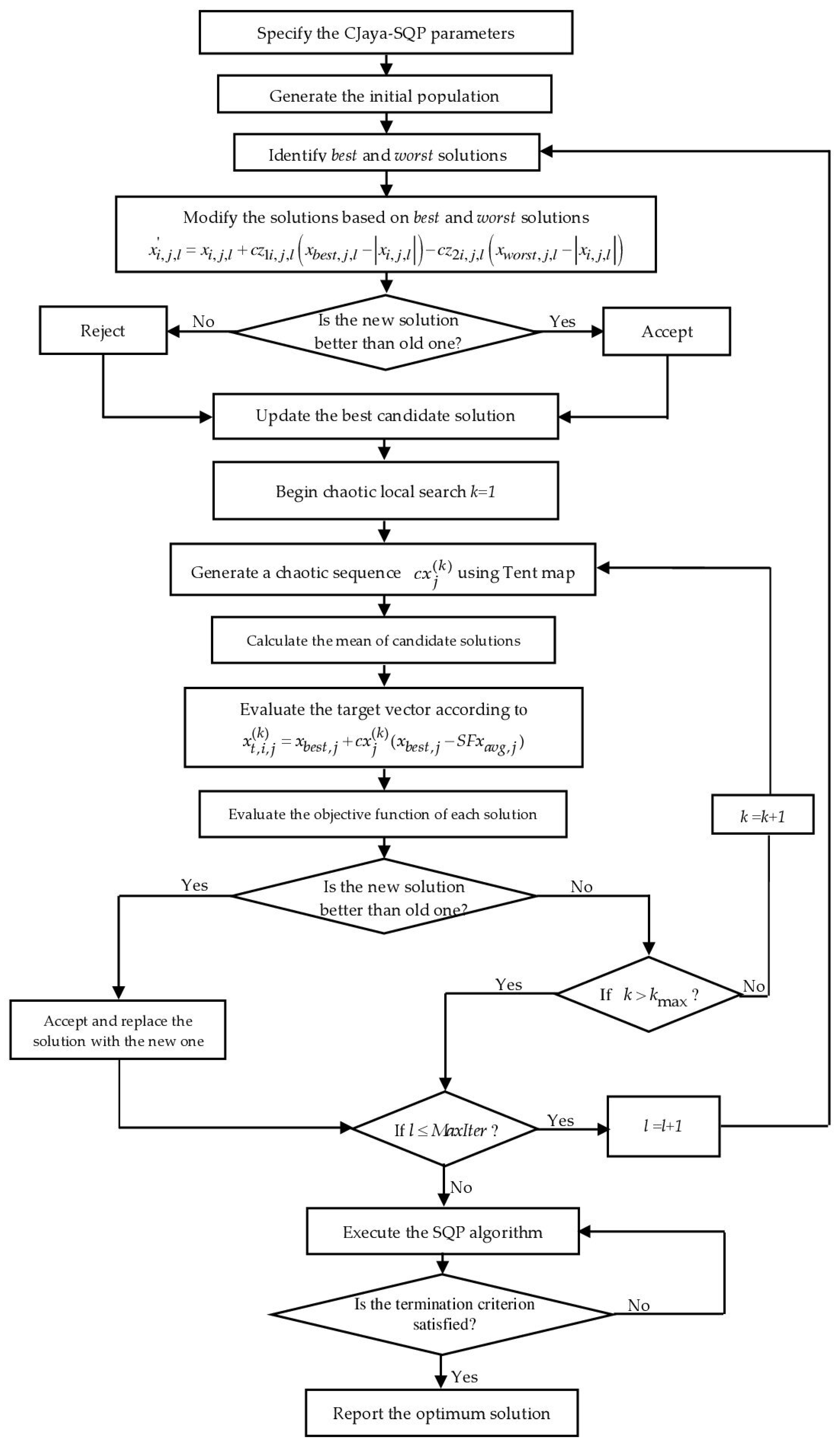
3.5. Hybrid CJaya-SQP Method
| Algorithm 1: The procedure of CJaya-SQP algorithm. |
| 1: Set the number of design variables (D), population size (NP), maximum function evaluations (MaxFEs), the maximum iteration number and the maximum search length of CLS ; 2: Initialize: the iteration count l (l = 1), the initial conditions for the Lorenz system and for the Tent map; 3: Initialize the NP candidate solutions chaotically within their search boundaries using Equation (6); 4: Calculate the value of the objective functions of the initial solutions during iteration ; 5: Repeat 6: Identify the indexes assigned to the best candidate , and the worst candidate , and evaluate and ; 7: For To NP Do 8: Produce the new solution by updating the variables for the candidate solution using Equation (7); 9: Check the variables’ boundaries; {Compare the new solution with the old one }; 10: If Then , End If End For {Update the best candidate solution Xbest and its function value Fbest = F(Xbest) }; 11: For To NP Do 12: Initialize the iteration count of the CLS k (k = 1); 13: Repeat 14: Generate the chaotic variables for the Tent map using Equation (5); 15: Evaluate the components of the target vector Xt,i using Equation (8); 16: Check if the design variables are in the search space using Equation (9); {Compare the target vector with the candidate solution }; 17: If Then , , End If 18: ; {increment the iteration count of the CLS} 19: Until (End Repeat) {Update the best solution Xbest and the function value Fbest = F(Xbest) }; 20: If Then , End If End For 21: {increment the iteration count} 22: Until (End Repeat) 23: Let the best solution extracted by CJaya be the initial condition for SQP; 24: Use the SQP method for searching around which is derived by CJaya; 25: Output the global optimum solution found by SQP. |
4. Problem Statement
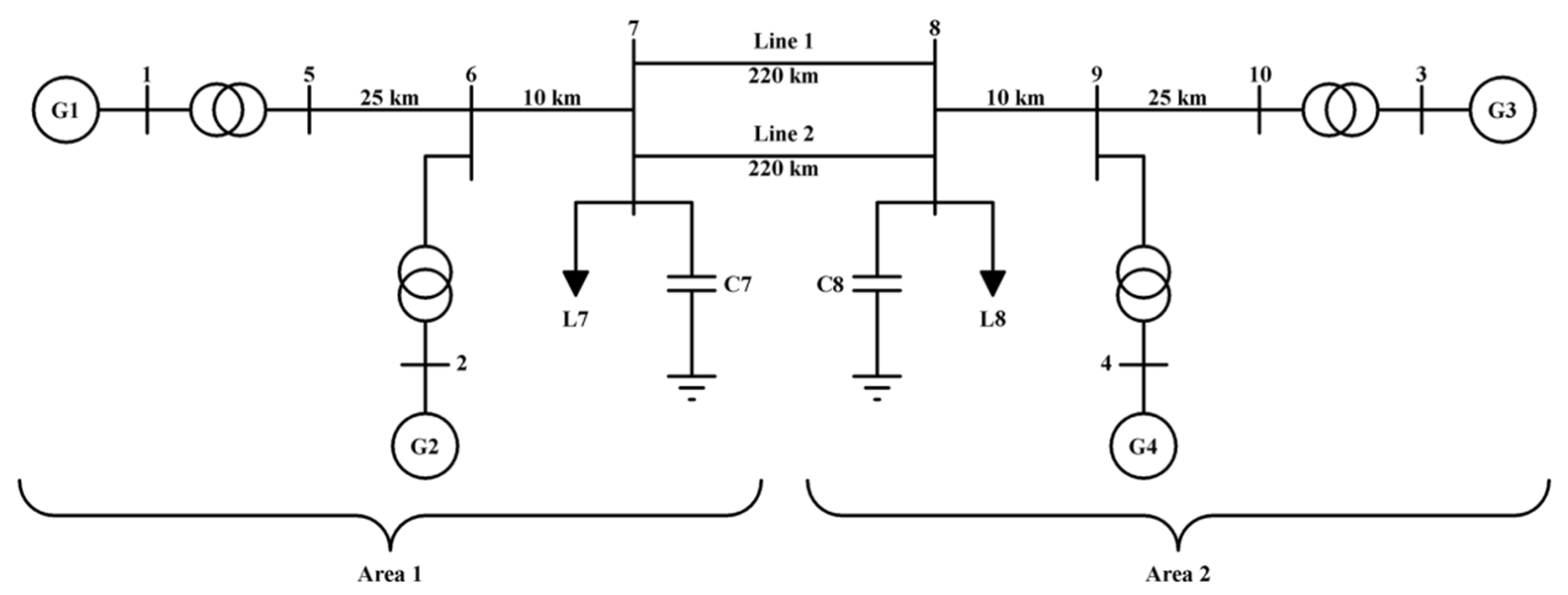
4.1. Power System Model
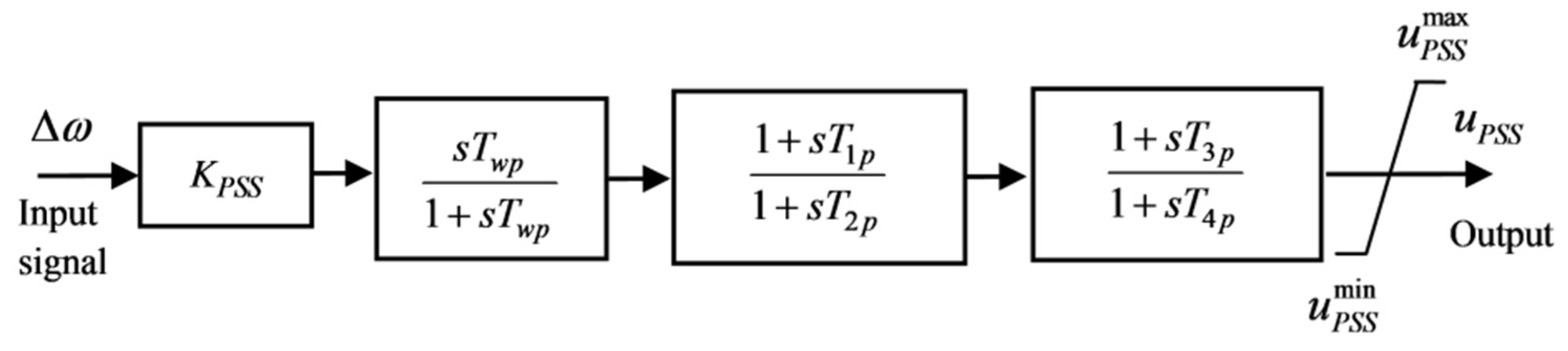
4.2. PSS Modeling and Damping Controller Structure
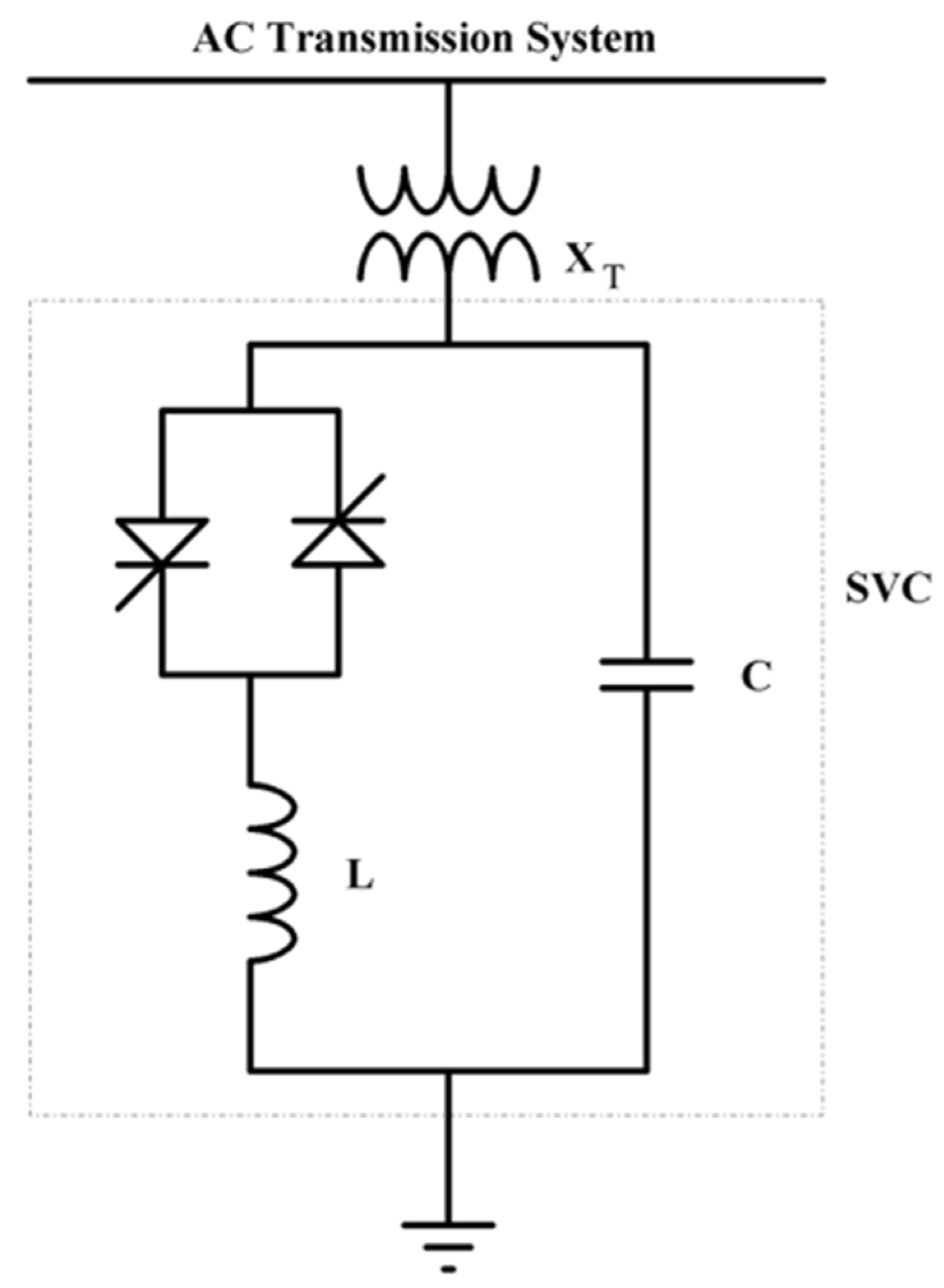
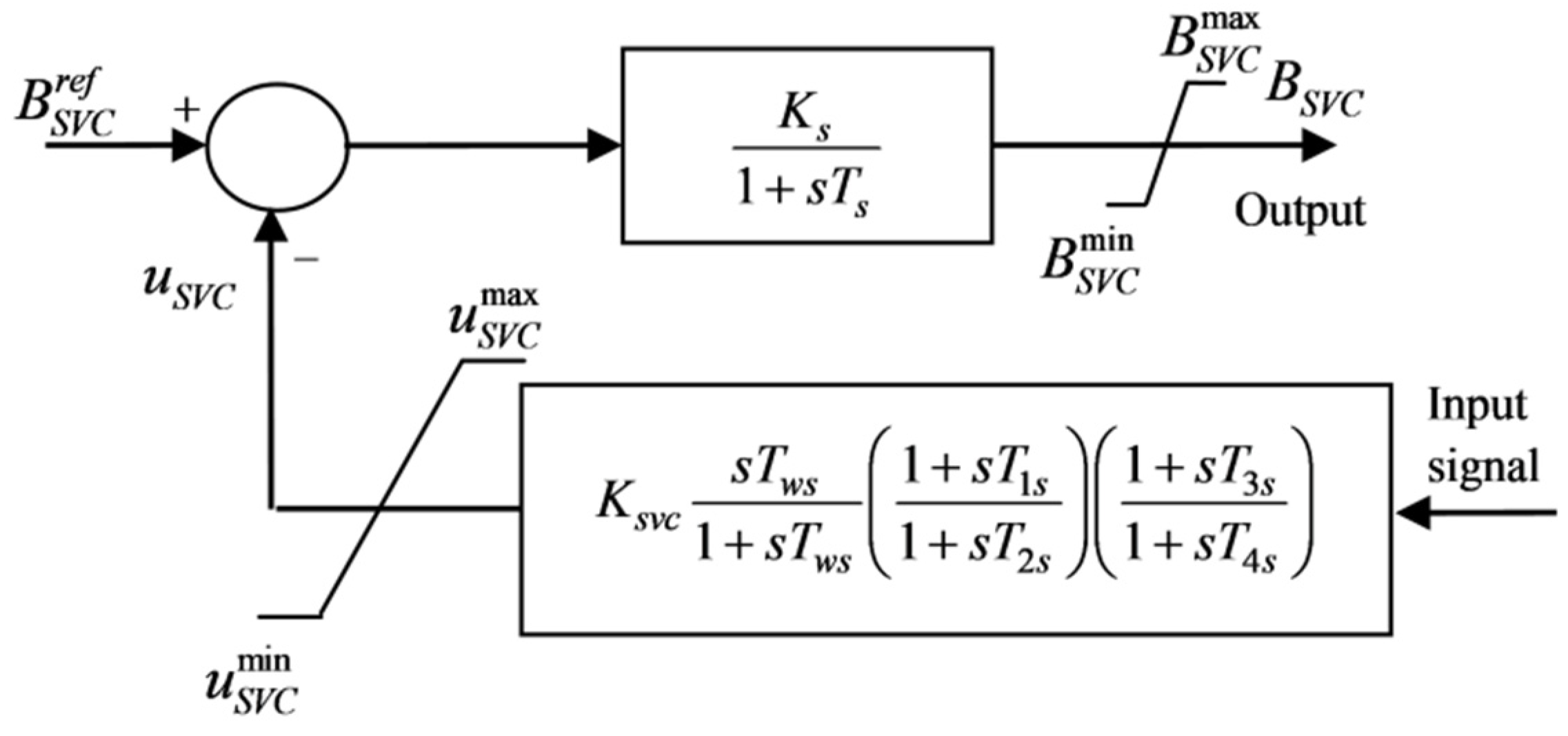
4.3. SVC Modeling and Damping Controller Structure
4.4. Optimal SVC Location Method
- The sensitivity factor which involves changes in RPL with respect to the change in the injection of reactive power is computed for all load buses. The bus having the largest absolute value of the sensitivity is considered as the best location for connecting an SVC controller;
- The SVC device should not be installed in the transmission lines containing the generation buses and transformers, even if the sensitivity factor is the largest there. Indeed, all generators are generally equipped with a PSS whose the main function consists in improving power system stability by producing a supplementary stabilizing signal through the excitation system. Moreover, the SVC device should not be placed in buses where there is no injected power.
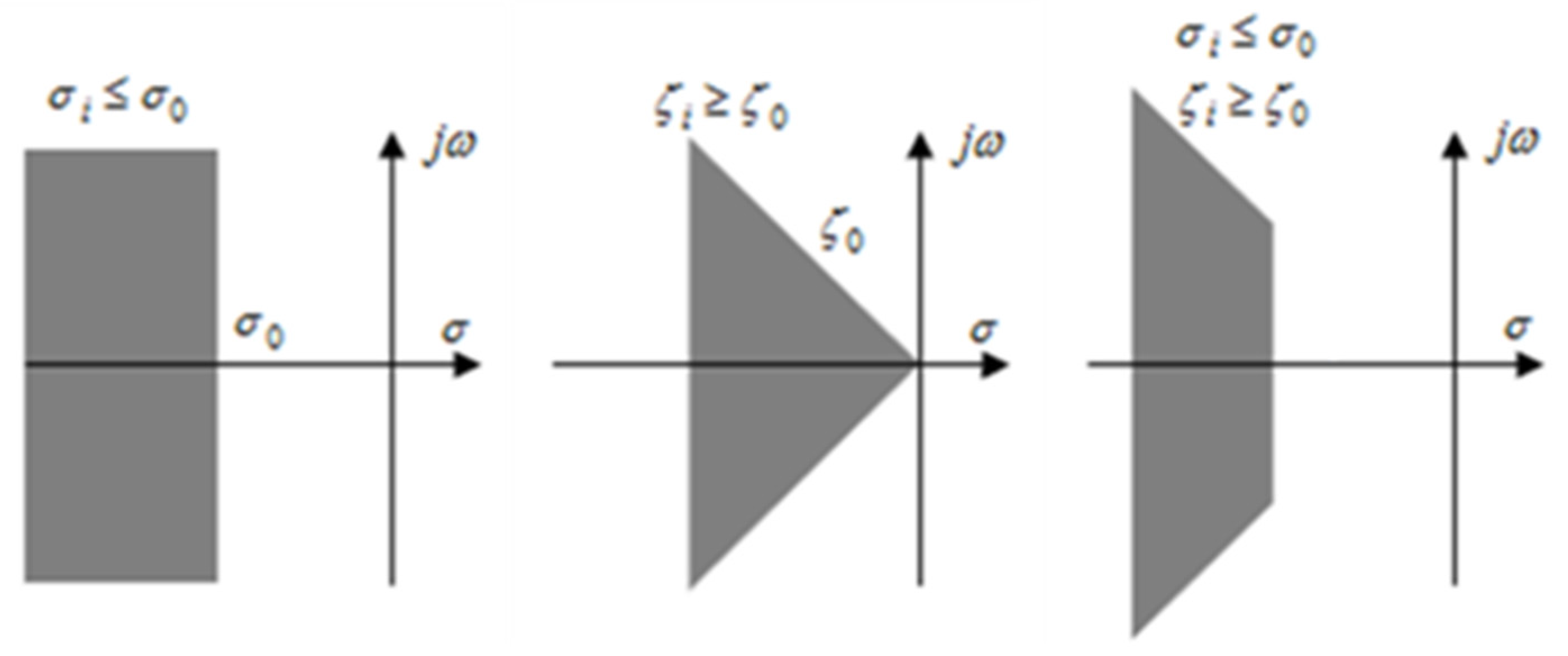
5. Coordinated Design of PSSs and SVC via Hybrid CJaya-SQP
6. Numerical Experiments
6.1. Benchmark Functions and Parameter Settings
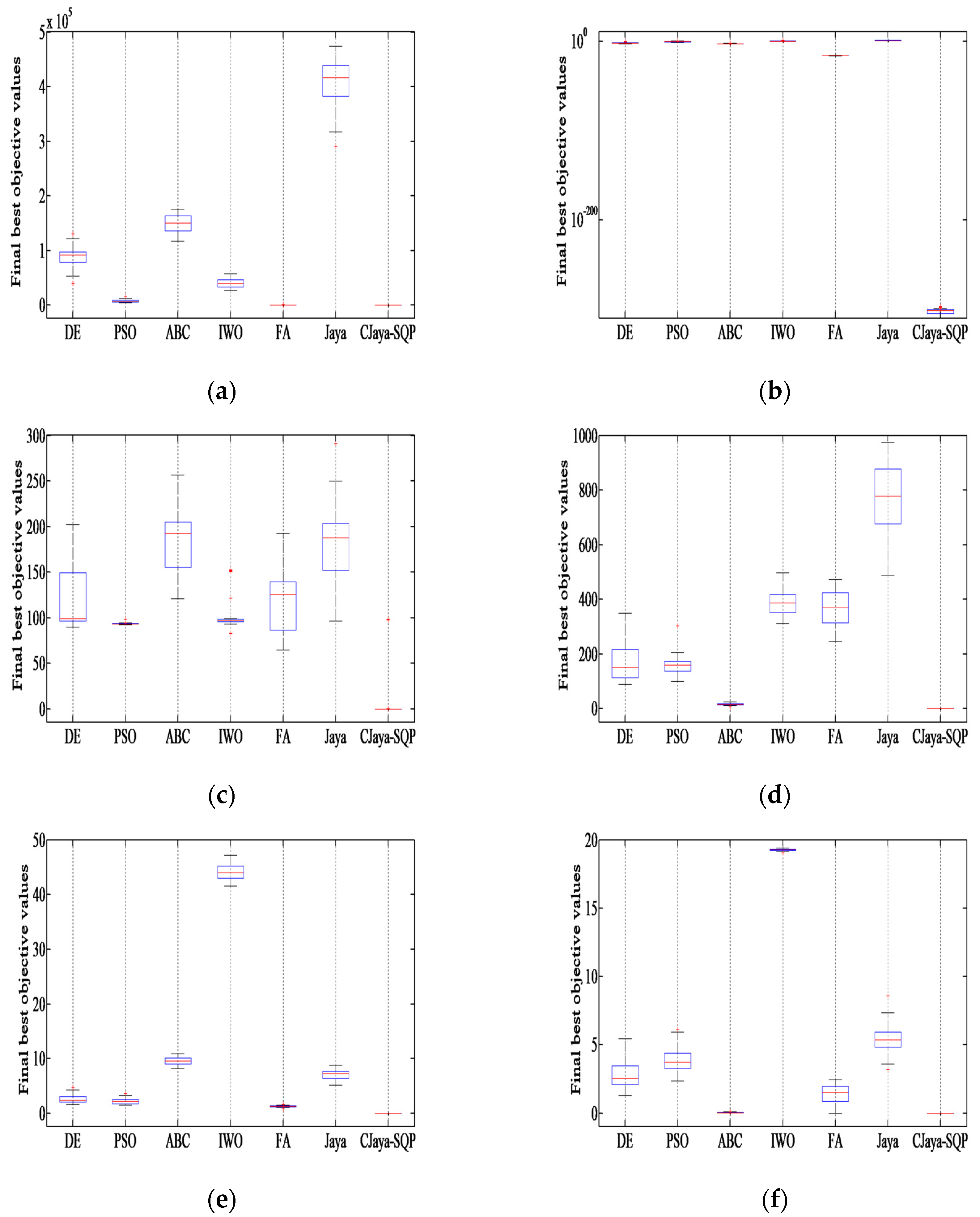
6.2. Results for Low-Dimensional Problems
6.2.1. Comparison of Solution Accuracy
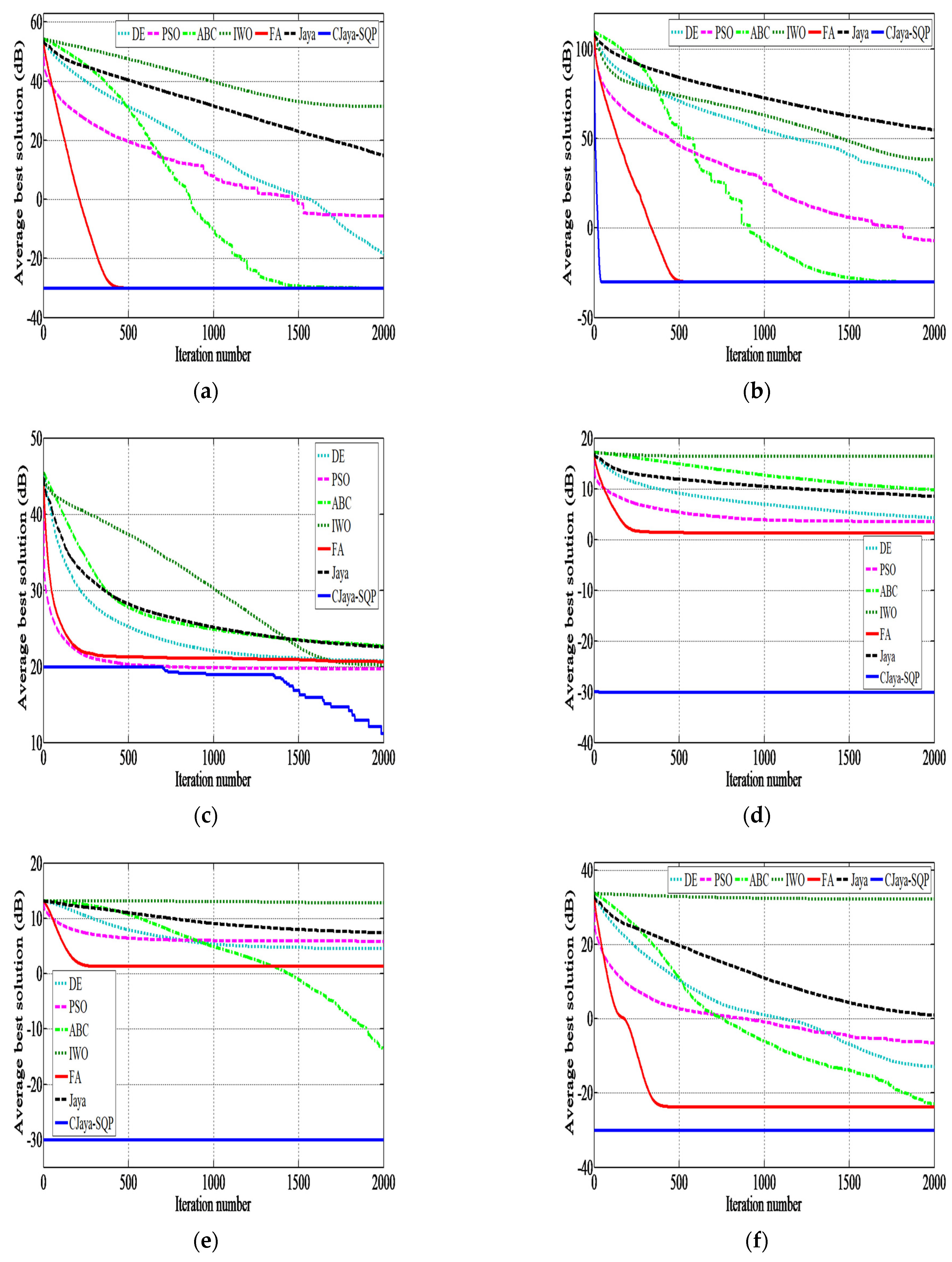
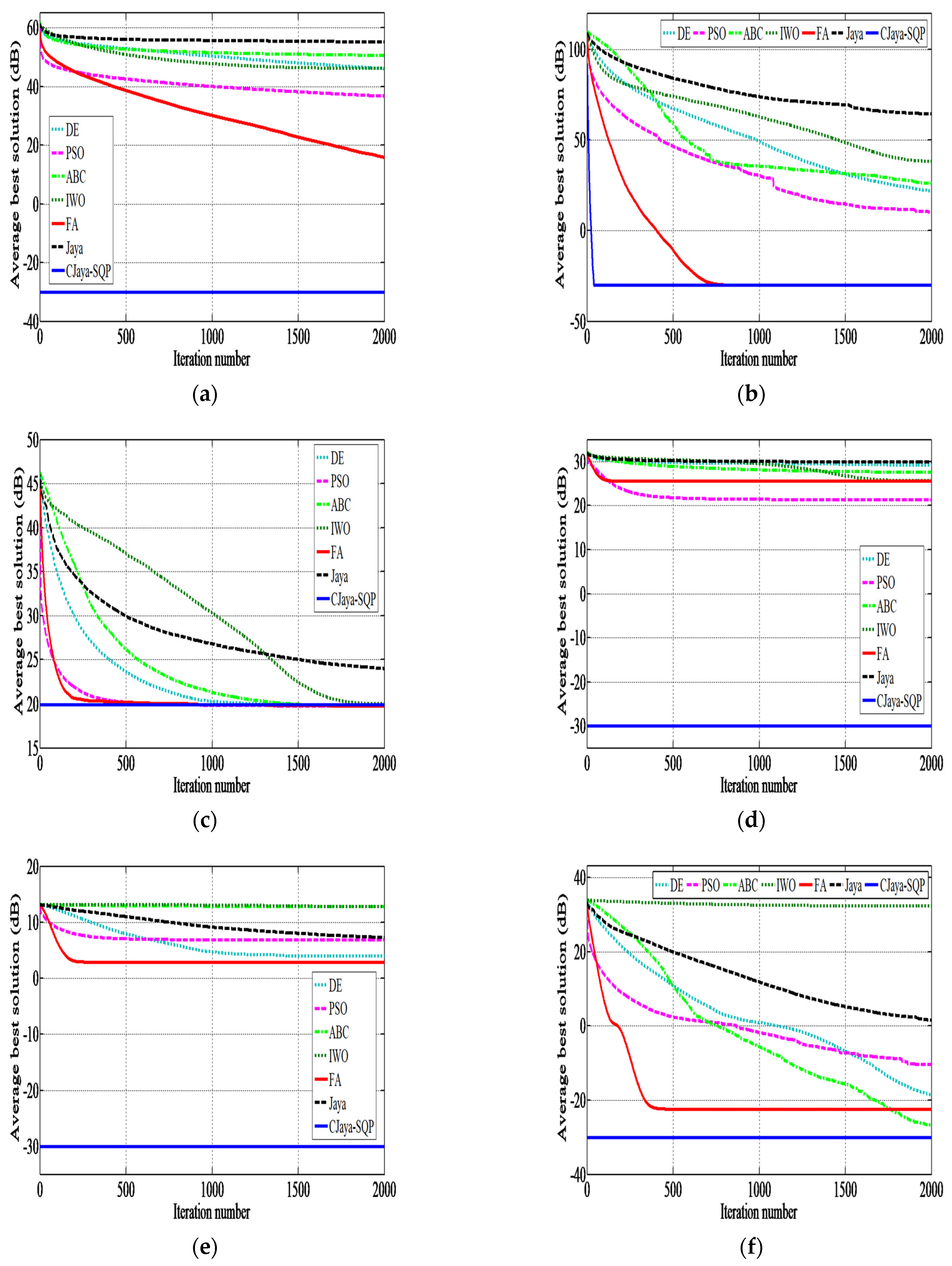
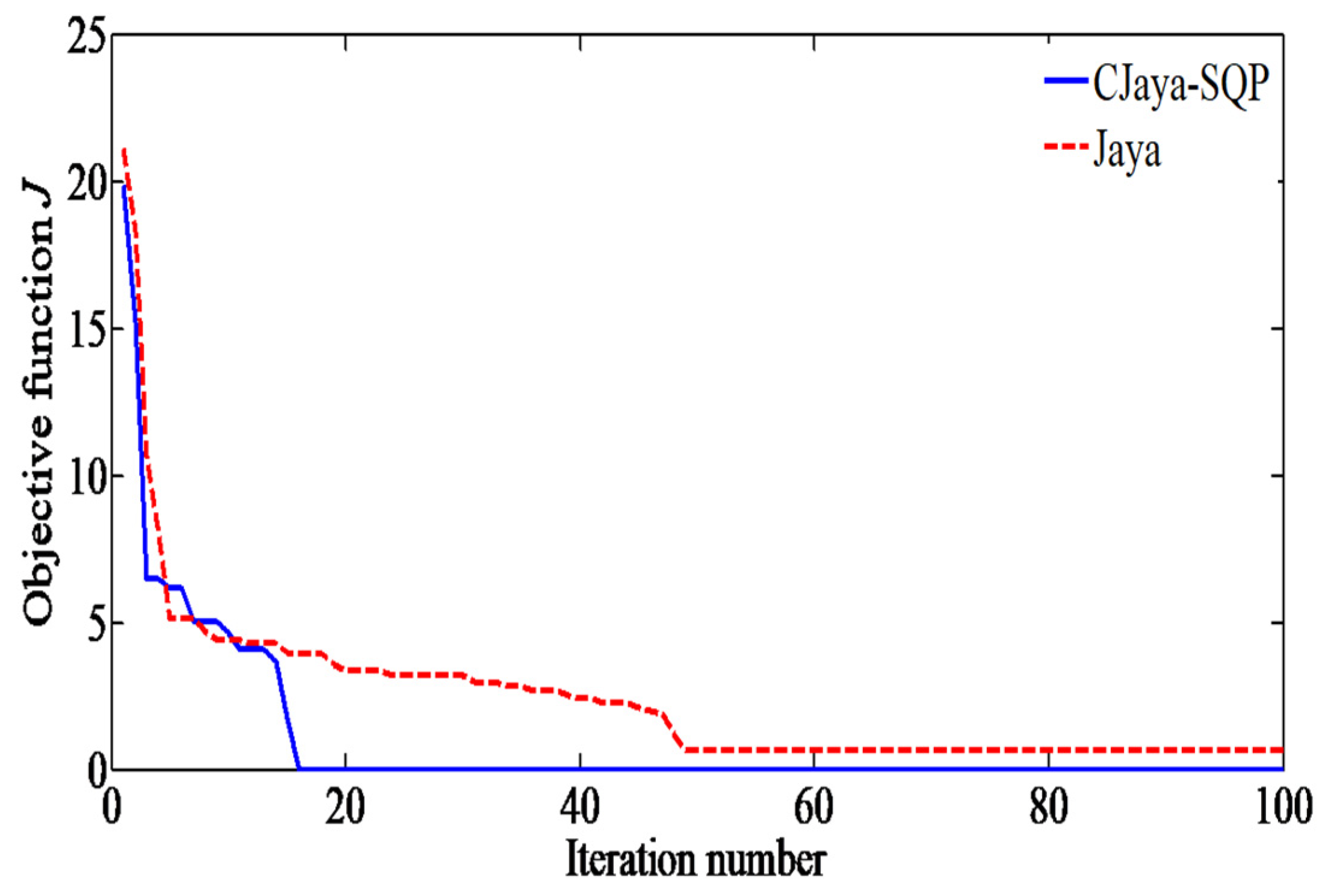
6.2.2. Comparison of Convergence and Success Ratios
6.2.3. Statistical Tests
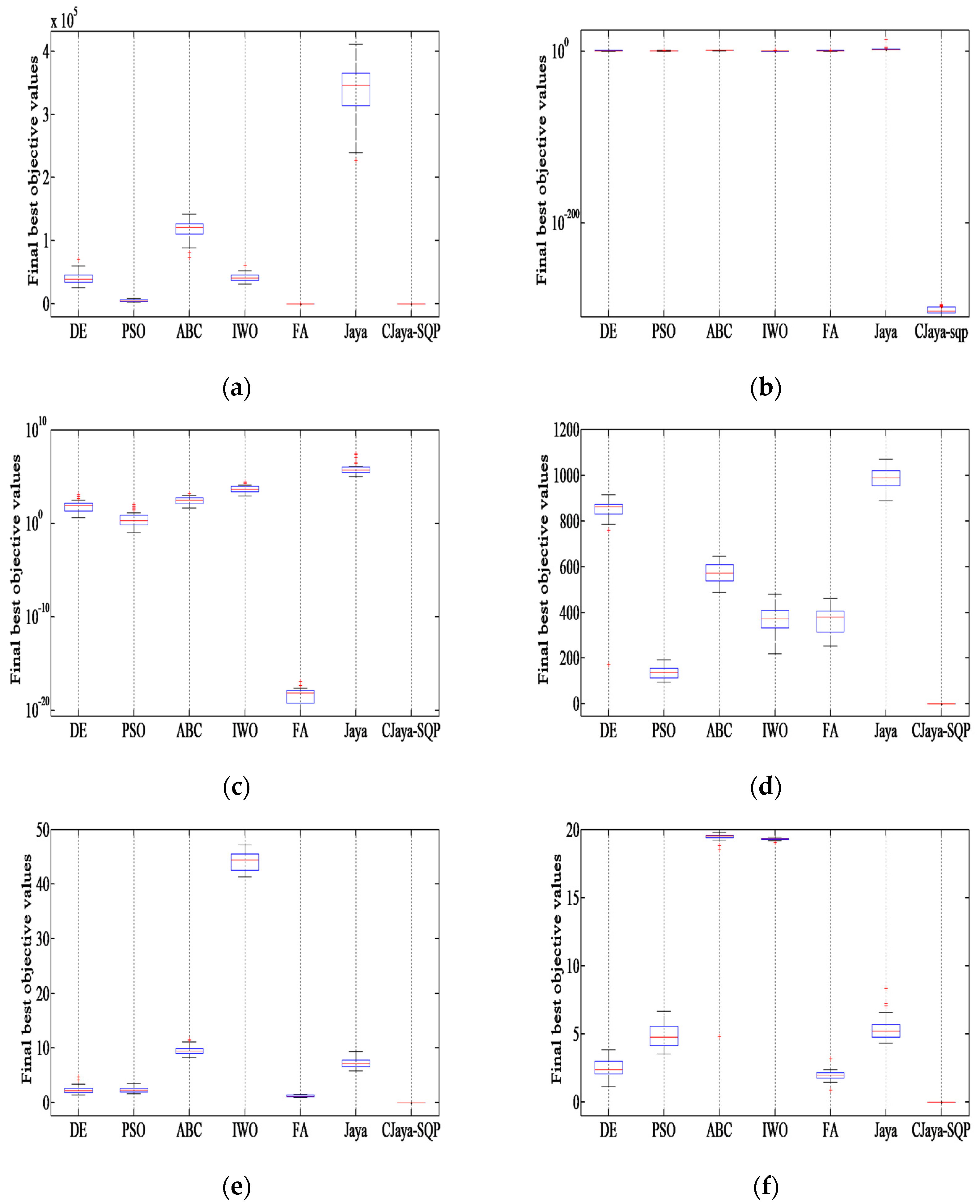
6.3. Results for High-Dimensional Problems
6.3.1. Comparison of Solution Accuracy
6.3.2. Comparison of Convergence and Success Ratios
6.3.3. Statistical Tests
7. Practical Application
7.1. PSSs Locations
7.2. SVC Location and Input Signal
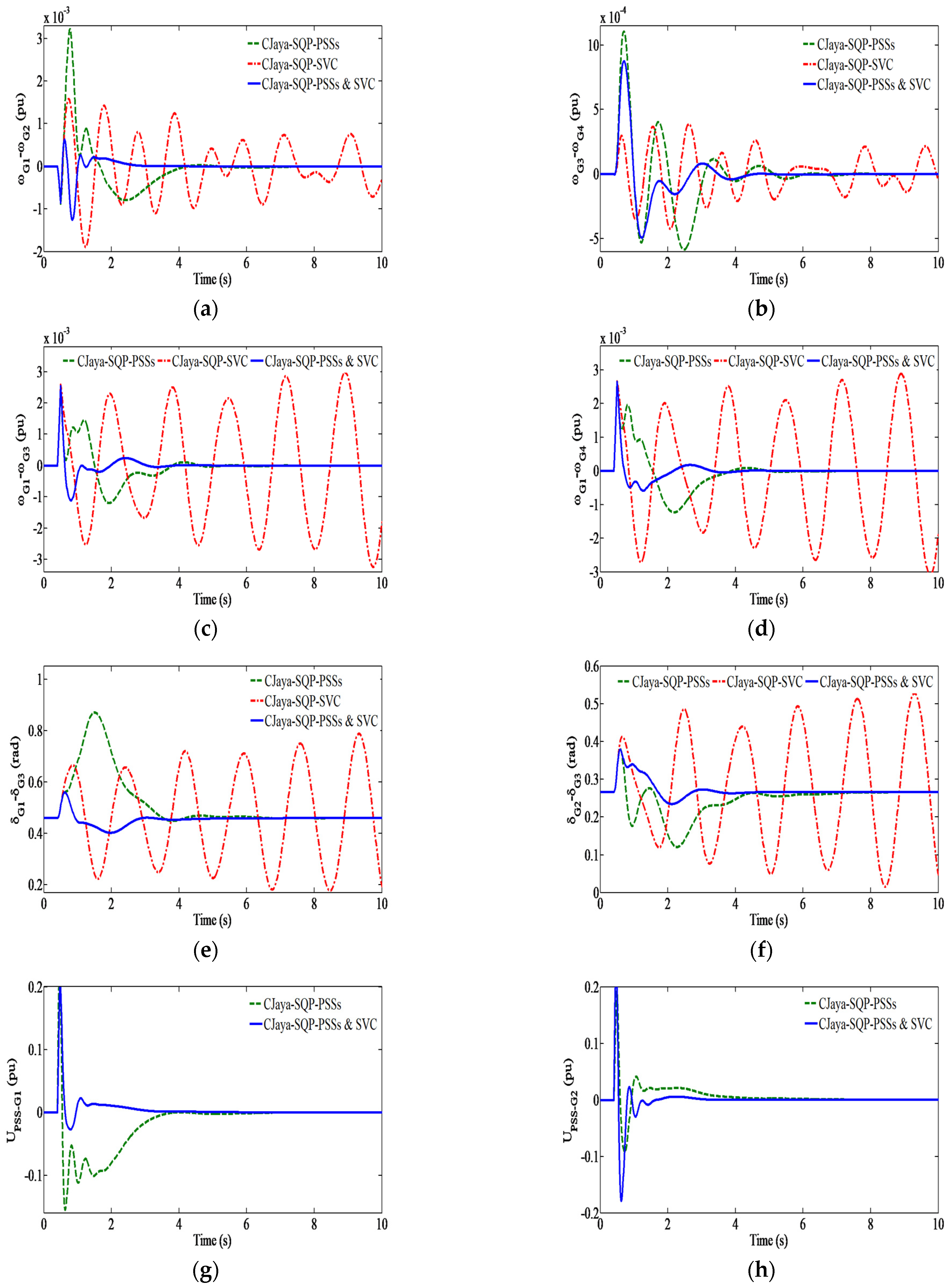
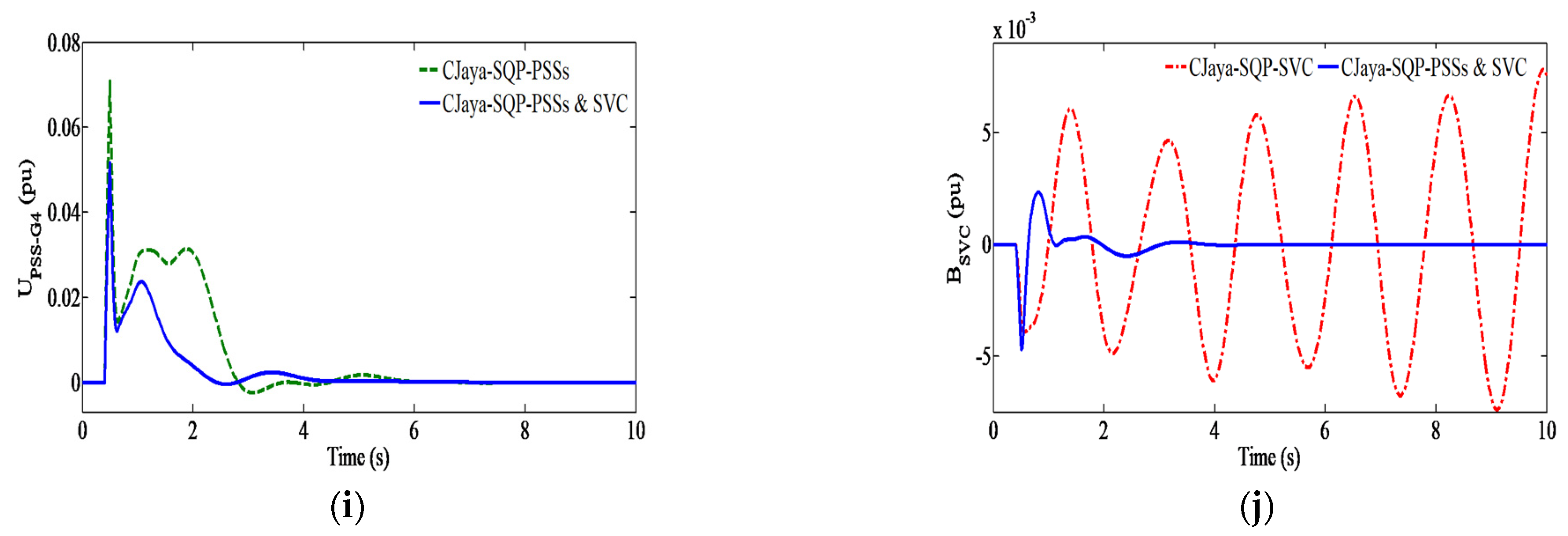
7.3. Damping Controllers Design and Robustness Analysis
7.4. Quantify the Enhancement of Proposed Approach
8. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Su, Q.; Khan, H.U.; Khan, I.; Choi, B.J.; Wu, F.; Aly, A.A. An optimized algorithm for optimal power flow based on deep learning. Energy Rep. 2021, 7, 2113–2124. [Google Scholar] [CrossRef]
- Farah, A.; Guesmi, T.; Hadj Abdallah, H.; Ouali, A. A novel chaotic teaching–learning-based optimization algorithm for multi-machine power system stabilizers design problem. Int. J. Electr. Power Energy Syst. 2016, 77, 197–209. [Google Scholar] [CrossRef]
- Welhazi, Y.; Guesmi, T.; Hadj Abdallah, H. Eigenvalue Assignments in Multimachine Power Systems using Multi-Objective PSO Algorithm. Int. J. Energy Optim. Eng. 2015, 4, 33–48. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Liang, J.; Jin, Y.; Wu, F. Model of Power System Stabilizer Adapting to Multi-Operating Conditions of Local Power Grid and Parameter Tuning. Sustainability 2018, 10, 2089. [Google Scholar] [CrossRef] [Green Version]
- Jolfaei, M.G.; Sharaf, A.M.; Shariatmadar, S.M.; Poudeh, M.B. A hybrid PSS-SSSC GA-stabilization scheme for damping power system small signal oscillations. Int. J. Electr. Power Energy Syst. 2016, 75, 337–344. [Google Scholar] [CrossRef]
- Singh, B.; Kumar, R. A comprehensive survey on enhancement of system performances by using different types of FACTS controllers in power systems with static and realistic load models. Energy Rep. 2020, 6, 55–79. [Google Scholar] [CrossRef]
- Bruno, S.; De Carne, G.; La Scala, M. Distributed FACTS for Power System Transient Stability Control. Energies 2020, 13, 2901. [Google Scholar] [CrossRef]
- Farah, A.; Guesmi, T.; Hadj Abdallah, H. A new method for the coordinated design of power system damping controllers. Eng. Appl. Artif. Intell. 2017, 64, 325–339. [Google Scholar] [CrossRef]
- Hasanvand, H.; Arvan, M.R.; Mozafari, B.; Amraee, T. Coordinated design of PSS and TCSC to mitigate interarea oscillations. Int. J. Electr. Power Energy Syst. 2016, 78, 194–206. [Google Scholar] [CrossRef]
- Movahedi, A.; Niasar, A.H.; Gharehpetian, G.B. Designing SSSC, TCSC, and STATCOM controllers using AVURPSO, GSA, and GA for transient stability improvement of a multi-machine power system with PV and wind farms. Int. J. Electr. Power Energy Syst. 2019, 106, 455–466. [Google Scholar] [CrossRef]
- Singh, B.; Agrawal, G. Enhancement of voltage profile by incorporation of SVC in power system networks by using optimal load flow method in MATLAB/Simulink environments. Energy Rep. 2018, 4, 418–434. [Google Scholar] [CrossRef]
- Yorino, N.; El-Araby, E.E.; Sasaki, H.; Harada, S. A new formulation for FACTS allocation for security enhancement against voltage collapse. IEEE Trans. Power Syst. 2003, 18, 3–10. [Google Scholar] [CrossRef]
- Minguez, R.; Milano, F.; Zarate-Minano, R.; Conejo, A.J. Optimal network placement of SVC devices. IEEE Trans. Power Syst. 2007, 22, 1851–1860. [Google Scholar] [CrossRef]
- Chang, R.W.; Saha, T.K. Maximizing Power System Loadability by OPTIMAL allocation of SVC Using Mixed Integer Linear Programming. In Proceedings of the IEEE Power & Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar]
- Chang, R.W.; Saha, T.K. A novel MIQCP method for FACTS allocation in complex real-world grids. Int. J. Electr. Power Energy Syst. 2014, 62, 735–743. [Google Scholar] [CrossRef]
- Jordehi, A.R. Brainstorm optimization algorithm (BSOA): An efficient algorithm for finding optimal location and setting of FACTS devices in electric power systems. Int. J. Electr. Power Energy Syst. 2015, 69, 48–57. [Google Scholar] [CrossRef]
- Raj, S.; Bhattacharyya, B. Optimal placement of TCSC and SVC for reactive power planning using Whale optimization algorithm. Swarm Evol. Comput. 2018, 40, 131–143. [Google Scholar] [CrossRef]
- Weiss, M.; Abu-Jaradeh, B.N.; Chakrabortty, A.; Jamehbozorg, A.; Habibi-Ashrafi, F.; Salazar, A. A wide-area SVC controller design for inter-area oscillation damping in WECC based on a structured dynamic equivalent model. Electr. Power Syst. Res. 2016, 133, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Panda, S.; Yegireddy, N.K.; Mohapatra, S.K. Hybrid BFOA–PSO approach for coordinated design of PSS and SSSC-based controller considering time delays. Int. J. Electr. Power Energy Syst. 2013, 49, 221–233. [Google Scholar] [CrossRef]
- Bian, X.Y.; Tse, C.T.; Zhang, J.F.; Wang, K.W. Coordinated design of probabilistic PSS and SVC damping controllers. Int. J. Electr. Power Energy Syst. 2011, 33, 445–452. [Google Scholar] [CrossRef]
- Furini, M.A.; Pereira, A.L.S.; Araujo, P.B. Pole placement by coordinated tuning of Power System Stabilizers and FACTS-POD stabilizers. Int. J. Electr. Power Energy Syst. 2011, 33, 615–622. [Google Scholar] [CrossRef]
- Robak, S. Robust SVC controller design and analysis for uncertain power systems. Control. Eng. Pract. 2009, 17, 1280–1290. [Google Scholar] [CrossRef]
- Panda, S.; Patidar, N.P.; Singh, R. Simultaneous Tuning of Static Var Compensator and Power System Stabilizer Employing Real-Coded Genetic Algorithm. Int. J. Electr. Comput. Eng. 2008, 2, 948–955. [Google Scholar]
- Abd-Elazim, S.M.; Ali, E.S. Coordinated design of PSSs and SVC via bacteria foraging optimization algorithm in a multi-machine power system. Int. J. Electr. Power Energy Syst. 2012, 41, 44–53. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Khajehzadeh, M. Optimal design of damping controllers using a new hybrid artificial bee colony algorithm. Int. J. Electr. Power Energy Syst. 2013, 52, 42–54. [Google Scholar] [CrossRef]
- Baadji, B.; Bentarzi, H.; Bakdi, A. Comprehensive learning bat algorithm for optimal coordinated tuning of power system stabilizers and static VAR compensator in power systems. Eng. Optim. Syst. 2019, 52, 1761–1779. [Google Scholar] [CrossRef]
- Narne, R.; Panda, P.C. PSS with multiple FACTS Controllers Coordinated Design and Real-Time Implementation Using Advanced Adaptive PSO. Int. J. of Electr. Comput. Eng. 2014, 8, 137–147. [Google Scholar]
- Ali, E.S.; Abd-Elazim, S.M. Stability improvement of multimachine power system via new coordinated design of PSSs and SVC. Complexit 2014, 21, 256–266. [Google Scholar] [CrossRef]
- Ali, E.S.; Abd-Elazim, S.M. Stability Enhancement of Multimachine Power System via New Coordinated Design of PSSs and SVC. WSEAS Trans. Syst. 2014, 13, 345–356. [Google Scholar]
- Esmaili, M.R.; Hooshmand, R.A.; Parastegari, M.; Panah, P.G.; Azizkhani, S. New coordinated design of SVC and PSS for multi-machine power system using BF-PSO algorithm. Proc. Technol. 2013, 11, 65–74. [Google Scholar] [CrossRef] [Green Version]
- Shayeghi, H.; Shayanfar, H.A.; Safari, A.; Aghmasheh, R. A robust PSSs design using PSO in a multi-machine environment. Energy Convers. Manag. 2010, 51, 696–702. [Google Scholar] [CrossRef]
- Jordehi, A.R. Time varying acceleration coefficients particle swarm optimisation (TVACPSO): A new optimisation algorithm for estimating parameters of PV cells and modules. Energy Convers. Manag. 2016, 129, 262–274. [Google Scholar] [CrossRef]
- Rao, R.V. A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–Learning-Based Optimization: An optimization method for continuous non-linear large scale problems. Inform. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Rao, R.V.; More, K.C. Design optimization and analysis of selected thermal devices using self-adaptive Jaya algorithm. Energy Convers. Manag. 2017, 140, 24–35. [Google Scholar] [CrossRef]
- Rao, R.V.; Rai, D.P.; Balic, J. A multi-objective algorithm for optimization of modern machining processes. Eng. Appl. Artif. Intell. 2017, 61, 103–125. [Google Scholar] [CrossRef]
- Rao, R.V.; Saroj, A. Economic optimization of shell-and-tube heat exchanger using Jaya algorithm with maintenance consideration. Appl. Therm. Eng. 2017, 116, 473–487. [Google Scholar] [CrossRef]
- Singh, S.P.; Prakash, T.; Singh, V.P.; Babu, M.G. Analytic hierarchy process based automatic generation control of multi-area interconnected power system using Jaya algorithm. Eng. Appl. Artif. Intell. 2017, 60, 35–44. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Abdul-Wahab, N.I. Optimal power flow using the jaya algorithm. Energies 2016, 9, 678. [Google Scholar] [CrossRef]
- Rao, R.V.; Waghmare, G.G. A new optimization algorithm for solving complex constrained design optimization problems. Eng Optim. 2017, 49, 60–83. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.; Qu, B.Y.; Chen, X.; Wang, H. Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Convers. Manag. 2017, 150, 742–753. [Google Scholar] [CrossRef]
- Majumdar, M.; Mitra, T.; Nishimura, K. Optimization and Chaos; Springer: New York, NY, USA, 2000. [Google Scholar]
- Farah, A.; Belazi, A. A novel chaotic Jaya algorithm for unconstrained numerical optimization. Nonlinear Dyn. 2018, 93, 1451–1480. [Google Scholar] [CrossRef]
- Gokhale, S.S.; Kale, V.S. An application of a tent map initiated chaotic firefly algorithm for optimal overcurrent relay coordination. Int. J. Electr. Power Energy Syst. 2016, 78, 336–342. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H. Chaotic gravitational constants for the gravitational search algorithm. Appl. Soft Comput. 2017, 53, 407–419. [Google Scholar] [CrossRef]
- Boggs, P.T.; Tolle, J.W. Sequential quadratic programming. Acta Numer. 1995, 4, 1–51. [Google Scholar] [CrossRef] [Green Version]
- Morshed, M.J.; Asgharpour, A. Hybrid imperialist competitive-sequential quadratic programming (HIC-SQP) algorithm for solving economic load dispatch with incorporating stochastic wind power: A comparative study on heuristic optimization techniques. Energy Convers. Manag. 2014, 84, 30–40. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Xia, X.; Shehata, A.M. Hybrid DE-SQP and hybrid PSO-SQP methods for solving dynamic economic emission dispatch problem with valve-point effects. Electr. Power Syst. Res. 2013, 103, 192–200. [Google Scholar] [CrossRef]
- Krishnasamy, U.; Nanjundappan, D. Hybrid weighted probabilistic neural network and biography based optimization for dynamic economic dispatch of integrated multiple-fuel and wind power plants. Int. J. Electr. Power Energy Syst. 2016, 77, 385–394. [Google Scholar] [CrossRef]
- Modares, H.; Naghibi Sistani, M.-B. Solving nonlinear optimal control problems using a hybrid IPSO-SQP algorithm. Eng. Appl. Artif. Intell. 2011, 24, 476–484. [Google Scholar] [CrossRef]
- Xu, W.; Geng, Z.; Zhu, Q.; Gu, X. A piecewise linear chaotic map and sequential quadratic programming based robust hybrid particle swarm optimization. Inform. Sci. 2013, 218, 85–102. [Google Scholar] [CrossRef]
- Muhammad, M.A.; Mokhlis, H.; Naidu, K.; Amin, A.; Franco, J.F.; Othman, M. Distribution Network Planning Enhancement via Network Reconfiguration and DG Integration Using Dataset Approach and Water Cycle Algorithm. J. Mod. Power Syst. Clean Energy 2020, 8, 86–93. [Google Scholar] [CrossRef]
- Helmi, A.M.; Carli, R.; Dotoli, M.; Ramadan, H.S. Efficient and Sustainable Reconfiguration of Distribution Networks via Metaheuristic Optimization. IEEE Trans. Autom. Sci. Eng. 2022, 19, 82–98. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Teh, J.S.; Samsudin, A.; Akhavan, A. Parallel chaotic hash function based on the shuffle-exchange network. Nonlinear Dyn. 2015, 81, 1067–1079. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Alizadeh, M.; Ganjefar, S.; Alizadeh, M. Wavelet neural adaptive proportional plus conventional integral-derivative controller design of SSSC for transient stability improvement. Eng. Appl. Artif. Intell. 2013, 26, 2227–2242. [Google Scholar] [CrossRef]







| Characteristics | CJaya-SQP | Other Metaheuristic Optimizers |
|---|---|---|
| Algorithm formulation | Very simple formulation. | Sometimes very complicated formulations, especially for hybrid algorithms. |
| Setting of control parameters | Not required. There are no algorithm-specific parameters. | Often required. The convergence behavior is very sensitive to tuning of algorithm-specific control parameters. |
| Gradient information | The gradient-based SQP method is utilized for the adjustment of the best solution derived by CJaya. | Not utilized. |
| Population diversity | The diversity of generated solutions is enhanced by embedding the chaotic maps to substitute random numbers in search equations and implementing chaotic local search strategy. | Not guaranteed. |
| Solutions quality | There is a high probability of generating high quality solutions. Current best candidate can be improved in each design cycle. | Best candidate design of population is not necessarily improved during the update of decision variables. |
| Elitism | Intrinsically elitist. There are no additional structural analyses. | Sometimes elitist. Additional structural analyses are usually required. |
| Exploration/Exploitation | Naturally balanced with just one mathematical model. The exploitation and exploration capabilities are further enhanced by using chaos theory, a local search strategy and SQP technique. | Not necessarily balanced. |
| Symbol | Variable Description | Symbol | Variable Description |
|---|---|---|---|
| Internal and the field voltages, respectively. | SVC susceptance. | ||
| Rotor angle and speed, respectively. | Reference susceptance of SVC. | ||
| Reference and terminal voltages, respectively. | Total number of buses. | ||
| PSS and SVC stabilizing signals, respectively. | Total number of load buses. | ||
| Gain of the PSS. | Real power injected at the slack bus s. | ||
| Washout time constant of PSS. | Real power generation at the slack bus s. | ||
| Lead-lag time constants of PSS. | Real power demand at the slack bus s. | ||
| Change in speed for machine i. | Voltages at the end buses s and j. | ||
| Gain and time constant of the excitation system, respectively. | element of the power system admittance matrix. | ||
| SVC gain and time constant, respectively. | Total real power demand. | ||
| Gain of lead-lag circuits of SVC. | Real power loss. | ||
| Washout time constant of SVC. | Real and reactive powers generated by machine i. | ||
| Lead-lag time constants of SVC. |
| Case | Lower Limit | Upper Limit | |
|---|---|---|---|
| PSS | KPSS | 1 | 100 |
| Ti (i = 1,2,3,4) | 0.001 | 2 | |
| SVC | Ksvc | 1 | 150 |
| Ti (i = 1,2,3,4) | 0.001 | 2 |
| Function | Formula | Range | T-Value |
|---|---|---|---|
| Category I: Conventional problems | |||
| Sphere | [−100, 100] | 1 × 10−2 | |
| Schwefel 1.2 | [−100, 100] | 1 × 10−5 | |
| Schwefel 2.22 | [−10, 10] | 1 × 10−5 | |
| Zakharov | [−5, 10] | 1 × 10−5 | |
| Rosenbrock | [−2.048, 2.048] | 5 | |
| Rastrigin | [−5.12, 5.12] | 1 × 10−5 | |
| Salomon | [−100, 100] | 1 × 10−5 | |
| Ackley | [−32.768, 32.768] | 1 × 10−5 | |
| Griewank | [−600, 600] | 1 × 10−5 | |
| Category II: Rotated problems | |||
| Rotated Schwefel 1.2 | [−100, 100] | 1 × 10−5 | |
| Rotated Schwefel 2.22 | [−10, 10] | 1 × 10−5 | |
| Rotated Zakharov | [−5, 10] | 1 × 10−5 | |
| Rotated Rosenbrock | [−2.048, 2.048] | 50 | |
| Rotated Rastrigin | [−5.12, 5.12] | 1 × 10−5 | |
| Rotated Salomon | [−100, 100] | 1 × 10−5 | |
| Rotated Ackley | [−32.768, 32.768] | 1 × 10−5 | |
| Rotated Griewank | [−600, 600] | 1 × 10−5 |
| Function | DE | PSO | ABC | IWO | FA | Jaya | CJaya-SQP | |
|---|---|---|---|---|---|---|---|---|
| f1 | Mean | 1.78 × 10−29 | 8.32 × 10−39 | 5.67 × 10−16 | 3.29 × 10−5 | 4.72 × 10−34 | 2.45 × 10−10 | 0.00 |
| SD | 1.87 × 10−29 | 1.55 × 10−38 | 1.01 × 10−16 | 4.95 × 10−6 | 5.85 × 10−35 | 1.75 × 10−10 | 0.00 | |
| SEM | 3.42 × 10−30 | 2.83 × 10−39 | 1.85 × 10−17 | 9.04 × 10−7 | 1.06 × 10−35 | 3.20 × 10−11 | 0.00 | |
| f2 | Mean | 5.54 × 10−1 | 4.54 × 10−3 | 7.89 × 103 | 4.39 × 10−4 | 8.73 × 10−33 | 2.57 × 104 | 0.00 |
| SD | 5.53 × 10−1 | 4.90 × 10−3 | 2.03 × 103 | 2.31 × 10−4 | 3.13 × 10−33 | 6.56 × 103 | 0.00 | |
| SEM | 1.01 × 10−1 | 8.95 × 10−4 | 3.71 × 102 | 4.23 × 10−5 | 5.72 × 10−34 | 1.19 × 103 | 0.00 | |
| f3 | Mean | 1.21 × 10−16 | 4.93 × 10−16 | 6.26 × 10−15 | 2.55 × 10−2 | 9.17 × 10−18 | 4.75 × 10−6 | 6.80 × 10−297 |
| SD | 9.13 × 10−17 | 2.21 × 10−15 | 2.83 × 10−15 | 2.27 × 10−3 | 7.23 × 10−19 | 2.38 × 10−6 | 0.00 | |
| SEM | 1.67 × 10−17 | 4.03 × 10−16 | 5.17 × 10−16 | 4.15 × 10−4 | 1.32 × 10−19 | 4.35 × 10−7 | 0.00 | |
| f4 | Mean | 8.00 × 10−28 | 1.38 × 10−38 | 5.39 × 10−16 | 4.99 × 10−1 | 1.65 × 10−34 | 5.68 × 10−10 | 0.00 |
| SD | 1.82 × 10−27 | 2.65 × 10−38 | 9.65 × 10−17 | 2.95 × 10−1 | 2.87 × 10−35 | 3.76 × 10−10 | 0.00 | |
| SEM | 3.33 × 10−28 | 4.83 × 10−39 | 1.76 × 10−17 | 5.40 × 10−2 | 5.25 × 10−36 | 6.86 × 10−11 | 0.00 | |
| f5 | Mean | 2.49 × 101 | 1.95 × 101 | 1.36 × 101 | 2.66 × 101 | 1.12 × 101 | 1.90 × 101 | 3.12 × 10−1 |
| SD | 1.79 × 100 | 2.24 × 100 | 7.26 × 100 | 1.40 × 100 | 1.16 × 100 | 1.91 × 101 | 1.32 | |
| SEM | 3.27 × 10−1 | 4.09 × 10−1 | 1.33 × 100 | 2.55 × 10−1 | 2.13 × 10−1 | 3.48 × 100 | 2.41 × 10−1 | |
| f6 | Mean | 2.74 × 101 | 4.91 × 101 | 3.31 × 10−15 | 6.30 × 101 | 4.98 × 101 | 2.05 × 102 | 0.00 |
| SD | 1.81 × 101 | 1.70 × 101 | 1.71 × 10−14 | 1.82 × 101 | 1.56 × 101 | 1.70 × 101 | 0.00 | |
| SEM | 3.31 × 100 | 3.11 × 100 | 3.13 × 10−15 | 3.32 × 100 | 2.85 × 100 | 3.11 × 100 | 0.00 | |
| f7 | Mean | 2.07 × 10−1 | 4.37 × 10−1 | 1.15 × 100 | 1.75 × 101 | 1.96 × 10−1 | 4.04 × 10−1 | 0.00 |
| SD | 2.54 × 10−2 | 9.64 × 10−2 | 1.73 × 10−1 | 1.47 × 100 | 1.82 × 10−2 | 7.07 × 10−2 | 0.00 | |
| SEM | 4.63 × 10−3 | 1.76 × 10−2 | 3.16 × 10−2 | 2.69 × 10−1 | 3.33 × 10−3 | 1.29 × 10−2 | 0.00 | |
| f8 | Mean | 3.10 × 10−2 | 5.95 × 10−1 | 4.96 × 10−13 | 1.76 × 101 | 1.85 × 10−14 | 4.46 × 10−2 | 8.88 × 10−16 |
| SD | 1.70 × 10−1 | 6.83 × 10−1 | 1.87 × 10−13 | 4.80 × 100 | 5.15 × 10−15 | 2.44 × 10−1 | 0.00 | |
| SEM | 3.10 × 10−2 | 1.25 × 10−1 | 3.42 × 10−14 | 8.77 × 10−1 | 9.40 × 10−16 | 4.46 × 10−2 | 0.00 | |
| f9 | Mean | 4.35 × 10−3 | 1.44 × 10−2 | 1.08 × 10−3 | 2.70 × 102 | 3.53 × 10−3 | 9.17 × 10−2 | 0.00 |
| SD | 7.30 × 10−3 | 1.51 × 10−2 | 2.84 × 10−3 | 3.62 × 101 | 4.87 × 10−3 | 1.39 × 10−1 | 0.00 | |
| SEM | 1.33 × 10−3 | 2.75 × 10−3 | 5.18 × 10−4 | 6.61 × 100 | 8.89 × 10−4 | 2.54 × 10−2 | 0.00 | |
| f10 | Mean | 4.67 × 10−2 | 1.83 × 10−3 | 5.54 × 103 | 4.55 × 10−4 | 5.68 × 10−33 | 1.30 × 104 | 0.00 |
| SD | 4.06 × 10−2 | 1.86 × 10−3 | 1.59 × 103 | 1.78 × 10−4 | 1.71 × 10−33 | 5.21 × 103 | 0.00 | |
| SEM | 7.41 × 10−3 | 3.40 × 10−4 | 2.90 × 102 | 3.25 × 10−5 | 3.12 × 10−34 | 9.52 × 102 | 0.00 | |
| f11 | Mean | 6.36 × 10−12 | 1.30 × 10−1 | 7.58 × 10−2 | 2.48 × 10−2 | 9.37 × 10−18 | 2.15 × 101 | 1.91 × 10−302 |
| SD | 3.41 × 10−11 | 5.63 × 10−1 | 8.39 × 10−2 | 2.41 × 10−3 | 7.10 × 10−19 | 3.46 × 101 | 0.00 | |
| SEM | 6.23 × 10−12 | 1.03 × 10−1 | 1.53 × 10−2 | 4.41 × 10−4 | 1.29 × 10−19 | 6.31 × 100 | 0.00 | |
| f12 | Mean | 1.76 × 10−11 | 4.11 × 10−21 | 5.01 × 100 | 6.51 × 10−1 | 2.48 × 10−34 | 4.53 × 101 | 0.00 |
| SD | 5.10 × 10−11 | 1.68 × 10−20 | 5.90 × 100 | 2.82 × 10−1 | 4.93 × 10−35 | 2.46 × 102 | 0.00 | |
| SEM | 9.32 × 10−12 | 3.07 × 10−21 | 1.07 × 100 | 5.15 × 10−2 | 9.01 × 10−36 | 4.49 × 101 | 0.00 | |
| f13 | Mean | 2.39 × 101 | 1.93 × 101 | 2.39 × 101 | 2.64 × 101 | 1.22 × 101 | 2.89 × 101 | 2.87 × 101 |
| SD | 1.19 × 100 | 1.49 × 100 | 2.95 × 100 | 1.60 × 100 | 1.88 × 100 | 7.64 × 10−1 | 2.74 × 10−2 | |
| SEM | 2.17 × 10−1 | 2.73 × 10−1 | 5.39 × 10−1 | 2.93 × 10−1 | 3.44 × 10−1 | 1.39 × 10−1 | 5.00 × 10−3 | |
| f14 | Mean | 1.53 × 102 | 3.92 × 101 | 1.30 × 102 | 5.47 × 101 | 5.86 × 101 | 2.25 × 102 | 0.00 |
| SD | 4.63 × 101 | 1.12 × 101 | 1.35 × 101 | 1.46 × 101 | 1.90 × 101 | 1.82 × 101 | 0.00 | |
| SEM | 8.45 × 100 | 2.04 × 100 | 2.47 × 100 | 2.68 × 100 | 3.48 × 100 | 3.32 × 100 | 0.00 | |
| f15 | Mean | 2.09 × 10−1 | 4.60 × 10−1 | 1.16 × 100 | 1.75 × 101 | 1.93 × 10−1 | 3.97 × 10−1 | 0.00 |
| SD | 4.04 × 10−2 | 9.68 × 10−2 | 1.17 × 10−1 | 1.26 × 100 | 2.53 × 10−2 | 6.09 × 10−2 | 0.00 | |
| SEM | 7.38 × 10−3 | 1.77 × 10−2 | 2.14 × 10−2 | 2.30 × 10−1 | 4.63 × 10−3 | 1.11 × 10−2 | 0.00 | |
| f16 | Mean | 3.85 × 10−2 | 1.83 × 100 | 7.09 × 100 | 1.88 × 101 | 1.80 × 10−14 | 7.75 × 10−2 | 8.88 × 10−16 |
| SD | 2.11 × 10−1 | 6.11 × 10−1 | 7.21 × 100 | 2.71 × 10−1 | 6.79 × 10−15 | 3.00 × 10−1 | 0.00 | |
| SEM | 3.85 × 10−2 | 1.11 × 10−1 | 1.31 × 100 | 4.95 × 10−2 | 1.24 × 10−15 | 5.48 × 10−2 | 0.00 | |
| f17 | Mean | 4.99 × 10−3 | 1.03 × 10−2 | 2.31 × 10−5 | 2.73 × 102 | 4.93 × 10−4 | 1.33 × 10−1 | 0.00 |
| SD | 1.06 × 10−2 | 1.58 × 10−2 | 6.46 × 10−5 | 3.20 × 101 | 1.87 × 10−3 | 1.80 × 10−1 | 0.00 | |
| SEM | 1.93 × 10−3 | 2.89 × 10−3 | 1.18 × 10−5 | 5.85 × 100 | 3.42 × 10−4 | 3.29 × 10−2 | 0.00 |
| Function | DE | PSO | ABC | IWO | FA | Jaya | CJaya-SQP | |
|---|---|---|---|---|---|---|---|---|
| f1 | MeanFEs | 15,963 | 9556 | 11,655 | 65,471 | 8593.3 | 37,517 | 3.33 |
| SR (%) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| f2 | MeanFEs | NaN | NaN | NaN | NaN | 19,125 | NaN | 8.06 |
| SR (%) | 0 | 0 | 0 | 0 | 100 | 0 | 100 | |
| f3 | MeanFEs | 32,199 | 25,373 | 35,040 | NaN | 25,160 | 76,022.67 | 10.43 |
| SR (%) | 100 | 100 | 100 | 0 | 100 | 100 | 100 | |
| f4 | MeanFEs | 25,470.67 | 16,504 | 20,672 | NaN | 14,408 | 56,173.33 | 1122.83 |
| SR (%) | 100 | 100 | 100 | 0 | 100 | 100 | 100 | |
| f5 | MeanFEs | NaN | NaN | 57,856 | NaN | NaN | 603,80 | 17,826.21 |
| SR (%) | 0 | 0 | 16.66 | 0 | 0 | 13.33 | 96.66 | |
| f6 | MeanFEs | NaN | NaN | 42,561.33 | NaN | NaN | NaN | 7.63 |
| SR (%) | 0 | 0 | 100 | 0 | 0 | 0 | 100 | |
| f7 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 20.46 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f8 | MeanFEs | 32,580.69 | 23,925 | 41,117.33 | NaN | 23,965.33 | 77,400 | 27.5 |
| SR (%) | 96.66 | 53.33 | 100 | 0 | 100 | 86.66 | 100 | |
| f9 | MeanFEs | 24,464.76 | 16,008.89 | 31,547.69 | NaN | 16,073.68 | 61,088 | 23.5 |
| SR (%) | 70 | 30 | 86.66 | 0 | 63.33 | 16.66 | 100 | |
| f10 | MeanFEs | NaN | NaN | NaN | NaN | 18,386.67 | NaN | 10.16 |
| SR (%) | 0 | 0 | 0 | 0 | 100 | 0 | 100 | |
| f11 | MeanFEs | 39,573.33 | 44,388 | NaN | NaN | 25,192 | NaN | 11.90 |
| SR (%) | 100 | 66.66 | 0 | 0 | 100 | 0 | 100 | |
| f12 | MeanFEs | 46,014.67 | 26,560 | NaN | NaN | 14,850.67 | NaN | 1278.66 |
| SR (%) | 100 | 100 | 0 | 0 | 100 | 0 | 100 | |
| f13 | MeanFEs | 5794.66 | 1226.66 | 7540 | 45,032 | 834.66 | 15,921.33 | 36.76 |
| SR (%) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| f14 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 9.33 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f15 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 23.56 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f16 | MeanFEs | 33,384.83 | 22,480 | NaN | NaN | 23,966.67 | 78,511.11 | 29.83 |
| SR (%) | 96.66 | 3.33 | 0 | 0 | 100 | 30 | 100 | |
| f17 | MeanFEs | 26,200 | 17,637.33 | 47,376.67 | NaN | 16,048.57 | 64,885 | 25.43 |
| SR (%) | 66.66 | 50 | 80 | 0 | 93.33 | 26.66 | 100 |
| Test for Mean Solutions | Test for SEM Solutions | ||||||
|---|---|---|---|---|---|---|---|
| Algorithms | Friedman Value | Normalized Value | Rank | Algorithms | Friedman value | Normalized Value | Rank |
| DE | 3.94 | 3.05 | 3 | DE | 4.05 | 3.85 | 3 |
| PSO | 4.05 | 3.13 | 4 | PSO | 4.23 | 4.02 | 4 |
| ABC | 4.52 | 3.50 | 5 | ABC | 4.82 | 4.59 | 5 |
| IWO | 5.82 | 4.51 | 6 | IWO | 5.52 | 5.25 | 6 |
| FA | 2.47 | 1.91 | 2 | FA | 2.70 | 2.57 | 2 |
| Jaya | 5.88 | 4.55 | 7 | Jaya | 5.58 | 5.31 | 7 |
| CJaya-SQP | 1.29 | 1.00 | 1 | CJaya-SQP | 1.05 | 1.00 | 1 |
| Function | DE | PSO | ABC | IWO | FA | Jaya | CJaya-SQP | |
|---|---|---|---|---|---|---|---|---|
| f1 | Mean | 1.34 × 10−2 | 2.72 × 10−1 | 6.06 × 10−6 | 1.41 × 103 | 2.78 × 10−32 | 3.08 × 101 | 0.00 |
| SD | 3.12 × 10−2 | 1.16 × 100 | 7.59 × 10−6 | 7.79 × 102 | 4.82 × 10−33 | 1.66 × 101 | 0.00 | |
| SEM | 5.69 × 10−3 | 2.12 × 10−1 | 1.38 × 10−6 | 1.42 × 102 | 8.80 × 10−34 | 3.03 × 100 | 0.00 | |
| f2 | Mean | 8.72 × 104 | 7.32 × 103 | 1.49 × 105 | 4.05 × 104 | 1.04 × 102 | 4.05 × 105 | 0.00 |
| SD | 1.90 × 104 | 2.50 × 103 | 1.60 × 104 | 7.65 × 103 | 1.60 × 102 | 4.67 × 104 | 0.00 | |
| SEM | 3.48 × 103 | 4.57 × 102 | 2.92 × 103 | 1.39 × 103 | 2.92 × 101 | 8.53 × 103 | 0.00 | |
| f3 | Mean | 5.53 × 10−2 | 7.02 × 10−1 | 2.64 × 10−3 | 1.82 × 100 | 1.15 × 10−16 | 8.00 × 100 | 4.07 × 10−298 |
| SD | 1.47 × 10−1 | 7.58 × 10−1 | 9.26 × 10−4 | 2.73 × 100 | 9.25 × 10−18 | 4.01 × 100 | 0.00 | |
| SEM | 2.69 × 10−2 | 1.38 × 10−1 | 1.69 × 10−4 | 5.00 × 10−1 | 1.69 × 10−18 | 7.33 × 10−1 | 0.00 | |
| f4 | Mean | 2.51 × 102 | 2.00 × 10−1 | 1.05 × 10−5 | 6.59 × 103 | 2.49 × 10−31 | 3.10 × 105 | 0.00 |
| SD | 7.45 × 102 | 3.69 × 10−1 | 9.27 × 10−6 | 4.28 × 103 | 8.71 × 10−32 | 6.15 × 105 | 0.00 | |
| SEM | 1.36 × 102 | 6.74 × 10−2 | 1.69 × 10−6 | 7.82 × 102 | 1.59 × 10−32 | 1.12 × 105 | 0.00 | |
| f5 | Mean | 1.20 × 102 | 9.34 × 101 | 1.85 × 102 | 1.05 × 102 | 1.16 × 102 | 1.80 × 102 | 1.30 × 101 |
| SD | 3.26 × 101 | 1.08 × 100 | 3.41 × 101 | 2.16 × 101 | 3.42 × 101 | 4.67 × 101 | 3.39 × 101 | |
| SEM | 5.95 × 100 | 1.98 × 10−1 | 6.24 × 100 | 3.96 × 100 | 6.26 × 100 | 8.54 × 100 | 6.19 × 100 | |
| f6 | Mean | 1.71 × 102 | 1.62 × 102 | 1.73 × 101 | 3.88 × 102 | 3.71 × 102 | 7.72 × 102 | 0.00 |
| SD | 7.69 × 101 | 3.50 × 101 | 4.16 × 100 | 4.42 × 101 | 6.19 × 101 | 1.27 × 102 | 0.00 | |
| SEM | 1.40 × 101 | 6.39 × 100 | 7.59 × 10−1 | 8.07 × 100 | 1.13 × 101 | 2.32 × 101 | 0.00 | |
| f7 | Mean | 2.68 × 100 | 2.27 × 100 | 9.60 × 100 | 4.40 × 101 | 1.33 × 100 | 7.08 × 100 | 0.00 |
| SD | 7.94 × 10−1 | 5.72 × 10−1 | 7.20 × 10−1 | 1.40 × 100 | 1.63 × 10−1 | 8.45 × 10−1 | 0.00 | |
| SEM | 1.45 × 10−1 | 1.04 × 10−1 | 1.31 × 10−1 | 2.56 × 10−1 | 2.97 × 10−2 | 1.54 × 10−1 | 0.00 | |
| f8 | Mean | 2.84 × 100 | 3.89 × 100 | 4.14 × 10−2 | 1.92 × 101 | 1.36 × 100 | 5.51 × 100 | 8.88 × 10−16 |
| SD | 1.10 × 100 | 9.08 × 10−1 | 2.94 × 10−2 | 8.75 × 10−2 | 7.94 × 10−1 | 1.16 × 100 | 0.00 | |
| SEM | 2.01 × 10−1 | 1.65 × 10−1 | 5.38 × 10−3 | 1.59 × 10−2 | 1.45 × 10−1 | 2.13 × 10−1 | 0.00 | |
| f9 | Mean | 5.07 × 10−2 | 2.30 × 10−1 | 4.15 × 10−3 | 1.71 × 103 | 3.28 × 10−3 | 1.25 × 100 | 0.00 |
| SD | 6.99 × 10−2 | 3.87 × 10−1 | 9.14 × 10−3 | 8.95 × 101 | 5.93 × 10−3 | 1.57 × 10−1 | 0.00 | |
| SEM | 1.27 × 10−2 | 7.07 × 10−2 | 1.67 × 10−3 | 1.63 × 101 | 1.08 × 10−3 | 2.86 × 10−2 | 0.00 | |
| f10 | Mean | 4.11 × 104 | 4.75 × 103 | 1.16 × 105 | 4.24 × 104 | 3.82 × 101 | 3.37 × 105 | 0.00 |
| SD | 1.13 × 104 | 1.66 × 103 | 1.72 × 104 | 6.87 × 103 | 3.28 × 101 | 4.32 × 104 | 0.00 | |
| SEM | 2.07 × 103 | 3.04 × 102 | 3.14 × 103 | 1.25 × 103 | 5.99 × 100 | 7.89 × 103 | 0.00 | |
| f11 | Mean | 6.76 × 100 | 5.26 × 100 | 1.36 × 101 | 3.17 × 100 | 8.83 × 100 | 3.23 × 1012 | 1.54 × 10−296 |
| SD | 3.64 × 100 | 3.51 × 100 | 5.57 × 100 | 4.48 × 100 | 7.97 × 100 | 1.77 × 1013 | 0.00 | |
| SEM | 6.65 × 10−1 | 6.41 × 10−1 | 1.01 × 100 | 8.19 × 10−1 | 1.45 × 100 | 3.23 × 1012 | 0.00 | |
| f12 | Mean | 1.56 × 102 | 1.12 × 101 | 4.11 × 102 | 6.75 × 103 | 1.38 × 10−18 | 2.81 × 106 | 0.00 |
| SD | 2.53 × 102 | 2.40 × 101 | 3.49 × 102 | 6.01 × 103 | 2.52 × 10−18 | 6.79 × 106 | 0.00 | |
| SEM | 4.63 × 101 | 4.39 × 100 | 6.37 × 101 | 1.09 × 103 | 4.60 × 10−19 | 1.24 × 106 | 0.00 | |
| f13 | Mean | 9.81 × 101 | 9.44 × 101 | 9.65 × 101 | 1.01 × 102 | 9.45 × 101 | 2.53 × 102 | 9.89 × 101 |
| SD | 9.85 × 100 | 2.00 × 100 | 1.50 × 100 | 1.57 × 101 | 1.80 × 101 | 1.82 × 102 | 2.12 × 10−2 | |
| SEM | 1.79 × 100 | 3.65 × 10−1 | 2.74 × 10−1 | 2.87 × 100 | 3.29 × 100 | 3.33 × 101 | 3.87 × 10−3 | |
| f14 | Mean | 8.33 × 102 | 1.38 × 102 | 5.72 × 102 | 3.68 × 102 | 3.60 × 102 | 9.88 × 102 | 0.00 |
| SD | 1.29 × 102 | 2.69 × 101 | 3.98 × 101 | 5.52 × 101 | 6.10 × 101 | 4.36 × 101 | 0.00 | |
| SEM | 2.36 × 101 | 4.92 × 100 | 7.27 × 100 | 1.00 × 101 | 1.11 × 101 | 7.97 × 100 | 0.00 | |
| f15 | Mean | 2.38 × 100 | 2.40 × 100 | 9.63 × 100 | 4.43 × 101 | 1.25 × 100 | 7.29 × 100 | 0.00 |
| SD | 7.40 × 10−1 | 4.94 × 10−1 | 7.86 × 10−1 | 1.71 × 100 | 1.52 × 10−1 | 8.45 × 10−1 | 0.00 | |
| SEM | 1.35 × 10−1 | 9.02 × 10−2 | 1.43 × 10−1 | 3.13 × 10−1 | 2.78 × 10−2 | 1.54 × 10−1 | 0.00 | |
| f16 | Mean | 2.51 × 100 | 4.87 × 100 | 1.89 × 101 | 1.93 × 101 | 1.95 × 100 | 5.41 × 100 | 8.88 × 10−16 |
| SD | 6.20 × 10−1 | 8.23 × 10−1 | 2.68 × 100 | 7.75 × 10−2 | 3.91 × 10−1 | 9.34 × 10−1 | 0.00 | |
| SEM | 1.13 × 10−1 | 1.50 × 10−1 | 4.90 × 10−1 | 1.41 × 10−2 | 7.14 × 10−2 | 1.70 × 10−1 | 0.00 | |
| f17 | Mean | 1.28 × 10−2 | 9.16 × 10−2 | 1.10 × 10−3 | 1.72e × 103 | 4.76 × 10−3 | 1.42 × 100 | 0.00 |
| SD | 1.27 × 10−2 | 1.36 × 10−1 | 1.75 × 10−3 | 8.97 × 101 | 6.39 × 10−3 | 5.93 × 10−1 | 0.00 | |
| SEM | 2.31 × 10−3 | 2.49 × 10−2 | 3.20 × 10−4 | 1.63 × 101 | 1.16 × 10−3 | 1.08 × 10−1 | 0.00 |
| Function | DE | PSO | ABC | IWO | FA | Jaya | CJaya-SQP | |
|---|---|---|---|---|---|---|---|---|
| f1 | MeanFEs | 74,322 | 66,373 | 43,039 | NaN | 12704 | NaN | 9.86 |
| SR (%) | 66.66 | 60 | 100 | 0 | 100 | 0 | 100 | |
| f2 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 12.5 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f3 | MeanFEs | NaN | NaN | NaN | NaN | 30140 | NaN | 14.3 |
| SR (%) | 0 | 0 | 0 | 0 | 100 | 0 | 100 | |
| f4 | MeanFEs | NaN | NaN | 76,290.91 | NaN | 21,966.67 | NaN | 1498.66 |
| SR (%) | 0 | 0 | 73.33 | 0 | 100 | 0 | 100 | |
| f5 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 55,755.38 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 86.66 | |
| f6 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 12.03 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f7 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 23.10 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f8 | MeanFEs | NaN | NaN | NaN | NaN | 26,793.33 | NaN | 31.16 |
| SR (%) | 0 | 0 | 0 | 0 | 20 | 0 | 100 | |
| f9 | MeanFEs | NaN | NaN | 79,240 | NaN | 19,405.71 | NaN | 24.53 |
| SR (%) | 0 | 0 | 3.33 | 0 | 70 | 0 | 100 | |
| f10 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 16.43 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f11 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 22.19 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f12 | MeanFEs | NaN | NaN | NaN | NaN | 32,870.67 | NaN | 1564 |
| SR (%) | 0 | 0 | 0 | 0 | 100 | 0 | 100 | |
| f13 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| f14 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 20.76 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f15 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 26.86 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f16 | MeanFEs | NaN | NaN | NaN | NaN | NaN | NaN | 33.73 |
| SR (%) | 0 | 0 | 0 | 0 | 0 | 0 | 100 | |
| f17 | MeanFEs | NaN | NaN | NaN | NaN | 19,456.47 | NaN | 29.36 |
| SR (%) | 0 | 0 | 0 | 0 | 56.66 | 0 | 100 |
| Test for Mean Solutions | Test for SEM Solutions | ||||||
|---|---|---|---|---|---|---|---|
| Algorithms | Friedman Value | Normalized Value | Rank | Algorithms | Friedman Value | Normalized Value | Rank |
| DE | 4.17 | 3.39 | 4 | DE | 4.58 | 3.91 | 5 |
| PSO | 3.52 | 2.86 | 3 | PSO | 3.58 | 3.05 | 3 |
| ABC | 4.35 | 3.53 | 5 | ABC | 3.82 | 3.26 | 4 |
| IWO | 5.70 | 4.63 | 6 | IWO | 5.05 | 4.31 | 6 |
| FA | 2.64 | 2.14 | 2 | FA | 3.35 | 2.86 | 2 |
| Jaya | 6.35 | 5.16 | 7 | Jaya | 6.41 | 5.47 | 7 |
| CJaya-SQP | 1.23 | 1.00 | 1 | CJaya-SQP | 1.17 | 1.00 | 1 |
| Eigenvalues | Frequency | Modes | Damping Ratio | Generators | State Variables | |
|---|---|---|---|---|---|---|
| 0.0720 ± j3.7192 | 0.5919 | Interarea | −0.0194 | 1.0000, 1.0000 | ||
| 0.6012, 0.6012 | ||||||
| 0.7181, 0.7181 | ||||||
| 0.7445, 0.7445 | ||||||
| −0.2166 ± j5.9569 | 0.9481 | Local | 0.0363 | 0.8053, 0.8053 | ||
| 1.0000, 1.0000 | ||||||
| 0.0316, 0.0316 | ||||||
| 0.0119, 0.0119 | ||||||
| −0.2161 ± j6.1273 | 0.9752 | Local | 0.0352 | 0.0145, 0.0145 | ||
| 0.0229, 0.0229 | ||||||
| 0.9941, 0.9941 | ||||||
| 1.0000, 1.0000 |
| Bus No. | Base Case | % Load Increase | ||||
|---|---|---|---|---|---|---|
| 10 | 15 | 20 | 25 | 30 | ||
| Bus 7 | 0.0038 | 0.0055 | 0.0064 | 0.0073 | 0.0081 | 0.0087 |
| Bus 8 | 0.0279 | 0.0390 | 0.0448 | 0.0509 | 0.0574 | 0.0646 |
| Uncoordinated Design | Coordinated Design | |||||||
|---|---|---|---|---|---|---|---|---|
| PSS-G1 | PSS-G2 | PSS-G4 | SVC | PSS-G1 | PSS-G2 | PSS-G4 | SVC | |
| K | 17.5059 | 28.0717 | 11.5571 | 33.3058 | 32.2919 | 30.2838 | 9.2705 | 11.6793 |
| T1 | 1.1324 | 1.1831 | 1.2220 | 0.1464 | 0.9337 | 0.7207 | 1.8364 | 1.3573 |
| T2 | 0.2664 | 0.6197 | 0.5310 | 0.8140 | 0.6893 | 0.5714 | 1.3917 | 0.9393 |
| T3 | 1.4371 | 1.1725 | 1.4376 | 1.6985 | 0.8732 | 1.5084 | 1.3293 | 1.0909 |
| T4 | 1.0159 | 1.3452 | 1.1442 | 1.2474 | 0.6431 | 0.6918 | 0.5001 | 1.3336 |
| Case | Eigenvalues | Damping Ratios |
|---|---|---|
| CJaya-SQP-PSSs | −2.7659 ± j7.7039 | 0.3379 |
| −2.1961 ± j1.8797 | 0.7597 | |
| −1.2187 ± j2.0866 | 0.5043 | |
| CJaya-SQP-SVC | 0.0731 ± j3.7180 | −0.0197 |
| −0.2164 ± j5.9569 | 0.0363 | |
| −0.2167 ± j6.1283 | 0.0353 | |
| CJaya-SQP-PSSs&SVC | −2.7881 ± j7.6715 | 0.3416 |
| −2.6014 ± j1.9392 | 0.8018 | |
| −2.0017 ± j3.2075 | 0.5294 |
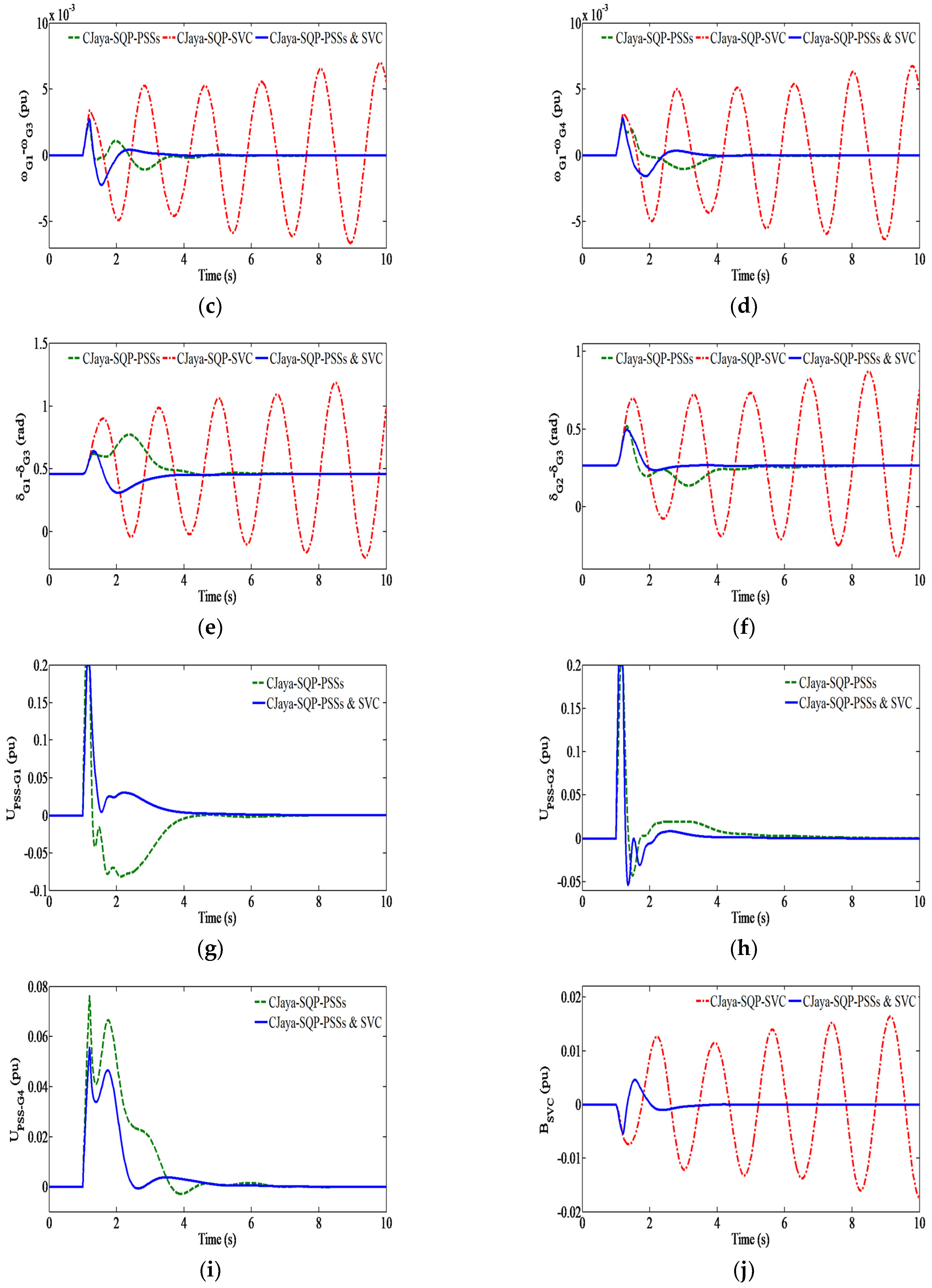
| Controller type | ITAE1 (tsim = 10 s) | ||||
|---|---|---|---|---|---|
| Scenario I | Scenario II | Scenario III | Scenario IV | Total | |
| CJaya-SQP-PSSs | 0.0141 | 0.0192 | 9.0501 | 3.9026 | 12.9860 |
| CJaya-SQP-SVC | 0.3100 | 0.6942 | 29.7768 | 19.3631 | 50.1441 |
| CJaya-SQP-PSSs&SVC | 0.0049 | 0.0122 | 0.0778 | 0.0988 | 0.1937 |
| Controller type | ITAE2 (tsim = 10 s) | ||||
|---|---|---|---|---|---|
| Scenario I | Scenario II | Scenario III | Scenario IV | Total | |
| CJaya-SQP-PSSs | 0.0064 | 0.0095 | 0.0698 | 0.4432 | 0.5289 |
| CJaya-SQP-SVC | 0.0286 | 0.0468 | 0.0941 | 0.9933 | 1.1628 |
| CJaya-SQP-PSSs&SVC | 0.0016 | 0.0040 | 0.0075 | 0.0097 | 0.0228 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Welhazi, Y.; Guesmi, T.; Alshammari, B.M.; Alqunun, K.; Alateeq, A.; Almalaq, Y.; Alsabhan, R.; Abdallah, H.H. A Novel Hybrid Chaotic Jaya and Sequential Quadratic Programming Method for Robust Design of Power System Stabilizers and Static VAR Compensator. Energies 2022, 15, 860. https://doi.org/10.3390/en15030860
Welhazi Y, Guesmi T, Alshammari BM, Alqunun K, Alateeq A, Almalaq Y, Alsabhan R, Abdallah HH. A Novel Hybrid Chaotic Jaya and Sequential Quadratic Programming Method for Robust Design of Power System Stabilizers and Static VAR Compensator. Energies. 2022; 15(3):860. https://doi.org/10.3390/en15030860
Chicago/Turabian StyleWelhazi, Yosra, Tawfik Guesmi, Badr M. Alshammari, Khalid Alqunun, Ayoob Alateeq, Yasser Almalaq, Robaya Alsabhan, and Hsan Hadj Abdallah. 2022. "A Novel Hybrid Chaotic Jaya and Sequential Quadratic Programming Method for Robust Design of Power System Stabilizers and Static VAR Compensator" Energies 15, no. 3: 860. https://doi.org/10.3390/en15030860
APA StyleWelhazi, Y., Guesmi, T., Alshammari, B. M., Alqunun, K., Alateeq, A., Almalaq, Y., Alsabhan, R., & Abdallah, H. H. (2022). A Novel Hybrid Chaotic Jaya and Sequential Quadratic Programming Method for Robust Design of Power System Stabilizers and Static VAR Compensator. Energies, 15(3), 860. https://doi.org/10.3390/en15030860








