A Polynomial Approximation to Self Consistent Solution for Schrödinger–Poisson Equations in Superlattice Structures

Abstract

The paper deals with a new approach to iterative solving the Schrödinger and Poisson equations in the first type of semiconductor superlattice. Assumptions of the transfer matrix method are incorporated into the approach, which allows to take into account the potential varying within each single layer of bias voltage superlattice. The key process of the method is to approximate the charge density and wave functions with polynomials. It allows to obtain semi-analytical solutions for the Schrödinger and Poisson equations, which in turn have significant impact on the accuracy and speed of superlattice simulations. The presented procedure is also suifihue for finding eigenstates extended over relatively large superlattice area, and it can be used as an effective pro-gram module for a superlattice finite model. The obtained quantum states are very similar to the Wannier-Stark functions, and they can serve as the base under non-equilibrium Green’s function formalism (NEGF). Exemplary results for Schrödinger and Poisson solutions for superlattices based on the GaAs/AlGaAs heterostructure are presented to prove all the above.

1. Introduction

Semiconductor superlattices (SL) are nanostructures whose properties were discovered in the 1970s [1], still the first real devices were produced twenty years later [2]. Currently, they are used for building quantum cascade lasers [3,4] which are used in several important industry sectors [5]. Due to the high complexity of the physical processes occurring in the SL structures, their computer simulations require either high computing power, or highly effective computational methods. Therefore, over the recent years, many numerical models have been developed for SL structures. In the simplest one [5,6,7,8] a constant potential and the effective mass of electrons in each layer of the structure are assumed. A popular approach to solving the Schrödinger equation in cascade struktures is provided by the rate equation method (RE) [9,10,11,12] where the boundary conditions in the form of hard walls at the edges of the structure composed of three consecutive periods of SL are assumed, and the solutions obtained for the central period are considered to be representative for the whole system. The Monte Carlo method (ME) [13,14,15], based on solving the Boltzman equation, is another approach. Non-equilibrium Green’s function formalism (NEGF) [16,17] however, is the approach that offers the most versatile opportunities for simulating superlattices. This approach relies on self-consistent solving of Dyson, Keldysh and selfenergy equations either in the real space (real space method—RSM) [18,19,20], or by means of the Wannier functions (Wannier function method—WFM) [21,22]. Under WFM infinite geometrical dimensions of the superlattice, and periodic delocalised Bloch functions over the whole structure are considered. To provide an alternative to such approaches we have built a finite model of the superlattice (FMSL) [23], where the base of the wave functions that is the solution to the Schrödinger equation for the SL model of finite geometrical dimensions is applied. Despite many studies on the semiconductor superlattices properties, conducted both from the empirical and theoretical perspective, many factors that influence the transport parameters of the devices based on such structures still remain unexplored. We believe them to be the ground for the observed discrepancies between the simulation results and measurements performed on real devices. Thus, the pressure to find new tools for studying SL properties under different conditions and fields is still considerable. The influence of finite geometrical sizes on the quantum phenomena occurring in these structures is one of many issues to be studied. Our FMSL [24] where the base of wave functions being the solution to the Schrödinger equation for the superlattice model with a finite geometry is applied, provides quite a suitable tool for such studies.

This paper presents new elements of the FMSL that allows quick studies on the influence of an unbalanced charge, and the voltage applied, on the tested device transport parameters, to be performed. Polynomials used to approximate the charge and potential distribution functions in a SL allow to obtain semi-analytical solutions for the Schrödinger and Poisson equations, where the variable potential in a single structure layer is taken into account without the necessity of dividing it into many sub-areas once the voltage to the system is applied. The presented method is effective in finding eigenstates extended over relatively large superlattice areas. The obtained quantum states are very similar to the Wannier-Stark functions and they can form the basis for the NEGF formalism. In order to confirm such a thesis, exemplary results for Schrödinger and Poisson solutions for superlattices based on GaAs/AlGaAs heterostructure are presented.

2. Formulation of the Problem

In most cases SL are simply stratified unipolar, n-type nanodevices [25]. Figure 1. shows an example of the AlGaAs-GaAs device presented in [26].

Hence, the electrons are subject to the quantum laws, i.e., under the Schrödinger equation with 1D Hamiltonian in the growth d(z) direction within the plane kinetic energy term ${\hslash }^2{k}^2/2m_e(z)$, where $k=\left|k\right|$ is the magnitude of the in-plane momentum k. In total, it can be written as

$$\left[\frac{-{\hslash }^2}{2}\frac{d^{}}{dz}\frac{1}{m_e(z)}\frac{d^{}}{d{z}^{}}+V(z)+\frac{{\hslash }^2{k}^2}{m_e(z)}\right] \Psi (z)=E\Psi (z)$$

(1)

where Ψ(z) are envelope functions, m_e(z) is the effective mass constant within each semiconductor layer, whereas V(z) is a spatially dependent total potential energy which can be written as

V(z) = V_SL(z) + V_B(z) + V_S(z)

(2)

where V_SL(z) represents the superlattice potential, V_B(z) is the potential from the applied voltage, and V_S(z) denotes the potential derived from impurities and unbalanced charge carriers.

The numerical model of SL presented so far [23,24] have some problems. It consists in the necessity to divide the superlattice layers into many sub-areas with a constant potential (see Figure 2A). In the case of an applied voltage this significantly increases the Hamiltonian device matrix in size. The previous model also does not allow for the consideration of an unbalanced charge. In the present work we propose a solution to these problems by using a polynomial approximation of the potential (see Figure 2B) and then to the charge distribution in the whole SL structure.

Many previous calculations (e.g., [27,28]) have shown, that in SL the conduction band is divided into minibands. With the wave functions in the above-mentioned minibands known, it is possible to determine the electron charge distribution within the SL as

$$n(z)={\displaystyle \sum _i{n}_i{\left|{\psi }_i(z)\right|}^2}$$

(3)

where n_i describes the electrons concentration in the miniband i according to

$$n_i=\frac{m}{\pi {\hslash }^2}{\displaystyle \sum _i{\displaystyle \underset{E_i}{\overset{\infty }{\int }}\frac{dE}{\exp \left[\left(E-E_F\right)/k_{B}T\right]+1}}},$$

(4)

The total charge distribution can be written as

ρ(z)= e[n(z)−N_D(z)],

(5)

where N_D is the donor dopant concentration. The charge ρ(z) generates a potential consistent with the Poisson equation

$$\frac{\mathrm{d}}{\mathrm{d}z}\epsilon (z)\frac{\mathrm{d}{V}_{\mathrm{S}}(z)}{\mathrm{d}z}=-e\rho (z),$$

(6)

where ε is dielectric function. On the border of each layer of the structure, the potential must meet the continuity conditions

$$V_j\left(z_{j+1}\right)=V_{j+1}\left(z_{j+1}\right)$$

(7)

$${\epsilon }_j{\left.\frac{\mathrm{d}{V}_j}{\mathrm{d}z}\right|}_{z_{j+1}}={\left.{\epsilon }_{j+1}\frac{\mathrm{d}{V}_{j+1}}{\mathrm{d}z}\right|}_{z_{j+1}}$$

(8)

where z_j represents the coordinate of the beginning of the j-th SL layer (see Figure 1), while V is the function of the potential within this layer. The same conditions are fulfilled by the wave function

$${\psi }_j\left(z_{j+1}\right)={\psi }_{j+1}\left(z_{j+1}\right)$$

(9)

$$m_e{}_j{\left.\frac{\mathrm{d}{\psi }_j}{\mathrm{d}z}\right|}_{z_{j+1}}={\left.m_e{}_{j+1}\frac{\mathrm{d}{\psi }_{j+1}}{\mathrm{d}z}\right|}_{z_{j+1}}$$

(10)

In addition, the boundary conditions at the beginning and the end of the structure need to be considered. In our model (see Figure 1) they correspond to the source and the drain, respectively. For the potential function such conditions result from the applied voltage U and it can be written as

$$V_1\left(z_1\right)-V_L\left(z_{L+1}\right)=U,$$

(11)

For the wave function, the conditions correspond to the amplitudes of waves coming from the source and drain, and generally it can be formulated differently [26]. All in all, the problem is to determine three coupled fields V, Ψ, and ρ, described by Equations (1)–(6), under boundary conditions (7)–(11).

3. The Main Algorithm of Calculations

The solution of the problem formulated in the previous section requires the fields V, Ψ, ρ, to be self-consistent, which is achievable by calculations with an iterative algorithm applied. The first step is to find the energies and eigenfunctions of the Equation (1) for the V_SL and the V_B potentials. For V_B = 0, the solution of the Equation (1) can be presented as a linear combination of elementary functions, namely plane waves running opposite each other. The standard TMF method is convenient for determining their amplitudes. Incorporating in the next iteration steps the potential of V_B, as well as the potential of V_S, the solutions to Equation (1) are no longer possible to be presented as elementary functions. Hence, we propose to use solution to the Equation (1) in the form of power series. Such a representation can be obtained analytically, for the potential expressed as a polynomial, or generally, as a power series. By Equation (6) the charge density function takes an analogous form. Therefore, it is suggested to approximate the charge density function with a polynomial, separately for each of the layers, at each step of the calculation procedure, following the solution of Equation (1) and by applying (3)–(5).

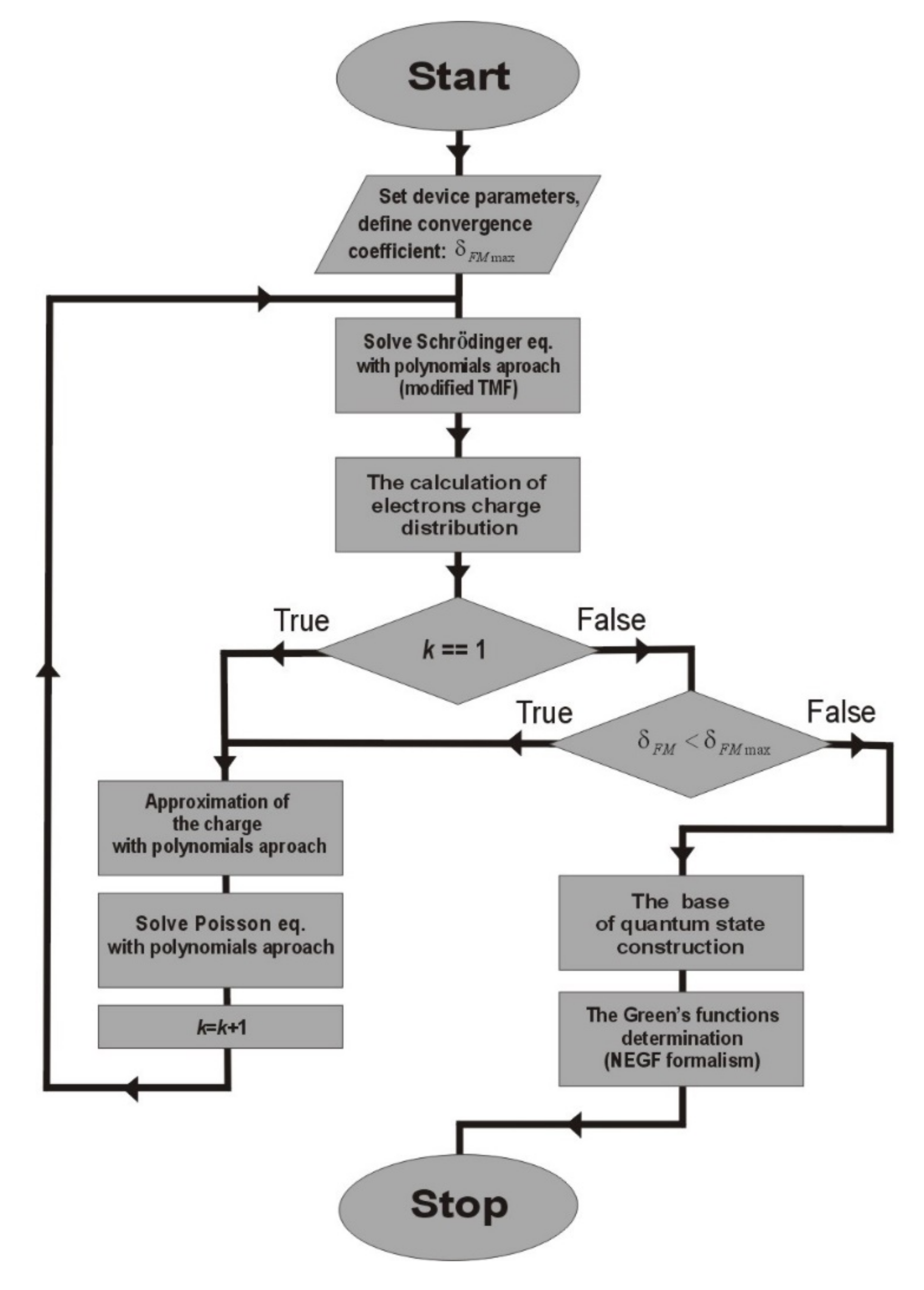
The main algorithm of the method under consideration is shown in Figure 3.

One of the basic input parameters is the convergence coefficient defined as

$${\delta }_{FM}=\sqrt{\frac{{{\displaystyle \int \left({\rho }_k-{\rho }_{k-1}\right)}}^{2}dz}{{\displaystyle \int {\rho }_k^{2}dz}}}·100\%$$

(12)

where ρ_k represents the electron charge density for the kth iteration. The algorithm runs a loop for δ > δ_{FM max}. The next programmed operation involves applying the computed wave functions for constructing the quantum states base, to be used in NEGF procedures.

It is worth noting that the self-consistent method for solving the Poisson and Schrödinger equations with the presented algorithm is less complex than the algorithm presented earlier [29], where repeated running of the NEGF blocks have been required that engaged most of the computing power.

The algorithm proposed under the paper significantly speeds up the simulation process and provides an important element of an effective SL model. A detailed description of each of its elements is provided in the following sections.

4. Solving the Schrödinger Equation

The main task of the procedure described above is to find, separately for each layer of the structure, a general solution to Equation (1) with a given potential in the polynomial form

$$V_j\left(z\right)={\displaystyle \sum _{k=0}^M{b}_{j,k}{\left(z-z_j\right)}^k},$$

(13)

For this purpose, it is advisable to write Equation (1) in dimensionless form, which is obtained by introducing dimensionless variables

$$u_j=\frac{\sqrt{2m_{\mathrm{e}}{}_{j}eE}}{\hslash }\left(z-z_j\right)$$

(14)

and

$$W_j\left(u\right)=\frac{V_j\left(z\right)}{E}$$

(15)

For quantities defined his way, Equation (1) takes the form

$$\frac{{\partial }^2\psi }{\partial u_{}^2}+\left[1-W_j\left(u\right)\right] \psi \left(u\right)=0,$$

(16)

where

$$W_j\left(u\right)={\displaystyle \sum _{k=0}^M{d}_{j,k}{u}_{}^k},\hspace{1em}{d}_{j,k}=\frac{b_{j,k}}{E{\sigma }_j^k},\hspace{1em}{\sigma }_j=\frac{\sqrt{2m_{\mathrm{e}}{}_{j}eE}}{\hslash }$$

(17)

Solution of Equation (16) can be also represented as a power series

$$\psi \left(u\right)={\displaystyle \sum _{n=0}^{\infty }{c}_n{u}^n}.$$

(18)

Substituting (17) and (18) to (16) a recursive relationship of the coefficients c_j,n is obtained

$$c_{j,n}=\frac{1}{n(n-1)}\left[\left(d_{j,0}-1\right) c_{j,n-2}+{\displaystyle \sum _{k=1}^{\max \left(M,n-2\right)}{d}_{j,k}{c}_{j,n-k-2}}\right], \mathrm{dla} n>1,$$

(19)

The coefficients c_j,0 and c_j,1 can be assumed arbitrarily, instead of adopting specific numerical values, which allows to obtain different pairs of independent solutions to Equation (16). For further analysis, a pair of functions $F_j^{\mathrm{I}}\left(u\right)$, and $F_j^{\mathrm{II}}\left(u\right)$ defined by dependencies (18), (19)

$$c_{j,0}=1,c_{j,1}=\mathrm{i}\sqrt{1-d_{j,0}}, \mathrm{for} F_j^{\mathrm{I}}\left(u\right)$$

(20)

and

$$c_{j,0}=1,c_{j,1}=-\mathrm{i}\sqrt{1-d_{j,0}}, \mathrm{for} F_j^{\mathrm{II}}\left(u\right)$$

(21)

where $\mathrm{i}=\sqrt{-1}$ are applied. By this choice, compliance with the solutions representing counter-rotating waves is achieved for W_j(u) = const = d_j,0, i.e., $F_j^{\mathrm{I}}\left(u\right)=\exp \left(\mathrm{i}\sqrt{1-d_{j,0}}u\right)$, $F_j^{\mathrm{II}}\left(u\right)=\exp \left(-\mathrm{i}\sqrt{1-d_{j,0}}u\right)$. The general solution of Equation (16) is presented as

$$\psi \left(u\right)=C^{\mathrm{I}}{F}^{\mathrm{I}}\left(u\right)+C^{\mathrm{II}}{F}^{\mathrm{II}}\left(u\right).$$

(22)

Under continuity conditions (9), (10) we get the following dependencies

$$C_{j+1}^{\mathrm{I}}+C_{j+1}^{\mathrm{II}}=C_j^{\mathrm{I}}{D}_j^{\mathrm{I}}+C_j^{\mathrm{II}}{D}_j^{\mathrm{II}},$$

(23)

$$C_{j+1}^{\mathrm{I}}-C_{j+1}^{\mathrm{II}}=C_j^{\mathrm{I}}{\beta }_j{G}_j^{\mathrm{I}}+C_j^{\mathrm{II}}{\beta }_j{G}_j^{\mathrm{II}},$$

(24)

where

$$D_j^K=F_j^K\left({\sigma }_j{s}_j\right), s_j=z_{j+1}-z_j, {\beta }_j=-\mathrm{i}\frac{m_{j+1}{\sigma }_j}{m_j{\sigma }_{j+1}}$$

(25)

and

$$G_j^K={\left.\frac{\mathrm{d}{F}_j^K}{\mathrm{d}u}\right|}_{u={\sigma }_j{s}_j}={\displaystyle \sum _{n=1}^{\infty }n{c}_n{\left({\sigma }_j{s}_j\right)}^{n-1}},K=\mathrm{I}, \mathrm{II}.$$

(26)

The Equations (23) and (24) can be transformed with the matrix notation

$$\left[\begin{array}{c}{C}_{j+1}^{\mathrm{I}}\\ C_{j+1}^{\mathrm{II}}\end{array}\right]=M_j\left[\begin{array}{c}{C}_j^{\mathrm{I}}\\ C_j^{\mathrm{II}}\end{array}\right],$$

(27)

where

$$M_j=\frac{1}{2}\left[\begin{array}{cc}{D}_j^{\mathrm{I}}+{\beta }_j{G}_j^{\mathrm{I}}& D_j^{\mathrm{II}}+{\beta }_j{G}_j^{\mathrm{II}}\\ D_j^{\mathrm{I}}-{\beta }_j{G}_j^{\mathrm{I}}& D_j^{\mathrm{II}}-{\beta }_j{G}_j^{\mathrm{II}}\end{array}\right]$$

(28)

is the state-transition matrix for j- layer of the structure. By using (27) we get

$$\left[\begin{array}{c}{C}_{L+1}^{\mathrm{I}}\\ C_{L+1}^{\mathrm{II}}\end{array}\right]=M\left[\begin{array}{c}{C}_0^{\mathrm{I}}\\ C_0^{\mathrm{II}}\end{array}\right]’$$

(29)

where

$$M={\displaystyle \prod _{j=L}^{j=0}{M}_j}$$

(30)

is the state-transition matrix for whole structure. In the Equation (29) the constants $C_0^{\mathrm{I}}$ and $C_{L+1}^{\mathrm{II}}$ are the amplitudes of incident waves from the source and drain respectively. According to the assumption $C_0^{\mathrm{I}}=0$, $C_{L+1}^{\mathrm{II}}=0$, by substituting to (30) we arrive at

$$C_{L+1}^{\mathrm{I}}=m_{1,2}{C}_0^{\mathrm{II}},$$

(31)

$$m_{2,2}=0$$

(32)

where $m_{1,2}$ and $m_{2,2}$ are the elements of the matrix M. By solving Equation (32), numerically we obtain the set of eigenenergies of the system under analysis.

5. Solving the Poisson Equation

According to the assumptions, the right side of the Equation (5) is approximated in the j-th superlattice layer by an N-degree polynomial

$${\rho }_j\left(z\right)={\displaystyle \sum _{k=0}^N{a}_{j,k}{\left(z-z_j\right)}^k}.$$

(33)

The approximation procedure consists in comparing the charge density function calculated in the previous iteration step with the function described by Equation (33) at N + 1 selected points (nodes) of each structure layer. This leads to the algebraic systems of equations of N + 1 degree, by solving which, the values of the coefficients a_j,k are obtained. Substituting (33) to (6), and following double integration, we get

$$V_{\mathrm{S}}{}_j\left(z\right)={\displaystyle \sum _{k=0}^{N+2}{b}_{j,k}^{*}{\left(z-z_j\right)}^k},$$

(34)

where

$$b_{j,k+2}^{*}=\frac{a_{j,k}}{\left(k+1\right)\left(k+2\right){\epsilon }_j}.$$

(35)

Comparing (33) with (12) we get M = N + 2; moreover $b_{j,0}^{*}=b_{j,0}^{}+V_{\mathrm{SL},j}$, $b_{j,1}^{*}=b_{j,1}^{}-U/d$, $b_{j,k}^{*}=b_{j,k}^{}$ for k > 1. Undetermined coefficient values b_j,0, and b_j,1 under Equation (34) can be found by applying the boundary conditions (7), (8), i.e.,

$$b_{j+1,0}=b_{j,0}+b_{j,1}{s}_j+{\displaystyle \sum _{k=2}^{N+2}{b}_{j,k}{s}_j{}^k},$$

(36)

$$b_{j+1,1}=\frac{{\epsilon }_j}{{\epsilon }_{j+1}}\left(b_{j,1}+{\displaystyle \sum _{k=2}^{N+2}k{b}_{j,k}{s}_j{}^{k-1}}\right),$$

(37)

Equations (36) and (37) can be written in matrix form

$$\left[\begin{array}{c}{b}_{j+1,0}^{}\\ b_{j+1,1}^{}\end{array}\right]=\left[\begin{array}{cc}1& s_j\\ 0& {\eta }_j\end{array}\right]\left[\begin{array}{c}{b}_{j,0}^{}\\ b_{j,1}^{}\end{array}\right]+\left[\begin{array}{c}{B}_j^{}\\ {\eta }_j{B^{\prime }}_j^{}\end{array}\right],$$

(38)

where

$${\eta }_j=\frac{{\epsilon }_j}{{\epsilon }_{j+1}},$$

(39)

$$B_j={\displaystyle \sum _{k=2}^{N+2}{b}_{j,k}{s}_j{}^k},$$

(40)

$${B^{\prime }}_j={\displaystyle \sum _{k=2}^{N+2}k{b}_{j,k}{s}_j{}^{k-1}}.$$

(41)

Equation (38) allows coefficients b_j,0 and b_j,1 in the subsequent layers to be calculated recursively and along with (34) it is possible to determine the full potential distribution within the superlattice structure. The coefficient values for the first layer (b_1,0 and b_1,1) should be determined from the condition (11). For this purpose, it is necessary to link them with the coefficients of the last layer (b_L,0, b_L,1). Using (38) we get

$$\left[\begin{array}{c}{b}_{L,0}^{}\\ b_{L,1}^{}\end{array}\right]=A\left[\begin{array}{c}{b}_{1,0}^{}\\ b_{1,1}^{}\end{array}\right]+P,$$

(42)

where

$$A={\displaystyle \prod _{j=L-1}^{j=1}{A}_j},$$

(43)

with

$$A_j=\left[\begin{array}{cc}1& s_j\\ 0& {\eta }_j\end{array}\right],$$

(44)

Matrix P in (42) is written:

$$P={\displaystyle \sum _{i=1}^{L-2}\left({\displaystyle \prod _{j=L-1}^{j=i+1}{A}_j}\right)T_i}+T_{L-1},$$

(45)

where

$$T_j=\left[\begin{array}{c}{B}_j^{}\\ {\eta }_j{B^{\prime }}_j^{}\end{array}\right].$$

(46)

Using (11), (34) and (38) we get

$$b_{1,0}=0,$$

(47)

$$b_{1,1}=-\frac{\left(a_{1,1}+a_{2,1}{s}_L\right) U+p_1+p_2{s}_L+B_L}{a_{1,2}+a_{2,2}{s}_L}$$

(48)

As we can see, the proposed method for determining the potential distribution within the superlattice consist mainly in performing multiplying and adding operations on 2-rank matrices, which highly speeds up calculations.

6. NEGF Modelling of Superlattice Structure

The FMSL under the paper incorporated the NEGF formalism into calculating transport parameters. As a part of the NEGF procedure, the Dyson and Keldysh equations are solved to determine the retarted Green’s (G^R) and correlation (G^<) functions, respectively. the model described here has an implemented procedure for calculating Green’s function based on the WFM method [29] where we solve Dyson equation in the form

$$(E I-H-{\Sigma }^R)G^R=I,$$

(49)

where H is the Hamiltonian of the device, $G^R$ is the matrix of the retarded Green’s functions and Σ^R is the matrix of self energies. The Keldysh equation takes the form

$$G^{<}=G^R {\Sigma }^{<} G^R{}^{†}$$

(50)

where $G^{<}$ is the matrix of non-equilibrium Green functions, also called density or correlation functions. The elements of the self energy matrices (Σ^< and Σ^R) are found in the procedure of solving self-consistent solution equations together with the matrix elements G^< and G^R, respectively for the considered electron scattering mechanisms. This allows to determine transport parameters of the tested device, such as the density of state (DOS) [23].

$$N\left(E,k_{\left|\right|}\right)=-\frac{1}{\pi }\mathrm{Im}\left\{ G^R\left(E,k_{\left|\right|}\right) \right\},$$

(51)

and electron density

$$n\left(E,k_{\left|\right|}\right)=\frac{2}{\pi }\mathrm{Im}\left\{ G^{<}\left(E,k_{\left|\right|}\right) \right\},$$

(52)

Transport parameters under this study were calculated with a module into which the Büttiker probes had been implemented [25]. It is a well known approach to solving Equations (49) and (50), the essence of which is the exchange of electrons between each quantum state of the active device and the virtual electrode attached to it (a Büttiker probe) containing the electron reservoir. As the result, self-consistent Fermi levels for the quantum and electrochemical state of the electrode are attained. It allows to determine the occupation of states in a wide energy range. It is also worth noting that such a method for determining Green’s function is very effective, as shown in our earlier paper [28].

Under another research [29], we found that the calculation speed can be significantly reduced when the approach with the WFM method is applied, according to which the Hamiltonian matrix is written as a sum, $H=H_0+H_R$ with the matrix $H_0$ representing the sum of states for the non-polarized ($H_{SL}$) and polarized ($H_{\xi }$) superlattice, and the matrix $H_R$ containing all electron scattering effects. Detailed definitions of all of the above Hamiltonian matrices are given in our previous papers [29,30] whereas this article has been focused on one of them only, related to the applied voltage, which appears in the form

$$H_{\xi }={\displaystyle \sum _{n,\nu }{\displaystyle \sum _k\left\{\begin{array}{l}-e\xi R_0^{\mu \nu }{\stackrel{⌢}{a}}_{\mathrm{n},k}^{\nu †}{\stackrel{⌢}{a}}_{\mathrm{n},k}^{\nu }-ne\xi d{\delta }_{\mu \nu }{\stackrel{⌢}{a}}_{\mathrm{n},k}^{\nu †}{\stackrel{⌢}{a}}_{\mathrm{n},k}^{\nu }-\\ +e\xi R_1^{\mu \nu }\left[{\stackrel{⌢}{a}}_{\mathrm{n}+1,k}^{\nu †}{\stackrel{⌢}{a}}_{\mathrm{n},k}^{\nu }+{\stackrel{⌢}{a}}_{\mathrm{n}-1,k}^{\nu †}{\stackrel{⌢}{a}}_{\mathrm{n},k}^{\nu }\right]\end{array}\right\}}},$$

(53)

where e is the electron charge, ξ is the electric field, n stands for the number of the considered superlattice period of length—d, k is the wave vector, and the parameters ${\stackrel{⌢}{a}}_{\mathrm{n},k}^{\nu †}$ and ${\stackrel{⌢}{a}}_{\mathrm{n},k}^{\nu }$ are state operators, namely creation and annihilation of the ν state, respectively. The variable $R_l^{\mu \nu }$ included in the definition (51) calculated as

$$R_l^{\mu \nu }={\displaystyle \int dz} W_{}^{\mu *}(z-ld)z{W}_{}^{\nu }(z),$$

(54)

is called overlapping states integral. The interaction between the minibands (indices μ, ν) and the superlattice periods (index l) are taken into account by this relation. Under IMS model [28] the W (z) functions correspond to the Wannier and Wannier-Stark basis for unpolarised and polarised superlattice structures, respectively, whereas under the FMS model they correspond to the constructed quantum states described elsewhere [23]. Under this paper, we use the base of eigenstates that was created by solving the Schrödinger equation on the basis of the procedure presented elsewhere [23].

7. Simulations Results

The correctness and effectiveness of the developed numerical method has been checked by simulating typical superlattice structures whose parameters are widely available elsewhere [26,28] that for the purpose of this paper are called structure 1 and structure 2, respectively. They are presented in

Table 1. Basic parameters of simulated superlattice structures; structure 1 is presented in [28], and structure 2 reported in [26].

Number of Structure	Materials of Heterostructures	The Dimensions of the Structures (Barriers are Denoted in Bold) [nm]	ΔEc [eV]
1.	AlGaAs/GaAs	6.5, 2.5	0.22
2.		7.8, 2.4, 6.4, 3.8, 14.8, 2.4, 9.4, 5.4	0.15

.

An important part of numerical research was concerned with assessing the impact of the SL geometrical sizes on the quantum states properties. The results of the research in this area are illustrated in Figure 4. The energy eigenvalues distributions calculated with the FMSL are clearly dependent on the number of the superlattice periods considered. Picture (A) presents the results for a simple symmetrical superlattice that consists of one well and one barrier in the period (structure 1), while picture (B) displays the eigenvalues of energy for a typical terahertz laser structure (structure 2). The results show a general tendency for the energy eigenvalues to group within the minibands. The minibands boundaries are defined by the number of SL periods. This is very clearly seen in the graphs presented in Figure 4A, thought it is less clearly pronounced in Figure 4B, due to the very narrow minibands for this SL.

It is also worth noting that the eigenstates located near the upper edge of the minibands exceed the energy barrier levels (ΔE_C) already for 4 periods for structure 1, and 8 periods for structure 2. When these states are occupied by electrons, it may have a significant impact on transport.

In Figure 4. it can also be observed that the greater number of the periods considered in the calculations, the more precisely the minibands edges are determined. It indicates the necessity of considering the greatest possible number of SL periods in simulations. Regretfully, it practically brings very high load to calculating machines, as well as decreases simulations efficiency.

Therefore, a question arises on the SL periods number to be taken into account in simulations that would give the exact results for the miniband distribution, without the efficiency loss for calculating SL parameters. A comparison of the presented results with the results obtained by means of IMSL may provide an answer. To compare we used the coefficient defined as

$${\Delta }_{IM->FM}=\frac{{\delta }_{IM}^{\upsilon }-{\delta }_{FM}^{\upsilon }}{{\delta }_{IM}^{\upsilon }}·100\%,$$

(55)

where ${\delta }_{IM}^{\upsilon }$—is the value of the parameter for the υ - miniband calculated using the IMSL, while ${\delta }_{FM}^{\upsilon }$ it is the value of the same parameter determined by using of the FMSL.

From important parameters that characterize superlattices the minibands width (ΔE) and the location of the miniband centers energy (E_center) were selected to compare both models. Then the values were determined for each miniband of the considered structure, and their dependence on the number of SL periods with the FSML model, and compared to the results obtained with IMSL. The results are illustrated in Figure 5. Both models were found to converge nicely for simulations with 40 SL periods taken into account under FMSL. The differences increased to less than 1%, and to 0.1% for the width of the minibands (ΔE) and the position of their centers (E_center), respectively. It was observed for both simulated structures. It is worth noting here that the obtained results are also consistent with the results published in [29]. In addition practical implementations for structure 1 contain several hundred periods, whereas for structure 2 the number of periods to be considered is equal to 190 [26]. Hence, any errors due to assumed infinite sizes in IMSL seem negligible.

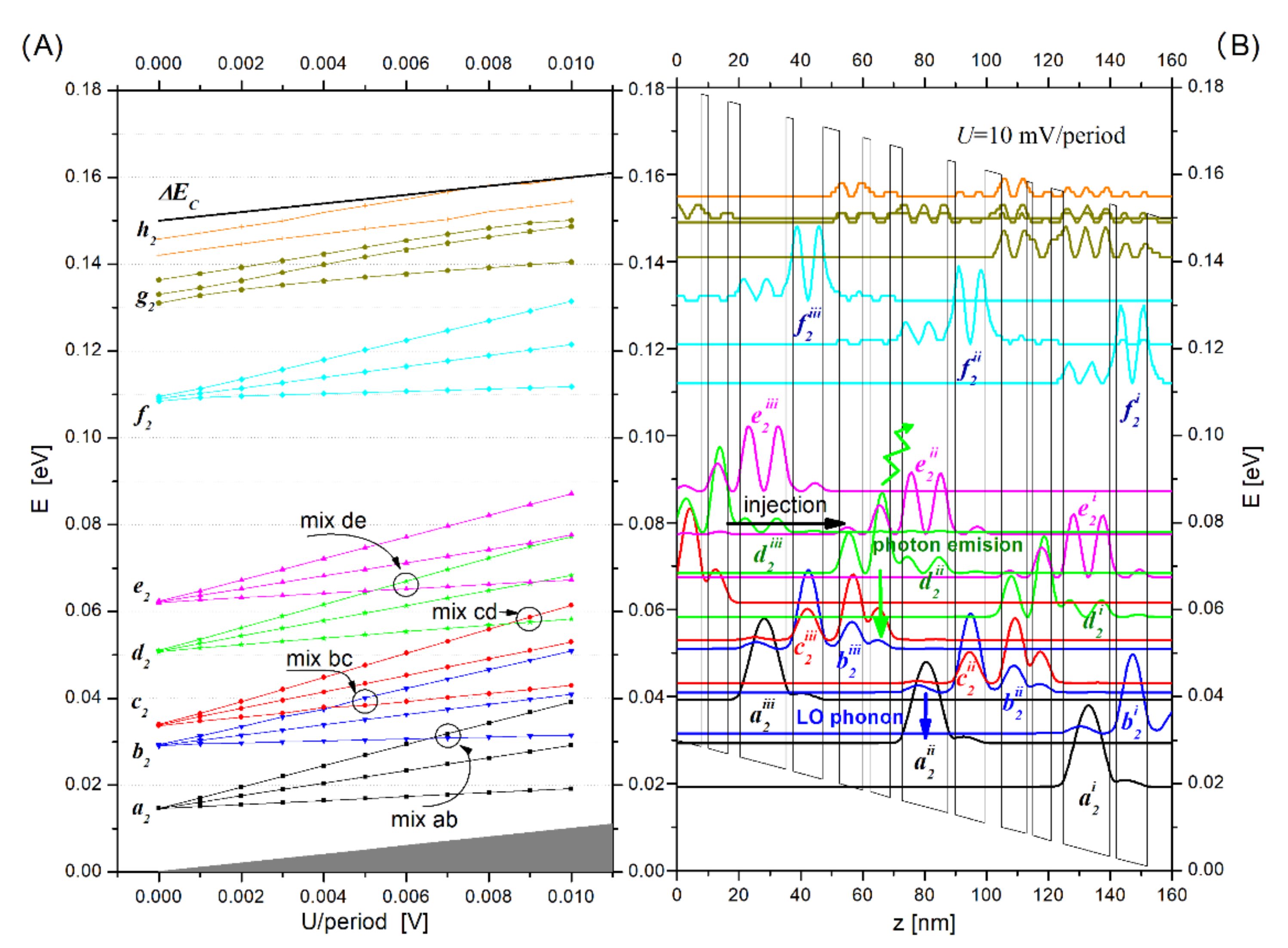
On the other hand, it can be also argued that slight differences observed in the results are encouraging with regards to applying the FMSL to a greater extent than it has been practiced so far. It is clear that the developed method allows to engage the structure bias voltage directly in the process of solving the Schrödinger and Poisson equations. The calculations showing the results are presented in Figure 6A shows the bias voltage influence on the eigenenergy distribution for the structure 2, calculated by means of the FMSL. The effect of so-called mixing eigenstates from different minibands can be observed. For example, from the voltage of 5 mV/period, the energy for the highest state of miniband b₂ is greater than the lowest state of miniband c₂ (mix bc). From the voltage of 6 mV/period, it can be seen that the highest state of the d₂ miniband occupies a higher energy level than the lowest state of the e₂ miniband (mix de). For another case, the energy of the highest state of miniband a₂ is greater than for the lowest state of miniband b₂ (mix ab) already from the voltage of 7 mV/period, and from the voltage of 9 mV/period, the energy for the highest state of miniband c₂ is greater than the lowest level of miniband d₂ (mix ab). All the cases can result in the interband transitions combined with tunneling effects through the potential barriers. These are the electronic transport features characteristic for this type of SL structures.

Potential occurrences of such quantum effects are illustrated with Figure 6B, where we can see the wave functions (modules squared) for the bias voltage of 10 mV/period applied to the structure.

Mixed quantum states with similar eigenvalues, for example $d_2^{iii}$ and $e_2^{ii}$, drawn in green and pink, respectively, located in adjacent quantum wells separated by narrow potential barriers are found there. It enables the electron tunnel transport in the local area of the superlattice, even as far as to the next period, to the energy level from the higher mini-band. This is a process known as charge carrier injection. In the next stage, electrons from a higher energy level due to local inversion of occupations can be subject to a coherent transition to the average level (for example $d_2^{ii}\to c_2^{ii}$) emitting a photon with an energy characteristic for the simulated structure (here 14 meV). Vertical transitions incoherent between quantum states emitting LO phonons with the energy of 37.5 meV, such as transitions $b_2^{ii}\to a_2^{ii}$, are also possible, with appropriately biased voltage. Such processes result in a electron cascade flux transporting the charge along the superlattice structure, and they provide the basis for cascade lasers operation. However, the precise conditions for such transport can be established only following the NEGF formalism.

In order to perform such calculations, a base of quantum states adequate to the current bias voltage should be constructed and applied to creating the tested device Hamiltonian matrix (51), which comprises the input data of the program block calculating Green’s functions. Calculations results for several various quantum states bases are known [31,32] and they can serve as the bases for positional quantum states, the quantum states Wannier functions, or the Wannier - Stark functions. So far all the models developed by our team have applied the Wannier and Wannier-Stark base for the IMSL [29], and the base of quantum states defined for the FMSL [23]. The disadvantage of the latter is that the quantum states representing individual minibands are not localized within one SL period. It implies the necessity of including at least five structure periods in the tested device Hamiltonian matrix, while in the IMSL only three structure periods are required for the same purpose. In the approach under the paper, all the obtained quantum states are very well localized within a single SL period, as is the case with the base of quantum states of the IMSL. Hence, the size of the Hamiltonian matrix can be limited to 3 SL periods, as in the IMSL.

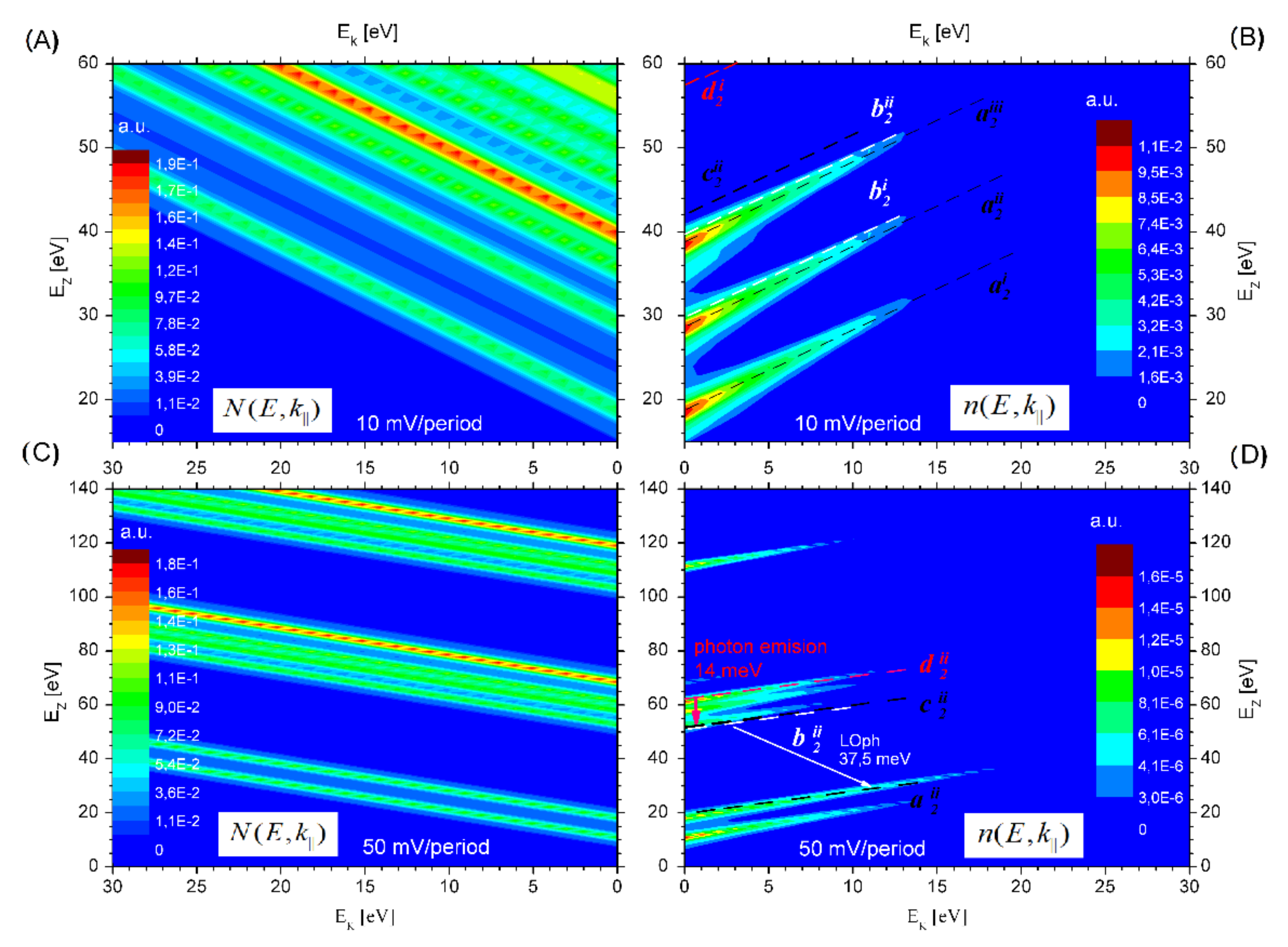
With the quantum states base shown in Figure 6 and the size of the Hamiltonian matrix limited to three SL periods, the transport parameters for structure 2 are simulated and selected examples of the results are shown in Figure 7.

Maps of DOS ($N(E,k_{\left|\right|})$) and occupation by electrons ($n(E,k_{\left|\right|})$) functions in the energy space of the wave vector k are also presented. The calculations run at the assumed temperature T = 77 K. The graphs (A) and (B) were made for the bias voltage of U = 10 mV/period, while the graphs (C) and (D) are related to the voltage U = 50 mV/period. By analyzing the results, it can be concluded that for a small voltage applied to the structure (10 mV/period) we observe a high density of states in the energy range corresponding to their eigen energies (see Figure 6B). Electrons occupy only the lowest states ($a_2^{}$ and $b_2^{}$) and there is no visible inversion of occupations opening the possibility for photons emission (transitions $d_2^{}\to c_2^{}$), or phonons (transitions $d_2^{}\to a_2^{}$). The situation is different for the superlattice biased with voltage of 50 mV/period (see Figure 7D). The higher energy states (e.g., $d_2^{ii}$) show then a greater occupation than the mid-states ($b_2^{ii}$), so electronic transitions emitting photons with an energy of 14 meV may occur. Additionally, transitions in the k-vector space emitting optical phonons with an energy of 37.5 meV are also likely to occur. More detailed research with NEGF applied in this area was published earlier [23,29].

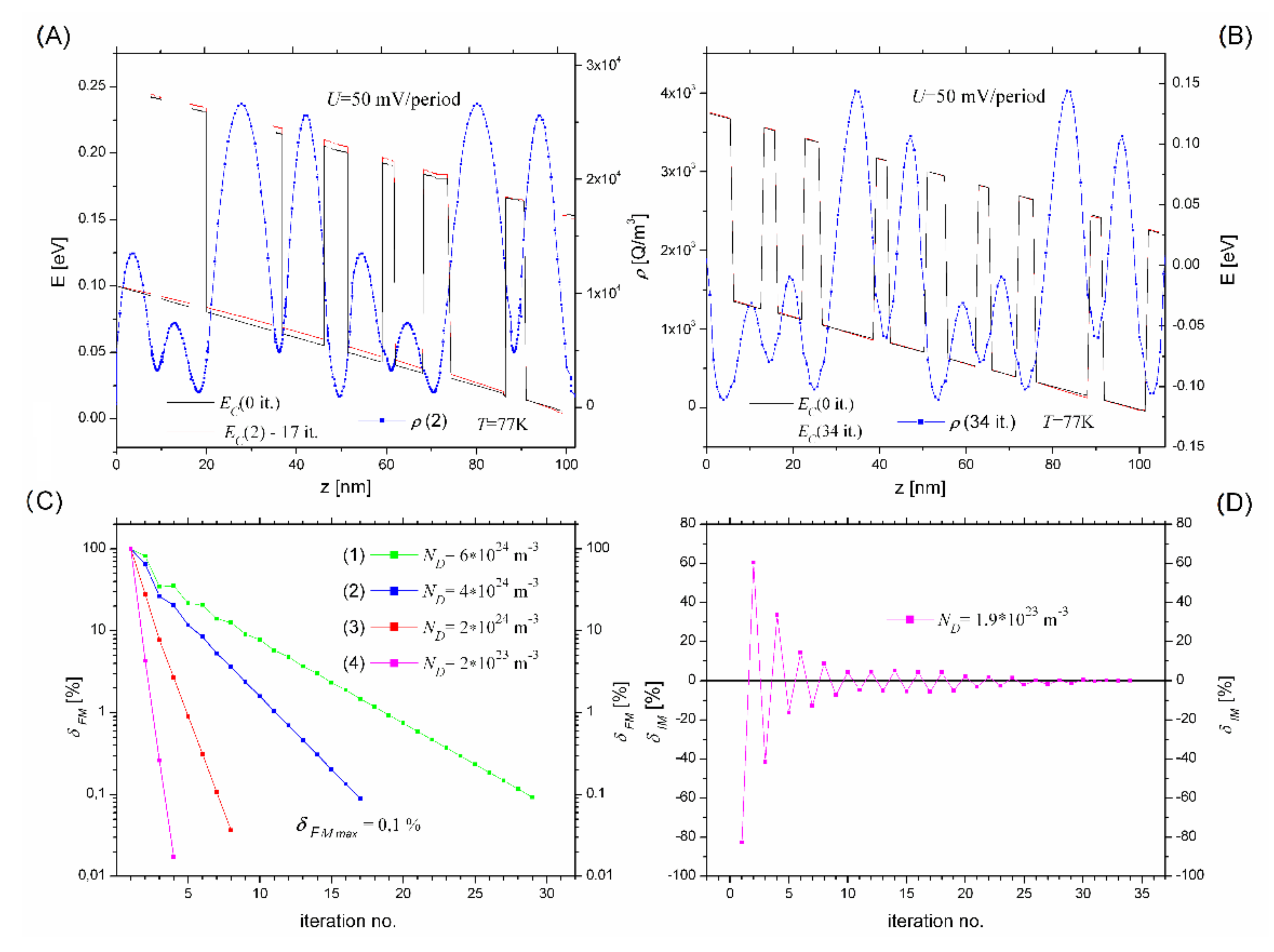
This article has been aimed at testing the correctness of a newly developed computational module, whose main task is to effectively find self-consistent potential and charge in a biased voltage SL structure. For this purpose, simulations for typical SL structures were carried out, the results of which are presented in Figure 8A shows the results of a self-consistent solution for the Schrödinger and Poisson equations with regards to potential and total charge distributions in the structure 2 with a bias voltage at 50 mV/period; the structure has been doped at N_D = 4 × 10²⁴ m⁻³. Graph (C) shows convergence of the method for different doping levels, i.e., δ_FM coefficient (see Equation (12)) versus the iteration number dependencies.

The convergence of the method was tested in a relatively wide range of impurity concentrations, namely from N_D = 2 × 10²³ m⁻³ to N_D = 6 × 10²⁴ m⁻³. The results prove the method to be quickly convergent and to require a maximum of 30 iterations, with the minimum charge change of δ _FMmax < 0.1% assumed. Simulations for the same structure with the input parameter defined with the Newton-Rapson method [33] were performed for comparison purposes. The results are represented by charts (B) and (D). Chart (B) presents the potential energy E_C distributions and the total charge ρ(z) for the polarized structure, doped at the level of N_D = 1.9 × 10²³ m⁻³, while graph (D) displays the dependence between δ_IM coefficient and the number of iterations. The convergence coefficient δ_IM is calculated from

$${\delta }_{IM}=\frac{\delta V_k-\delta V_{\max }}{\delta V_{\max }}·100\%$$

(56)

where k is the iteration number, $\delta V_{\max }$ stands for the input parameter assumed at 10⁻⁴ V, and $\delta V$ denotes the potential correction calculated according to the procedure presented in [33].

By analyzing the results shown in Figure 8A in relation to the graphs presented in Figure 8B correctness of the new method can be considered confirmed, as similar results with regards to both total charge density distribution and its influence on the E_C potential were obtained. With regards to the results shown in graphs (C) it should be noted that the very high doping N_D = 6 × 10²⁴ m⁻³ has not prevented us from achieving good convergence. However, it is not the case for the Newton-Rapson method. As seen from chart (D) a relatively low level of doping, namely N_D = 1.9 × 10²³ m⁻³, requires 34 iterations for the charge and potential within the structure to be elf-consistent under the conditions specified in Figure 8, and for very high doping levels convergence problems may occur. Similar cases have been reported [34] and PID blocks were recommended for the method algorithm in order to obtain stable and self-balanced procedure for the charge and potential, which in turn is associated with a significant extension of the simulation time.

The linear relationships on Figure 8C suggest that the convergence of the developed method is exponential (ordinate axis is on a logarithmic scale). This is its great advantage, because it means fast convergence as well as allows to predict simulation time.

8. Conclusions

The method presented here introduces a significant change in the approach to solving the Schrödinger and Poisson equations in I type superlattices, which—to the best of our knowledge, has not been used in any model for such structures so far.

The polynomial approximation of the charge density function allows to obtain analitycal solutions of the Poisson and Schrodinger equations, which significantly accelerates the procedure for obtaining self-consistent fields in tested system.

As the method was tested on relatively simple structures, with maximum 8 layers in the period, the study of more complex structures remains to be carried out. It requires, however, a better adjustment of polynomial approximation coefficients to more complex wave functions. This topic is currently under research.