1. Introduction
Following the Paris Agreement and the more recent Glasgow Climate Pact [
1,
2], a framework was established to keep the global average temperature increase within 2 °C of pre-industrial levels by 2050. At the same time, a plan of action was outlined to confine global warming within the upper limit of 1.5 °C [
3]. To this end, national and regional policies have focused on a global energy transition that consists of increased use of renewable sources for electricity generation [
4] and direct use of renewable heat and biomass, fast electrification processes, including direct use of clean electricity in transport and heat applications, improved energy efficiency, and increased use of green hydrogen and bioenergy with carbon capture and storage [
5]. Currently, the renewable energy sources with the widest range of applications in the industrial sector are hydroelectric, geothermal, biomass, tidal, wind, and solar. Solar energy is used to desalinate seawater or brackish water [
6,
7], to generate electricity using large-scale power plants or building installations, to produce domestic hot water, and to supply space heating or cooling to meet the energy demands of both residential and tertiary users. The most widely used solar technologies for direct electricity generation are photovoltaic (PV) and concentrating photovoltaic (CPV) systems, both of which convert solar radiation into energy but exploit different operating mechanisms and have different conversion efficiencies and investment costs [
8]. The concentrating solar power (CSP) systems currently being developed are very promising [
9] because they are characterised by a low environmental impact, low land consumption, and excellent energy performance [
10]. However, they have poor commercial penetration if compared to PV systems. At the end of 2020, more than 707 GW of solar photovoltaic systems were installed worldwide, of which approximately 127 GW were commissioned in 2020 alone. This growth in installed capacity was the highest recorded in that year when compared to all other renewable technologies. CSP installed capacity grew globally between 2010 and 2020, reaching around 6.5 GW at the end of 2020, of which only 150 MW was commissioned in the same year [
11]. The share of energy generation by CSP plants increased by 34% in 2019 [
12], closely reflecting the growing trend of the global share of renewable generation, which reached 27% in 2019 and 29% in 2020 [
13].
A solar concentrator essentially consists of a collector, which, through a series of mirrors or lenses, concentrates the collected direct normal irradiance (DNI) onto a receiver, thus, obtaining high-temperature thermal energy, which is subsequently converted into mechanical and electrical energy [
14]. There are four types of solar concentrator systems currently available in the renewable power technologies market, namely: linear Fresnel reflectors and parabolic trough collectors, known as linear-focusing systems, and central solar towers and parabolic dishes (usually equipped with a Stirling engine), known as point-focusing systems [
15]. The dish–Stirling system is the least widespread, commercially, and the least mature from a technological point of view since, firstly, the installation cost of the parabolic dish concentrator is still too high compared to other CSP technologies [
11], and, secondly, coupling with a thermal storage system is more difficult to realise [
16]. Nevertheless, this technology appears to be the most promising in terms of its high values of solar-to-electric energy conversion efficiency, ease of installation, and modularity [
17].
The main factors affecting the energy producibility of a dish–Stirling solar concentrator, and which directly influence the design and optimisation of such a system, are the characteristic climate conditions of the installation site, i.e., DNI and ambient air temperature, and the level of soiling of the mirrors of the collector [
18]. Therefore, once an installation site is selected, it is easy to understand how extremely complicated it is to reliably predict the amount of electricity that can be generated by a dish–Stirling solar concentrator. In the continuation of our research, therefore, two different input datasets are defined, one as complete as possible and the other as limited as possible, in order to include all the combinations within these two extremes.
Several studies in the scientific literature have presented numerical models used to assess the energy output of a dish–Stirling system, although only very few of them were based on the real performance data of an operational dish–Stirling system; among these, the Stine model is the most widely used [
19]. Generally, these models were developed from a linear or quasi-linear correlation between electrical power output and incident direct normal irradiance, such as the recent physical–numerical model calibrated on experimental data collected during the period of operation of the demo 33 kWe dish–Stirling plant built at a facility test site at Palermo University [
18].
Several studies have proposed the energy modelling of solar power systems by artificial neural networks (ANNs) as alternatives to the analytical models developed and presented in the literature. ANNs represent a valuable, intelligent method for optimising and predicting the performance of buildings [
20] and of various solar energy systems, such as solar collectors, solar-assisted heat pumps, solar air and water heaters, photovoltaic/thermal (PV/T) systems [
21,
22], solar stills, solar cookers, and solar dryers [
23].
Referring to concentrating solar power systems, [
24] assessed the energy performance of a dish–Stirling system, considering its installation in Natal, RN, Brazil, and investigating four hybrid methods, including the adaptive neuro-fuzzy inference system (ANFIS) and multiple-layer perceptron (MLP), both of which were trained with particle swarm optimization (PSO) or a genetic algorithm (GA) [
25,
26]. The authors of [
27] compared the performance of two analytical methods and one based on neural networks to assess the hourly electrical production of a parabolic trough solar plant (PTSTPP) located in Ain Beni-Mathar in eastern Morocco. Simulations conducted using an annual series of operating data showed that the performance of the ANN model was better than that of the analytical models analysed. The authors of [
28] demonstrated the effectiveness of a model based on a feedforward artificial neural network optimised with particle swarm optimisation to predict the power output of the solar Stirling heat engine, first using input data from literature and then experimental data.
In this work, different artificial neural networks (ANNs) are investigated and trained to predict the energy performance of an existing demo dish–Stirling solar concentrator installed on the university campus in Palermo. To this aim, employing the open-source platform TensorFlow, two different classes of feedforward neural networks, multilayer perceptron (MLP) and radial basis function (RBF), are developed and validated using a set of experimental input data collected during the real operation period of the cited system. The two different classes of networks are tested by varying the number of neurons (depth and computing resources involved) and other sensitive parameters in order to identify the best possible architecture. Finally, the predictive performance of the networks is compared with a previously developed analytical model.
The aleatory nature of solar energy sources and the need to have available power generation plants, which ensure the dispatchability of the resource and make the energy supply secure, drive the development of reliable energy prediction tools. Especially in the case of plants not yet fully mature from a commercial point of view, such as the dish–Stirling plants here investigated, their diffusion cannot disregard the development of a predictive model that considers the most influencing environmental and technical variables.
The paper is organised as follows:
Section 2 presents the experimental set-up;
Section 3 describes the analytic energy model of the analysed dish–Stirling solar concentrator;
Section 4 introduces, explains, and discusses all the ANNs developed;
Section 5 discusses the results obtained; and, lastly,
Section 6 outlines the conclusions of the study.
3. Experimental Set-Up
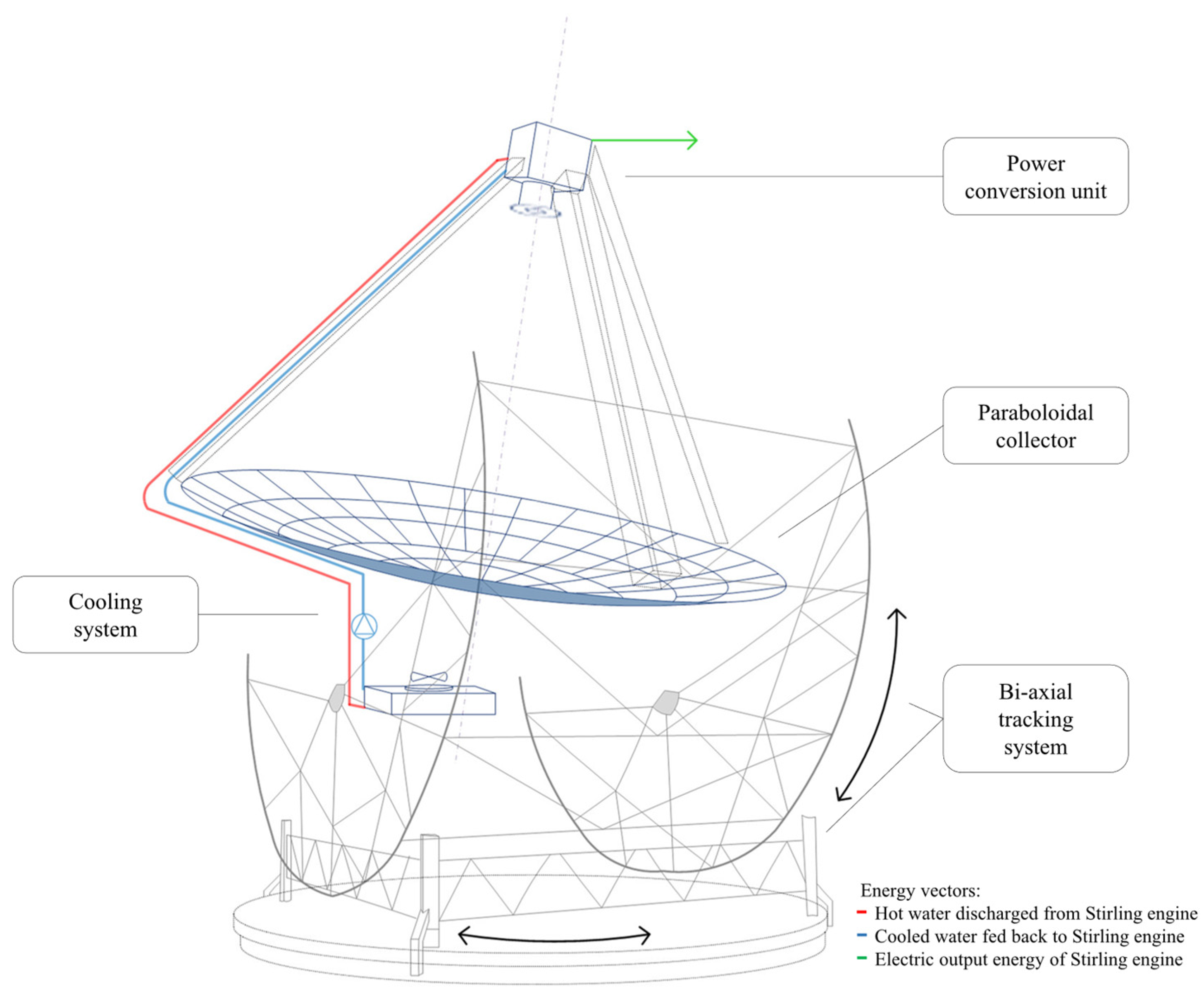
This paper proposes a neural approach to predict the electric energy production of a dish–Stirling solar concentrator at a specific, selected installation site. The reference system that is considered for the development of a neural prediction model is the demo commercial dish–Stirling solar concentrator installed on the university campus in Palermo (see
Figure 1) as well as its real operational data.
This dish–Stirling plant has a net peak electric output power of 33 kW
e and features a geometric concentration ratio equal to 3217 (see
Table 1). The reference system has a paraboloidal collector consisting of an assembly of 54 mirrors with a high reflection coefficient; each mirror is characterised by a sandwich structure and a double curvature calibrated in order to concentrate the incident DNI on a fixed point corresponding to the small aperture of the cavity receiver. Subsequently, the Stirling engine and the electric generator convert the thermal energy into mechanical power and then electricity [
34]. The power conversion unit (see zoom in
Figure 1), including the receiver, the Stirling engine, and the electric generator, is placed at the focal point of the paraboloidal collector by a tripod.
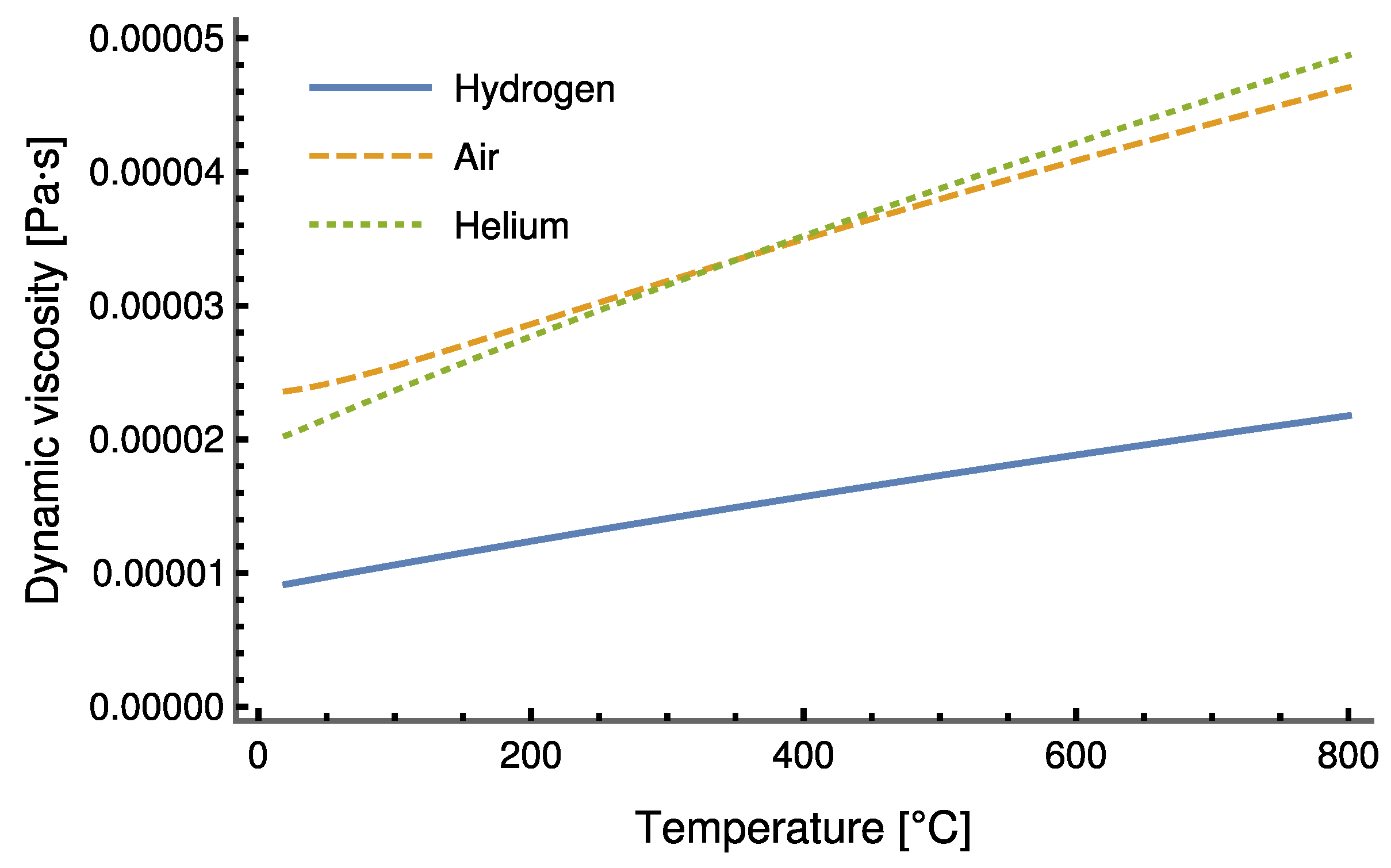
Inside the Stirling engine, hydrogen is used as the working fluid; the fundamental reason why hydrogen is selected as the working fluid is to minimise internal losses due to viscous friction.
Figure 2 shows a comparison with two other possible fluids, air and helium, under the same working conditions. It is evident that hydrogen is less viscous than the other fluids considered. The curves drawn in
Figure 2 were produced using the well-known database of thermodynamic properties provided by [
35].
Moreover, the perfect alignment between the focal axis of the collector and the direction of the sun’s rays is ensured by a biaxial solar tracking system throughout the day [
34].
3.1. Description of the Experimental Dataset
The installation site of the plant, on the outskirts of Palermo (see
Figure 3), is characterised by typically Mediterranean climatic conditions. In this location, winters are generally characterised by very moderate temperatures ranging from 8 to 14 degrees. The summer period typically features rather high temperatures, sometimes even reaching 45 °C. Throughout most of the year, hot south-easterly winds, known as Sirocco winds, occur sporadically. Usually, the Sirocco winds bring with them a large amount of dust or sand from the North African coast, which tends to adhere to the external surfaces, strongly decreasing the amount of DNI available on the ground and, at the same time, decreasing the reflective properties of the mirrors of CSP systems.
The geographical coordinates specifying the installation site of the reference dish–Stirling system (described in
Section 2) are long. 13°20′43″ E and lat. 38°06′17″ N.
All variables observed and recorded by the monitoring systems of the CSP plant are listed in
Table 2.
The index of cleanness (
) is a measure of the amount of soiling or dirt deposited on the reflector compared to the condition of clean mirrors, and, along with the reflectivity of mirrors (
), the interception factor (
) of the concentrator (which is defined as the fraction of rays incident upon the aperture that reaches the receiver for a given incidence angle) and the absorption coefficient (
) of the inner surface of the cavity receiver affect the optical efficiency (
) of the CSP system (see Equation (1)) [
18,
36].
For the 165 days from 5 January 2018 to 2 July 2018, the monitoring system acquired 14,256,000 records (on a second-by-second basis). A large proportion of these records related to events when the plant was not operating because they corresponded to the night periods or day periods affected by weather conditions that were unsuitable for plant operation or to periods when the plant was under maintenance. The records relating to the remaining events were further aggregated with a simple average operation by single minutes, thus, we obtained 7971 records (data on a minute basis).
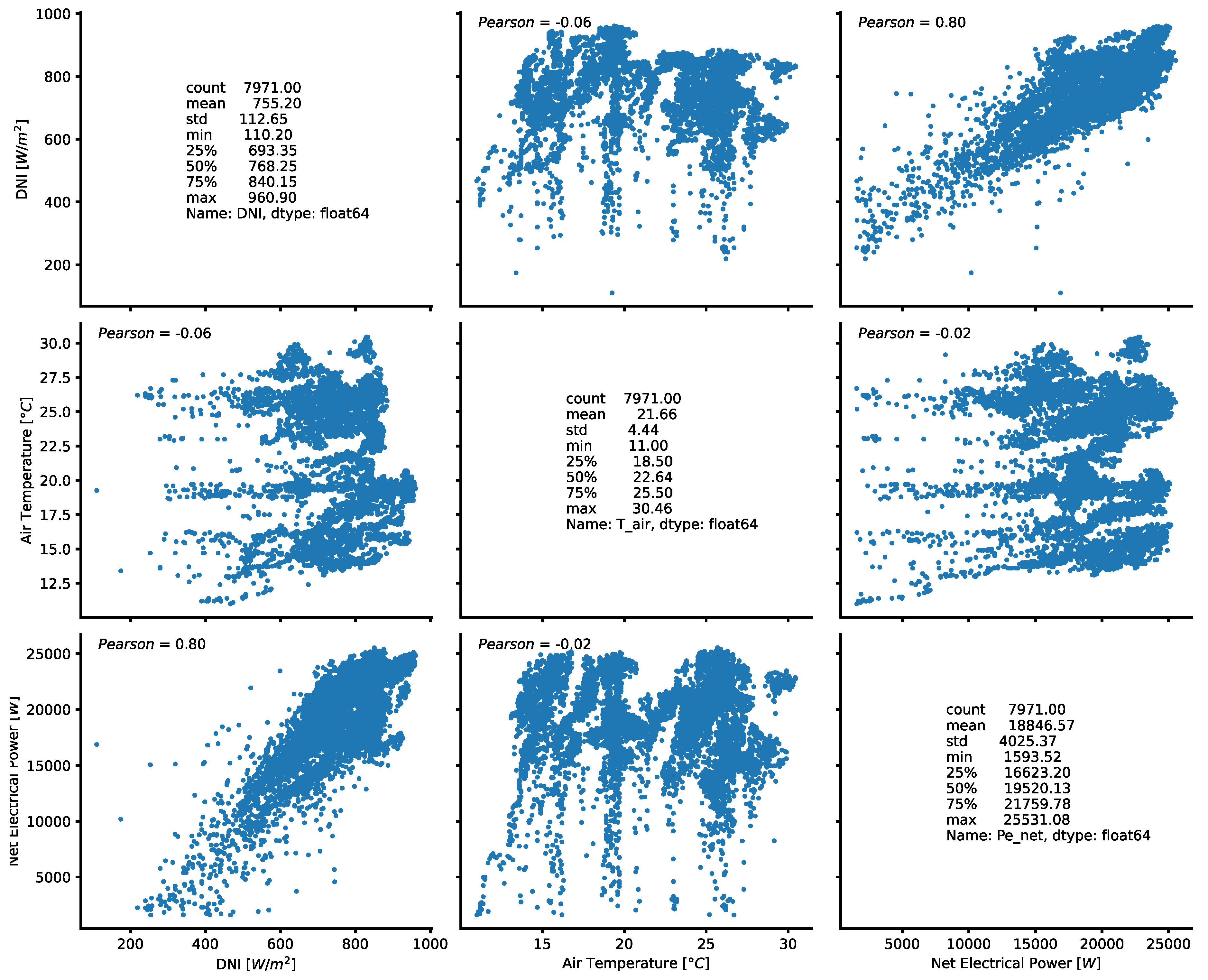
Figure 4 shows some results of the statistical analysis carried out on those variables of the original dataset which, from a physical and thermodynamic point of view, are the most relevant to the operation of an engine based on a Stirling cycle. From a physical and thermodynamic point of view, the variables that are certainly most significant in determining the performance of a dish–Stirling system are the DNI, on which the power input to the system depends, and the outside air temperature, which affects, on the one hand, the heat exchange between the receiver and the external environment and, on the other hand, the heat exchange between the cold side of the Stirling engine and the environment. The Pearson coefficient (ρ
p) illustrated in
Figure 5 shows that the net electrical power output of the dish–Stirling system is strongly correlated with the DNI.
3.2. Outlier Removal Procedure
As is usually the case, any population of samples or data can exhibit large deviations, meaning anomaly points or individual data points that deviate significantly from the rest of the distribution data. These data points are called outliers. The presence of outliers in a dataset can be due to a variety of factors, such as the experimental nature of the same data, human or measurement instrument errors, or wrong data handling; therefore, they are considered normal. In order to prevent outliers in the dataset from affecting the performance of any model developed, it is common practice to preliminarily identify and remove them to reduce the variability of the input dataset. Outliers can be either univariate or multivariate, depending on whether it is possible to identify them by observing a distribution of values in a single-dimensional space or an n-dimensional space. Obviously, in the latter case, the removal of outliers requires the training of an appropriate model able to replace the human brain. Several techniques are useful for detecting outliers in a dataset, of which the most widely used is the Z-score. The Z-score method uses standard deviation to identify outliers in a dataset with a Gaussian distribution (or those where the distribution is assumed to be Gaussian). Such a statistical quantity is a measure of how the observed data deviate from the most probably occurring data in the dataset, in other words, the mean of the data [
37]. Referring to a Gaussian distribution of the data, the standard deviation (
) is defined as in Equation (2) below:
where
is the number of records in the dataset,
is the i-th record in the dataset, and
is the mean of the data (see Equation (2)). Thus, the Z-score (
) can be calculated by Equation (3) as:
In our case, the Z-score technique was applied considering three variables from the dataset, which were: the DNI, the net electric output power, and the outdoor air temperature. This is because, according to our experience of running the solar power plant installed at the Palermo University campus, these variables are the ones that most influence the behaviour of the system and can also vary very quickly. It should also be noted that abrupt variations can induce operating transients that can lead to system shutdown or restart within seconds. According to the Gaussian distribution of the data, all records falling within the range of extremes were considered. The resulting filtered dataset included 7417 records, approximately 93% of the originally available, valid data.
3.3. Statistical Analysis of Input Datasets
To describe and define the dataset, purified of outliers, a statistical analysis was carried out, investigating the quantities that are listed and explained in
Table 3. These quantities were calculated for each variable of the original dataset without outliers, which included 7417 records, and were analysed by using the statistical variables summarised in
Table 3 below.
The results of the preliminary statistical analysis of the data, summarised in
Table 4, describe the main characteristics of the data and provide precise quantitative information on the data distribution, variability, skewness, and taililedness of the actual data sample available to the authors. The analysed data sample refers to all monitored variables listed in
Table 2 and to the variable “Clean day”, which indicates the number of days since the last cleaning event affecting the mirrors.
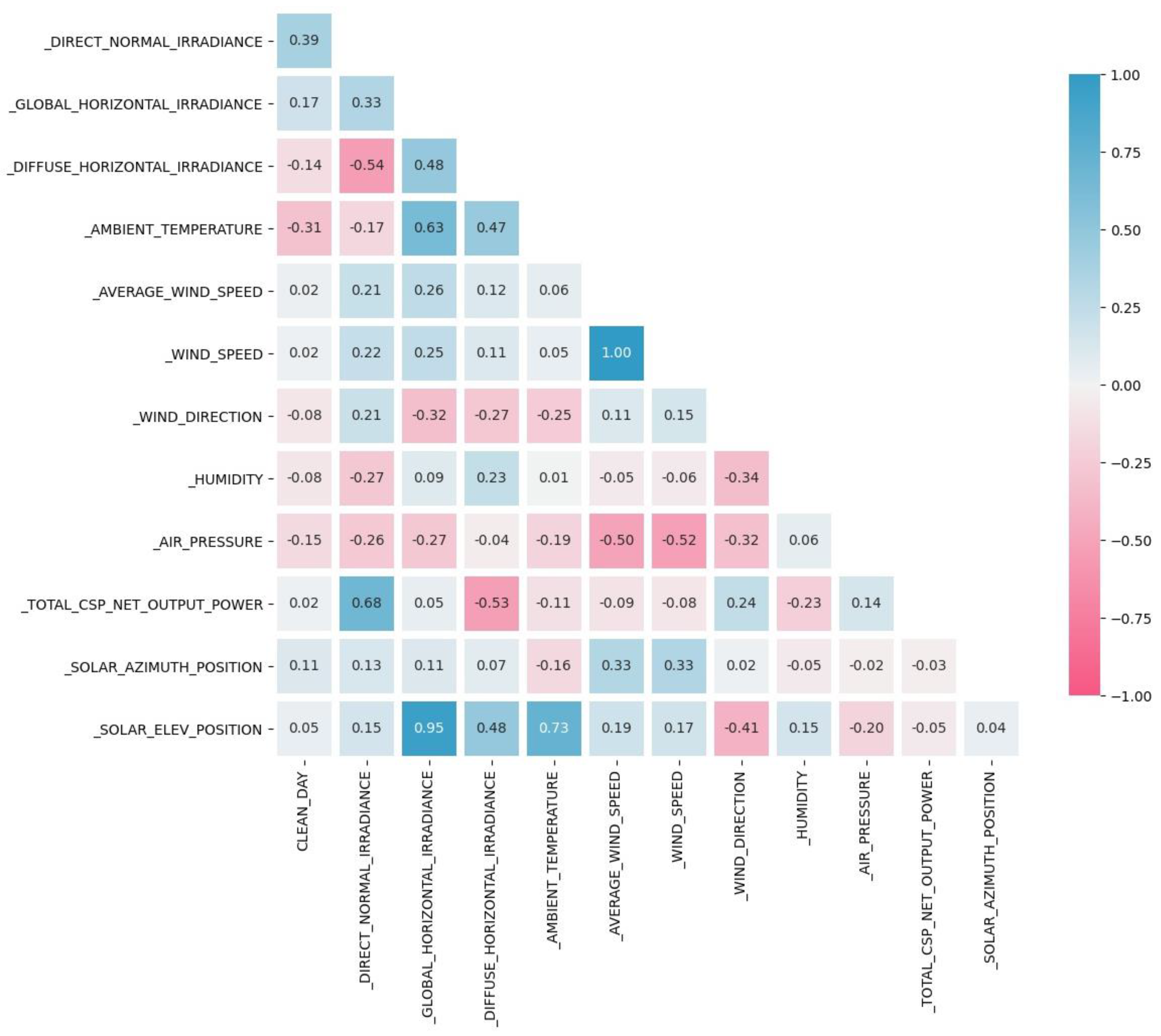
The full input dataset of 7417 samples was always randomly split to obtain an input dataset for the training process of the neural networks and another input dataset to be used for the validation process of the same neural networks; the training dataset included 85% of the original data; the validation dataset resembles the other 15%. Preliminary statistical analysis of the data made it possible to evaluate the correlation coefficients between each of the variables covered, and the results are exemplified by
Figure 5.
To avoid any form of direct influence or manipulation in order to improve the predictive performance of the developed neural models, training and validation datasets were autonomously extracted by the software in random mode from the set of data monitored on our prototype system. Therefore, no filter or algorithm was applied for the above splitting operation except for that used for the removal of outliers. In this sense, punctual data used for the training of the network were never used to validate the results and vice versa. Although, in theory, point data might be used for the training phase, and the one immediately following in time used for validation, it is necessary to underline that we did not applied algorithms specifically indicated for time series. The data, before being used, were purposely remixed, eliminating any temporal succession. In addition, the operation of the dish–Stirling was characterised by extreme and fast variability due to a continuous variability of weather and solar parameters.
5. Artificial Neural Network Models
5.1. Machine Learning Deployment Using TensorFlow and Python
In recent years, the use of neural network technologies and algorithms applied to physical and engineering problems has become increasingly common, and software companies have made increasingly sophisticated tools available for analysing complex systems. However, such software often requires the user to have detailed knowledge of artificial intelligence, which has slowed the spread of these interesting methodologies. The cost of purchasing such software has been another limiting factor for the spread of machine learning techniques. The diffusion of open-source libraries characterised by high reliability and effectiveness has facilitated the success of this ground-breaking technology. In this context, Google’s TensorFlow 2 library represents an extremely powerful, free tool, which, at the same time, is characterised by extreme ease of use for the production of machine learning algorithms in several programming environments [
42]. For the development of the models described below, the authors used the Python code language, which is very well suited to some of the particular functionalities of TensorFlow 2 [
43], such as saving and restoring the state of a neural network in order to predict at a time following the training of the network itself [
44]. Python is a programming language, developed in the 1990s, that is particularly suited to the development of applications that rely on numerical computation. It is free of charge and is available for a wide range of operating systems, a feature that has made it particularly popular in academic circles [
45,
46]. All the machine learning models described below, therefore, use libraries and environments that are completely free and reusable for absolute transparency and replicability of the results.
5.2. Artificial Neural Networks
The artificial neural network (ANN) is a powerful tool, the sophisticated rationale of which is inspired by the way the human brain analyses and elaborates information [
47]. ANNs are largely used for the modelling, prediction, assessment, and optimisation of the performance of many different engineering technologies, such as solar energy systems, which often require the solving of complex and non-linear problems [
48].
In this paper, from all the different types of ANNs, the multilayer perceptron (MLP) and the radial basis function (RBF) models were selected.
5.2.1. Multilayer Perceptron Neural Network
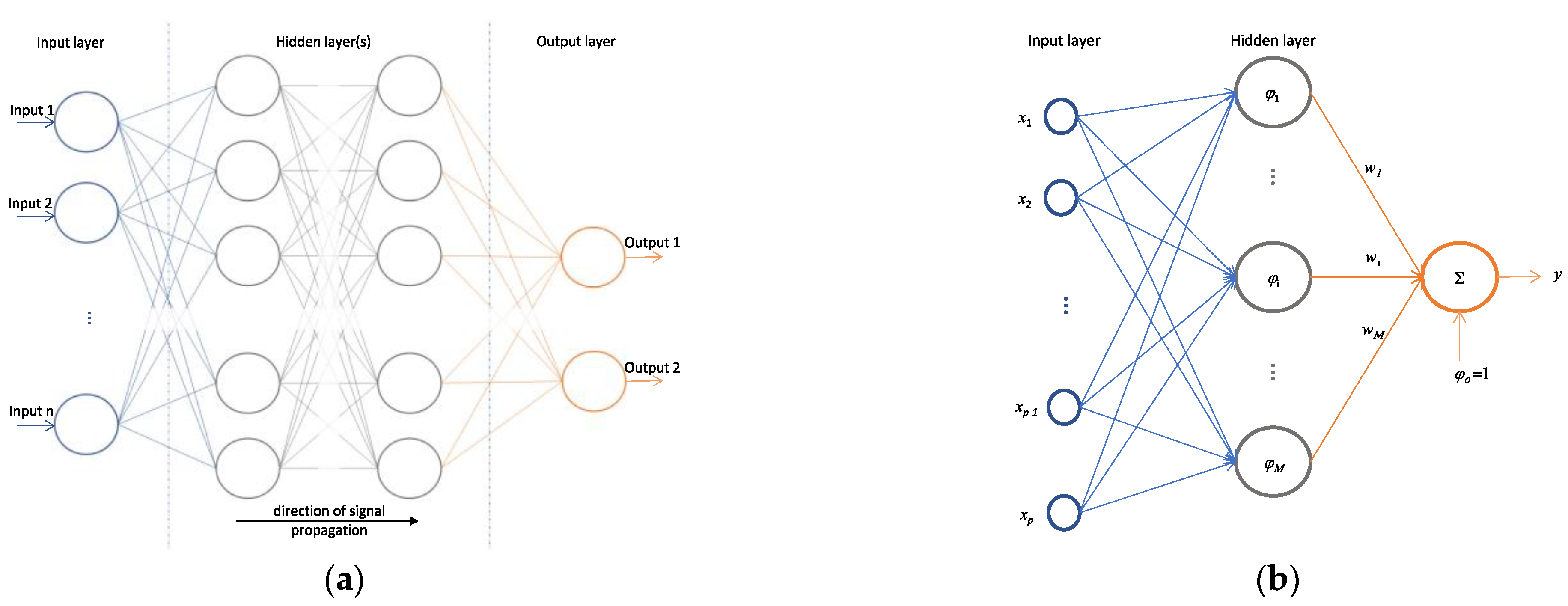
The MLP neural network (see
Figure 8a) consists of several layers (an input layer, several hidden layers, and an output layer) in which the neurons are ordered to transmit signals from the input to the output of the network. The output (
) of each neuron of the hidden layer and the network output (
) are mathematically described by the following Equation (9):
where
is a non-linear function,
is the weight of the first layer,
is the input information,
is the bias, and
is the weight of the output layer [
48].
5.2.2. Radial Basis Function
As can be seen in
Figure 8b, which shows the architecture of a general RBF network, each neuron of the hidden layer has a vector of parameters called centre (
), which is compared with the input vector (
) of the network, producing a radial, symmetric response [
49]. The responses of the hidden layer are also scaled by the connection weights (
) to the output layer and then combined to generate the output of the network [
50]. The output (
) of each neuron of the hidden layer and the network output (
) are mathematically described by Equation (10) as:
where
can be a Gaussian function [
48].
Keras layers are the basic building blocks of neural networks in Keras, the open-source framework used in our research. A layer consists of a tensor-in tensor-out computation function (the layer’s call method) and a state, held in TensorFlow variables (the layer’s weights). While Keras offers a wide range of built-in layers, it does not cover every possible use case. Indeed, a radial basis function layer was achieved by customising the already available layers in Keras [
42,
51].
5.3. Development of Neural Network Models
This section defines the models and the description of the neural network architectures, both MLP and RBF, which were used for the prediction of the energy producibility of the analysed dish–Stirling plant. As indicated in
Table 6, for both types of ANN models, the total net output power of the CSP was the only output variable of the networks, and two different datasets were defined for the input variables to these same networks; the first included twelve variables (long dataset), and the second one included only two variables (short dataset). It is important to highlight that the identification of a restricted group of variables, to be used in the training phase, was carried out after a preliminary sensitivity analysis of the energy performance of the plant with respect to the environmental and operating conditions of the technology, also taking into account the physical features of the phenomena occurring in a CSP plant such as the one being investigated.
Two possible types of input datasets are presented in the research described here: long and short. The long dataset consisted of all significant variables made available by our monitoring system. The short dataset, on the other hand, considered only the two climate variables that are absolutely necessary from the physical point of view to describe the energy balance and the related analytical model of the dish–Stirling system. The two possible datasets, therefore, delimit the widest interval within which the input variables can be selected.
For both MLP and RBF models, several neural network architectures characterised by different levels of depth were tested for each of the two datasets of variables defined. Specifically, the performance of each network architecture was investigated for four different depth levels, varying the number of neurons in the layers and the number of layers making up the neural network. Therefore, a total of 16 networks were trained, of which eight were of the MLP type, and the other eight were of the RBF type.
From this point on, for ease of writing and to better identify the different neural networks examined, each of them is associated with the nomenclature X-Y-N, in which: X is a letter that indicates the level of depth of the network, which can be superficial (S), medium deep (M), deep (D), or very deep (V); Y is an acronym that can be MLP or RBF depending on the type of neural network implemented; and N is a number that can be equal to 2 or 12 depending on how many input variables were used.
Table 7 summarises the main characteristics of all 16 neural networks tested to predict the energy producibility of the dish–Stirling plant, reporting for each network: the number of layers, the number of neurons in each layer, and the total number of parameters involved in the training process.
The programming language used to build the artificial neural network models defined in
Table 7 was Python employing TensorFlow libraries.
Supplementary Materials include all scripts and data necessary to ensure the complete replicability of the neural network models examined and proposed for predicting the electrical producibility of a dish–Stirling system. Among them, the master script defines the network architecture of the neural model (see ‘NN_script.py’), and the reader can examine it to recreate, modify, and review the modelling procedures and data used in both the training and validation phases. With regard to the input data of the neural networks examined, although the complete original dataset is not provided due to confidentiality issues, a limited dataset used for the validation phase of the neural networks is nevertheless provided both for the long input dataset, which includes twelve variables (see ‘y_test.txt’), and for the short input dataset, which includes two variables (see ‘X_test.txt’). Various strategies were used to avoid overfitting, involving the definition of different checkpoints. The checkpoint configures the early stopping of the training phase in order to avoid overfitting by using a measure of the loss of accuracy in the validation phase and setting a maximum number of training repetitions (epochs) for which no improvement in the accuracy of the prediction is detected.
Finally, a simplified script is provided (see “NN_reload_script.py”), which allows the user to instantly execute the best neural network by reading a file in which all the parameters of the best neural network are stored (see “best_dish_model_achieve.h5”). This set of files allows the user to directly verify the results of the present study and possibly modify and reuse these architectures even in other cases.
5.5. Definition of Performance Measures
With the aim of assessing the quality and reliability of the neural models developed, several statistical indices were calculated, starting from the validation dataset, including the determination coefficient R squared explained by Equation (11) in
Table 8, which provides a synthetic measure of the goodness of the approximate function. This index can assume a value between 0 and 1 and indicates how far the predicted values deviate from the expected ones. Moreover, starting from the validation dataset again, the mean absolute error (MAE) was produced for each trained neural network. The MAE, explained in Equation (12), is the average of the absolute differences between the prediction and the actual value of the output variable of the neural network, providing information on the average magnitude of errors in a set of predictions, regardless of their direction.
In addition, a statistical analysis of the resulting residuals was carried out after the validation process for each neural network. Being residuals (), the set of differences was obtained by subtracting the actually measured values from those predicted as the output variable of the networks. The following quantities were then evaluated to examine the frequency distribution of these residuals, such as the mean value, the size of the validation dataset (count), the standard deviation value, the minimum and maximum values, and quartiles at 25% (first quartile, Q1), at 50% (second quartile, Q2), and 75% (third quartile, Q3). In order to graphically compare all the developed neural networks in terms of the accuracy of predicting the energy production of the dish–Stirling plant, the following graphs were produced for each of them:
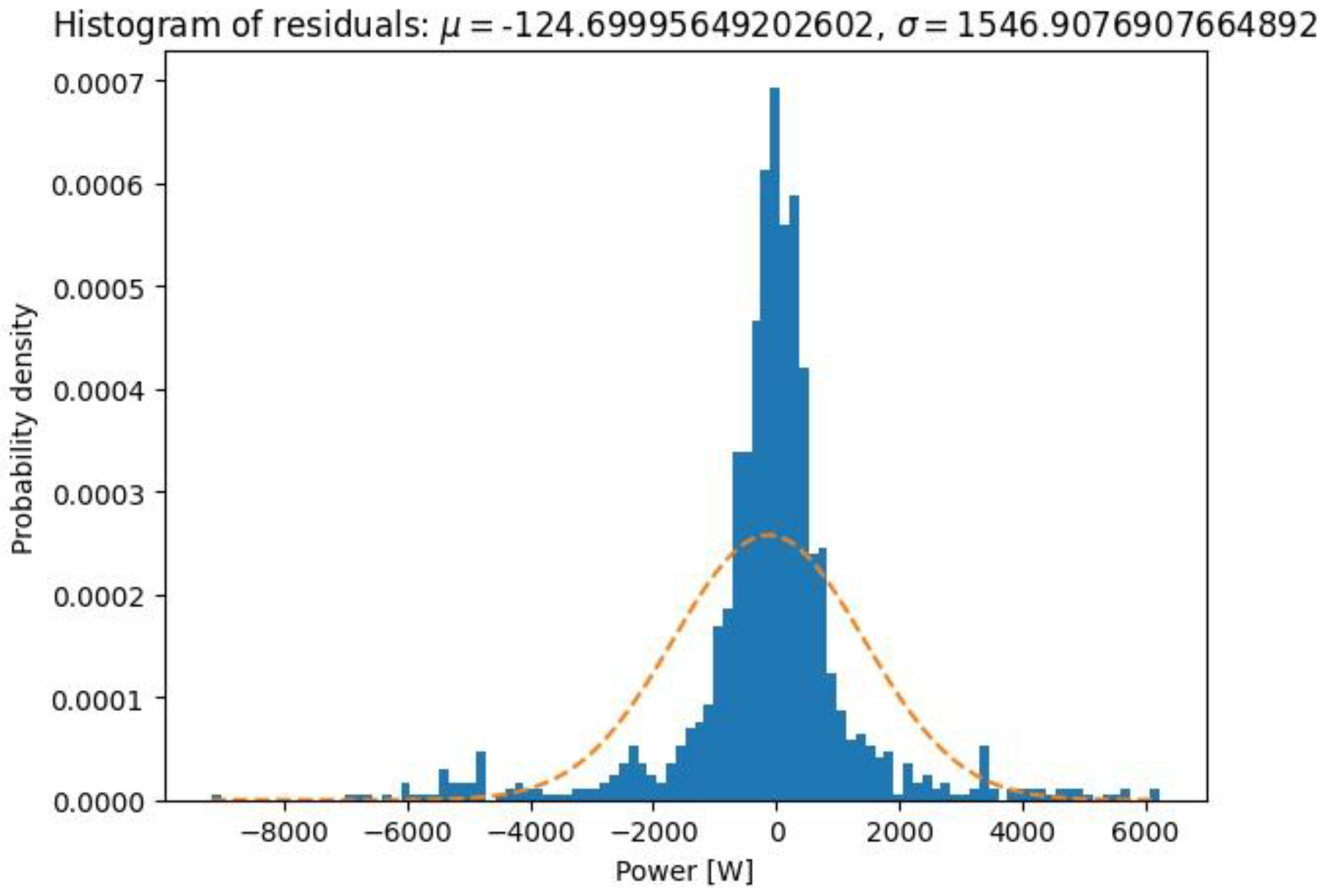
(1) A histogram of residuals showing the distribution of residuals obtained by comparing the values of the electrical output power of the dish–Stirling system predicted against that measured. From this comparison, the mean () and standard deviation () values of the residuals were calculated and displayed. In general, it is expected that the distribution is centred on the value 0 and is close to a Gaussian distribution. However, in this graph, it is also possible to graphically compare the probability density distribution obtained with a normal distribution having the same mean value and the same standard deviation value;
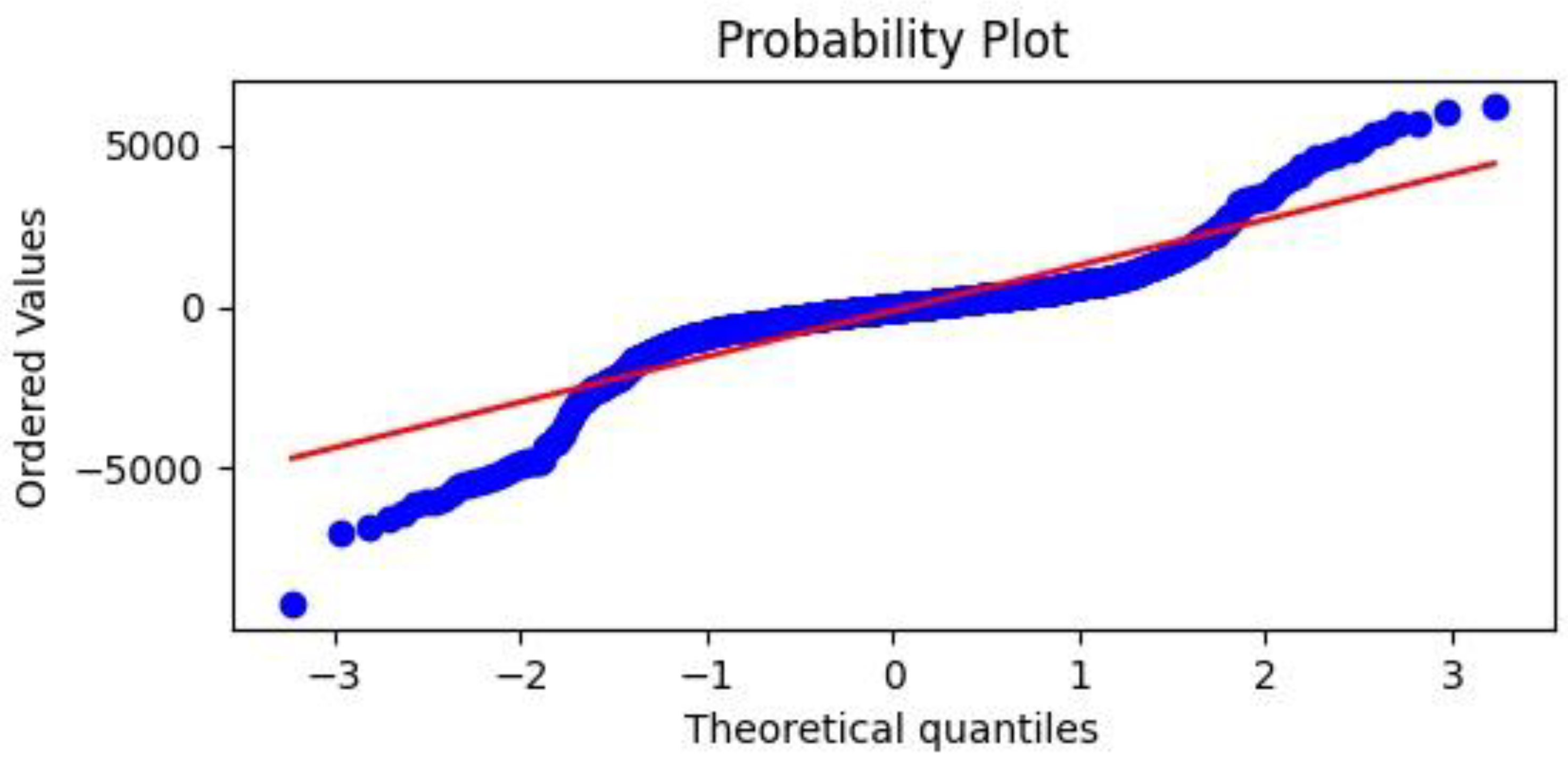
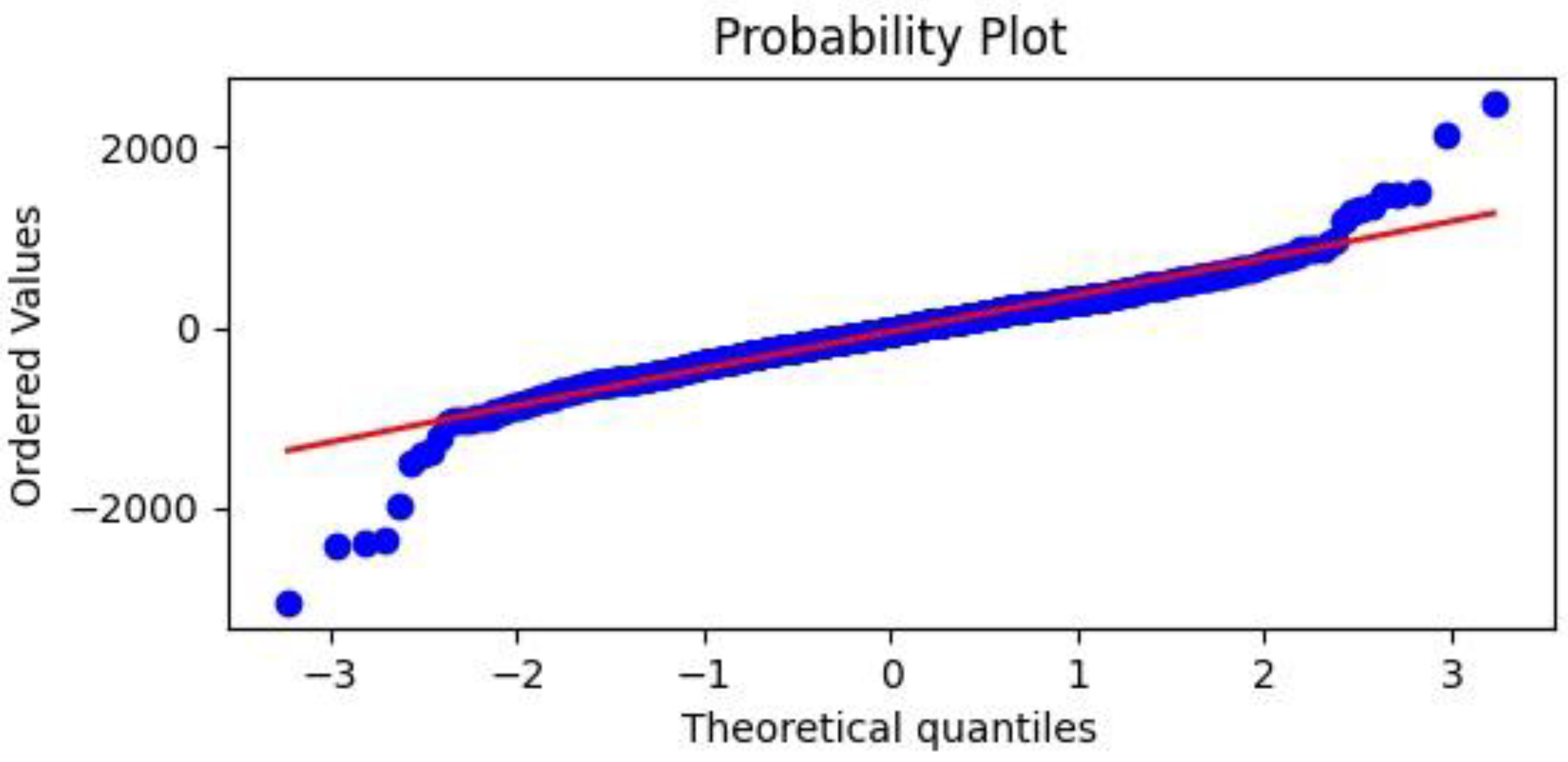
(2) A Q–Q (quantile–quantile) plot, a probability plot in which the probability distributions of the residuals obtained after the validation process are compared with a normal distribution by plotting their quantiles against each other;
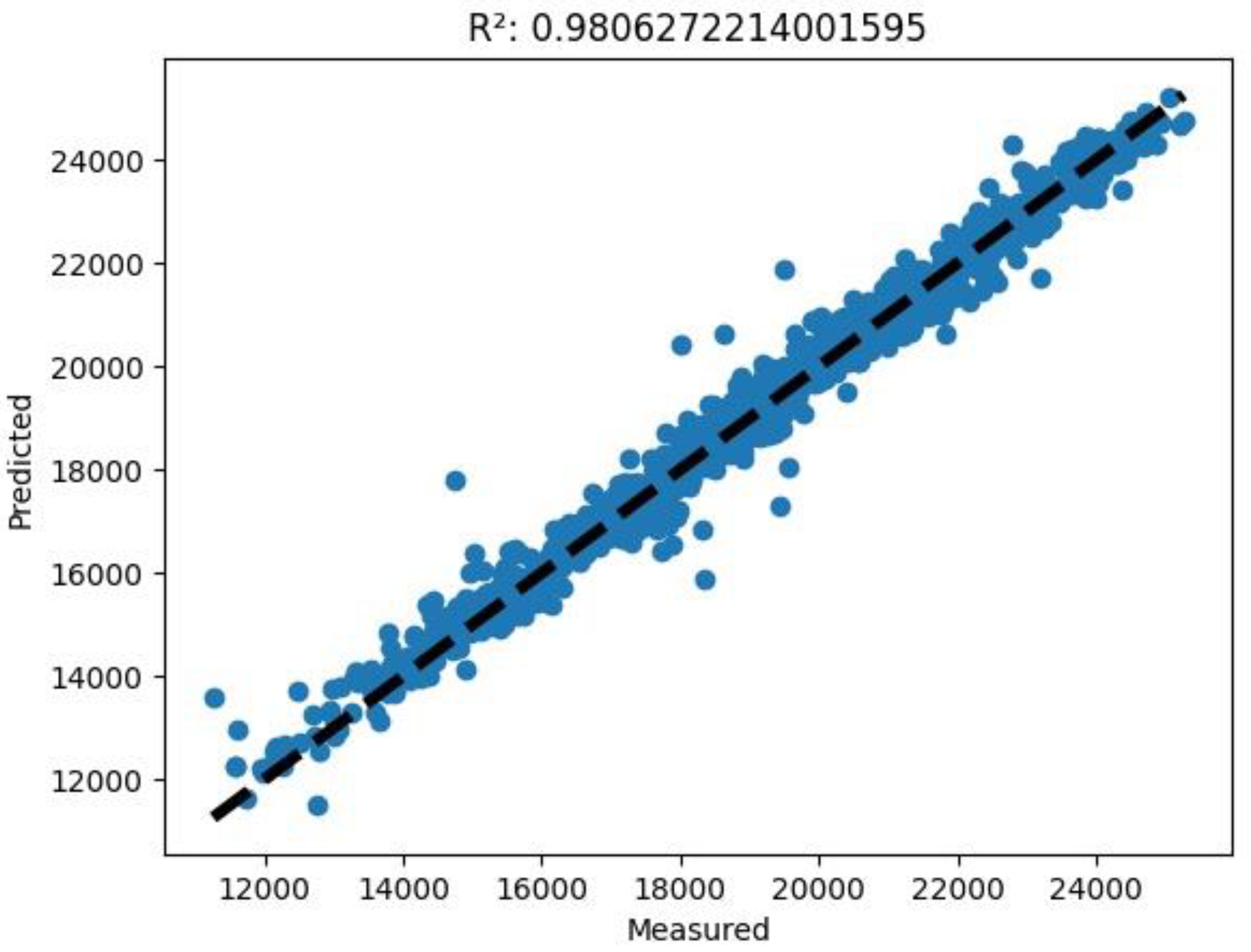
(3) A predicted versus measured graph showing points of coordinates expected and actual measured electrical output power values. In this graph, it is possible to appreciate, through the coefficient of determination R squared explained in Equation (11) (see
Table 8), the spatial distribution of the points with respect to the bisector of the first quadrant, which represents an ideally perfect regression.
7. Conclusions
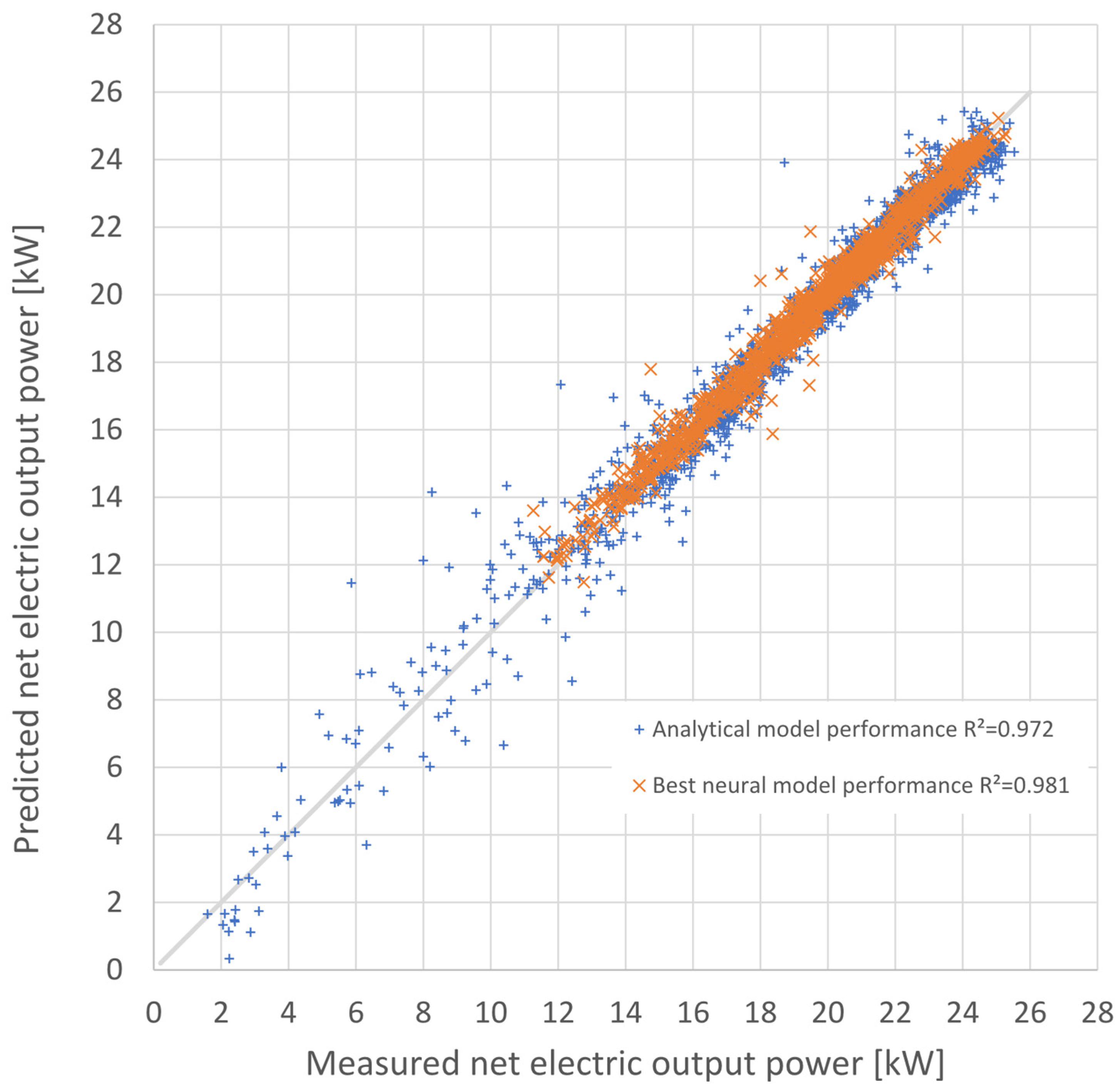
The study here presented aimed to test and optimise a forecasting model for the energy performance of a dish–Stirling solar-concentrating plant based upon the use of artificial neural networks. Contrary to most of the models already tested in the most recent literature in this scientific sector, the data used for the training phase of the networks were real data from a monitoring campaign of a real working plant on the university campus in Palermo. Neural networks of different architectures and sizes were also tested to better understand the link between the complexity and quality of the obtained results. All the different tested network architectures were trained alternately with two inputs (in the case of only standard data such as DNI and external temperature being available) and 12 inputs (in the case of more complete climatic data being available). A further reason for the novelty is the introduction of the input variables of information regarding the cleaning of the reflector mirrors, which has never before been tested in this type of model. The results made it possible to appreciate the good performance of the MLP models compared to the RBF models, traditionally characterised by better performance in the approximation of functions. Compared to a modern analytical model developed by the authors themselves, the best of the developed neural models obtained an even higher determination index between expected and calculated results, with a value equal to 0.98. The comparison is not, therefore, to be considered singularly, but it is useful to understand how a sophisticated neural network can be absolutely equivalent and sometimes superior to analytical models.
The results confirmed the maximum reliability of the developed ANN models.
It was not unexpected that the best neural model using the long input dataset, i.e., the one extended to twelve input variables, had a slightly higher accuracy than that achieved with the analytical energy model. The latter, being fundamentally based on a lumped parameter analysis of the dish–Stirling system, could not take into account the effect on its operation of all those meteorological and climatic variables that were, instead, considered in the extended dataset. For instance, it would be extremely complex to include the variability induced by air humidity or wind speed in the analytical model for predicting the electrical producibility of the solar concentrator, although these certainly influence the availability of direct solar radiation. The neural model, on the other hand, was based on a black-box approach, which simply learns from the available data without having to assume any analytical cause-and-effect relations between input and output. Thus, the present work demonstrates that the neural approach, using real data collected experimentally, is competitive with an analytical approach.
A neural model, already trained, together with the same input data used, is made available as attachments in “
Supplementary Materials”. The digital neural model is directly provided with the script in Python language, allowing maximum transparency of the algorithms described in the research work. The availability of the dataset and the used Python scripts allow, thanks to the exclusive use of open-source software, maximum transparency and replicability. Finally, it should be noted that the results of the best of the neural networks tested (V-MLP-12) were better, in terms of coefficient of determination than one of the most advanced and highest performing analytical models developed by the same authors [
18]. Further improvements in the performance of the neural network models could be achieved by using different activation functions and different optimisers (fine tuning) using the Python script and dataset provided as a complement to this study.