Optimal Ultra-Local Model Control Integrated with Load Frequency Control of Renewable Energy Sources Based Microgrids
Abstract
1. Introduction
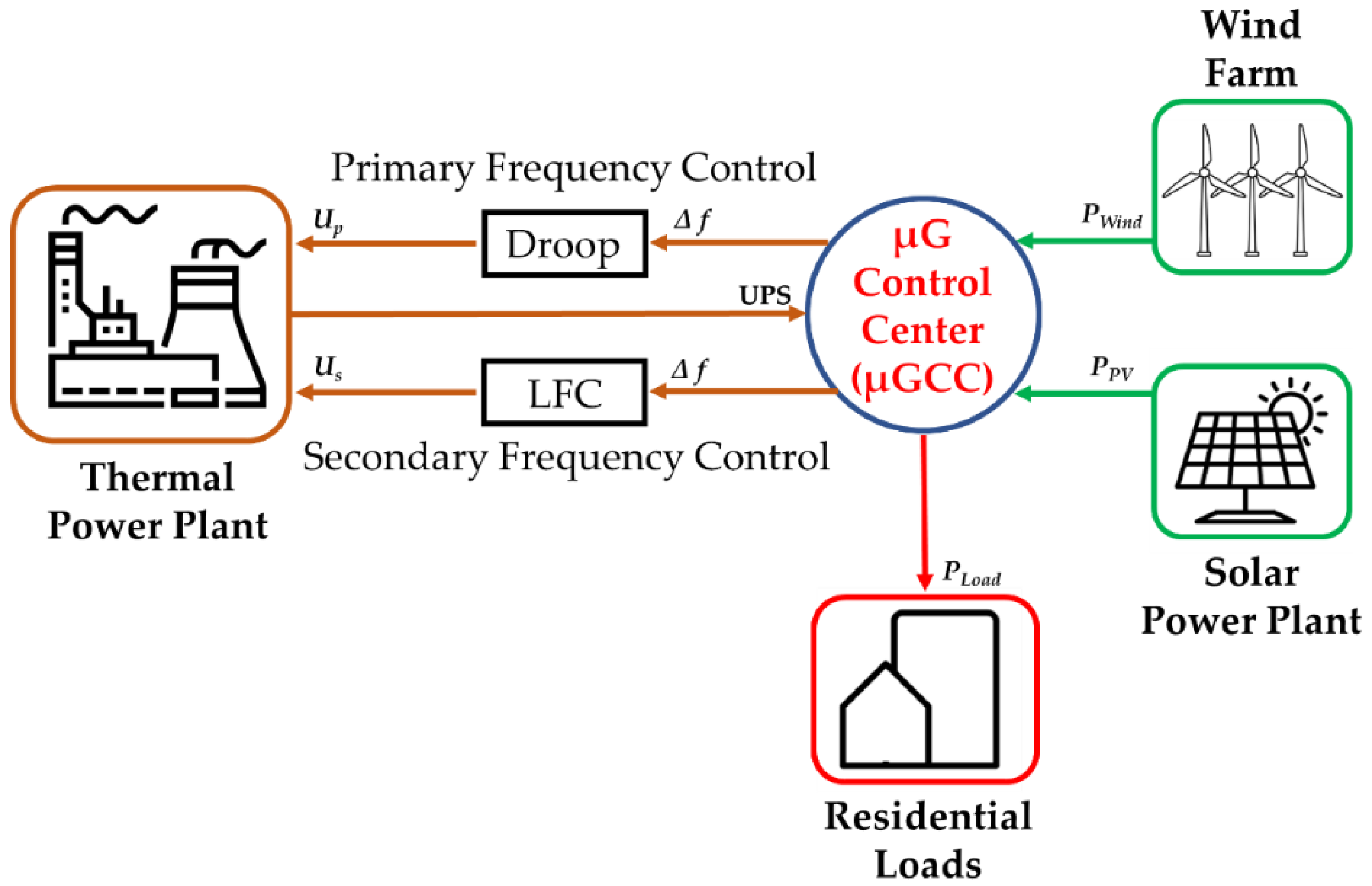
2. Configuration and Modeling of the Studied Islanded µG
2.1. Structural Details of the Islanded µG
- The valve gate’s limits (upper limit ‘VU’ and lower limit ‘VL’) regulate the valve’s opening and shutting.
- The generation rate constraints (GRCs) are used to restrict the rate of the produced power. The non-reheat thermal PP’s GRC is set at 20% pu. MW/minute [22].
2.2. Dynamic Modeling in the State-Space
3. Proposed Optimal Ultralocal Model for LFC of µG
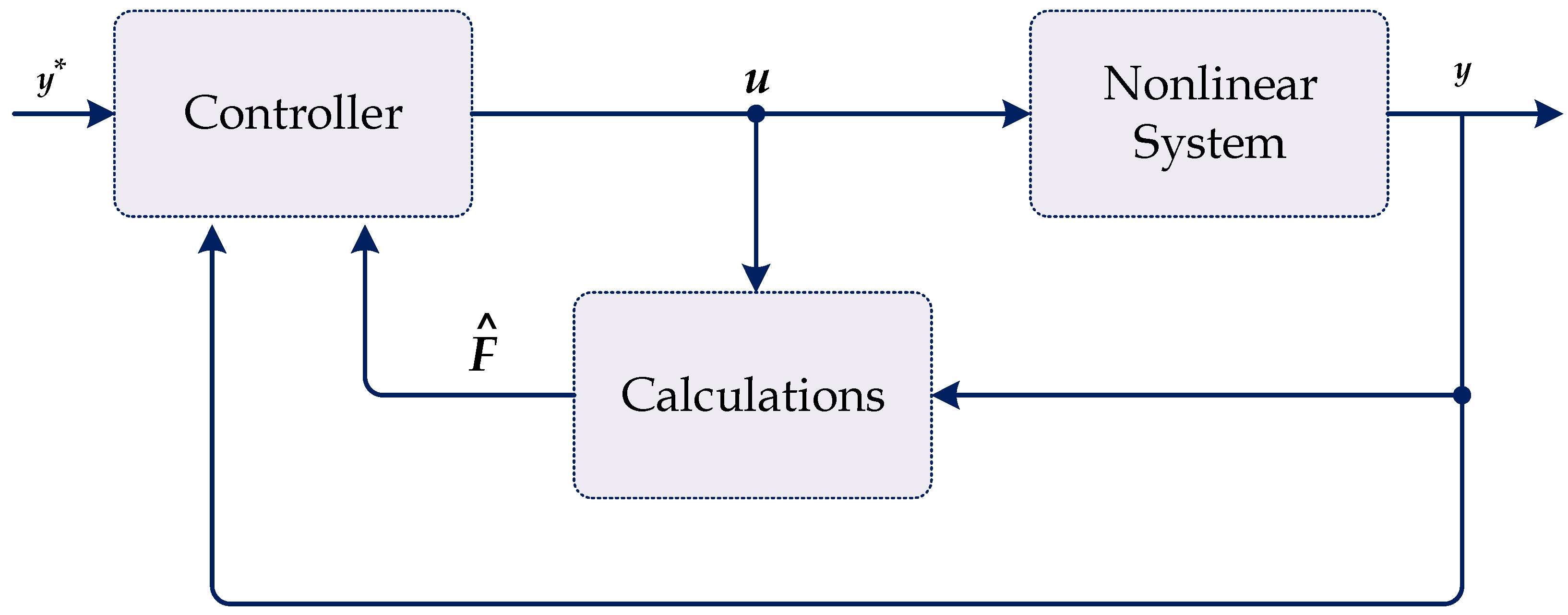
3.1. Description of the Ultralocal Model Control
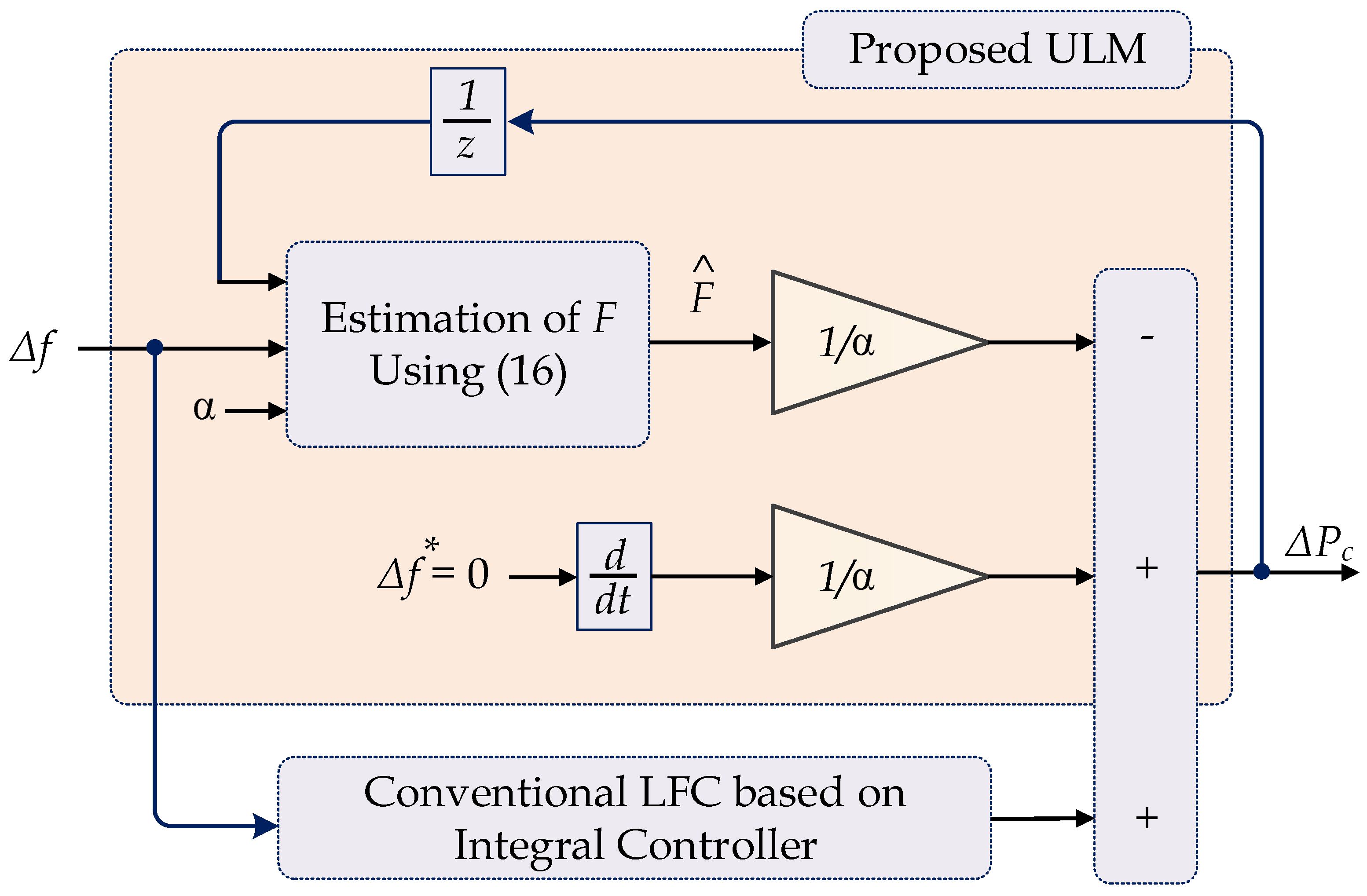
3.2. Proposed Optimal Ultralocal Model Control for LFC
3.3. A metaheuristic Optimization Method Based on the African Vulture Optimization Algorithm:
- The AV population consists of N Avs, each with a d-dimensional position space.
- There are three different groups within the AV population. The fitness value of the viable solution determines the quality rank; the best solution is ranked as the leading and first AV, the second-best solution is ranked as the second-best AV, and the remaining Avs are assigned to the third group.
- The three groups were established in the population to define the most significant natural function of Avs. Therefore, diverse vulture species have unique functions to fulfill.
- Additionally, the fitness value of a potential solution may indicate both the advantages and disadvantages of Avs. In light of this, the most vulnerable and ravenous vultures tend to be the worst. In contrast, the strongest and most numerous vultures tend to be the best vultures. All Avs in the AVOA often try to stay close to the best ones and stay away from the worst.
3.3.1. Step 1: Population Classification
3.3.2. Step 2: The Rate of Vulture Starvation
3.3.3. Step 3: Stage of Exploration
3.3.4. Step 4: Stage of Exploitation (Phase 1)
3.3.5. Step 5: Stage of Exploitation (Phase 2)
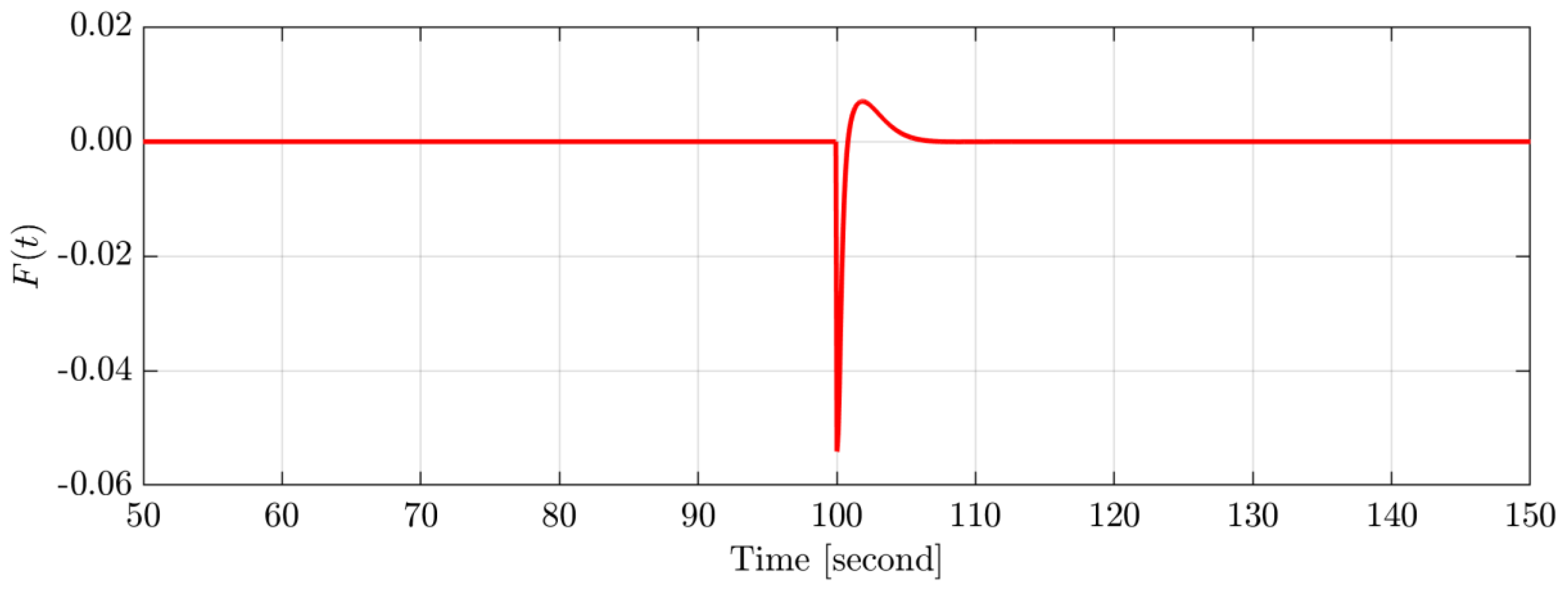
4. Simulation Results and Discussion
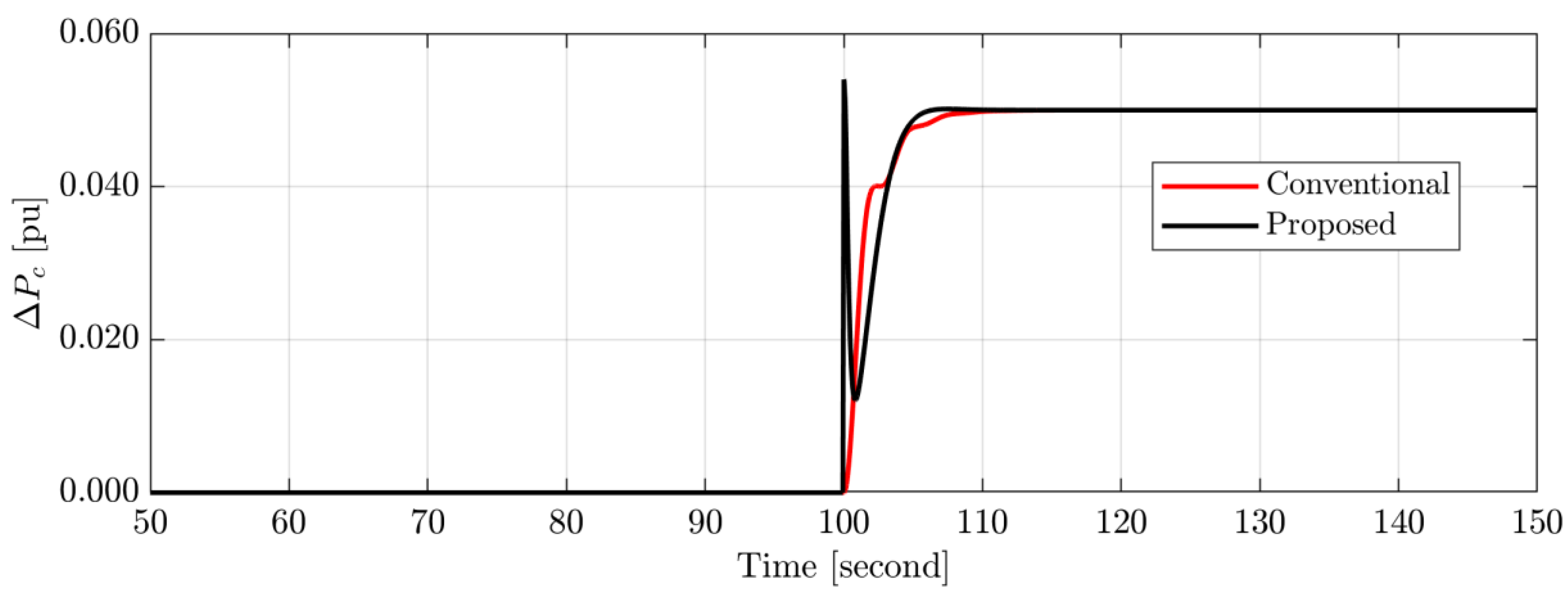
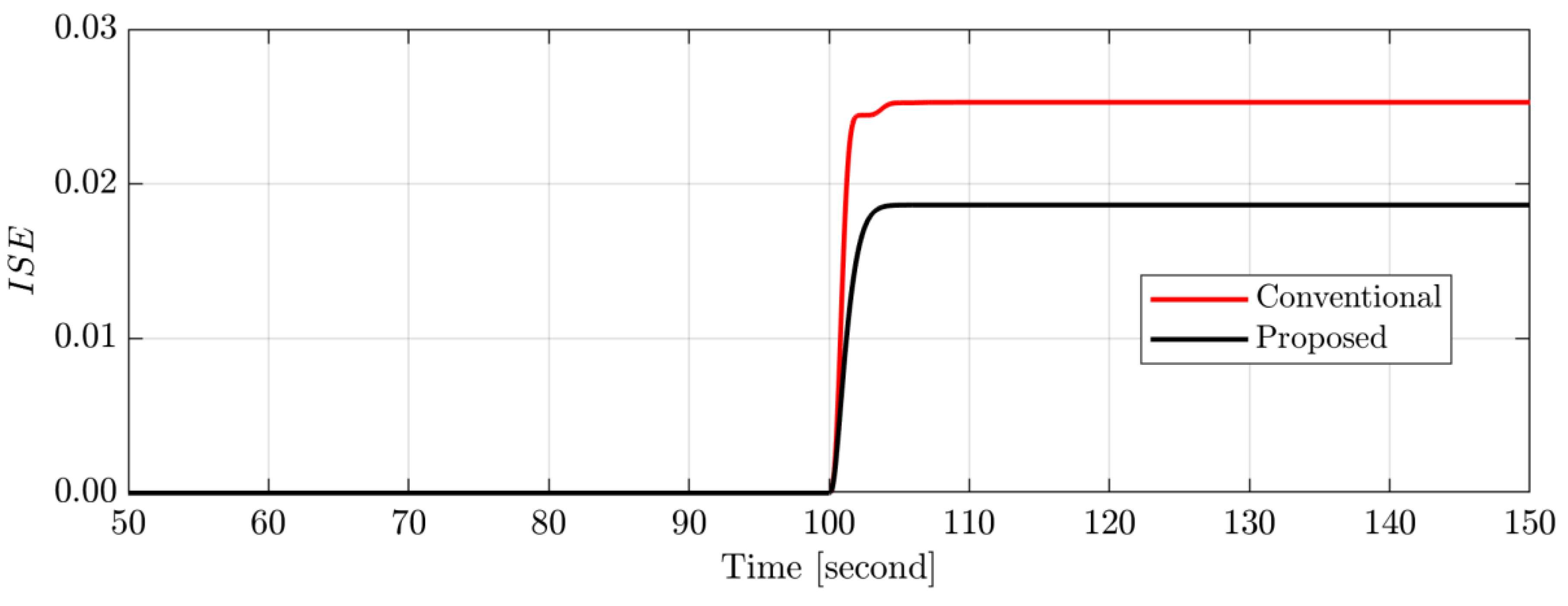
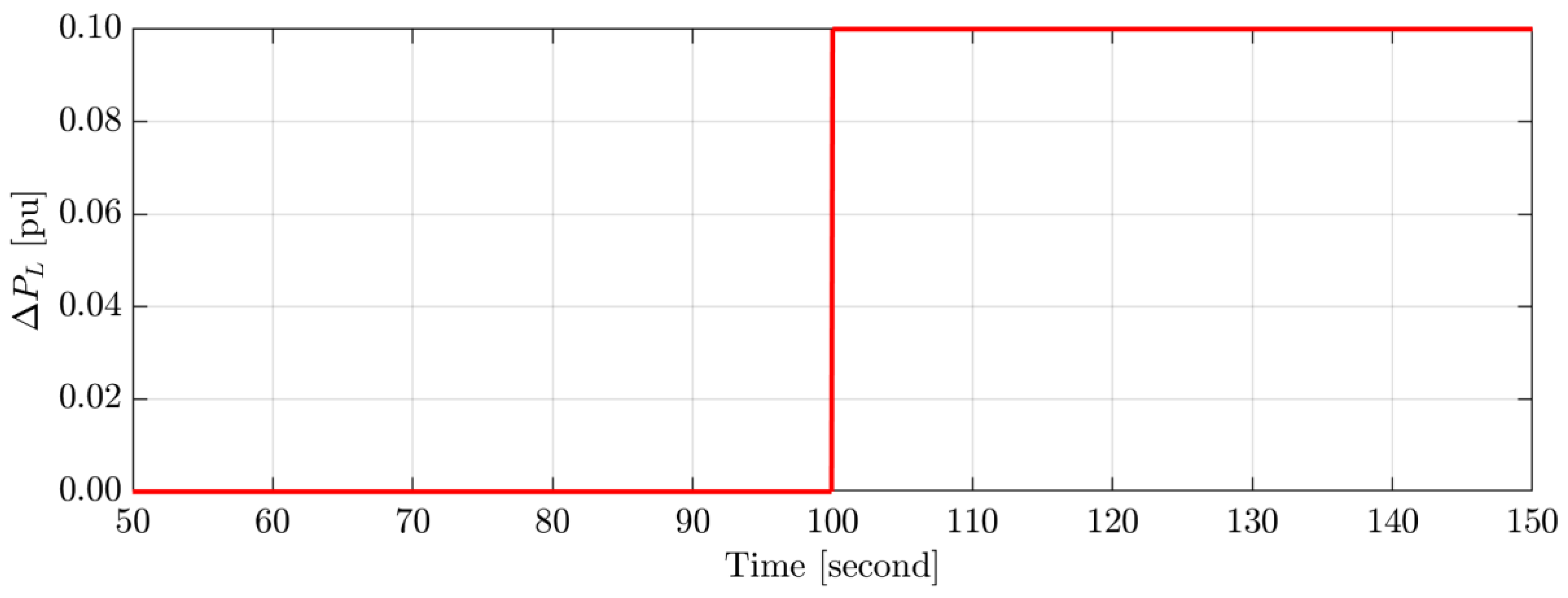
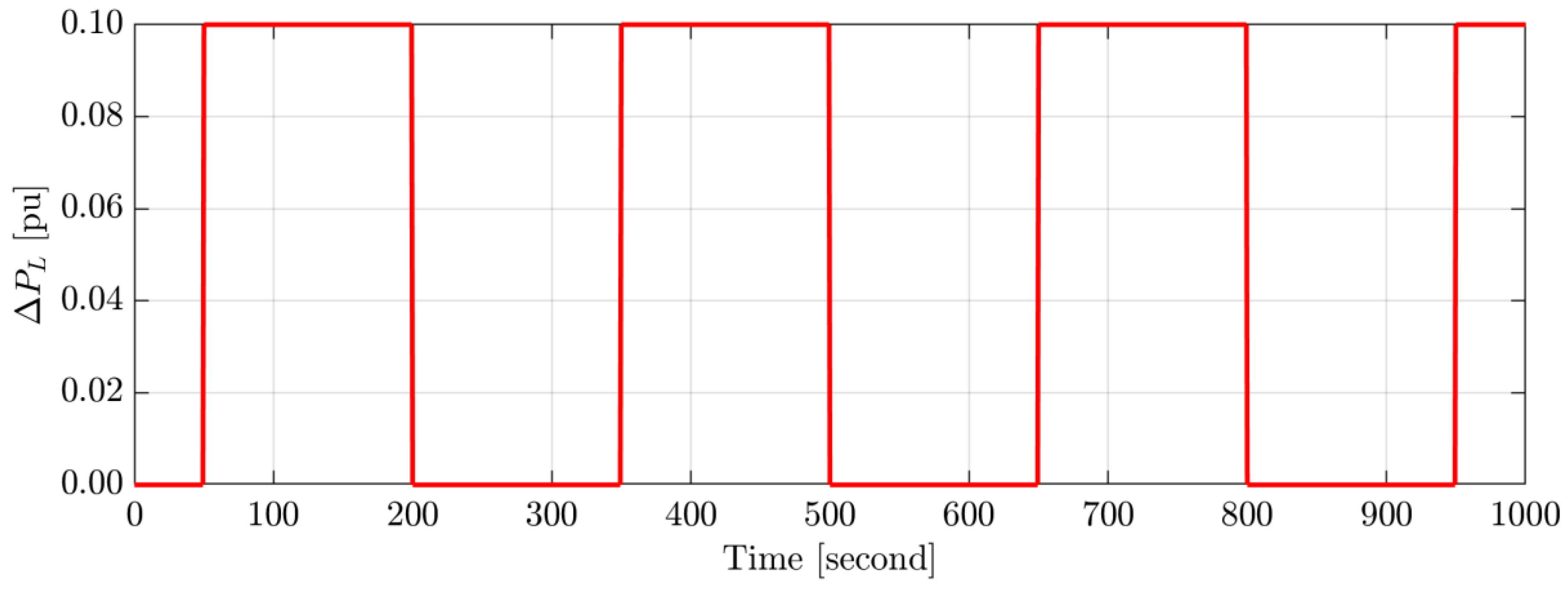
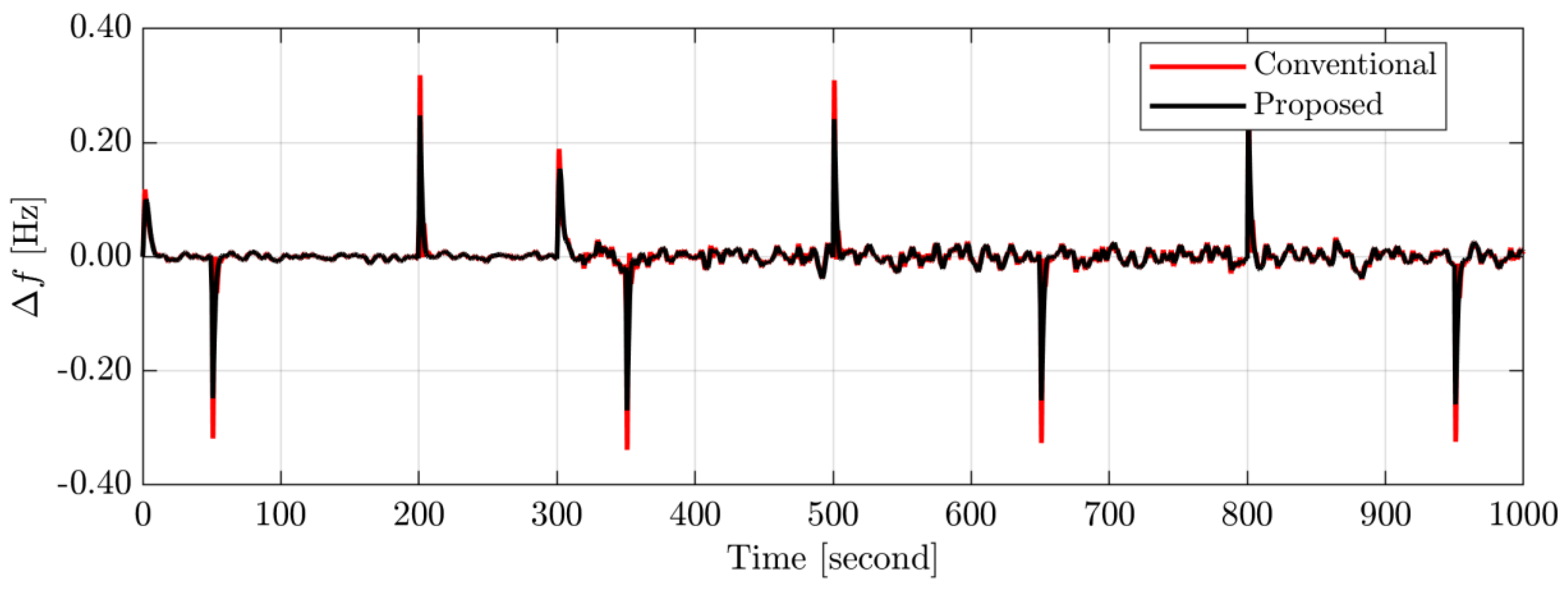
4.1. Scenario A: System Performance Appraisal during Abrupt Load Variations
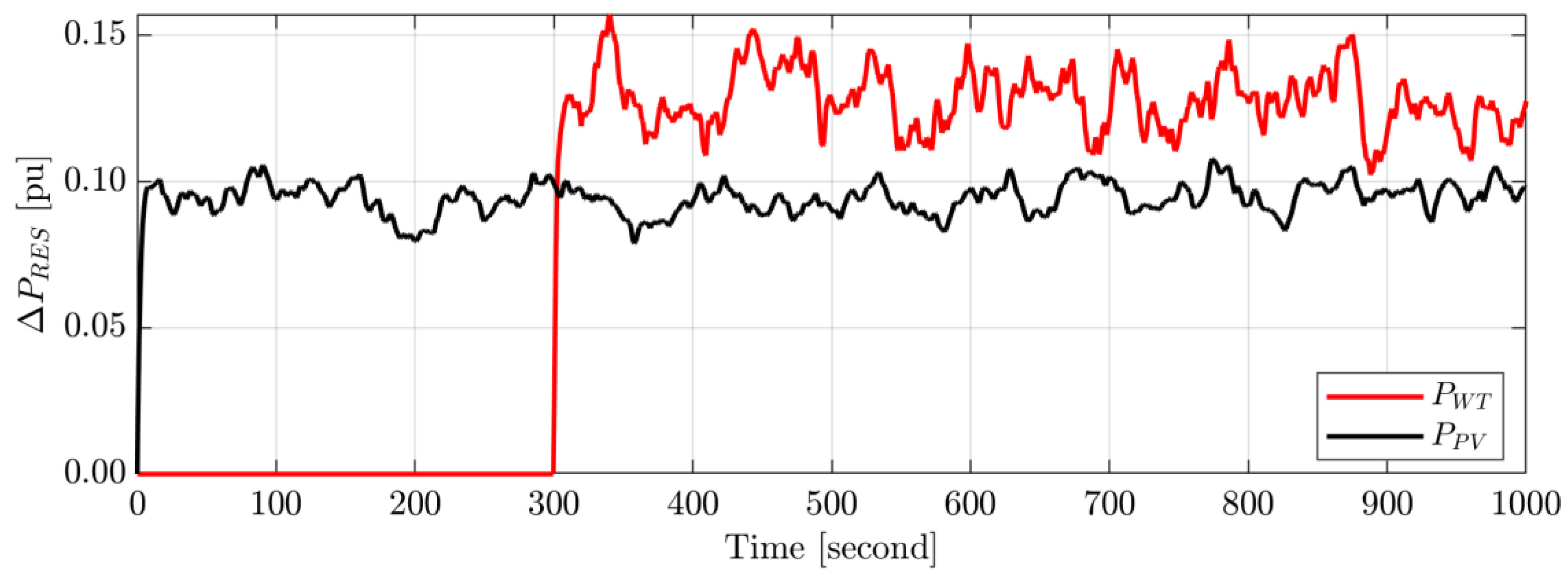
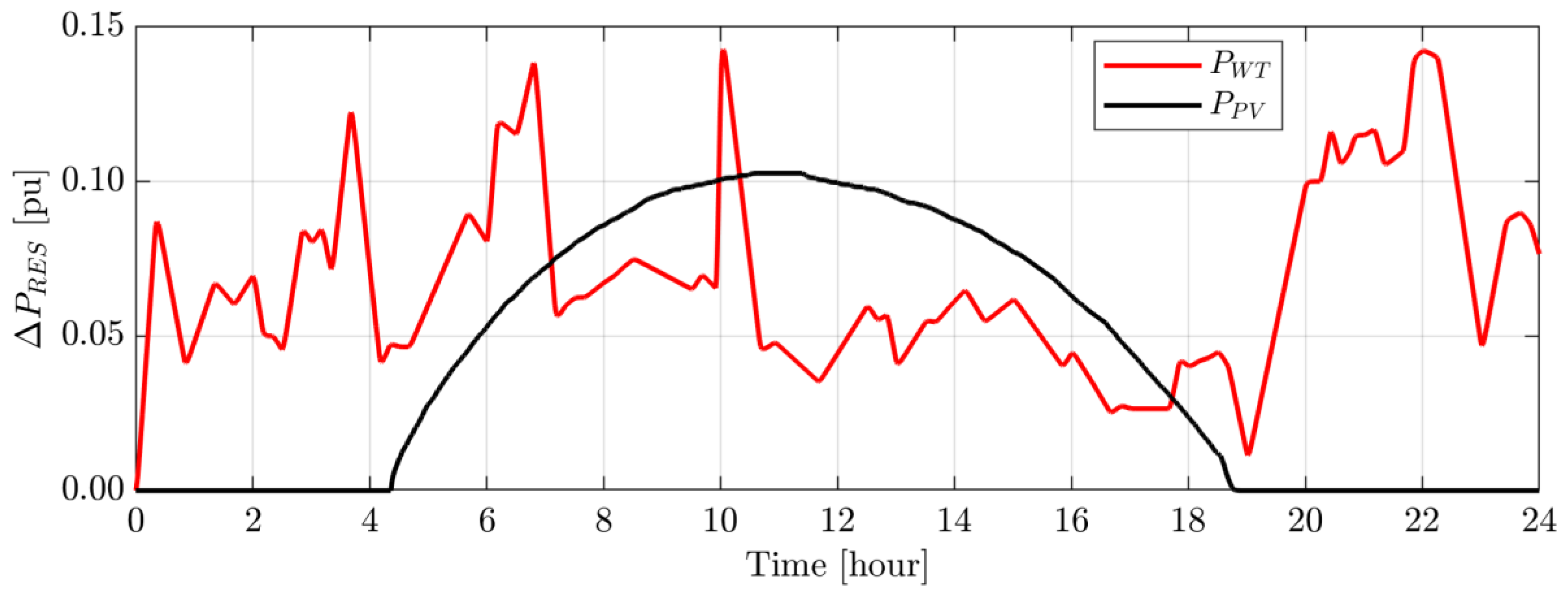
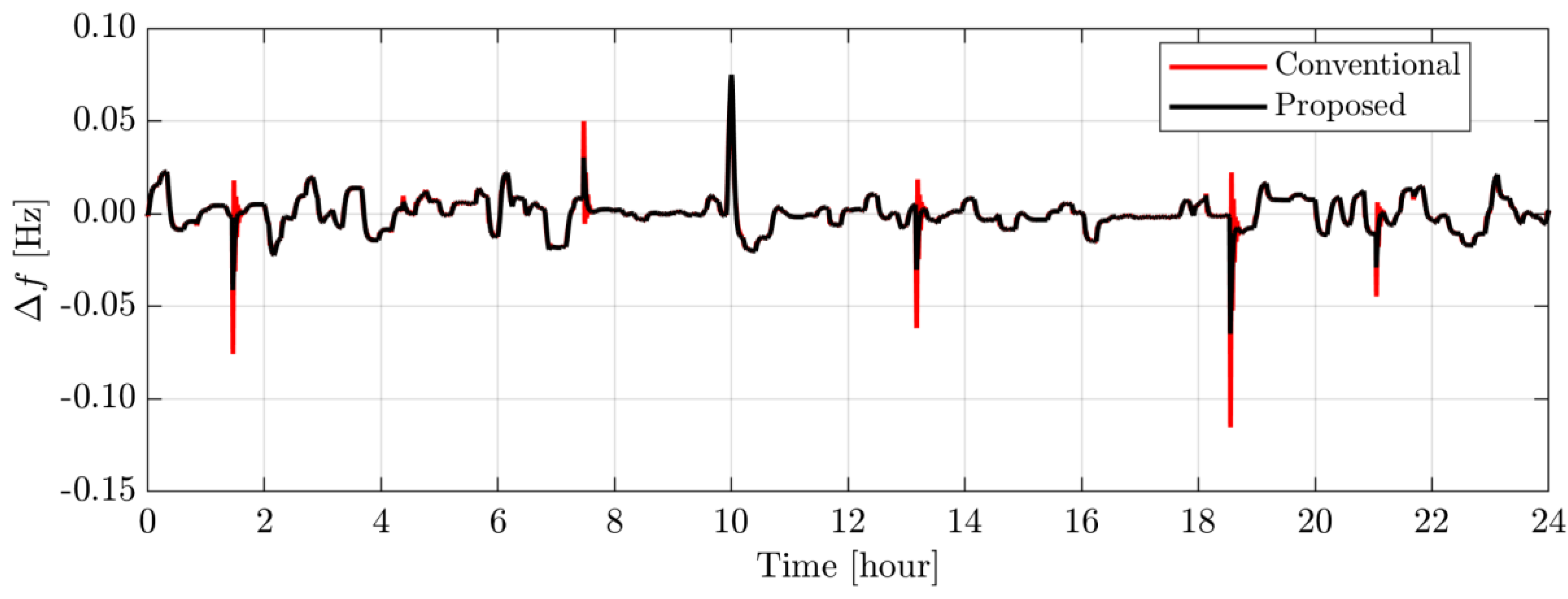
4.2. Scenario B: System Performance Assessment under Random Load Change and Random Renewables Generation
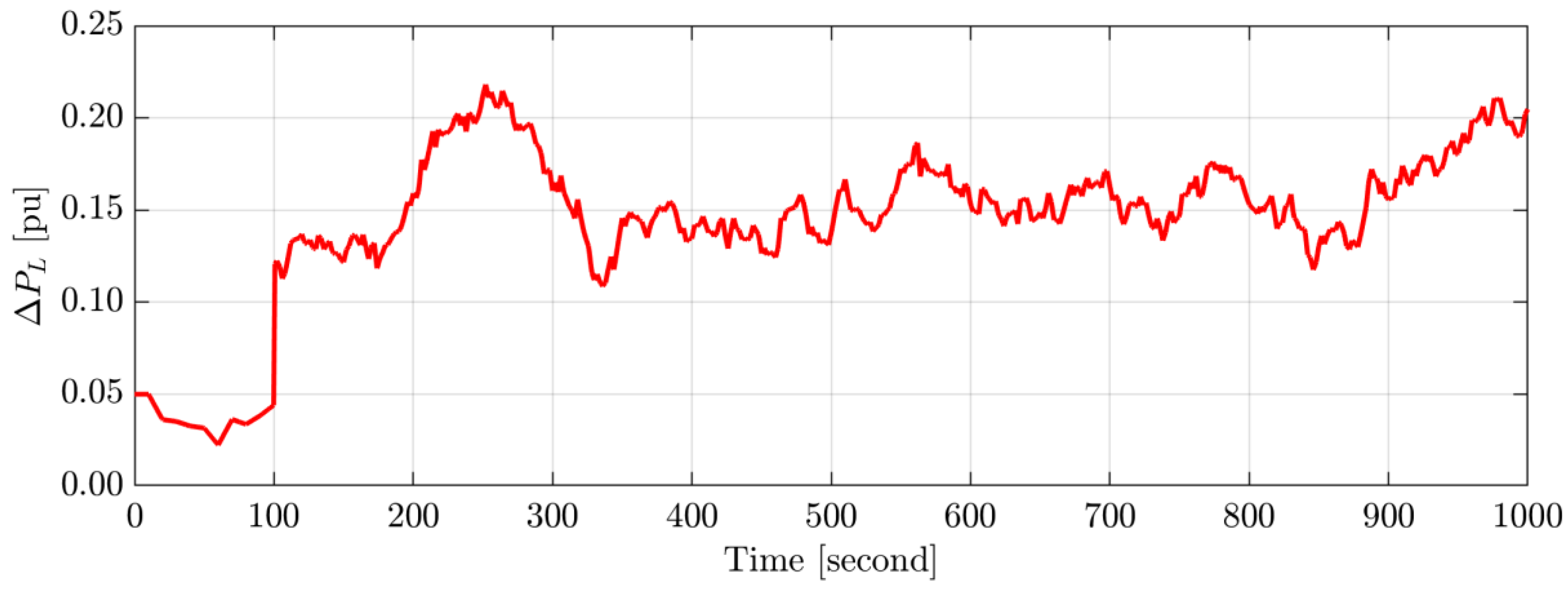
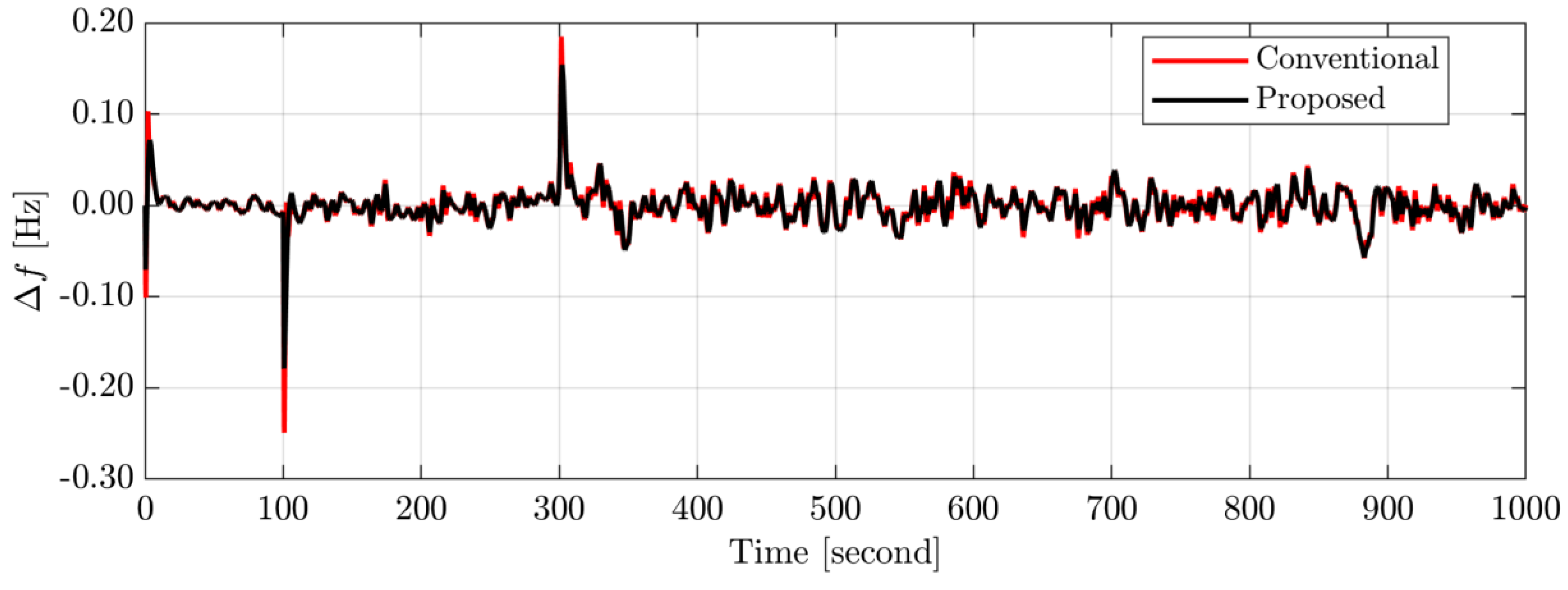
4.3. Scenario C: Long-Term Impact of Random Loads/RESs on System Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| RESs | Renewable energy sources |
| LFC | Load frequency control |
| ULM | Ultralocal model |
| µG | Microgrid |
| AVOA | African vultures optimization algorithm |
| PS | Power systems |
| ESSs | Energy storage systems |
| PV | Photovoltaic |
| PID | Proportional integral derivative |
| iPID | Intelligent proportional integral derivative |
| DGs | Distributed generators |
| PPs | Power plants |
| VU | Upper limit |
| VL | Lower limit |
| GRC | Generation rate constraint |
| D | Microgrid damping coefficient (pu MW/Hz) |
| H | Microgrid inertia constant (pu MW s) |
| Tg | Governor time constant (s) |
| Tt | Turbine time constant (s) |
| KI | Integral control gain |
| R | Speed regulation of μG, (Hz/pu MW) |
| TWT | Wind turbine time constant (s) |
| TPV | PV system time constant (s) |
| f | Nominal frequency (Hz) |
| SSM | State-space model |
| Δf | Frequency deviation (Hz) |
| ΔPWind | Wind speed change (pu) |
| ΔPSolar | PV solar change (pu) |
| ΔPL | Load power change (pu) |
| ∆PPV | PV output power (pu) |
| ∆PWT | Wind turbine output power (pu) |
| ∆PC | Incremental power (pu) |
| ∆Pm | Mechanical power change (pu) |
| ∆Pg | Governor power (pu) |
| E | Nonlinear unknown function |
| u | Control input of the system |
| y | Output variable of the system |
| m | Order of the control input |
| n | Order of the system output |
| F | Sum of the known and unknown parameters of the system |
| α | Nonphysical parameter of ULM |
| s | Laplace operator |
| Ts | Sampling time |
| Nf | Window length |
| y* | Reference of the system output |
| e | The error between the desired and actual output |
| AV | African vultures |
| N | Number of vultures |
| L1,L2,rand3, rand4, rand5, rand6,v, u | Random numbers ranging from 0 and 1 |
| Fi | The rate of vulture satiation calculated in the current iteration |
| n | Total number of the first and second groups of vultures |
| z | Variable of a random value ranging from −1 and 1 |
| h | Variable of a random value ranging from −2 and 2 |
| ω | A parameter with a predetermined value |
| R(i) | One of the finest vultures determined in the current iteration |
| D(i) | Distance between the vulture and the current optimum vulture |
| ub | Variable upper boundary |
| Lb | Variable lower boundary |
| P(i) | The location of the ith vulture |
| X | Random variable ranging from 0 and 2 |
| d(t) | The distance that separates the vulture and one of the two “best vultures” groups |
| LF | Lévy flight |
| β | Constant |
References
- Rihan, M.; Nasrallah, M.; Hasanin, B.; El-Shahat, A. A Proposed Controllable Crowbar for a Brushless Doubly-Fed Reluctance Generator, a Grid-Integrated Wind Turbine. Energies 2022, 15, 3894. [Google Scholar] [CrossRef]
- Murtaza, A.F.; Sher, H.A.; Usman Khan, F.; Nasir, A.; Spertino, F. Efficient MPP Tracking of Photovoltaic (PV) Array Through Modified Boost Converter With Simple SMC Voltage Regulator. IEEE Trans. Sustain. Energy 2022, 13, 1790–1801. [Google Scholar] [CrossRef]
- Bakeer, A.; Magdy, G.; Chub, A.; Bevrani, H. A sophisticated modeling approach for photovoltaic systems in load frequency control. Int. J. Electr. Power Energy Syst. 2022, 134, 107330. [Google Scholar] [CrossRef]
- Zakir, M.; Arshad, A.; Sher, H.A.; Lehtonen, M. An Optimal Power Management System Based on Load Demand and Resources Availability for PV Fed DC-Microgrid with Power-Sharing among Multiple Nanogrids. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Espoo, Finland, 18–21 October 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Nour, M.; Magdy, G.; Chaves-Ávila, J.P.; Sánchez-Miralles, Á.; Petlenkov, E. Automatic Generation Control of a Future Multisource Power System Considering High Renewables Penetration and Electric Vehicles: Egyptian Power System in 2035. IEEE Access 2022, 10, 51662–51681. [Google Scholar] [CrossRef]
- Sohrabzadi, E.; Gheisarnejad, M.; Esfahani, Z.; Khooban, M.H. A novel intelligent ultra-local model control-based type-II fuzzy for frequency regulation of multi-microgrids. Trans. Inst. Meas. Control 2021, 44, 1134–1148. [Google Scholar] [CrossRef]
- Tu, Z.; Fan, B.; Khazaei, J.; Zhang, W.; Liu, W. October. Optimal Reset-Control-Based Load Frequency Regulation in Isolated Microgrids. IEEE Trans. Sustain. Energy 2022, 13, 2239–2249. [Google Scholar] [CrossRef]
- Magdy, G.; Ali, H.; Xu, D. A new synthetic inertia system based on electric vehicles to support the frequency stability of low-inertia modern power grids. J. Clean. Prod. 2021, 297, 126595. [Google Scholar] [CrossRef]
- Jan, M.U.; Xin, A.; Rehman, H.U.; Abdelbaky, M.A.; Iqbal, S.; Aurangzeb, M. Frequency Regulation of an Isolated Microgrid With Electric Vehicles and Energy Storage System Integration Using Adaptive and Model Predictive Controllers. IEEE Access 2021, 9, 14958–14970. [Google Scholar] [CrossRef]
- Farrokhabadi, M.; Cañizares, C.A.; Bhattacharya, K. Frequency Control in Isolated/Islanded Microgrids Through Voltage Regulation. IEEE Trans. Smart Grid. 2017, 8, 1185–1194. [Google Scholar] [CrossRef]
- Ali, H.; Magdy, G.; Xu, D. A new optimal robust controller for frequency stability of interconnected hybrid microgrids considering non-inertia sources and uncertainties. Int. J. Electr. Power Energy Syst. 2021, 128, 106651. [Google Scholar] [CrossRef]
- Sibtain, D.; Murtaza, A.F.; Ahmed, N.; Sher, H.A.; Gulzar, M.M. Multi control adaptive fractional order PID control approach for PV/wind connected grid system. Int. Trans. Electr. Energy Syst. 2021, 31, e12809. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; El-Hameed, M.A. Efficient frequency controllers for autonomous two-area hybrid microgrid system using social-spider optimiser. IET Gener. Trans. Distrib. 2017, 11, 637–648. [Google Scholar] [CrossRef]
- Khooban, M.H.; Gheisarnejad, M. A Novel Deep Reinforcement Learning Controller Based Type-II Fuzzy System: Frequency Regulation in Microgrids. IEEE Trans. Emergy Top. Comput. Intell. 2020, 5, 689–699. [Google Scholar] [CrossRef]
- Aluko, A.O.; Dorrell, D.G.; Pillay-Carpanen, R.; Ojo, E.E. Frequency Control of Modern Multi-Area Power Systems Using Fuzzy Logic Controller. In Proceedings of the 2019 IEEE PES/ IAS PowerAfrica, Abuja, Nigeria, 20–23 August 2019; pp. 645–649. [Google Scholar] [CrossRef]
- Liao, K.; Xu, Y. A Robust Load Frequency Control Scheme for Power Systems Based on Second-Order Sliding Mode and Extended Disturbance Observer. IEEE Trans. Ind. Inform. 2018, 14, 3076–3086. [Google Scholar] [CrossRef]
- Magdy, G.; Ali, H.; Xu, D. Effective control of smart hybrid power systems: Cooperation of robust LFC and virtual inertia control system. CSEE J. Power Energy Systems 2022, 8, 1583–1593. [Google Scholar] [CrossRef]
- Bevrani, H.; Feizi, M.R.; Ataee, S. Robust Frequency Control in an Islanded Microgrid: H∞ and μ-Synthesis Approaches. IEEE Trans. Smart Grid. 2016, 7, 706–717. [Google Scholar] [CrossRef]
- Ma, M.; Liu, X.; Zhang, C. LFC for multi-area interconnected power system concerning wind turbines based on DMPC. IET Gener. Trans. Distrib. 2017, 11, 2689–2696. [Google Scholar] [CrossRef]
- Liu, T.; Chen, A.; Gao, F.; Liu, X.; Li, X.; Hu, S. Double-Loop Control Strategy With Cascaded Model Predictive Control to Improve Frequency Regulation for Islanded Microgrids. IEEE Trans. Smart Grid. 2022, 13, 3954–3967. [Google Scholar] [CrossRef]
- Magdy, G.; Shabib, G.; Elbaset, A.A.; Mitani, Y. A Novel Coordination Scheme of Virtual Inertia Control and Digital Protection for Microgrid Dynamic Security Considering High Renewable Energy Penetration. IET Renew. Power Gener. 2019, 13, 462–474. [Google Scholar] [CrossRef]
- Magdy, G.; Bakeer, A.; Nour, M.; Petlenkov, E. A New Virtual Synchronous Generator Design Based on the SMES System for Frequency Stability of Low-Inertia Power Grids. Energies 2020, 13, 5641. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y.; Watanabe, M.; Küfeoǧlu, S.K. Robust Virtual Inertia Control of an Islanded Microgrid Considering High Penetration of Renewable Energy. IEEE Access 2018, 6, 625–636. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Model-free control and intelligent pid controllers: Towards a possible trivialization of nonlinear control? IFAC Proc. Vol. 2009, 42, 1500–1531. [Google Scholar] [CrossRef]
- Michel, L.; Join, C.; Fliess, M.; Sicard, P.; Chériti, A. Model-free control of dc/dc converters. In Proceedings of the 2010 IEEE 12th Workshop on Control and Modeling for Power Electronics (COMPEL), Boulder, CO, USA, 28–30 June 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Thabet, H.; Ayadi, M.; Rotella, F. Experimental comparison of new adaptive PI controllers based on the ultra-local model parameter identification. Int. J. Control Autom. Syst. 2016, 14, 1520–1527. [Google Scholar] [CrossRef][Green Version]
- Zhang, Y.; Liu, X.; Liu, J.; Rodriguez, J.; Garcia, C. Model-free predictive current control of power converters based on ultra-local model. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020; pp. 1089–1093. [Google Scholar] [CrossRef]
- Magdy, G.; Bakeer, A.; Alhasheem, M. Superconducting energy storage technology-based synthetic inertia system control to enhance frequency dynamic performance in microgrids with high renewable penetration. Prot. Control Mod. Power Syst. 2021, 6, 36. [Google Scholar] [CrossRef]
- Ghazi, G.A.; Hasanien, H.M.; Al-Ammar, E.A.; Turky, R.A.; Ko, W.; Park, S.; Choi, H.-J. African Vulture Optimization Algorithm-Based PI Controllers for Performance Enhancement of Hybrid Renewable-Energy Systems. Sustainability 2022, 14, 8172. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]







| Variable | Value | Variable | Value |
|---|---|---|---|
| D | 0.015 | TWT | 1.5 |
| H | 0.083 | TPV | 1.8 |
| Tg | 0.1 | VU | 0.3 |
| Tt | 0.4 | VL | −0.3 |
| Ki | 0.05 | GRC | 20% |
| R | 2.4 | f | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakeer, A.; Magdy, G.; Chub, A.; Jurado, F.; Rihan, M. Optimal Ultra-Local Model Control Integrated with Load Frequency Control of Renewable Energy Sources Based Microgrids. Energies 2022, 15, 9177. https://doi.org/10.3390/en15239177
Bakeer A, Magdy G, Chub A, Jurado F, Rihan M. Optimal Ultra-Local Model Control Integrated with Load Frequency Control of Renewable Energy Sources Based Microgrids. Energies. 2022; 15(23):9177. https://doi.org/10.3390/en15239177
Chicago/Turabian StyleBakeer, Abualkasim, Gaber Magdy, Andrii Chub, Francisco Jurado, and Mahmoud Rihan. 2022. "Optimal Ultra-Local Model Control Integrated with Load Frequency Control of Renewable Energy Sources Based Microgrids" Energies 15, no. 23: 9177. https://doi.org/10.3390/en15239177
APA StyleBakeer, A., Magdy, G., Chub, A., Jurado, F., & Rihan, M. (2022). Optimal Ultra-Local Model Control Integrated with Load Frequency Control of Renewable Energy Sources Based Microgrids. Energies, 15(23), 9177. https://doi.org/10.3390/en15239177











