A Modified Calculation Method for a Centered Water Nozzle Steam–Water Injector
Abstract
1. Introduction
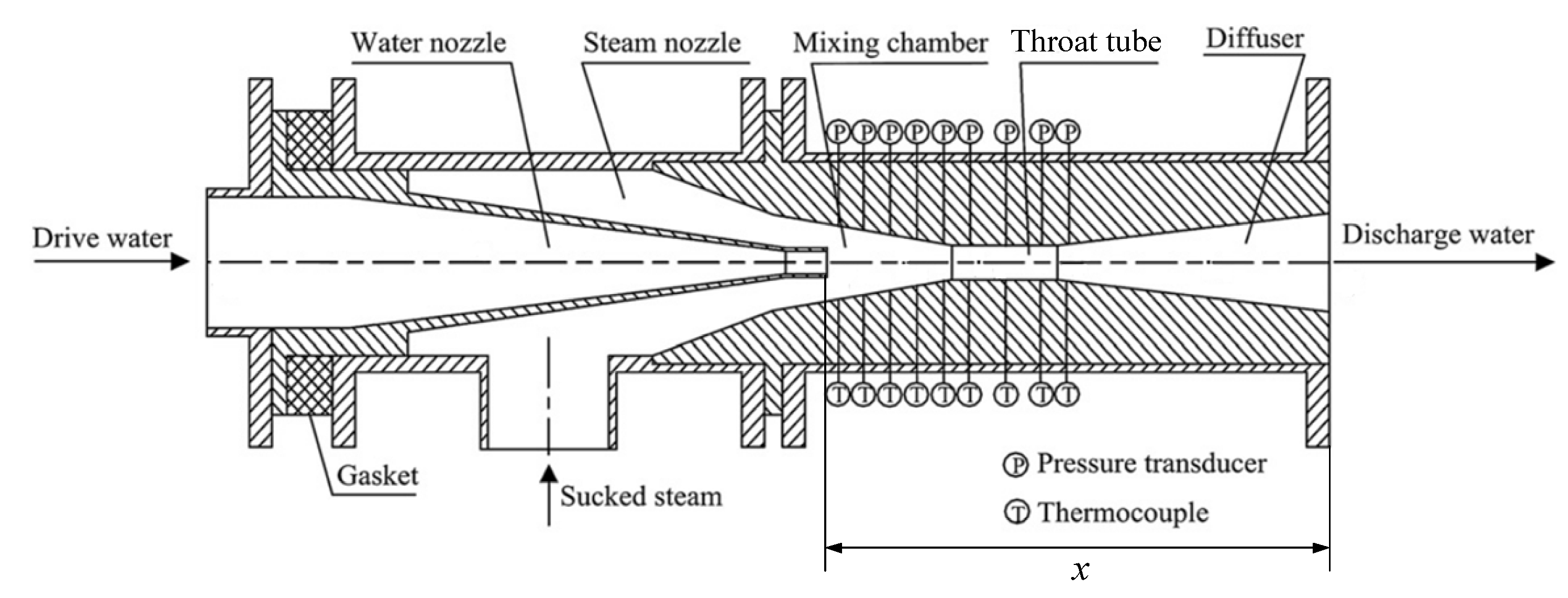
2. Modeling of Centered Water Nozzle Steam–Water Injector
2.1. Modeling of Water Nozzle
2.2. Modeling of the Steam Nozzle
2.3. Modeling of Mixing Section
2.3.1. Steam–Water Two-Phase Flow Model
2.3.2. Single-Phase Flow Model
2.4. Modeling of Shock Wave
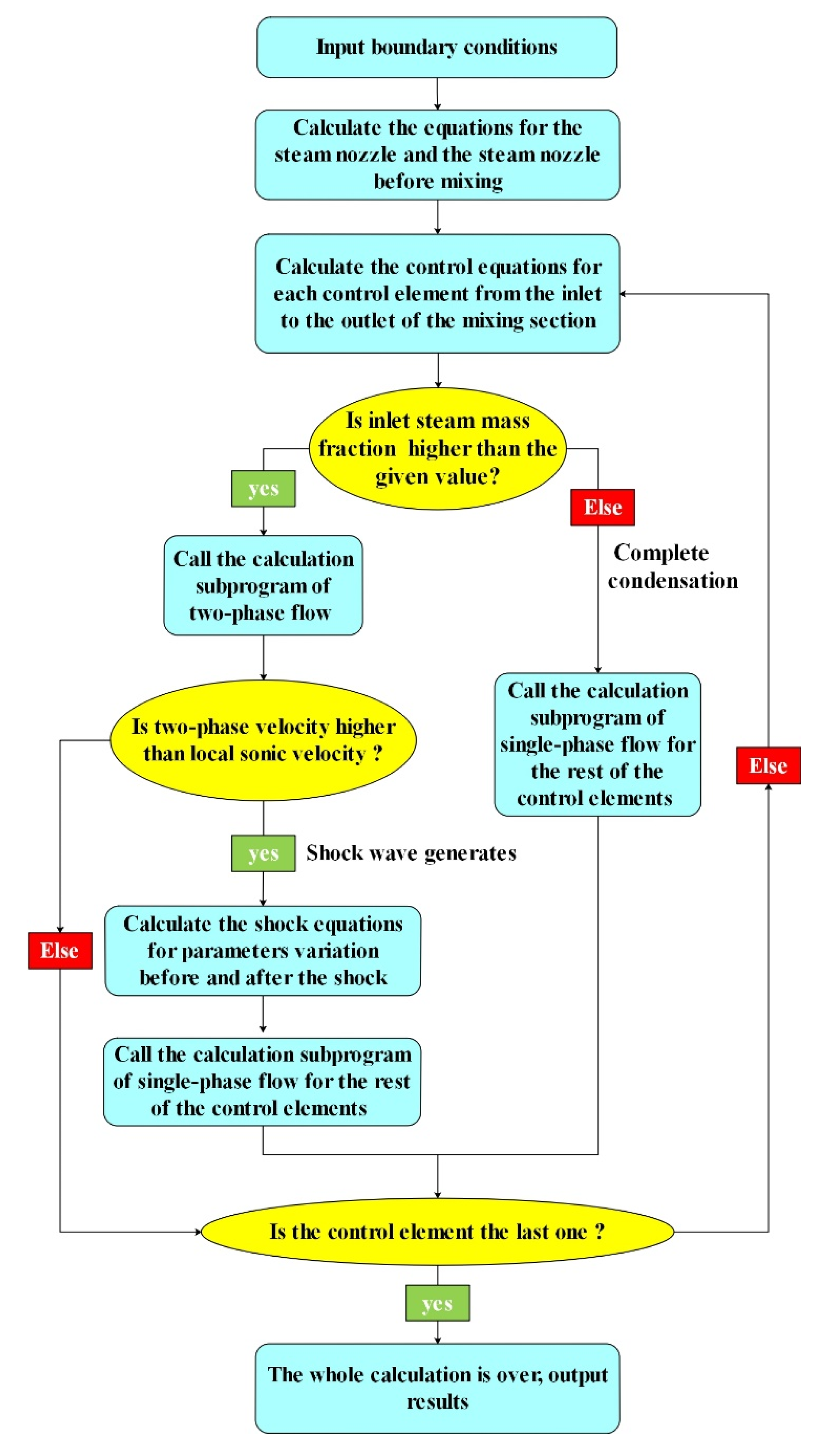
2.5. Solution of the Model
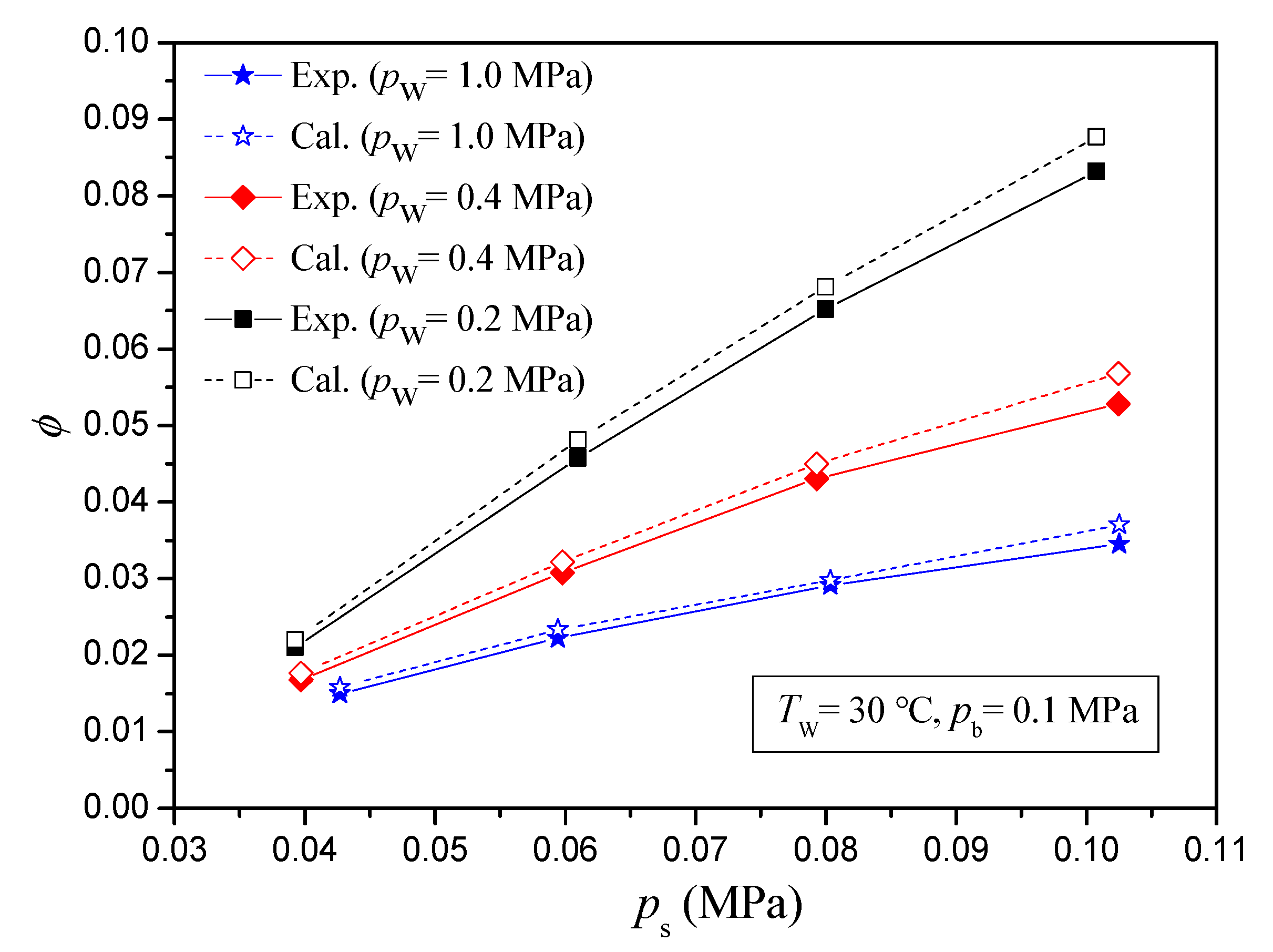
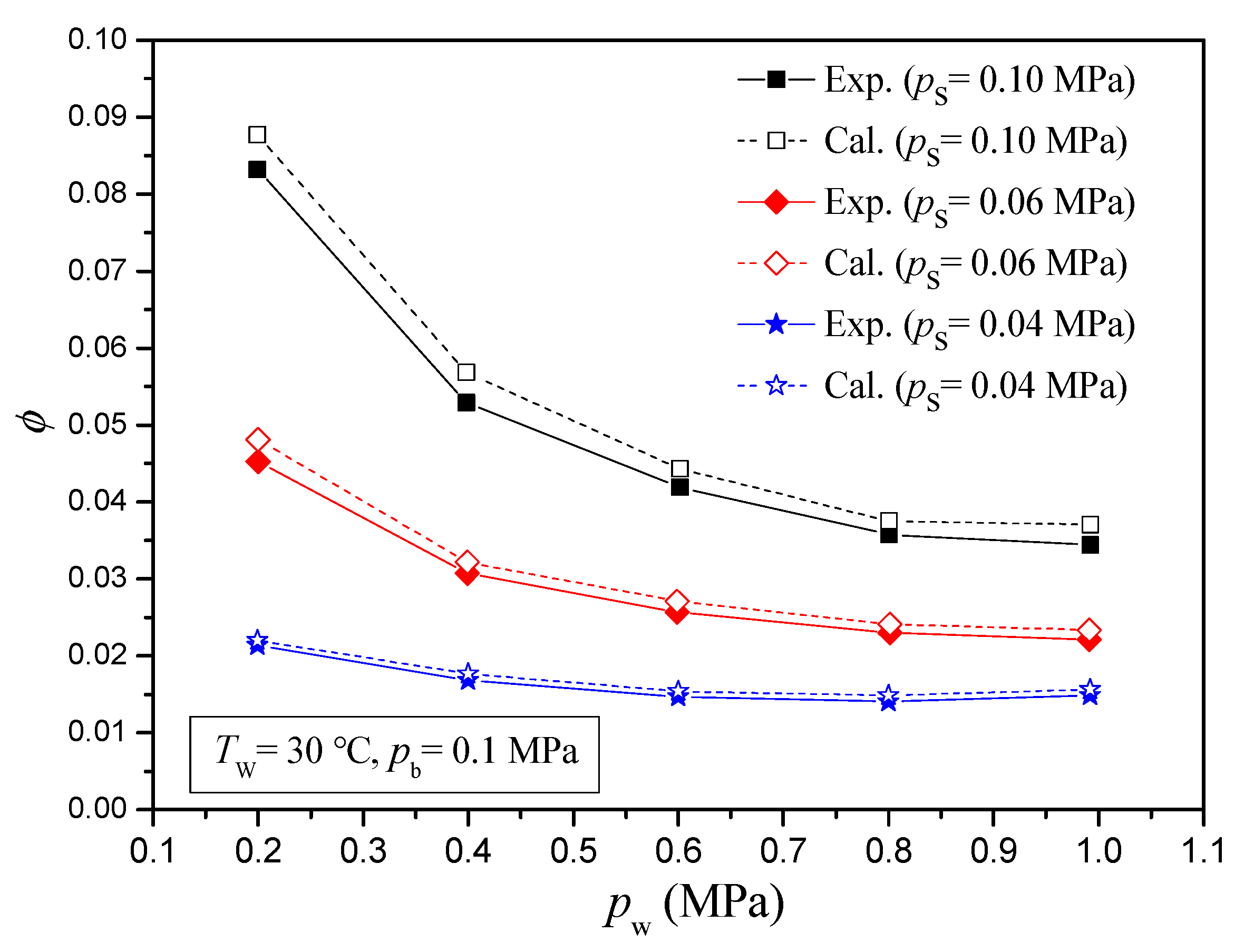
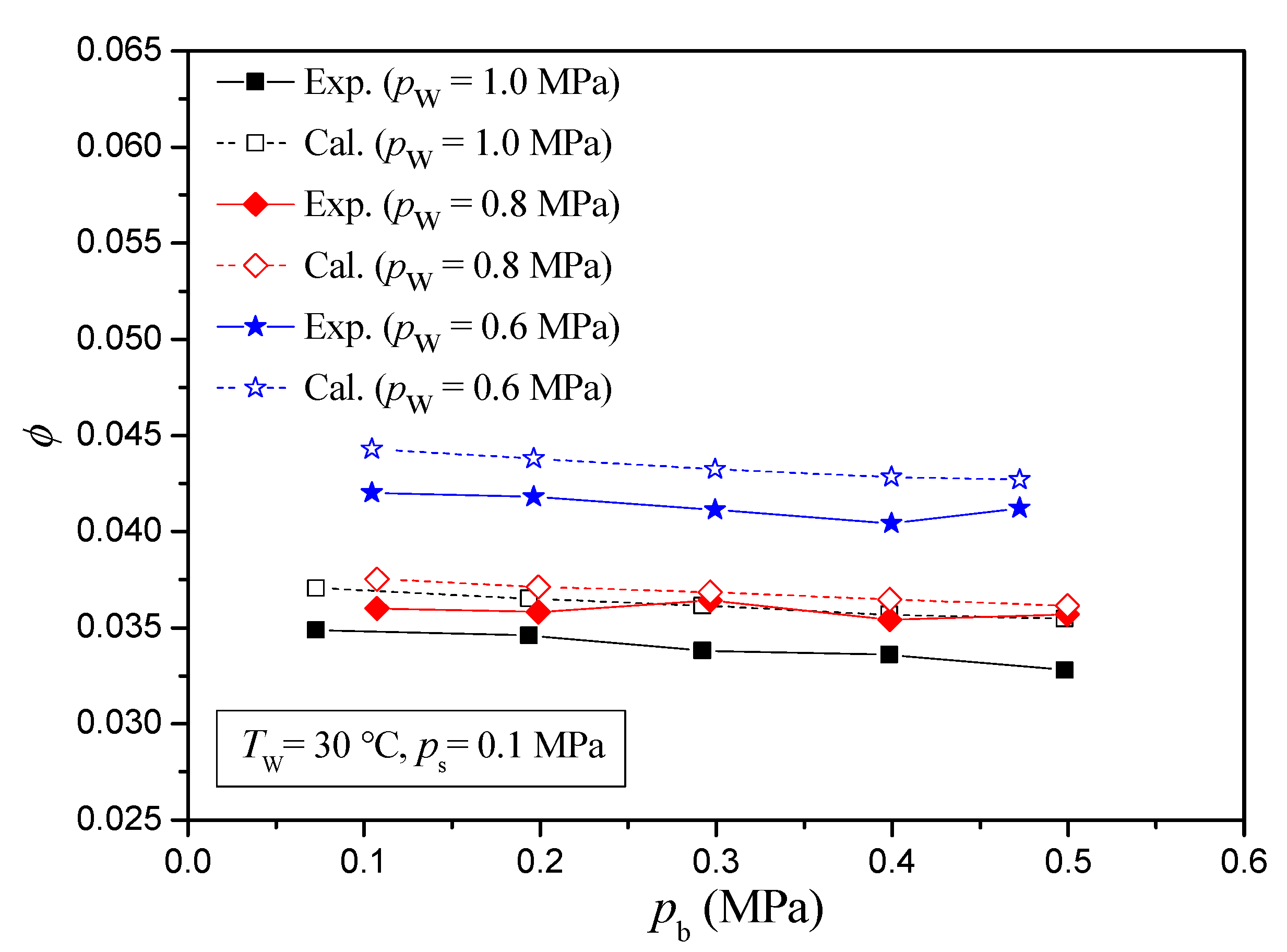
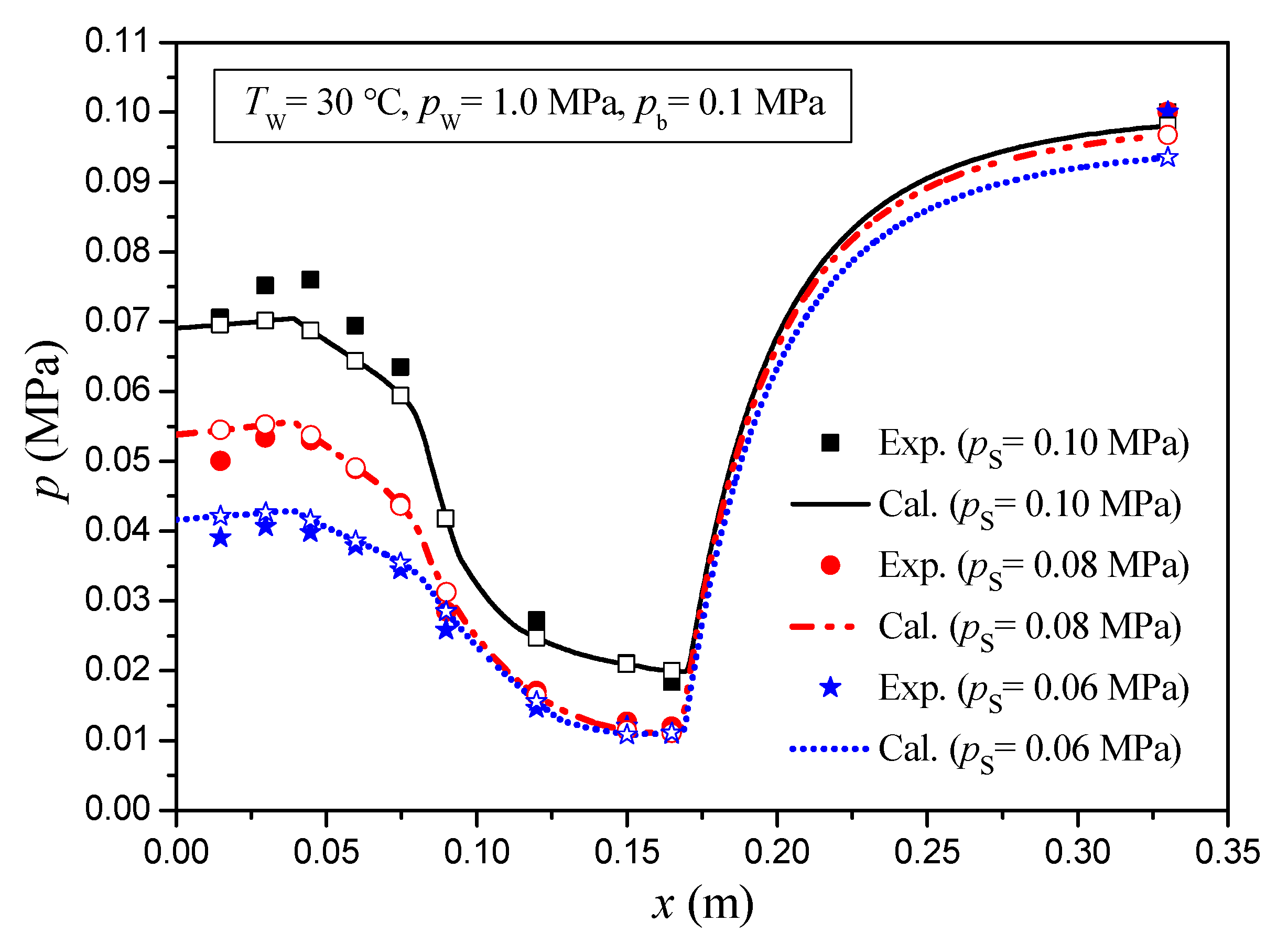
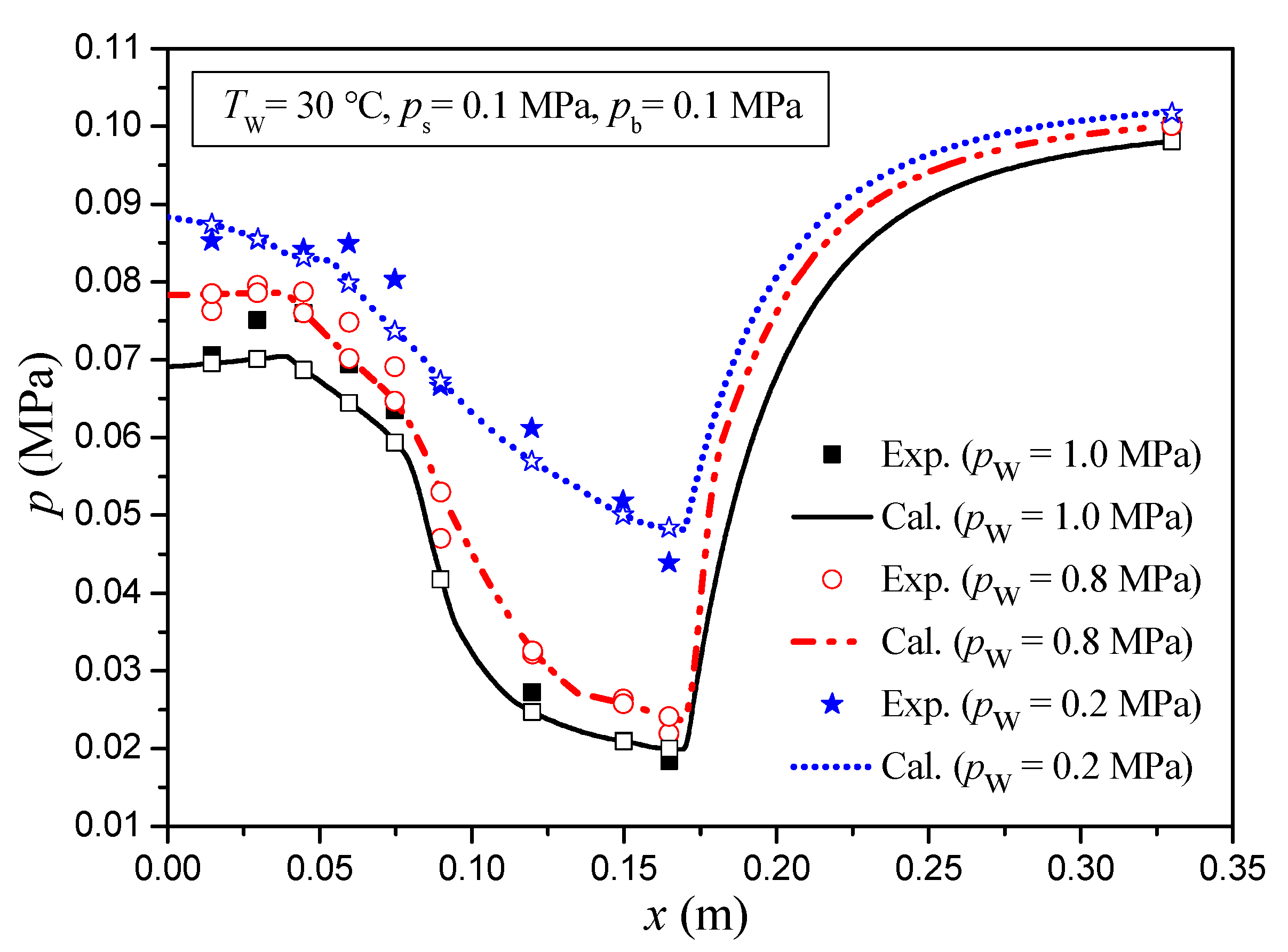
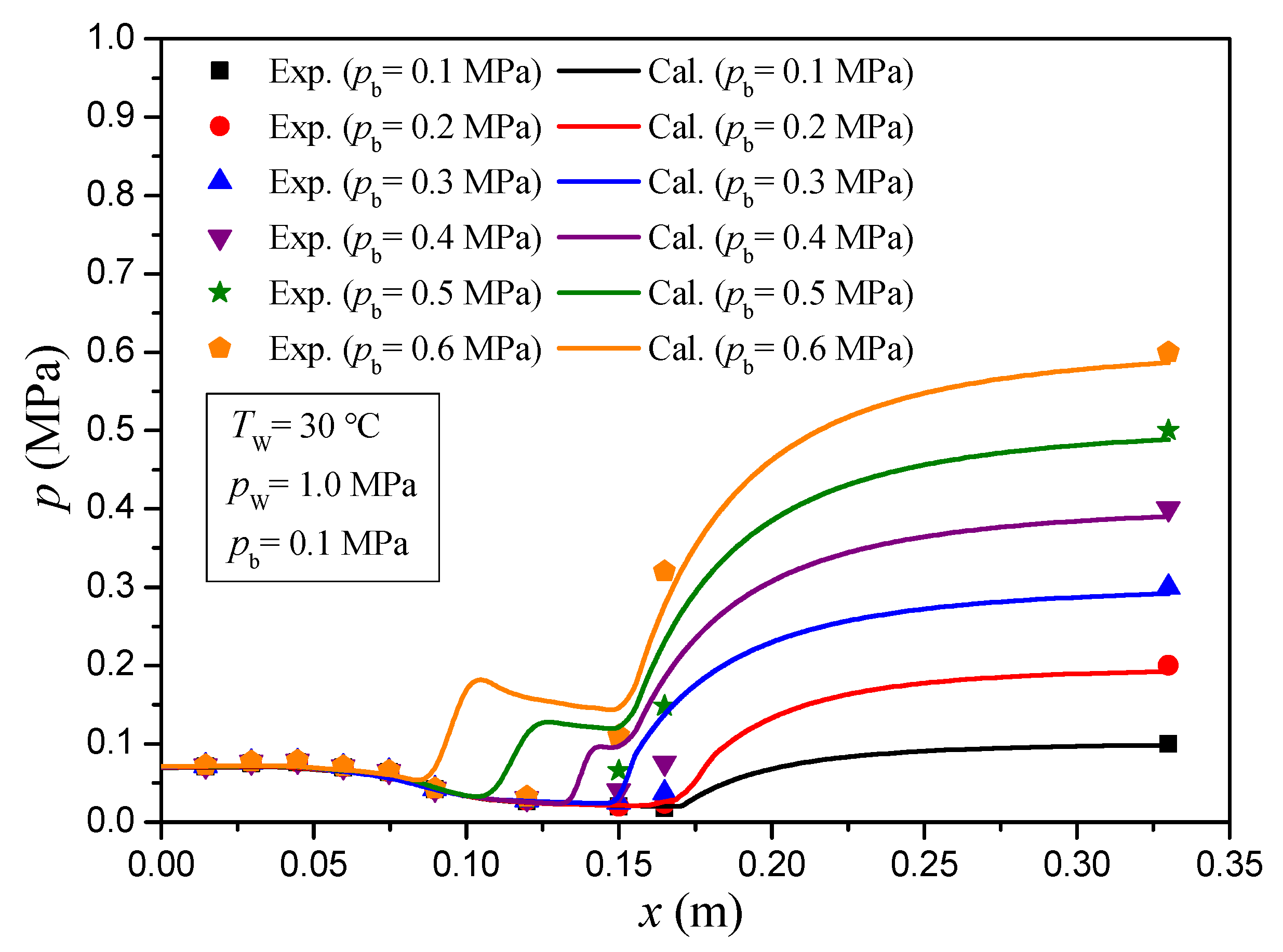
3. Model Validation and Discussion
4. Conclusions
- (1)
- The calculation method consists of a water nozzle model, a steam nozzle model, a mixing section model, and a shock wave model.
- (2)
- From the comparisons under different inlet steam pressures, different inlet water pressures, and different back pressures, it is known that the calculated results are in good agreement with the experimental results.
- (3)
- The model in this study can predict the operating characteristics in the injector under different conditions. When the back pressure is small, no shock wave occurs in the mixing section, but with the back pressure increasing, the pressure undergoes a dramatic increase in the throat tube, and the shock wave position moves towards the inlet of the mixing section. However, due to the complexity of shock wave characteristics, it is necessary to conduct a more in-depth study of shock wave characteristics in the mixing section to determine more detailed boundary conditions for the shock wave generation.
Author Contributions
Funding
Conflicts of Interest
References
- Takeya, Y.; Miwa, S.; Hibiki, T.; Mori, M. Application of steam injector to improved safety of light water reactors. Prog. Nucl. Energy 2015, 78, 80–100. [Google Scholar] [CrossRef]
- Fukuichi, A.; Abe, Y.; Fujiwara, A.; Kawamoto, Y.; Iwaki, C.; Narabayashi, T.; Mori, M.; Ohmori, S. Study on turbulent behavior of water jet in supersonic steam injector. In Proceedings of the 16th International Conference on Nuclear Engineering, Orlando, FL, USA, 11–15 May 2008. [Google Scholar]
- Yan, J.; Chong, D.; Wu, X. Effect of swirling vanes on performance of steam-water jet injector. Appl. Therm. Eng. 2010, 30, 623–630. [Google Scholar] [CrossRef]
- Li, W.; Liu, M.; Yan, J.; Wang, J.; Chong, D. Exergy analysis of centered water nozzle steam-water injector. Exp. Therm. Fluid Sci. 2018, 94, 77–88. [Google Scholar] [CrossRef]
- Miwa, S.; Endo, H.; Moribe, T.; Sakashita, H.; Mori, M.; Hibiki, T. Investigation of the thermal-hydraulic characteristics of supersonic steam injector. Appl. Therm. Eng. 2016, 109, 261–271. [Google Scholar] [CrossRef]
- Miwa, S.; Endo, H.; Moribe, T.; Mori, M. Investigation of the supersonic steam injector operation mode. Nucl. Eng. Des. 2018, 334, 57–65. [Google Scholar] [CrossRef]
- Miwa, S.; Xu, Y.; Hibiki, T.; Sakashita, H.; Sawa, K. Pressure elevation of high-performance steam-water condensing-injector. Int. J. Heat Mass Transf. 2021, 170, 120971. [Google Scholar] [CrossRef]
- Abe, Y.; Shibayama, S. Study on the characteristics of the supersonic steam injector. Nucl. Eng. Des. 2014, 268, 191–202. [Google Scholar] [CrossRef]
- Zhang, Z.; Chong, D.; Yan, J. Modeling and experimental investigation on water-driven steam injector for waste heat recovery. Appl. Therm. Eng. 2012, 40, 189–197. [Google Scholar] [CrossRef]
- Yan, J.; Shao, S.; Liu, J.; Zhang, Z. Experiment and analysis on performance of steam-driven jet injector for district-heating system. Appl. Therm. Eng. 2005, 25, 1153–1167. [Google Scholar] [CrossRef]
- Trela, M.; Kwidzinski, R.; Butrymowicz, D.; Karwacki, J. Exergy analysis of two-phase steam-water injector. Appl. Therm. Eng. 2010, 30, 340–346. [Google Scholar] [CrossRef]
- Kwidzinski, R. Experimental investigation of condensation wave structure in steam-water injector. Int. J. Heat Mass Transf. 2015, 91, 594–601. [Google Scholar] [CrossRef]
- Kwidzinski, R. Experimental and theoretical investigations of two-phase flow in low pressure steam-water injector. Int. J. Heat Mass Transf. 2019, 144, 118618. [Google Scholar] [CrossRef]
- Kwidzinski, R. Condensation heat and mass transfer in steam-water injectors. Int. J. Heat Mass Transf. 2021, 164, 120582. [Google Scholar] [CrossRef]
- Deberne, N.; Leone, J.F.; Duque, A.; Lallemand, A. A model for calculation of steam injector performance. Int. J. Multiphase Flow 1999, 25, 841–855. [Google Scholar] [CrossRef]
- Xu, Q.; Liang, L.; She, Y.; Xie, X.; Guo, L. Numerical investigation on thermal hydraulic characteristics of steam jet condensation in subcooled water flow in pipes. Int. J. Heat Mass Transf. 2022, 184, 122277. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, C.; Liu, Q.; Zhu, Y.; Zhou, H.; Guo, L. Interfacial characteristics of steam jet condensation in subcooled water pipe flow—An experimental and numerical study. Chem. Eng. Sci. 2022, 251, 117457. [Google Scholar] [CrossRef]
- Zhao, Q.; Fu, P.; Chong, D.; Chen, W.; Liu, J.; Yan, J. Steam entrainment and heat transfer characteristic of steam submerged jet condensation within steam-water mixture layer. Int. J. Heat Mass Transf. 2023, 201, 123600. [Google Scholar] [CrossRef]
- Munson, B.R.; Youn, D.F.; Okiishi, T.H. Fundamentals of Fluid Mechanics, 4th ed.; John Wiley & Sons Inc.: New York, NY, USA, 2002. [Google Scholar]
- Reisel, J.R. Principles of Engineering Thermodynamics, 1st ed.; Cengage Learning: Stamford, CT, USA, 2015. [Google Scholar]
- Beithou, N.; Aybar, H.S. A mathematical model for steam-driven jet pump. Int. J. Multiph. Flow 2000, 26, 1609–1619. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, H.; Wang, L.; Yu, Z.; Mao, X. Modeling and investigation of a steam-water injector. Energ. Convers. Manage. 2017, 151, 170–178. [Google Scholar] [CrossRef]
- Lee, W.H. A pressure iteration scheme for two-phase flow modeling. In Multiphase Transport Fundamentals, Reactor Safety, Applications; Veziroglu, T.N., Ed.; Hemisphere Publishing: Washington, DC, USA, 1980; Volume 1. [Google Scholar]
- Lee, W.H.; Lyczkowski, R.W. The basic character of five two-phase flow model equation sets. Int. J. Numer. Meth. Fluids 2000, 33, 1075–1098. [Google Scholar] [CrossRef]
- Liu, X.; Hao, Y. Numerical simulation of vapor-liquid two-phase flow in a closed loop oscillating heat pipe. In Proceedings of the ASME International Mechanical Engineering Congress & Exposition, Lake Buena Vista, FL, USA, 13–19 November 2009. [Google Scholar]
- Wang, J.; Ma, H.; Zhu, Q.; Dong, Y.; Yue, K. Numerical and experimental investigation of pulsating heat pipes with corrugated configuration. Appl. Therm. Eng. 2016, 102, 158–166. [Google Scholar] [CrossRef]
- Chen, J.; Huang, Y.; Niu, Z.; Chen, Y.; Luo, X. Performance analysis of a novel organic Rankine cycle with a vapor-liquid ejector. Energ. Convers. Manage. 2018, 157, 382–395. [Google Scholar] [CrossRef]
- Liu, D. The speed of sound in two-phase flows under the condition of velocity-equilibrium between phases. Acta Mech. Sin. 1999, 22, 660–669. (In Chinese) [Google Scholar]


| References | Injector | Model | Calculation Results |
|---|---|---|---|
| Zhang et al. [9] | Centered water nozzle steam–water injector | The calculation method consisted of water nozzle model, steam nozzle model, mixing chamber model, throat tube model, and diffuser model, but no shock wave model. It was assumed that steam completely condensed into water in the mixing chamber and throat tube, and only the water existed in the diffuser. | The shock wave characteristics were not reflected in the calculation results, and the pressure distribution along the flow direction in the diffuser was not calculated. |
| Yan et al. [10] | Centered steam nozzle steam–water injector | The calculation method consisted of water nozzle model, steam nozzle model, mixing chamber model, and diffuser model, but shock wave model was not considered. It was assumed that steam completely condensed into water at the end section of the mixing chamber, and only the water existed in the diffuser. | An empirical equation to calculate the outlet water pressure of the water nozzle was given according to the experimental results, and the performance parameters of the injector were not calculated. |
| Kwidzinski [13] | Centered steam nozzle steam–water injector | A model consisting of a water nozzle, steam nozzle, mixing chamber, condensation wave, and diffuser was considered. It was assumed that steam completely condensed into water in the mixing chamber, and only the water existed in the diffuser. | Based on his calculation method, the pressure along the flow direction in the diffuser was calculated according to the Bernoulli equation. |
| Deberne et al. [15] | Centered steam nozzle steam–water injector | A model consisting of a water nozzle, steam nozzle, mixing chamber, shock wave, and diffuser was considered. It was assumed that steam completely condensed into water in the mixing chamber, and only the water existed in the diffuser. | The shock wave characteristics were experimentally measured but not calculated, and the calculated pressure along the flow direction in the injector was not given. |
| This study | Centered water nozzle steam–water injector | A model consisting of a water nozzle, steam nozzle, mixing chamber, shock wave, and diffuser is considered. Steam may not completely condense into water in the mixing chamber or throat tube, so the continuous condensation of steam in the diffuser must be considered. | Steam continues to condense into water in the diffuser based on the calculation method under a certain operating condition, and the calculated results show that the calculation method can predict the shock wave characteristics. |
| Parameters | Symbol/Unit | Values |
|---|---|---|
| Inlet water pressure | pw/MPa | 0.1–1.0 |
| Inlet water temperature | Tw/°C | 25–70 |
| Inlet steam pressure | ps/MPa | 0.02–0.1 |
| Inlet steam temperature | Ts/°C | 95–120 |
| Water nozzle inlet diameter | d1/mm | 80 |
| Water nozzle outlet diameter | d2/mm | 14 |
| Water nozzle inlet straight length | L1/mm | 80 |
| Water nozzle convergence length | L2/mm | 267 |
| Water nozzle outlet straight length | L3/mm | 33 |
| Steam nozzle inlet diameter | d5/mm | 113 |
| Mixing chamber convergence length | L4/mm | 85 |
| Throat tube diameter | d3/mm | 21 |
| Throat tube length | L5/mm | 70 |
| Diffuser outlet diameter | d4/mm | 60 |
| Diffuser divergence length | L6/mm | 180 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, H.; Xiao, Q.; Long, C.; Liu, J.; Shi, L.; Tang, L. A Modified Calculation Method for a Centered Water Nozzle Steam–Water Injector. Energies 2022, 15, 9159. https://doi.org/10.3390/en15239159
Ke H, Xiao Q, Long C, Liu J, Shi L, Tang L. A Modified Calculation Method for a Centered Water Nozzle Steam–Water Injector. Energies. 2022; 15(23):9159. https://doi.org/10.3390/en15239159
Chicago/Turabian StyleKe, Hanbing, Qi Xiao, Chengyi Long, Jialun Liu, Leitai Shi, and Linghong Tang. 2022. "A Modified Calculation Method for a Centered Water Nozzle Steam–Water Injector" Energies 15, no. 23: 9159. https://doi.org/10.3390/en15239159
APA StyleKe, H., Xiao, Q., Long, C., Liu, J., Shi, L., & Tang, L. (2022). A Modified Calculation Method for a Centered Water Nozzle Steam–Water Injector. Energies, 15(23), 9159. https://doi.org/10.3390/en15239159








