Using Machine Learning to Predict Multiphase Flow through Complex Fractures
Abstract
1. Introduction
2. Data
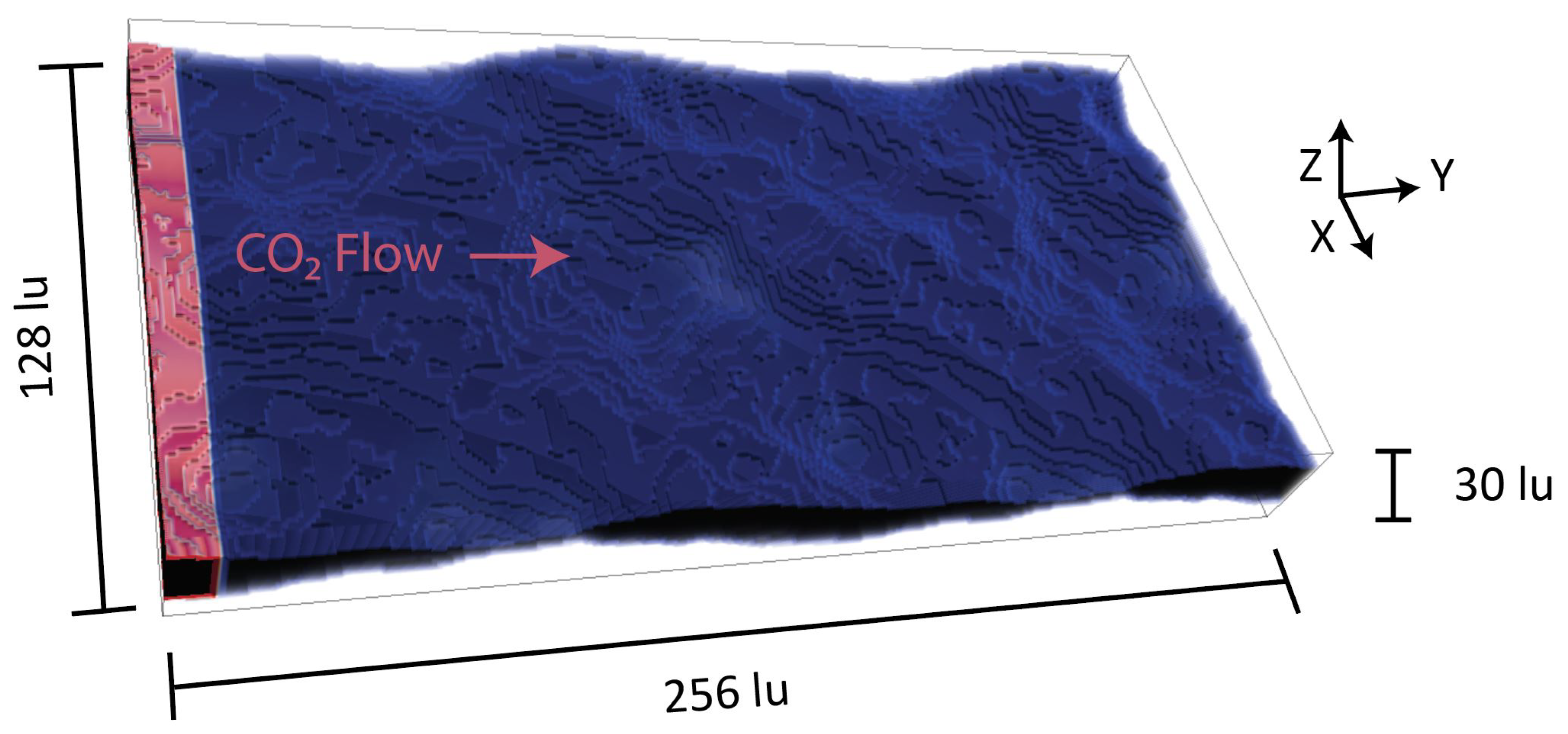
2.1. Physics Based Simulations
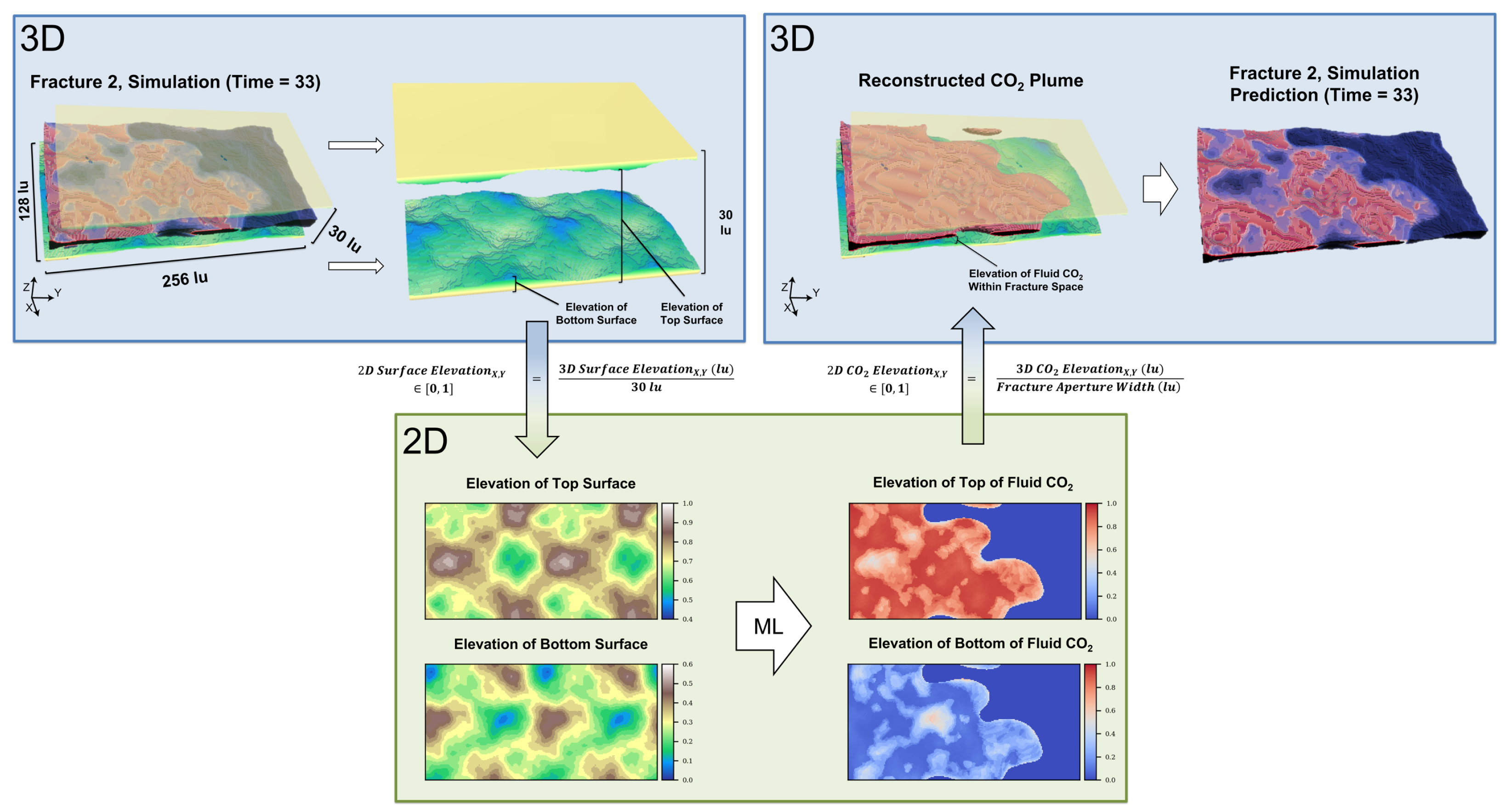
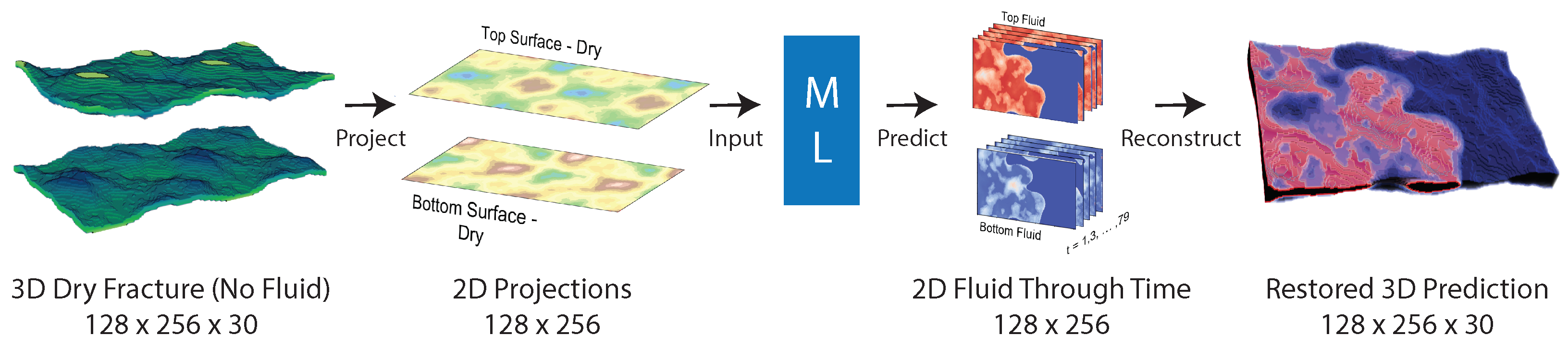
2.2. Data Processing
| Algorithm 1 3D to 2D fracture conversion. |
|
|
|
|
|
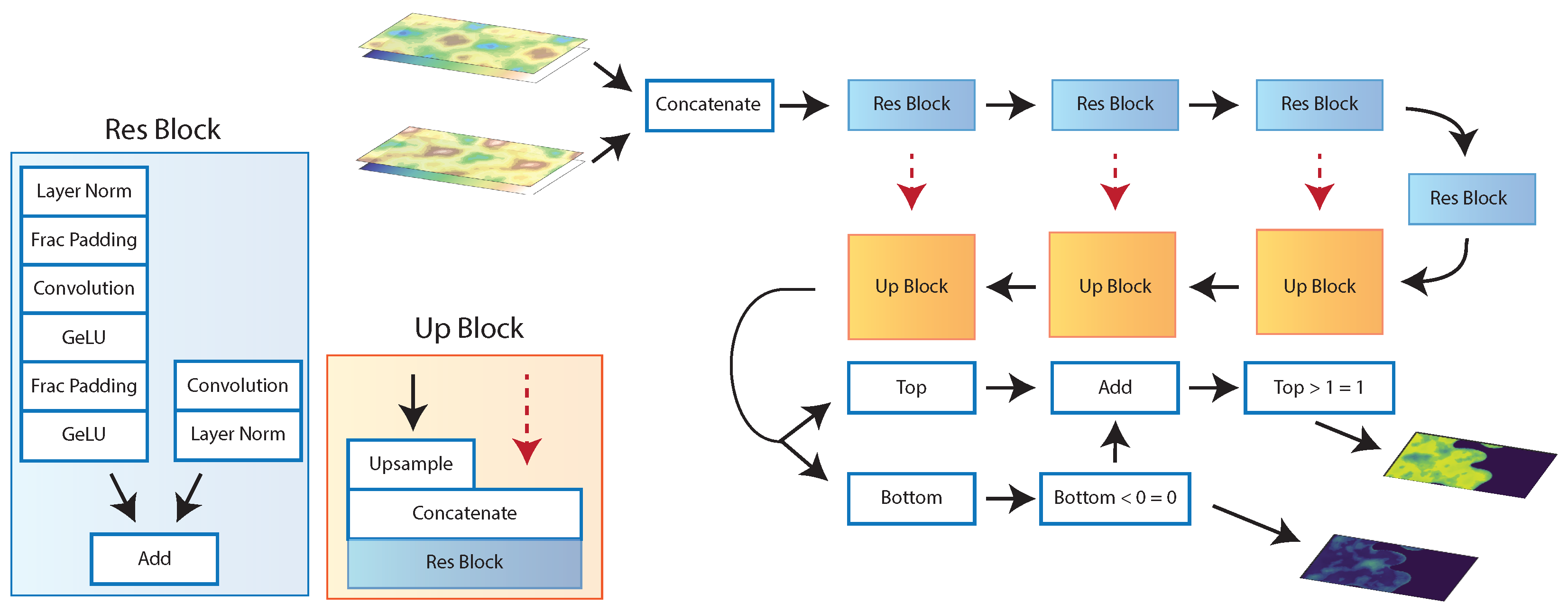
3. Machine Learning Model
3.1. Network Architecture Development
3.2. Loss Function
3.3. Training
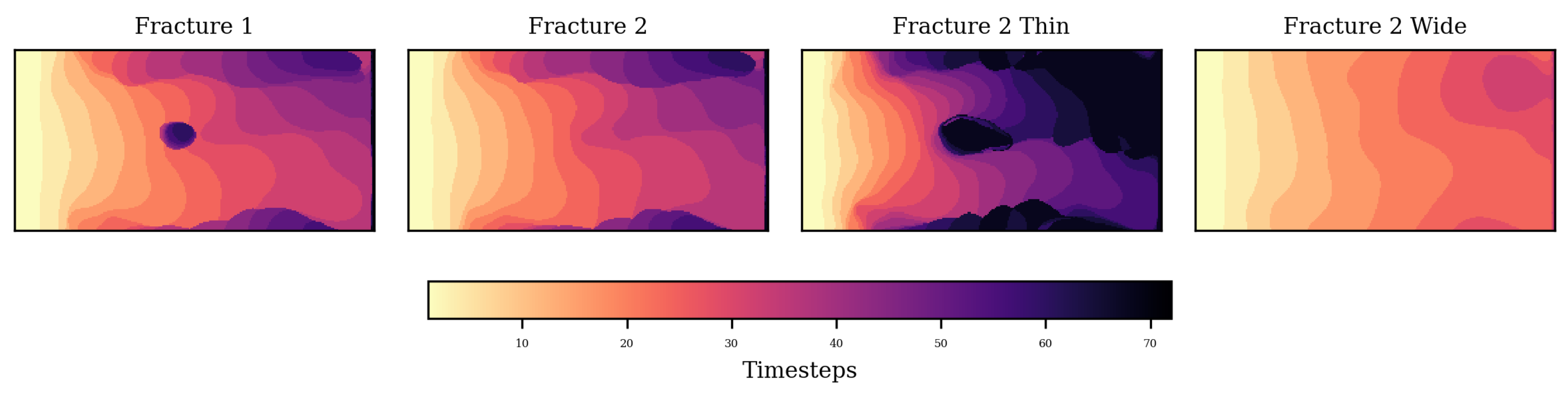
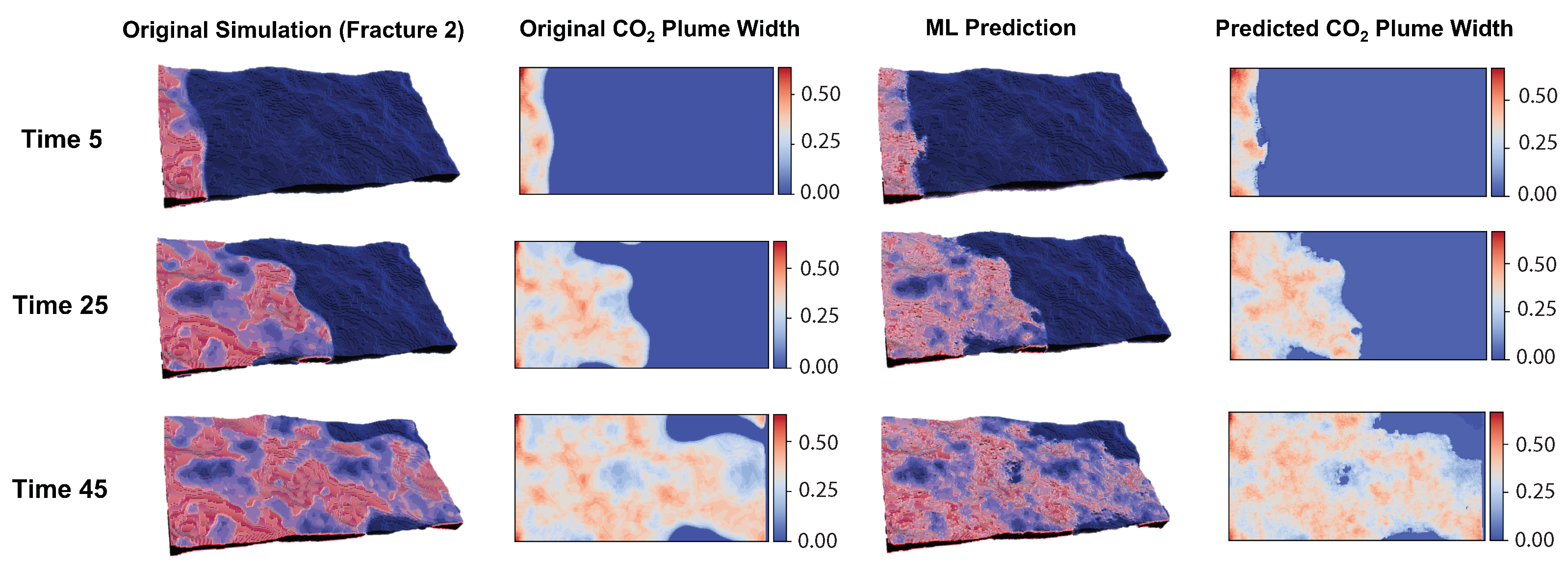
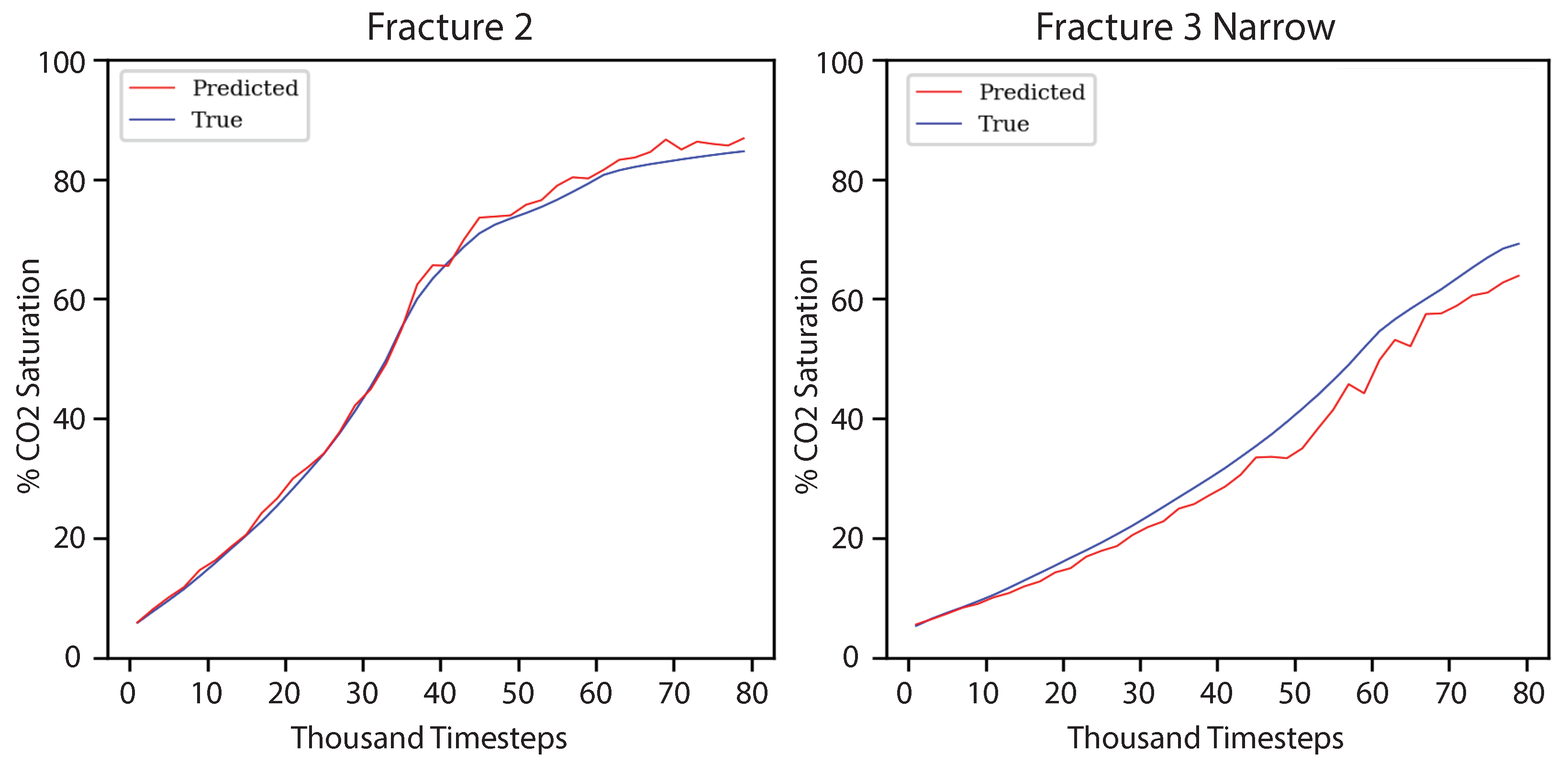
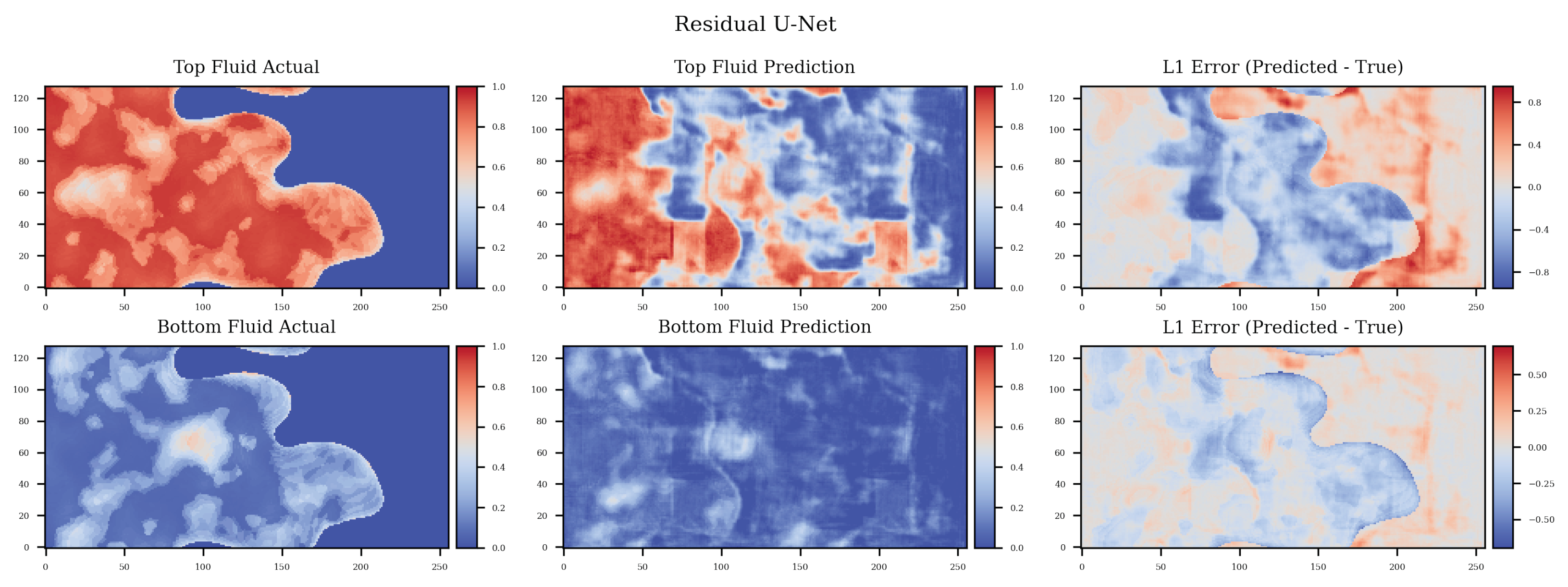
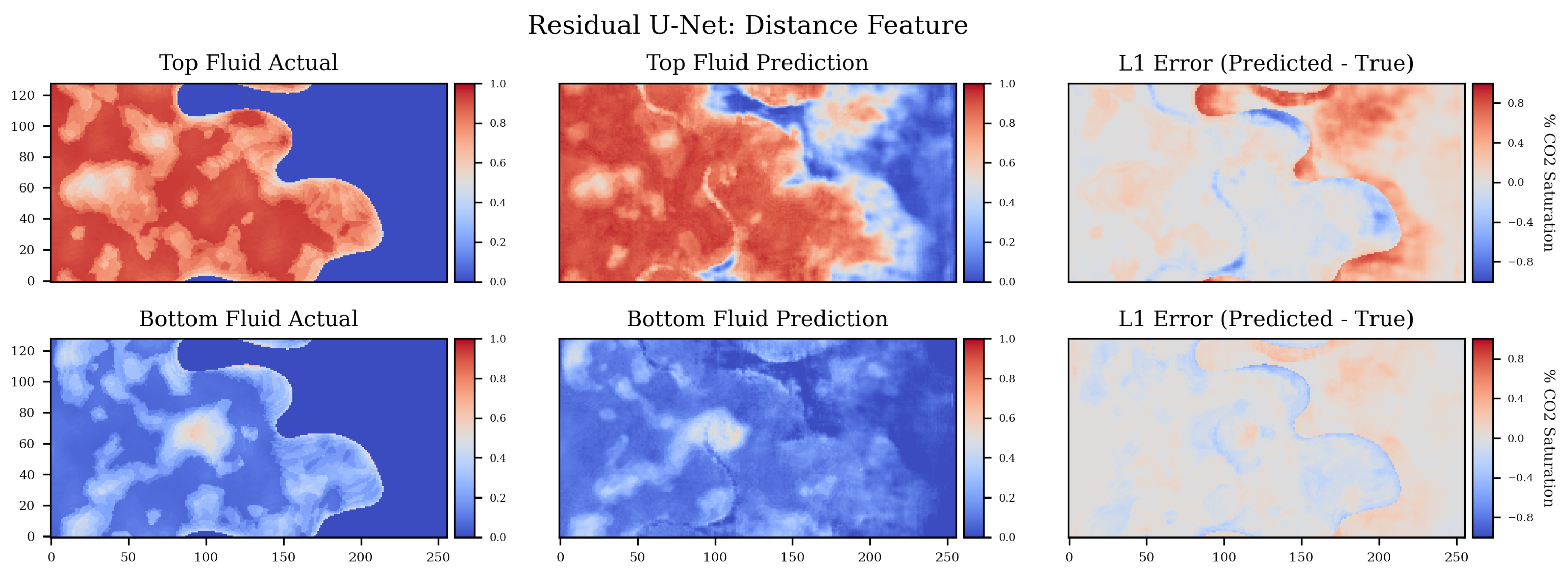
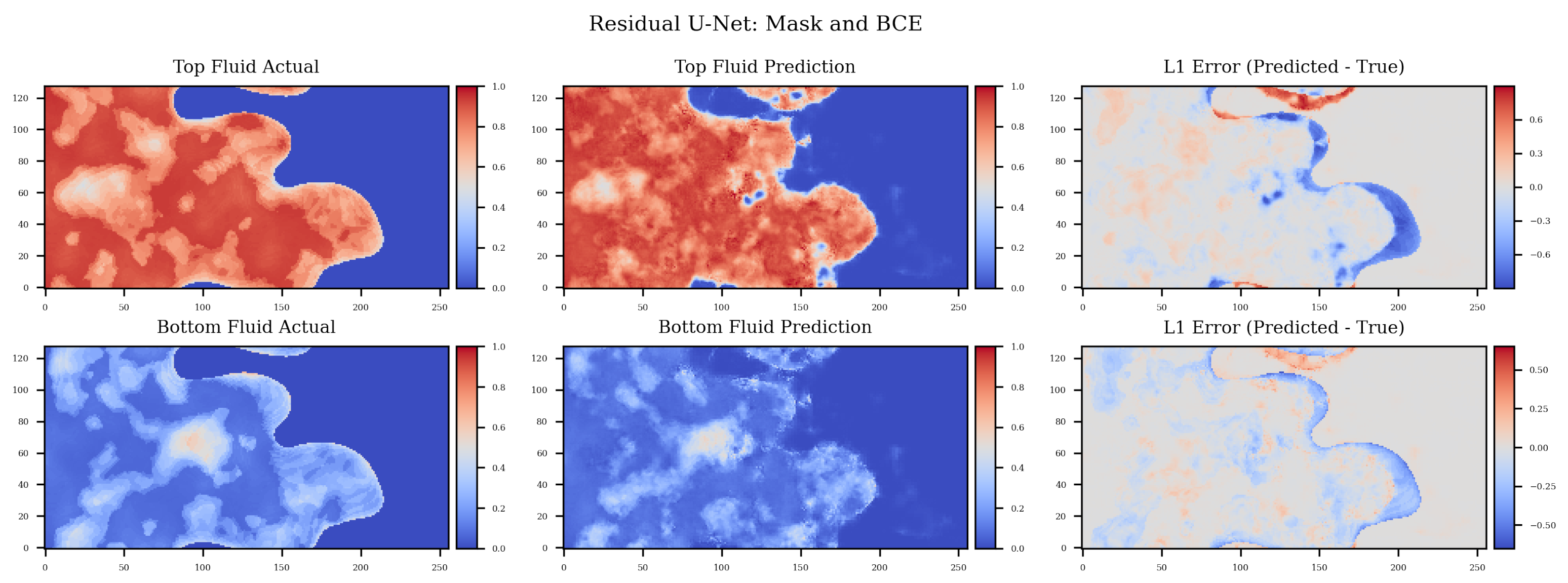
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CO | Carbon Dioxide |
| LBM | Lattice-Boltzmann Method |
| ML | Machine Learning |
| ConvNet | Convolutional Neural Network |
References
- Guiltinan, E.J.; Cardenas, M.B.; Bennett, P.C.; Zhang, T.; Espinoza, D.N. The effect of organic matter and thermal maturity on the wettability of supercritical CO2 on organic shales. Int. J. Greenh. Gas Control 2017, 65, 15–22. [Google Scholar] [CrossRef]
- Renshaw, C.E. On the relationship between mechanical and hydraulic apertures in rough-walled fractures. J. Geophys. Res. Solid Earth 1995, 100, 24629–24636. [Google Scholar] [CrossRef]
- Vogler, D.; Settgast, R.R.; Annavarapu, C.; Madonna, C.; Bayer, P.; Amann, F. Experiments and Simulations of Fully Hydro-Mechanically Coupled Response of Rough Fractures Exposed to High-Pressure Fluid Injection. J. Geophys. Res. Solid Earth 2018, 123, 1186–1200. [Google Scholar] [CrossRef]
- Wang, L.; Cardenas, M.B.; Slottke, D.T.; Ketcham, R.A.; Sharp, J.M. Modification of the Local Cubic Law of fracture flow for weak inertia, tortuosity, and roughness. Water Resour. Res. 2015, 51, 2064–2080. [Google Scholar] [CrossRef]
- Dou, Z.; Zhou, Z.; Sleep, B.E. Influence of wettability on interfacial area during immiscible liquid invasion into a 3D self-affine rough fracture: Lattice Boltzmann simulations. Adv. Water Resour. 2013, 61, 1–11. [Google Scholar] [CrossRef]
- Eker, E.; Akin, S. Lattice Boltzmann simulation of fluid flow in synthetic fractures. Transp. Porous Media 2006, 65, 363–384. [Google Scholar] [CrossRef]
- Ju, Y.; Zhang, Q.; Zheng, J.; Chang, C.; Xie, H. Fractal model and Lattice Boltzmann Method for Characterization of Non-Darcy Flow in Rough Fractures. Sci. Rep. 2017, 7, 41380. [Google Scholar] [CrossRef] [PubMed]
- Kim, I.; Lindquist, W.B.; Durham, W.B. Fracture flow simulation using a finite-difference lattice Boltzmann method. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2003, 67, 9. [Google Scholar] [CrossRef]
- Landry, C.J.; Karpyn, Z.T.; Ayala, O. Relative permeability of homogenous-wet andmixed-wet porousmedia as determined by pore-scale lattice Boltzmann modeling. Water 2014, 50, 3672–3689. [Google Scholar] [CrossRef]
- Santos, J.E. Lattice-Boltzmann Modeling of Multiphase Flow through Rough Heterogeneously Wet Fractures. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2018. [Google Scholar] [CrossRef]
- Guiltinan, E.; Estrada Santos, J.; Kang, Q.; Cardenas, B.; Espinoza, D.N. Fractures with Variable Roughness and Wettability. 2020. Available online: https://www.digitalrocksportal.org/projects/314 (accessed on 10 October 2022).
- Guiltinan, E.J.; Santos, J.E.; Cardenas, M.B.; Espinoza, D.N.; Kang, Q. Two-phase fluid flow properties of rough fractures with heterogeneous wettability: Analysis with lattice Boltzmann simulations. Water Resour. Res. 2020, 57, e2020WR027943. [Google Scholar] [CrossRef]
- Guiltinan, E.; Santos, J.E.; Kang, Q. Residual Saturation During Multiphase Displacement in Heterogeneous Fractures with Novel Deep Learning Prediction. In Proceedings of the Unconventional Resources Technology Conference (URTeC), Online, 20–22 July 2020; Society of Petroleum Engineers (SPE): Austin, TX, USA, 2020. [Google Scholar] [CrossRef]
- Zhou, X.H.; McClure, J.E.; Chen, C.; Xiao, H. Neural network-based pore flow field prediction in porous media using super resolution. Phys. Rev. Fluids 2022, 7, 074302. [Google Scholar] [CrossRef]
- Santos, J.E.; Xu, D.; Jo, H.; Landry, C.J.; Prodanović, M.; Pyrcz, M.J. PoreFlow-Net: A 3D convolutional neural network to predict fluid flow through porous media. Adv. Water Resour. 2020, 138, 103539. [Google Scholar] [CrossRef]
- Santos, J.E.; Yin, Y.; Jo, H.; Pan, W.; Kang, Q.; Viswanathan, H.S.; Prodanović, M.; Pyrcz, M.J.; Lubbers, N. Computationally Efficient Multiscale Neural Networks Applied to Fluid Flow in Complex 3D Porous Media. Transp. Porous Media 2021, 140, 241–272. [Google Scholar] [CrossRef]
- Kashefi, A.; Mukerji, T. Point-cloud deep learning of porous media for permeability prediction. Phys. Fluids 2021, 33, 097109. [Google Scholar] [CrossRef]
- Wang, H.; Yin, Y.; Hui, X.Y.; Bai, J.Q.; Qu, Z.G. Prediction of effective diffusivity of porous media using deep learning method based on sample structure information self-amplification. Energy AI 2020, 2, 100035. [Google Scholar] [CrossRef]
- Marcato, A.; Boccardo, G.; Marchisio, D. A computational workflow to study particle transport and filtration in porous media: Coupling CFD and deep learning. Chem. Eng. J. 2021, 417, 128936. [Google Scholar] [CrossRef]
- Marcato, A.; Estrada Santos, J.; Boccardo, G.; Viswanathan, H.; Marchisio, D.; Prodanović, M. Prediction of Local Concentration Fields in Porous Media with Chemical Reaction Using a Multi Scale Convolutional Neural Network. Chem. Eng. J. 2022, 140367. [Google Scholar] [CrossRef]
- Wang, Y.D.; Chung, T.; Armstrong, R.T.; McClure, J.; Ramstad, T.; Mostaghimi, P. Accelerated Computation of Relative Permeability by Coupled Morphological and Direct Multiphase Flow Simulation. J. Comput. Phys. 2020, 401, 108966. [Google Scholar] [CrossRef]
- Chang, B.; Santos, J.; Prodanovic, M. ElRock-Net: Assessing the Utility of Machine Learning to Initialize 3D Electric Potential Simulations; Society of Core Analysists: 2022. Available online: http://jgmaas.com/SCA/2022/SCA2022-11.pdf (accessed on 10 October 2022).
- ecoon/Taxila-LBM: Lattice Boltzmann code from LANL. Available online: https://github.com/ecoon/Taxila-LBM (accessed on 10 October 2022).
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation. Phys. Rev. E 1994, 49, 2941–2948. [Google Scholar] [CrossRef] [PubMed]
- Porter, M.L.; Coon, E.T.; Kang, Q.; Moulton, J.D.; Carey, J.W. Multicomponent interparticle-potential lattice Boltzmann model for fluids with large viscosity ratios. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 86, 036701. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Yang, H.; Fan, L.-S. Numerical simulation of bubble interactions using an adaptive lattice Boltzmann method. Chem. Eng. Sci. 2011, 66, 3441–3451. [Google Scholar] [CrossRef]
- Ogilvie, S.R.; Isakov, E.; Glover, P.W. Fluid flow through rough fractures in rocks. II: A new matching model for rough rock fractures. Earth Planet. Sci. Lett. 2006, 241, 454–465. [Google Scholar] [CrossRef]
- Glover, P.W.; Matsuki, K.; Hikima, R.; Hayashi, K. Fluid flow in synthetic rough fractures and application to the Hachimantai geothermal hot dry rock test site. J. Geophys. Res. Solid Earth 1998, 103, 9621–9635. [Google Scholar] [CrossRef]
- Glover, P.W.; Matsuki, K.; Hikima, R.; Hayashi, K. Synthetic rough fractures in rocks. J. Geophys. Res. Solid Earth 1998, 103, 9609–9620. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. Lect. Notes Comput. Sci. (Includ. Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinform.) 2015, 9351, 234–241. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Wang, Y. Road Extraction by Deep Residual U-Net. IEEE Geosc. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef]
- Su, Z.; Fang, L.; Kang, W.; Hu, D.; Pietikäinen, M.; Liu, L. Dynamic Group Convolution for Accelerating Convolutional Neural Networks. In Proceedings of the European Conference on Computer Vision, Online, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 138–155. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A ConvNet for the 2020s. arXiv 2022, arXiv:2201.03545. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A System for Large-Scale Machine Learning. 2015. In Proceedings of the 12th USENIX symposium on operating systems design and implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Musy, M.; Jacquenot, G.; Dalmasso, G.; Neoglez; Bruin, R.D.; Pollack, A.; Claudi, F.; Badger, C.; icemtel; Sullivan, B.; et al. Vedo. 2021. Available online: https://zenodo.org/record/4609336 (accessed on 10 October 2022).
- Santos, J.E.; Gigliotti, A.; Bihani, A.; Landry, C.; Hesse, M.A.; Pyrcz, M.J.; Prodanović, M. MPLBM-UT: Multiphase LBM library for permeable media analysis. SoftwareX 2022, 18, 101097. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ting, A.K.; Santos, J.E.; Guiltinan, E. Using Machine Learning to Predict Multiphase Flow through Complex Fractures. Energies 2022, 15, 8871. https://doi.org/10.3390/en15238871
Ting AK, Santos JE, Guiltinan E. Using Machine Learning to Predict Multiphase Flow through Complex Fractures. Energies. 2022; 15(23):8871. https://doi.org/10.3390/en15238871
Chicago/Turabian StyleTing, Allen K., Javier E. Santos, and Eric Guiltinan. 2022. "Using Machine Learning to Predict Multiphase Flow through Complex Fractures" Energies 15, no. 23: 8871. https://doi.org/10.3390/en15238871
APA StyleTing, A. K., Santos, J. E., & Guiltinan, E. (2022). Using Machine Learning to Predict Multiphase Flow through Complex Fractures. Energies, 15(23), 8871. https://doi.org/10.3390/en15238871





