Abstract
Current methods of oil and gas field development design rely on reservoir simulation modeling. A reservoir simulation model is a tool to reproduce field development processes and forecast production data. Reservoir permeability is one of the basic properties that determines fluid flow. From existing approaches, the porosity and permeability values should be consistent with petrophysical correlations obtained from core sample tests in the course of development of an absolute permeability cube in the reservoir simulation model. For carbonate reservoirs with complex pore space structure and fractures, the petrophysical correlations are often unstable. To factor in the fluid flow in a fractured rock system, dual-medium models are developed, allowing for matrix and fracture components. Yet in this case, the degree of uncertainty only increases with the introduction of a new parameter: a cross-flow index of fluid migration from matrix to fracture, which is only determined indirectly by results of fluid flow studies conducted in the initial development period, and therefore most often is adaptive. Clearly, for well-studied fields there is an extensive data pool drawn on research findings: core studies, well logging, well flow testing, flowmetry, special well-logging methods (FMI, Sonic Scanner, etc.); the dual-medium model development for such reservoirs is fairly well-founded and supported by actual studies. However, at the start of the field development, the data are incomplete, which renders qualitative dual-medium modeling impossible. This paper proposes an approach to factor in the target’s permeability anisotropy at an early development stage through the integration of well, core and 3D seismic surveys. The reservoir was classified into pore space types, to which different petrophysical correlations were assigned to develop a permeability array, and relative phase permeabilities were studied. The fluid flow model was history-matched with allowance for permeability anisotropy and rock types. Comparative calculations were conducted on the resulting model to select the optimum development strategy for the target.
1. Introduction
There is a growing share of hard-to-recover reserves in the structure of the world’s oil reserves. Such reserves are typical of complex carbonate reservoirs that account for 60% of global oil reserves. With this background, much consideration has been given lately to the study of complex carbonate reservoirs, as well as approaches and technologies for their development. Efficient exploration and production drilling of such reservoirs is a crucial and demanding task. The success of various improved oil recovery activities, such as horizontal drilling, acid treatments and other well interventions, is largely determined by the type of rock and void space [1,2,3,4]. With many uncertainties arising in the development strategy effectiveness assessment, it is therefore essential to factor in the reservoir heterogeneity and the anisotropy of its properties. Reservoir simulation modeling is a critical stage in the design of this kind of field development.
Being an unconventional task, the problem of complex reservoir modeling is addressed by many scientists [5,6,7]. Permeability is one of the key parameters determining fluid flow in reservoirs. Standard approaches to permeability prediction during carbonate reservoir modeling are not feasible, since permeability–porosity petrophysical correlations are unstable and show a high variance. Permeability values for the same porosity values may differ by an order of magnitude. There are also different types of voids: fractures, vugs, pores, and mixed types. Fluid flow in such rocks is mainly determined by fractures and vugs [8,9,10].
In some cases, in addition to fractures and vugs, the development of carbonate reservoirs is challenging due to paleokarst processes [11,12,13]. In such cases, two neighbouring wells may show fundamentally different lateral and vertical rock properties. There may be super reservoirs with layers of excessively high permeability across a number of wells. The design of injection wells should also take such features into account. Premature flooding of wells often occurs through such a reservoir [14].
The heterogeneity and anisotropy of carbonate reservoir properties—particularly permeability, laterally and vertically—strongly affects their development processes [15]. Carbonate reservoir modeling factors in these rock features. There is a range of approaches to complex carbonate reservoir modeling. The primary approach involves the development of a dual-medium model [16], a method that has been assessed by a number of scientists. Yet, a large amount of input data—core studies, well logging, well tests, 3D seismic surveys results—are needed. The reservoir has to be uniformly explored by volume. In the initial stages of development, this approach is ineffective due to limited data volume [17]. When using dual media, an additional sigma parameter is introduced that characterises the cross-flow between a matrix and a fracture. The sigma value is defined by calculation, thus being an additional uncertainty in modeling [18].
To analyse and factor in uncertainties in reservoir properties, multivariate modeling is applied, allowing the search of a range of key reservoir parameters (porosity, permeability, aquifer, etc.), conduct more substantiated history-matching, obtain multiple model implementations, and make optimistic, pessimistic and realistic forecasts of production data. The technique is well proven for assessing uncertainties, yet it has its weaknesses. As a rule, no criteria of geological realism and consistency of parameters are selected, resulting in non-physical model implementations. Regarding the permeability cube, it may be noted that in multivariate modeling, heterogeneity and vertical anisotropy are partially factored in. However, the lateral permeability anisotropy of a formation, fracture zones, super reservoirs and ancient karst are left out, which can strongly affect the development process [19].
Some works present a more comprehensive allowance for heterogeneity and reservoir permeability prediction [20,21,22,23].
A number of papers describe permeability prediction in the reservoir volume with allowance for seismic attributes, which is particularly relevant at the initial stages of target development, where drilled wells are insufficient to characterise permeability and other properties at volume [24,25,26,27,28].
For more mature fields, it is proposed to develop the permeability array by integrating surveys at various scales to factor in reservoir permeability heterogeneity [29].
There are various approaches to factoring in permeability anisotropy, as well [30,31]. For example, the works [32,33] offer well test analysis. The relationship between permeability and well-log curves parameters is closely studied. First derivatives of average permeability values and their distribution histograms are plotted and lateral anisotropy is determined by their results. Some studies [34,35,36] determine permeability anisotropy by core data. Techniques and approaches to factor in permeability anisotropy in reservoir simulation modeling are described in the works [37,38,39].
Allowing for reservoir heterogeneity, it should be understood that fluid flow varies in different reservoir zones [40]. Therefore, the phase permeability curves will be shaped differently [41,42,43].
When selecting a development strategy, all of the above factors have to be taken into account, as they significantly impact production data. Therefore, the study objective is building the fluid-flow model-permeability cube with allowance for heterogeneity and permeability anisotropy, fluid flow model history-matching, and comparing different reservoir development strategies.
The Section 2 provides a geological description of the reservoir in which we describe approaches and methods to integrate available input data, analyse heterogeneity and permeability anisotropy, classify the reservoir, and plot phase-permeability curves.
The Section 3 describes the obtained discrete arrays of rock types and permeability arrays in different directions. We provide the results of the fluid-flow model history-matching allowing for permeability anisotropy. We also present the results of comparisons of two reservoir development options with different directions of horizontal wellbores.
The Section 4 points to the significance of the results for the selection of an optimum reservoir development strategy, and defines future studies to cover field development.
2. Materials and Methods
A complex carbonate reservoir of the field code-named Alpha was selected for the study. The reservoir rocks feature vuggy, fractured, occasionally dolomitic organogenic detrital and organogenic clastic limestones of the Serpukhovian age.
The study analyzed the data evidencing the development of fracturing, zones of secondary reservoir alteration and decompaction including the results of laboratory-based core studies, high permeability values from well-flow tests, seismic studies (duplex waves), and mud losses while drilling.
As noted in the Introduction, this deposit is in the initial stage of development. No special logging surveys were conducted to determine fracturing, yet significant fracturing was observed in neighboring analogue fields. The studies of core from two wells identified fractured and vuggy samples. Three-dimensional seismic studies (duplex wave migration, DWM) determined rock decompaction zones in different directions [44].
Given the limited data for the distribution of properties in the reservoir volume, it was decided to conduct reservoir classification based on the duplex wave migration results. Duplex waves are reflections that bounce twice: successively from the near-horizontal interface, and then from the near-vertical interface, or vice versa [45,46]. Regularised Kirchhoff depth migration (duplex wave migration) where the Green’s function is calculated based on the duplex wave kinematics, was applied for duplex wave migration for near-vertical interface imaging. The VTI anisotropy application to the migration allowed for the improvement of depth-imaging accuracy to a level of error of the first tens of meters [47,48].
Thus, the most probable zones of high value—the zones of decompaction, fracturing, vugginess, as well as the matrix zones—can be determined. Such zones are identified in three directions: X, Y, Z, which in the future will allow the factoring in of the permeability anisotropy in different directions.
Next, the core analysis enabled us to distinguish samples with fractures and discernible vugs, as well as pure porous-type samples. For these types, different permeability–porosity petrophysical correlations were plotted.
The relative phase permeability curves were normalised and approximated. A range of possible relative phase permeability curve modifications was determined. Different phase permeabilities that most accurately describe the fluid flow for a particular type were specified for different types of reservoir rocks. A key feature of DWM is that the fracture-zone tracing within target horizons is not based on the identification of phase shifts of the latter, but on the direct seismic near-vertical heterogeneity imaging, in this case, the fracture zone. Duplex wave migration has been frequently applied in the studies of carbonate reservoir fractured zones, specifically, in a number of fields in the Timan-Pechora basin province, where the field under study is located. For example, for one field, the DWM prediction was fully confirmed by drilling mud loss in the intervals of two horizontal wells, precisely in the areas of predicted anomalies [49].
Thus, the duplex wave migration arrays were rebuilt into discrete rock-type cubes. That is, the predicted fracture zones were allocated to one type, and the rock matrix zone to another type (Figure 1). The rock types were identified in three directions: X, Y, Z, to further factor in the formation permeability anisotropy.

Figure 1.
Classification of the reservoir in the volume according to the aperture of the distribution of duplex waves: (a) in the X-direction, (b) in the Y-direction, (c) in the Z-direction.
In the next step, the results of studies of 112 full-diameter core samples (d = 100 mm) from two wells were analysed. Initially identified were fractured samples, and samples characterising the matrix part of the rock.
In this case the main task of rock typing was to identify fractures. For this we used visual analysis of samples, and x-ray tomography to identify fractures inside them [50]. Twenty-four samples confirmed fractures. An example of a core sample (100 × 100 mm) with fractures is shown below (Figure 2).

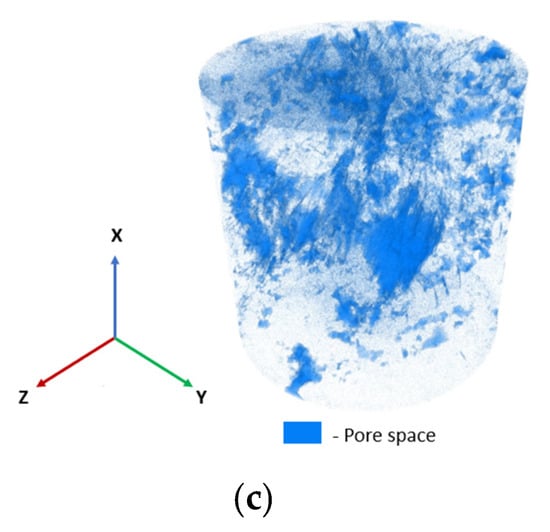
Figure 2.
Results of x-ray tomography study of rock samples: (a) XY slice; (b) YZ slice; (c) 3D model of pore space.
At the next stage, this classification statistical analysis was carried out. Results of standard statistical tests (t-test, F-test) are shown in Table 1.

Table 1.
Comparing different types of rock.
Results of analysis (Table 1) showed statistically significant differences between the two types of rocks by permeability.
For these samples, permeability was determined in three different directions: X, Y, Z. Therefore, permeability-porosity petrophysical correlations were plotted for each rock type and measurement direction (Figure 3).

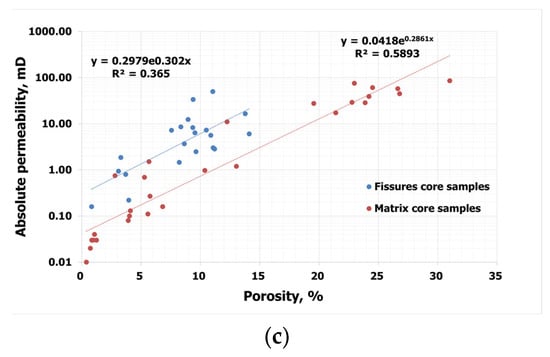
Figure 3.
Permeability–porosity correlation: (a) in the X-direction, (b) in the Y-direction, (c) in the Z-direction.
The resulting permeability–porosity correlations are as follows (1)–(6), where φ is porosity coefficient, and k is absolute permeability in different directions:
- (a)
- X-direction
- (b)
- Y-direction
- (c)
- Z-direction
A static model of the field was built subject to reserves estimation standards and regulations, and used as input data in this study [51]. The model includes a porosity array obtained from stochastic distribution [52]. Therefore, in the next step, the permeability–porosity correlations for rock types and different directions were integrated into the model with allowance for discrete rock type arrays (Figure 4).
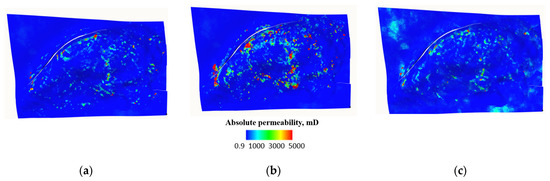
Figure 4.
Permeability arrays (plane view): (a) X-direction, (b) Y-direction, (c) Z-direction.
Figure 3 shows that permeability varies according to direction, which will allow factoring in the permeability anisotropy at history-matching and predicting the development strategy.
Further to the model’s absolute permeability array, the fluid flow processes in the reservoir are significantly impacted by relative phase permeabilities that are set in the reservoir simulation model [53].
Actual studies of phase permeabilities on core samples were analysed with a total of six studies of phase permeabilities in an oil-water system. To form curves of relative phase permeabilities of the model, the results of studies were normalised and approximated. Relative phase permeability curves are normally approximated subject to various theoretical correlations of Corey, LET, etc. [54,55].
Therefore, in this study, the relative phase permeability curves from the laboratory results were processed by the following algorithm: 1. Normalisation of the relative phase permeabilities values; 2. Approximation of the obtained values using the Corey correlation; 3. Identification of a range of acceptable modifications of the relative phase permeabilities; 4. Selection of curves for fractured and pore types.
Water saturation values are normalised by the formula given below:
where SWn—normalised water saturation, SWCR—critical water saturation, SOWCR—critical oil saturation, SGL—gas saturation.
The Corey correlations below (8) and (9) were selected as the approximation function.
where Kro is the relative phase permeability to oil, and Krw is the relative phase permeability to water.
The results of normalization and approximation are shown in Figure 5, where Kro is oil relative permeability and Krw is water relative permeability.
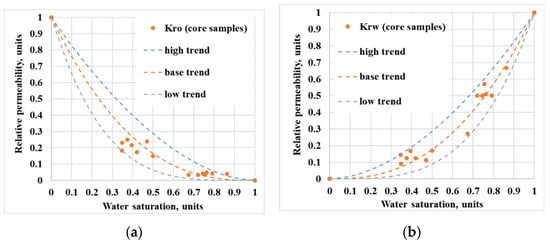
Figure 5.
Relative permeability to: (a) oil (b) water.
Figure 5 shows an acceptable range of modification of the relative phase permeability curves, which is required at history-matching. At the initial modeling stage it was decided to assign the low trend to the matrix type and the high trend to the fractured type of the rock. This approach is expected to provide the most accurate description of the fluid migration through the rocks during the initial history-match.
All of the above approaches are then integrated into the fluid flow simulation model to further history-match the indicators and predict various field development strategies.
3. Results and Discussions
The fluid flow simulation model was history-matched by taking the formation permeability anisotropy and phase permeability classification into account (Figure 6).
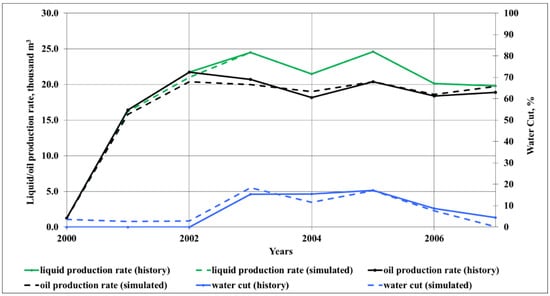
Figure 6.
Results of history-matching.
Based on the history-matching, the discrepancy between the actual values and the values from the model does not exceed 5%. Factoring in the permeability anisotropy allowed to promptly history-match the model (three iterations).
The oilfield was under development from 2000 to 2007, with two production wells. The field was then shut down for economic reasons. Currently, the field development start is expected in 2022.
Proposed are two development strategies (Figure 7) that include additional drilling of nine wells. Thus, a total of eleven wells will be developing the reservoir: six production wells, three of which are horizontal wellbores, and five injection wells. The differences between the options arise from orientation of the horizontal wellbores. For Option 1, horizontal wellbores are oriented along the strike; for Option 2, horizontal wellbores are oriented perpendicular to the strike.
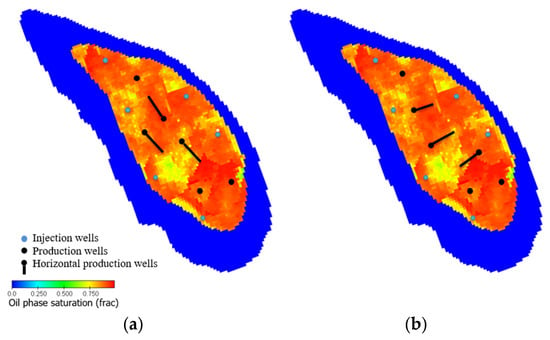
Figure 7.
Development strategies: (a) Option 1 (b) Option 2.
Production figures were calculated according to the two options. However, to factor in the formation anisotropy impact, the options were calculated on two models. Model 1 was obtained from the study with allowance for the permeability anisotropy and different phase permeabilities by zones; in Model 2, anisotropy by different directions was not taken into account.
For Model 2, a permeability cube along the X-direction was developed from the petrophysical correlation for all core samples:
In the Y- and Z-directions, permeability is equal to values in the X-direction. Phase permeabilities for Model 2 are taken as the base trend (Figure 5).
Identical injection and production levels were assigned to the options. Thus, the difference between the options was only expected by oil production and watercut (Figure 8).
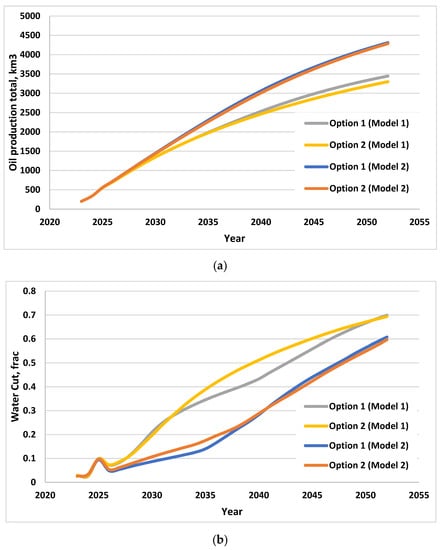
Figure 8.
Development strategies: (a) oil production, total, (b) water cut.
On the basis of the calculations, the following conclusions were drawn:
- Model 2 calculations made minimum difference between the options (oil production is 30,000 m3, watercut is 0.01).
- Model 2 calculations indicated notably low watercut performance during development and values at the end of development. Model 2 did not expose flooding risks in higher reservoir porosity and permeability zones, and permeability anisotropy.
- In Model 1 calculations, the difference between the options in terms of cumulative oil production was 145,000 m3. In terms of watercut at the end of development, the difference was insignificant, while the watercut trends were completely different. Model 1, with allowance for anisotropy, shows that different orientation of horizontal wellbores considerably impacted the cumulative production and watercut.
- Model 1 calculations suggested that Option 1, i.e., the orientation of horizontal wellbores along the strike, was a better choice. With the probability of fracture zones and permeability anisotropy, a faster flooding from the injection wells was predicted for the perpendicular wellbore option; there was a substantial risk of the horizontal wellbore heel flooding, which would cause the rapid flooding of wells.
4. Conclusions
The work included indirect allowance for fracture zones and anisotropy in the C1S1 fluid flow simulation model of the Alpha field:
- -
- three-dimensional parameters reflecting the directivity of fracture intensity distribution in the lateral and vertical strike were integrated into the fluid flow simulation model;
- -
- rock reservoirs in the reservoir volume were classified into fractured and porous;
- -
- permeability–porosity petrophysical correlations describing lateral and vertical anisotropy were plotted for different rock types and factored into the fluid flow model;
- -
- phase permeabilities were differentiated by rock type;
- -
- the fluid flow model was history-matched, the discrepancy in the cumulative oil production not exceeding 5%;
- -
- predicted options for the reservoir development were calculated;
- -
- it was discovered that Model 2 (with no allowance for anisotropy) does not allow reliable estimates of fluid flow processes in a complex carbonate reservoir;
- -
- Model 1 calculations showed Option 1 as the most effective, as it allows the production of 145,000 m3 more oil compared to Option 2.
A method for integrating different scale information for improving the forecasting of production data quality was proposed. The technique allows zones of higher flow properties and probable fracturing to be indirectly factored in. The study shows that the failure to take permeability anisotropy into account may strongly affect the calculation of development options. Conventional approaches to fluid flow modeling normally do not allow a reliable reflection of flooding performance in complex carbonate reservoirs. With allowance for anisotropy, the forecasts are more pessimistic, yet they allow water breakthrough risks to be factored in under lateral heterogeneity of reservoir properties. To refine the model and the anisotropy parameter, it is recommended to take oriented core samples from new wells.
As a follow-up, the authors intend to check model parameters and refine the fluid flow model following the drilling of new wells in 2022, and develop correlations between seismic attributes and reservoir properties. This will enable prompt management of the field development using the reliable fluid flow model.
Author Contributions
Conceptualization, S.K.; methodology, S.K.; software, A.K.; validation, S.K., A.K. and N.K.; formal analysis, E.O.; investigation, S.K. and E.O.; resources, S.K.; data curation, A.K. and N.K.; writing—original draft preparation, A.K.; writing—review and editing, S.K.; visualization, N.K. and E.O.; supervision, S.K.; project administration, S.K.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
The study was conducted under Russian Science Foundation grant No. 22-17-00111.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lake, L.W. Short Course Manual, Enhanced Oil Recovery Fundamentals; SPE: Richardson, TX, USA, 1985; p. 449. [Google Scholar]
- Novokreshchenny, D.V.; Raspopov, A.V. Perspectives of development of technologies of radial opening of a layer on deposits of the Perm region. Oil Ind. 2014, 3, 54–57. [Google Scholar]
- Pivovar, A.V.; Kolesov, V.A.; Kalistratov, S.A.; Zagrivniy, F.A.; Mishakov, M.V. Influence of Geological Conditions on Wear-out of the Bits in the Riphean Deposits of the Yurubcheno-Tokhomskoye Field. Oil Ind. 2022, 1, 50–53. [Google Scholar] [CrossRef]
- Zaripov, A.T.; Razumov, A.R.; Beregovoy, A.N.; Knyazeva, N.A.; Vasilyev, E.P.; Amerkhanov, M.I. Improved Production Performance of Heavy Oil Reservoirs with Compacted and Shaled-Out Interlayers. Oil Ind. 2021, 7, 28–31. [Google Scholar] [CrossRef]
- Putilov, I.S.; Vinokurova, E.E.; Guliaeva, A.A.; Yuzhakov, A.L.; Popov, N.A. Creation of a Conceptual Geological Model based on Lithological-Petrographic Research on the Example of the Permo-Carboniferous Deposit of the Usinskoe Deposit. Perm J. Pet. Min. Eng. 2020, 3, 214–222. [Google Scholar] [CrossRef]
- Ke, X.Y.; Zhao, J.; Li, Z.; Guo, Y.; Kang, Y. Production Simulation of Oil Reservoirs with Complex Fracture Network using Numerical Simulation. Energies 2022, 15, 4050. [Google Scholar] [CrossRef]
- Churanova, N.Y.; Khayrullin, M.M.; Chorniy, A.V.; Solovyev, A.V.; Kurelenkov, S.K. Reservoir Properties Distribution Forecast in a Complex Carbonate Reservoir and Drilling Risk Evaluation. In Proceedings of the Russian Petroleum Technology Conference, Moscow, Russia, 15–17 October 2018. [Google Scholar] [CrossRef]
- Fonta, O.; Verma, N.; Matar, S.; Divry, V.; Al-Qallaf, H. The Fracture Characterization and Fracture Modeling of a Tight Carbonate Reservoir. SPE Reserv. Eval. Eng. 2007, 10, 695–710. [Google Scholar] [CrossRef]
- Tavakoli, V. Carbonate Reservoir Heterogeneity: Overcoming the Challenges; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Gimazov, A.A.; Fokeeva, E.E.; Khairullin, R.U.; Minikhanov, D.M. Integrated Approach to Adapting and Forecasting the Parameters of Secondary Porosity for the R. Trebs Oilfield. Oil Ind. 2018, 10, 20–23. [Google Scholar] [CrossRef]
- Lu, X.B.; Gao, B.Y.; Chen, S.M. Study on Characteristics of Paleokarst Reservoir in Lower Ordovician Carbonate of Tahe Oil Field. Kuangwu Yanshi 2003, 23, 87–92. [Google Scholar]
- Jiu, B.; Huang, W.; Mu, N.; Li, Y. Types and Controlling Factors of Ordovician Paleokarst Carbonate Reservoirs in the Southeastern Ordos Basin, China. J. Petrol. Sci. Eng. 2021, 198, 108162. [Google Scholar] [CrossRef]
- Lopez, D.D.; Pickup, G.E.; Corbett, P.W.M. The Effects of Relative Permeability and Capillary Pressure Curves on a 2D Karst Reservoir Model. In Proceedings of the 77th EAGE Conference and Exhibition, Madrid, Spain, 1–4 June 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Du, Y.; Wang, J.; Fang, J.; Wang, Z.; Xin, J.; Ma, W.; Wang, H.; Huang, T.; Chen, M.; Fu, X. The Karst Reservoir Evolution and Genesis of Abnormal High Permeability Zone of the Upper Cretaceous Khasib Formation in Central Iraq. Sci. Geol. Sinica 2015, 50, 1218–1234. [Google Scholar] [CrossRef]
- Alkhimenkov, Y.A.; Bayuk, I.O. Analysis of Anisotropy Parameters of Fractured Carbonate Reservoir. In Proceedings of the 6th EAGE Saint Petersburg International Conference and Exhibition, Saint Petersburg, Russia, 7–10 April 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Grigoriev, A.V.; Laevsky, Y.M.; Yakovlev, P.G. On a Double Porosity Model of Fractured-Porous Reservoirs Based on a Hybrid Flow Function. Numerical Anal. Appl. 2018, 11, 121–133. [Google Scholar] [CrossRef]
- Krivoshchekov, S.N.; Kochnev, A.A.; Kozyrev, N.D.; Mengaliev, A.G. Modification of Permeability Cube of Geologic and Hydrodynamic Model Under various Volumes of Input Data. IOP Conf. Ser. Earth Environ. Sci. 2022, 988, 042020. [Google Scholar] [CrossRef]
- Nie, R.S.; Meng, Y.F.; Jia, Y.L.; Zhang, F.X.; Yang, X.T.; Niu, X.N. Dual porosity and dual permeability modeling of horizontal well in naturally fractured reservoir. Transp. Porous Media 2012, 92, 213–235. [Google Scholar] [CrossRef]
- Hutahaean, J.; Demyanov, V.V.; Christie, M. Many-objective optimization algorithm applied to history matching. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence, Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Anifowose, F.A.; Abdulraheem, A.; Al-Shuhail, A.; Schmitt, D.P. Improved Permeability Prediction From Seismic and Log Data using Artificial Intelligence Techniques. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 10–13 March 2013. [Google Scholar] [CrossRef]
- Subasi, A.; El-Amin, M.F.; Darwich, T.; Dossary, M. Permeability prediction of petroleum reservoirs using stochastic gradient boosting regression. J. Ambient Intell. Human Comput. 2020, 13, 3555–3564. [Google Scholar] [CrossRef]
- Chen, G.; Meng, Y.; Huan, J.; Wang, Y.; Xiao, L.; Zhang, L.; Feng, D. A new predrilling reservoir permeability prediction model and its application. J. Petrol. Sci. Eng. 2021, 210, 110086. [Google Scholar] [CrossRef]
- Zolotukhin, A.; Gayubov, A. Machine learning in reservoir permeability prediction and modelling of fluid flow in porous media. IOP Conf. Ser. Mater. Sci. Eng. 2019, 700, 012023. [Google Scholar] [CrossRef]
- Takougang, E.M.T.; Bouzidi, Y.; Ali, M.Y. Characterization of small faults and fractures in a carbonate reservoir using waveform inversion, reverse time migration, and seismic attributes. J. Appl. Geophys. 2019, 161, 116–123. [Google Scholar] [CrossRef]
- Thararoop, P.; Karpyn, Z.; Gitman, A.; Ertekin, T. Integration of seismic attributes and production data for infill drilling strategies—A virtual intelligence approach. J. Petrol. Sci. Eng. 2008, 63, 43–52. [Google Scholar] [CrossRef]
- Iturrarán-Viveros, U.; Parra, J.O. Artificial Neural Networks applied to estimate permeability, porosity and intrinsic attenuation using seismic attributes and well-log data. J. Appl. Geophys. 2014, 107, 45–54. [Google Scholar] [CrossRef]
- Yang, P.; Sun, Z.; Liang, X.; Li, H.; Dan, G. Seismic strategy for predicting highly profitable wells in the fractured-vuggy carbonate reservoirs. Petrol. Explor. Dev. 2013, 40, 537–541. [Google Scholar] [CrossRef]
- Boadu, F.K. Predicting the transport properties of fractured rocks from seismic information: Numerical experiments. J. Appl. Geophys. 2000, 44, 103–113. [Google Scholar] [CrossRef]
- Katterbauer, K.; Arango, S.; Sun, S.; Hoteit, I. Multi-data reservoir history matching for enhanced reservoir forecasting and uncertainty quantification. J. Petrol. Sci. Eng. 2015, 128, 160–176. [Google Scholar] [CrossRef]
- Moradi, A.; Samani, N.A.; Kumara, A.S.; Moldestad, B.M.E. Evaluating the Performance of Advanced Wells in Heavy Oil Reservoirs Under Uncertainty in Permeability Parameters. Energy Reports 2022, 8, 8605–8617. [Google Scholar] [CrossRef]
- Wang, Z.; Ge, H.; Wei, Y.; Wang, Y.; Jia, K.; Xu, N.; Zhang, Y.; Du, S. Characterizing the Microscopic Anisotropic Permeabilities of Tight Oil Reservoirs Impacted by Heterogeneous Minerals. Energies 2022, 15, 6552. [Google Scholar] [CrossRef]
- Kozyrev, N.D.; Kochnev, A.A.; Mengaliev, A.G.; Putilov, I.S.; Krivoshchekov, S.N. Refinement of the Geological and Hydrodynamic Model of a Complex Oil Reservoir by Means of a Comprehensive Data Analysis. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2022, 331, 164–177. [Google Scholar] [CrossRef]
- Mengaliev, A.G.; Martyushev, D.A. Accounting the Parameter of Anisotropy of Permeability in Geological and Hydrodynamic Models of Carbonate Objects (on the Example of the Gagarin Deposit). Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2020, 331, 7–17. [Google Scholar] [CrossRef]
- Clavaud, J.-B.; Maineult, A.; Zamora, M.; Rasolofosaon, P.; Schlitter, C. Permeability Anisotropy and its Relations with Porous Medium Structure. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Aziz, E.A.A.E.; Gomaa, M.M. Petrophysical Analysis of Well Logs and Core Samples for Reservoir Evaluation: A Case Study of Southern Issaran Field, Gulf of Suez Province, Egypt. Environ. Earth Sci. 2022, 81, 341. [Google Scholar] [CrossRef]
- Kovalenko, Y.F.; Karev, V.I.; Gavura, A.V.; Shafikov, R.R. About Necessity of Taking into Account the Anisotropy of Strength and Filtration Rocks Properties in Geomechanical Modeling of Wells. Oil Ind. 2016, 11, 114–117. [Google Scholar]
- Yermekov, R.I.; Merkulov, V.P.; Chernova, O.S.; Korovin, M.O. Features of Permeability Anisotropy Accounting in the Hydrodynamic Model. J. Min. Inst. 2020, 243, 299–304. [Google Scholar] [CrossRef]
- Kolbikov, S.; Kuznetsova, Y.; Smirnov, A. Method of Anisotropy Modeling and its Application to Hydrodynamic Simulation. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 15–17 October 2018. [Google Scholar] [CrossRef]
- Martyushev, D.A.; Galkin, V.I.; Ponomareva, I.N. Study of Regularities of Distribution of Filtering Properties within Complexly Constructed Carbonate Reservoirs. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2021, 332, 117–126. [Google Scholar] [CrossRef]
- Shipaeva, M.; Sudakov, V.; Khairtdinov, R.; Sattarov, A. Analysis of Flow Distribution in Fractured-Cavernous Carbonate Reservoir Basing on Tracer Tests and Isotope Survey. In Proceedings of the 19th International Multidisciplinary Scientific GeoConference SGEM, Albena, Bulgaria, 28 June–7 July 2019; pp. 635–642. [Google Scholar] [CrossRef]
- Dmitriev, N.M.; Maksimov, V.M. Determining Equations of Two-Phase Flows through Anisotropic Porous Media. Fluid Dyn. 1998, 33, 224–229. [Google Scholar] [CrossRef]
- Pergament, A.K.; Tomin, P.Y. The Study of Relative Phase-Permeability Functions for Anisotropic Media. Math. Models Comp. Sim. 2012, 4, 1–9. [Google Scholar] [CrossRef]
- Johnson, E.F.; Bossler, D.P.; Naumann, V.O. Calculation of relative permeability from displacement experiments: Transl. AIME 1959, 216, 370–376. [Google Scholar] [CrossRef]
- Khromova, I.; Link, B.; Marmelevskyi, N. Comparison of Seismic-Based Methods for Fracture Permeability Prediction. First Break 2011, 29, 37–44. [Google Scholar] [CrossRef]
- Marmalevskyi, N.; Khromova, I.; Kostyukevych, A. Duplex Wave AVO for Predicting Properties of Subvertical Boundaries. In Proceedings of the 4th EAGE St. Petersburg International Conference and Exhibition on Geosciences, St. Petersburg, Russia, 5–8 April 2010. [Google Scholar] [CrossRef]
- Jin, S.; Xu, S.; Walraven, D. One-Return Wave Equation Migration: Imaging of Duplex Waves. In Proceedings of the 2006 SEG Annual Meeting, New Orleans, LO, USA, 1–6 October 2006; SEG Technical Program Expanded Abstracts. pp. 2338–2342. [Google Scholar] [CrossRef]
- Dubrova, G.B.; Khromova, I.; Kostyukevych, A.; Luo, D.; Liang, W.; Li, B. Duplex Wave Migration Based AVO for Determination Properties of Vertical Boundaries. In Proceedings of the 73rd EAGE Conference and Exhibition Incorporating SPE EUROPEC, Vienna, Austria, 23–27 May 2011. [Google Scholar] [CrossRef]
- Marmalevskyi, N.; Gorbachev, S.; Gornyak, Z.; Dubrova, G.; Link, B. Velocity Detection by Duplex Wave Migration. In Proceedings of the 5th EAGE St. Petersburg International Conference and Exhibition on Geosciences, St. Petersburg, Russia, 2–5 April 2012. [Google Scholar] [CrossRef]
- Khromova, I. Migration of duplex waves-a method for mapping of fracture zones of tectonic genesis. Oil Gas Geol. 2008, 3, 37–47. (In Russian) [Google Scholar]
- Galkin, S.V.; Efimov, A.A.; Krivoshchekov, S.N.; Savitskiy, Y.V.; Cherepanov, S.S. X-ray tomography in petrophysical studies of core samples from oil and gas fields. Rus. Geol. Geophys. 2015, 5, 782–792. [Google Scholar] [CrossRef]
- Zakrevsky, K.E. Geological 3D Modeling. M. European Association of Geoscientists & Engineers. 2011. Available online: https://www.earthdoc.org/content/books/9789462820043 (accessed on 20 November 2022).
- Yarus, J.M. Stochastic Modeling and Geostatistics; AAPG: Tulsa, OK, USA, 1994; p. 231. [Google Scholar]
- Richmond, P.C.; Watson, A.T. Estimation of multiphase flow functions from displacement experiments. SPE Res. Eng. 1990, 5, 121–127. [Google Scholar] [CrossRef]
- Li, K.; Horne, R.N. Comparison of Methods to Calculate Relative Permeability from Capillary Pressure in Consolidated Water-Wet Porous Media. Water Resources Res. 2006, 42. [Google Scholar] [CrossRef]
- Ghoodjani, E.; Bolouri, S.H. A Novel Two-Parameter Relative Permeability Model. J. Porous Media 2012, 15, 1061–1066. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).