Abstract
Gas reservoirs discovered in the southern margin of the Junggar Basin generally have high temperatures (up to 172.22 °C) and high pressures (up to 171.74 MPa). If using the PVT laboratory to get the gas compressibility factor, data from the laboratory are so little that it will not satisfy the demands of reservoir engineering calculations. There are many empirical correlations for calculating the Z-factor; however, these correlations give large errors at high gas reservoir pressures. The errors in estimating the Z-factor will lead to large errors in estimating all the other gas properties such as gas formation volume factor, gas compressibility, and gas in place. In this paper, a new accurate Z-factor correlation has been developed based on PVT data by correcting the high-pressure part of the most commonly used Dranchuk-Purvis-Robinson Correlation. Multivariate nonlinear regression is used to establish the independent variable function of pseudo-critical temperatures and pressures. By comparing it with the PVT data, the DPR correlation is continuously corrected to be suitable for ultra-deep gas reservoirs with HTHP. The new correlation can be used to determine the Z-factor at any pressure range, especially for high pressures, and the error is less than 1% compared to the PVT data. Then, based on the corrected Z-factor, the Cullender-Smith method is used to calculate the bottom hole pressure in the middle of the reservoir. Finally, the Z-factor under reservoir conditions of well H2 is predicted and the Z-factor chart at different temperatures is provided.
1. Introduction
Facing increasing energy demands, fossil fuel exploration and development have been directed toward deep-layer unconventional oil and gas reservoirs [1,2]. Due to the relatively high degree of thermal evolution, deep oil and gas resources are dominated by natural gas, and these gas reservoirs generally have complex characteristics such as strong ground stress, strong heterogeneity, and HTHP [3,4]. For example, the formation depth of some gas reservoirs in Xinjiang, China is more than 8000 m, and the matrix has characteristics of low porosity (the average porosity is 6%) and low permeability (the average permeability is 0.05 × 10−3 μm2). The formation temperature is as high as 190 °C (the average temperature is 143 °C), and the formation pressure is as high as 170 MPa (the average pressure is 118 MPa). The ground stress is as high as 180 MPa (the average ground stress is 130 MPa, and the stress difference is 60 MPa). For this kind of gas reservoir, it is very important to accurately calculate the PVT property parameters of reservoir fluid. For example, the gas Z-factor is of great significance to the production dynamic analysis and dynamic reserve calculation in the process of oil and gas field development [5,6,7,8].
Generally speaking, the compressibility factor is a dimensionless quantity, and it has different names such as the compressibility factor, gas super compressibility, Z-factor, and gas deviation factor [9]. It represents the deviation of a real gas from the ideal behavior, and it is a function of temperature (T), pressure (P), and gas composition. It is generally defined as the ratio of the actual volume of the gas (at its pressure and temperature) to the ideal volume of the gas (at standard conditions) that its molecules do not have attraction forces [10]. A Z-factor value of unity represents an ideal gas behavior [11]. At present, the methods to obtain the gas Z-factor of high temperatures and high pressures mainly include the experimental measurement method, the Standing-Katz chart method, and the formula method. Among them, the experimental measurement method has a long test cycle, and high experimental cost, and the test temperature and pressure range are limited by the experimental conditions [12]. The experimental measurement method is usually used less in well-test designs and interpretations to obtain the gas Z-factor. The Standing-Katz chart is a diagram of the relationship of the Z-factor to the pseudo-critical temperature and pseudo-critical pressure established experimentally by Standing and Katz (1942) [13]. At the same time, the Standing-Katz chart is currently recognized by the industry as a highly reliable method for calculating the gas Z-factor, but this method is difficult to implement by programming. The formula method is the most common calculation method of the gas Z-factor in well testing, and the formula method is convenient for computer programming, but the application scope of different methods is different, and the applicable calculation method needs to be preferred. Hall and Yarborough obtained a method for calculating the gas Z-factor based on the Starling-Carnahan equation of state, called the H-Y method (1973, 1974) [14,15]. Based on the Benedict-Webb-Rubin (1940) equation of state, Dranchuk, Purvis, and Robinson (1973) obtained a method for calculating the gas Z-factor with eight coefficients, namely the DPR method [16,17]. Based on the Starling-Carnahan equation of state, Dranchuk and Abu-Kassem (1975) derived a calculation method for gas Z-factor with 11 coefficients, namely the Dranchuk-Abu-Kassem method [18]. Beggs and Brill (1977) proposed a method for calculating the gas Z-factor called the BB method [19]. Londono et al. (2002) refitted the chart with an expanded data set resulting in a modified method that can be used to accurately determine the Z-factor [20]. They provide two equations: one fit to an expanded data set from the Standing-Katz Z-factor chart and another that included single component data. Li et al. (2012) proposed a calculation method of the gas Z-factor that is suitable for full temperature and pressure range by fitting the Standing-Katz chart. Shariaty S. et al. (2019) proposed a new model for estimating the Z-factor [21]. Ekechukwu G K. et al. (2019) obtained a novel mathematical correlation for the accurate prediction of the Z-factor [22]. Hemmati-Sarapardeh A. et al. (2020) and Mogensen, K. et al. (2021) used a lot of PVT data for modeling the Z-factor [23,24]. Wang Y. et al. (2022) and Towfighi S. (2020) proposed an accurate correlation for calculating the Z-factor [25,26]. Unfortunately, most of these Z-factor methods have a pressure range below 150 MPa. Moreover, to the best of our knowledge, these correlations give large errors at high gas reservoir pressures, and this error could be more than 100%. The error in estimating the Z-factor will lead to large errors in estimating all the other gas properties such as gas formation volume factor, gas compressibility, and gas in place [27].
To address the gap, based on the DPR correlation, the independent variable function of pseudo-critical temperature and pseudo-critical pressure is established by the multivariate nonlinear regression method. A Z-factor calculation method suitable for high-temperature and high-pressure gas reservoirs is developed by correcting the high-pressure data in the DPR correlation. Furthermore, we use the corrected Z-factor to calculate the bottom hole pressure of well H1 based on the Cullender-Smith method [28]. Finally, the bottom hole pressure of well H2 is calculated, the Z-factor of well H2 under formation conditions is predicted, and the relationship between the Z-factor and pressure at different temperatures is provided.
2. Methodology
In this study, the errors of different gas Z-factor calculation methods and experimental data of well H1 under high-pressure conditions were compared. It is found that the calculation errors of different methods are large under ultrahigh-pressure conditions. Then, based on the experimental data, the coefficients of the DPR method are corrected by the multivariate nonlinear regression method to obtain a new DPR correlation. The new DPR correlation is used to obtain the accurate gas Z-factor and calculate the bottom hole pressure. Finally, the gas Z-factor and bottom hole pressure of a new well in the same oilfield block under any temperature and pressure are predicted. The detailed calculation process is shown in Figure 1.

Figure 1.
Flowchart of gas Z-factor correction and prediction in ultra-deep gas reservoir with high temperature and pressure.
2.1. Gas Z-Factor Correction
The highest formation pressure of the Qingshuihe formation gas reservoir in the southern margin of the Junggar Basin is 170 MPa, the highest formation temperature is 172 °C, and the burial depth is between 7000 and 8000 m. It is an ultra-deep gas reservoir with a high temperature and high pressure. For this kind of ultra-deep gas reservoir, due to its formation pressure exceeding 120 MPa, the Z-factor error is close to 4.00%, and the bottom hole pressure error is close to 3.00%, which brings great trouble to the early dynamic reserve calculation, production performance analysis, and vertical pipe flow calculation of the reservoir. If the calculation error of the Z-factor can be less than 0.50%, the calculation results of dynamic reserves and vertical pipe flow will be greatly improved.
Standing and Katz have developed a chart (SKC) according to the theory of corresponding states for calculating the Z-Factor which is widely used in high-temperature and high-pressure gas reservoirs. The SKC has been digitalized by Poettmann and Carppenter in the range of 0.2 ≤ Ppr ≤ 15 and 1.05 ≤ Tpr ≤ 3.0, which brings a lot of inconvenience to the calculation of the ultra-high pressure gas Z-factor. Moreover, the calculation range of various empirical formulas of the Z-factor cannot meet the Z-factor calculation requirements (Table 1) at 146.07 MPa and 158.63 °C of well H1 in the southern margin of the Junggar Basin. Therefore, it is urgent to develop a new method that is suitable for the calculation of the Z-factor under ultra-high-pressure conditions.

Table 1.
Recommended application range of natural gas Z-factor.
2.1.1. Feasibility Analysis of Linear Extrapolation
Some scholars believe that in the ultra-high-pressure stage, the Z-factor has a linear relationship with pressure, and it can be obtained by linear extrapolation of high-pressure stage data at different temperatures. The specific arguments are as follows.
According to thermodynamics, the general equation of the fluid state equation is:
where P is intermolecular interaction, MPa; PR is intermolecular repulsion, MPa; and PA is intermolecular attraction, MPa.
According to Equation (1), the general two-parameter state equation can be written as:
where R is State equation constant, R = 8.3145; T is temperature, K; V is volume, m3; and a and b are empirical constants of the VDW state equation.
When u and w take different values, Equation (2) can be transformed into common VDW, RK, SRK, and PR equations. According to the theory of molecular motion, there are interactions between gas molecules. When the molecular spacing is large, the force is generally gravitational, but as the molecules get closer, the gravity gradually weakens and is mainly manifested as repulsion. At ultra-high pressures, gas molecules are in close contact with each other. Due to the mutual repulsion between electron clouds and atomic nuclei, the intermolecular force is prominently manifested as repulsion. Thus, Equation (2) can be simplified to:
Introducing the Z-factor
Bring Equation (4) into Equation (3)
It can be seen from Equation (4) that when the gas molecules are under high pressure and the intermolecular interaction is mainly manifested as a repulsive force, the Z-factor changes linearly with pressure, and the slope is positive, that is, b/RT. Equation (4) is theoretically applicable to pure components but can be generalized to mixtures by mixing rules. By introducing a pseudo-reduced pressure and a pseudo-reduced temperature, Equation (4) can be transformed to:
where:
where ppr is pseudo-reduced pressure, dimensionless; Tpr is pseudo-reduced temperature, dimensionless; ppc is pseudo critical pressure, MPa; Tpc is pseudo critical temperature, K; pci is the critical pressure of component i, MPa; Tci is the critical temperature of component i, K; and xi is mole fraction of component i.
It can be seen from Equation (6) that the Z-factor has a linear relationship with the pseudo-reduced pressure at a given temperature or pseudo-reduced temperature. In addition, according to the experimental data of well H1, when the pressure is greater than 60 MPa, the Z-factor and pressure at three temperatures (158.63 °C, 138.63 °C, and 118.63 °C) show a linear relationship (Figure 2), and the correlation coefficient is 1. To sum up, under the condition of ultra-high pressure, the linear extrapolation of the Z-factor according to the data of the high-pressure stage is theoretically established or approximately established.
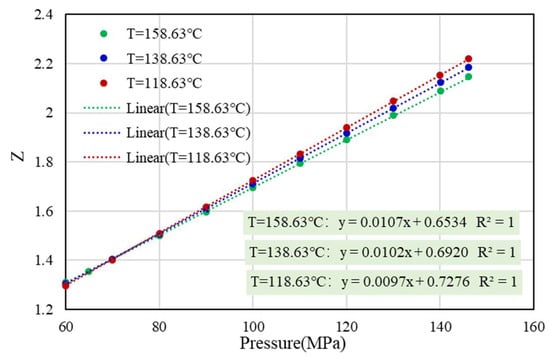
Figure 2.
Regression relation curve of Z-factor experimental data of well H1 under high pressure.
2.1.2. Error Analysis of Z-Factor Empirical Formula
Well H1 is located in the southern margin of the Junggar Basin, Xinjiang. The formation pressure of this well is 146.07 MPa, the formation temperature is 158.63 °C, and it is a condensate gas reservoir with a buried depth of 7374 m. It belongs to a typical high-temperature and high-pressure well. According to the composition of producing the well stream, the experiment data of constant composition expansion (CCE), constant volume depletion (CVD), and the compositions of natural gas are shown in Table 2, and the parameters such as gas critical properties are shown in Table 3. Among them, the relative density of the gas is 0.66, the dew point pressure is 53.76 MPa, and the critical condensation temperature is 376.73 °C. Since the formation pressure is much higher than the dew point pressure, the pressure drop will not appear as an obvious retrograde condensation phenomenon, so there is a single-phase flow in the reservoir. It is particularly important to accurately calculate the PVT parameters of such gas wells, which can provide accurate pre-processing for subsequent well testing interpretation and productivity prediction.

Table 2.
The compositions of natural gas.

Table 3.
Gas critical property parameters.
Using the Z-factor calculation methods of the PVT module in commercial software, these methods include the Dranchuk-Purvis-Robinson method, the Hall-Yarborough method, the Brill-Beggs method, and the Standing and Cranmer method. From the linear extrapolation of pressure to 160 MPa and comparison with experimental data from well H1, the results show that the various empirical formulas have good fitting effects between the pressure of 0–60 MPa (Figure 3a), but the calculation of the Z-factor after 60 MPa at three temperature conditions completely deviates from the experimental data (Figure 3b,d), and the error gradually increases with the increase of pressure. Although it seems that the error between the HY method and experimental data is small at 158.63 °C, the calculation results of the HY method gradually deviate from the experimental data at 138.63 °C and 118.63 °C. Similarly, although it seems that the error between the BB method and experimental data is small at 138.63 °C, the calculation results of the BB method gradually deviate from the experimental data at 158.63 °C and 118.63 °C. The other calculation methods also have large deviations from the experimental data of well H1 under high-pressure conditions.
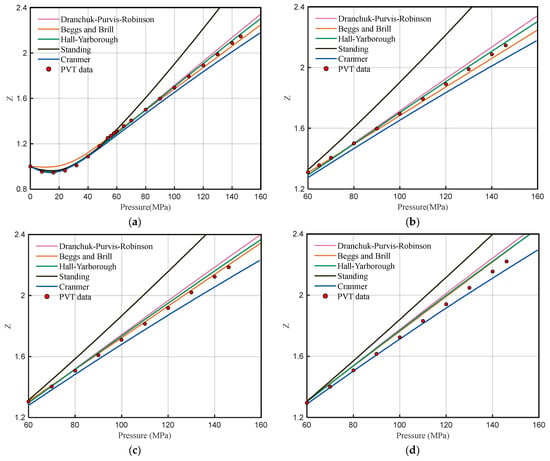
Figure 3.
Comparison between calculated results of Z-factor empirical formula and experimental data. (a) Full pressure comparison at 158.63 °C. (b) High-pressure comparison, 158.63 °C. (c) High-pressure comparison, 138.63 °C. (d) High-pressure comparison, 118.63 °C.
Based on the above analysis, considering that the DPR method is the most widely used for Z-factor calculation in commercial software and the DPR method is based on the correlation obtained from the digitization of 1500 Standing-Katz experimental data points with high applicability and accuracy, the DPR method is corrected to obtain a new ultra-high-pressure Z-factor calculation method. The error results of the DPR method and well H1 experimental data (Figure 4) show that the error increases gradually with the increase of pressure after 60 MPa under three temperature conditions. Therefore, it is considered to correct the DPR method from 60 Mpa based on experimental data.
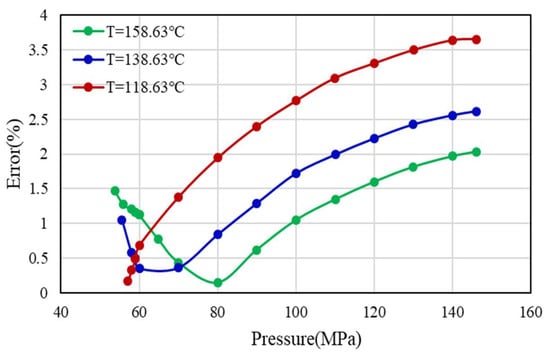
Figure 4.
Error analysis of Z-factor under high pressure and three temperature conditions.
2.1.3. Coefficients Sensitivity Analysis of DPR Method
Based on the Benedict-Webb-Rubin equation of state, Dranchuk, Purvis, and Robinson (1973) introduced the gas-reduced density to calculate the gas Z-factor. The reduced density is defined as the ratio of the density at a specific pressure and temperature to the density at the critical pressure and temperature:
The Z-factor of the critical gas is about 0.27, and the reduced density expression can be simplified as:
The equation for calculating the reduced density:
where
A1 = 0.31506237; A2 = −1.0467099; A3 = −0.57832729; A4 = 0.53530771;
A5 = −0.61232032; A6 = −0.10488813; A7 = 0.68157001; A8 = 0.68157001;
in Equation (13) needs to be solved by the Newton iteration method.
The DPR method contains eight coefficients of A1~A8. The sensitivity analysis of the coefficient value and Z-factor is performed. The value of the coefficient increases or decreases by 0.02 each time. The influence range of each coefficient on the Z-factor is shown in Figure 5.
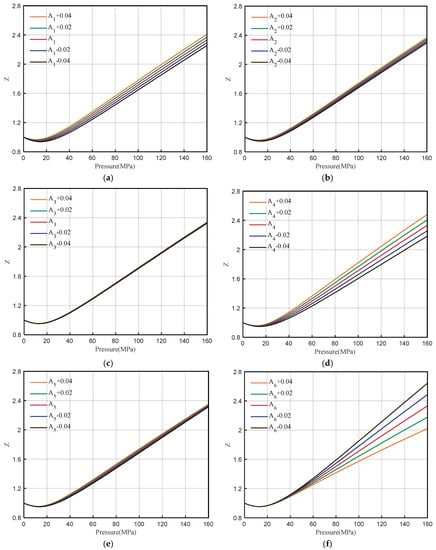
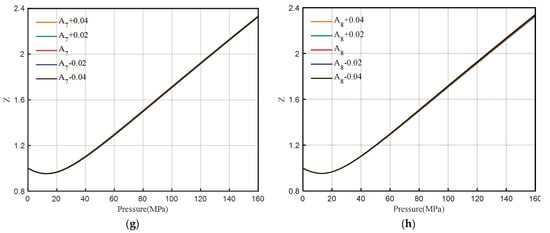
Figure 5.
Sensitivity analysis of coefficients A1~A8. (a) A1, (b) A2, (c)A3, (d) A4, (e) A5, (f) A6, (g) A7, (h) A8.
From Figure 5, it can be seen that with the change of the coefficient A1 value, the Z-factor has different amplitude changes in the whole pressure range (0–160 MPa), which does not meet the requirements of high-pressure correction, so correction A1 is not considered. The sensitivity analysis of A2 and A5 shows that with the change of value, the Z-factor has different amplitude changes (small change range) in the whole interval, without considering the correction. After a small change in the value of A3, A7, and A8, the change in the Z-factor is not obvious, and the correction is not considered.
The value of coefficient A4 varies between 0~10 MPa, and Z-factor is basically unchanged. However, when the pressure is greater than 60 MPa, the Z-factor changes greatly with pressure. A4 is more sensitive to high pressures and meets the requirements of correction. Similarly, the value of coefficient A6 changes between 0~40 MPa, and the Z-factor is basically unchanged. However, when the pressure is greater than 60 MPa, the Z-factor changes greatly with the pressure. A6 is more sensitive to high pressures, and it also meets the requirements of correction. Therefore, the coefficients A4 and A6 are corrected by multivariate nonlinear regression.
2.1.4. Correction of DPR Method by Multivariate Nonlinear Regression
In regression analysis, if there are two or more independent variables, it is called multiple regression. In fact, a phenomenon is often associated with multiple factors. The optimal combination of multiple independent variables to predict or estimate the dependent variable is more effective and more realistic than using only one independent variable to predict or estimate. This study specifies the multivariate nonlinear regression model (inline function) as the DPR Correlation (13). It returns a vector of estimated coefficients for the nonlinear regression of the responses in Z-factor on the predictors in using the model DPR. The coefficients are estimated using iterative least squares estimation, with initial values specified by A4 and A6.
Based on the Z-factor experimental data at 158.63 °C, the new A4 and A6 values are obtained after regression. Then, the new A4 and A6 values are substituted into Equation (13) to obtain a new reduced density. The above steps were repeated until the obtained A4 and A6 values were stable at a constant value, that is, the accurate value after the final regression. The specific calculation process is shown in Figure 6. After regression, A4′ = 0.570799074 and A6′= −0.067283104. The corrected coefficient is substituted into Equation (14) to obtain the corrected DPR correlation. The comparison between the calculated Z-factor before and after correction at 158.63 °C and the PVT data is shown in Figure 7.
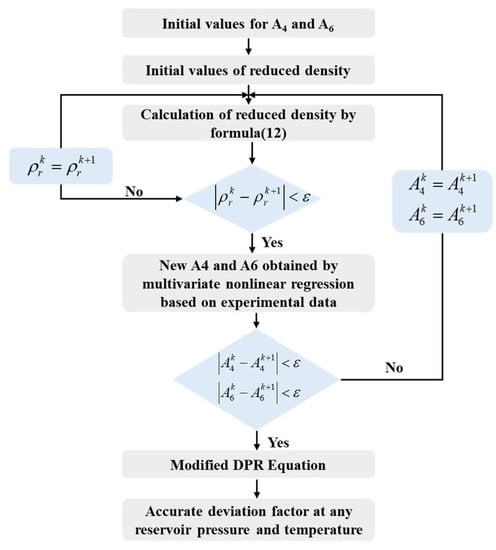
Figure 6.
The flow chart of multivariate nonlinear regression.
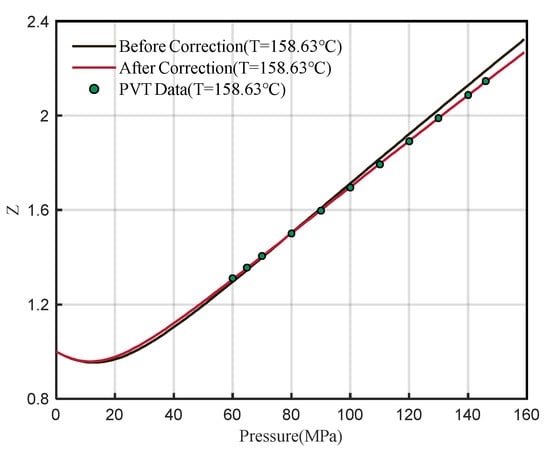
Figure 7.
Comparison of Z-factor with experimental data before and after correction at 158.63 °C.
The corrected DPR correlation is used to calculate the Z-factor at 138.63 °C and 118.63 °C. Compared with the uncorrected Z-factor and experimental data (Figure 8), the calculated results of the corrected DPR correlation are more accurate, which verifies the correctness of the corrected correlation and improves the applicability to the southern margin of the Junggar Basin.
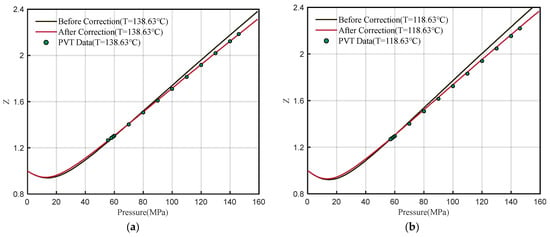
Figure 8.
Comparison of Z-factor with experimental data before and after correction (a) 138.63 °C (b) 118.63 °C.
The comparison of the Z-factor error results at 158.63 °C, 138.63 °C, and 118.63 °C is shown in Figure 9, Figure 10 and Figure 11.
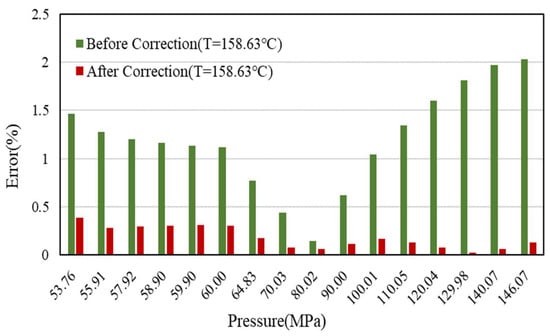
Figure 9.
Error comparison of Z-factor with experimental data before and after correction (158.63 °C).
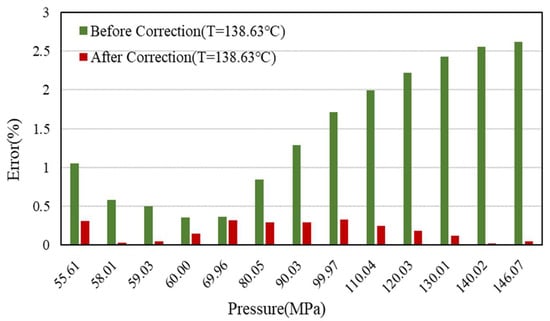
Figure 10.
Error comparison of Z-factor with experimental data before and after correction (138.63 °C).
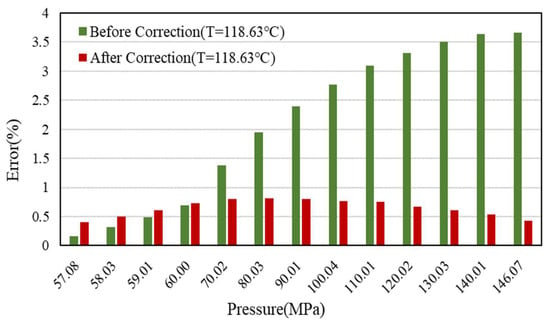
Figure 11.
Error comparison of Z-factor with experimental data before and after correction (118.63 °C).
The detailed data are shown in Table 4. It can be seen that the effect is better after correction, and the error of Z-factor is less than 1%, which can greatly improve the calculation accuracy of early dynamic reserves and vertical pipe flow.

Table 4.
Error results analysis after Z-Factor correction.
2.2. PVT Parameter Calculation
As we all know, the density of natural gas is used in the calculation of bottom hole pressure. It is particularly significant to accurately calculate the density of natural gas. The corrected Z-factor is substituted into Equation (15), and the accurate gas density (ρg) distribution with pressure at 158.63 °C can be obtained. The error analysis between the corrected gas density and the experimental data of well H1 is shown in Figure 12, and the error is within 1%, and the correction effect is better.
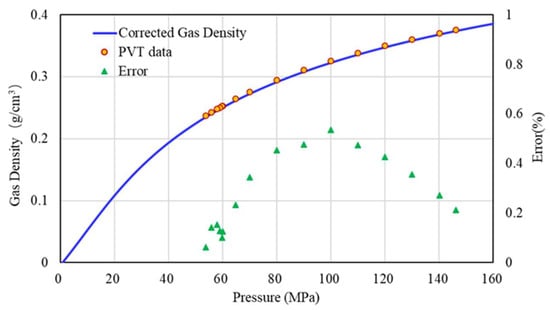
Figure 12.
Error analysis of corrected gas density and experimental data.
Similarly, substituting the corrected Z-factor into Equation (16) will get the accurate formation volume factor (Bg). The error between the corrected formation volume factor and the experimental data is within 0.5% (Figure 13), and the correction works very well.
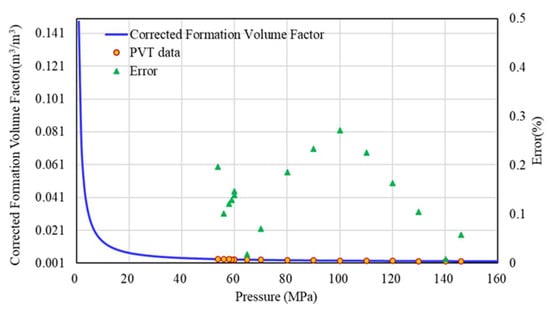
Figure 13.
Error analysis of corrected formation volume factor and experimental data.
In the PVT experiment of well H1, the isothermal compressibility coefficient (Cg) and gas viscosity (μg) were not tested. The variation of the isothermal compressibility coefficient and gas viscosity of well H1 with pressure is calculated by the relevant empirical formulas. The predicted results are shown in Figure 14.
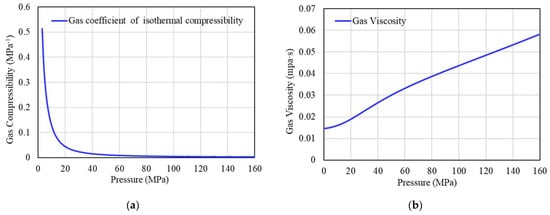
Figure 14.
(a) Gas coefficient of isothermal compressibility under different pressures. (b) Gas viscosity under different pressures.
2.3. Bottom Hole Pressure Calculation of Gas Well
In this study, the Cullender-Smith method commonly used in dry gas reservoirs is used to calculate the bottom hole pressure of gas wells. This method is calculated by the numerical integration method, considering the common tubing production situation:
According to Equation (17), the bottom hole pressure can be calculated by using the piecewise integral numerical calculation method, that is, multiple calculation position points are set from the wellhead to the bottom hole, and the pressure of each position point is calculated from top to bottom according to the wellhead pressure, and finally the bottom hole pressure is calculated. The trapezoidal method is applied to Equation (17). Considering that the production is 0, the equation for calculating the bottom hole pressure of the static gas column is obtained:
where, subscript 1 represents the upper position point of the adjacent calculated position point, subscript 2 represents the lower position point, and subscript m represents the middle position point of the two. The specific calculation steps are as follows:
- (1)
- According to the wellhead pressure and temperature conditions, the value of the subscript 1 numerical term in the denominator of Equation (18) is calculated. Assuming that the midpoint numerical term is equal to the subscript 1 numerical term, the initial value of the pressure in the middle of the wellbore is calculated;
- (2)
- According to the temperature in the middle of the wellbore and the above-calculated pressure value, the numerical value of the subscript m in the denominator of Equation (18) is calculated, and the pressure value in the middle of the wellbore is calculated again according to Equation (18);
- (3)
- Comparing the pressure difference between step (2) and the last calculation (the first step is the estimation), if the difference is large, step (2) iterative calculation is repeated until the calculation error meets the requirements;
- (4)
- After determining the pressure in the middle of the wellbore, the above steps are used to further iteratively calculate the bottom hole pressure.
Substituting the corrected Z-factor and gas density of well H1 into Equation (18) for an iterative solution, the wellbore pressure distribution of well H1 is obtained. The comparison with the uncorrected wellbore pressure distribution is shown in Figure 15. When the buried depth of the reservoir is 7374 m, the bottom hole pressure calculated by the uncorrected Z-factor is 143.58 MPa, and the bottom hole pressure calculated by the corrected Z-factor is 146.32 MPa. Compared with the actual measured value of 146.07 MPa, the corrected Z-factor calculation result is closer to the actual value. It shows that this method can obviously improve the calculation accuracy of bottom hole pressure and provide great help for field construction.
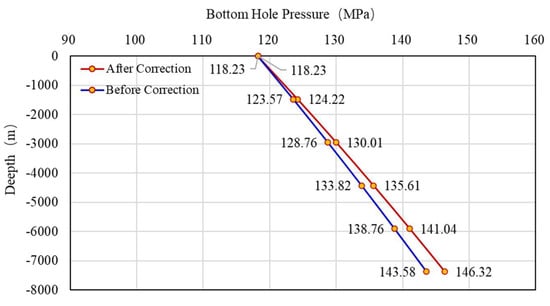
Figure 15.
Wellbore pressure distribution before and after correction.
3. Case Study and Prediction
3.1. Case 1
There are many publications devoted to correlations in explicit form for the Z-factor, such as Wang Y. et al. (2022), the authors have analyzed the most widely used of them, dating back to the ’70s of the last century. They used a lot of measured compressibility factor data to validate the accuracy of the proposed correlation in practice applications. Under the condition of using the same natural gas composition, when Ppr is less than 30, our results are close to their results (Figure 16), and it can validate the accuracy of our method. However, when Ppr is between 30 and 40, the results of Wang Y. et al. have an obvious upwarping phenomenon (Figure 17), which violates the linear law of pressure and Z-factor under high-pressure conditions. Therefore, when Ppr is greater than 30, the calculation results of this paper are more reliable.
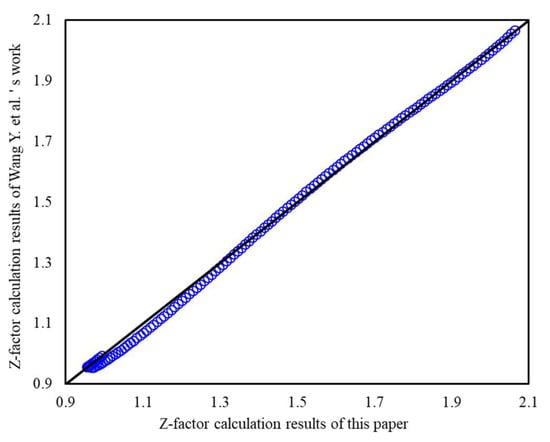
Figure 16.
Z-factor calculation results of this paper versus works from Wang Y. et al. (0.2 < Ppr < 30).
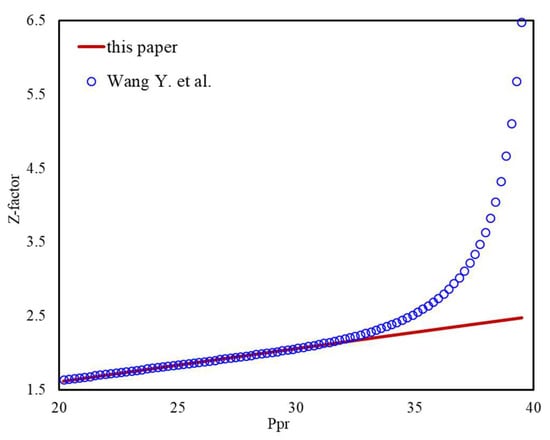
Figure 17.
Z-factor calculation results of this paper versus work from Wang Y. et al. (20 < Ppr < 40).
3.2. Case 2
Similar to well H1, well H2 is also located in the Qingshuihe Formation in the southern margin of the Junggar Basin, Xinjiang, and is close to well H1 (Figure 18). The depth of the reservoir is 8079 m, but the pressure gauge is located at 7875 m of the reservoir. The measured formation pressure at the pressure gauge position is 170.52 MPa, and the temperature is 170.2 °C. It belongs to a typical ultra-deep gas reservoir with a high temperature and high pressure.
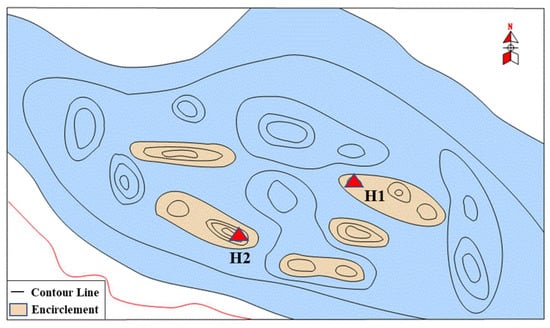
Figure 18.
Schematic diagram of the relative position of well H1 and well H2.
Due to the high temperature and pressure after downhole sampling in Well H2, PVT experiments cannot be performed to analyze the composition of natural gas and related parameters such as the Z-factor. Therefore, the PVT parameters of well H2 are calculated by using the method in this study with the same gas composition as well H1. First, the pressure of the measured pressure gauge is converted to the wellhead, and the wellhead pressure is 142.83 MPa. Then, the formation pressure at the depth of 8079 m is calculated to be 171.74 MPa, and the temperature is 172.22 °C. The wellbore pressure distribution is shown in Figure 19. Finally, the relationship between the Z-factor and the pressure of well H2 under reservoir conditions is calculated (Figure 20), and the Z-factor is 2.3548. The relationship between the Z-factor and pressure at different temperatures is shown in Figure 21.
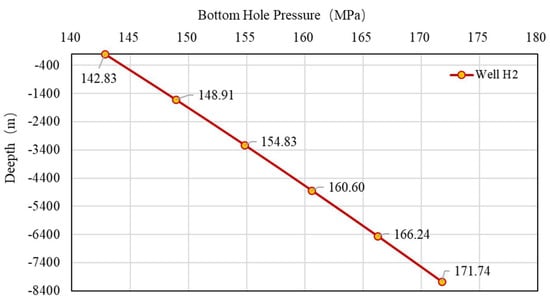
Figure 19.
Wellbore pressure distribution of well H2.
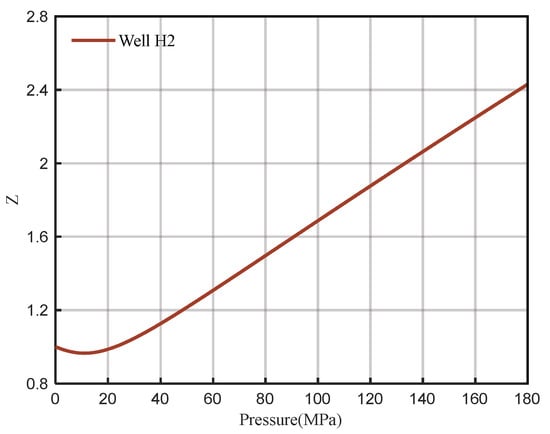
Figure 20.
Z-factor of H2 at 171.74 MPa and 172.22 °C.
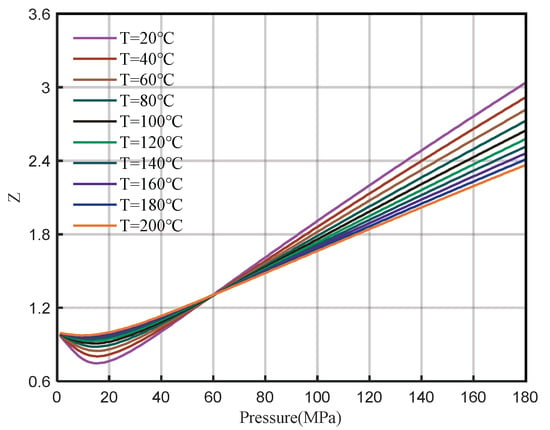
Figure 21.
Z-factor chart at different temperatures.
4. Conclusions
Based on the PVT laboratory data of well H1, we used the multivariate nonlinear regression method to correct the high-pressure part of the DPR correlation to obtain a new correlation, which will be suitable for the calculation of the Z-factor of ultra-deep gas reservoirs with high temperature and high pressure. When the PVT laboratory conditions cannot reach ultra-high pressures and temperatures, the new correlation can greatly improve the calculation efficiency and accuracy of the Z-factor, thus improving the calculation accuracy of the single-well bottom hole pressure, production capacity, and dynamic reserves. The contributions and conclusions of this work can be summarized as follows:
- (1)
- The sensitivity analysis of DPR correlation shows that the coefficients A4 and A6 are sensitive to high pressure and satisfy the demand for correction. The new correlation can be used to determine the Z-factor at any pressure range, especially for high pressures, and the error is less than 1% compared to the PVT data;
- (2)
- The error between the natural gas density calculated by the corrected Z-factor and the PVT data is within 1%, and the error between the formation volume factor and the PVT data is within 0.5%. At the same time, the variation trend of the gas isothermal compressibility coefficient and gas viscosity of well H1 with pressure is predicted;
- (3)
- Under the condition of a formation depth of 7374 m, the bottom hole pressure calculated before and after the correction of the Z-factor is 143.58 MPa and 146.32 MPa, respectively. Compared with the actual measured value of 146.07 MPa, the corrected Z-factor is closer to the actual value;
- (4)
- It is predicted that the bottom hole pressure of well H2 is 171.84 MPa and the gas Z-factor is 2.3548 when the formation depth is 8079 m, and the Z-factor chart at different temperatures is provided.
Author Contributions
Conceptualization, S.C.; methodology, Y.X.; validation, Z.X.; investigation, W.W.; formal analysis, Q.G.; writing—review and editing, W.B.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Science Foundation of China University of Petroleum, Beijing grant number 2462022BJRC004.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in this article.
Acknowledgments
The authors would like to acknowledge the financial support by the Science Foundation of China University of Petroleum, Beijing (2462022BJRC004).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Z | gas compressibility factor |
| Tpr | pseudo-reduced temperature |
| Ppr | pseudo-reduced pressure |
| P | intermolecular interaction (MPa) |
| PR | intermolecular repulsion (MPa) |
| PA | intermolecular attraction (MPa) |
| R | state equation constant |
| T | temperature (K) |
| V | Volume (m3) |
| a | empirical constants of VDW state equation |
| b | empirical constants of VDW state equation |
| Ppc | pseudo critical pressure (MPa) |
| Tpc | pseudo critical temperature (K) |
| pci | critical pressure of component i (MPa) |
| Tci | critical temperature of component i (K) |
| xi | mole fraction of component i |
| ρr | gas reduced density |
| ρg | gas density (g/cm3) |
| Ma | gas relative molecular weight |
| Bg | formation volume factor (m3/m3) |
| pwf | bottom hole pressure (MPa) |
| pwh | wellhead pressure (MPa) |
| D | tubing inner-diameter (m) |
| f | frictional coefficient |
| q | rate of the gas (m3/d) |
| γg | gas relative density |
| H | depth of tubing down to the middle of formation (m) |
| HTHP | high temperature and high pressure |
| DPR | Dranchuk, Purvis, and Robinson |
References
- Wang, Y.; Ayala, L.F. Explicit Determination of Reserves for Variable Bottom-hole Pressure Conditions in Gas Well Decline Analysis. SPE J. 2020, 25, 369–390. [Google Scholar] [CrossRef]
- Wei, C.; Liu, Y.; Deng, Y.; Cheng, S.; Hassanzadeh, H. Temperature Transient Analysis of Naturally Fractured Geothermal Reservoirs. SPE J. 2022, 27, 2723–2745. [Google Scholar] [CrossRef]
- Luo, L.; Cheng, S.Q.; Lee, J. Characterization of refracture orientation in poorly propped fractured wells by pressure transient analysis: Model, pitfall, and application. J. Nat. Gas Sci. Eng. 2020, 79, 1875–5100. [Google Scholar] [CrossRef]
- Mahmoud, M.A. Development of a New Correlation of Gas Compressibility Factor (Z-Factor) for High Pressure Gas Reservoir. In Proceedings of the North Africa Technical Conference and Exhibition, Cairo, Egypt, 15–17 April 2013. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, S.; Zhang, F.; Feng, N.; Li, L.; Shen, X.; Li, J.; Yu, H. Big Data Technique in the Reservoir Parameters’ Prediction and Productivity Evaluation: A Field Case in Western South China Sea. Gondwana Res. 2021, 96, 22–36. [Google Scholar] [CrossRef]
- Wei, C.; Liu, Y.; Deng, Y.; Cheng, S.; Hassanzadeh, H. Analytical well-test model for hydraulicly fractured wells with multiwell interference in double porosity gas reservoirs. J. Nat. Gas Sci. Eng. 2022, 103, 1875–5100. [Google Scholar] [CrossRef]
- Zhang, C.; Cheng, S.; Wang, Y.; Chen, G.; Yan, K.; Ma, Y. Rate Transient Behavior of Wells Intercepting Non-Uniform Fractures in a Layered Tight Gas Reservoir. Energies 2022, 15, 5705. [Google Scholar] [CrossRef]
- Abolghasemi, E.; Andersen, P.Ø. The influence of adsorption layer thickness and pore geometry on gas production from tight compressible shales. Adv. Geo-Energy Res. 2021, 6, 4–22. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, Y.; Han, D.; Sun, M.; Huang, Q. Combined effects of permeability and fluid saturation on seismic wave dispersion and attenuation in partially-saturated sandstone. Adv. Geo-Energy Res. 2021, 5, 181–190. [Google Scholar] [CrossRef]
- Kumar, M.N. Compressibility Factors for Natural and Sour Reservoir Gases by Correlations & Cubic Equations of State; Texas Tech University: Lubbock, TX, USA, 2004; Available online: http://hdl.handle.net/2346/15386 (accessed on 6 September 2022).
- Ghanem, A.; Gouda, M.F.; Alharthy, R.D.; Desouky, S.M. Predicting the Compressibility Factor of Natural Gas by Using Statistical Modeling and Neural Network. Energies 2022, 15, 1807. [Google Scholar] [CrossRef]
- Jia, D.; Zhu, X.; Song, L.; Liang, X.; Li, L.; Li, H.; Li, Z. New Model of Granite Buried-Hill Reservoir in PL Oilfield, Bohai Sea, China. Energies 2022, 15, 5702. [Google Scholar] [CrossRef]
- Standing, M.B.; Katz, D.L. Density of Natural Gases. Trans. AIME 1942, 146, 140–149. [Google Scholar] [CrossRef]
- Yarborough, L.; Hall, K.R. A New Equation of State for Z-Factor Calculations. Oil Gas J. 1973, 71, 82–92. [Google Scholar]
- Yarborough, L.; Hall, K.R. How to Solve Equation of State for Z-Factors. Oil Gas J. 1974, 72, 86–88. [Google Scholar]
- Benedict, M.; Webb, G.B.; Rubin, L.C. An Empirical Equation of Thermodynamic Properties of Light Hydrocarbon and Their Mixtures, I. Methane, Ethane, Propane, and n-Butane. J. Chem. Phys. 1940, 8, 334–345. [Google Scholar] [CrossRef]
- Dranchuk, P.M.; Purvis, R.A.; Robinson, D.B. Computer Calculation of Natural Gas Compressibility Factors Using the Standing and Katz Correlation. In Proceedings of the Annual Technical Meeting, Edmonton, AB, Canada, 7–11 May 1973. [Google Scholar] [CrossRef]
- Dranchuk, P.M.; Abou-Kassem, J.H. Calculation of Z Factor for Natural Gases Using Equation of State. J. Can. Pet. Technol. 1975, 14, 34–36. [Google Scholar] [CrossRef]
- Brill, J.P.; Beggs, D.H. Two-Phase Flow in Pipes; University of Tulsa: Tulsa, Oklahoma, 1974. [Google Scholar]
- Londono, F.E.; Archer, R.A.; Blasingame, T.A. Simplified Correlations for Hydrocarbon Gas Viscosity and Gas Density—Validation and Correlation of Behavior Using a Large-Scale Database. In Proceedings of the SPE Gas Technology Symposium, Calgary, AB, Canada, 30 April–2 May 2002. [Google Scholar] [CrossRef]
- Shariaty, S.; Khorsand Movaghar, M.R.; Vatandoost, A. A new model for estimating the gas compressibility factor using Group Method of Data Handling algorithm (case study). Asia-Pac. J. Chem. Eng. 2019, 14, e2307. [Google Scholar] [CrossRef]
- Ekechukwu, G.K.; Orodu, O.D. Novel mathematical correlation for accurate prediction of gas compressibility factor. Nat. Gas Ind. B 2019, 6, 629–638. [Google Scholar] [CrossRef]
- Hemmati-Sarapardeh, A.; Hajirezaie, S.; Soltanian, M.R.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Chau, K.W. Modeling natural gas compressibility factor using a hybrid group method of data handling. Eng. Appl. Comput. Fluid Mech. 2020, 14, 27–37. [Google Scholar] [CrossRef]
- Mogensen, K.; Robert, M. Comparison of Z-Factor Correlations Using a Large PVT Dataset with Emphasis on the GERG-2008 EOS. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 15–18 November 2021. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, J.; Wu, S. An accurate correlation for calculating natural gas compressibility factors under a wide range of pressure conditions. Energy Rep. 2022, 8, 130–137. [Google Scholar] [CrossRef]
- Towfighi, S. An empirical equation for the gas compressibility factor, Z. Pet. Sci. Technol. 2020, 38, 24–27. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, B.; Yan, L. Characteristics and Genesis Mechanism of Wellhead Pressure Fluctuation for Well Hutan-1. Xin Jiang Pet. Geol. 2022, 43, 587–591. [Google Scholar]
- Cullender, M.H.; Smith, R.V. Practical Solution of Gas-Flow Equations for Wells and Pipelines with Large Temperature Gradients. Trans. AIME 1956, 207, 281–287. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).