Tuning Model Predictive Control for Rigorous Operation of the Dalsfoss Hydropower Plant
Abstract
:1. Introduction
2. System Description
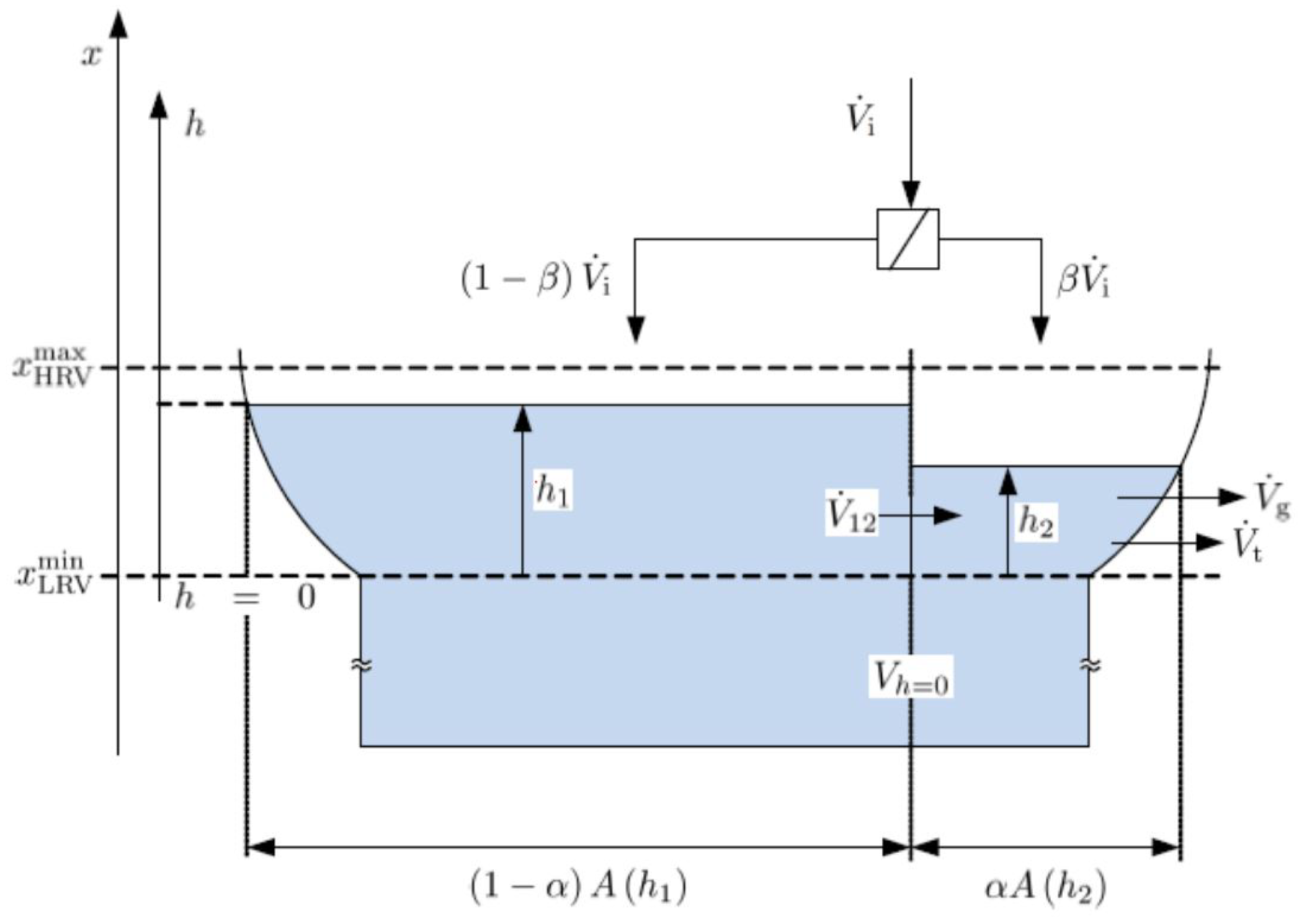
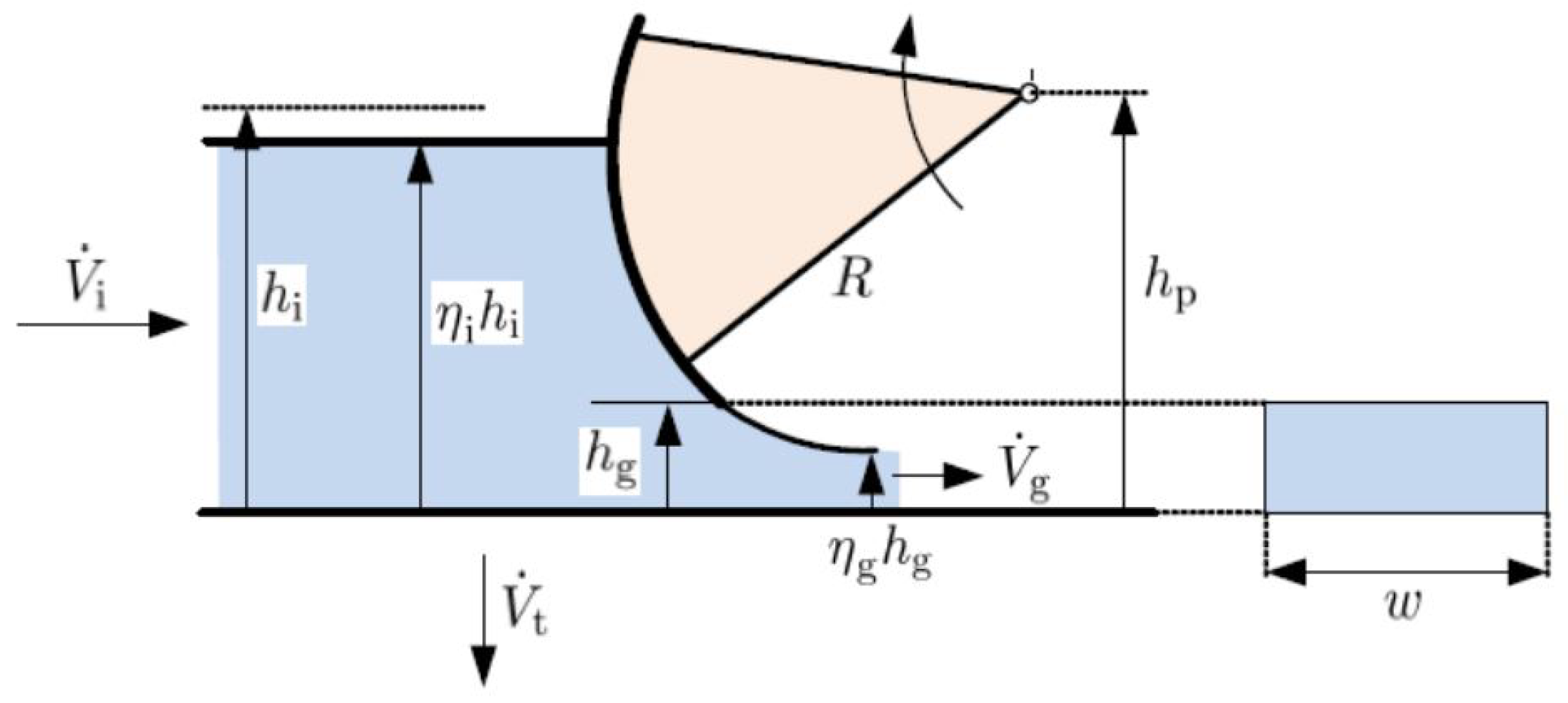
2.1. System Model
2.2. Operational Constraints
- The sudden change in the flowrate at downstream, , can endanger the properties and ecosystem along the watercourse. Therefore, the flowrate at downstream must be kept as constant as possible. The change of the flowrate at downstream is desired to keep less than 50 on every time step.
- The flowrate at downstream, , must be more than . This constraint is to ensure that fishes in downstream can move freely along the water course.
- The water level at Merkebekk, , must be maintained within a certain range as:where and mean the low and the high regulated value for the water level, respectively. The range changes seasonally as shown in Table 2.
- The maximum flowrate through the turbine, , is limited up to 36 .
2.3. Optimal Control Problem
3. Simulation Setting
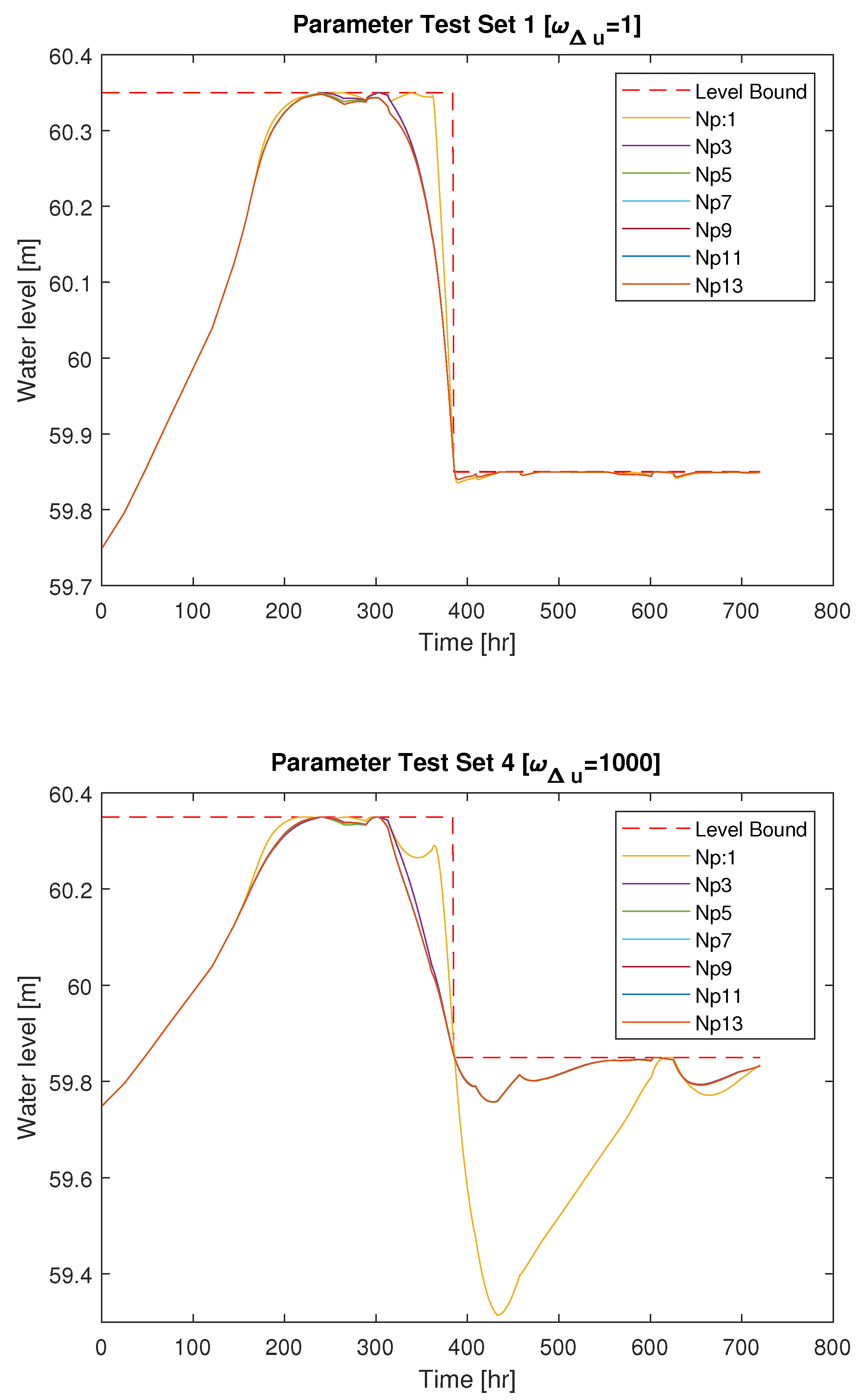
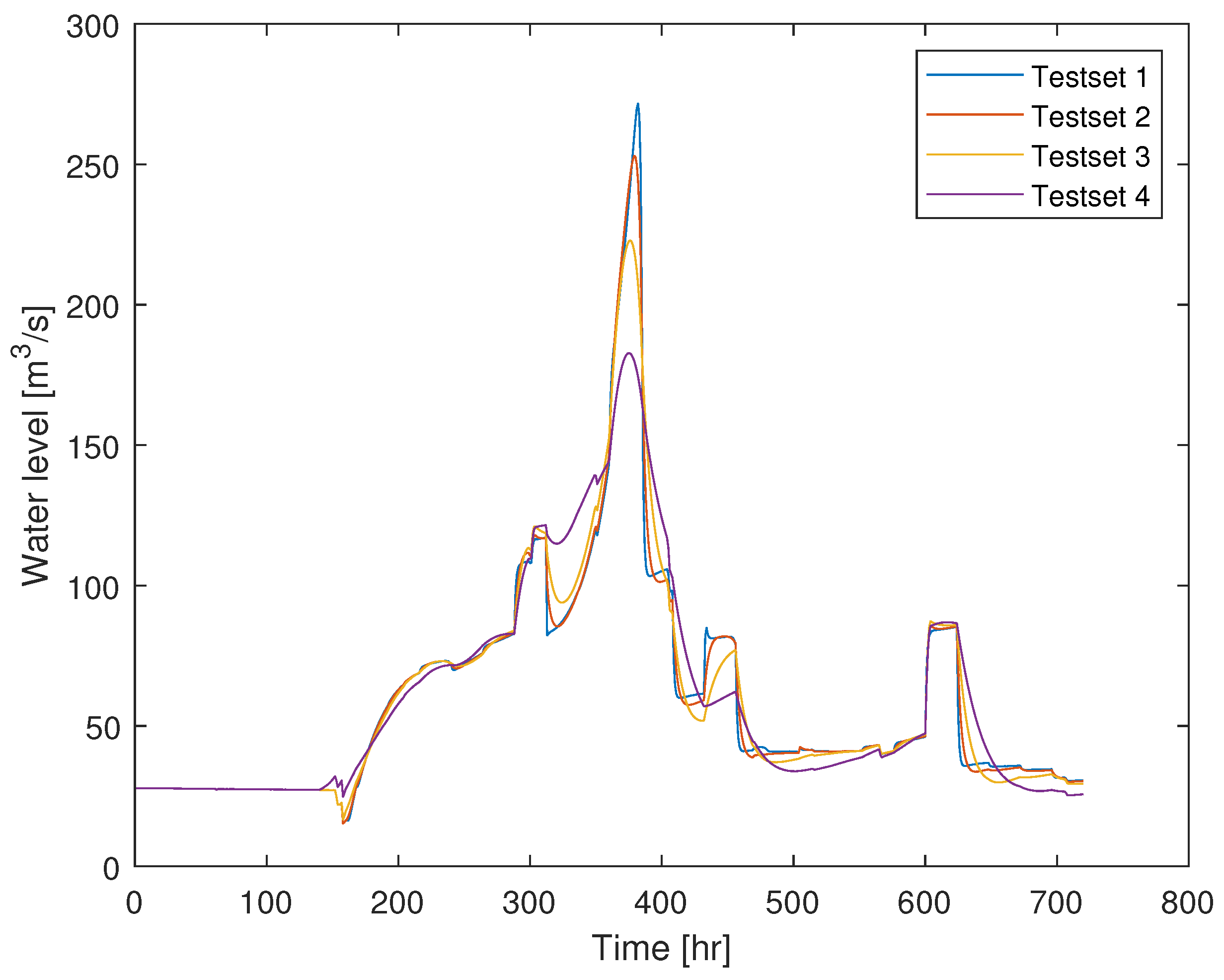
3.1. Test Sets of Parameters
3.2. Simulation Condition
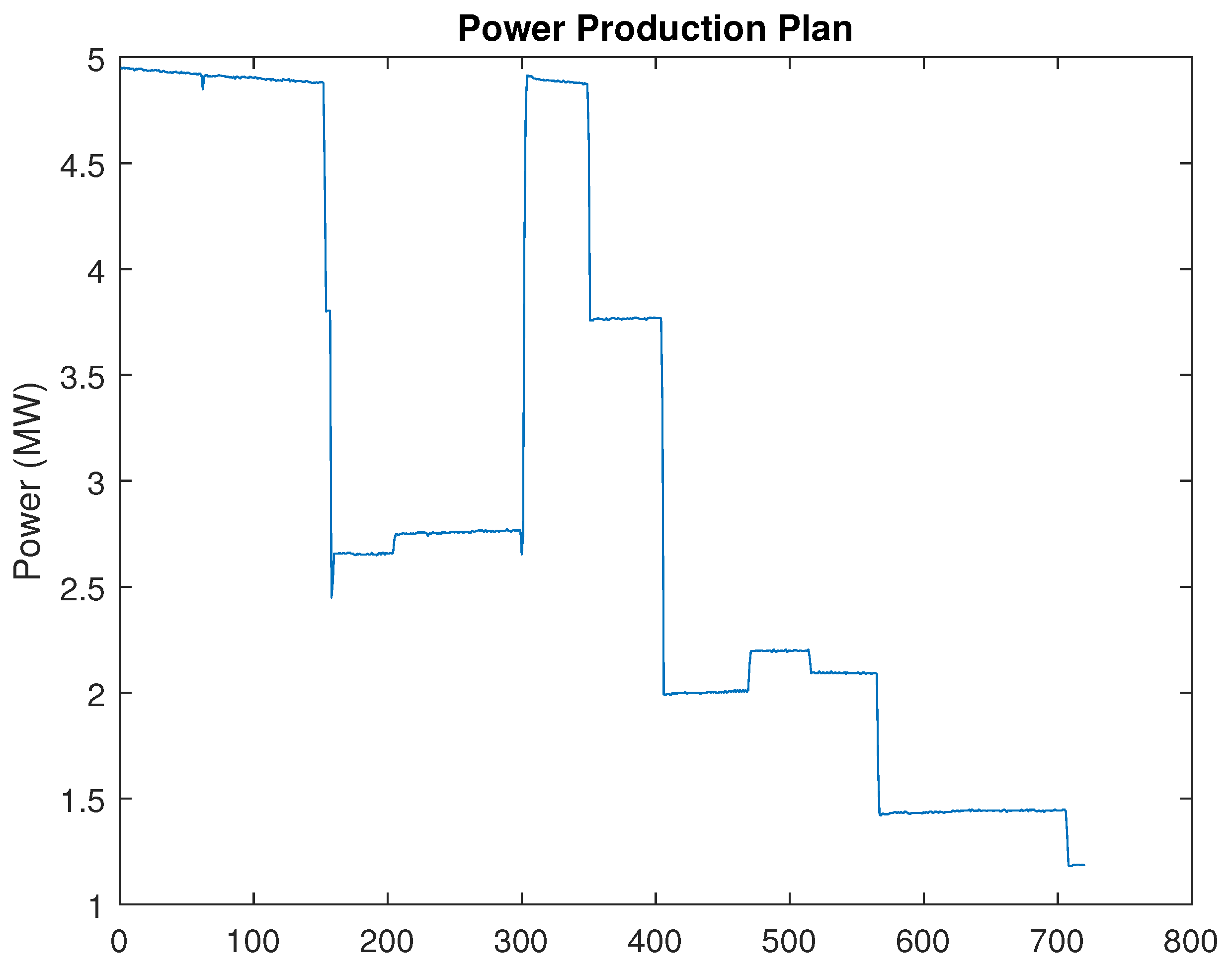
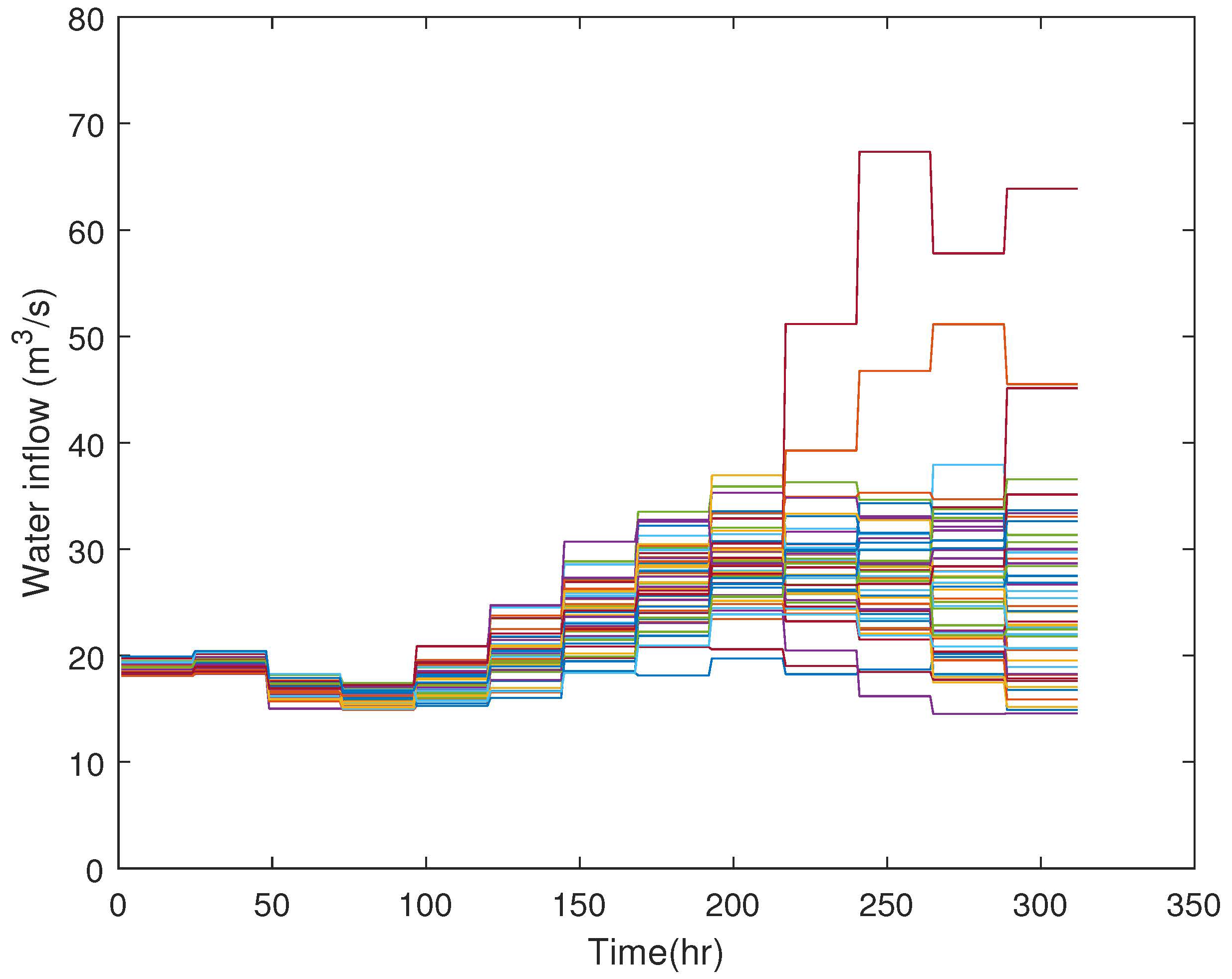
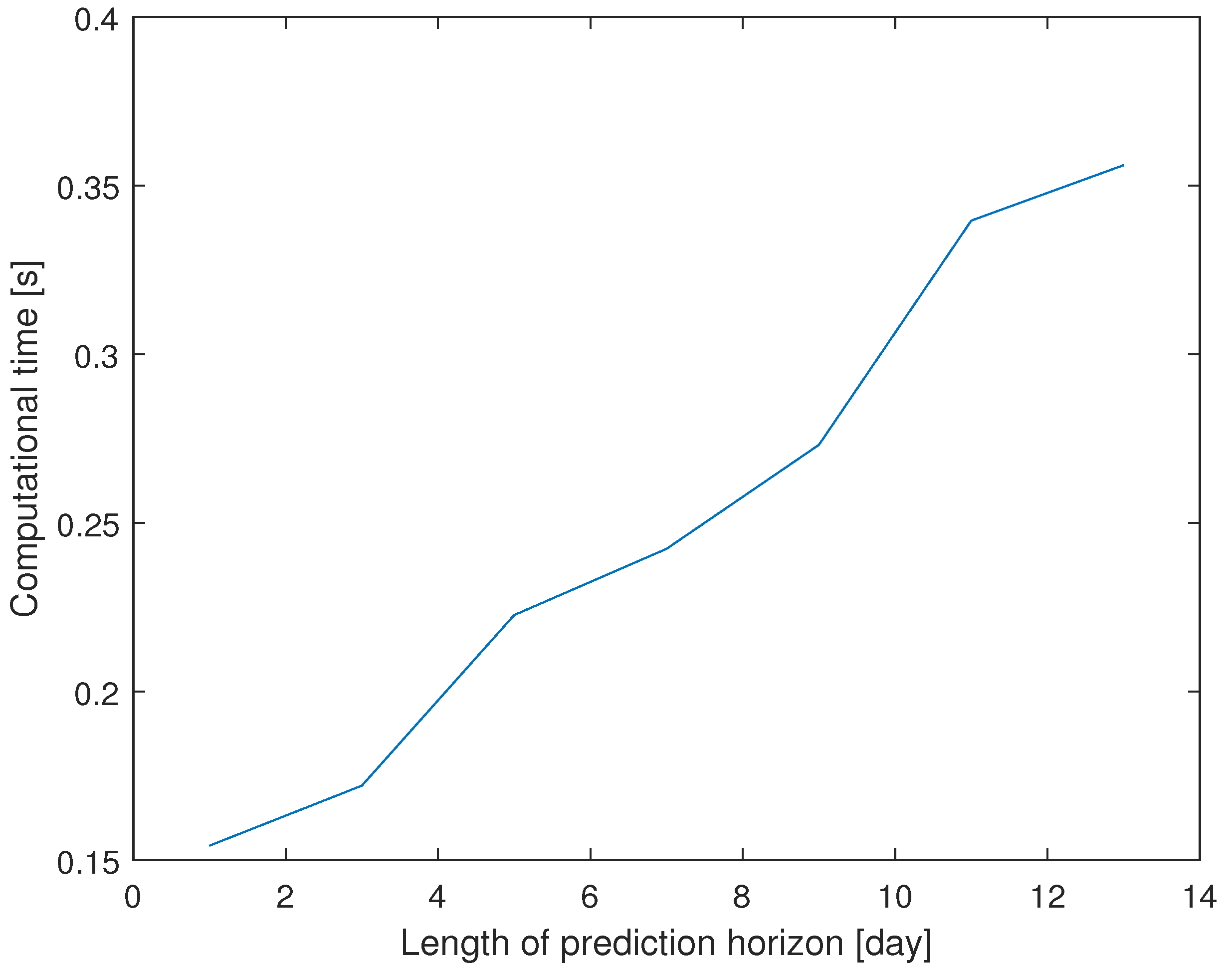
4. Simulation Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmed, T.; Muttaqi, K.; Agalgaonkar, A. Climate change impacts on electricity demand in the State of New South Wales, Australia. Appl. Energy 2012, 98, 376–383. [Google Scholar] [CrossRef]
- Torabi Haghighi, A.; Ashraf, F.B.; Riml, J.; Koskela, J.; Kløve, B.; Marttila, H. A power market-based operation support model for sub-daily hydropower regulation practices. Appl. Energy 2019, 255, 113905. [Google Scholar] [CrossRef]
- IEA. Hydropower Special Market Report—Analysis and Forecast to 2030; IEA: Paris, France, 2021. [Google Scholar]
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Mayne, D.; Rawlings, J.; Rao, C.; Scokaert, P. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Lee, J.H. Model predictive control: Review of the three decades of development. Int. J. Control. Autom. Syst. 2011, 9, 415–424. [Google Scholar] [CrossRef]
- SkagerakKraft. Dalsfos. 2021. Available online: https://www.skagerakkraft.no/dalsfos/category1277.html (accessed on 24 May 2021).
- SkagerakKraft. Kragerø Watercourse System. 2021. Available online: https://www.skagerakkraft.no/kragero-watercourse/category2391.html (accessed on 24 May 2021).
- NVE. Supervision of Dams. 2021. Available online: https://www.nve.no/supervision-of-dams/?ref=mainmenu (accessed on 24 May 2021).
- Lie, B. Final Report: KONTRAKT NR INAN-140122 Optimal Control of Dalsfos Flood Gates—Control Algorithm; Telemark University College: Porsgrunn, Norway, 2014. [Google Scholar]
- Kvam, K.D.; Furenes, B.; Hasaa, Å.; Gjerseth, A.Z.; Skeie, N.O.; Lie, B. Flood Control of Lake Toke: Model Development and Model Fitting. In Proceedings of the 58th Conference on Simulation and Modelling (SIMS 58), Reykjavik, Iceland, 25–27 September 2017. [Google Scholar]
- Menchacatorre, I.; Sharma, R.; Furenes, B.; Lie, B. Flood Management of Lake Toke: MPC Operation under Uncertainty. In Proceedings of the 60th SIMS Conference on Simulation and Modelling SIMS 2019, Västerås, Sweden, 12–16 August 2019; pp. 9–16. [Google Scholar] [CrossRef]
- Jeong, C.; Furenes, B.; Sharma, R. MPC Operation with Improved Optimal Control Problem at Dalsfoss Power Plant. In Proceedings of the First SIMS EUROSIM Conference on Modelling and Simulation, SIMS EUROSIM 2021, and 62nd International Conference of Scandinavian Simulation Society, SIMS 2021, Virtual Conference, Finland, 21–23 September 2021; Volume 11, pp. 226–233. [Google Scholar] [CrossRef]
- Jeong, C.; Sharma, R. Stochastic MPC For Optimal Operation of Hydropower Station under Uncertainty. IFAC-PapersOnLine 2022, 55, 155–160. [Google Scholar] [CrossRef]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]

| Parameter | Value | Unit | Comment |
|---|---|---|---|
| 0.05 | - | Fraction of surface area in compartment 2 | |
| 0.02 | - | Fraction of inflow to compartment 2 | |
| 800 | m/s | Flow coefficient | |
| 0.7 | - | Discharge coefficient, Dalsfoss gate | |
| 11.6 | m | Width of Dalsfoss gate 1 | |
| 11.0 | m | Width of Dalsfoss gate 2 | |
| 55.75 | m MSL | Minimal low regulated level value | |
| g | 9.81 | m/s | Acceleration of gravity |
| a | 124.69 | Pa | Coefficient in Equation (6) |
| b | 3.161 | m/s | Coefficient in Equation (6) |
| 0.13152 | W/m | Polynomial coefficient in Equation (7) | |
| −9.5241 | W/m | Polynomial coefficient in Equation (7) | |
| 1.7234 · 10 | W/m | Polynomial coefficient in Equation (7) | |
| −7.7045 · 10 | Pa/m | Polynomial coefficient in Equation (7) | |
| −8.7359 · 10 | W | Polynomial coefficient in Equation (7) |
| Date | ||
|---|---|---|
| 1 January–30 April | 55.75 | 60.35 |
| 1 May–30 August | 58.85 | 59.85 |
| 1 September–14 September | 55.75 | 59.35 |
| 28 October–11 November | 55.75 | 59.85 |
| 12 November–31 December | 55.75 | 60.35 |
| Parameter | Test Set 1 | Test Set 2 | Test Set 3 | Test Set 4 |
|---|---|---|---|---|
| 10 | 10 | 10 | 10 | |
| 1 | 10 | 100 | 1000 | |
| 1 | 1 | 1 | 1 | |
| 10,000 | 10,000 | 10,000 | 10,000 |
| [d] | Testset 1 | Testset 2 | Testset 3 | Test Set 4 |
|---|---|---|---|---|
| 1 | 4.2637 | 4.2625 | 4.2595 | 4.1644 |
| 3 | 4.2554 | 4.2537 | 4.2472 | 4.2314 |
| 5 | 4.2545 | 4.2528 | 4.2463 | 4.2290 |
| 7 | 4.2542 | 4.2526 | 4.2462 | 4.2294 |
| 9 | 4.2542 | 4.2526 | 4.2462 | 4.2294 |
| 11 | 4.2542 | 4.2526 | 4.2462 | 4.2294 |
| 13 | 4.2542 | 4.2526 | 4.2462 | 4.2294 |
| [d] | Testset 1 | Testset 2 | Testset 3 | Test Set 4 |
|---|---|---|---|---|
| 1 | 139.1463 | 71.9443 | 38.7613 | 31.4636 |
| 3 | 57.2664 | 33.3261 | 18.6869 | 17.2223 |
| 5 | 57.0969 | 33.1774 | 19.7069 | 14.8696 |
| 7 | 57.0943 | 33.1746 | 19.6943 | 16.4958 |
| 9 | 57.0941 | 33.1746 | 19.6950 | 16.3057 |
| 11 | 57.0941 | 33.1746 | 19.6935 | 16.3650 |
| 13 | 57.0941 | 33.1746 | 19.6934 | 16.3708 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, C.; Sharma, R. Tuning Model Predictive Control for Rigorous Operation of the Dalsfoss Hydropower Plant. Energies 2022, 15, 8678. https://doi.org/10.3390/en15228678
Jeong C, Sharma R. Tuning Model Predictive Control for Rigorous Operation of the Dalsfoss Hydropower Plant. Energies. 2022; 15(22):8678. https://doi.org/10.3390/en15228678
Chicago/Turabian StyleJeong, Changhun, and Roshan Sharma. 2022. "Tuning Model Predictive Control for Rigorous Operation of the Dalsfoss Hydropower Plant" Energies 15, no. 22: 8678. https://doi.org/10.3390/en15228678
APA StyleJeong, C., & Sharma, R. (2022). Tuning Model Predictive Control for Rigorous Operation of the Dalsfoss Hydropower Plant. Energies, 15(22), 8678. https://doi.org/10.3390/en15228678






