Heat Transport in Rotating Annular Duct: A Short Review
Abstract
1. Introduction
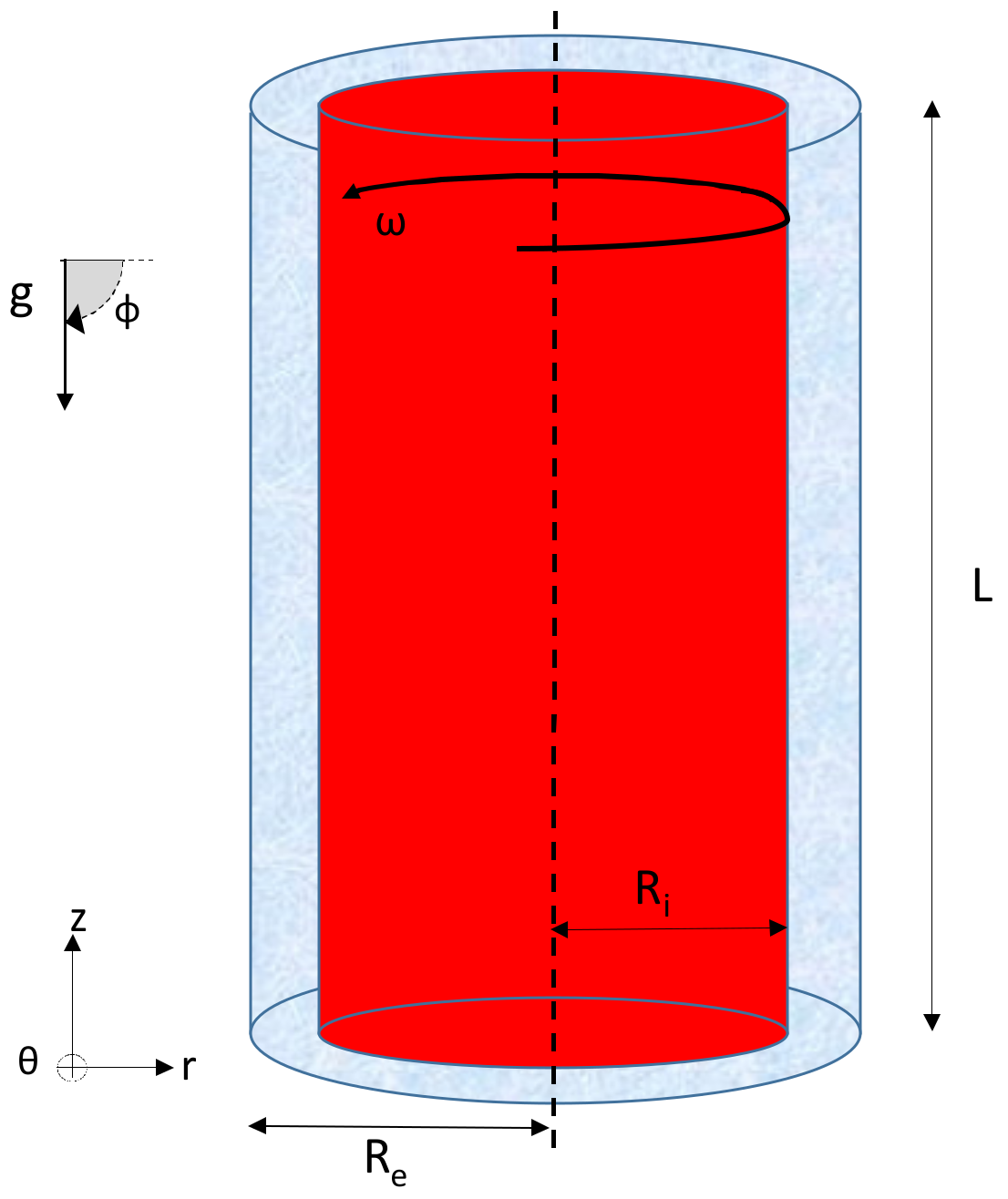
2. Iso-Thermal Condition
- -
- The Taylor-Couette instability is a vortex confined between two coaxial cylinders with the outer cylinder stationary and the inner cylinder rotating at a constant angular velocity.
- -
- The Dean instability is a flow induced by the curvature of the streamlines of a fully developed Newtonian flow. Above a critical value of the Dean number, a pair of vortex cells appears within the flow near the outer wall of the pipe.
- -
- The Görtler instability is a secondary flow appearing in the boundary layer of the flow along a concave wall. This flow appears as longitudinal rolls, counter-rotating in pairs, aligned in the direction of the mean flow. Its appearance is caused by a competition between pressure and centrifugal forces.
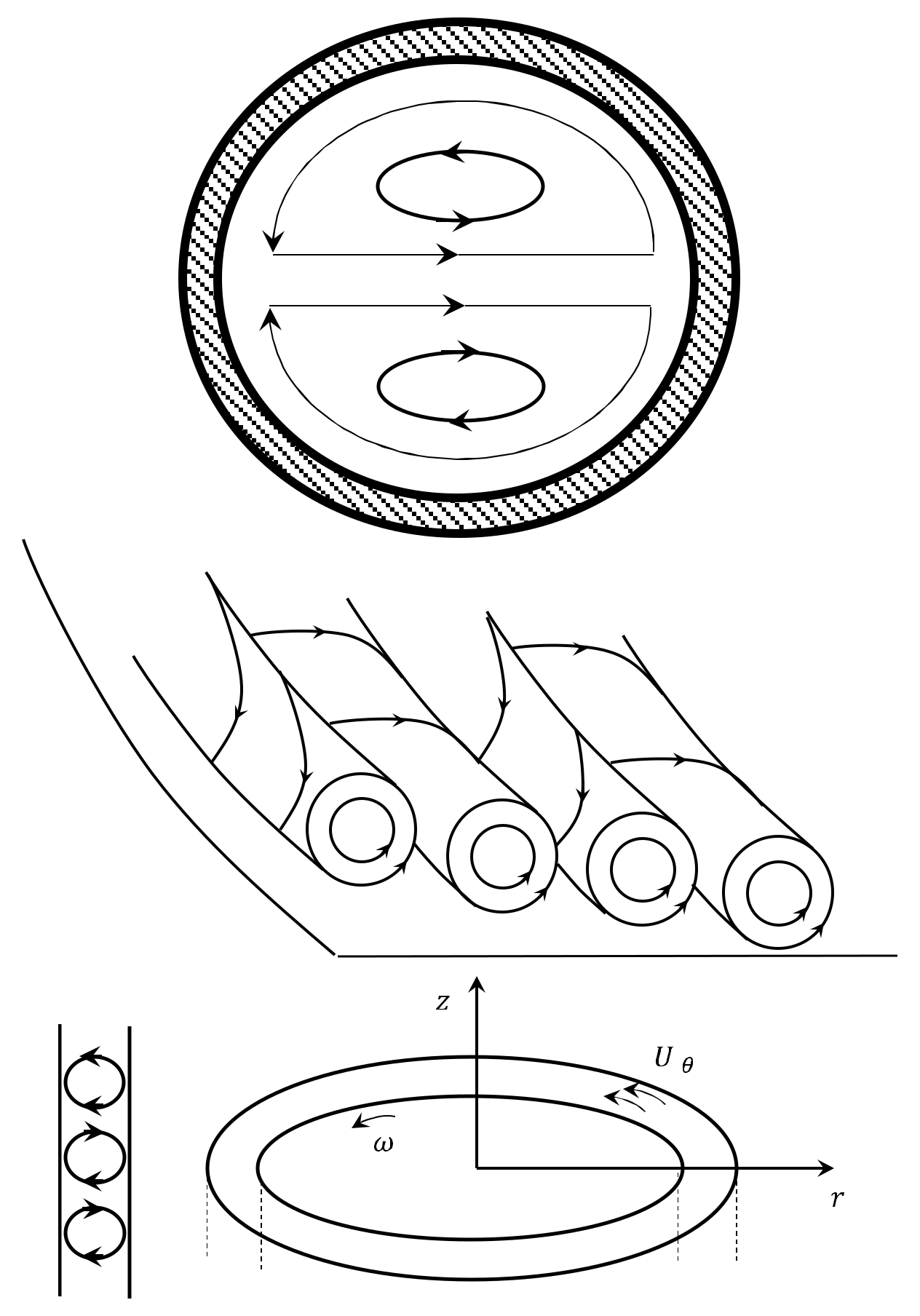
2.1. Taylor-Couette Flow
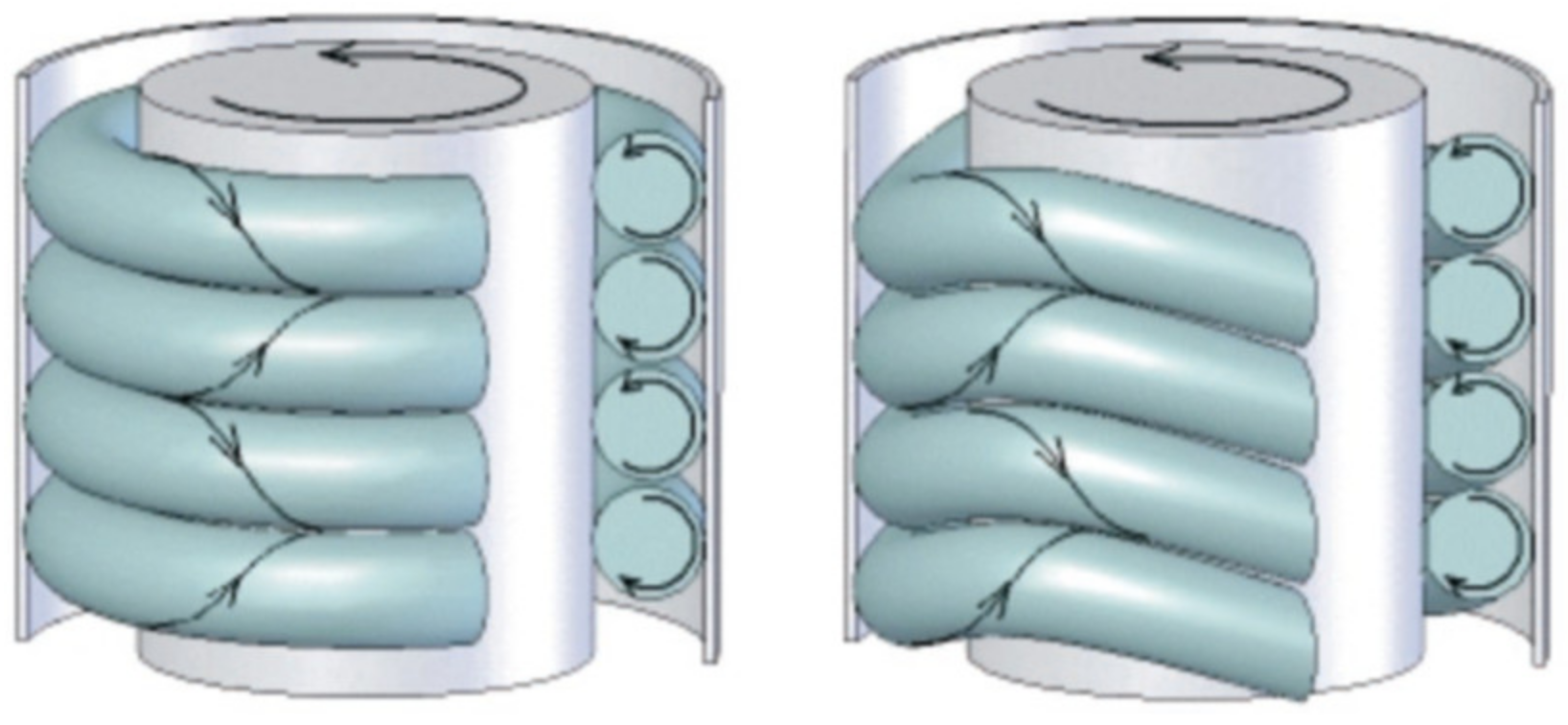
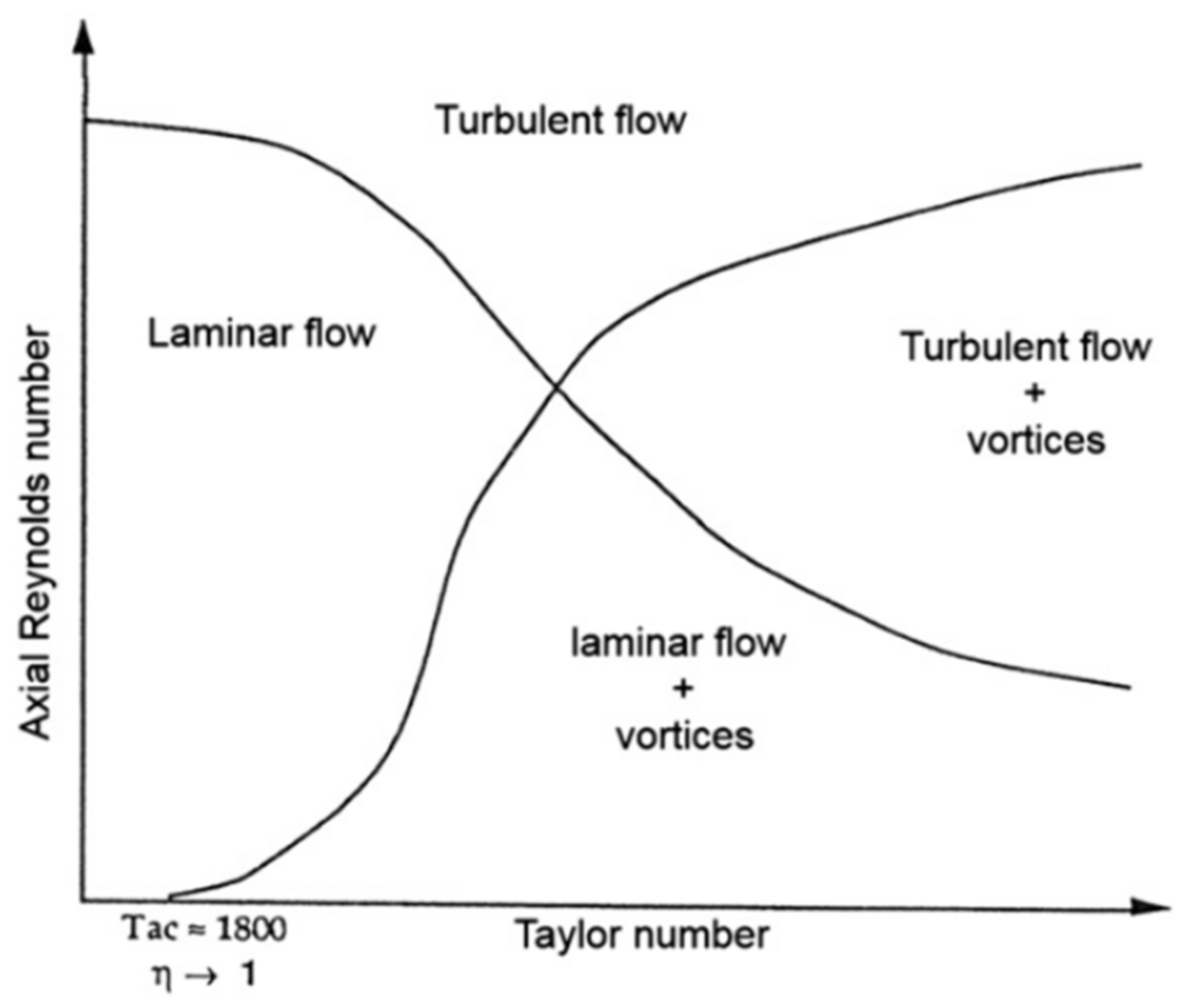
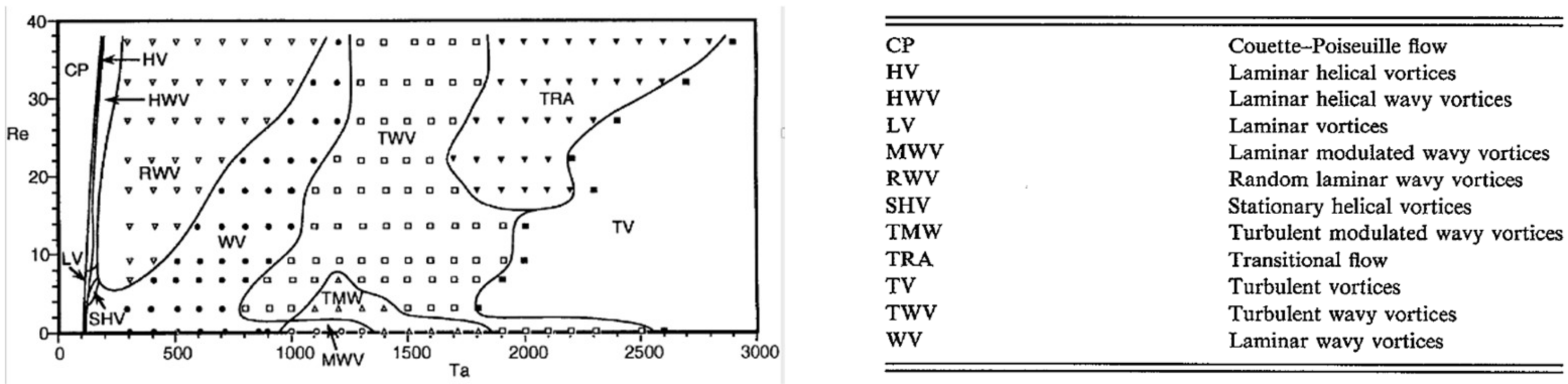
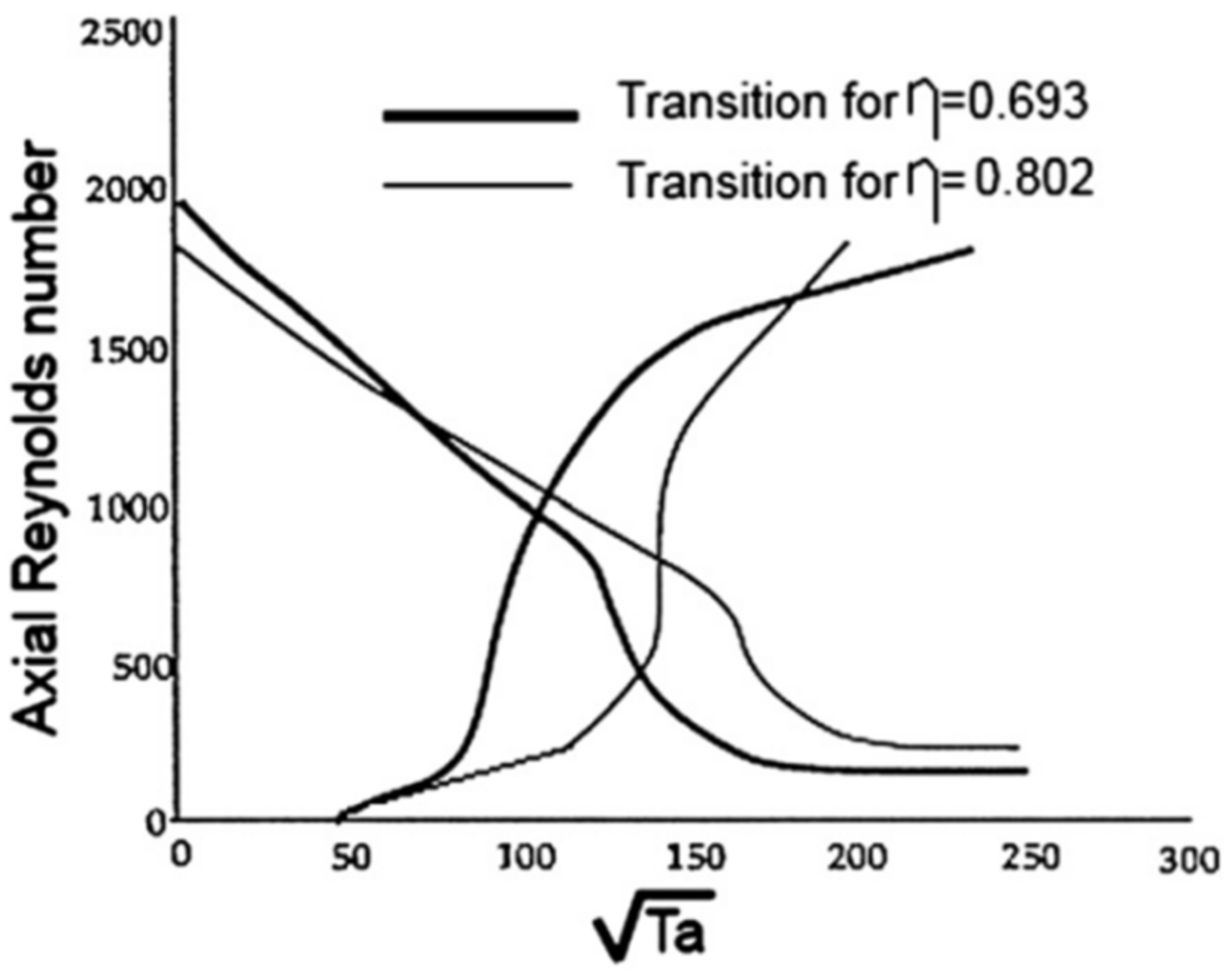
2.2. Taylor–Couette–Poiseuille Flow
- Laminar flow,
- Laminar flow with Taylor structures,
- Turbulent flow,
- Turbulent flow with Taylor structures.
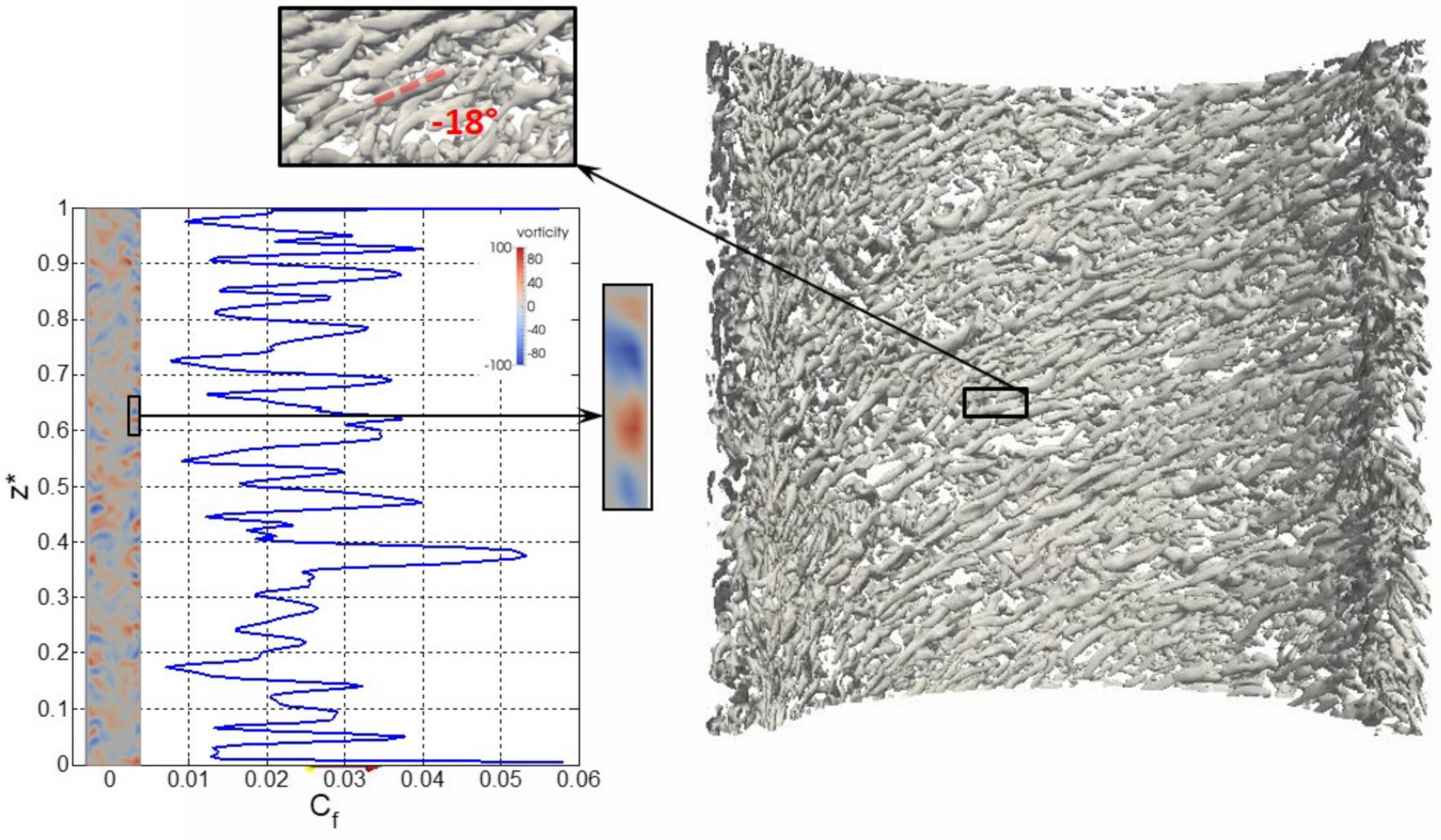
2.3. Numerical Simulation in Taylor–Couette–Poiseuille Flow
3. Non-Isothermal Condition
4. Conclusions
- -
- The open- and closed-gap;
- -
- The radial and axial heat flux densities.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | ||
| D | m | External diameter of the cylinder |
| Dh | m | Hydraulic diameter |
| m | Thickness of the annular space (=Re- Ri) | |
| g | m.s−2 | Gravity |
| k | m2.s−2 | Turbulent kinetic energy |
| L | m | Length of the cylinders |
| N | - | Rotational parameters (=) |
| Nu | - | Nusselt number |
| q | W/m2 | Wall heat density |
| Ri | m | Internal raduis |
| Re | m | External raduis |
| Ra | - | Rayleigh Number |
| Rea | - | Axial Reynolds number |
| Reeff | - | Effective Reynolds number |
| Rew | - | Rotational Reynolds number |
| T | °K | Temperature |
| °K | Wall temperature | |
| Ta | - | Taylor number |
| Tac | - | Critical Taylor number |
| m.s−1 | Tangential or spanwise velocity component | |
| m.s−1 | Axial or streamswise velocity component | |
| m2.s−2 | Reynolds stress tensor | |
| (m, rad, m) | Cylindrical coordinate | |
| - | Dimensionless radial coordinate | |
| - | Dimensionless axial coordinate (=z/L) | |
| Greek symbols | ||
| °K−1 | Thermal dilatation coefficient | |
| m3.s−2 | Turbulent kinetic energy dissipation rate | |
| - | Shape factor ( ) | |
| m.s−2 | Thermal diffusivity | |
| W.m−1.K−1 | Themal conductivity | |
| - | Aspect ratio ( ) | |
| m.s−2 | Kinematic viscosity | |
| rad | ||
| - | Volume fraction | |
| - | Mass fraction | |
| rad.s−1 | Angular velocity of the cylinder | |
| rad.s−1 | Crictical angular velocity | |
| Abbreviations | ||
| DNS | Direct Numerical Simulation | |
| LB | Lattice Boltzman method | |
| LDA | Laser Doppler Anemometry | |
| LES | Large Eddy Simulation | |
| RANS | Reynolds Averaged Navier Stokes | |
| TC | Taylor-Couette | |
| TCP | Taylor-Couette-Poiseuille | |
| Turbulent closure model | ||
References
- Bouafia, M.; Bertin, Y.; Saulnier, J.-B.; Ropert, P. Analyse expérimentale des transferts de chaleur en espace annulaire étroit et rainuré avec cylindre intérieur tournant. Int. J. Heat Mass Transf. 1998, 41, 1279–1291. [Google Scholar] [CrossRef]
- Yoo, W.; Jeon, S.; Son, C.; Yang, J.; Ahn, D.; Kim, S.; Hwang, K.; Ha, S. Full surface heat transfer characteristics of rotor ventilation duct of a turbine generator. Appl. Therm. Eng. 2016, 94, 385–394. [Google Scholar] [CrossRef]
- Caputo, A.C.; Pelegagge, P.M.; Salini, P. Performance modeling of radiant heat recovery exchangers for rotary kilns. Appl. Therm. Eng. 2011, 31, 2578–2589. [Google Scholar] [CrossRef]
- Swann, P.B.; Russel, H.; Jahn, I.H. Taylor-Couette-Poiseuille flow heat transfer in a high Taylor number test rig. J. Glob. Power Propuls. Soc. 2021, 5, 126–147. [Google Scholar] [CrossRef]
- Lorusso, P.; Martelli, E.; Del Nevo ADel Narcisi, V.; Giannetti, F.; Tarantino, M. Development of a PbLi heat exchanger for EU DEMO fusion reactor: Experimental test and system code assessment. Fusion Eng. Des. 2021, 169, 112462. [Google Scholar] [CrossRef]
- Poncet, S.; Schiestel, R. Numerical modeling of heat transfer and fluid flow in rotor–stator cavities with throughflow. Int. J. Heat Mass Transf. 2007, 50, 1528–1544. [Google Scholar] [CrossRef]
- Nemri, M.; Charton, S.; Climent, E. Mixing and axial dispersion in Taylor-Couette flows: The effect of the flow regime. Chem. Eng. Sci. 2015, 139, 109–124. [Google Scholar] [CrossRef]
- Abou-Ziyan, H.; Ameen, R.; Elsayed, K. Fluid flow and convection heat transfer in concentric and eccentric cylindrical annuli of different radii ratios for Taylor-Couette-Poiseuille flow. Adv. Mech. Eng. 2021, 13, 1–22. [Google Scholar] [CrossRef]
- Avila, K.; Moxey, D.; De Lozar, A.; Avila, M.; Barkley, D.; Hof, B. The onset of turbulence in pipe flow. Science 2011, 33, 192–196. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D.; Sun, C. High Reynolds numbers Taylor-Couette turbulence. Annu. Rev. Fluid Mech. 2016, 48, 53–80. [Google Scholar] [CrossRef]
- Leclercq, C.; Partridge, J.; Augier, P.; Dalziel, S.; Kerswell, R. Using stratification to mitigate end effects in quasi-Keplerian Taylor-Couette flow. J. Fluid Mech. 2016, 791, 608–630. [Google Scholar] [CrossRef]
- Naimi, M.; Devienne, R.; Lebouche, M. Etude dynamique et thermique de l’écoulement de Couette-Taylor-Poiseuille; cas d’un fluide présentant un seuil d’´écoulement. Int. J. Heat Mass Transf. 1990, 33, 381. [Google Scholar] [CrossRef]
- Jenny, M.; De Richter, S.K.; Louvet, N.; Skali-Lami, S.; Dossmann, Y. Taylor-Couette instability in thixotropic yield stress fluids. Phys. Rev. Fluids Am. Phys. 2017, 2, 023302. [Google Scholar] [CrossRef]
- Huchet, F.; Piton, M.; Del Barrio, A.; Le Corre, O.; Cazacliu, B. Air-cooled heat exchanger applied to external rotary kiln wall in forced and natural draft. Energy Convers. Manag. 2017, 154, 517–525. [Google Scholar] [CrossRef]
- Nouri-Borujerdi, A.; Nakhchi, M.E. Heat transfer enhancement in annular flow with outer grooved cylinder and rotating inner cylinder: Review and experiments. Appl. Therm. Eng. 2017, 120, 257–268. [Google Scholar] [CrossRef]
- Vahl Davis, G.; Thomas, R.W. Natural convection between concentric vertical cylinders. Phys. Fluids Suppl. II 1969, 12, 198–207. [Google Scholar]
- Sorour, M.M.; Coney, J.E.R. The effect of temperature gradient on the stability of flow between vertical, concentric, rotating cylinders. J. Mech. Eng. Sci. 1979, 21, 403–409. [Google Scholar] [CrossRef]
- Lopez, J.M.; Marques, F.; Avila, M. Conductive and convective heat transfer in fluids flows between differentially heated and rotating cylinder. Int. J. Heat Mass Transf. 2015, 90, 959–967. [Google Scholar] [CrossRef]
- Dawood, H.K.; Mohammed, H.A.; Azwadi Che Sidik, N.; Munisamy, K.M.; Wahid, M.A. Forced, natural and mixed-convection heat transfer and fluid flow in annulus: A review. Int. Commun. Heat Mass Transf. 2015, 62, 45–57. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Tyrinov, A.I.; Shevchuk, I.V.; Dmitrenko, N.P. Dean instability of nanofluids with radial temperature and concentration non-uniformity. Phys. Fluids 2016, 28, 034104. [Google Scholar] [CrossRef]
- Davaille, A.; Gueslin, B.; Massmeyer, A.; Giuseppe, E.D. Thermal instabilities in a yield stress fluid: Existence and morphology. J. Non-Newton. Fluid Mech. 2013, 193, 144–153. [Google Scholar] [CrossRef]
- Varé, T.; Nouar, C.; Métivier, C.; Bouteraa, M. Stability of hexagonal pattern in Rayleigh–Bénard convection for thermodependent shear-thinning fluids. J. Fluid Mech. 2020, 905, A33. [Google Scholar] [CrossRef]
- Peixinho, J.; Desaubry, C.; Lebouché, M. Heat transfer of a non-Newtonian fluid (Carbopol aqueous solution) in transitional pipe flow. Int. J. Heat Mass Transf. 2008, 51, 198–209. [Google Scholar] [CrossRef]
- Maleki, A.; Frigaard, I.A. Axial dispersion in weakly turbulent flows of yield stress fluids. J. Non-Newton. Fluid Mech. 2016, 235, 1–19. [Google Scholar] [CrossRef]
- Tso, C.P.; Mahulikar, S.P. Combined evaporating meniscus-driven convection and radiation in annular microchannels for electronics cooling application. Int. J. Heat Mass Transf. 2000, 43, 1007–1023. [Google Scholar] [CrossRef]
- Ozerdem, B. Measurement of convective heat transfer coefficient for a horizontal cylinder rotating in quiescent air. Int. Commun. Heat Mass Transf. 2000, 27, 389–395. [Google Scholar] [CrossRef]
- Harmand, S.; Pellé, J.; Poncet, S.; Shevchuk, I.V. Review of fluid flow and convective heat transfer within rotating disk cavities with impinging jet. Int. J. Therm. Sci. 2013, 67, 1–30. [Google Scholar] [CrossRef]
- Cavazzuti, M.; Agnani, E.; Corticelli, M.A. Optimization of a finned concentric pipes heat exchanger for industrial recuperative burners. Appl. Therm. Eng. 2015, 84, 110–117. [Google Scholar] [CrossRef]
- Douaire, M.; Mercade, M.; Morchain, J.; Loubière, P. A unique phenotypic modification of Lactococcus lactis cultivated in a couette bioreactor. Biotechnol. Bioeng. 2011, 108, 559–571. [Google Scholar] [CrossRef]
- Seddegh, S.; Joybari, M.M.; Wang, X.; Haghighat, F. Experimental and numerical characterization of natural convection in a vertical shell-and-tube latent thermal energy storage system. Sustain. Cities Soc. 2017, 35, 13–24. [Google Scholar] [CrossRef]
- Lepiller, V.; Goharzadeh, A.; Prigent, A.; Mutabazi, I. Weak temperature gradient effect on the stability of the circular Couette flow. Eur. Phys. J. B 2008, 61, 445–455. [Google Scholar] [CrossRef]
- Farias, M.H.; Braga, C.V.M.; Souza Mendes, P.R. Heat transfer coefficients for the laminar fully developed flow of viscoplastic liquids through annuli. Int. J. Heat Mass Transf. 2009, 52, 3257–3260. [Google Scholar] [CrossRef]
- Ahmed, H.E.; Ahmed, M.I. Thermal performance of annulus with its applications; A review. Renew. Sustain. Energy Rev. 2017, 71, 170–190. [Google Scholar] [CrossRef]
- Taylor, G.I. Stability of viscous liquid contained between two rotating cylinders. Philos. Trans. R. Soc. Lond. Ser. A 1923, 223. [Google Scholar]
- Coles, D. Transactions in circular Couette flows. J. Fluid Mech. 1965, 21, 385–425. [Google Scholar] [CrossRef]
- Fenstermacher, P.R.; Swinney, H.L.; Gollub, J.P. Dynamical instabilities and the transition to chaotic Taylor vortex flow. J. Fluid Mech. 1979, 94, 103–128. [Google Scholar] [CrossRef]
- Andereck, D.; Liu, S.S.; Swinney, H.L. Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 1986, 164, 155–183. [Google Scholar] [CrossRef]
- Esser, A.; Grossmann, S. Analytic expression for Taylor-Couette stability boundary. Physic Fluids 1996, 8, 1814. [Google Scholar] [CrossRef]
- Domanski, J. Determination of the parameters of fluid motion in Taylor-Couette Flow. Tech. Sci. Pap. Rep. 2006, 9, 73–78. [Google Scholar]
- Kaye, J.; Elgar, E.C. Modes of adiabatic and diabatic fluid flow in an annulus with an inner rotating cylinder. Trans. ASME 1958, 80, 753–765. [Google Scholar] [CrossRef]
- Piton, M. Heat Recovery Exchanger Applied to the Rotary Kiln Equipment. Ph.D. Thesis, Ecole des Mines de Nantes, Nantes, France, 6 November 2015. [Google Scholar]
- Chandrasekhar, S. The stability of spiral flow between rotating cylinders. Proc. R. Soc. Lond. Ser. A 1962, 265, 188–197. [Google Scholar]
- Yamada, Y. Resistance of a flow through an annulus with an inner rotating cylinder. Bull. JSME 1962, 5, 302–310. [Google Scholar] [CrossRef]
- Polkowski, J.W. Turbulent flow between coaxial cylinders with the inner cylinder rotating. J. Eng. Gas Turbines Power 1984, 106, 128–135. [Google Scholar] [CrossRef]
- Jakoby, R.; Kim, S.; Wittig, S. Correlations of the convection heat transfer in annular channels with rotating inner cylinder. J. Eng. Gas Turbines Power 1999, 121, 670–677. [Google Scholar] [CrossRef]
- Lueptow, R.M.; Docter, A.; Min, K. Stability of axial flow in an annulus with a rotating inner cylinder. Phys. Fluids 1992, A4, 2446–2456. [Google Scholar] [CrossRef]
- Wan, C.C.; Coney, J.E.R. Transition modes in adiabatic spiral vortex flow in narrow and wide annular gaps. Int. J. Heat Fluid Flow 1980, 2, 131–138. [Google Scholar] [CrossRef]
- Molki, M.; Astill, K.N.; Leal, E. Convective heat-mass transfer in the entrance region of a concentric annulus having a rotating inner cylinder. Int. J. Heat Fluid Flow 1990, 11, 120–128. [Google Scholar] [CrossRef]
- Fénot, M.; Bertin, Y.; Dorignac, E.; Lalizel, G. A review of heat transfer between concentric rotating cylinders with or without axial flow. Int. J. Therm. Sci. 2011, 50, 1138–1155. [Google Scholar] [CrossRef]
- Nourri, J.M.; Whitelaw, J.H. Flow of Newtonian and non-Newtonian fluids in a concentric annulus with rotation of inner cylinder. J. Fluid Eng. 1994, 116, 821–827. [Google Scholar] [CrossRef]
- Escudier, M.P.; Gouldson, I.W. Concentric annular flow with centerbody rotation of a Newtonian and a shear-thinnig liquid. Int. J. Heat Fluid Flow 1995, 16, 156–162. [Google Scholar] [CrossRef]
- Chung, S.Y.; Rhee, G.H.; Sung, H.J. Direct numerical simulation of turbulent concentric annular pipe flow. Part. 1: Flow field. Int. J. Heat Fluid Flow 2002, 23, 426–440. [Google Scholar] [CrossRef]
- Chung, S.Y.; Sung, H.J. Large-eddy simulation of turbulent flow in concentric annulus with rotation of an inner cylinder. Int. J. Heat Fluid Flow 2005, 26, 191–203. [Google Scholar] [CrossRef]
- Jung, S.Y.; et Sung, H.J. Characterization of the three-dimensional turbulent boundary layer in a concentric annulus with a rotating inner cylinder. Phys. Fluids 2006, 18, 115102. [Google Scholar] [CrossRef]
- Hadziabdic, M.; Hanjalic, K.; Mullyadzhanov, R. LES of turbulent flow in a concentric annulus with rotating outer wall. Int. J. Heat Fluid Flow 2013, 43, 74–84. [Google Scholar] [CrossRef]
- Poncet, S.; Viazzo, S.; Oguic, R. Large eddy simulation of Taylor-Couette-Poiseuille flows in a narrow-gap system. Phys. Fluids 2014, 26, 105108. [Google Scholar] [CrossRef]
- Poncet, S.; Haddadi, S.; Viazzo, S. Numerical modeling of fluid flow and heat transfer in a narrow Taylor-Couette-Poiseuille system. Int. J. Heat Fluid Flow 2011, 32, 128–144. [Google Scholar] [CrossRef]
- Pawar, S.B.; Thorat, B.N. CFD simulation of Taylor-Couette flow in scraped surface heat exchanger. Chem. Eng. Res. Des. 2012, 90, 313–322. [Google Scholar] [CrossRef]
- Naser, A. Prediction of Newtonian and non-Newtonian flow through concentric annulus with centerbody rotation. In Proceedings of the 1st International Conference on CFD in Mineral and Metal Processing and Power Generation, Melbourne, Australia, 3–4 July 1997. [Google Scholar]
- Ohsawa, A.; Murata, A.; Iwamoto, K. Through-flow effects on Nusselt number and torque coefficient in Taylor-Couette-Poiseuille flow investigated by large eddy simulation. J. Therm. Sci. Technol. 2016, 11, 1–12. [Google Scholar] [CrossRef]
- Mehrez, I.; Gheith, R.; Aloui, F.; Nasrallah, S.B. Theoretical and numerical study of Couette-Taylor flow with an axial flow-using lattice Boltzmann method. Int. J. Numer. Meth. Fluids 2019, 90, 427–441. [Google Scholar] [CrossRef]
- Piton, M.; Huchet, F.; Cazacliu, B.; Le Corre, O. Numerical Turbulent Flow Analysis through a Rotational Heat Recovery System. Energies 2022, 15, 6792. [Google Scholar] [CrossRef]
- Guillerm, R.; Kang, C.; Savaro, C.; Lepiller, V.; Prigent, A.; Yang, K. Flow regimes in a vertical Taylor-Couette system with a radial thermal gradient. Phys. Fluids 2015, 27, 094101. [Google Scholar] [CrossRef]
- Bjorklund, I.; Kays, W. Heat transfer between concentric rotating cylinders. Trans. ASME J. Heat Transf. 1959, 84, 97–105. [Google Scholar] [CrossRef]
- Vafai, K.; Desai, C.P.; Iyer, S.V.; Dyko, M.P. Buoyancy induced convection in a narrow open-ended annulus. J. Heat Transf. 1997, 19, 483–494. [Google Scholar] [CrossRef]
- Grossman, S.; Lohse, D. Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 2011, 23, 045108. [Google Scholar] [CrossRef]
- Boffeta, G.; Mazzino, A. Incompressible Rayleigh-Taylor turbulence. Annu. Rev. Fluid Mech. 2017, 49, 119–143. [Google Scholar] [CrossRef]
- Leng, X.Y.; Zhong, J.Q. Mutual coherent structures for heat and angular momentum transport in turbulent Taylor-Couette flows. Phys. Rev. Fluids 2022, 7, 043501. [Google Scholar] [CrossRef]
- Howey, D.A.; Childs, P.R.N.; Holmes, A.S. Air-Gap convection in rotating electrical machines. IEEE Trans. Ind. Electron. 2012, 59, 1367–1375. [Google Scholar] [CrossRef]
- Nouri-Borujerdi, A.; Nakhchi, M.E. Optimization of the heat transfer coefficient and pressure drop of Taylor-Couette-Poiseuille flows between an inner rotating cylinder and an outer grooved stationary cylinder. Int. J. Heat Mass Transf. 2017, 108, 1449–1459. [Google Scholar] [CrossRef]
- Becker, K.; Kaye, J. The influence of a radial temperature gradient on the instability of fluid flow in an annulus with inner rotating cylinder. Trans. ASME 1962, 80, 79–90. [Google Scholar] [CrossRef]
- Gazley, C. Heat-Transfer Characteristics of the Rotational and Axial Flow between Concentric Cylinders. J. Turbomach. 1958, 80, 79–90. [Google Scholar] [CrossRef]
| Control Parameters | Lower Values | Upper Values |
|---|---|---|
| (m) | ||
| Microelectronics cooling device [25] | Space vehicle technology, ball bearing [26] | |
| L Gas turbine discs cooling [27] | L > 0 Heat recovery of burners [28] | |
| Bioreactor for culture cells [29] | CO2 turbine diffuser [4] | |
| Angle | Double-pipe heat exchanger [19] | Vertical thermal energy storage tank [30] |
| −1Geostrophic motion [31] | +1 Most of the applications [14,15] | |
| Al2O3/water Nanofluids [19] | Viscoplastic type fluid [32] |
| Authors | Method | Flow Regime | |||||
|---|---|---|---|---|---|---|---|
| Nourri and Whitelaw (1994) [50] | LDA | 0.5 | 98 | Turbulent | |||
| Escudier and Gouldson (1995) [51] | LDA | Turbulent | |||||
| Chung et al. (2002) [52] | DNS | - | Turbulent | - | |||
| Chung and Sung (2005) [53] | LES | 0.5 | - | Turbulent | |||
| Jung and Sung (2006) [54] | DNS | 0.5 | - | Turbulent | |||
| Hadziabdic et al. (2013) [55] | LES | 0.5 | - | Turbulent | 12,500 | ||
| Poncet et al. (2014) [56] | LES | 0.889 | 10 | Turbulent | |||
| Poncet et al. (2011) [57] | 0.961 | 76.9 | Laminar-Turbulent | ||||
| Pawar and Thorat (2012) [58] | RANS (RSM) | 0.745 | 5.85–1 | Turbulent | 0 | ||
| Nasser et al. (1990) [59] | 0.5 | 244 | Laminar-Turbulent | ||||
| Ohsawa et al. (2016) [60] | LES | 0.87 | 18 | Turbulent | = 4000 | ||
| Mehrez et al. (2019) [61] | Lattice Boltzman | 0.5–0.6–0.7 | 2–3.8–5–6–7–8–9–10 | Laminar-Wavy | |||
| Piton et al. (2022) [62] | 0.809 | 10 | Turbulent |
| Geometry | Authors | Range of Applicability | Nu-Correlation | Remarks |
|---|---|---|---|---|
| Closed gap | Bjorklund and kays (1959) [64] | Diffusive regime (Ra < 400.Γ) Ta << Tac | Equation (4) | Conduction |
| Vahl Davis G. and Thomas (1969) [16] | Ra > Rac; Ta << Tac | Equation (5) | Natural convection | |
| Open gap | Huchet et al. (2017) [14] | 2.5 × 107 > Ra > 2.5 × 108 0 < Rew < 6980 1000 < Rea < 15,000 | Equation (6) | Heated rotor–Mixed Convection |
| Geometry | Authors | Range of Applicability | Nu-Correlation | Remarks |
|---|---|---|---|---|
| Closed-gap | Beker and Kays (1962) [71] | 1994 < Ta < 104 104 < Ta < 3.3105 | Nuw = 0.128(Ta)0.367 Nuw = 0.409(Ta)0.241 | Radial heat flux |
| Open gap | Gazley (1958) [72] | Rea < 12,000 Rew < 110,000 | = 0.03Reeff0.8 | Calculation made from Trot-Tst |
| Bouafia (1998) [1] | 11,000 < Rea < 31,000 500 < Rew < 31,000 | Nuw = 0.021Reeff0.8 | Heated rotor |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piton, M.; Huchet, F.; Cazacliu, B.; Le Corre, O. Heat Transport in Rotating Annular Duct: A Short Review. Energies 2022, 15, 8633. https://doi.org/10.3390/en15228633
Piton M, Huchet F, Cazacliu B, Le Corre O. Heat Transport in Rotating Annular Duct: A Short Review. Energies. 2022; 15(22):8633. https://doi.org/10.3390/en15228633
Chicago/Turabian StylePiton, Maxime, Florian Huchet, Bogdan Cazacliu, and Olivier Le Corre. 2022. "Heat Transport in Rotating Annular Duct: A Short Review" Energies 15, no. 22: 8633. https://doi.org/10.3390/en15228633
APA StylePiton, M., Huchet, F., Cazacliu, B., & Le Corre, O. (2022). Heat Transport in Rotating Annular Duct: A Short Review. Energies, 15(22), 8633. https://doi.org/10.3390/en15228633








