Virtual Modeling and Experimental Validation of the Line-Start Permanent Magnet Motor in the Presence of Harmonics
Abstract
1. Introduction
- Model the LSPMM in the FEM software based on its physical dimensions;
- Apply the harmonic waveforms to the electric motor through the FEM software;
- Validate the results obtained from measurement campaigns in CEAMAZON with an LSPMM of 0.75 kW.
2. Induction Motors
2.1. Minimum Energy Performance Standards
2.2. Finite Elements Formulation for Time-Harmonic Magnetic Problems
2.3. Finite Elements Formulation for Thermal Analysis
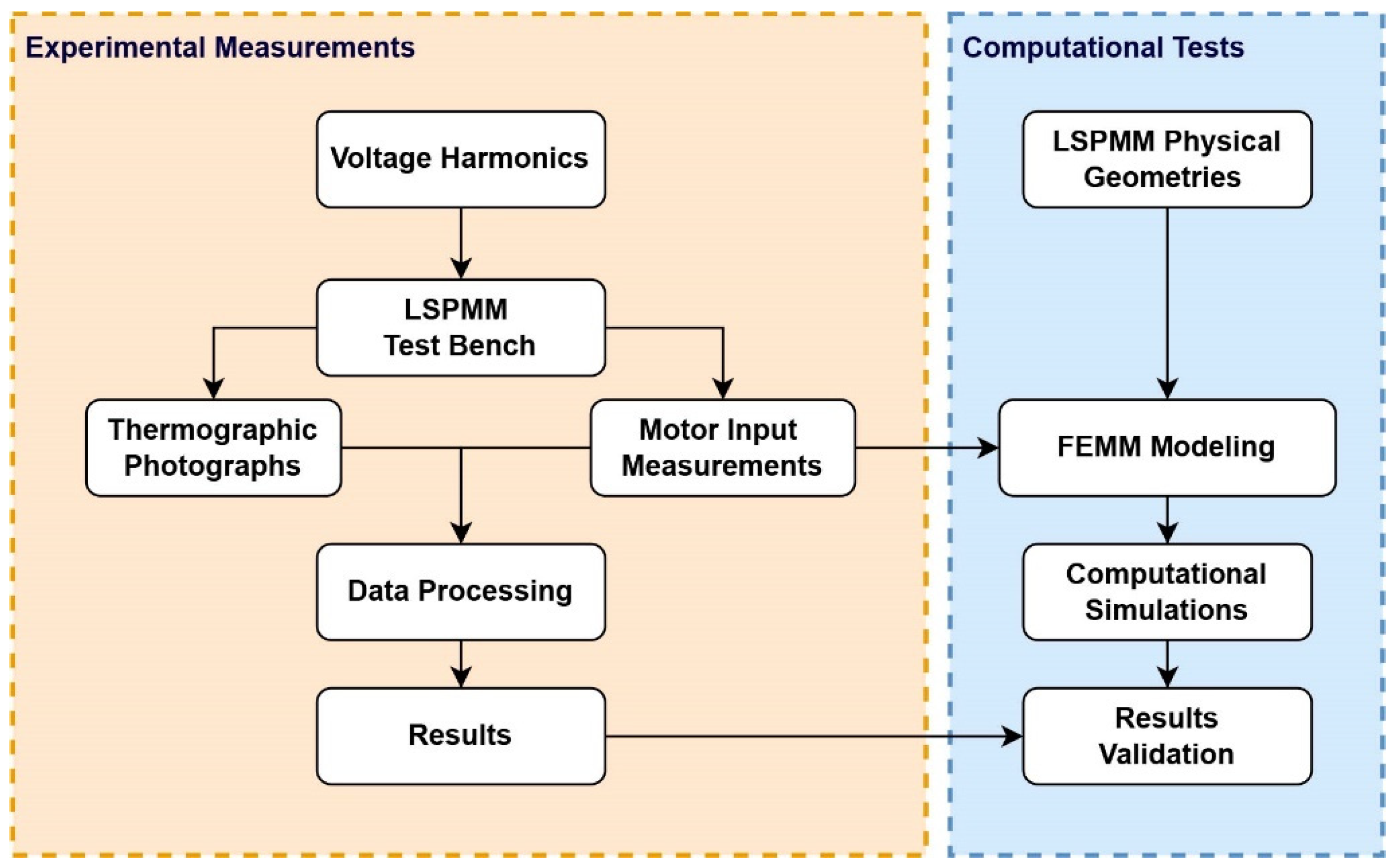
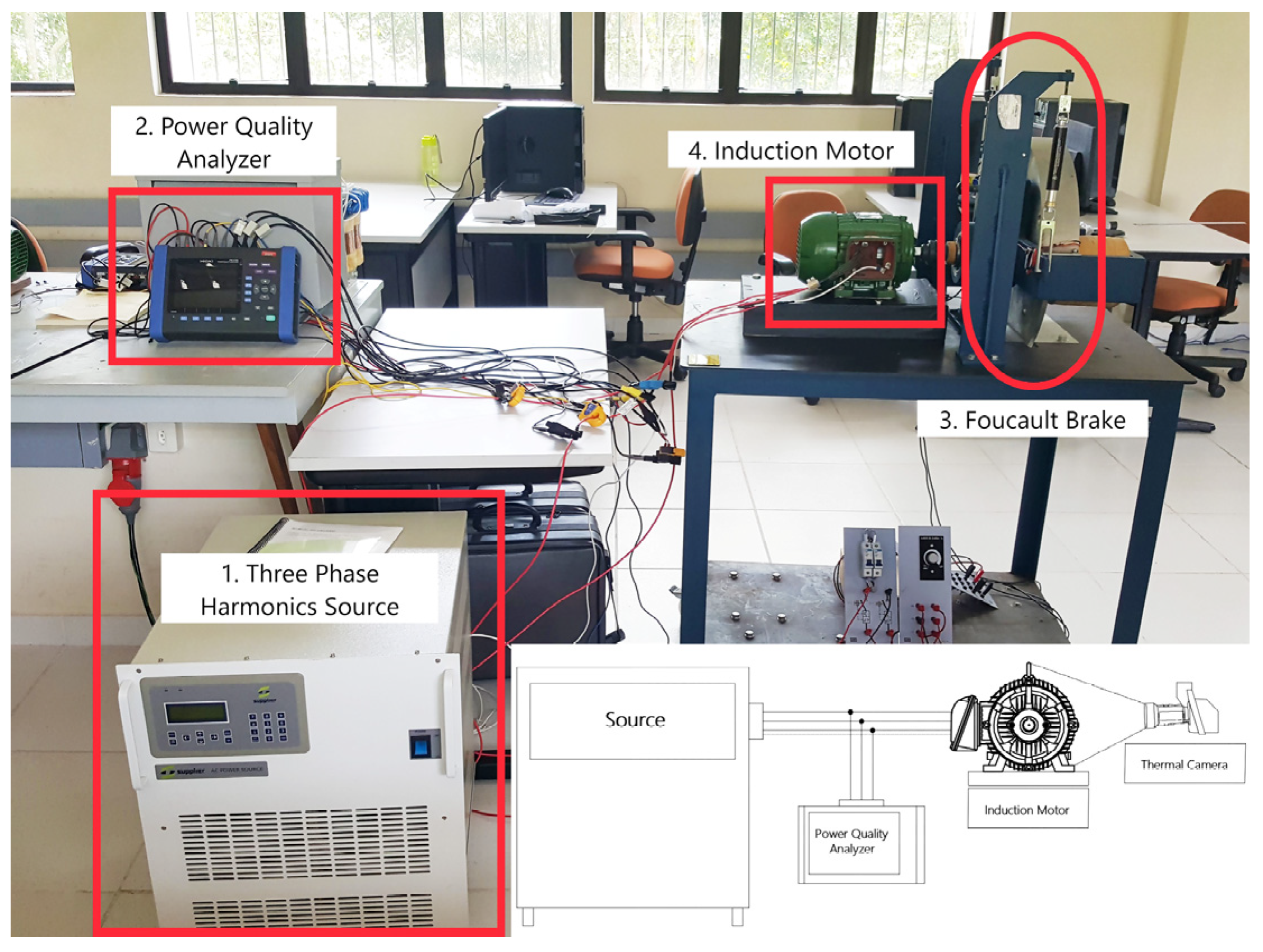
3. Methodology
4. Results
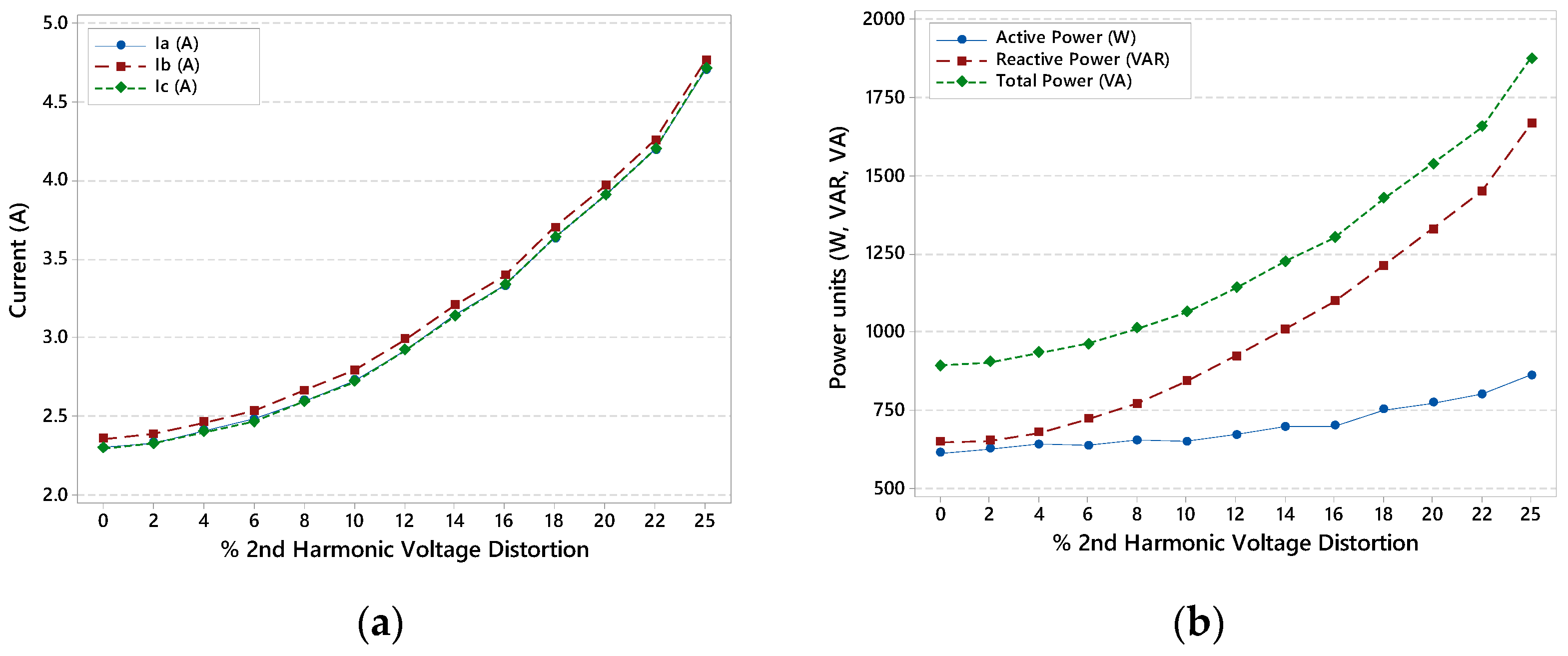
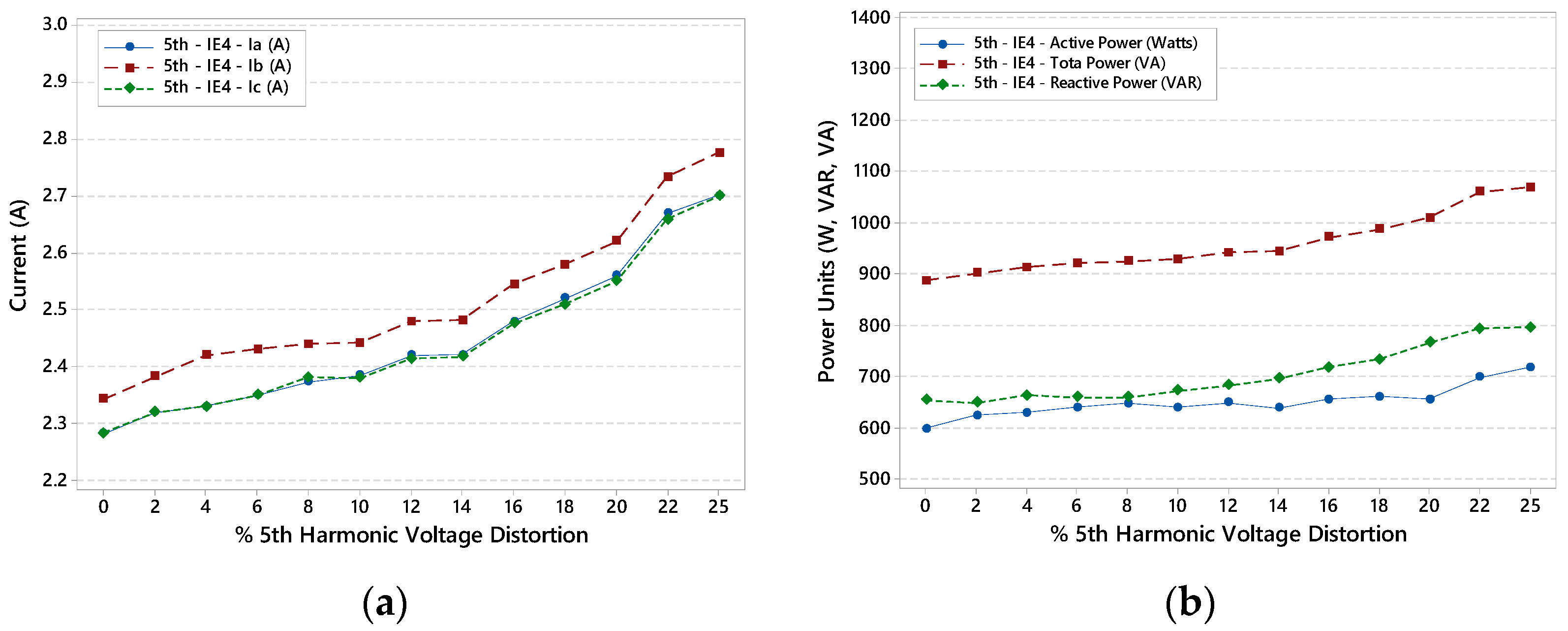
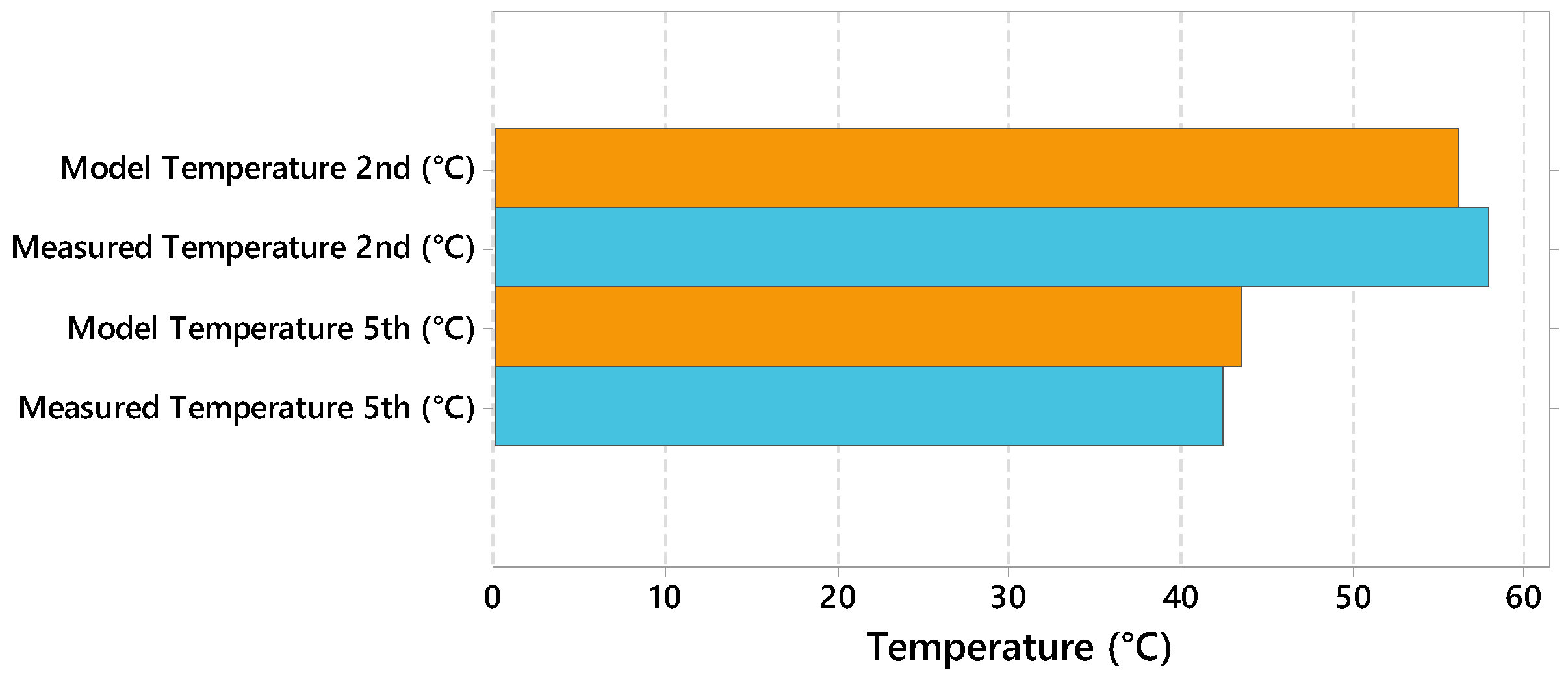
4.1. Experimental Results
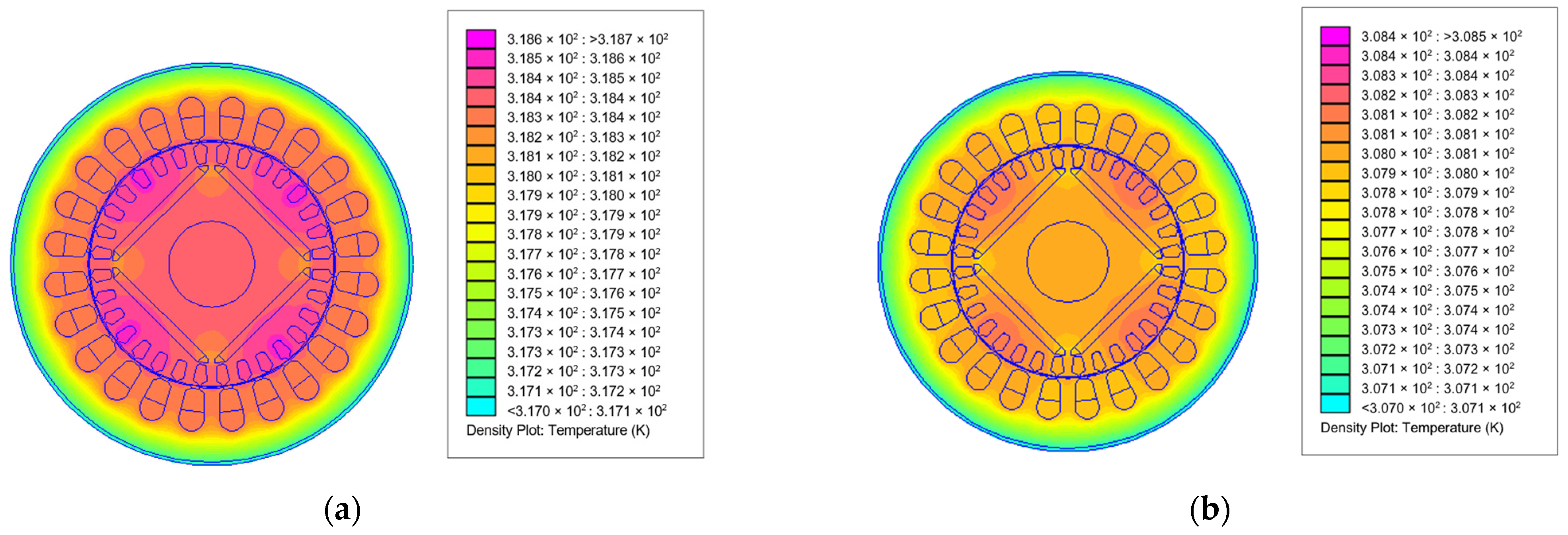
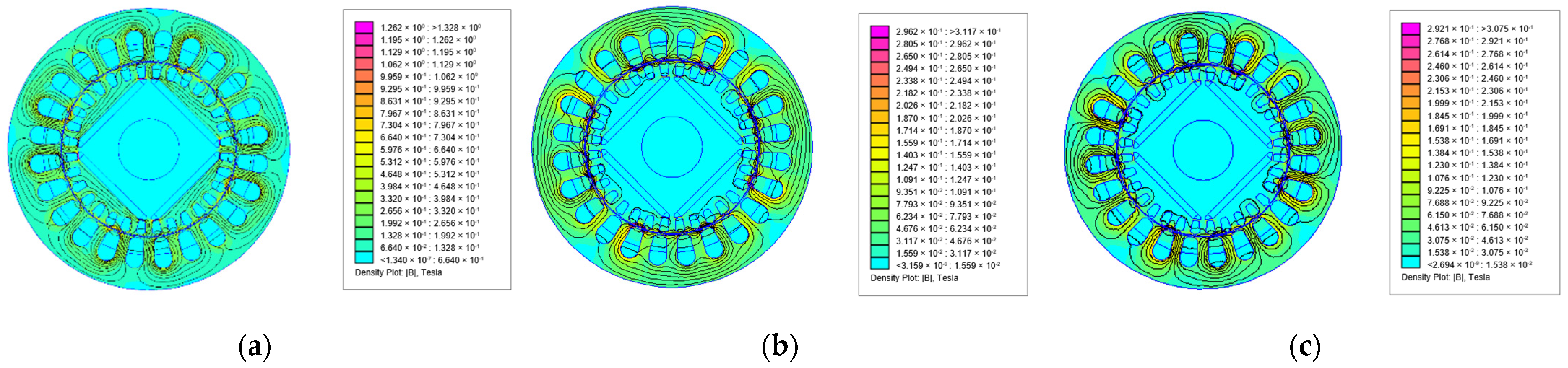
4.2. Finite Elements Analysis Results

5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sarac, V.J.; Stefanov, G. Various Rotor Topologies of Line-Start Synchronous Motor for Efficiency Improvement. Power Electron. Drives 2019, 5, 83–95. [Google Scholar] [CrossRef]
- Zeng, X.; Quan, L.; Zhu, X.; Xu, L.; Liu, F. Investigation of an Asymmetrical Rotor Hybrid Permanent Magnet Motor for Approaching Maximum Output Torque. IEEE Trans. Appl. Supercond. 2019, 29, 1–4. [Google Scholar] [CrossRef]
- Study on Line-Start Permanent Magnet Assistance Synchronous Reluctance Motor for Improving Efficiency and Power Factor. Available online: https://www.mdpi.com/1996-1073/13/2/384 (accessed on 16 March 2022).
- Zöhra, B.; Akar, M. Design Trends for Line Start Permanent Magnet Synchronous Motors. In Proceedings of the 2019 3rd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 11–13 October 2019; pp. 1–7. [Google Scholar]
- Lyskawinski, W. Comparative Analysis of Energy Performance of Squirrel Cage Induction Motor, Line-Start Synchronous Reluctance and Permanent Magnet Motors Employing the Same Stator Design. Arch. Electr. Eng. 2020, 69, 967–981. [Google Scholar] [CrossRef]
- Ferreira, F.J.T.E.; Leprettre, B.; de Almeida, A.T. Comparison of Protection Requirements in IE2-, IE3-, and IE4-Class Motors. IEEE Trans. Ind. Appl. 2016, 52, 3603–3610. [Google Scholar] [CrossRef]
- Tshoombe, B.K.; Muñoz Tabora, J.; da Silva Fonseca, W.; Emília Lima Tostes, M.; de Matos, E.O. Voltage Harmonic Impacts on Line Start Permanent Magnet Motor. In Proceedings of the 2021 14th IEEE International Conference on Industry Applications (INDUSCON), São Paulo, Brazil, 16–18 August 2021; pp. 962–968. [Google Scholar]
- Muñoz Tabora, J.; de Lima Tostes, M.E.; Ortiz de Matos, E.; Mota Soares, T.; Bezerra, U.H. Voltage Harmonic Impacts on Electric Motors: A Comparison between IE2, IE3 and IE4 Induction Motor Classes. Energies 2020, 13, 3333. [Google Scholar] [CrossRef]
- Influence of Voltage Subharmonics on Line Start Permanent Magnet Synchronous Motor. Available online: https://ieeexplore.ieee.org/document/9641816 (accessed on 16 March 2022).
- Debruyne, C.; Sergeant, P.; Derammelaere, S.; Desmet, J.J.M.; Vandevelde, L. Influence of Supply Voltage Distortion on the Energy Efficiency of Line-Start Permanent-Magnet Motors. IEEE Trans. Ind. Appl. 2014, 50, 1034–1043. [Google Scholar] [CrossRef]
- Debruyne, C. Impact of Voltage Distortion on Energy Efficiency of Induction Machines and Line Start Permanent Magnet Machines; Ghent University: Ghent, Belgium, 2014. [Google Scholar]
- Tabora, J.M.; De Lima Tostes, M.E.; De Matos, E.O.; Bezerra, U.H.; Soares, T.M.; De Albuquerque, B.S. Assessing Voltage Unbalance Conditions in IE2, IE3 and IE4 Classes Induction Motors. IEEE Access 2020, 8, 186725–186739. [Google Scholar] [CrossRef]
- Tabora, J.M.; De Lima Tostes, M.E.; Bezerra, U.H.; De Matos, E.O.; Filho, C.L.P.; Soares, T.M.; Rodrigues, C.E.M. Assessing Energy Efficiency and Power Quality Impacts Due to High-Efficiency Motors Operating Under Nonideal Energy Supply. IEEE Access 2021, 9, 121871–121882. [Google Scholar] [CrossRef]
- López-Pérez, D.; Antonino-Daviu, J. Application of Infrared Thermography to Failure Detection in Industrial Induction Motors: Case Stories. IEEE Trans. Ind. Appl. 2017, 53, 1901–1908. [Google Scholar] [CrossRef]
- Diagnosis of the Three-Phase Induction Motor Using Thermal Imaging-ScienceDirect. Available online: https://www.sciencedirect.com/science/article/abs/pii/S1350449516306259 (accessed on 16 March 2022).
- Ferreira, F.J.T.E.; de Almeida, A.T.; Carvalho, J.F.S.; Cistelecan, M.V. Experiments to Observe the Impact of Power Quality and Voltage-Source Inverters on the Temperature of Three-Phase Cage Induction Motors Using an Infra-Red Camera. In Proceedings of the 2009 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 1311–1318. [Google Scholar]
- Singh, G.; Anil Kumar, T.C.; Naikan, V.N.A. Fault Diagnosis of Induction Motor Cooling System Using Infrared Thermography. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–4. [Google Scholar]
- Mahami, A.; Rahmoune, C.; Bettahar, T.; Benazzouz, D. Induction Motor Condition Monitoring Using Infrared Thermography Imaging and Ensemble Learning Techniques. Adv. Mech. Eng. 2021, 13, 16878140211060956. [Google Scholar] [CrossRef]
- Azari, M.N.; Mirsalim, M. Performance Analysis of a Line-Start Permanent Magnet Motor with Slots on Solid Rotor Using Finite-Element Method. Electr. Power Compon. Syst. 2013, 41, 1159–1172. [Google Scholar] [CrossRef]
- Fonseca, D.; Santos, C.C.; Cardoso, A. Modelling of a Line-Start Permanent Magnet Synchronous Motor, Using Empirical Parameters. In Proceedings of the International Conference on Engineering ICEUBI2017, Covilhã, Portugal, 5–7 December 2017. [Google Scholar]
- Robust Design Optimization of a Five-Phase PM Hub Motor for Fault-Tolerant Operation Based on Taguchi Method. Available online: https://ieeexplore.ieee.org/document/9076301 (accessed on 10 October 2022).
- Sun, X.; Xu, N.; Yao, M. Sequential Subspace Optimization Design of a Dual Three-Phase Permanent Magnet Synchronous Hub Motor Based on NSGA III. IEEE Trans. Transp. Electrif. 2022, 1. Available online: https://ieeexplore.ieee.org/document/9828489 (accessed on 13 July 2022). [CrossRef]
- Xu, J.; Zhang, L.; Meng, D.; Su, H. Simulation, Verification and Optimization Design of Electromagnetic Vibration and Noise of Permanent Magnet Synchronous Motor for Vehicle. Energies 2022, 15, 5808. [Google Scholar] [CrossRef]
- Liu, X.; Lin, Q.; Fu, W. Optimal Design of Permanent Magnet Arrangement in Synchronous Motors. Energies 2017, 10, 1700. [Google Scholar] [CrossRef]
- Yeo, H.-K.; Ro, J.-S. Novel Analytical Method for Overhang Effects in Surface-Mounted Permanent-Magnet Machines. IEEE Access 2019, 7, 148453–148461. [Google Scholar] [CrossRef]
- Li, J.; Song, J.; Cho, Y. High Performance Line Start Permanent Magnet Synchronous Motor for Pumping System. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 1308–1313. [Google Scholar]
- Cavagnino, A.; Vaschetto, S.; Ferraris, L.; Gmyrek, Z.; Agamloh, E.B.; Bramerdorfer, G. Striving for the Highest Efficiency Class With Minimal Impact for Induction Motor Manufacturers. IEEE Trans. Ind. Appl. 2020, 56, 194–204. [Google Scholar] [CrossRef]
- Influence of Magnetic Slot Wedge on the Performance of 10-kV, 1000-kW Permanent Magnet Synchronous Motor-Qiu-2020-International Transactions on Electrical Energy Systems-Wiley Online Library. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/2050-7038.12332 (accessed on 16 March 2022).
- Frosini, L.; Pastura, M. Analysis and Design of Innovative Magnetic Wedges for High Efficiency Permanent Magnet Synchronous Machines. Energies 2020, 13, 255. [Google Scholar] [CrossRef]
- IEC 60034-30-1:2014|IEC Webstore|Pump, Motor, Water Management, Smart City, Energy Efficiency. Available online: https://webstore.iec.ch/publication/136 (accessed on 10 June 2022).
- Fong, J.; Ferreira, F.J.T.E.; Silva, A.M.; de Almeida, A.T. IEC61800-9 System Standards as a Tool to Boost the Efficiency of Electric Motor Driven Systems Worldwide. Inventions 2020, 5, 20. [Google Scholar] [CrossRef]
- Electric Motors. Available online: https://ec.europa.eu/info/energy-climate-change-environment/standards-tools-and-labels/products-labelling-rules-and-requirements/energy-label-and-ecodesign/energy-efficient-products/electric-motors_en (accessed on 12 May 2021).
- Ferreira, F.J.T.E.; Silva, A.M.; Aguiar, V.P.B.; Pontes, R.S.T.; Quispe, E.C.; de Almeida, A.T. Overview of Retrofitting Options in Induction Motors to Improve Their Efficiency and Reliability. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–12. [Google Scholar]
- European Committee of Manufacturers of Electrical Machines and Power Electronics (CEMEP). Ecodesign Regulations (EU) 2019/1781 for Motor and Drives and (EU) 2021/341 (Amendment) from CAPIEL and CEMEP. 10 May 2021. Available online: https://www.nord.com/cms/en/product_catalogue/ie2_motors/country_regulations/cp_countryregulations.jsp (accessed on 2 August 2020).
- WEG. Energy Efficiency Primer. Available online: http://Materiais.Motores.Weg.Net/Cartilha (accessed on 27 July 2022).
- Hughes, A.; Drury, B. Electric Motors and Drives, 4th ed.; Elsevier Ltd.: Leeds, UK, 2013; ISBN 978-0-08-098332-5. [Google Scholar]
- Meeker, D. Finite Element Method Magnetics; User’s Manual; Version 4.2. Available online: http://www.femm.info/Archives/doc/manual34.pdf (accessed on 1 October 2022).
- A Thermal Analysis of Induction Motors Using a Weak Coupled Modeling. Available online: https://ieeexplore.ieee.org/document/582603 (accessed on 18 October 2022).
- IEC 60034-2-1:2014|IEC Webstore|Energy Efficiency, Smart City. Available online: https://webstore.iec.ch/publication/121 (accessed on 27 July 2022).
- HomePage: Finite Element Method Magnetics. Available online: https://www.femm.info/wiki/HomePage (accessed on 27 July 2022).
- Kumar, L.A.; Alexander, S.A. Computational Paradigm Techniques for Enhancing Electric Power Quality; CRC Press: Boca Raton, FL, USA, 2018; ISBN 978-0-429-80990-3. [Google Scholar]
- Saha, S.; Cho, Y.H. Starting Characteristic Analysis of LSPM for Pumping System Considering Demagnetization. Int. J. Mech. Mechatron. Eng. 2015, 9, 1305–1311. [Google Scholar]
- Palangar, M.F. Design, Analysis and Optimization of Line-Start Permanent-Magnet Synchronous Motors: Simultaneous Electromagnetic and Thermal Analysis. Available online: https://theses.flinders.edu.au/view/8616886a-3b6f-4c97-a9d0-95452aa86a65/1 (accessed on 1 November 2022).







| Induction Motor Class | IE4 Class |
|---|---|
| Technology | LSPMM |
| Power | 0.75 kW |
| Voltage | 220 V/380 V |
| Speed (rpm) | 1800 |
| Torque (Nm) | 3.96 |
| Current (A) | 3.08/1.78 |
| Efficiency (%) | 87.4 |
| Power Factor | 0.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabora, J.M.; Tshoombe, B.K.; Fonseca, W.d.S.; Tostes, M.E.d.L.; Matos, E.O.d.; Bezerra, U.H.; Silva, M.d.O.e. Virtual Modeling and Experimental Validation of the Line-Start Permanent Magnet Motor in the Presence of Harmonics. Energies 2022, 15, 8603. https://doi.org/10.3390/en15228603
Tabora JM, Tshoombe BK, Fonseca WdS, Tostes MEdL, Matos EOd, Bezerra UH, Silva MdOe. Virtual Modeling and Experimental Validation of the Line-Start Permanent Magnet Motor in the Presence of Harmonics. Energies. 2022; 15(22):8603. https://doi.org/10.3390/en15228603
Chicago/Turabian StyleTabora, Jonathan Muñoz, Bendict Katukula Tshoombe, Wellington da Silva Fonseca, Maria Emília de Lima Tostes, Edson Ortiz de Matos, Ubiratan Holanda Bezerra, and Marcelo de Oliveira e Silva. 2022. "Virtual Modeling and Experimental Validation of the Line-Start Permanent Magnet Motor in the Presence of Harmonics" Energies 15, no. 22: 8603. https://doi.org/10.3390/en15228603
APA StyleTabora, J. M., Tshoombe, B. K., Fonseca, W. d. S., Tostes, M. E. d. L., Matos, E. O. d., Bezerra, U. H., & Silva, M. d. O. e. (2022). Virtual Modeling and Experimental Validation of the Line-Start Permanent Magnet Motor in the Presence of Harmonics. Energies, 15(22), 8603. https://doi.org/10.3390/en15228603







