Forecasting Monthly Wind Energy Using an Alternative Machine Training Method with Curve Fitting and Temporal Error Extraction Algorithm
Abstract
1. Introduction
1.1. Literature Review
1.2. Motivation
1.3. Main Contribution
1.4. Algorithm Justification
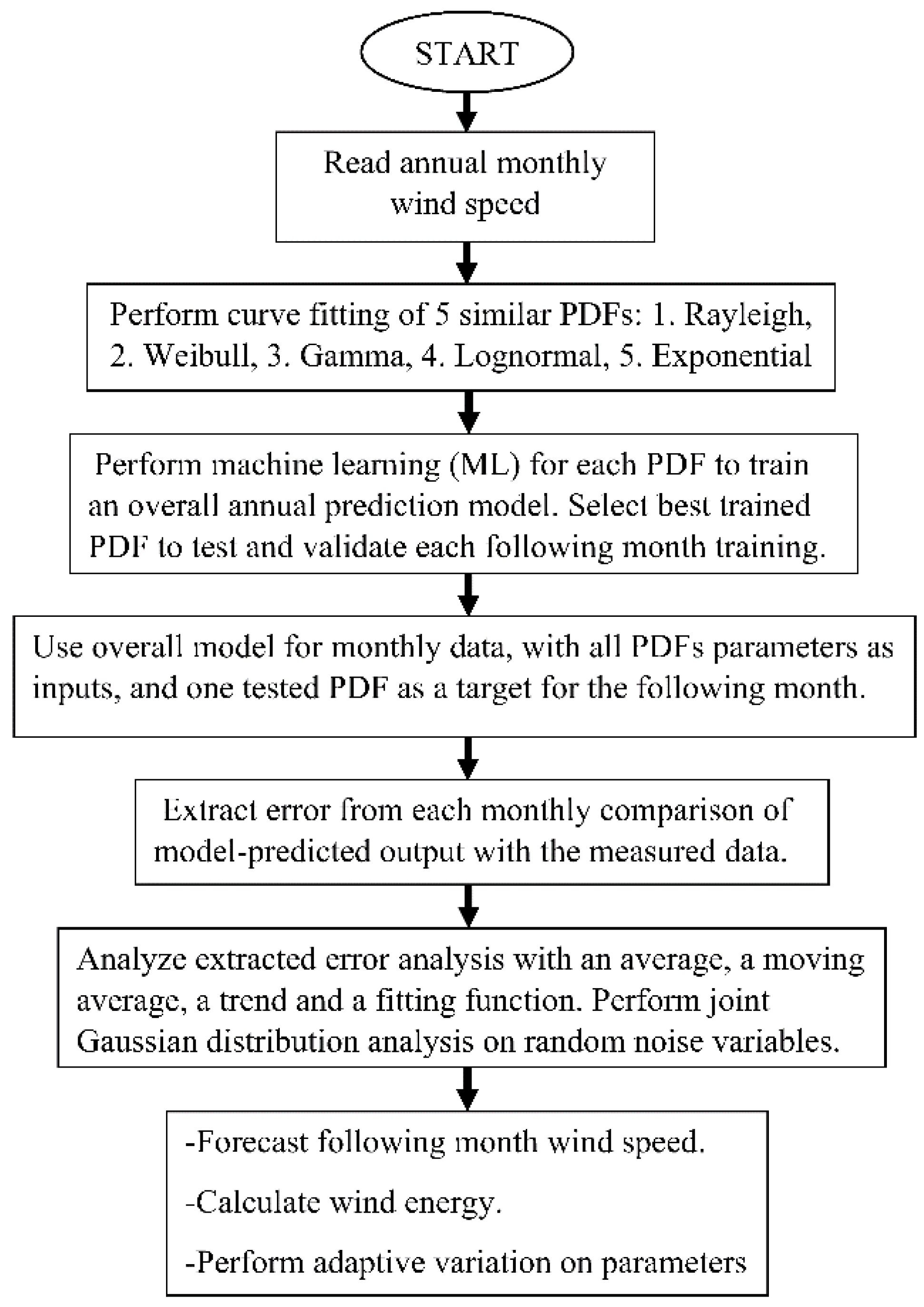
2. Procedural Methodology
3. Wind Speed Curve Fitting
- 1.
- Rayleigh PDF, where σ is the scale parameter.
- 2.
- Weibull PDF, where a is the inverse of the scale parameter, and b is the shape parameter.
- 3.
- Lognormal PDF, where μ and σ are related to the mean (or average) and standard deviation parameters.
- 4.
- Gamma PDF, where a is the shape parameter and b is the inverse of the scale parameter.
- 5.
- Exponential PDF, where b is the rate parameter.
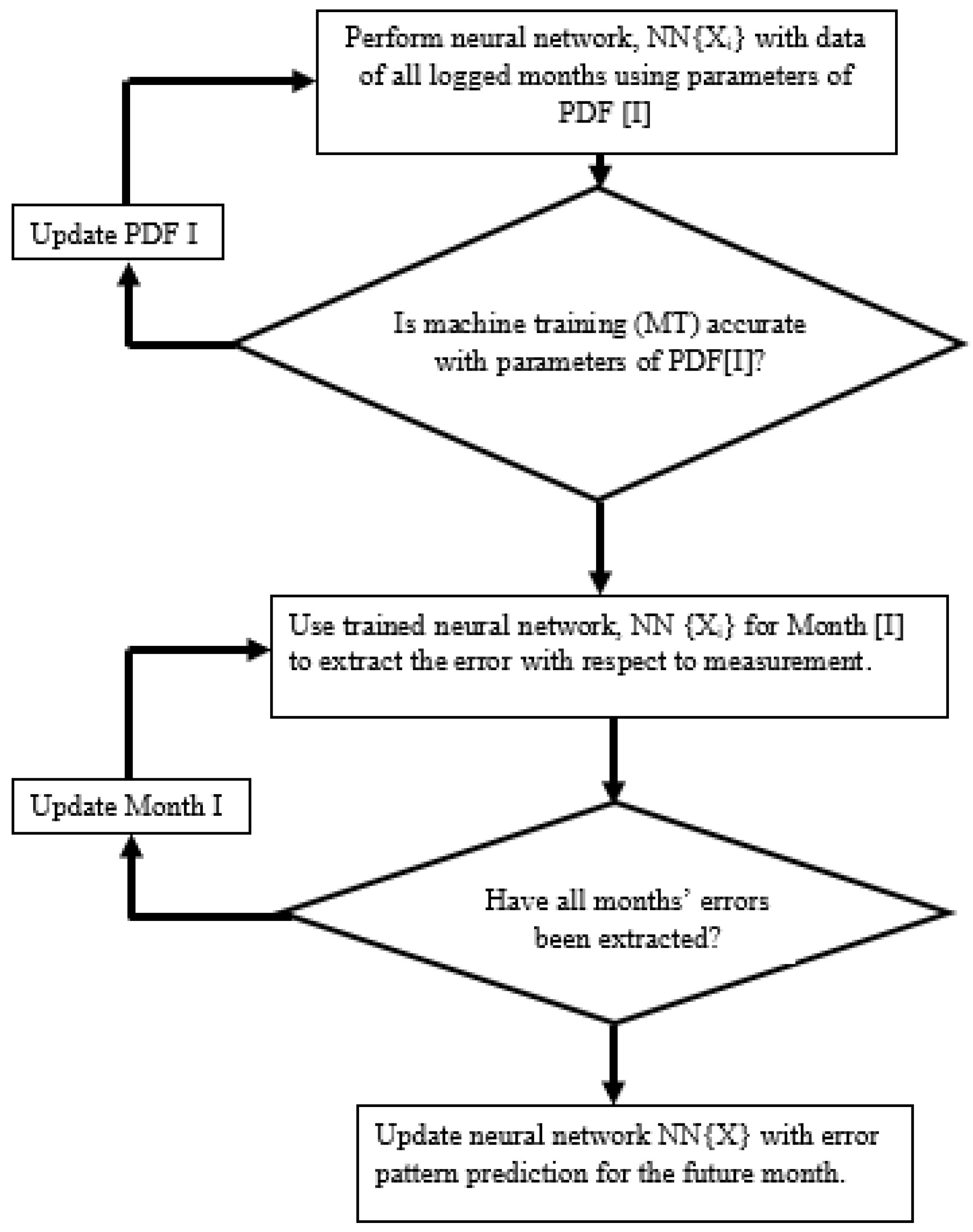
4. ML Forecasting Model
5. Analysis and Results
- (a)
- New concept of neural network modeling:
- (b)
- Probability distribution functions’ parameters are used as input NN abstracts:
- (c)
- Annual wind energy forecast is performed:
- (d)
- Adaptive analysis of extracted energy:
- (e)
- Accuracy of the adopted method:
5.1. Lognormal Pdf Prediction
5.2. Error Extracting Algorithm
5.3. Forecasting Wind Energy
5.4. Algorithm Adaptive Analysis
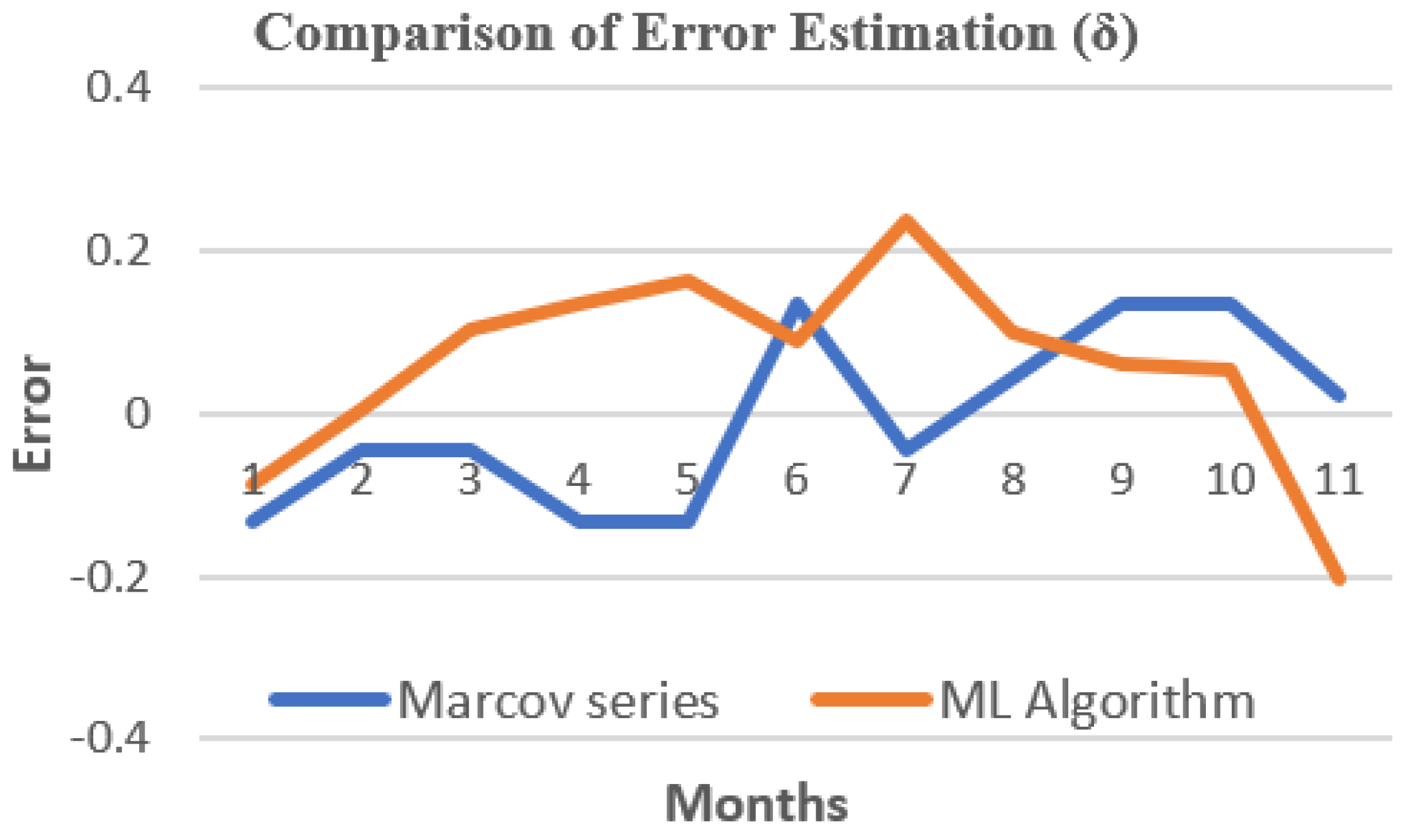
5.5. Estimating Algorithm Error
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| AR | Autoregressive part |
| ARIMA | Auto Regressive Integrated Moving Average |
| ARMA | Auto Regressive Moving Average |
| EWT | Empirical wavelet transformation |
| IDMDN | Improved deep mixture density network |
| IEMD | Improved empirical mode decomposition |
| KDE | Kernel Density Estimation |
| LUBE | Lower Upper Bound Estimation |
| MA | Moving average |
| ML | Machine learning |
| NN | Neural Network |
| Probability Density Function | |
| QR | Quantile Regression |
| SVM | Support Vector Machine |
References
- Bazionis, I.K.; Georgilakis, P.S. Reviews of deterministic and probabilistic wind power forecasting: Models, methods, and Future Research. Electricity 2021, 2, 13–47. [Google Scholar] [CrossRef]
- Wu, Y.K.; Po, E.S.; Jing, S.H. An overview of wind power probabilistic forecasts. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference, Xi’an, China, 25–28 October 2016. [Google Scholar]
- Giebel, G.; Brownsword, R.; Kariniotakis, G.; Denhart, M.; Draxl, C. The State-of-the-Art in Short-Term Prediction of Wind Power, A Literature Overview, 2nd ed. Available online: https://orbit.dtu.dk/en/publications/the-state-of-the-art-in-short-termprediction-of-wind-power-a-lit (accessed on 10 October 2020).
- Cadenas, E.; Rivera, W. Wind speed forecasting in three different regions of Mexico, using a hybrid ARIMA–ANN model. Renew. Energy 2010, 35, 2732–2738. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Short-term wind power forecasting in Portugal by neural networks and wavelet transform. Renew. Energy 2011, 36, 1245–1251. [Google Scholar] [CrossRef]
- Gomes, P.; Castro, R. Wind speed and wind power forecasting using statistical models: Auto Regressive moving average (ARMA) and artificial neural networks (ANN). Int. J. Sustain. Energy Dev. 2012, 1, 41–50. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, Y.; Zhang, D.; Wang, W.; Chen, Z. Wind power ultra-short-term forecasting method combined with pattern-matching and ARMA-model. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013. [Google Scholar]
- Tseng, F.; Yu, H.; Tzeng, G. Applied hybrid Grey model to forecast seasonal time series. Technol. Forecast. Soc. Change 2001, 67, 291–302. [Google Scholar] [CrossRef]
- Catalao, J.P.S.; Pousinho, H.M.I.; Mendez, V.M.F. An artificial neural network approach for short-term wind power forecasting in Portugal. In Proceedings of the 15th International Conference of Intelligent System Applications to Power Systems, Curitiba, Brazil, 8–12 November 2009. [Google Scholar]
- Haque, A.; Nehrir, M.; Mandal, P. A Hybrid intelligent model for deterministic and quantile regression approach for probabilistic wind power forecasting. IEEE Trans. Power Syst. 2014, 29, 1663–1672. [Google Scholar] [CrossRef]
- Bofinger, S.; Luig, A.; Beyer, H. Qualification of wind power forecasts. In Proceedings of the Global Wind Power Conference, Paris, France, 2–5 April 2002. [Google Scholar]
- Zeng, J.; Qiao, W. Support vector machine-based short-term wind power forecasting. In Proceedings of the IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011. [Google Scholar]
- Zhang, W.; Liu, F.; Zheng, X.; Li, Y. A hybrid EMD-SVM based short-term wind power forecasting model. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference, Brisbane, QLD, Australia, 15–18 November 2015. [Google Scholar]
- Lin, L.; Xia, D.; Dai, L.; Zheng, Q.; Qin, Z. Chaotic analysis and prediction of wind speed based on wavelet decomposition. Processes 2021, 9, 1793. [Google Scholar] [CrossRef]
- Peng, L.; Wang, L.; Xia, D.; Gao, Q. Effective energy consumption forecasting using empirical wavelet transform and long short-term memory. Energy 2022, 238, 121756. [Google Scholar] [CrossRef]
- Liu, H.; Yu, C.; Wu, H.; Duan, Z.; Yan, G. A new hybrid ensemble deep reinforcement learning model for wind speed short term forecasting. Energy 2020, 202, 117794. [Google Scholar] [CrossRef]
- Lv, S.; Wang, L. Deep learning combined wind speed forecasting with hybrid time series decomposition and multi-objective parameter optimization. Appl. Energy 2022, 311, 118674. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Y.; Wang, J. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar] [CrossRef]
- Wan, C.; Lin, J.; Wang, J.; Song, Y.; Dong, Z.Y. Direct quantile regression for nonparametric probabilistic forecasting of wind power generation. IEEE Trans. Power Syst. 2017, 32, 2767–2778. [Google Scholar] [CrossRef]
- Juban, J.; Siebert, N.; Kariniotakis, G. Probabilistic short-term wind power forecasting for the optimal management of wind generation. In Proceedings of the IEEE Power Tech, Lausanne, Switzerland, 1–5 July 2007. [Google Scholar]
- Khosravi, A.; Nahavandi, S.; Creighton, D. Prediction intervals for short-term wind farm power generation forecasts. IEEE Trans. Sustain. Energy 2013, 4, 602–610. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A. Short-Term Load and Wind Power Forecasting Using Neural Network-Based Prediction Intervals. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Probabilistic forecasting of wind power generation using extreme learning machine. IEEE Trans. Power Syst. 2014, 29, 1033–1044. [Google Scholar] [CrossRef]
- Wu, Y.K.; Wu, Y.C.; Hong, J.S.; Phan, L.H.; Quoc, D.P. Forecast of wind power generation with data processing and numerical weather prediction. IEEE Trans. Ind. Appl. 2021, 57, 36–45. [Google Scholar] [CrossRef]
- Wu, Y.; Su, P.; Wu, T.; Hong, J.; Hassan, M. Probabilistic wind power forecasting using weather ensemble models. IEEE Trans. Ind. Appl. 2018, 54, 5609–5620. [Google Scholar] [CrossRef]
- Afrasiabi, M.; Mohammadi, M.; Afrasiabi, M.R.S. Advanced deep learning approach for probabilistic wind speed forecasting. IEEE Trans. Ind. Inform. 2021, 17, 720–727. [Google Scholar] [CrossRef]
- Dehnavi, S.D.; Shirani, A.; Mehrjerdi, H.; Baziar, M. New deep learning-based approach for the wind turbine output power modeling and forecasting. IEEE Trans. Ind. Appl. 2020, 17, 720–727. [Google Scholar] [CrossRef]
- Abedinia, O.; Lotfi, M.; Bagheri, M.; Sobhani, B.; Shafie-khah, M.; Catalao, J.P.S. Improved EMD-based complex prediction model for wind power forecasting. IEEE Trans. Sustain. Energy 2020, 11, 2790–2802. [Google Scholar] [CrossRef]
- Rajagopalan, S.; Santoso, S. Wind power forecasting and error analysis using the autoregressive moving average modeling. In Proceedings of the IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Tsikalakis, A.; Katsigiannis, Y.; Georgilakis, P.; Hatziargyriou, N. Impact of wind power forecasting error bias on the economic operation of autonomous power systems. Wind Energy 2009, 12, 315–331. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, M.; Wan, C.; Wang, J.; Song, Y. A multi-model combination approach for probabilistic wind power forecasting. IEEE Trans. Sustain. Energy 2019, 10, 226–237. [Google Scholar] [CrossRef]
- Hodge, B.K. Wind Energy. In Alternative Energy Systems and Applications; John Wiley: Hoboken, NJ, USA, 2010; pp. 56–87. ISBN 978-0-470-14250-9. [Google Scholar]
- Haykin, S. Learning processes. In Neural Networks, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Abdul Majid, A. Accurate and efficient forecasted wind energy using selected temporal metrological variables and wind direction. Energy Convers. Manag. X 2022, 16, 100286. [Google Scholar] [CrossRef]
- Abdul Majid, A. The Evaluation of Wind Energy Based on the Inherent Nature of Wind Speed Assessment at Fujairah of UAE. Instrum. Mes. Métrologie 2021, 20, 121–130. [Google Scholar] [CrossRef]
- Abdul Majid, A. Wind energy forecasting by fitting predicted probability density functions of wind speed measurements. Int. J. Energy Environ. Eng. 2022, 13, 573–585. [Google Scholar] [CrossRef]
- Miller, S.; Childers, D. Multiple random variables. In Probability and Random Processes with Applications to Signal Processing and Communications; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 978-0-12-386981-4. [Google Scholar]
- Mahmud, S.; Bhuiyan, A.M.; Sarmin, N.; Elahee, S. Study of wind speed and relative humidity using stochastic technique in a semi-arid climate region. AIMS Environ. Sci. 2020, 7, 156–173. [Google Scholar] [CrossRef]

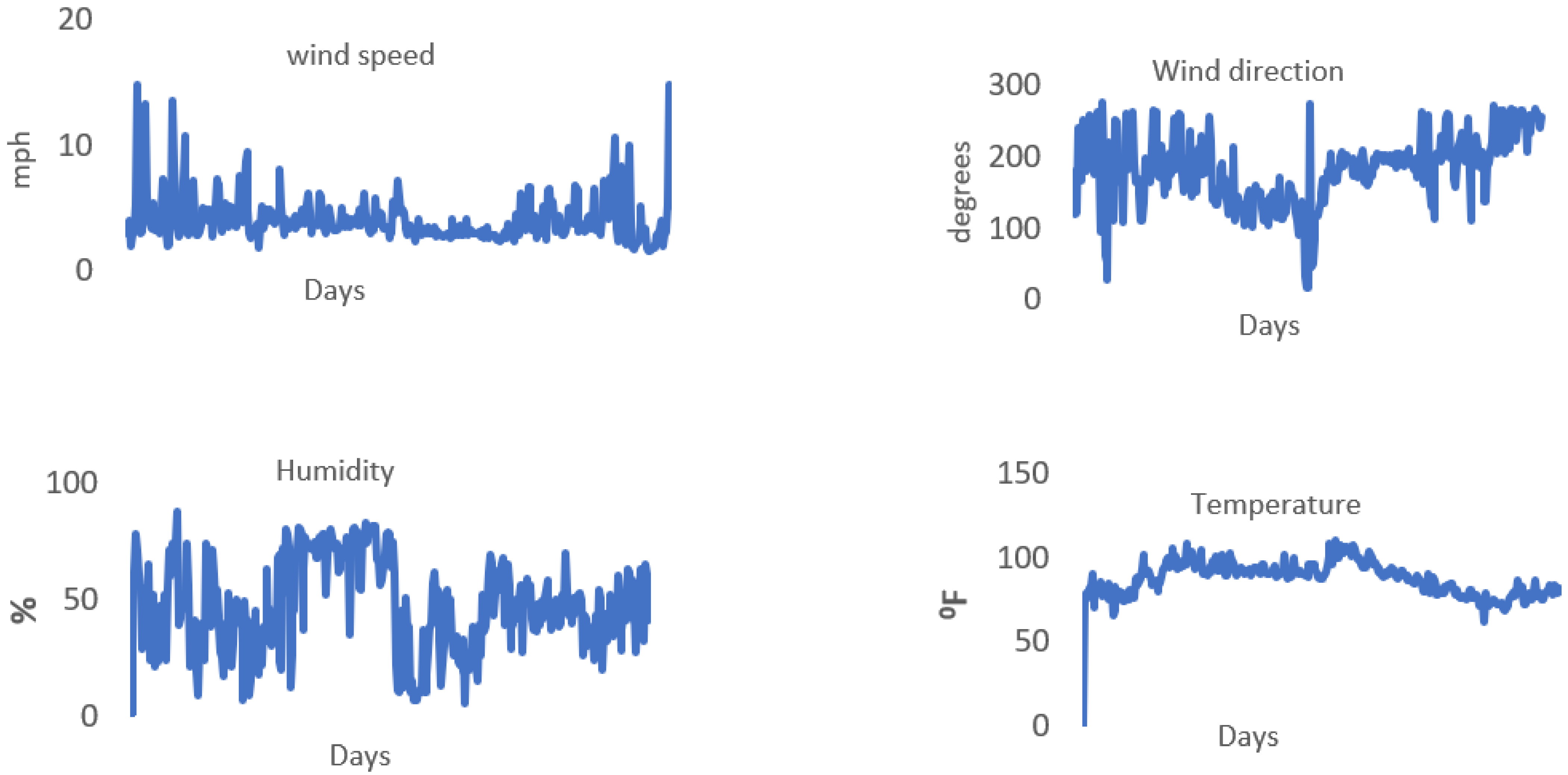
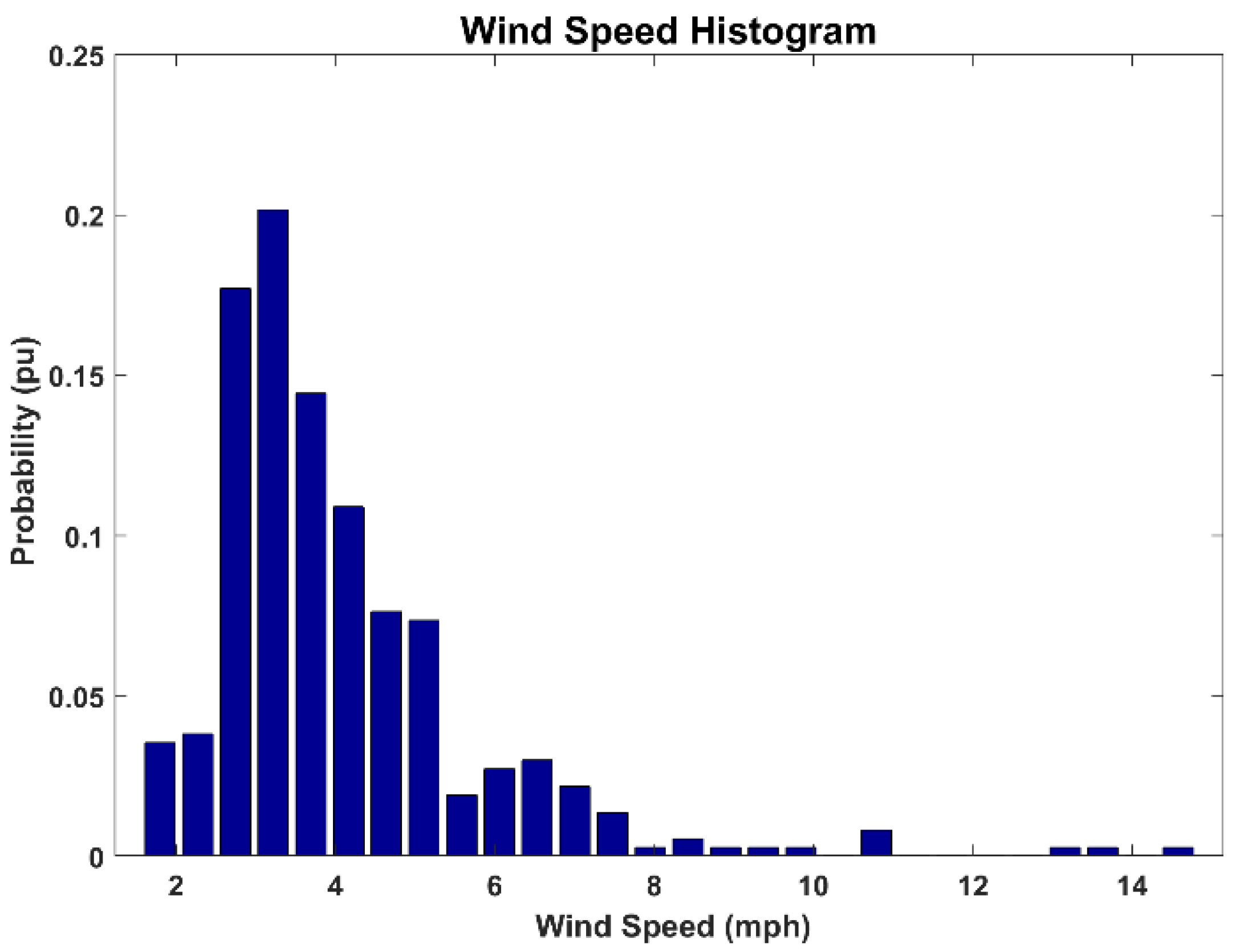


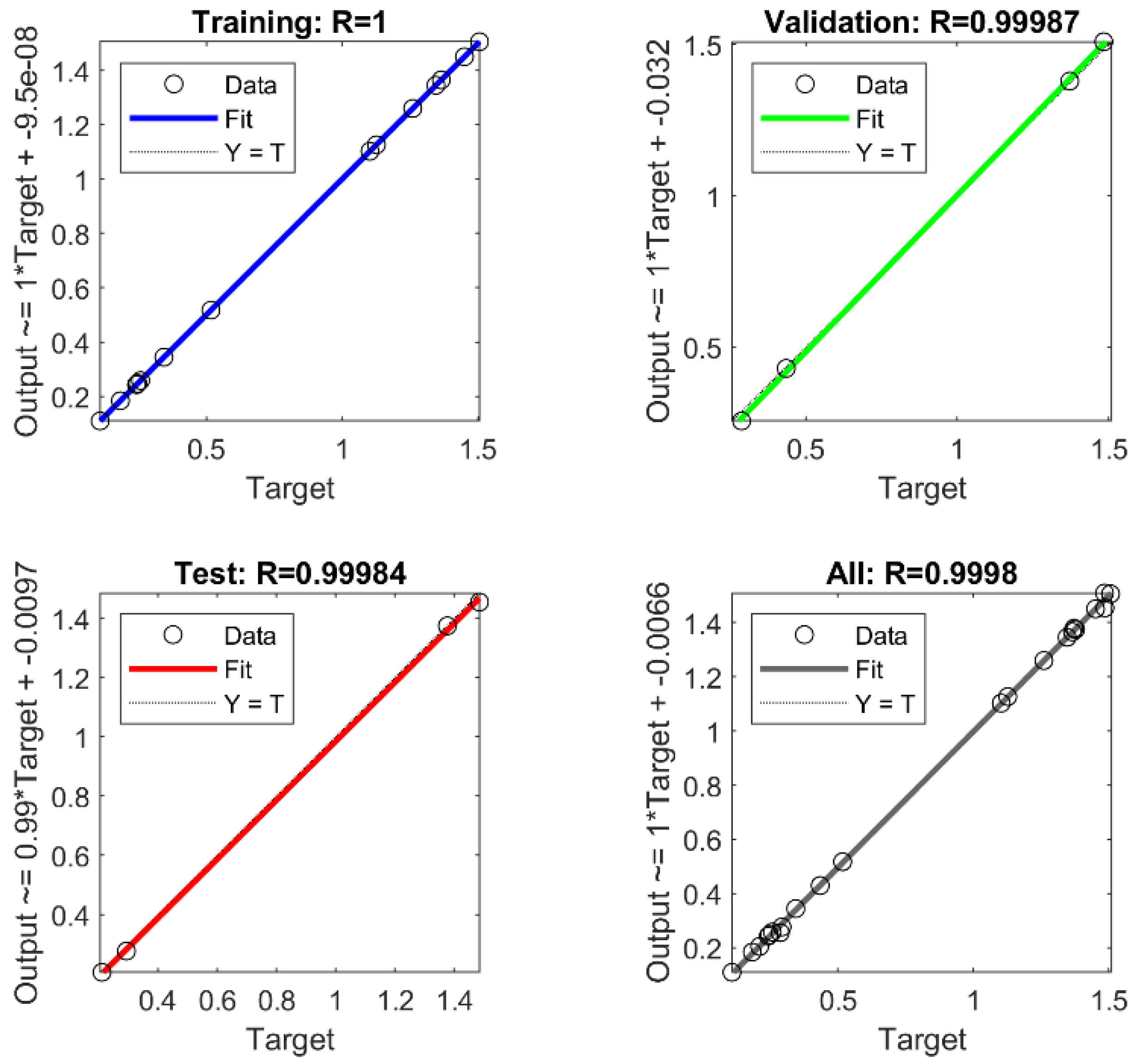
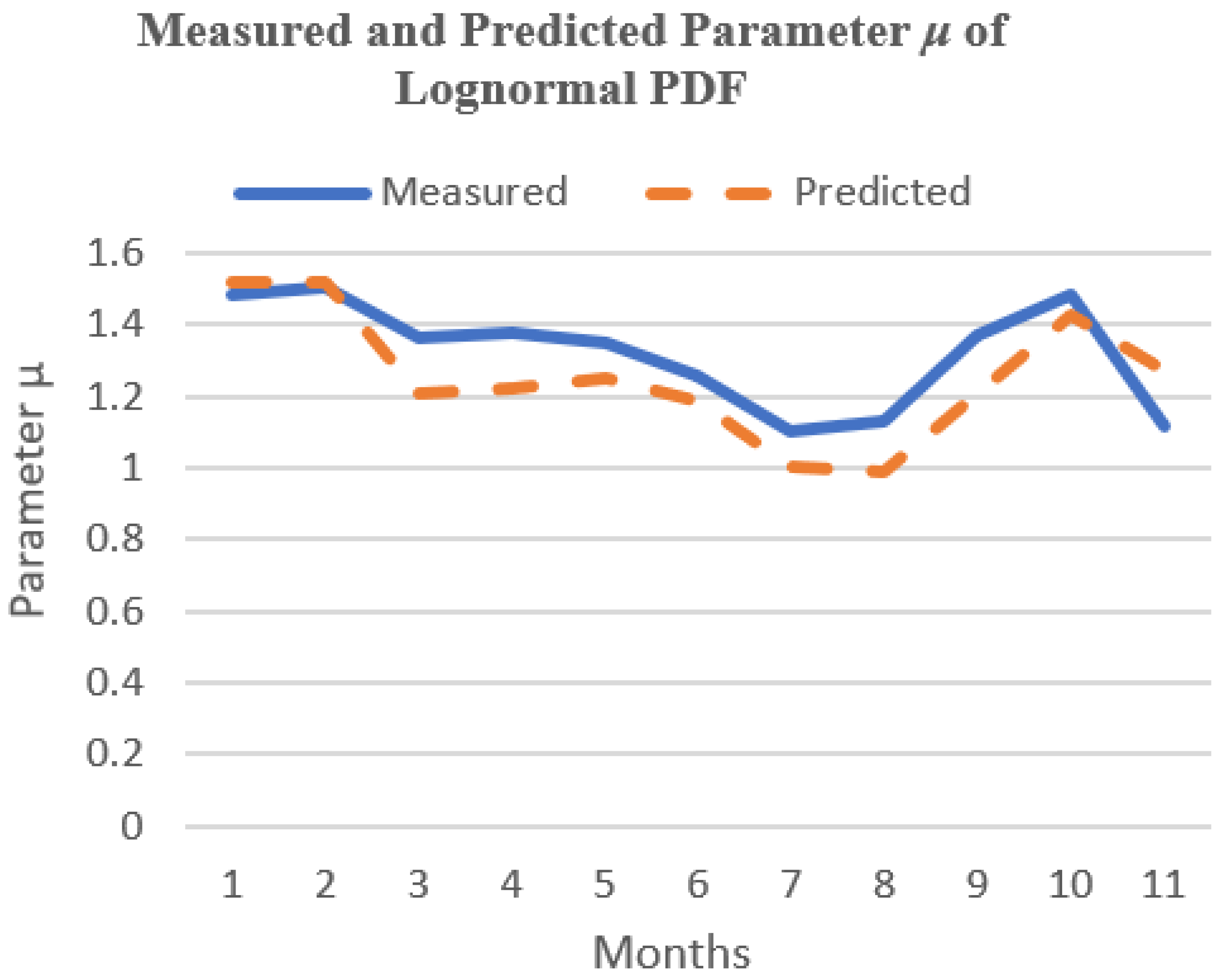




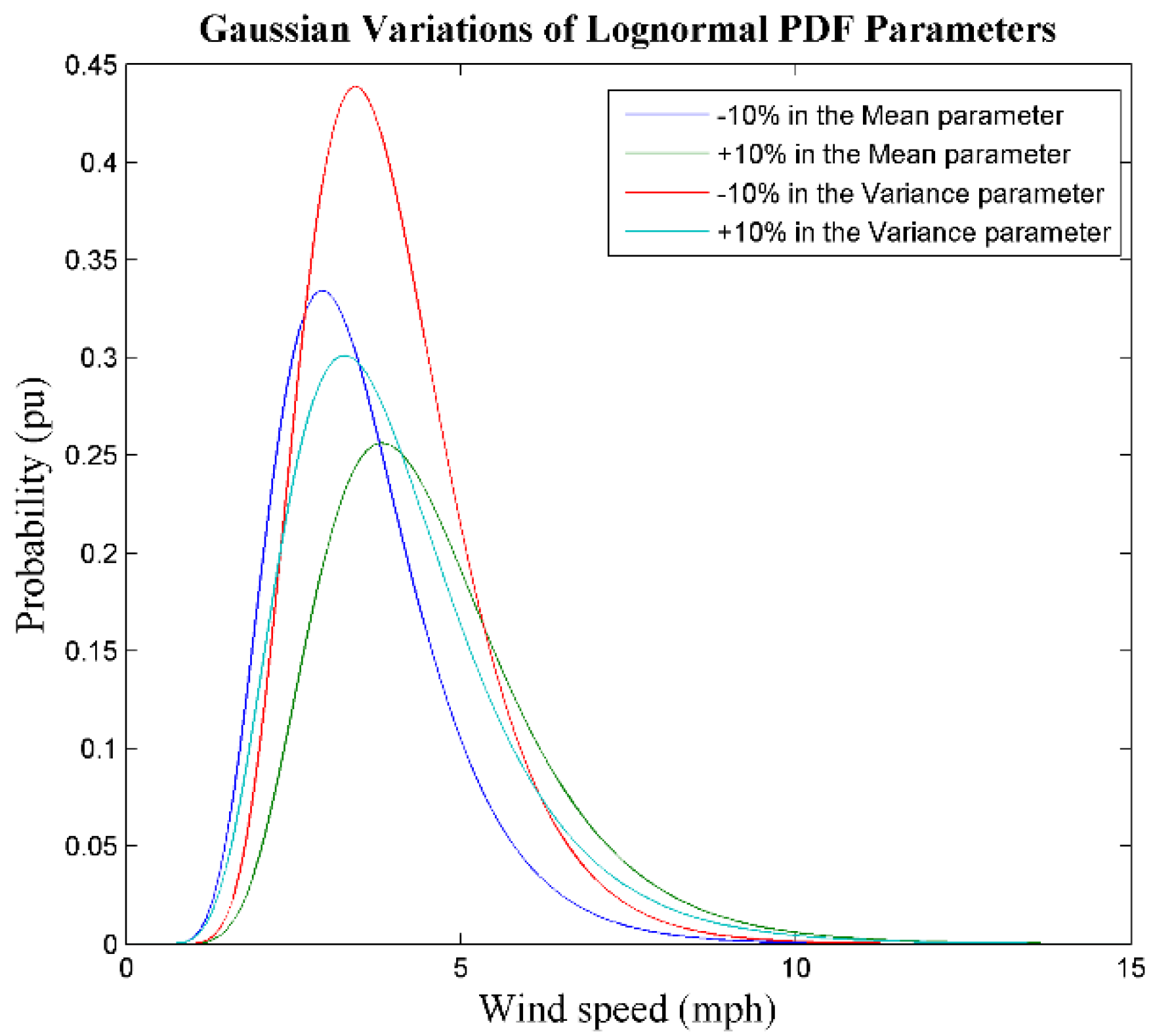
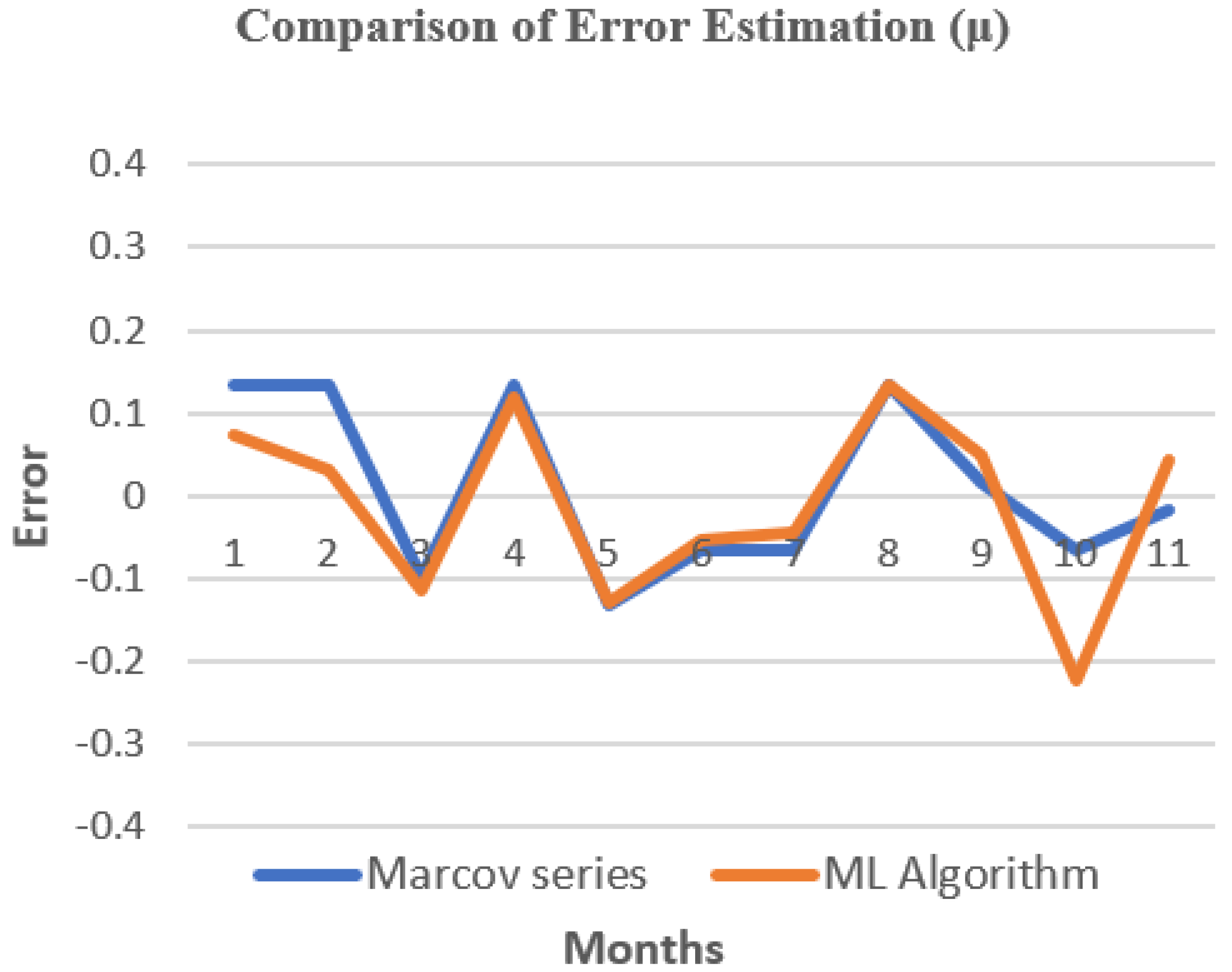
| Parameter | Value |
|---|---|
| Latitude (deg N) | 25007′ N |
| Longitude | 56018′ E |
| Mean wind speed at 10 m | 4.072664 mph |
| Mean wind direction | 182.46510 |
| Average temperature | 28 °C |
| Mean pressure | 900–1100 m bar |
| Relative humidity | 50–100% |
| Air density | 1.188 kg/m3 |
| Terrain | flat land |
| Obstacles | Hills |
| Surface roughness class | 0.5 Sa |
| Case | Input Abstracts | Output Target | All R |
|---|---|---|---|
| 1 | b of Exponential pdf a and b of Weibull pdf a and b of Gamma pdf μ and σ of Lognormal pdf | σ of Rayleigh pdf | 0.659 |
| 2 | σ of Rayleigh pdf a and b of Weibull pdf a and b of Gamma pdf μ and σ of Lognormal pdf | b of Exponential pdf | 0.785 |
| 3 | σ of Rayleigh pdf b of Exponential pdf a and b of Gamma pdf μ and σ of Lognormal pdf | a and b of Weibull pdf | 0.652 |
| 4 | σ of Rayleigh pdf b of Exponential pdf a and b of Weibull pdf μ and σ of Lognormal pdf | a and b of Gamma pdf | 0.358 |
| 5 | σ of Rayleigh pdf b of Exponential pdf a and b of Weibull pdf a and b of Gamma pdf | μ and σ of Lognormal pdf | 0.981 |
| Month | Measured | Predicted | ||
|---|---|---|---|---|
| μ | σ | μ | σ | |
| 1 | 1.4508 | 0.5174 | ||
| 2 | 1.484 | 0.4347 | ||
| 3 | 1.5061 | 0.3442 | 1.52 | 0.35 |
| 4 | 1.3654 | 0.243 | 1.52 | 0.24 |
| 5 | 1.377 | 0.2113 | 1.21 | 0.13 |
| 6 | 1.3457 | 0.184 | 1.22 | 0.15 |
| 7 | 1.2603 | 0.2582 | 1.25 | 0.17 |
| 8 | 1.1027 | 0.1092 | 1.19 | 0.28 |
| 9 | 1.1267 | 0.2478 | 1 | 0.17 |
| 10 | 1.3717 | 0.2874 | 0.99 | 0.26 |
| 11 | 1.4854 | 0.2938 | 1.21 | 0.35 |
| 12 | 1.1135 | 0.5519 | 1.43 | 0.4 |
| Month | Error of Parameter μ | Error of Parameter σ | ||
|---|---|---|---|---|
| μ Error | % μ | σ Error | % σ | |
| 1 | ||||
| 2 | ||||
| 3 | 0.0139 | 0.92 | 0.0058 | 1.69 |
| 4 | 0.1546 | 11.32 | 0.003 | 1.23 |
| 5 | 0.167 | 12.13 | 0.0813 | 38.48 |
| 6 | 0.1257 | 9.34 | 0.034 | 18.48 |
| 7 | 0.0103 | 0.82 | 0.0882 | 34.16 |
| 8 | 0.0873 | 7.92 | 0.1708 | 156.41 |
| 9 | 0.1267 | 11.25 | 0.0778 | 31.4 |
| 10 | 0.3817 | 27.83 | 0.0274 | 9.53 |
| 11 | 0.2754 | 18.54 | 0.0562 | 19.13 |
| 12 | 0.3165 | 28.42 | 0.1519 | 27.52 |
| Trained μ | Trained σ | Actual μ | Actual σ | Error μ | Error σ |
|---|---|---|---|---|---|
| 1.4238 | 0.3469 | 1.484 | 0.4347 | −0.0602 | −0.0878 |
| 1.4052 | 0.3424 | 1.5061 | 0.3442 | −0.1009 | −0.0018 |
| 1.3502 | 0.2351 | 1.3654 | 0.243 | −0.0152 | −0.0079 |
| 1.3609 | 0.1886 | 1.377 | 0.2113 | −0.0161 | −0.0227 |
| 1.3504 | 0.1934 | 1.3457 | 0.184 | 0.0047 | 0.0094 |
| 1.2733 | 0.2469 | 1.2603 | 0.2582 | 0.013 | −0.0113 |
| 1.124 | 0.1798 | 1.1027 | 0.1092 | 0.0213 | 0.0706 |
| 1.1266 | 0.1796 | 1.1267 | 0.2478 | 1.0E−4 | −0.0682 |
| 1.4028 | 0.3408 | 1.3717 | 0.2874 | 0.0311 | 0.0534 |
| 1.3307 | 0.2602 | 1.4854 | 0.2938 | −0.1547 | −0.0336 |
| 1.1742 | 0.4185 | 1.1135 | 0.5519 | 0.0607 | −0.1334 |
| Method | μ | σ |
|---|---|---|
| Measured | 1.1135 | 0.5519 |
| Predicted | 1.43 | 0.4 |
| Trained without error extraction | 1.1742 | 0.4185 |
| Trained with moving average of extracted error | 1.1242 | 0.3385 |
| Trained with trended extraction error | 1.1242 | 0.2685 |
| Trained with average extracted error | 1.1545 | 0.4620 |
| Method | Error w.r.t Measurement | |
|---|---|---|
| Measurement | 3.3526 | |
| Predicted | 4.3573 | +300% |
| Trained | 3.4915 | +4% |
| Trained with moving error | 3.2565 | −2.8% |
| Trained with trend error | 3.1907 | −4.8% |
| Trained with average error | 3.4537 | +3% |
| Velocity (m/s) | Power Density Watt/m2 | Energy kWh/m2/yr. |
|---|---|---|
| 22.293 | 195,292 | |
| 31.636 | 277,800 |
| Month | μ | Pu | μ1 | μ2 | Eu1 | Eu2 |
|---|---|---|---|---|---|---|
| 1 | 1.4508 | |||||
| 2 | 1.484 | 0.4 | 1.4238 | 1.6173 | ||
| 3 | 1.5061 | 0.4 | 1.4052 | 1.6394 | 0.214 | 0.506 |
| 4 | 1.3654 | 0.3 | 1.3502 | 1.2654 | 0.644 | 0.287 |
| 5 | 1.377 | 0.4 | 1.3609 | 1.5103 | 0.077 | 0.386 |
| 6 | 1.3457 | 0.4 | 1.3504 | 1.2123 | 1.104 | 0.792 |
| 7 | 1.2603 | 0.2 | 1.2733 | 1.1936 | 2.207 | 2.627 |
| 8 | 1.1027 | 0.2 | 1.124 | 1.0360 | 3.338 | 3.836 |
| 9 | 1.1267 | 0.4 | 1.1266 | 1.2600 | 5.451 | 3.589 |
| 10 | 1.3717 | 0.05 | 1.4028 | 1.3883 | 1.052 | 0.697 |
| 11 | 1.4854 | 0.2 | 1.3307 | 1.4187 | 1.199 | 0.448 |
| 12 | 1.1135 | 0.05 | 1.1742 | 1.0968 | 2.294 | 0.986 |
| Month | σ | Pσ | σ1 | σ2 | Eσ1 | Eσ2 |
|---|---|---|---|---|---|---|
| 1 | 0.517 | |||||
| 2 | 0.434 | −0.6 | 0.346 | 0.3013 | −0.1333 | −0.0878 |
| 3 | 0.344 | −0.2 | 0.342 | 0.2997 | −0.0444 | 0.0027 |
| 4 | 0.243 | −0.2 | 0.235 | 0.1985 | −0.0444 | 0.1039 |
| 5 | 0.211 | −0.6 | 0.188 | 0.0779 | −0.1333 | 0.1356 |
| 6 | 0.184 | −0.6 | 0.193 | 0.0506 | −0.1333 | 0.1629 |
| 7 | 0.258 | 0.6 | 0.246 | 0.3915 | 0.13333 | 0.0887 |
| 8 | 0.109 | −0.2 | 0.179 | 0.0647 | −0.0444 | 0.2377 |
| 9 | 0.247 | 0.2 | 0.179 | 0.2922 | 0.0444 | 0.0991 |
| 10 | 0.287 | 0.6 | 0.340 | 0.4207 | 0.1333 | 0.0595 |
| 11 | 0.293 | 0.6 | 0.260 | 0.4271 | 0.1333 | 0.0531 |
| 12 | 0.551 | 0.1 | 0.418 | 0.5741 | 0.0222 | −0.205 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdul Majid, A. Forecasting Monthly Wind Energy Using an Alternative Machine Training Method with Curve Fitting and Temporal Error Extraction Algorithm. Energies 2022, 15, 8596. https://doi.org/10.3390/en15228596
Abdul Majid A. Forecasting Monthly Wind Energy Using an Alternative Machine Training Method with Curve Fitting and Temporal Error Extraction Algorithm. Energies. 2022; 15(22):8596. https://doi.org/10.3390/en15228596
Chicago/Turabian StyleAbdul Majid, Amir. 2022. "Forecasting Monthly Wind Energy Using an Alternative Machine Training Method with Curve Fitting and Temporal Error Extraction Algorithm" Energies 15, no. 22: 8596. https://doi.org/10.3390/en15228596
APA StyleAbdul Majid, A. (2022). Forecasting Monthly Wind Energy Using an Alternative Machine Training Method with Curve Fitting and Temporal Error Extraction Algorithm. Energies, 15(22), 8596. https://doi.org/10.3390/en15228596






