Reducing the Exposure Dose by Optimizing the Route of Personnel Movement When Visiting Specified Points and Taking into Account the Avoidance of Obstacles

Abstract

The data on the collective dose reduction of a nuclear power plant’s personnel after the introduction of new dose limits by the International Commission for Radiological Protection (ICRP) (Publication 60) in 1990 are presented. The main methods of personnel irradiation reduction are formulated, which are namely: to impact on radiation parameters, to increase the distance between a radiation source and a person, and to reduce the exposure time in radiation fields. The ways to implement one of the basic principles of radiation safety, the principle of optimization, are described. The possibility of route optimization in minimizing the personnel dose costs when moving in heterogeneous radiation fields is shown. The results of the algorithm development for solving the “dosimetrist problem” using the Dijkstra algorithm and dynamic programming are presented, including determining the optimal route with visiting given points in the room and bypassing possible obstacles. An interpolation algorithm based on the method of radial basic functions for constructing a radiation map of a room is proposed and implemented. The results of a computational experiment using the “Uran” supercomputer and the assessment of the developed algorithm efficiency are given. The results of experimental verification of the developed algorithm for solving the “dosimetrist problem” using interpolation in the operating nuclear power plant conditions are presented.

1. Introduction

In accordance with the recommendations of the International Commission on Radiological Protection (ICRP) stated in Publication 60, (1990) the dose limit of personnel exposure was reduced from 50 to 20 mSv per year. As a result of organizational and technical measures, the annual collective doses of the personnel of foreign [1] and Russian nuclear power plants (NPPs) have decreased by 3–4 times from the 1990s to the present, reaching a certain level for each type of reactor and a slight change from year to year within this level depending on the duration of repairs (Figure 1) [2]. Further optimization of radiation protection of personnel should be determined by measures aimed at individual dose management [3], such as enhancement of the organization of works, improving the radiation situation at NPPs, and reducing the time spent by personnel in ionizing radiation fields.

The greatest reduction in dose loads on personnel is provided by the use of automated and robotic devices. However, close attention should be paid to optimizing radiation protection in all possible directions [4], for example, selection of the optimal composition of radiation protection materials [5,6,7] and selection of the optimal route of movement in heterogeneous radiation fields [8,9].

The optimization principle is of practical importance for ensuring radiation safety of personnel at all stages of the life cycle of existing and, especially, newly designed NPPs [10].

In 2007, the ICRP issued recommendations (Publication 103) that combine and complement the previous ones. The recommendations reemphasize and further reinforce the importance of optimization of radiation protection, thereby disseminating successful experience of putting this requirement into practice (now also in planned exposure situations).

The heterogeneity of radiation fields is determined by the qualitative and quantitative radioisotope composition of contamination of the walls, floor of the room, equipment and other structures, and the distance between the radiation source and the person. This leads to the dependence of the integral dose of personnel exposure when performing work in the given room on the choice of the movement trajectory and the sequence of dismantling radioactive system elements [11]. This circumstance discovers a significant potential in dose cost minimization due to the route optimization of work in heterogeneous radiation fields and the search for the optimal route of movement or the optimal sequence of works when dismantling radioactive equipment. At the same time, the shortest path in terms of length does not mean the minimum radiation dose [12,13].

2. Methods and Technologies

The term “dosimetrist task” was first formulated and used by the authors of the article in the process of analyzing the experimental operation of the subsystem of automated processing of non-regulatory measurements of the radiation situation data at finally stopped nuclear power plants in accordance with the program for optimizing radiation protection of Rosenergoatom JSC and optimizing the route of the dosimetrist when performing measurements [14,15].

To optimize the route of personnel movement during work in non-stationary fields, a movement plan is built for each performer. The dosimetrist needs to perform a number of preliminary works in order to build such a plan:

• The dosimetrist must first perform several measurements in the room where a team or a worker intends to work.
• The radiation map of the room is drawn based on the preliminary measurements.
• Facilities to be maintained (visited) by a nuclear power plant’s employees are assigned.
• Based on the data obtained at the second step, the functions of the cost of movements between previously selected objects are calculated, considering bypassing possible obstacles, as well as the terminal function.
• The optimal route for the performer to visit all designated objects is built, considering possible restrictions in the form of antecedent conditions.

After these operations, the team starts work, using the route found by the dosimetrist (or with the help of the dosimetrist) for movements. In this regard, we call the entire 1-5 system the task of a dosimetrician.

As a part of the dosimetrist’s task, an algorithm is developed for constructing the optimal route of movement of the dosimetrist (considering obstacles to be avoided) for visiting the specified points of the room, where it is necessary to perform work to determine the parameters of the radiation situation (measuring the dose rate, taking samples, etc.). To find the cost functions in view of the possibility of avoiding obstacles, the Dijkstra algorithm [16] was considered, with the help of which the shortest paths were found in the graph. This procedure is described in detail in [17].

3. General Designations and Task Statement

First, we note some of the general concepts and designations used below. Through ≜ we denote equality by definition. A family is a set whose elements are sets. Denote by $ℝ$ the real line, ${ℝ}_{+}\triangleq \left\{\mathcal{E}\le ℝ | 0\le \mathcal{E}\right\}$, $\mathbb{N}\triangleq \left\{1;2;\dots \right\}$ и ${\mathbb{N}}_0\triangleq \mathbb{N}\cup \left\{0\right\}$ =$\left\{0;1;2;\dots \right\}$, $\mathbb{N}\subset {\mathbb{N}}_0\subset$ $ℝ$. With $p\in {\mathbb{N}}_0$ and $q\in {\mathbb{N}}_0$, denote $\overline{p,q}\triangleq \left\{t\in {\mathbb{N}}_0| \left(p\le m\right)\right\}$. For each ordered pair (OP) z = (a, b) of arbitrary objects a and b, through ${\mathrm{pr}}_1\left(z\right)$ and ${\mathrm{pr}}_2\left(z\right)$ we denote the first and second elements of OP z: ${\mathrm{pr}}_1\left(z\right)=a, {\mathrm{pr}}_2\left(z\right)=b$, respectively. The ${\mathcal{R}}_{+}\left[S\right]$ denotes the set of all functions acting from the non-empty set $S$ to ${ℝ}_{+}$, that is, the set of all non-negative real functions on $S$. If $H$ is the set, then through $\mathcal{P}\left(H\right) and \mathcal{P}\prime \left(H\right)$ we denote, respectively, families of all and all non-empty subsets of $H$.

We fix the natural number of $\mathrm{N}\in \mathbb{N}, \mathrm{N}\ge 2$. Our goal is to investigate movements of the following kind:

$$0\to \mathsf{\alpha }\left(1\right)\to \cdots \to \mathsf{\alpha }\left(\mathrm{N}\right),$$

where α is the permutation of indices from $\overline{1,\mathrm{N}}$. We must visit each city exactly once and return to the base if necessary. In the future, the mentioned permutations are called routes.

We believe that the choice of $\mathsf{\alpha }$ may be constrained by additional restrictions (conditions of precedence). Elements of $\mathbb{K}$ are OP. We conditionally name the first elements—the sender, and the second—the recipients; the elements of $\mathbb{K}$ themselves are called address pairs. Everywhere in the future we believe that

$$\forall {\mathbb{K}}_0\in \mathcal{P}\prime \left(\mathbb{K}\right) \exists {\mathrm{z}}_0\in {\mathbb{K}}_0:{\mathrm{pr}}_1\left({\mathrm{z}}_0\right)\ne {\mathrm{pr}}_2\left(\mathrm{z}\right)\forall \mathrm{z}\in {\mathbb{K}}_0$$

Then, the set of all valid routes according to the previous route can be written as follows:

$$\mathbb{A}\triangleq \{\mathsf{\alpha }\in \mathbb{P} |\forall \mathrm{z}\in \mathbb{K} \forall {\mathrm{t}}_1\in \overline{1,\mathrm{N}} \forall {\mathrm{t}}_2\in \overline{1,\mathrm{N}} \left(\mathrm{z}=\left(\mathsf{\alpha }\left({\mathrm{t}}_1\right),\mathsf{\alpha }\left({\mathrm{t}}_2\right)\right)\right)\Rightarrow \left({\mathrm{t}}_1<{\mathrm{t}}_2\right)\},$$

where $\mathbb{P}\triangleq \left(\mathrm{bi}\right)\left[\overline{1,\mathrm{N}}\right]$.

We have a set of all valid routes in the sense of the conditions of precedence determined by $\mathbb{K}$. That is, we are only interested in those routes where for each address pair the sender is visited before the recipient. Thus, $\mathbb{A}$ defines a plurality of allowable solutions to the problem formulated below.

Now, let us enter the value function. Suppose that two non-negative functions are given (their areas of definition are given below) involved in the formation of the additive criterion: c is the cost of movement and f is the terminal function; for example, the cost of returning to the base:

$$\mathrm{c}\in {\mathcal{R}}_{+}\left[\overline{0,\mathrm{N}}\times \overline{1,\mathrm{N}}\right], \mathrm{f}\in {\mathcal{R}}_{+}\left[\overline{1,\mathrm{N}}\right].$$

Then, the additive criterion is defined as follows:

$${ℭ}_{\mathsf{\alpha }}\triangleq \mathrm{c}\left(0, \mathsf{\alpha }\left(1\right)\right)+{\displaystyle \sum }_{\mathrm{t}=1}^{\mathrm{N}-1}\mathrm{c}\left(\mathsf{\alpha }\left(\mathrm{t}\right),\mathsf{\alpha }\left(\mathrm{t}+1\right)\right)+\mathrm{f}\left(\mathsf{\alpha }\left(\mathrm{N}\right)\right).$$

(1)

We consider the task of minimizing the additive criterion as the main Equation (1).

$${ℭ}_{\mathsf{\alpha }}\to \min , \mathsf{\alpha }\in \mathbb{A}.$$

(2)

Since $\mathbb{A}$ is a non-empty finite set, the value (extremum) is mapped to the problem in Equation (2)

$$\mathrm{V}\triangleq \underset{\mathsf{\alpha }\in \mathbb{A}}{\min }{ℭ}_{\mathsf{\alpha }}$$

(3)

and a non-empty set of optimal allowable routes:

$${\mathbb{A}}_{\mathrm{opt}}\triangleq \left\{{\mathsf{\alpha }}_0\in \mathbb{A} | {ℭ}_{{\mathsf{\alpha }}_0}=\mathrm{V}\right\}\in \mathcal{P}\prime \left(\mathbb{A}\right).$$

(4)

Our goal is to determine the value of $\mathrm{V}$ in Equation (3) and any element of the set Equation (4). To solve the problem in Equation (2), an independent calculation scheme [18,19] is used, based on the dynamic programming method [20,21,22,23].

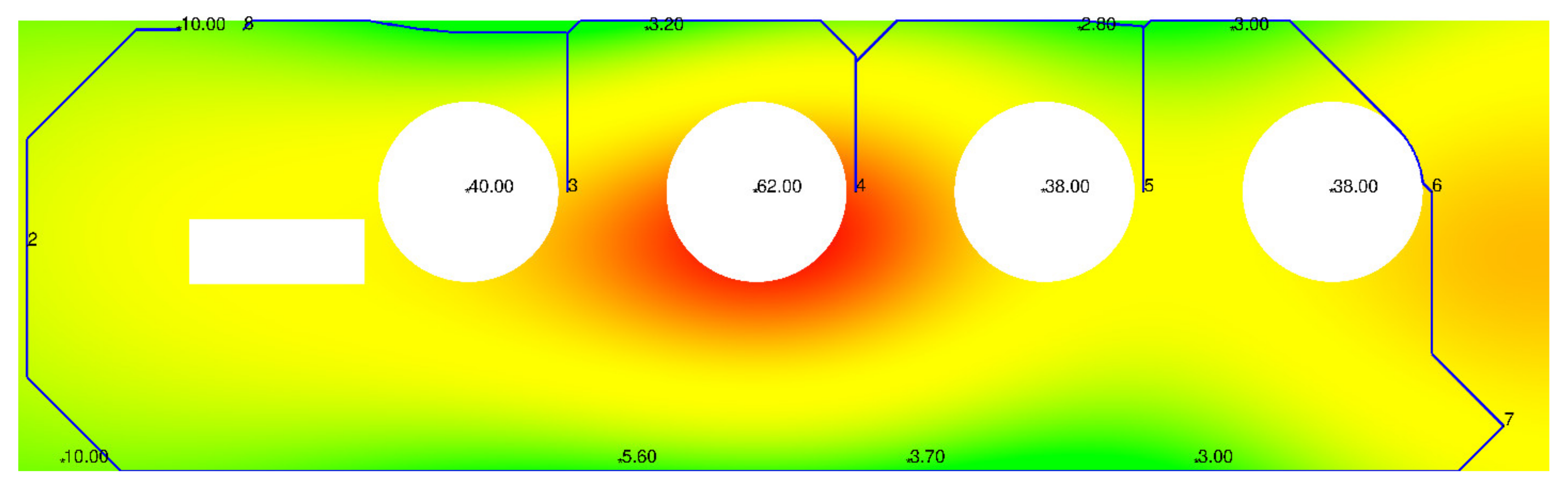
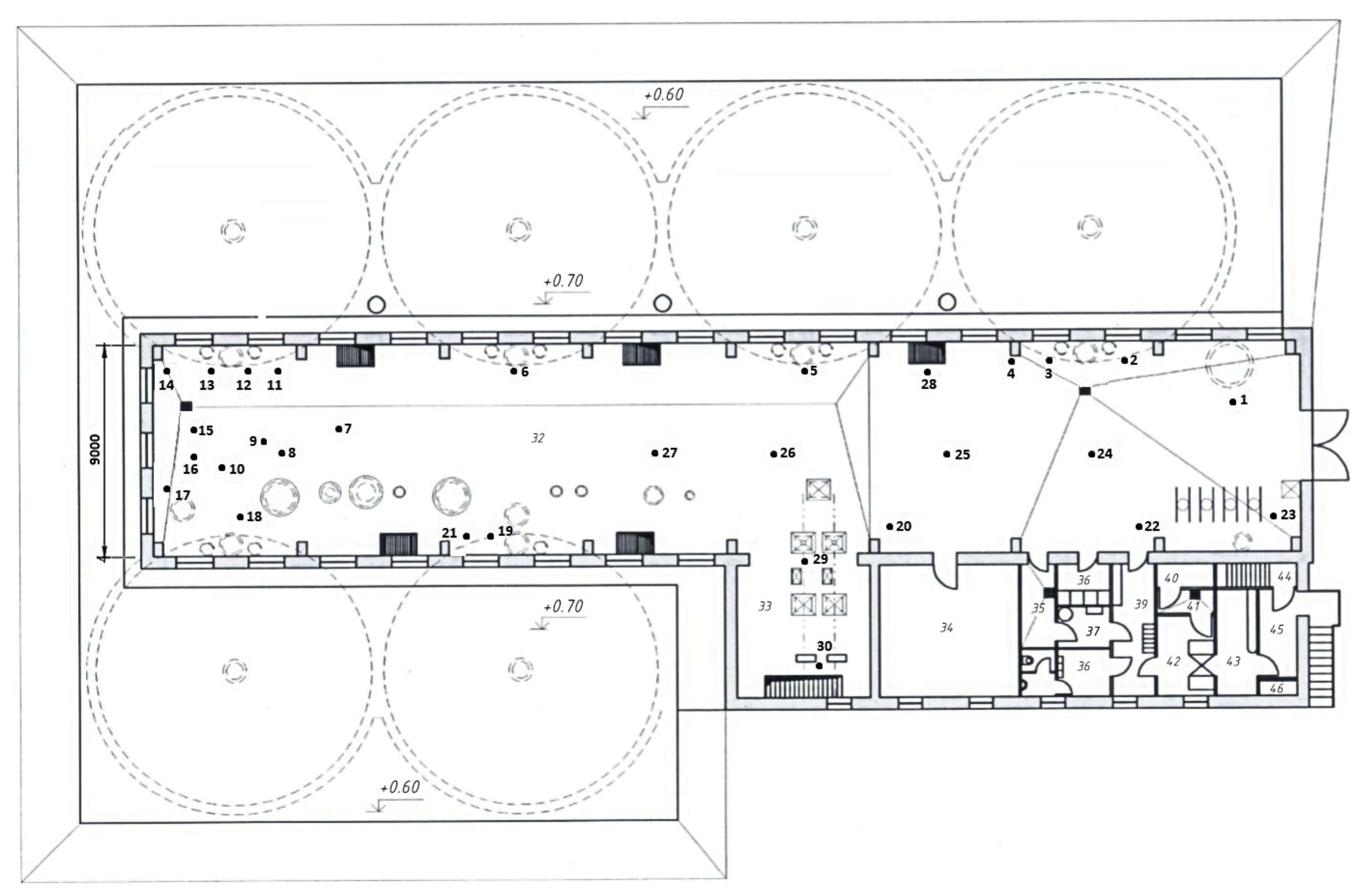
3.1. Building a Radiation Map of the Room

Radial basis functions [24,25] are applied in many directions, such as: topography, hydrology, geodesy, cartography, geophysics, visualization, and reconstruction of three-dimensional objects. The method of radial basis functions is a method of rigid interpolation, that is, the surface passes through given points; in addition, the method allows you to interpolate values above the maximum and below the minimum contained in the source data. In this work, we used this method to interpolate radiation levels from points with pre-measured radiation levels.

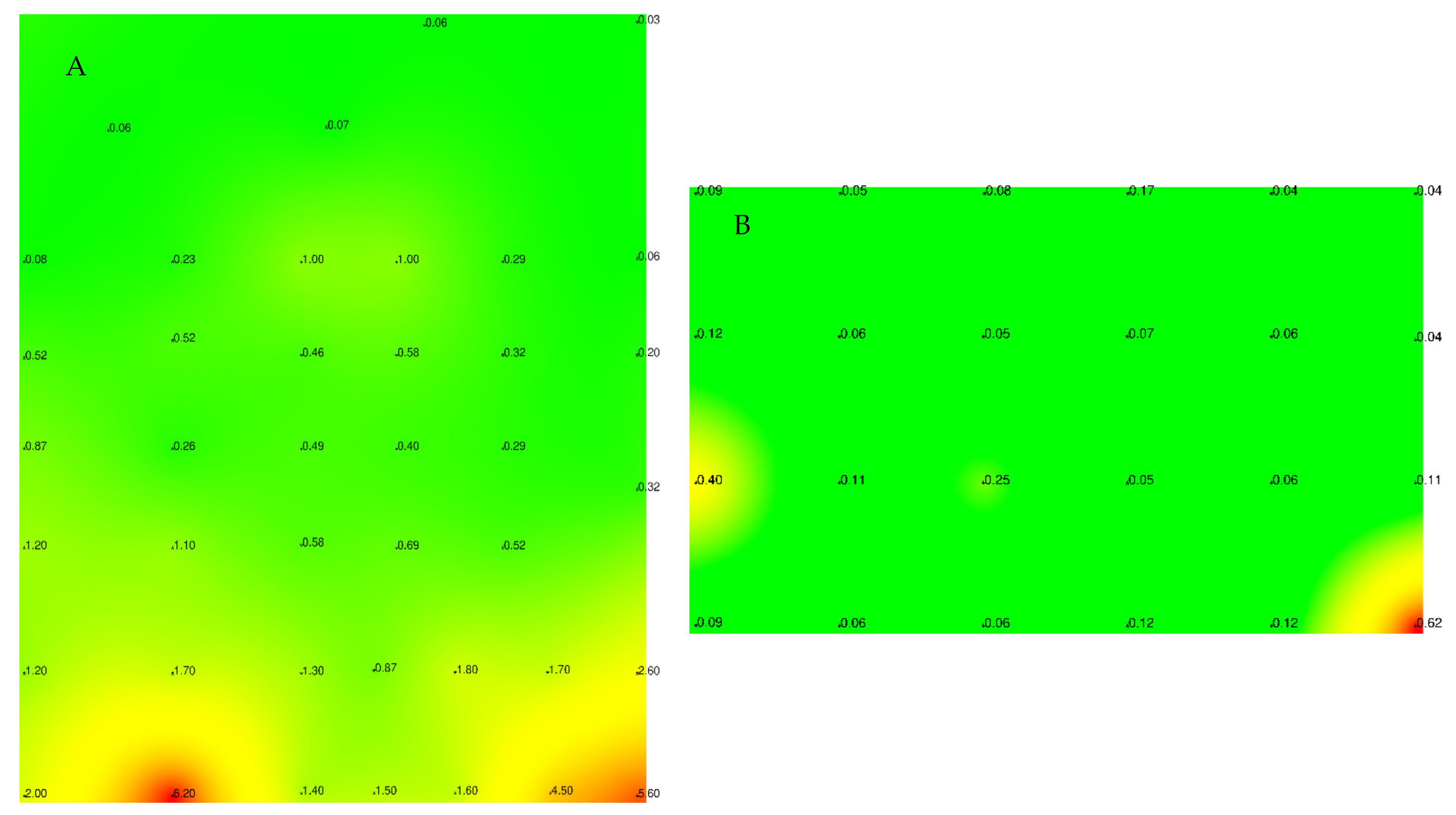
3.2. Solution Diagram Based on Radial Basis Functions

Let a set of $x_1,x_2,\dots ,x_n\subset {ℝ}^n$ datum points be specified. A radial basis function is a function of a real line whose value depends only on the distance from the reference point x to some other point $x_i$. In other words, it is the function meeting the following condition $\phi \left(x, x_i\right)={\phi }_i\left(x\right)=\phi \left(\Vert x-x_i\Vert \right), i=1,\dots ,n$ is considered a radial basic function, and her norm $\Vert \phi \left(x,x_i\right)\Vert$ is defined by the size of Euclidean distance $|x-x_i|$. Let the $y_1,y_2,\dots ,y_n\in ℝ$ values be defined on the corresponding set of $x_1,x_2,\dots ,x_n\subset {ℝ}^n$ datum points. As an interpolating function, we choose a linear combination of radial basis functions

$$F\left(x\right)={\displaystyle \sum }_{i=1}^n{\alpha }_i{\phi }_i\left(x\right)+{\alpha }_{n+1}.$$

(5)

Implementing the interpolation procedure using Equation (5), we obtain a system of $n+1$ linear equations with $n+1$ unknown coefficients ${\alpha }_i$

$$\left\{\begin{array}{c}{\displaystyle \sum _{j=1}^n}{\alpha }_j{\phi }_j\left(x_i\right)+{\alpha }_{n+1}=y_i=F\left(x_i\right). i=1,\dots ,n;\\ {\displaystyle \sum _{j=1}^n}{\alpha }_j=0 \end{array}\right.$$

where $y_i$ is the value of an unknown interpolation function at point $x_i$.

A number of the most commonly used types of radial basis functions are distinguished.

(a)

Linear $\phi =r$

(b)

Cubic $\phi =r^3$

(c)

Quintic $\phi =r^5$

(d)

ThinPlate $\phi =r^2\log r$

3.3. Building a Cost Function

To find the cost functions that take into account the possibility of bypassing obstacles, Dijkstra’s algorithm is considered to find the shortest path in the graph (see [16]). To do this, the grid is set on the plane and a connected graph is built, from which all edges and vertices falling into the obstacle region are removed. It is assumed that the radiation field is heterogeneous, so the edges of the graph can have significantly different weights. The following is a detailed algorithm for finding cost functions that consider the possibility of bypassing obstacles.

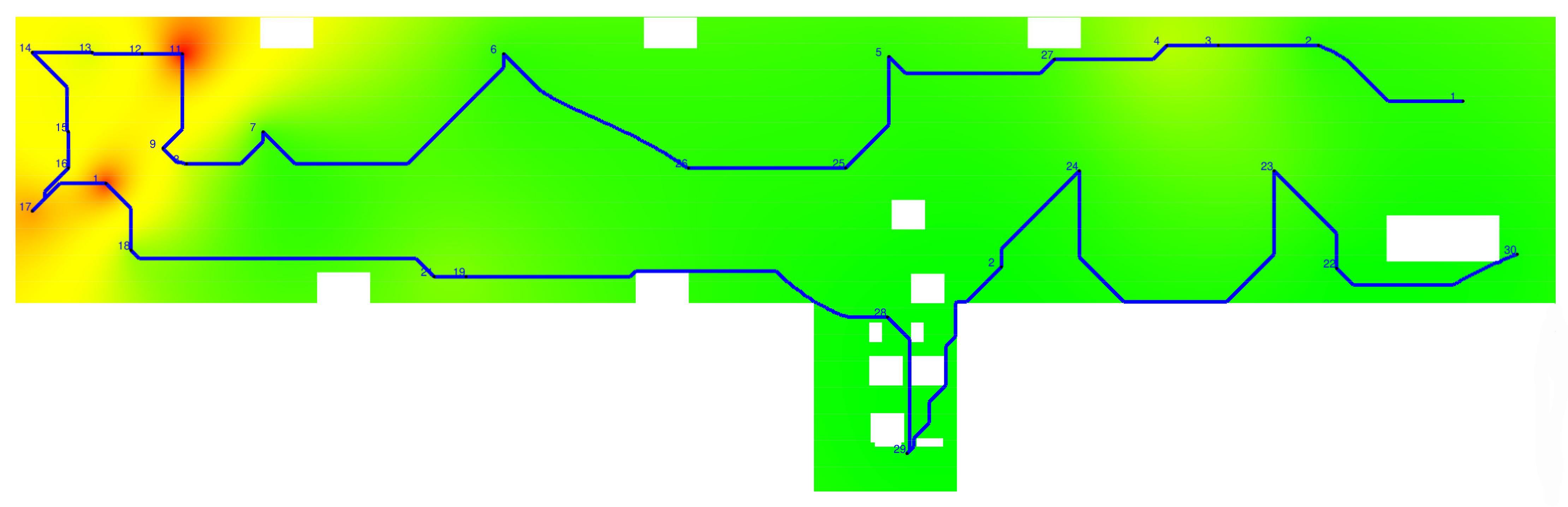
• At the first stage, we take a plan of the area with the increased level of radiation or an NPP room. We mark on it the objects that cannot be passed through, i.e., obstacles. We also highlight the points that need to be visited. Next, we build a quite fine grid on this plan, which completely covers it (Figure 2a). The nodes of this grid are discarded where it covers obstacles (Figure 2b). The grid spacing depends on the accuracy with which we want to achieve the values of the cost function. The smaller the grid spacing, the more accurate result we get, but at the same time, the counting time increases.
• Next, we move on to the construction of an undirected graph. The vertices of the graph are nodes of the constructed grid, and the edges are its faces.
• The shortest path problem on a graph can be defined for an undirected, oriented, or mixed graph. In our case, the setting of the problem for an undirected graph is considered.

A graph is made of a non-empty set of vertices and edges (pairs of edges). Two vertices are said to be adjacent if they are connected by an edge. A path in an undirected graph is the sequence of vertices $P=\left(k_1, k_2, \dots , k_n\right)\in K\times K\times \dots \times$, such that $k_i$ is adjacent to $k_{i+1}$ for $1\le i\le n$. Such a path $\mathrm{P}$ is said to be a length $\mathrm{n}$ path from $k_1$ to $k_n$ ($\mathrm{i}$ denotes the vertex’s number in the path and has no relation to the numbering of the vertices in the graph). Let $e_{i,j}$ be an edge connecting the vertices: $k_i$ and $k_j$. Given a weight function $\mathrm{f}:\mathrm{E}\to ℝ$, which maps the weights (real numbers) to edges and an undirected graph $\mathrm{G}$, call the shortest path from $\mathrm{k}$ to $k\prime$ the path $P=(k_1, k_2, \dots , k_n)$ (where $k_1=k$ and $k_{\mathrm{n}}=k\prime$) that achieves the minimum in the sum ${{\displaystyle \sum }}_{i=1}^{n-1}f(e_{i,i+1})$.

Thus, we find the cost of movements (values of the function c) between each pair of points that the performer needs to visit. After that, we can proceed to determine the optimal route (Figure 2c).

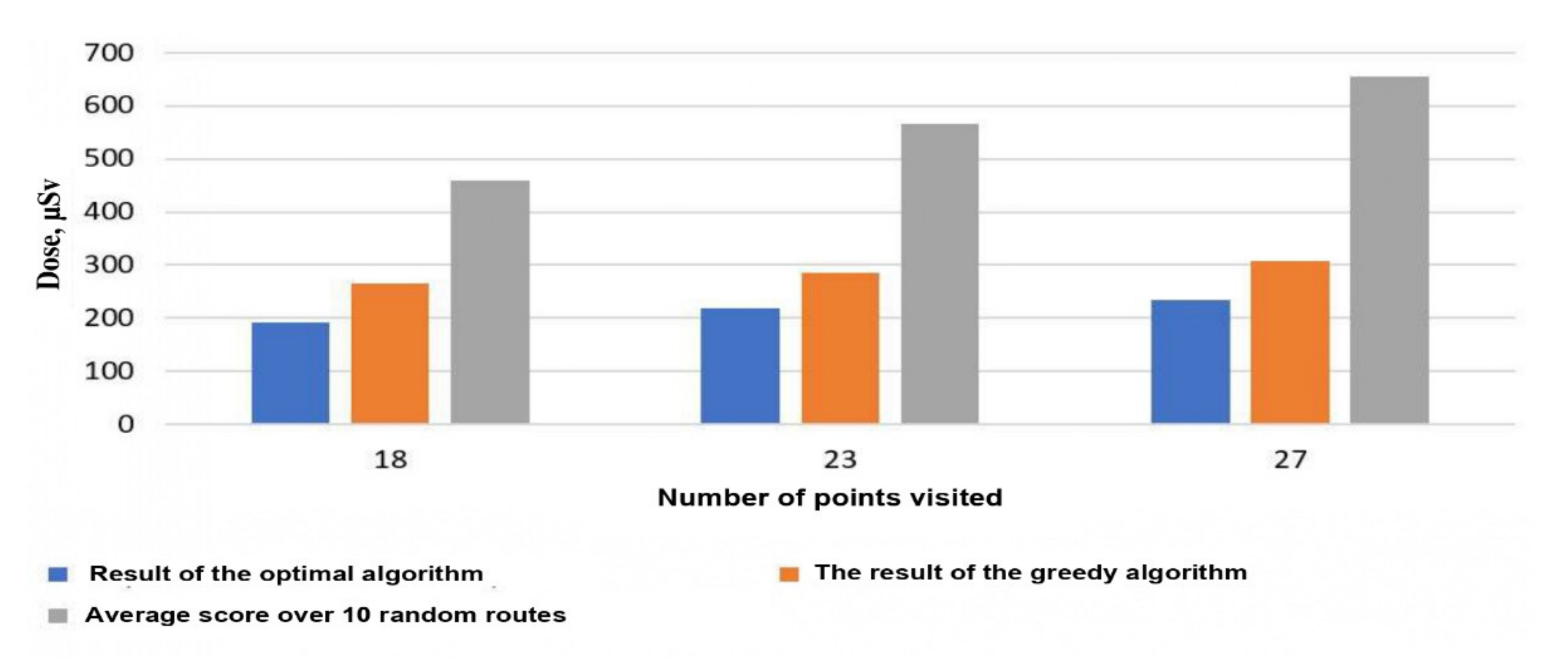
3.4. Computational Experiment

For practical verification of the theoretical research, a program in the C++ programming language was written and computational experiments were carried out on the “Uran” supercomputer of the Ural Branch of the Russian Academy of Sciences [17], including an experiment comparing the results of the proposed optimal algorithm with the so called “greedy” simplest heuristic algorithm (“go to the nearest”) and the result obtained in the case of random route selection (Figure 3).

Based on the radiation situation data, optimal routes were determined when visiting the specified points in various rooms, for example, rooms of a finally stopped for decommissioning NPP unit with a pressurized light-water-moderated and cooled reactor VVER-210 (Figure 4) [26].

4. Results and Discussion

Figure 5 shows the results of the computational experiment for the real premises “A” (11.2 × 13.5 m) and “B” (11.2 × 6.7 m) of the finally stopped NPPs. For room “A”, 40 reference points with known dose rates (from 0.033 mSv/h to 6.2 mSv/h) were specified, of which five and eight points were selected to check the simulation results. For room “B”, 24 reference points (from 0.036 mSv/h to 0.62 mSv/h) were specified, from which four and five points were selected to check the simulation results.

For these rooms, computational experiments were carried out to determine the optimal route of the dosimetrist with a visit to the specified points, considering the avoidance of obstacles with the preliminary construction of radiation maps based on a limited number of points with known values of the dose rate.

Table 1. Radiation doses when moving along the detected optimal route, visiting the specified points of room “B”, mSv.

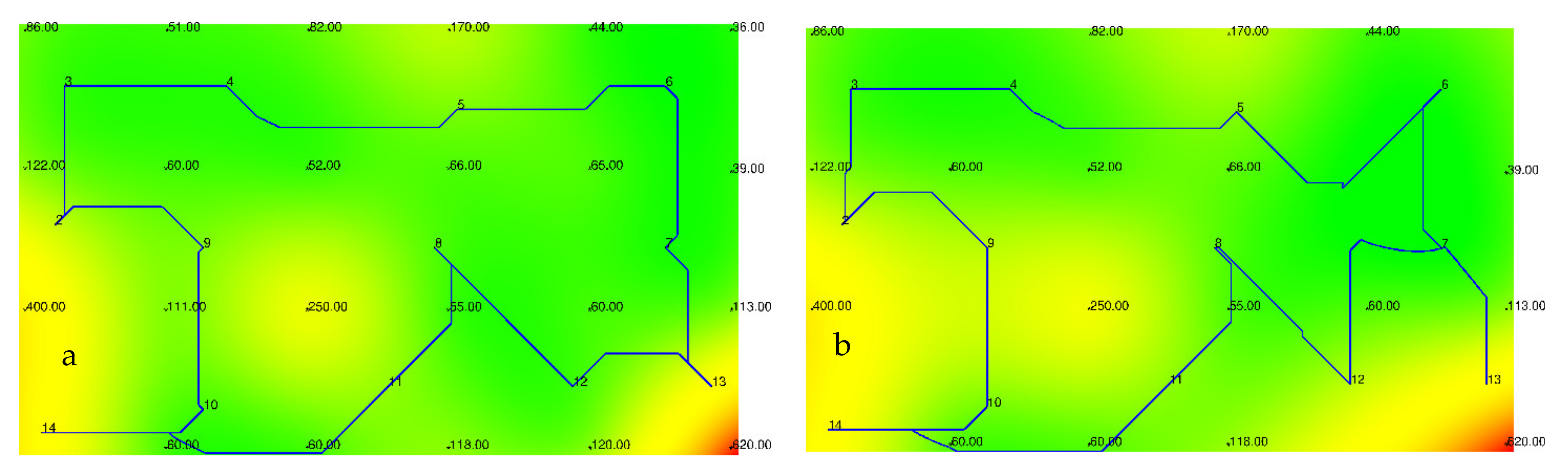
	Radial Basis Functions
	Cubic	Linear	Quintic	ThinPlate
All measurements	8.55674	9.2007	8.40472	8.59993
80% measurements	7.97714	8.78118	7.02262	8.16382
Deviation in %	7.27%	4.78%	19.68%	5.34%

shows data on radiation doses when moving along the found optimal route with complete and partial information on radiation parameters at the points for room “B”, when visiting 14 specified points, considering bypassing possible obstacles [27].

Calculations were performed using four radial basis functions. In the first case, all reference values presented in the radiation-monitoring protocols were used to build the radiation map of the room and the optimal route. In the second case, 20% of the reference values were randomly thrown out and then the radiation map of the room and the optimal route were built. Figure 6 shows the results of the graphical construction of the optimal route of the dosimetrist movement with a visit to the specified points in room B using the ThinPlate radial basis function ($\phi =r^2\log r$) [27]. Figure 6a shows the route for the case when all reference values from the radiation monitoring data were used; Figure 6b shows the route when using 80% of the reference values at the reference points.

In 2021, at the nuclear power plant, instrumental studies were carried to verify the program for determining the optimal route when measuring radiation parameters to minimize the dose loads of the dosimetrist. Measurements were carried out in the space of equipment room No. 2 (Figure 7,

Table 2. Values of the ambient radiation dose equivalent rate at the points of equipment room No. 2.

Point	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
AEDR, mSv/h	0.066	0.09	0.4	0.5	0.1	0.11	0.16	0.6	1.1	2.0	2.1	1.2	0.7	1.0	0.9
Тoчка	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
AEDR, mSv/h	1.1	1.7	0.4	0.3	0.02	0.3	0.019	0.03	0.2	0.1	0.08	0.09	0.16	0.009	0.0033

) when visiting 30 specified points in accordance with the cartogram of the rooms. The points fully comply with the real regulations for measuring the power of the ambient equivalent dose rate (AEDR) and the route of movement. The dose during measurements along the route of equipment room No. 2 was 0.080 mSv. An X-ray and gamma ray dosimeter DKS-AT1121 was used.

In accordance with the developed calculation program, the values of the total radiation dose during the routine route and the determination of the optimal route of visiting the specified points of the premises under consideration were determined. Dose reduction when optimizing the routes of movement of the dosimetrist, taking into account the avoidance of obstacles, was 22.01% for equipment room No. 2. Deviations of the calculated values of the total radiation dose from the measured values were 4.1% for equipment room No. 2.

Computational experiments on building a radiation map of the space and determining the optimal route using interpolation methods and comparing the results of using various RBF methods were carried out for the rooms of equipment room No. 2, including points No. 8–17 (see Figure 8,

Table 3. Using interpolation methods.

Point/ Func	Linear		Cubic		Quintic		ThinPlate		Measured Value
	Deviation from the Real Value, mSv/h	Deviation from the Real Value in %	Deviation from the Real Value, mSv/h	Deviation from the Real Value in %	Deviation from the Real Value, mSv/h	Deviation from the Real Value in %	Deviation from the Real Value, mSv/h	Deviation from the Real Value in %
8	0.0267944	4.47%	0.00346935	0.58%	−0.0117228	1.95%	0.0143474	2.39%	0.6
9	−0.00983797	0.89%	0.0134573	1.22%	0.0363129	3.30%	0.00145992	0.13%	1.1
10	−0.106373	5.32%	−0.10339	5.17%	−0.0941109	4.71%	−0.106697	5.33%	2
11	−0.114607	5.46%	−0.0818156	3.90%	−0.0698758	3.33%	−0.0958796	4.57%	2.1
12	0.0281054	2.34%	0.0285196	2.38%	0.0223563	1.86%	0.0332057	2.77%	1.2
13	0.0389322	5.56%	0.00677445	0.97%	−0.00405566	0.58%	0.01932	2.76%	0.7
14	−0.014384	1.44%	−0.0635085	6.35%	−0.00003837	0.00%	−0.0453361	4.53%	1
15	0.0239413	2.66%	−0.0290123	3.22%	−0.0778416	8.65%	−0.00127017	0.14%	0.9
16	0.040386	3.67%	0.0540454	4.91%	0.0613541	5.58%	0.0495584	4.51%	1.1
17	−0.0711521	4.19%	−0.162506	9.56%	−0.1698	9.99%	−0.100038	5.88%	1.7
	Average value over all points:	3.60%	Average value over all points:	3.83%	Average value over all points:	3.99%	Average value over all points:	3.30%

).

Based on the developed algorithm, it is planned to implement a software that automates the process of forming an optimal route for minimizing the radiation doses of dosimetrists. The initial data for the software are the data of non-regulatory measurements of the NPP radiation situation.

5. Conclusions

The developed algorithm for solving the “dosimetrist problem”, which involves visiting the specified points of the space for measurements, allows us to find the optimal route of movement, taking into account the avoidance of obstacles. The results of a computational model experiment performed on the “Uran” supercomputer of the Ural Branch of the Russian Academy of Sciences demonstrate a significant reduction in the received radiation dose when using the built optimal route for virtual performers in heterogeneous radiation fields. Tests of the developed program, carried out under the operating conditions of the nuclear power plant, showed a reduction in the radiation dose (by more than 20%) when moving along the found optimal route compared to the routine route.

Interpolation of values of radiation parameters (for example, radiation dose rate) based on known values when building a radiation map of the space using radial basis functions allows us to solve routing problems with the necessary accuracy without additional dose costs for determining radiation parameters in the grid nodes of the map.