Abstract
Massive hydraulic fracturing (MHF) is currently the most effective technology used to create fracture networks with sufficient conductivity and maximize the stimulated reservoir volume (SRV) in tight oil and gas reservoirs. The newly initiated fracture networks during MHF usually exhibit complex fracture morphology and contain intersected fractures and fracture branches. The conductivity of these fractures plays a pivotal role in determining long-term productivity. Due to the complex geometry, it is difficult to accurately evaluate intersected fracture conductivity through traditional conductivity measurement methods and devices which are designed for a single primary fracture. Unlike previous studies where fracture conductivity was measured using two rock slabs under single-direction (vertical) loading, we establish a novel conductivity measurement apparatus that can mimic different fracture intersection scenarios under both vertical and transverse loading to facilitate the evaluation of intersected fracture conductivity. Based on this apparatus, a standard conductivity measurement framework for intersected fractures under biaxial compaction conditions is also proposed, and stable and reliable conductivity testing data are obtained. Sensitivity analyses are performed to find out the controlling factors of intersected fracture conductivity and the corresponding conductivity evolution law. Results indicate that the overall intersected fracture conductivity of intersected fractures can be divided into three stages, with closure pressure increasing, videlicet, the conductivity rapid reduction stage at low closure pressure, the conductivity slow reduction stage, and the conductivity stabilization stage. Higher proppant concentration results in higher conductivity. However, the conductivity differences among cases with different proppant concentration are relatively small at high closure pressure (conductivity stabilization stage). The more complex the fracture intersecting pattern is, the higher the conductivity would be. The experimental results can provide guidance for the design of proppant placement procedure for intersected fractures.
1. Introduction
With the rapid development of conventional reservoirs and increased demand of oil and gas resources, tight reservoirs, such as shale reservoirs, now have huge potential for world future oil and gas supply [1]. However, due to poor permeability, primary production from these reservoirs is extremely low [1,2,3,4,5]. Multistaged massive hydraulic fracturing (MMHF) is frequently used to extend fracture networks, maximize reservoir contact surface areas, and achieve economic rates in these reservoirs [6,7,8]. After MMHF, multiple intersected fractures within the fracture networks are observed, and they are a combination of tensile fractures, sheared weak discontinuities, natural fractures, and pressure solution interfaces [9,10]. Fracture conductivity is a crucial parameter that affects postfracturing productivity [11]. Laboratory tests are treated as direct, controllable, and repeatable methods to investigate fracture conductivity [12]. Thus, over the years, a lot of experimental work has been performed to directly measure fracture conductivity at different closure pressures.
Early in 1973, Cooke [13] performed fracture conductivity measurement procedures under stress using multilayer brittle proppants. The impacts of fluid type, temperature, and non-Darcy flow were investigated. In 1985, Cutler et al. [14] completed laboratory fracture conductivity studies to compare the performance of various proppants under intermediate- and high-stress conditions. Their results show that many oxide ceramics provide acceptable conductivity even the closure stress reaches 96.5 MPa. Resin-coated proppants offer smaller conductivity compared with uncoated oxide ones. Then, Penny [15] outlined equipment and procedures that can obtain repeatable long-term fracture conductivity at different temperatures and closures. The conductivity impairment caused by crosslinked fracturing fluids and fluid loss additives were studied. It was found that fracturing fluids reduce fracture conductivity due to the formation of the residual filter cake. The used additives generate 5% additional conductivity loss. Much and Penny [16] performed conductivity measurement experiments using two classes of proppants to reveal the effects of time, stress, proppant embedment, and gel damage on fracture conductivity. They concluded that traditional conductivity–stress evaluation would overestimate fracture conductivity under in situ conditions. The inclusion of time and temperature effects makes the measurement results more meaningful. In the same year, Parker and McDaniel [17] developed laboratory conductivity testing methods to mimic in situ conditions. Their results indicate that achieving high proppant concentration can reduce the impairment caused by gel filter cakes. Later on, a laboratory investigation was conducted by Bilden et al. [18] to analyze the effects of shut-in periods on fracture conductivity. They found that, under their experimental conditions, 7-day shut-in periods did not show a detrimental effect on conductivity. In 2001, Fredd et al. [19] conducted a series of fracture conductivity measurement experiments to understand how fracture properties affect conductivity. The impacts of fracture displacement, asperity, proppant concentration and strength, and rock mechanical properties on fracture conductivity were analyzed. They found that under asperity-dominated conditions, the conductivity variation is difficult to predict, while high-strength proppants with low concentration offer proppant-dominated conductivity and overcome the uncertainty of conductivity caused by formation properties. Weaver et al. [20] developed a method to examine the impact of geochemical reactions on proppant-pack conductivity. They used radial-conductivity cells and found that proppant dissolution and remineralization result in the proppant pack permeability reduction. Kurz et al. [21] measured the conductivity provided by various proppants at reservoir temperatures and pressures utilizing reservoir rock cores. They found that some fluids can influence both proppant and rock strength. The overall conductivity is controlled by proppant and rock strength and formation spalling and embedment.
More recently, Zhang et al. [22] tested the unpropped induced fracture, unpropped natural fracture, and propped fracture conductivity under realistic conditions for the Barnett shale. Their results indicate that unpropped displaced fracture conductivity is one order of magnitude higher than that of unpropped aligned fractures, while larger proppant size and higher proppant concentration enhance propped fracture conductivity. To measure complex fracture network conductivity, Wen et al. [23] established a new conductivity measurement device and used marble slabs to mimic nine fracture intersection scenarios for typical fracture networks. However, lateral compaction cannot be included in that device, which may produce inaccurate results compared with those from in situ conditions. Zhan et al. [24] developed core-scale complex fracture conductivity measurement equipment and simply tested unpropped fracture conductivity. Combining 3D scanning and 3D engraving technology, Chen et al. [25] proposed a new method to reproduce samples with identical fracture surface morphology and similar mechanical properties and used them to investigate the conductivity of fractures with rough surfaces under different conditions. Li et al. [26] experimentally studied the role of proppant size, concentration, effective stress, water soaking, and rock type on nonmonotonic fracture conductivity evolution. Based on the background of popular temporary plugging and diversion fracturing technology, Zhang et al. [27] placed a mixture of proppants and degradable particle diverter in the fracture to evaluate fracture conductivity and find the optimal combination of the two types of particles. Fan et al. [28] used sand and ceramic proppant monolayers to test how proppant embedment induces the conductivity loss in narrow fractures. From the above review, it can be seen that these studies help researchers and engineers to better understand the controlling factors of fracture conductivity. However, existing fracture conductivity measurement procedures mainly focus on the conductivity of a single fracture. The experimental apparatus they used is similar to or the same as the API standard conductivity cell, as shown in Figure 1. It can only deal with vertical compaction, although researchers may use different samples, such as a combination of two original rock slabs or a combination of multiple marble slabs [23]. The core-scale device used by Zhan et al. [24] is also a cuboid cell with a cylindrical core chamber. The laboratory work for complex fracture conductivity measurement still has some limitations. The conductivity of intersected fractures has not been comprehensively studied under conditions close to the in situ ones.
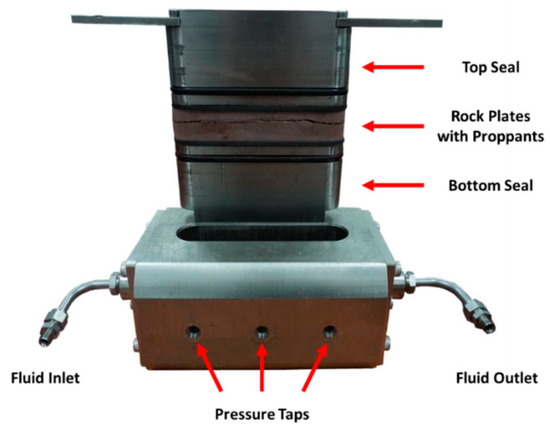
Figure 1.
A typical fracture conductivity cell [29].
This research aims at establishing a new fracture conductivity measurement system that can test intersected fracture conductivity under more realistic conditions. Based on this apparatus, we figure out a standard conductivity measurement framework for intersected fractures under biaxial compaction conditions. Dominant factors for intersected fracture conductivity evolution are documented according to our experimental results. The findings of this work are beneficial for MHF optimization design.
2. Experimental Apparatus
The newly developed conductivity measurement system consists of four sub-systems, namely the loading system, the fluid injection system, the data acquisition system, and the conductivity cell. Detailed components of the conductivity measurement system are shown in Figure 2. The conductivity cell is designed and improved based on the API cell of Cooke [13]. Unlike classical conductivity cells where the hydraulic load is added parallel to a certain direction (vertical direction), this conductivity cell involves both vertical and lateral loading so that biaxial compaction can be realized. The new cell uses the same hydraulic device as the API standard conductivity cell in the vertical direction. The difference is that the lateral stress-loading module is added to the loading system. The system pushes the side piston to achieve lateral stress loading by injecting flow pressure into the side pressure piston cylinder. This is closer to the actual in situ conditions for intersected fractures in the reservoir. Figure 3 and Figure 4 demonstrate the components of the conductivity cell and the intersected fracture patterns of the intersected fracture unit that will be placed in the conductivity cell. The length, width, and height of the inner chamber are 178 mm, 38 mm, and 81 mm, respectively. Note that in the length direction, there is a length of 38 mm occupied by the two semicircular ends of the chamber, so the effective length for the intersected fracture unit is 140 mm. The intersected fracture unit is fabricated into dimensions fit for chamber of the conductivity cell, and is 140 mm long, 34 mm wide, and 34 mm high. This unit is composed of several steel cuboid blocks representing rock blocks. Compared with rock samples, it is more flexible to create different fracture intersecting patterns if we utilize steel cuboid blocks. Since the conductivity is provided by the propped space and conductivity evolution is dominated by the proppant’s dynamic responses to external loading, the impact of adjacent cuboid block’s material on conductivity is negligible. The fracture patterns (types A, B, and C in Figure 4) used to represent different fracture intersecting scenarios are selected based on Wen et al. [23] and the typical sugar cube fracture network model. The conductivity cell’s biaxial loads that mimic closure pressure can reach up to 60 MPa with an accuracy of 0.01 MPa. The flux offered by the pump is in the range of 0 to 100 mL/min. The pressure transducer is connected to the three-way connector (Figure 2d) to collect pressure data. Different sizes of proppants, such as 30/50 mesh, 40/70 mesh, and 70/140 mesh, are used in our experiments to analyze the impact of the proppant size on intersected fracture unit conductivity. Sand-control screens are also added to the inlet and outlet of the intersected fracture unit (Figure 3d) to avoid crushed proppant flowing out.
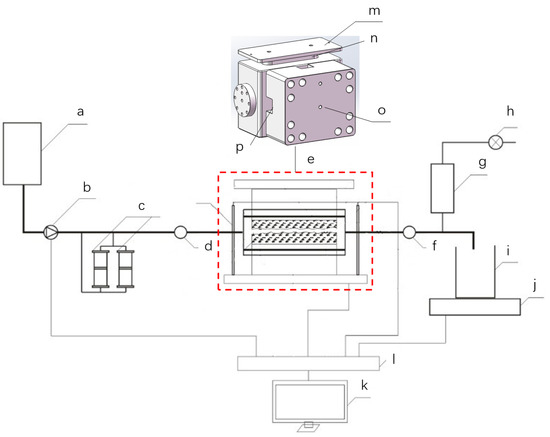
Figure 2.
Schematic of the experimental apparatus: (a) upstream fluid reservoir, (b) pump, (c) pre-treated fracturing fluid reservoir, (d) pressure transducer, (e) conductivity cell, (f) back pressure regulator, (g) vacuum buffer container, (h) vacuum pump, (i) downstream fluid collection container, (j) precision lab scale, (k) computer, (l) data acquisition panel, (m) hydraulic load frame, (n) vertical-direction piston, (o) lateral load frame, and (p) side piston.
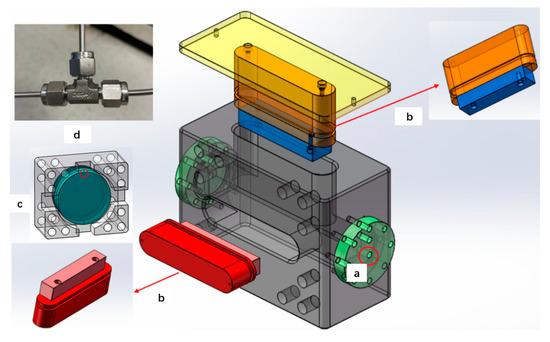
Figure 3.
Schematic of the new conductivity cell: (a) sealing assembly, (b) hydraulic load frame and side piston, (c) lateral load frame and displacement measurement device, and (d) three-way connector.
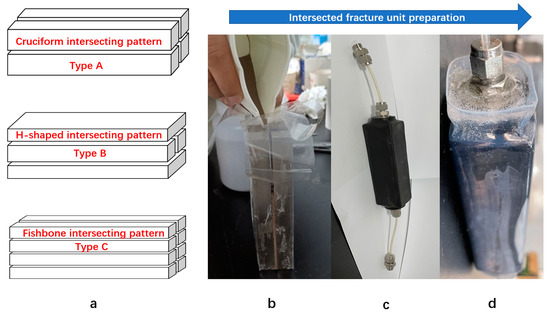
Figure 4.
Intersected fracture patterns and intersected fracture units: (a) three intersected fracture patterns used in the experiments, (b) proppant placement into the intersected fracture unit, (c) intersected fracture unit sealed by a black heat-shrink sleeve, and (d) intersected fracture unit sealed by another transparent heat-shrink sleeve outside the black sleeve.
3. Experimental Procedure
This research focuses on testing intersected fracture conductivity, investigating the conductivity’s controlling factors, and evaluating the conductivity evolution law. The conductivity was measured at varying closure pressure (from 3.45 MPa to 55.2 MPa) with different proppant concentration (from 3 kg/m2 to 10 kg/m2). Detailed description of the experimental procedure is as follows (see the flow chart in Figure 5).
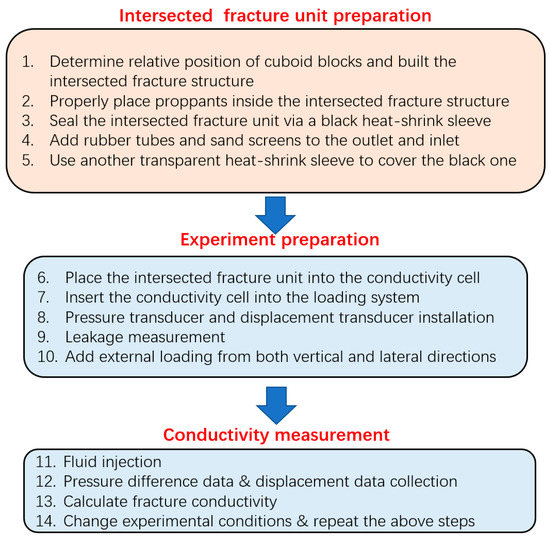
Figure 5.
Flow chart for the complete conductivity measurement process.
3.1. Intersected Fracture Unit Preparation
The intersected fracture unit needs to be prepared first before performing the conductivity measurement experiment. To mimic different fracture intersecting patterns, different combinations of cuboid blocks are used, as shown in Figure 4a. The relative position of the blocks is fixed by utilizing transparent plastic sheets (see Figure 4b), forming the intersected structure. Then, proppants are placed into the void space (fractures) of this unit through the inlet, while the outlet of this unit is sealed by the plastic sheets. When loading proppant, firstly the sample is fixed, a thin transparent plastic sheet is used to bond and fix the steel block to keep its relative position, and a physical model of intersected fractures is constructed. Then, the fixed steel block assembly is placed upright, the bottom of the sample is sealed with the same thin transparent plastic sheet, and the seam is filled with proppant by pouring. After the completion of proppant filling, a pressure-resistant heat shrinkable pipe is sheathed outside the proppant and steel block assembly and heated with a hot air gun to make it shrink and compact. After the fluid inlet and outlet are installed by bonding, sealant shall be poured on both sides of the sample inlet and outlet. For each intersecting pattern, we can calculate the total inner surface area of the fracture system. The corresponding proppant concentration can be calculated by , where and are total proppant mass (kg) and total inner fracture surface area (m2), respectively. After proppant placement, the intersected fracture unit is sealed by a black heat-shrink sleeve due to its reliable sealing quality. Rubber tubes are connected to the inlet and outlet with sand screens. The two sand screens are added to avoid crushed proppant flow-out. Another transparent heat-shrink sleeve is used to cover the black one to protect the test unit under loading conditions.
3.2. Conductivity Measurement
After intersected fracture unit preparation, the test unit is placed into the center of the conductivity cell. Then, the conductivity cell is inserted into the loading system to perform conductivity measurement. Pressure transducers are applied at the inlet and outlet through three-way connectors to collect the corresponding pressure data. Fluid (water) leakage measurement is also conducted to check the sealing quality of the whole system. Before adding the external biaxial loading, two displacement transducers are installed to record fracture aperture variation under vertical and lateral compaction. To mimic the in situ stress condition, the vertical loading is controlled by a computer, while the lateral loading is realized by the manual loading process. When the external loadings in the two directions become stable, fluids are injected through the pump, and the displacement and pressure transducers offer fracture aperture evolution data and the pressure difference between the inlet and the outlet. Finally, the above steps are repeated under different closure pressure, proppant concentration, and pump rate conditions to investigate the corresponding conductivity. In the experiment, the stability of fluid flow is achieved when the inlet and outlet pressure become stable. Thus, we evaluate the stability of the fluid through inlet and outlet pressure data. As for the time period required to achieve stabilization, it changes under different situations and varies from several minute to more than thirty minutes. For example, when the liquid is injected, the separated gas phases (bubbles) within the proppant pack affects the time required to realize flow stabilization. After collecting the required data, one can calculate fracture conductivity. According to Darcy’s law () [30] and the definition of fracture conductivity (fracture width multiplied by fracture permeability) [13], the conductivity can be calculated from the pressure difference and flux data:
where is the permeability, μm2; is the flux, cm3/s; is the cross-sectional area of the intersected fracture, cm2; is the pressure difference between the two pressure transducers, KPa; is the fluid viscosity, mPa·s; and is the length of the intersected fracture as the pressure drop outside the fracture can be ignored. Here, is a dimensionless coefficient used to convert the unit and is also related to the intersecting patterns. By using Equation (1), the conductivity can be obtained. Figure 6 shows the relationship between pressure difference across the equipment and the closure pressure. The flux is stable and is around 10 mL/min. As can be seen from Figure 6, the pressure difference increases dramatically as the closure pressure rises, indicating that the conductivity drops with the increase in closure pressure. Note that we did not plot the change in pressure difference with time under a certain closure pressure level. Time-dependent conductivity evolution is beyond the scope of this paper.
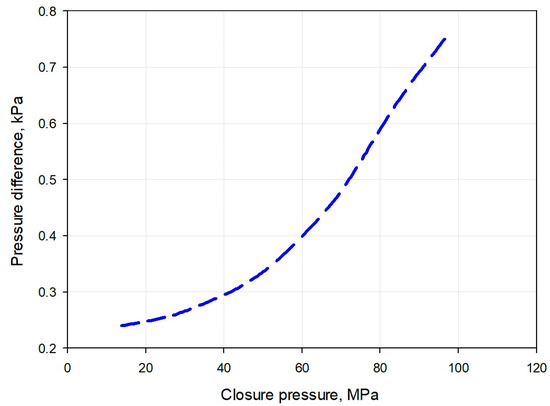
Figure 6.
Pressure difference variation with the increase in closure pressure.
4. Results and Discussion
The primary objective of this paper is to use the new apparatus to investigate intersected fracture conductivity evolution and its controlling factors under more realistic biaxial compaction conditions. To ensure the reliability of this apparatus, we compare the single-fracture conductivity measurement data obtained by using our equipment and FCES-100 (long-term fracture conductivity evaluation system) [31]. Here, the test unit only involves a single fracture. Note that the lateral loading is not applied here in order to perform the comparison under the sane condition. This is because FCES-100 cannot deal with lateral compaction. Figure 7 shows the comparison results. With the increase in closure pressure, the single-fracture conductivity drops continuously. In general, the measured conductivity values from our apparatus and FCES-100 are close to each other. When the closure pressure is larger than 5 MPa, the conductivity from our apparatus becomes smaller than that from FCES-100. The above results confirm the reliability of this apparatus. After checking new equipment’s reliability, the impacts of proppant concentration, proppant size, and intersected fracture patterns are analyzed.
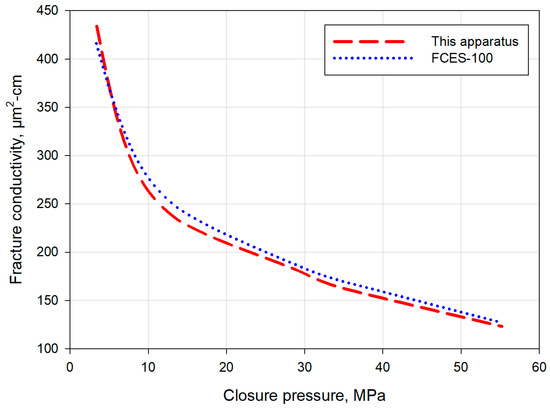
Figure 7.
Comparison between conductivity data collected by this apparatus and FCES-100 under identical conditions.
4.1. Conductivity of Cruciform Intersecting Pattern Fractures
The cruciform intersecting pattern (type A in Figure 4a) is relatively simple and involves two orthogonally intersected fracture planes. Figure 8 shows the conductivity variation with different proppant concentration using 40/70 mesh proppants. The overall conductivity evolution behavior can be divided three stages regardless of proppant concentration. In the first stage, the closure pressure is relatively low; conductivity drops dramatically with closure pressure’s increment. In the second stage, the conductivity decline rate becomes smaller at higher closure pressure. In the final stage, conductivity turns relatively stable, and only marginal conductivity variation can be observed with the increase in closure pressure. As expected, the larger the proppant concentration is, the higher the conductivity would be. However, with high proppant concentration, an additional increment in this concentration will not lead to significant conductivity enhancement. For example, when the concentration changes from 7 kg/m2 to 10 kg/m2, conductivity’s enhancement can even be lower than that obtained by increasing proppant concentration from 4 kg/m2 to 5 kg/m2. The conductivity enhancement caused by rising proppant concentration from 4 kg/m2 to 5 kg/m2 is close to that obtained by changing proppant concentration from 3 kg/m2 to 4 kg/m2. When the closure pressure rises from 3.45 MPa to 55.2 MPa, the conductivity is reduced by 56.69%, 60.63%, 62.09%, 68.41%, and 68.71% with proppant concentration increasing. Larger proppant concentration exhibits a heavier conductivity decreasing rate. The initial conductivity values are quite different, but the conductivity values at high closure pressure are close to each other. Figure 9 shows the impact of the proppant size on conductivity evolution. Here, the proppant concentration is fixed at 5 kg/m2. It can be seen that larger proppants offer higher conductivity, which is similar to the conductivity of a single fracture [32]. The conductivity reduction rate of larger proppants is also higher, possibly due to proppant pack deformation at low closure pressure and proppant crush at high closure pressure.
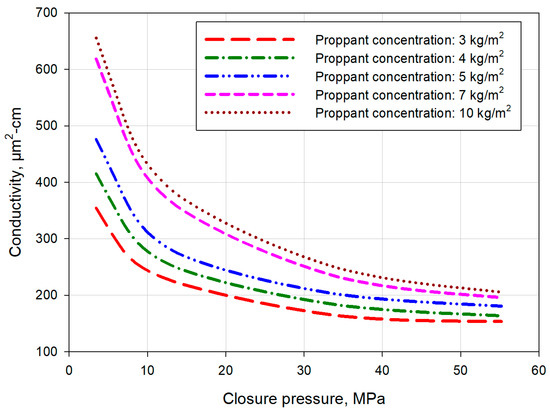
Figure 8.
Conductivity evolution of cruciform intersecting pattern fractures with different proppant concentrations.
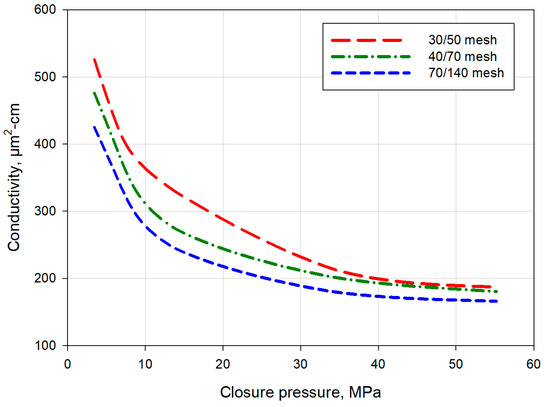
Figure 9.
Conductivity evolution of cruciform intersecting pattern fractures with different sizes of proppants.
4.2. Conductivity of H-Shaped Intersecting Pattern Fractures
As for H-shaped intersecting pattern fractures, the conductivity evolution behavior is similar to that of cruciform intersecting pattern fractures. As shown in Figure 10, when proppant concentration rises from 3 kg/m2 to 4 kg/m2; the conductivity increment is smaller than that obtained by changing proppant concentration from 4 kg/m2 to 5 kg/m2. However, a further increase in proppant concentration from 7 kg/m2 to 10 kg/m2 does not result in a more significant conductivity enhancement. Therefore, there is an optimal proppant concentration value that can provide sufficient conductivity and is also economical. Figure 11 illustrates the impact of the proppant size on the conductivity of H-shaped intersecting pattern fractures. Once again, larger proppants generate higher conductivity. For this case, the conductivity curves are close to each other, especially at high pressure, and the evolution laws are also similar to each other.
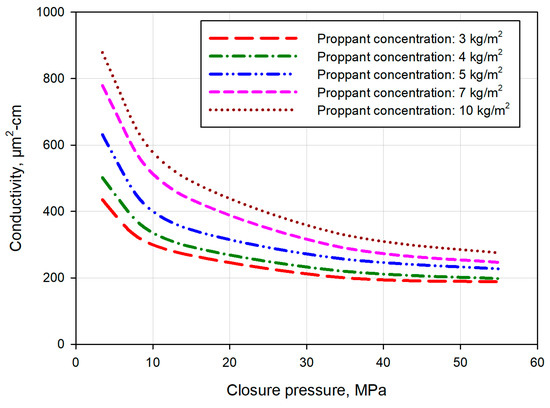
Figure 10.
Conductivity evolution of H-shaped intersecting pattern fractures with different proppant concentrations.
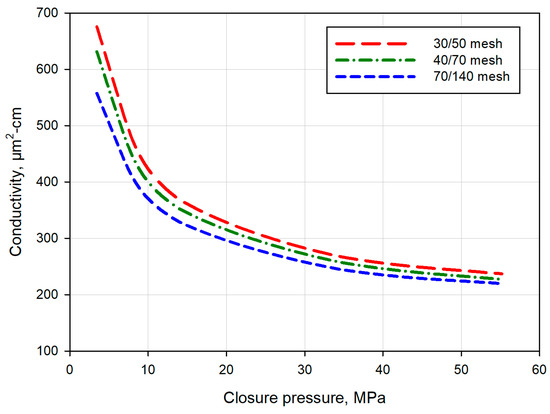
Figure 11.
Conductivity evolution of H-shaped intersecting pattern fractures with different sizes of proppants.
4.3. Conductivity of Fishbone Intersecting Pattern Fractures
This case involves the most complex fracture intersecting structure. Figure 12 and Figure 13 show conductivity evolution of fishbone intersecting pattern fractures with different proppant concentrations and proppant sizes, respectively. The overall conductivity values are higher than those of the previous fracture patterns and increase as proppant concentration becomes larger. With different proppant concentrations, the conductivity differences are more noticeable at low closure pressure and turn smaller at the stabilization stage. In terms of the proppant size, the shapes of the curves are similar to each other. With the increase in proppant size, the curves move upward.
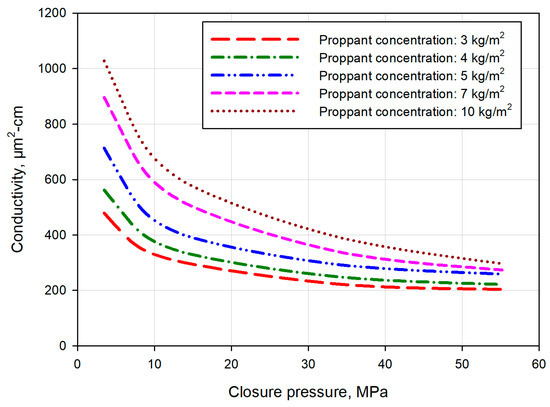
Figure 12.
Conductivity evolution of fishbone intersecting pattern fractures with different proppant concentrations.
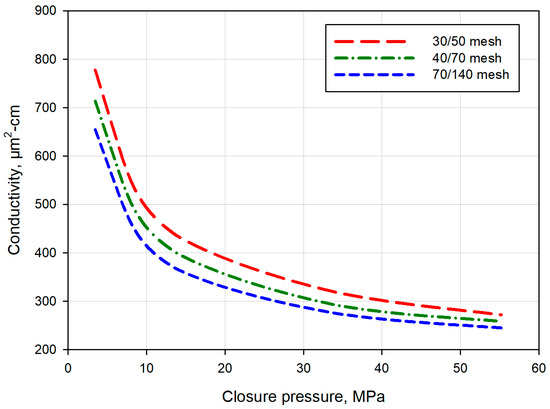
Figure 13.
Conductivity evolution of fishbone intersecting pattern fractures with different sizes of proppants.
4.4. Impact of Fracture Intersecting Patterns
In this section, we compare conductivity evolution behavior of three cases with different fracture intersecting patterns, namely the cruciform intersecting pattern, the H-shaped intersecting pattern, and the fishbone intersecting pattern. The proppant size and concentration for all the three cases are 40/70 mesh and 5 kg/m2, respectively. As can be seen from Figure 14, the more complex the fracture intersecting pattern is, the higher the conductivity would be. Even at high closure pressure, the differences in the conductivity of the three cases are still relatively large. Their conductivity values at 55.2 MPa closure pressure are 180.41 μm2-cm, 226.88 μm2-cm, and 258.38 μm2-cm, respectively. This indicates that intersected fractures with complex structures can still provide certain conductivity at high closure pressure.
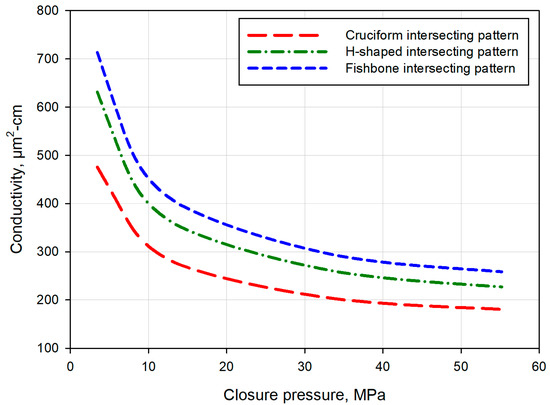
Figure 14.
Comparison evolution of fractures with different intersecting patterns but identical proppants (40/70 mesh) and proppant concentrations (5 kg/m2).
5. Conclusions
This study aims at establishing a new experimental apparatus to evaluate the conductivity evolution of different types of intersected fractures under more realistic biaxial compaction conditions. The novelty of the developed equipment is that both vertical and lateral loadings can be added to the intersected fracture unit through the special structure of the conductivity cell. Furthermore, the design of the fracture intersecting pattern is also flexible. Various fracture intersecting patterns can be constructed for conductivity measurement by using different combinations of cuboid blocks. Particularly, for this research, three types of fracture intersecting patterns are analyzed, including cruciform intersecting pattern fractures, H-shaped intersecting pattern fractures, and fishbone intersecting pattern fractures. Impacts of both proppant concentration and proppant size on fracture conductivity evolution with closure pressure increasing are investigated. Based on the analysis results, the following conclusions can be obtained.
For all the three types of fractures, the overall conductivity evolution upon closure pressure’s increase shows three stages, including the conductivity rapid reduction stage at low closure pressure, the conductivity slow reduction stage, and the conductivity stabilization stage.
As for proppant size, larger proppants provide higher intersected fracture conductivity at the same proppant concentrations and closure pressure conditions. In terms of proppant concentration, higher proppant concentration results in higher conductivity. However, the conductivity differences among cases with different proppant concentrations are relatively small at high closure pressure (conductivity stabilization stage).
Under the same closure pressure, proppant size, and proppant concentration conditions, the conductivity turns larger with the increase in fracture complexity. The conductivity differences among cases with different fracture complexity are still noticeable even at high closure pressure.
From the above understanding, to obtain sufficient conductivity for production at high closure pressure, low-concentration and relatively large proppants should be pumped into complex intersected fractures.
Author Contributions
Conceptualization, C.L. and J.Z.; methodology, C.L., H.W. and Q.Z.; validation, H.W., Y.Y. and J.Z.; formal analysis, C.C.; investigation, J.Z., H.W. and C.C.; resources, H.W., C.C. and Y.Y.; data curation, J.Z. and Q.Z.; writing—original draft preparation, J.Z. and C.L.; writing—review and editing, C.L. and H.W.; supervision, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China under a grant number 52022087 and the Basic Research Program on Deep Petroleum Resource Accumulation and Key Engineering Technologies under a grant number U19B6003.
Data Availability Statement
Data available on request from the authors.
Acknowledgments
The authors would like to give special recognition to the State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation at Southwest Petroleum University, for providing equipment and relevant experimental materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khlaifat, A.; Qutob, H.; Barakat, N. Tight gas sands development is critical to future world energy resources. In Proceedings of the SPE Middle East Unconventional Gas Conference and Exhibition, Muscat, Oman, 31 January–2 February 2011. [Google Scholar]
- Zeng, J.; Liu, J.; Li, W.; Leong, Y.K.; Elsworth, D.; Guo, J. Evolution of shale permeability under the influence of gas diffusion from the fracture wall into the matrix. Energy Fuels 2020, 34, 4393–4406. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, J.; Guo, J. Characterization of gas transport in shale: A multi-mechanism permeability modeling approach. Chem. Eng. J. 2022, 438, 135604. [Google Scholar] [CrossRef]
- Gao, Q.; Han, S.; Cheng, Y.; Li, Y.; Yan, C.; Han, Z. Apparent permeability model for gas transport through micropores and microfractures in shale reservoirs. Fuel 2021, 285, 119086. [Google Scholar] [CrossRef]
- Gao, Q.; Han, S.; Cheng, Y.; Shi, X.; Yan, C.; Han, Z. Flow-coupled-geomechanical modelling of CO2 transport in depleted shale from a microscopic perspective. Energy 2022, 257, 124727. [Google Scholar] [CrossRef]
- Du, C.M.; Zhang, X.; Zhan, L.; Gu, H.; Hay, B.; Tushingham, K.; Ma, Y.Z. Modeling hydraulic fracturing induced fracture networks in shale gas reservoirs as a dual porosity system. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010. [Google Scholar]
- Li, W.; Liu, J.; Zeng, J.; Leong, Y.K.; Elsworth, D.; Tian, J.; Li, L. A fully coupled multidomain and multiphysics model for evaluation of shale gas extraction. Fuel 2020, 278, 118214. [Google Scholar] [CrossRef]
- Gao, Q.; Cheng, Y.; Han, S.; Yan, C.; Jiang, L. Numerical modeling of hydraulic fracture propagation behaviors influenced by pre-existing injection and production wells. J. Pet. Sci. Eng. 2019, 172, 976–987. [Google Scholar] [CrossRef]
- Frash, L.P.; Hampton, J.; Gutierrez, M.; Tutuncu, A.; Carey, J.W.; Hood, J.; Mokhtari, M.; Huang, H.; Mattson, E. Patterns in complex hydraulic fractures observed by true-triaxial experiments and implications for proppant placement and stimulated reservoir volumes. J. Pet. Explor. Prod. Technol. 2019, 9, 2781–2792. [Google Scholar] [CrossRef]
- McClure, M.; Horne, R. Characterizing hydraulic fracturing with a tendency-for-shear-stimulation test. SPE Reserv. Eval. Eng. 2014, 17, 233–243. [Google Scholar] [CrossRef]
- Elsarawy, A.M.; Nasr-El-Din, H.A. Propped fracture conductivity in shale reservoirs: A review of its importance and roles in fracturing fluid engineering. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 23–26 April 2018. [Google Scholar]
- Zhang, J.; Kamenov, A.; Zhu, D.; Hill, A.D. Development of new testing procedures to measure propped fracture conductivity considering water damage in clay-rich shale reservoirs: An example of the Barnett Shale. J. Pet. Sci. Eng. 2015, 135, 352–359. [Google Scholar] [CrossRef]
- Cooke, C.E. Conductivity of fracture proppants in multiple layers. J. Pet. Technol. 1973, 25, 1101–1107. [Google Scholar] [CrossRef]
- Cutler, R.A.; Enniss, D.O.; Jones, A.H.; Swanson, S.R. Fracture conductivity comparison of ceramic proppants. SPE J. 1985, 25, 157–170. [Google Scholar] [CrossRef]
- Penny, G.S. An evaluation of the effects of environmental conditions and fracturing fluids upon the long-term conductivity of proppants. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 27–30 September 1987. [Google Scholar]
- Much, M.G.; Penny, G.S. Long-term performance of proppants under simulated reservoir conditions. In Proceedings of the SPE/DOE Joint Symposium on Low Permeability Reservoirs, Denver, CO, USA, 18–19 May 1987. [Google Scholar]
- Parker, M.A.; McDaniel, B.W. Fracturing treatment design improved by conductivity measurements under in-situ conditions. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 27–30 September 1987. [Google Scholar]
- Bilden, D.M.; Fletcher, P.A.; Montgomery, C.T.; Guillory, R.J.; Allen, T.P. The effect of long-term shut-in periods on fracture conductivity. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 22–25 October 1995. [Google Scholar]
- Fredd, C.N.; McConnell, S.B.; Boney, C.L.; England, K.W. Experimental study of fracture conductivity for water-fracturing and conventional fracturing applications. SPE J. 2001, 6, 288–298. [Google Scholar] [CrossRef]
- Weaver, J.; Rickman, R.; Luo, H. Fracture-conductivity loss caused by geochemical interactions between man-made proppants and formations. SPE J. 2010, 15, 116–124. [Google Scholar] [CrossRef]
- Kurz, B.; Darren Schmidt, P.E.; Cortese, P. Investigation of improved conductivity and proppant applications in the Bakken formation. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2013. [Google Scholar]
- Zhang, J.; Kamenov, A.; Zhu, D.; Hill, A.D. Measurement of realistic fracture conductivity in the Barnett shale. J. Unconv. Oil Gas Resour. 2015, 11, 44–52. [Google Scholar] [CrossRef]
- Wen, Q.; Wang, S.; Gao, J.; Duan, X.; Wang, F.; Liu, J.; Yang, L. Research on flow conductivity experiment in complex fracture network. Pet. Geol. Recovery Effic. 2016, 23, 116–121. (In Chinese) [Google Scholar]
- Zhan, Y.; Luo, M.; Ma, Y.; Lei, M.; Fu, C. Development of the Artificial Fracture Network Tool for Standard Core Size. Res. Explor. Lab. 2019, 38, 56–59+93. (In Chinese) [Google Scholar]
- Chen, C.; Wang, S.; Lu, C.; Liu, Y.; Guo, J.; Lai, J.; Tao, L.; Wu, K.; Wen, D. Experimental study on the effectiveness of using 3D scanning and 3D engraving technology to accurately assess shale fracture conductivity. J. Pet. Sci. Eng. 2022, 208, 109493. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Q.; Teng, Y.; Fan, M.; Ripepi, N.; Yin, X.; Chen, C. Experimental investigation of non-monotonic fracture conductivity evolution in energy georeservoirs. J. Pet. Sci. Eng. 2022, 211, 110103. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, F.; Zhang, S.; Wang, J.; Wang, J.; Pournik, M. Fracture conductivity analysis on the degradable particle diverter combined with engineered proppant. In Proceedings of the 53rd US Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019. [Google Scholar]
- Fan, M.; Li, Z.; Han, Y.; Teng, Y.; Chen, C. Experimental and Numerical Investigations of the Role of Proppant Embedment on Fracture Conductivity in Narrow Fractures (includes associated Errata). SPE J. 2021, 26, 324–341. [Google Scholar] [CrossRef]
- Zhang, D.; Ma, S.; Zhang, J.; Zhu, Y.; Wang, B.; Zhu, J.; Fan, X.; Yang, H.; Liang, T. Field experiments of different fracturing designs in tight conglomerate oil reservoirs. Sci. Rep. 2022, 12, 3220. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application des Principes à Suivre et des Formules à Employer Dans les Questions de Distribution d’eau: Ouvrage Terminé par un Appendice Relatif aux Fournitures d’eau de Plusieurs Villes, au Filtrage des Eaux et à la Fabrication des Tuyaux de Fonte, de Plomb, de Tôle et de Bitume; Dalmont, V., Ed.; Saraswati Press: Belghoria, India, 1856; Volume 2. [Google Scholar]
- Wen, Q.; Zhang, S.; Wang, L.; Liu, Y.; Li, X. The effect of proppant embedment upon the long-term conductivity of fractures. J. Pet. Sci. Eng. 2007, 55, 221–227. [Google Scholar] [CrossRef]
- Zhang, J.; Kamenov, A.; Zhu, D.; Hill, A.D. Laboratory measurement of hydraulic fracture conductivities in the Barnett shale. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).