Optimal Control of a PHEV Based on Backward-Looking Model Extended with Powertrain Transient Effects
Abstract
1. Introduction
2. Powertrain Models
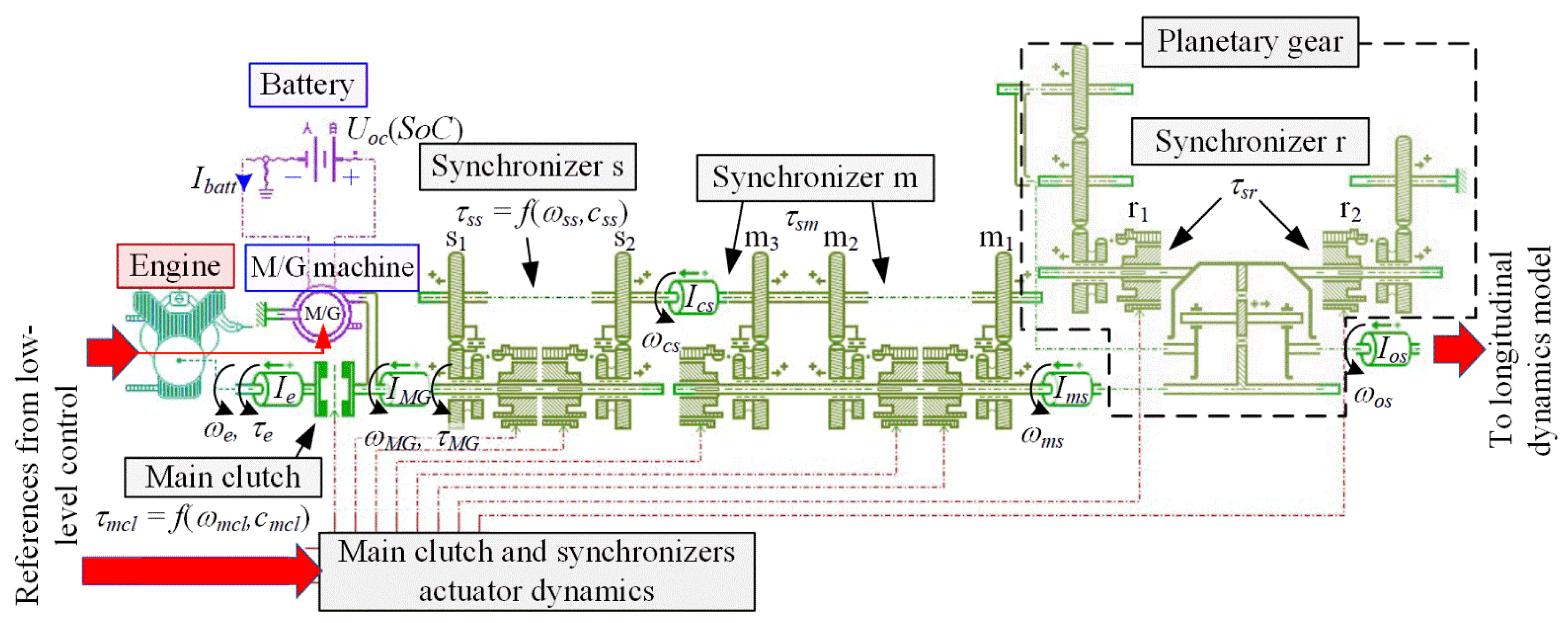
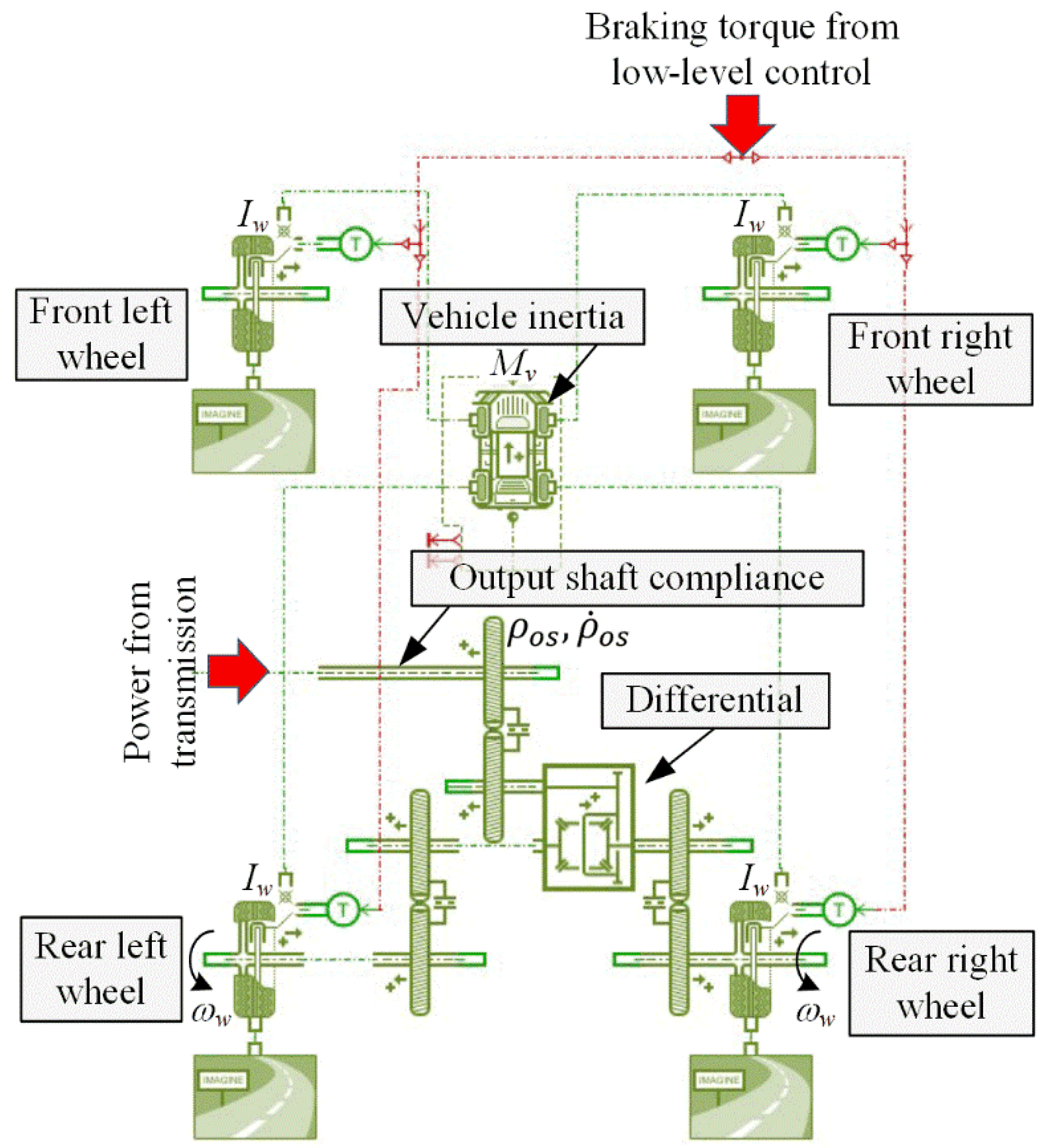
2.1. Powertrain Configuration
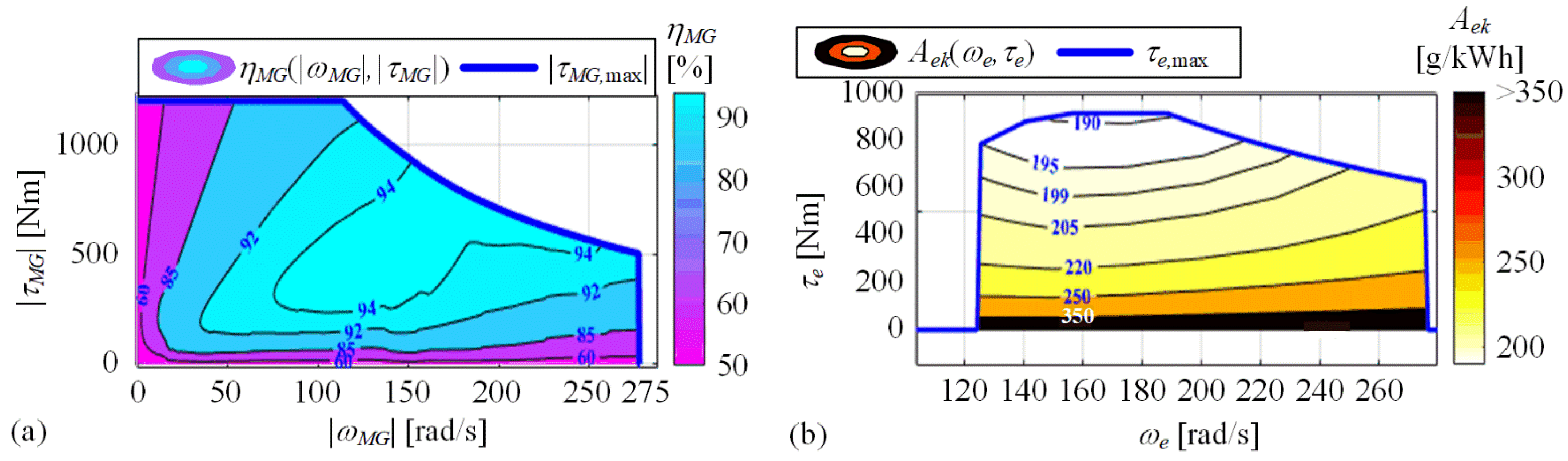
2.2. Backward-Looking Powertrain Model
2.3. Forward-Looking Powertrain Model
3. Control Strategy
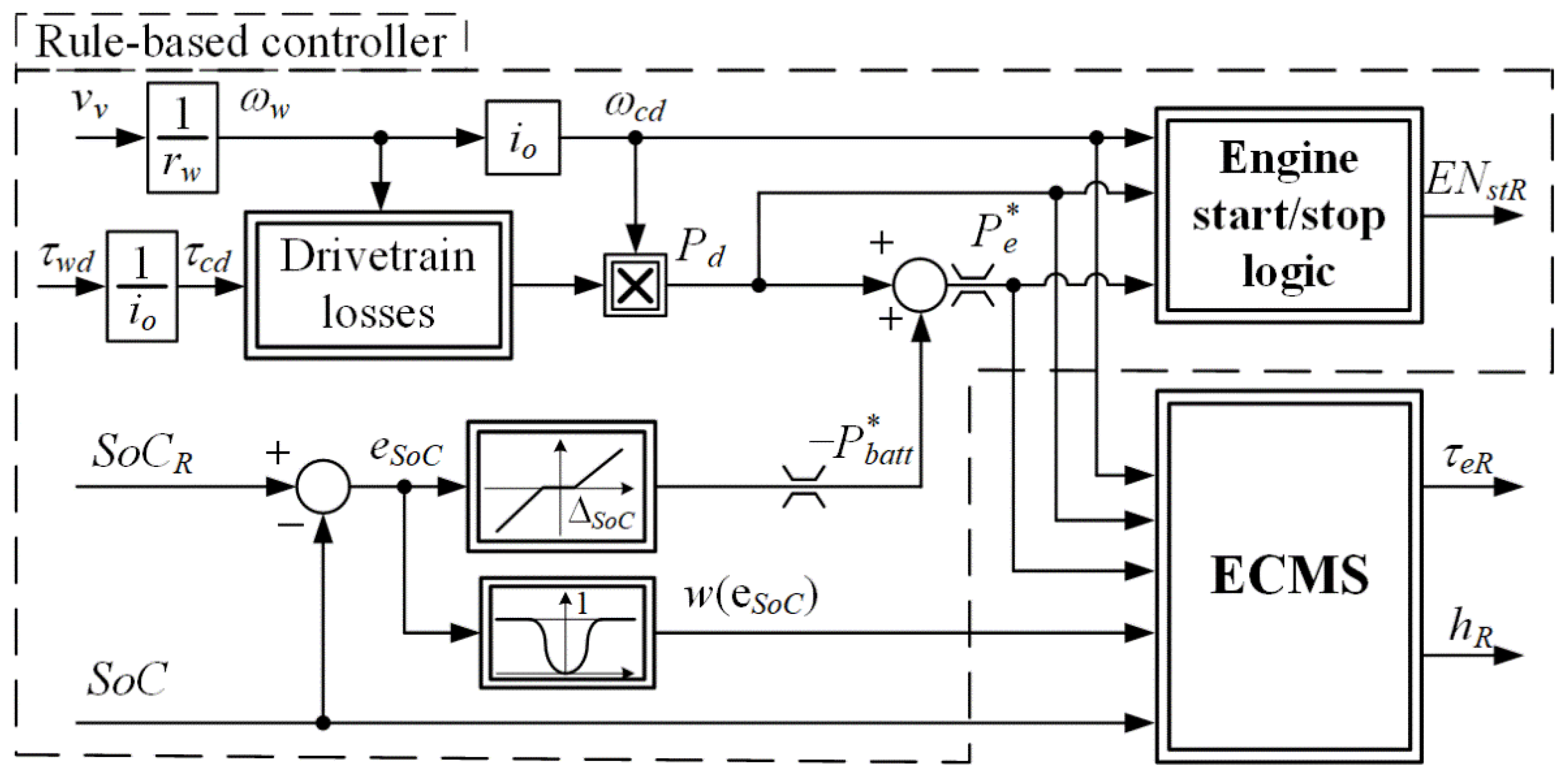
3.1. Structure of Overall Control Strategy
3.2. High-Level Control
3.3. Low-Level Control
3.3.1. Generation of M/G Machine and Mechanical Brake Torque References
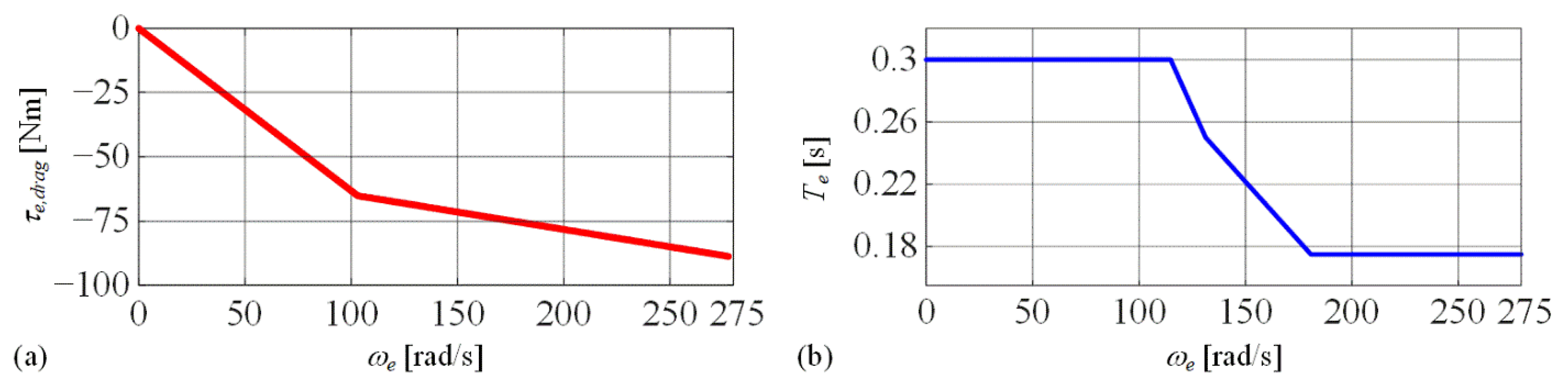
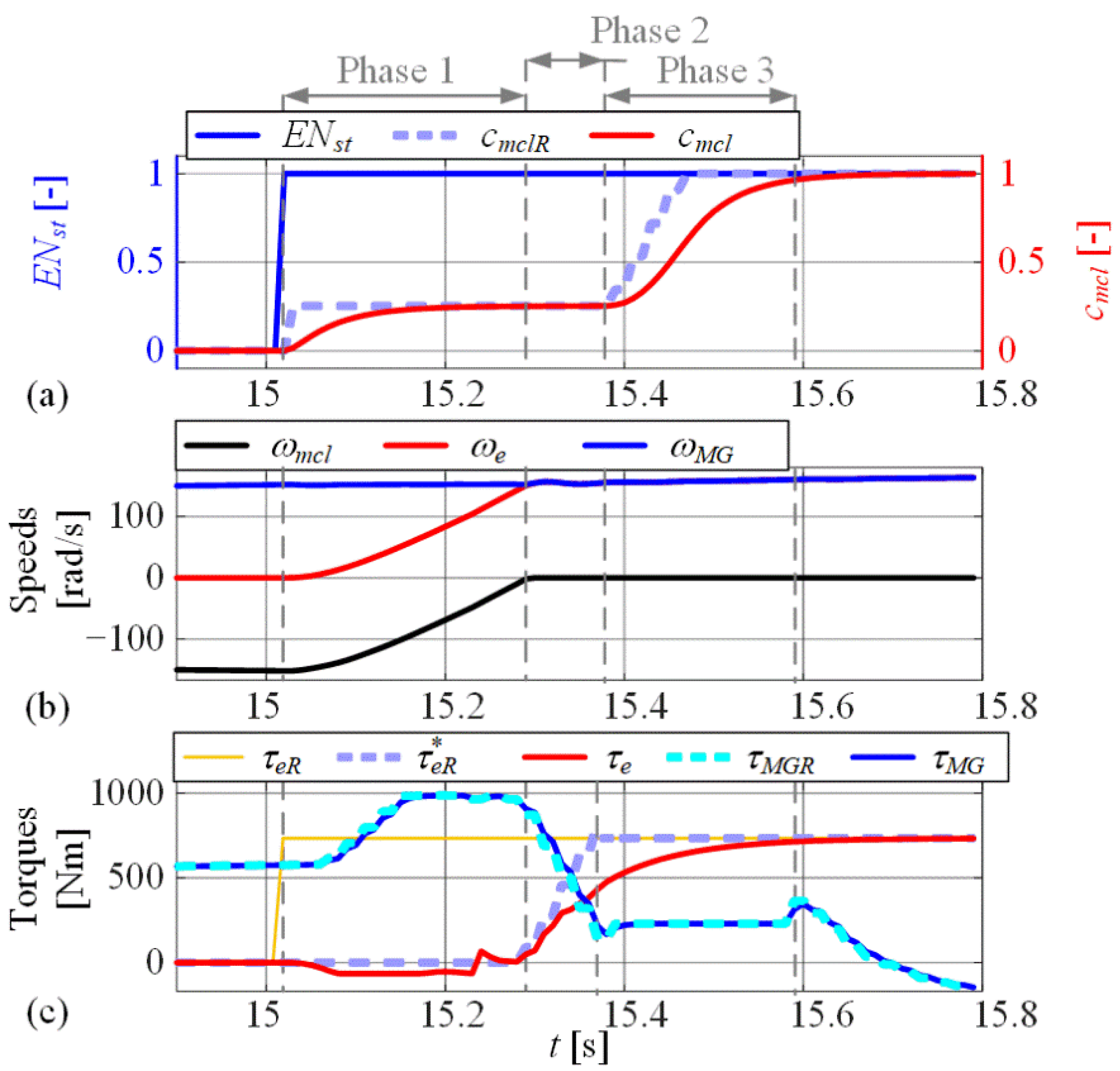
3.3.2. Low-Level Control for Engine-On Transient Mode
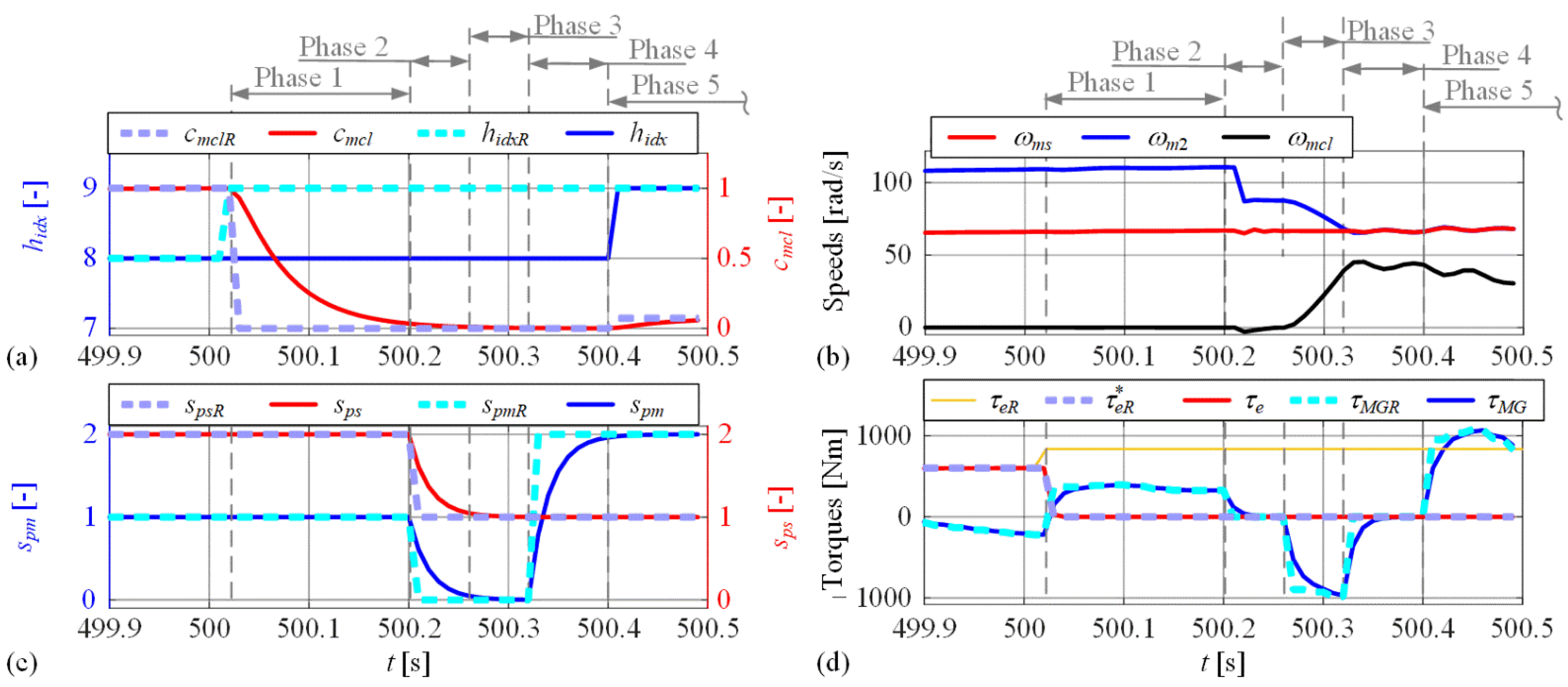
3.3.3. Low-Level Control during Gear Shifting
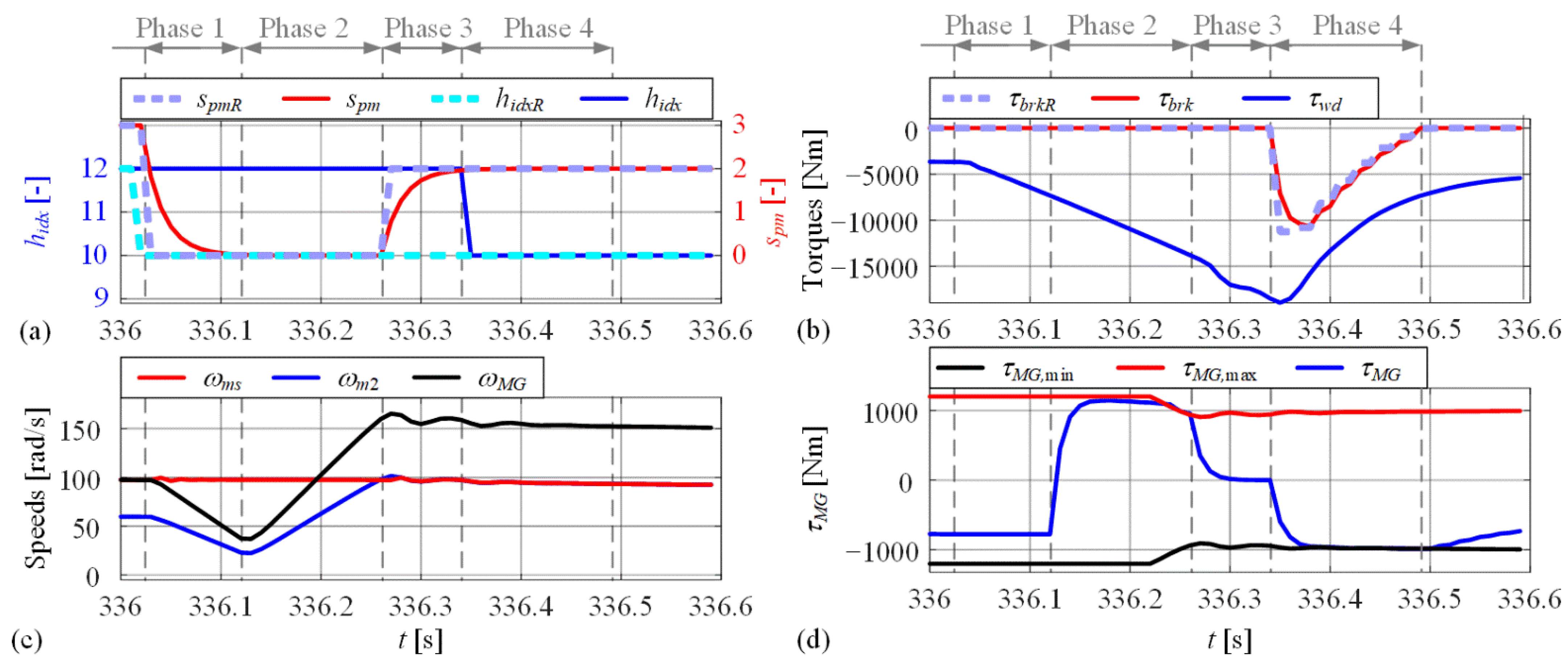
3.3.4. Low-Level Control during Braking Event
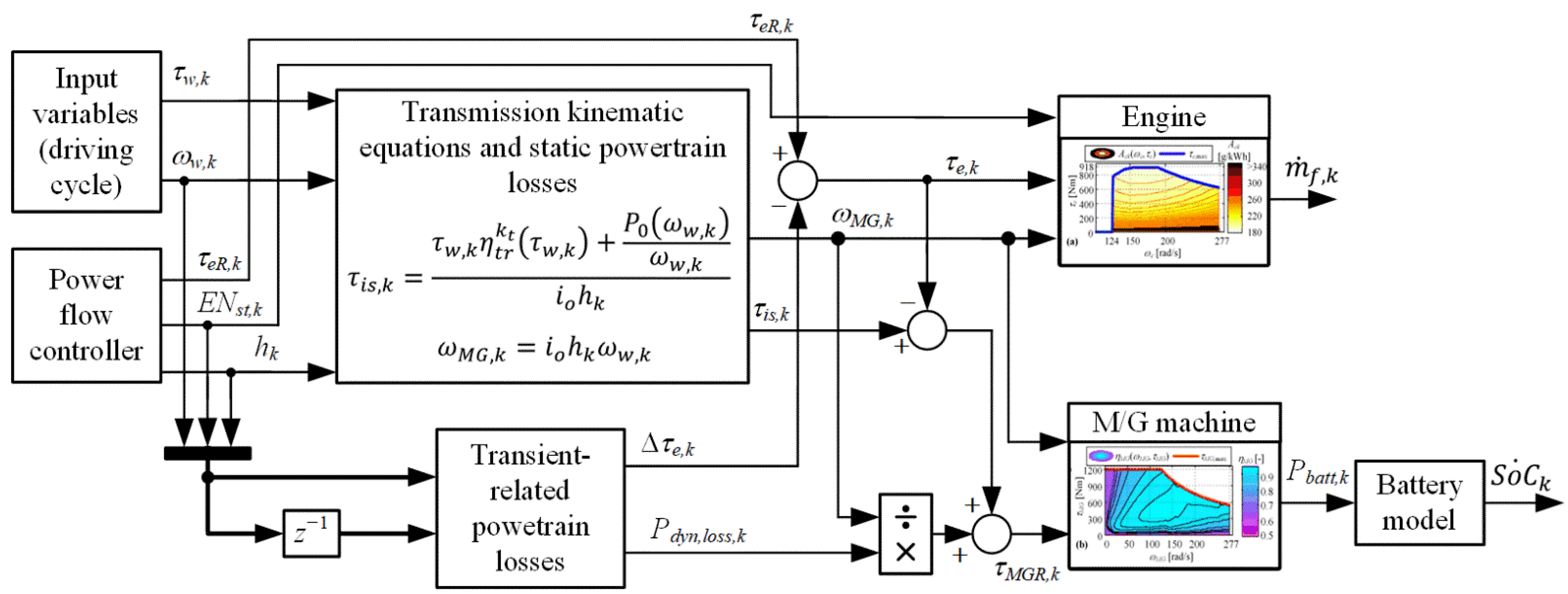
4. Extended Backward-Looking Powertrain Model
4.1. Model Structure Overview
4.2. Engine Torque Loss
4.3. Powertrain Transient Power Loss
4.3.1. Main Clutch Slippage Energy Loss
4.3.2. Synchronizer Slippage Energy Loss
4.3.3. M/G Machine-Based Synchronization Energy Loss
4.3.4. Engine-On Energy Losses While Switching On
4.3.5. Inertial Load of Powertrain Components
4.3.6. Use of EXT-BWD Model within ECMS+RB Control Strategy
5. Dynamic Programming-Based Control Variable Optimization and EXT-BWD Model Validation
5.1. Optimal Problem Formulation
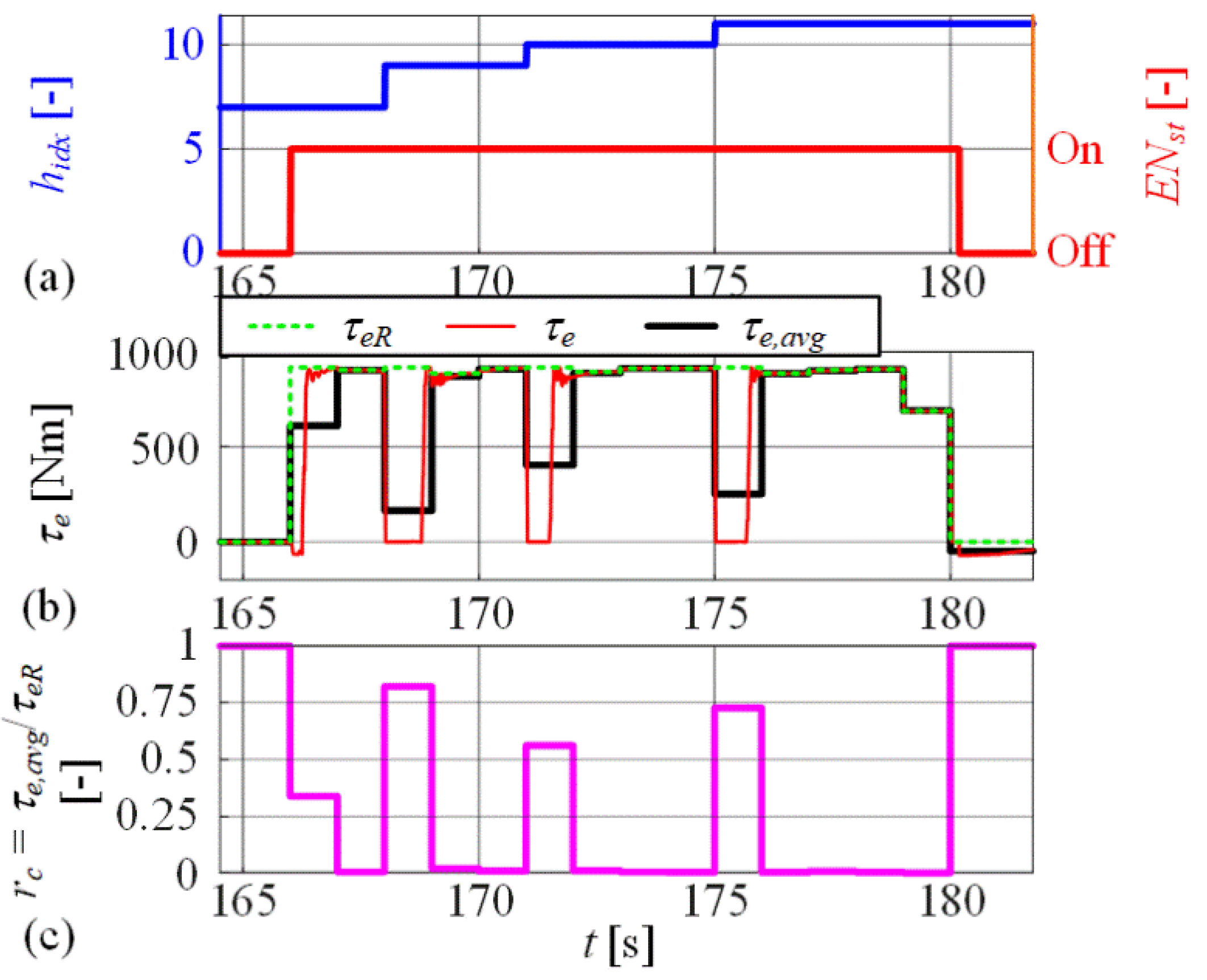
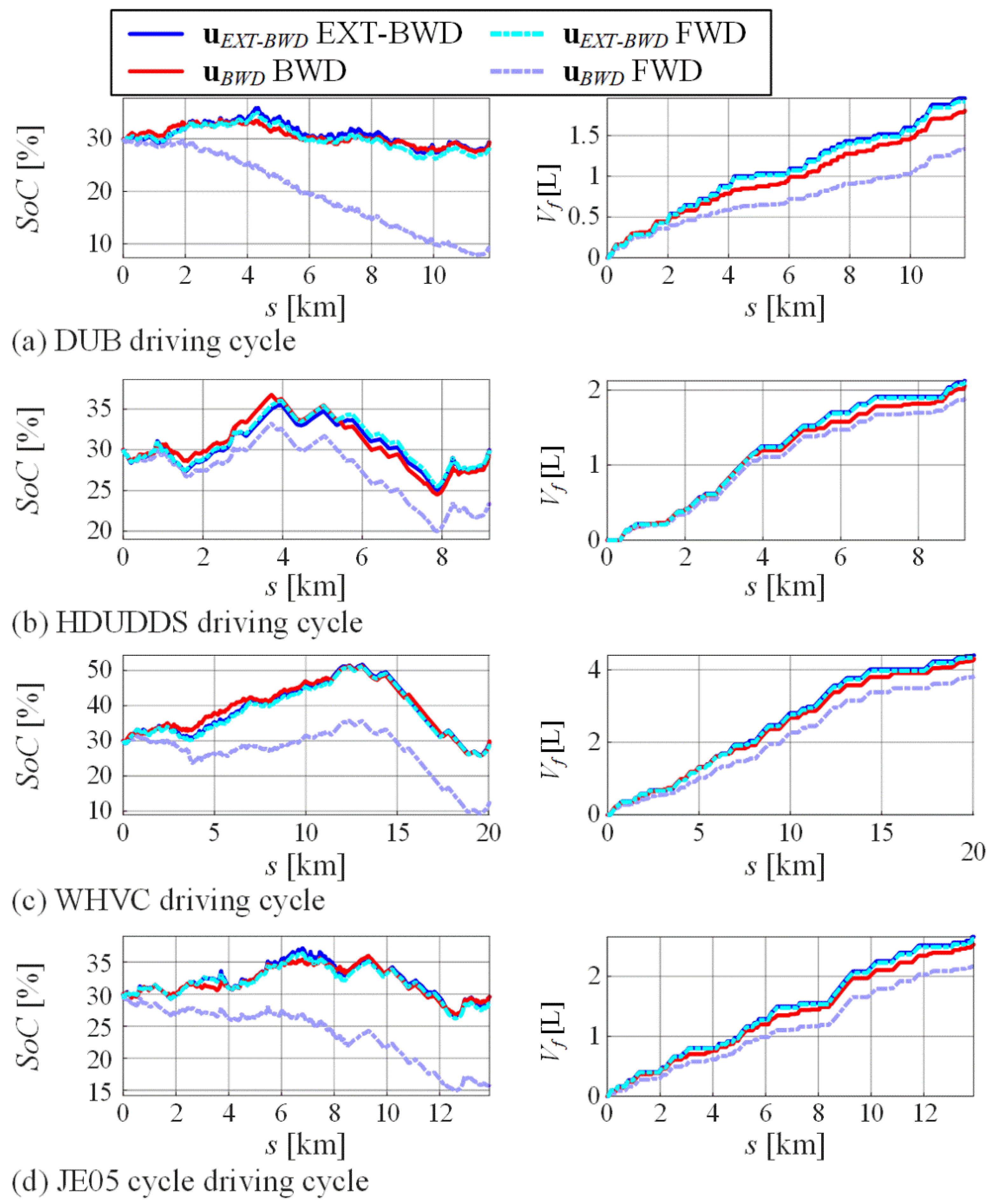
5.2. Optimization Results
5.3. Validation of EXT-BWD Model
6. Control System Simulation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Powertrain and Control Strategy Parameters
Appendix B. Generating Main Clutch Normalized Torque Capacity Reference
Appendix C. Engine Torque REDUCTION Coefficient

References
- Martinez, C.M.; Hu, X.; Cao, D.; Velenis, E.; Gao, B.; Wellers, M. Energy Management in Plug-in Hybrid Electric Vehicles: Recent Progress and a Connected Vehicles Perspective. IEEE Trans. Veh. Technol. 2017, 66, 4534–4549. [Google Scholar] [CrossRef]
- Ouddah, N.; Adouane, L. Hybrid Energy Management Strategy Based on Fuzzy Logic and Optimal Control for Tri-Actuated Powertrain System. IEEE Trans. Veh. Technol. 2019, 68, 5343–5355. [Google Scholar] [CrossRef]
- Lee, W.; Jeoung, H.; Park, D.; Kim, N. An Adaptive Concept of PMP-Based Control for Saving Operating Costs of Extended-Range Electric Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 11505–11512. [Google Scholar] [CrossRef]
- Enang, W.; Bannister, C. Robust proportional ECMS control of a parallel hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 99–119. [Google Scholar] [CrossRef]
- Škugor, B.; Deur, J.; Cipek, M.; Pavković, D. Design of a power-split hybrid electric vehicle control system utilizing a rule-based controller and an equivalent consumption minimization strategy. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2014, 228, 631–648. [Google Scholar] [CrossRef]
- Guzzella, L.; Sciaretta, A. Vehicle Propulsion Systems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Schmid, R.; Buerger, J.; Bajcinca, N. Energy Management Strategy for Plug-in-Hybrid Electric Vehicles Based on Predictive PMP. IEEE Trans. Control Syst. Technol. 2021, 29, 2548–2560. [Google Scholar] [CrossRef]
- Chen, D.; Kim, Y.; Stefanopoulou, A.G. Predictive Equivalent Consumption Minimization Strategy with Segmented Traffic Information. IEEE Trans. Veh. Technol. 2020, 69, 14377–14390. [Google Scholar] [CrossRef]
- Opila, D.F.; Wang, X.; McGee, R.; Gillespie, R.B.; Cook, J.A.; Grizzle, J.W. Real-world robustness for hybrid vehicle optimal energy management strategies incorporating drivability metrics. J. Dyn. Syst. Meas. Control Trans. ASME 2014, 136, 061011. [Google Scholar] [CrossRef]
- Soldo, J.; Cvok, I.; Deur, J. Bond Graph-Based Energy Balance Analysis of Forward and Backward Looking Models of Parallel Plug-In Hybrid Electric Vehicle. SAE Tech. Pap. 2022, 1, 743. [Google Scholar]
- Galvagno, E.; Guercioni, G.; Rizzoni, G. Effect of Engine Start and Clutch Slip Losses on the Energy Management Problem of a Hybrid DCT Powertrain. Int.J. Automot. Technol. 2020, 21, 953–969. [Google Scholar] [CrossRef]
- Opila, D.F.; Wang, X.; McGee, R.; Gillespie, R.B.; Cook, J.A.; Grizzle, J.W. An energy management controller to optimally trade off fuel economy and drivability for hybrid vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 1490–1505. [Google Scholar] [CrossRef]
- Tota, A.; Galvagno, E.; Dimauro, L.; Vigliani, A.; Velardocchia, M. Energy management strategy for hybrid multimode powertrains: Influence of inertial properties and road inclination. Appl. Sci. 2021, 11, 11752. [Google Scholar] [CrossRef]
- Škugor, B.; Ranogajec, V.; Deur, J. On smoothing HEV/EREV supervisory control action using an extended ECMS approach. In Proceedings of the 2013 World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013; IEEE: Piscataway, NJ, USA. [Google Scholar]
- Yakhshilikova, G.; Ruzimov, S.; Ezemobi, E.; Tonoli, A.; Amati, N. Development of Optimization Based Control Strategy for P2 Hybrid Electric Vehicle including Transient Characteristics of Engine. Appl. Sci. 2022, 12, 2852. [Google Scholar] [CrossRef]
- Kim, S.; Choi, S.B. Cooperative Control of Drive Motor and Clutch for Gear Shift of Hybrid Electric Vehicles with Dual-Clutch Transmission. IEEE/ASME Trans. Mechatron. 2020, 25, 1578–1588. [Google Scholar] [CrossRef]
- Yan, F.; Wang, J.; Huang, K. Hybrid electric vehicle model predictive control torque-split strategy incorporating engine transient characteristics. IEEE Trans. Veh. Technol. 2012, 61, 2458–2467. [Google Scholar] [CrossRef]
- Ganesan, A.; Gros, S.; Murgovski, N.; Lee, C.F.; Sivertsson, M. Effect of engine dynamics on optimal power-split control strategies in hybrid electric vehicles. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 18 November–16 December 2020. [Google Scholar]
- Bidarvatan, M.; Shahbakhti, M. Analysis and control of torque split in hybrid electric vehicles by incorporating powertrain dynamics. J. Dyn. Syst. Meas. Control. Trans. ASME 2018, 140, 111009. [Google Scholar] [CrossRef]
- Chen, R.; Zou, Y.; Hou, S. Heuristic Dynamic Programming Based Online Energy Management Strategy for Plug-In Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 843–851. [Google Scholar]
- Guercioni, G.R.; Galvagno, E.; Tota, A.; Vigliani, A. Adaptive equivalent consumption minimization strategy with rule-based gear selection for the energy management of hybrid electric vehicles equipped with dual clutch transmissions. IEEE Access 2020, 8, 190017–190038. [Google Scholar] [CrossRef]
- Volvo 7900 Electric Hybrid Specifications. Available online: https://www.volvobuses.co.uk/en-gb/our-offering/buses/volvo-7900-electric-hybrid/specifications.html (accessed on 17 March 2021).
- Soldo, J.; Škugor, B.; Deur, J. Optimal energy management and shift scheduling control of a parallel plug-in hybrid electric vehicle. Int. J. Powertrains 2020, 9, 240–264. [Google Scholar] [CrossRef]
- Siemens. Simcenter Amesim 2020.1: Integration Algorithms Used in Simcenter Amesim; Technical Bulletin No. 102; Siemens: Munich, Germany, 2020. [Google Scholar]
- Pacejka, H.B. Tire and Vehicle Dynamics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Deur, J.; Pavković, D. Fundamentals of electrical drive controls. In Electrical Engineering—Fundamentals of Electrical Drive Controls; EOLSS Publishers: Oxford, UK, 2011; pp. 1–59. [Google Scholar]
- Bellman, R.E.; Dreyfus, S.E. Applied Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Soldo, J.; Škugor, B.; Deur, J. Analysis of optimal battery state-of-charge trajectory patterns for blended mode of a parallel plug-in hybrid electric vehicle and a wide range of driving conditions. Optim. Eng. 2021, 22, 1955–1977. [Google Scholar] [CrossRef]
- Cipek, M.; Škugor, B.; Čorić, M.; Kasać, J.; Deur, J. Control variable optimisation for an extended range electric vehicle. Int. J. Powertrains 2016, 5, 30–54. [Google Scholar] [CrossRef]
- Škugor, B.; Hrgetić, M.; Deur, J. GPS measurement-based road grade reconstruction with application to electric vehicle simulation and analysis. In Proceedings of the 11th Conference on Sustainable Development of Energy, Water and Environment Systems (SDEWES 2015), Dubrovnik, Croatia, 27 September–2 October 2015. [Google Scholar]




| Gear hidx [-] | Ratio h [-] | s1 | s2 | m1 | m2 | m3 | r1 | r2 | sps | spm | spr |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 14.94 | x | x | x | 1 | 1 | 1 | ||||
| 2 | 11.73 | x | x | x | 2 | 1 | 1 | ||||
| 3 | 9.04 | x | x | x | 1 | 2 | 1 | ||||
| 4 | 7.09 | x | x | x | 2 | 2 | 1 | ||||
| 5 | 5.54 | x | x | x | 1 | 3 | 1 | ||||
| 6 | 4.35 | x | x | x | 2 | 3 | 1 | ||||
| 7 | 3.44 | x | x | x | 1 | 1 | 2 | ||||
| 8 | 2.70 | x | x | x | 2 | 1 | 2 | ||||
| 9 | 2.08 | x | x | x | 1 | 2 | 2 | ||||
| 10 | 1.63 | x | x | x | 2 | 2 | 2 | ||||
| 11 | 1.27 | x | x | x | 1 | 3 | 2 | ||||
| 12 | 1.00 | x | x | x | 2 | 3 | 2 |
| Cycle | Model | Vf [L] | SoC(tf) [%] | Ne [-] | Ng [-] |
|---|---|---|---|---|---|
| DUB | BWD | 1.80 (+0.0%) | 29.75 (+0.0%) | 64 (+0.0%) | 967 (+0.0%) |
| EXT-BWD | 1.96 (+8.9%) | 29.76 (+0.0%) | 28 (−56.3%) | 555 (−42,6%) | |
| HDUDDS | BWD | 2.02 (+0.0%) | 29.74 (+0.0%) | 25 (+0.0%) | 168 (+0.0%) |
| EXT-BWD | 2.12 (+5.0%) | 29.89 (+0.5%) | 13 (−48.0%) | 92 (−45.0%) | |
| WHVC | BWD | 4.22 (+0.0%) | 29.85 (+0.0%) | 51 (+0.0%) | 365 (+0.0%) |
| EXT-BWD | 4.40 (+4.3%) | 29.69 (−0.5%) | 26 (−49.0%) | 190 (−47.9%) | |
| JE05 | BWD | 2.54 (+0.0%) | 29.80 (+0.0%) | 54 (+0.0%) | 466 (+0.0%) |
| EXT-BWD | 2.66 (+4.7%) | 29.61 (−0.6%) | 22 (−59.3%) | 224 (−51.9%) |
| Strategy | Vf [L] | SoC(tf) [%] | Ne [-] | Ng [-] |
|---|---|---|---|---|
| DUB driving cycle | ||||
| RB+ECMS, w/o GSD | 2.11 (+9.0%) | 28.91 | 48 | 696 (0.0%) |
| RB+ECMS, w/GSD | 2.10 (+8.7%) | 28.93 | 48 | 383 (−45.0%) |
| RB+ECMS-EXT | 2.04 (+5.2%) | 28.95 | 45 | 371 (−46.7%) |
| HDUDDS driving cycle | ||||
| RB+ECMS, w/o GSD | 2.33 (+3.2%) | 32.99 | 11 | 167 (0.0%) |
| RB+ECMS, w/GSD | 2.34 (+3.4%) | 33.14 | 11 | 88 (−47.3%) |
| RB+ECMS-EXT | 2.31 (+2.1%) | 33.12 | 12 | 79 (−52.7%) |
| WHVC driving cycle | ||||
| RB+ECMS, w/o GSD | 4.64 (+3.8%) | 31.35 | 21 | 327 (0.0%) |
| RB+ECMS, w/GSD | 4.63 (+3.7%) | 31.35 | 22 | 187 (−42.8%) |
| RB+ECMS-EXT | 4.61 (+3.1%) | 31.38 | 22 | 188 (−42.5%) |
| JE05 driving cycle | ||||
| RB+ECMS, w/o GSD | 2.72 (+4.6%) | 28.15 | 24 | 480 (0.0%) |
| RB+ECMS, w/GSD | 2.72 (+4.6%) | 28.18 | 24 | 220 (−54.2%) |
| RB+ECMS-EXT | 2.68 (+3.0%) | 28.24 | 24 | 236 (−50.8%) |
| Strategy | Vf [L] | Vf,corr [L] | SoC(tf) [%] | Ne [-] | Ng [-] |
|---|---|---|---|---|---|
| DUB driving cycle | |||||
| RB+ECMS, w/GSD | 2.13 | 2.28 (0.0%) | 27.78 | 61 | 499 (0.0%) |
| RB+ECMS-EXT | 2.16 | 2.23 (−2.2%) | 28.45 | 59 | 452 (−9.4%) |
| HDUDDS driving cycle | |||||
| RB+ECMS, w/GSD | 2.29 | 2.18 (0.0%) | 32.60 | 17 | 97 (0.0%) |
| RB+ECMS-EXT | 2.30 | 2.16 (−0.9%) | 33.46 | 12 | 106 (+9.3%) |
| WHVC driving cycle | |||||
| RB+ECMS, w/GSD | 4.68 | 4.56 (0.0%) | 33.07 | 22 | 288 (0.0%) |
| RB+ECMS-EXT | 4.73 | 4.53 (−0.7%) | 34.79 | 29 | 266 (−7.6%) |
| JE05 driving cycle | |||||
| RB+ECMS, w/GSD | 2.71 | 2.79 (0.0%) | 28.07 | 22 | 239 (0.0%) |
| RB+ECMS-EXT | 2.84 | 2.77 (−0.7%) | 31.68 | 25 | 253 (−5.9%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soldo, J.; Cvok, I.; Deur, J. Optimal Control of a PHEV Based on Backward-Looking Model Extended with Powertrain Transient Effects. Energies 2022, 15, 8152. https://doi.org/10.3390/en15218152
Soldo J, Cvok I, Deur J. Optimal Control of a PHEV Based on Backward-Looking Model Extended with Powertrain Transient Effects. Energies. 2022; 15(21):8152. https://doi.org/10.3390/en15218152
Chicago/Turabian StyleSoldo, Jure, Ivan Cvok, and Joško Deur. 2022. "Optimal Control of a PHEV Based on Backward-Looking Model Extended with Powertrain Transient Effects" Energies 15, no. 21: 8152. https://doi.org/10.3390/en15218152
APA StyleSoldo, J., Cvok, I., & Deur, J. (2022). Optimal Control of a PHEV Based on Backward-Looking Model Extended with Powertrain Transient Effects. Energies, 15(21), 8152. https://doi.org/10.3390/en15218152








